Investigation of the Impact Factors on the Optimal Intermediate Temperature in a Dual Transcritical CO2 System with a Dedicated Transcritical CO2 Subcooler
Abstract
1. Introduction
2. System Description
2.1. System Configuration
2.2. Theoretical Analysis
3. Mathematical Model
3.1. The Seeking Process of Optimal Discharge Pressures
3.2. The Simulation Process of the Dual System’s Thermodynamic Performance
4. Results Discussion
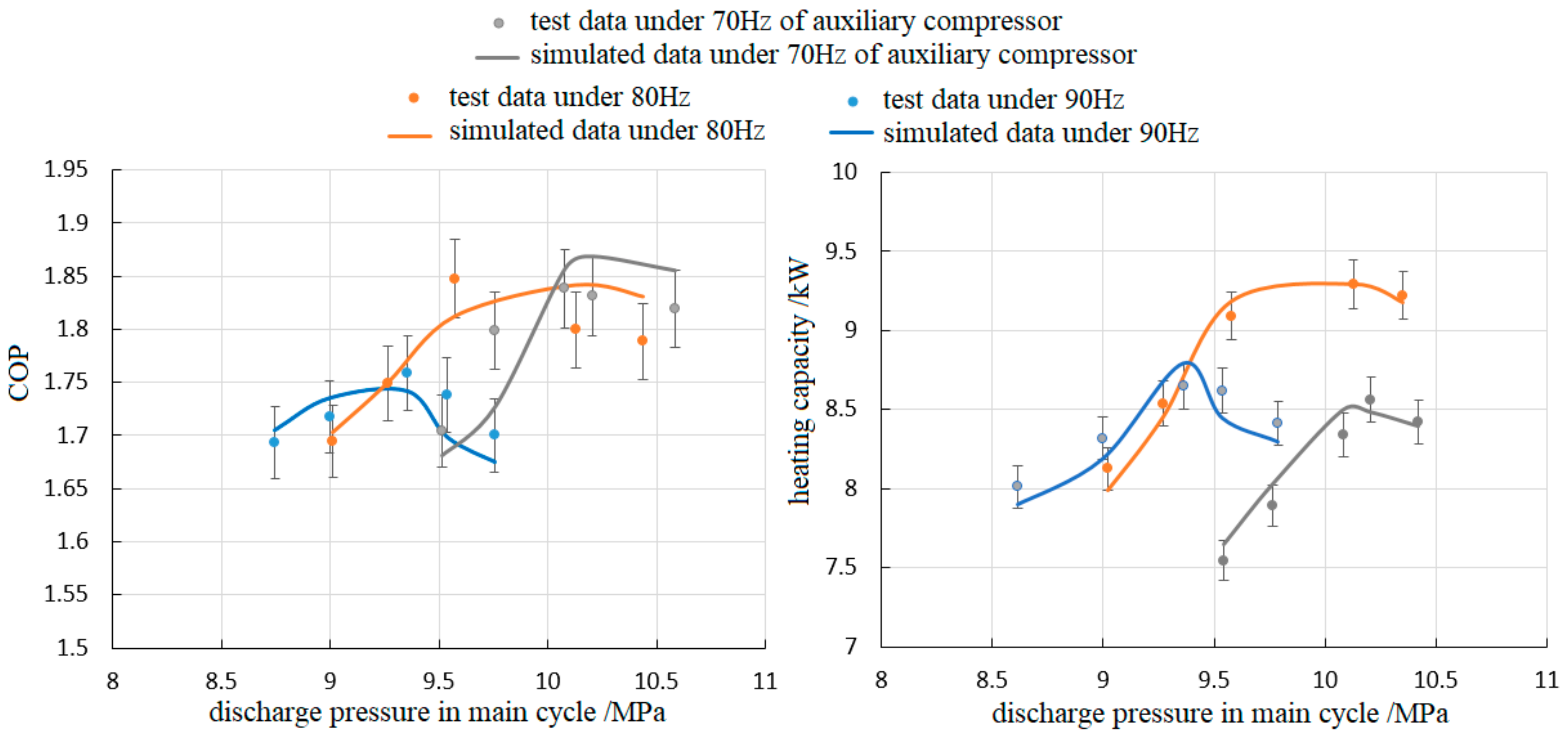
4.1. The Verification of the Simulation Model
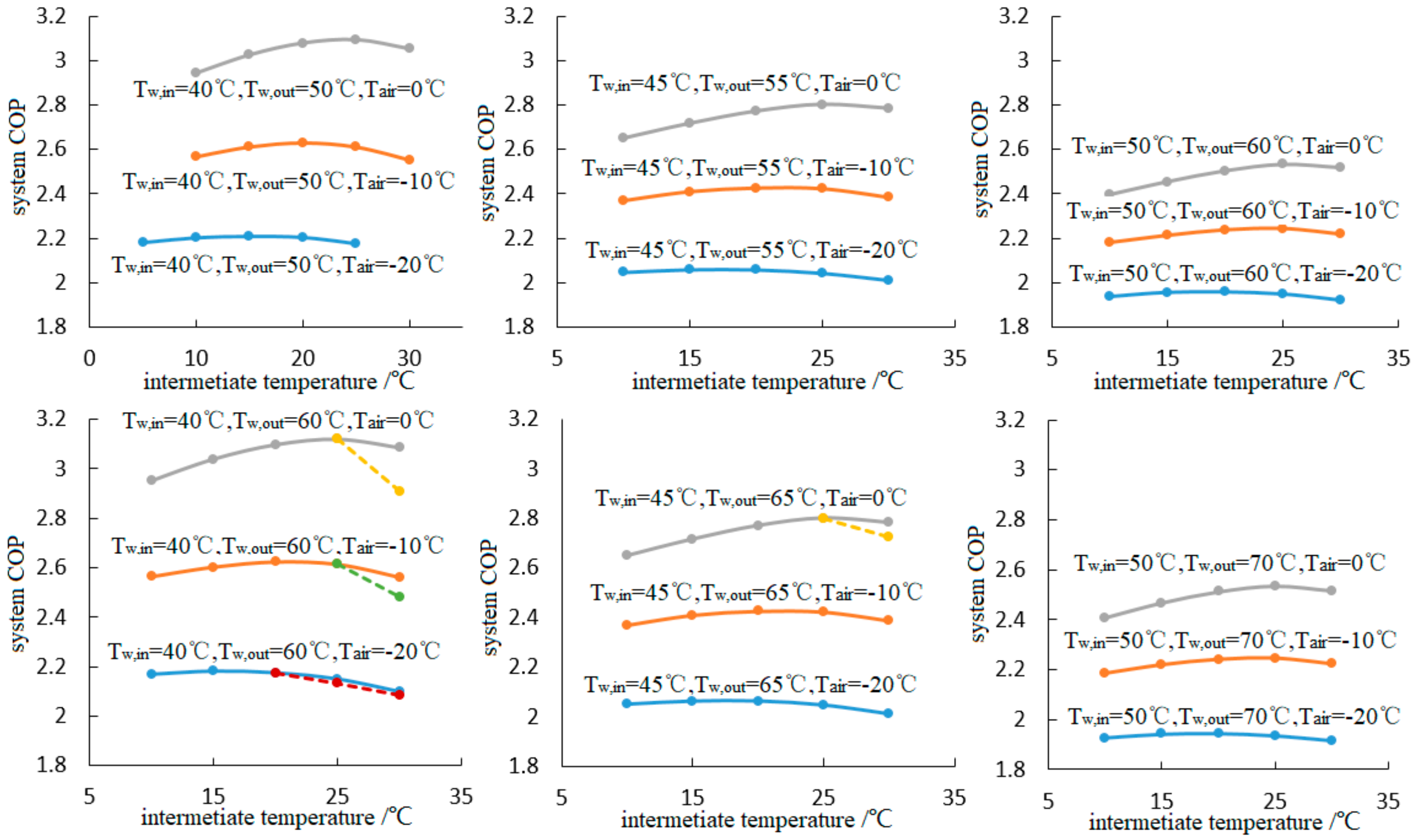
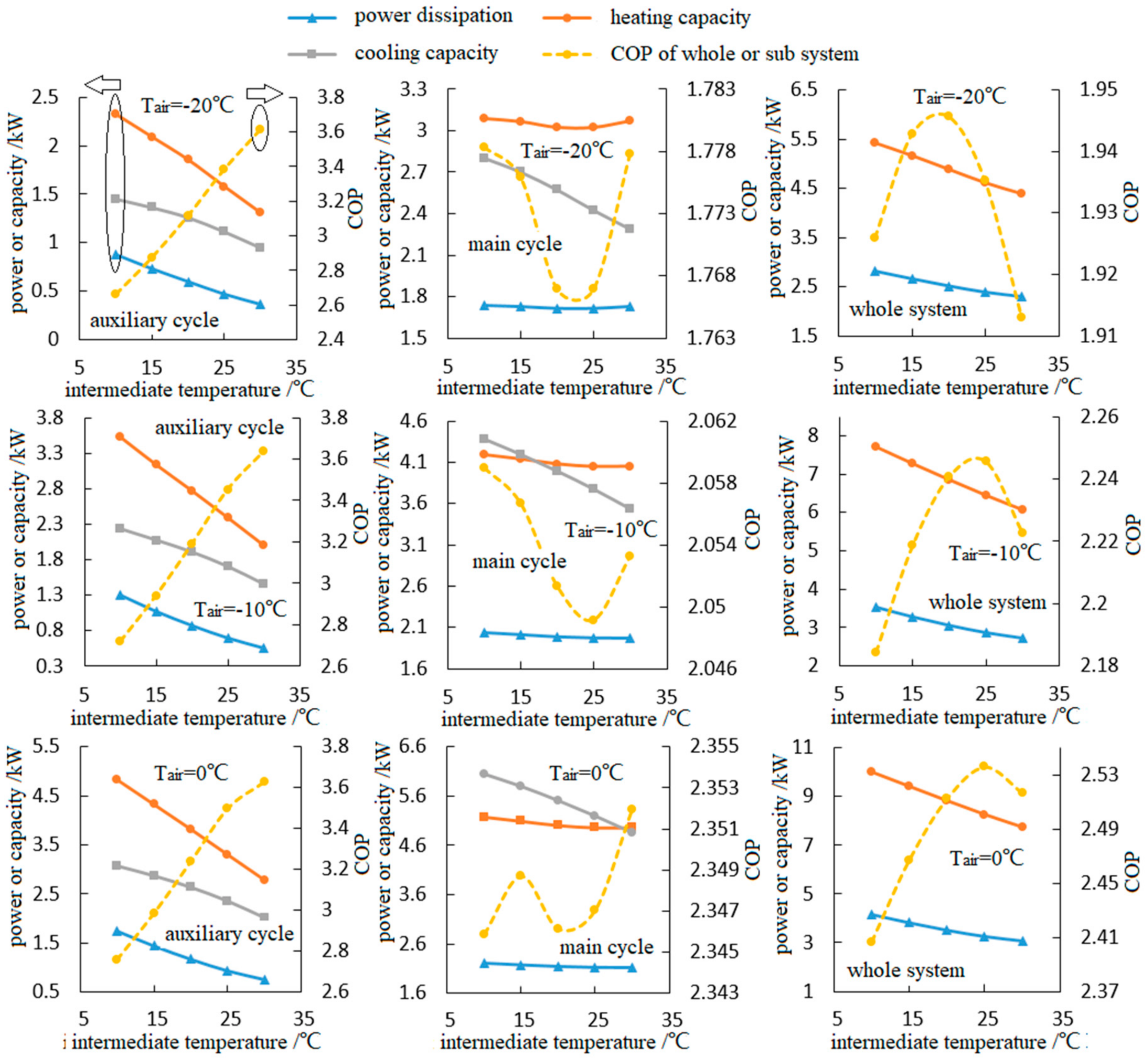
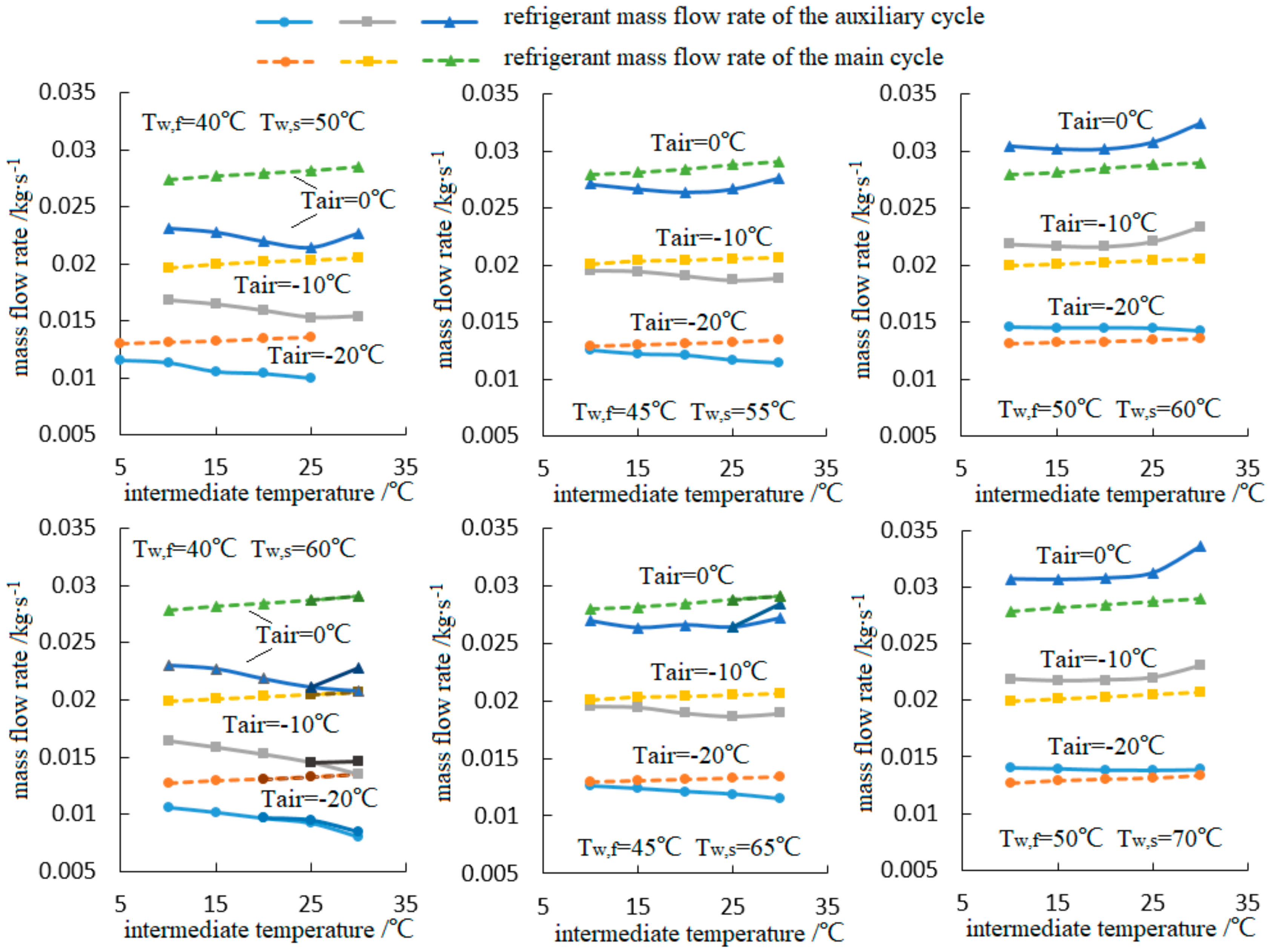
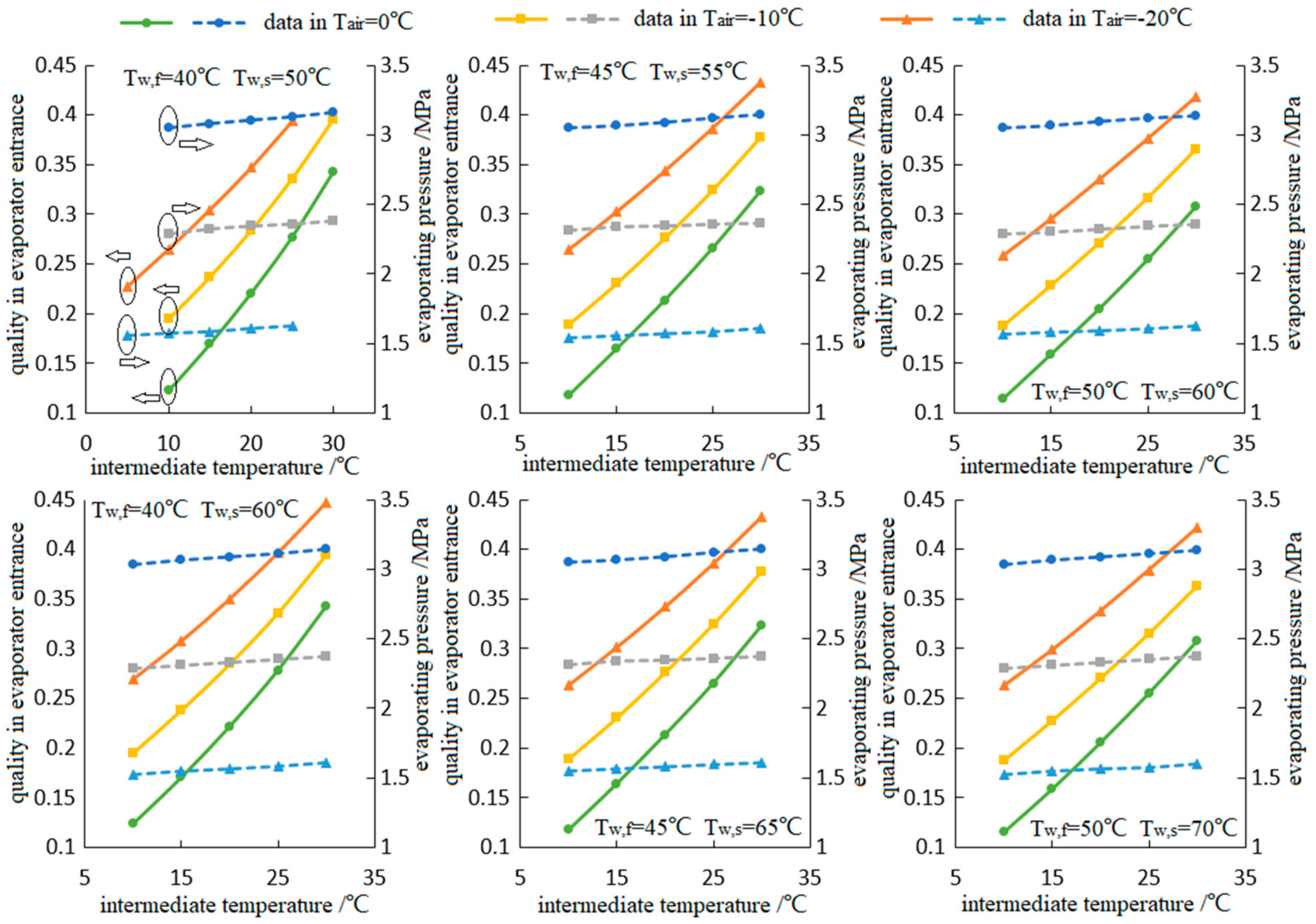
4.2. Discussion about the Intermediate Temperature
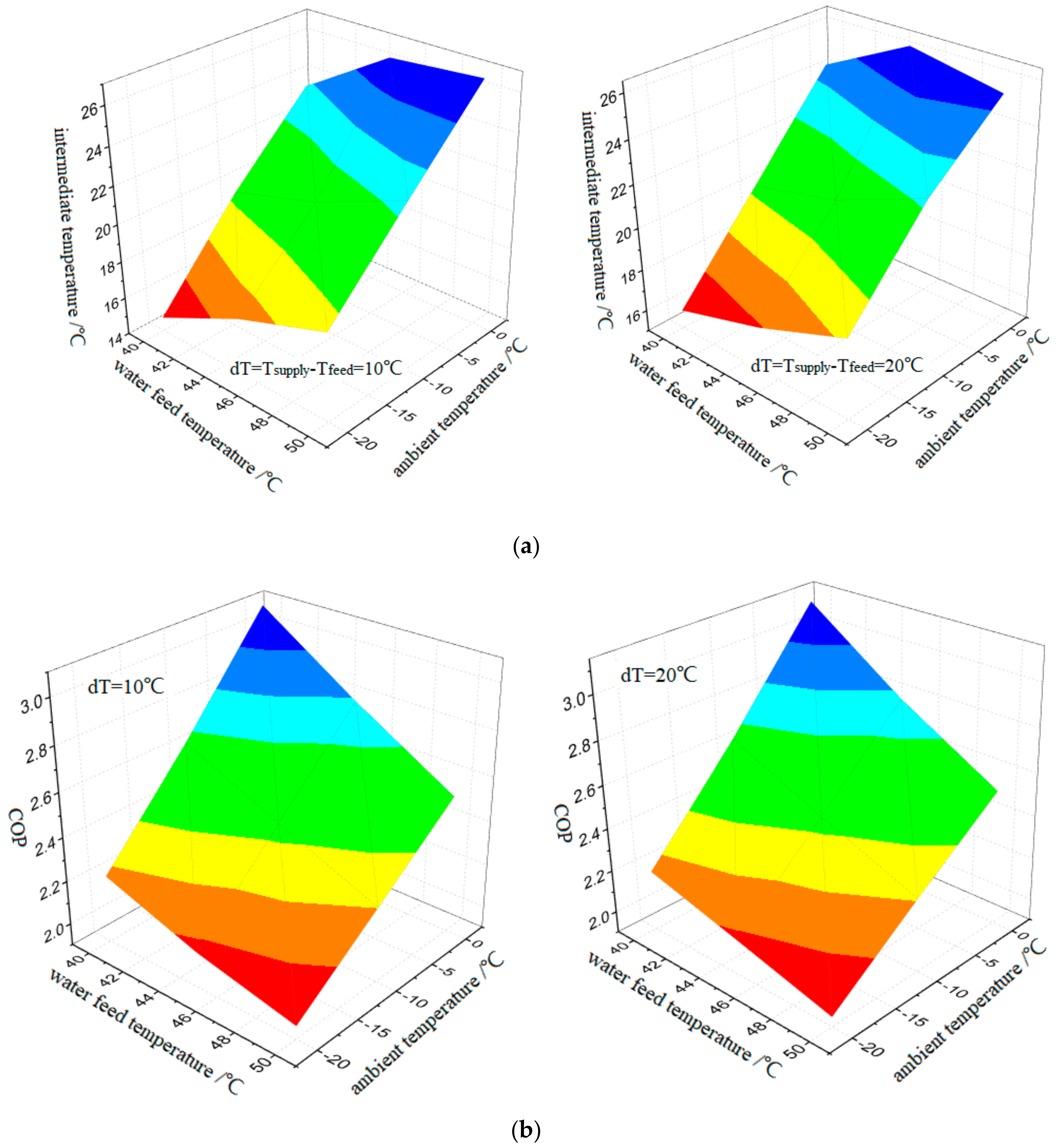
4.3. Predictive Correlation
4.4. Regulation of the Intermediate Temperature
5. Conclusions
- (i)
- After comparison with the measurement data from our previous works, the veracity of the simulation models could be verified, which gives us the convenience to carry on the most discussion based on only the simulation results.
- (ii)
- The existence of optimal intermediate temperature is validated, while optimal values of the intermediate temperature increase with an increase in ambient temperature and water-feed temperature. Subsequently, the system COP also increases with an increase in ambient temperature, but decreases with the water-feed temperature.
- (iii)
- Due to the existence of the optimal intermediate temperature, the system performance rises first and then declines, while the auxiliary cycle’s performance rises gradually with the increase in intermediate temperature. As for the main cycle’s performance, no obvious rule could be observed.
- (iv)
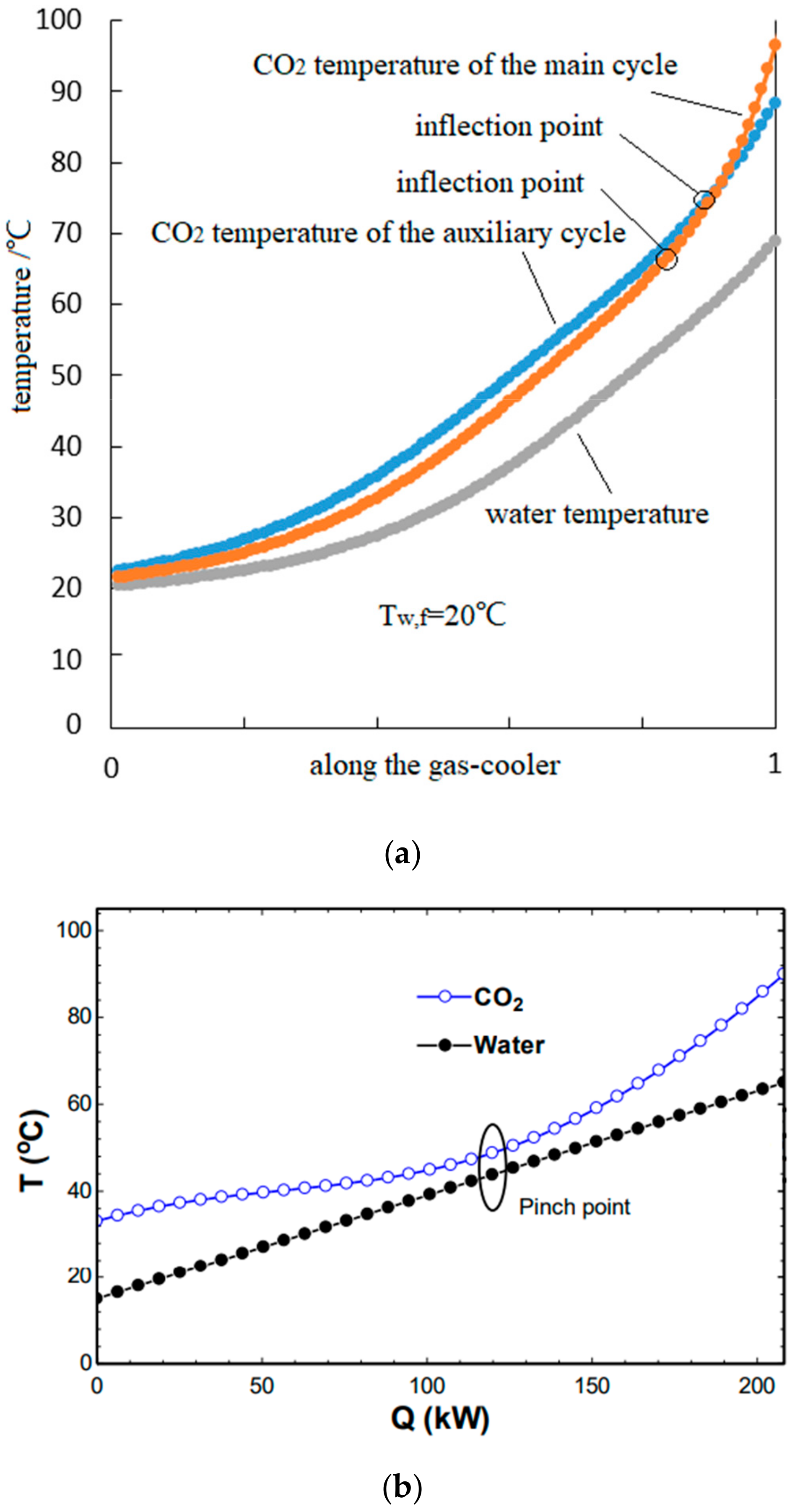
- By using the dual gas cooler (the heat rejection of the auxiliary and main cycles is installed inside a same gas cooler), the negative effects of the pinch point on the heat transfer inside the heat exchanger could be greatly reduced.
- (v)
- A predictive correlation for the optimal intermediate temperature determination, with the ambient and water-feed temperature as the independent variables, is proposed, while the relative prediction errors are no more than 5% across 18 working conditions.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | Heat-transfer area (m2) |
| Specific heat capacity (kJ∙kg−1∙K−1) | |
| d | Diameter (m) |
| f | Friction factor |
| h | Enthalpy (kJ∙kg−1) |
| m | Mass flow rate (kg∙s−1) |
| p | Pressure (MPa) |
| Pr | Prandtl number |
| Q | Heat-transfer rate (kW) |
| R | Fouling resistance (K∙m2∙W−1) |
| Re | Reynolds number |
| T | Temperature (℃) |
| Power consumption (kW) | |
| Convective heat-transfer coefficient (W∙K-1∙m-2) | |
| Thickness of the fin (m) | |
| γ | heat leakage coefficient |
| Efficiency | |
| Conductivity (W∙K-1∙m-2) | |
| Density (kg∙m-3) | |
| Dehumidification coefficient | |
| Subscripts | |
| av | Average |
| air | air |
| comp | Compressor |
| eq | Equivalent |
| eva | Evaporator |
| f | feed |
| gc | Gas cooler |
| h | Heating |
| i | Inner |
| in | System inlet |
| is | Isentropic |
| out | System outlet |
| o | Outer |
| r | Refrigerant |
| single | Single phase |
| tube | tube |
| v | Volumetric |
| w | Water |
| wall | Tube wall |
References
- Lorentzen, G.; Pettersen, J. A new, efficient and ambientally benign system for car air conditioning. Int. J. Refrig. 1993, 16, 4–12. [Google Scholar] [CrossRef]
- Lorentzen, G. The use of natural refrigerant: A complete solution to the CFC/HCFC predicament. Int. J. Refrig. 1994, 18, 190–197. [Google Scholar] [CrossRef]
- Song, Y.; Cao, F. The evaluation of the optimal medium temperature in a space heating used transcritical air-source CO2 heat pump with an R134a subcooling device. Energy Convers. Manag. 2018, 166, 409–423. [Google Scholar] [CrossRef]
- Song, Y.; Ye, Z.; Wang, Y.; Cao, F. The experimental verification on the optimal discharge pressure in a subcooler-based transcritical CO2 system for space heating. Energy Build. 2018, 158, 1442–1449. [Google Scholar] [CrossRef]
- White, S.D.; Yarrall, M.G.; Cleland, D.J.; Hedley, R.A. Modeling the performance of a transcritical CO2 heat pump for high temperature heating. Int. J. Refrig. 2002, 25, 479–486. [Google Scholar] [CrossRef]
- Aprea, C.; Maiorino, A. An experimental evaluation of the transcritical CO2 refrigerator performances using an internal heat exchanger. Int. J. Refrig. 2008, 31, 1006–1011. [Google Scholar] [CrossRef]
- Zhang, F.; Jiang, P.; Lin, Y. Efficiencies of subcritical and transcritical CO2 inverse cycles with and without an internal heat exchanger. Appl. Therm. Eng. 2011, 31, 432–438. [Google Scholar] [CrossRef]
- Kim, S.G.; Kim, Y.J.; Lee, G.; Kim, M.S. The performance of a transcritical CO2 cycle with an internal heat exchanger for hot water heating. Int. J. Refrig. 2005, 28, 1064–1072. [Google Scholar] [CrossRef]
- Torrella, E.; Sanchez, D.; Llopis, R. Energetic evaluation of an internal heat exchanger in a CO2 transcritical refrigeration plant using experimental data. Int. J. Refrig. 2011, 34, 40–49. [Google Scholar] [CrossRef]
- Bertsch, S.S.; Groll, E.A. Two-stage air-source heat pump for residential heating and cooling applications in northern U.S. climates. Int. J. Refrig. 2008, 31, 1282–1292. [Google Scholar] [CrossRef]
- Xu, S.X.; Ma, G.Y. Experimental study on two-stage compression refrigeration/heat pump system with dual-cylinder rolling piston compressor. Appl. Therm. Eng. 2014, 62, 803–808. [Google Scholar]
- Redón, A.; Navarro-Peris, E.; Pitarch, M.; Gonzálvez-Macia, J.; Corberán, J.M. Analysis and optimization of subcritical two-stage vapor injection heat pump systems. Appl. Energy 2014, 124, 231–240. [Google Scholar] [CrossRef]
- Agrawal, N.; Souvik, B.; Sarkar, J. Optimization of two-stage transcritical carbon dioxide heat pump cycles. Int. J. Therm. Sci. 2007, 46, 180–187. [Google Scholar] [CrossRef]
- Baek, C.; Heo, J.; Jung, J. Effects of vapor injection techniques on the heating performance of a CO2 heat pump at low ambient temperatures. Int. J. Refrig. 2014, 43, 26–35. [Google Scholar] [CrossRef]
- Baek, C.; Heo, J.; Jung, J. Performance characteristics of a two-stage CO2 heat pump water heater adopting a sub-cooler vapor injection cycle at various operating conditions. Energy 2014, 77, 570–578. [Google Scholar] [CrossRef]
- Baek, C.; Heo, J.; Jung, J. Effects of the cylinder volume ratio of a twin rotary compressor on the heating performance of a vapor injection CO2 cycle. Appl. Therm. Eng. 2014, 67, 89–96. [Google Scholar] [CrossRef]
- Nakagawa, M.; Takeuchi, H. Performance of two-phase ejector in refrigeration cycle. In Proceedings of the Third International Conference on Multiphase Flow, Lyon, France, 8–12 June 1998; pp. 1–8. [Google Scholar]
- Elbel, S. Historical and present developments of ejector refrigeration systems with emphasis on transcritical carbon dioxide air-conditioning applications. Int. J. Refrig. 2011, 34, 1545–1561. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, C.; Zhang, F.; Jiang, P. Comprehensive experimental study on a transcritical CO2 ejector-expansion refrigeration system. Energy Convers. Manag. 2017, 151, 98–106. [Google Scholar] [CrossRef]
- Boccardi, G.; Botticella, F.; Lillo, G. Experimental investigation on the performance of a transcritical CO2 heat pump with multi-ejector expansion system. Int. J. Refrig. 2017, 82, 389–400. [Google Scholar] [CrossRef]
- Sarkar, J. Performance optimization of transcritical CO2 refrigeration cycle with thermoelectric subcooler. Int. J. Energy Res. 2013, 37, 121–128. [Google Scholar] [CrossRef]
- Llopis, R.; Cabello, R.; Sanchez, D. Energy improvements of CO2 transcritical refrigeration cycles using dedicated mechanical subcooling. Int. J. Refrig. 2015, 55, 129–141. [Google Scholar] [CrossRef]
- Llopis, R.; Laura, A.; Cabello, R. Experimental evaluation of a CO2 transcritical refrigeration plant with dedicated mechanical subcooling. Int. J. Refrig. 2016, 69, 361–368. [Google Scholar] [CrossRef]
- Dai, B.; Liu, S.; Li, H. Energetic performance of transcritical CO2 refrigeration cycles with mechanical subcooling using zeotropic mixture as refrigerant. Energy 2018, 150, 205–221. [Google Scholar] [CrossRef]
- Dai, B.; Qi, H.; Liu, S. Evaluation of transcritical CO2 heat pump system integrated with mechanical subcooling by utilizing energy, exergy and economic methodologies for residential heating. Energy Convers. Manag. 2019, 192, 202–220. [Google Scholar] [CrossRef]
- Sarkar, J. Cycle parameter optimization of vortex tube expansion transcritical CO2 system. Int. J. Therm. Sci. 2009, 48, 1823–1828. [Google Scholar] [CrossRef]
- Song, Y.; Sun, Q.; Yang, S.; Xing, Q.; Cheng, L.; Cao, F. The theoretical and experimental research on the thermodynamic process in transcritical carbon dioxide piston compressor. IMech E Part E J. Process Mech. Eng. 2019, 233, 267–279. [Google Scholar] [CrossRef]
- Yang, D.; Song, Y.; Cao, F. Theoretical and experimental investigation of a combined R134a and transcritical CO2 heat pump for space heating. Int. J. Refrig. 2016, 72, 156–170. [Google Scholar] [CrossRef]
- Dang, C.; Eiji, H. In-tube cooling heat transfer of supercritical carbon dioxide, part 1. Experimental measurement. Int. J. Refrig. 2004, 27, 736–747. [Google Scholar] [CrossRef]
- Dang, C.; Eiji, H. In-tube cooling heat transfer of supercritical carbon dioxide, part 2. Comparison of numerical calculation with different turbulence models. Int. J. Refrig. 2004, 27, 748–760. [Google Scholar] [CrossRef]
- Cheng, L.; Ribatski, G.; Wojtan, L.; Thome, J.R. New flow boiling heat transfer model and flow pattern map for carbon dioxide evaporating inside horizontal tubes. Int. J. Heat Mass Transf. 2006, 49, 4082–4094. [Google Scholar] [CrossRef]
- Churchill, S.W.; Bernstein, M. A correlating equation for forced convection from gases and liquids to a circular cylinder in cross flow. ASME Transf. J. Heat Transf. 1977, 99, 300–306. [Google Scholar] [CrossRef]
- Cao, F.; Cui, C.; Wei, X. The experimental investigation on a novel transcritical CO2 heat pump combined system for space heating. Int. J. Refrig. 2019, 106, 539–548. [Google Scholar] [CrossRef]
- Sarkar, J.; Bhattacharyya, S.; Gopalm, M.R. Optimization of a transcritical CO2 heat pump cycle for simultaneous cooling and heating applications. Int. J. Refrig. 2004, 27, 830–838. [Google Scholar] [CrossRef]
- Chen, Y. Optimal heat rejection pressure of CO2 heat pump water heaters based on pinch point analysis. Int. J. Refrig. 2019, 106, 592–603. [Google Scholar] [CrossRef]
- Llopis, R.; Andres, L.; Sanchez, D. Subcooling methods for CO2 refrigeration cycles: A review. Int. J. Refrig. 2018, 93, 85–107. [Google Scholar] [CrossRef]

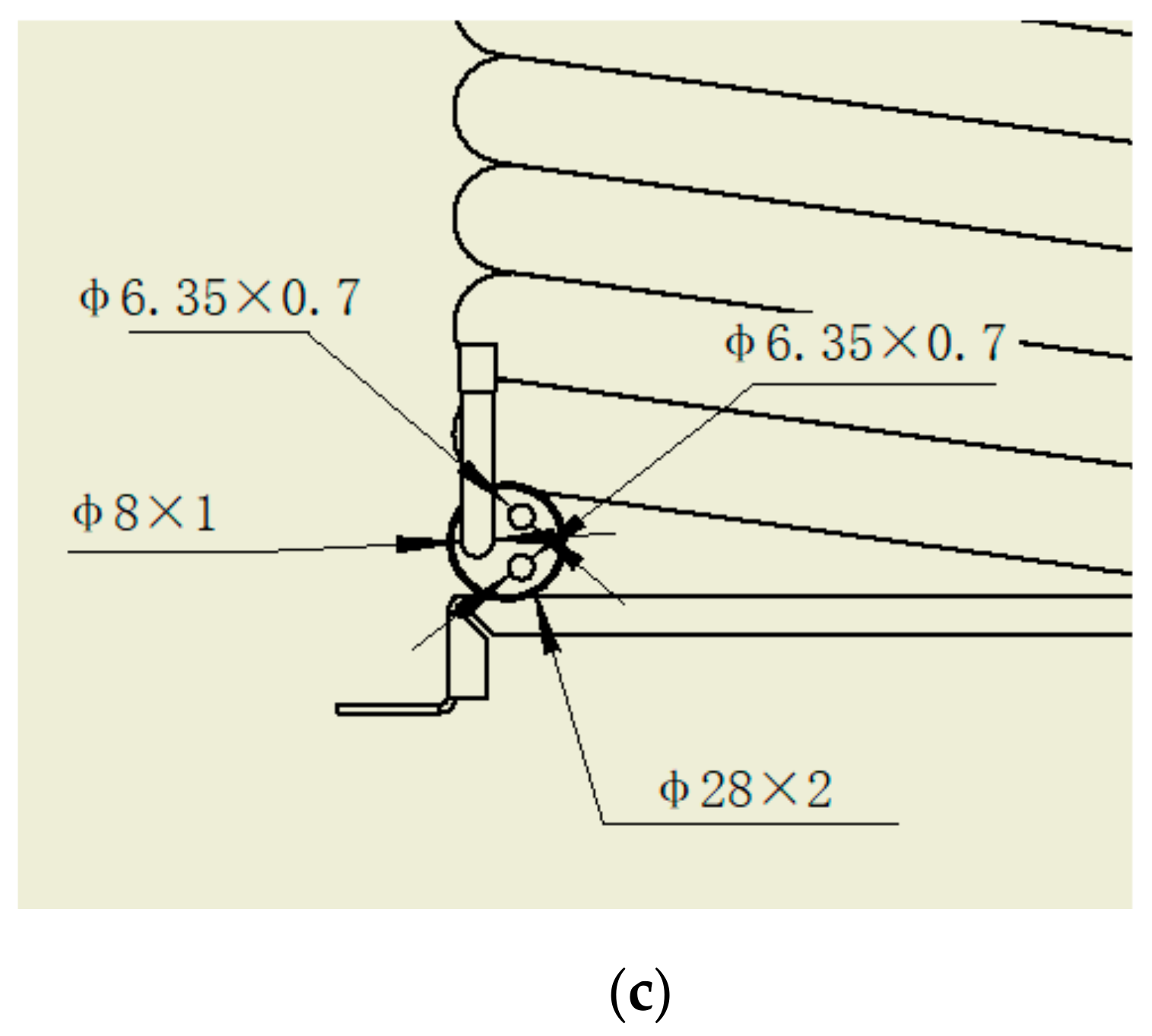
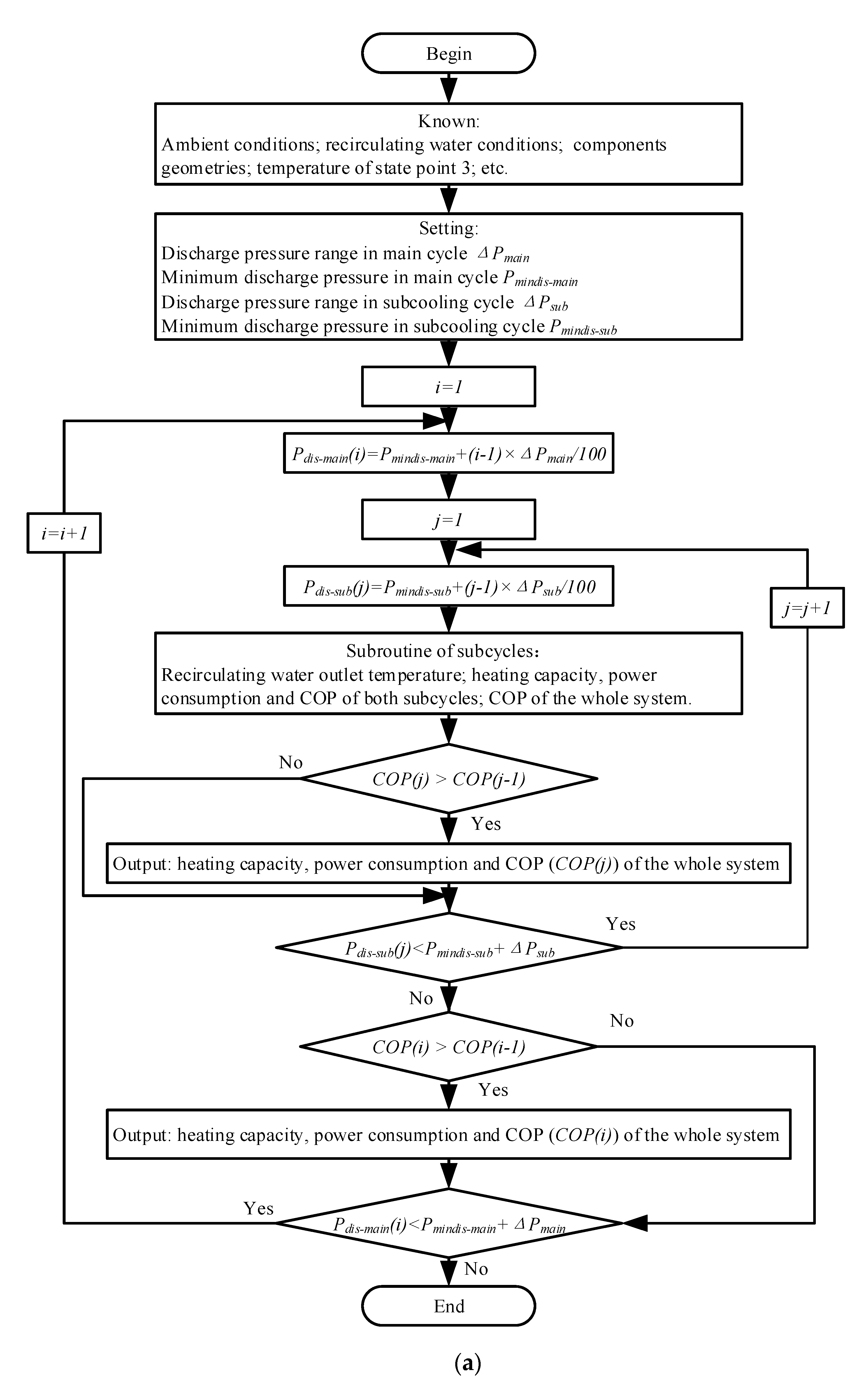
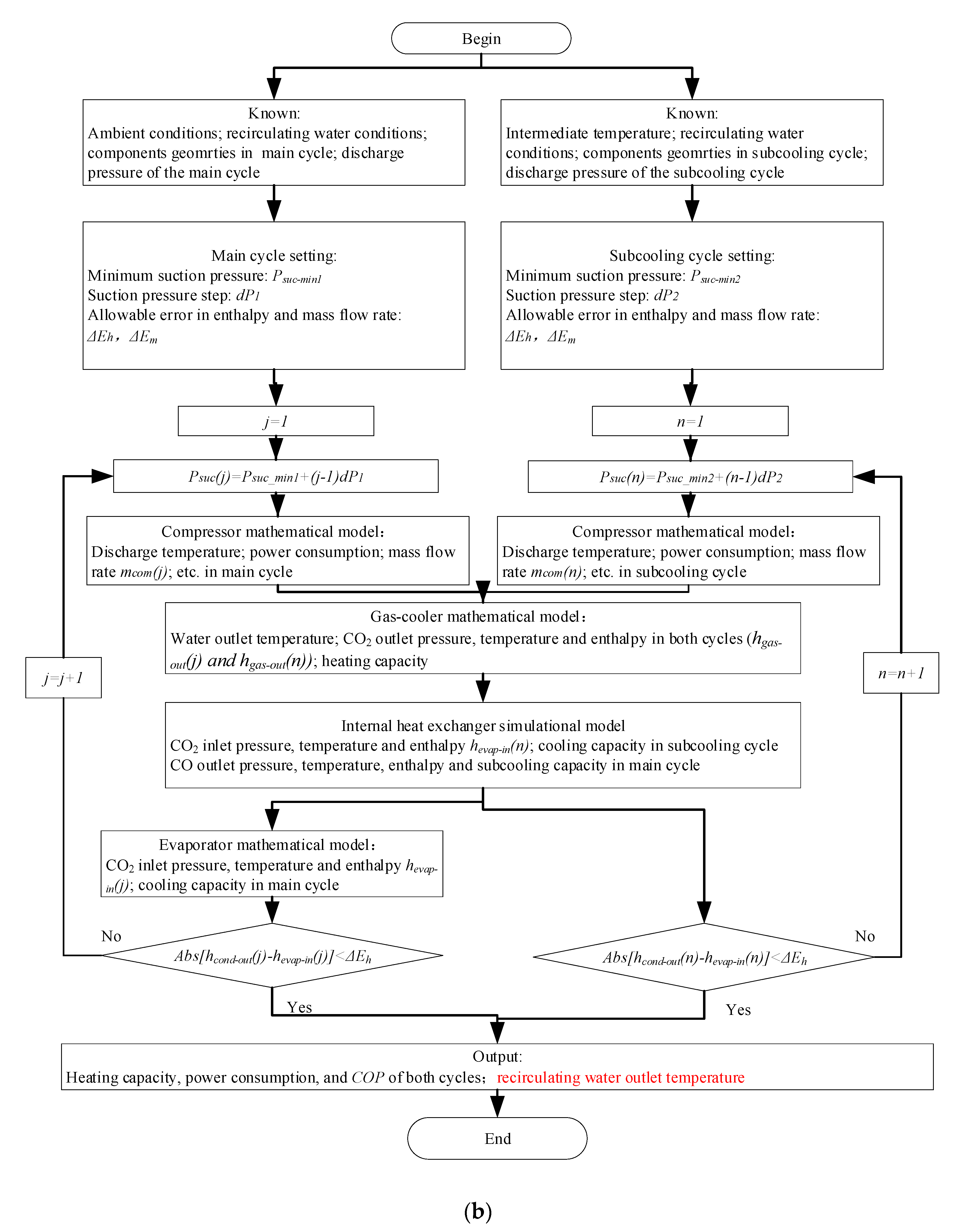

| Components | Detailed Models | |
|---|---|---|
| CO2 compression model [27] | Each time step was divided into: 1) the isentropic process with constant mass (1-2*); 2) the inner change with constant volume (2*-2). | |
| (1) | ||
| (2) | ||
| (3) | ||
| (4) | ||
| (5) | ||
| CO2 cooling model [29,30] | (6) | |
| (7) | ||
| (8) | ||
| (9) | ||
| CO2 evaporating model [31] | (10) | |
| (11) | ||
| (12) | ||
| (13) | ||
| (14) | ||
| (15) | ||
| (16) | ||
| Air flow through the fine-tube heat exchanger [32] | (17) | |
| (18) | ||
| Circulating water through the gas cooler [32] | (19) | |
| (20) |
| Main Components | Type | Characteristics | |
|---|---|---|---|
| Main cycle’s compressor | (Panasonic) DC-inventor rotary compressor | Displacement: 8.0 ml/rev | |
| Auxiliary cycle’s compressor | (Haili) DC-inverter rotary compressor | Displacement: 3.26 ml/rev | |
| Dual gas cooler | Tube-in-tube | Outside tube | Φ22 × 2.45 mm |
| Galvanized steel tube | |||
| Inside tube | Φ6.35 × 0.7 mm × 2 tubes | ||
| Φ7 × 1 mm × 1 tubes | |||
| Copper tube | |||
| Length | 17.6 m | ||
| Main cycle’s evaporator | Wavy-finned tube | Tube | Φ7 × 1 mm |
| Number of rows | 2 | ||
| Number of tubes per row | 40 | ||
| Tube length | 1.5 m | ||
| Internal heat exchanger | Plate heat exchanger | Primary channel volume | 0.549 L |
| Secondary channel volume | 0.610 L | ||
| Material | Channel plate: stainless steel | ||
| Brazing: Copper | |||
| Water-Feed Temperature/°C | Water-Supply Temperature/°C | Ambient Temperature/°C | Sought Value of Optimal Intermediate Temperature/°C | Calculated Value of Optimal Intermediate Temperature/°C | Relative Error/% |
|---|---|---|---|---|---|
| 40 | 50 | −20 | 14.74 | 15.30 | 3.65 |
| 40 | 50 | −10 | 19.55 | 19.65 | 0.51 |
| 40 | 50 | 0 | 23.53 | 24.00 | 1.97 |
| 45 | 55 | −20 | 16.99 | 16.70 | −1.72 |
| 45 | 55 | −10 | 20.84 | 21.05 | 1.01 |
| 45 | 55 | 0 | 26.41 | 25.40 | −3.97 |
| 50 | 60 | −20 | 18.65 | 18.10 | −3.07 |
| 50 | 60 | −10 | 22.79 | 22.45 | −1.51 |
| 50 | 60 | 0 | 26.78 | 26.80 | 0.07 |
| 40 | 60 | −20 | 15.87 | 15.30 | −3.71 |
| 40 | 60 | −10 | 20.07 | 19.65 | −2.12 |
| 40 | 60 | 0 | 24.31 | 24.00 | −1.29 |
| 45 | 65 | −20 | 17.09 | 16.70 | −2.33 |
| 45 | 65 | −10 | 21.02 | 21.05 | 0.16 |
| 45 | 65 | 0 | 26.36 | 25.40 | −3.80 |
| 50 | 70 | −20 | 18.72 | 18.10 | −3.42 |
| 50 | 70 | −10 | 22.73 | 22.45 | −1.24 |
| 50 | 70 | 0 | 25.56 | 26.80 | 4.65 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Wang, H.; Cao, F. Investigation of the Impact Factors on the Optimal Intermediate Temperature in a Dual Transcritical CO2 System with a Dedicated Transcritical CO2 Subcooler. Energies 2020, 13, 309. https://doi.org/10.3390/en13020309
Song Y, Wang H, Cao F. Investigation of the Impact Factors on the Optimal Intermediate Temperature in a Dual Transcritical CO2 System with a Dedicated Transcritical CO2 Subcooler. Energies. 2020; 13(2):309. https://doi.org/10.3390/en13020309
Chicago/Turabian StyleSong, Yulong, Haidan Wang, and Feng Cao. 2020. "Investigation of the Impact Factors on the Optimal Intermediate Temperature in a Dual Transcritical CO2 System with a Dedicated Transcritical CO2 Subcooler" Energies 13, no. 2: 309. https://doi.org/10.3390/en13020309
APA StyleSong, Y., Wang, H., & Cao, F. (2020). Investigation of the Impact Factors on the Optimal Intermediate Temperature in a Dual Transcritical CO2 System with a Dedicated Transcritical CO2 Subcooler. Energies, 13(2), 309. https://doi.org/10.3390/en13020309





