Fast Adaptive Robust Differentiator Based Robust-Adaptive Control of Grid-Tied Inverters with a New L Filter Design Method
Abstract
1. Introduction
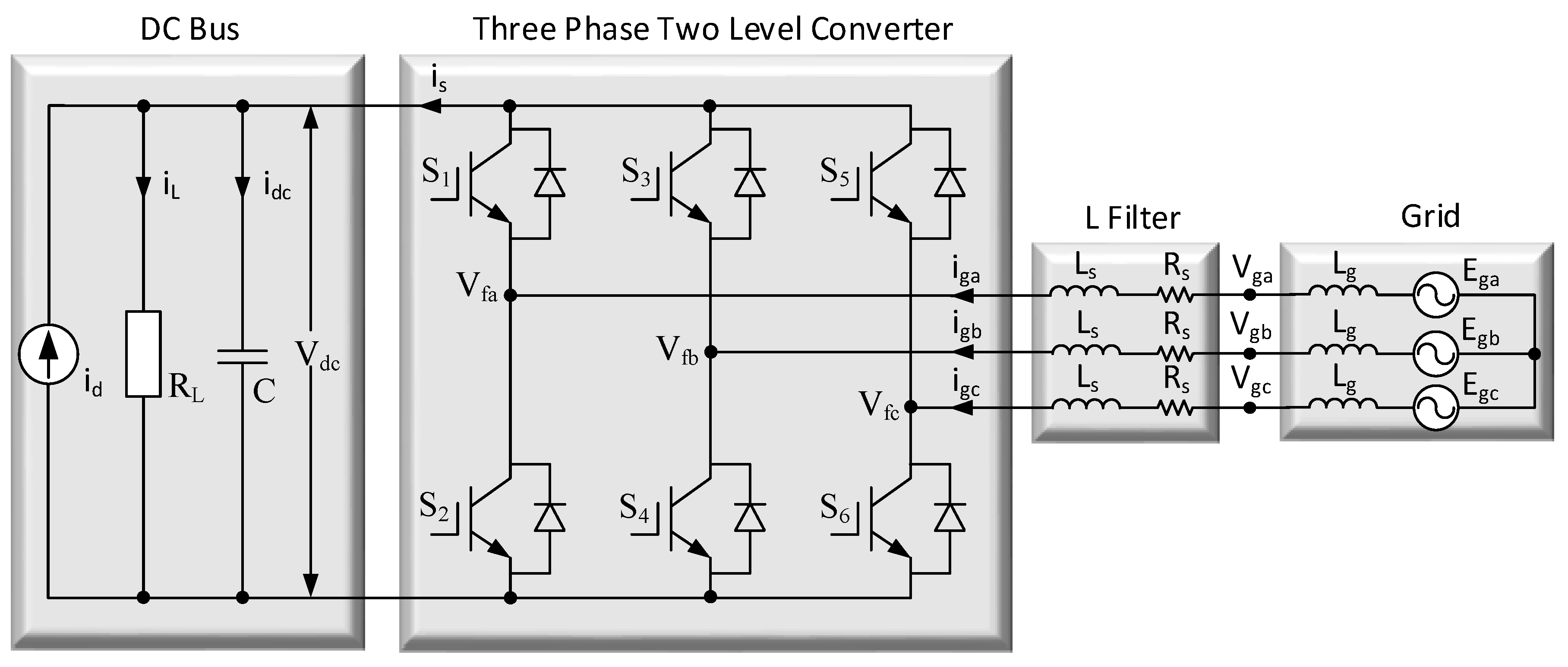
2. Dynamics of Grid-Tied Inverters
3. Control System Design for Grid-Tied Inverters
- All the signals in the closed loop must be bounded and the tracking errors in the DC bus voltage/current globally asymptotically converge to zero under all uncertainties and;
- To satisfy the unity power factor condition at the grid side;
- Considering all the dynamics of GTIs, some common assumptions are used in the control objectives in the following order;
- The three phase grid voltages Ega, Egb, and Egc are balanced. That is, the phase differences among the grid phase voltages are 120°, the peak values of them are 155 V, and the grid frequency is 50 Hz. Eventually the phase voltages are free of harmonic;
- A three-phase transformer with a conversion ratio of 220/110 in the phase voltages is used as a grid. In this case, the secondary leakage inductance of the transformer constitutes the grid inductance for the control system, and its value is maximum (0.5151 mH) at the rated power, 5 kVA. For lower power values, its value is smaller than the maximum. Exactly like that, one can deduce the same result for the grid impedance;
- The three-phase grid currents igabc and voltages Vgabc and DC bus voltage Vdc are present for feedback;
- All external disturbances and the lumped disturbance iL, id, and il are bounded, and considered uncertain in the controller design;
- In the adaptive control, it is an essential assumption that uncertainties are constants. The uncertainties with cap and with tilde represent values of estimations and estimation errors, respectively. Therefore, the time derivatives of uncertainties can be taken equal to zero, but not the derivatives of estimations and estimation errors [40];
- The signal is the reference DC bus voltage signal, which is differentiable and bounded with derivatives.
3.1. Proposed Controller Design
3.2. Proposed L Filter Design
3.3. Proposed Robust Differentiator Design
- The controller design can be carried out with ease, by avoiding the complexity in the existing backstepping;
- It can differentiate fast varying signals without the chattering;
- It enables differentiation of noisy signals to be possible without amplifying the noise;
- There is no need for using a filter, for example notch filter commonly preferred in DC bus voltage control loop [52].
3.4. Design of PLL
3.5. Design of Conventional PI Based Control System
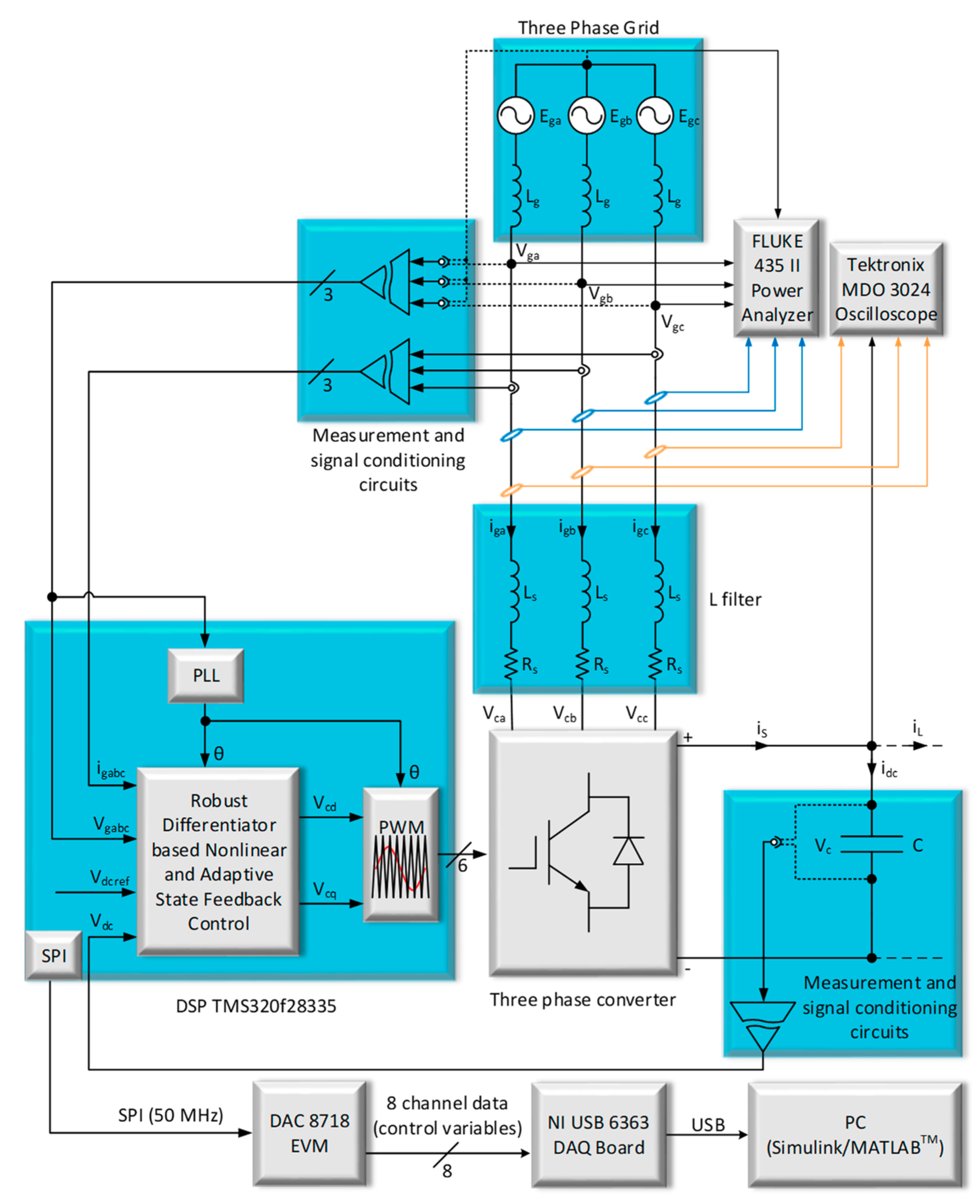
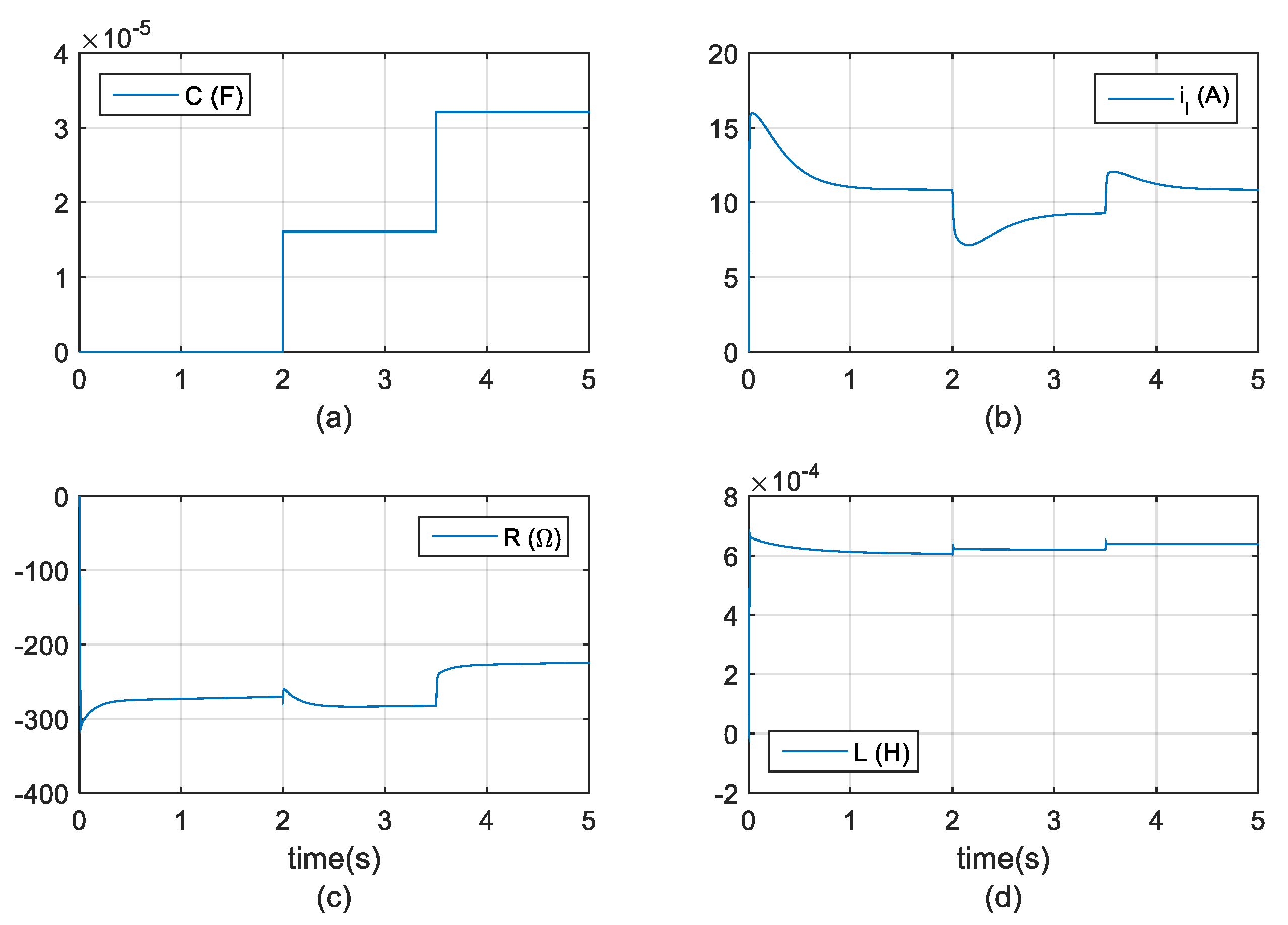
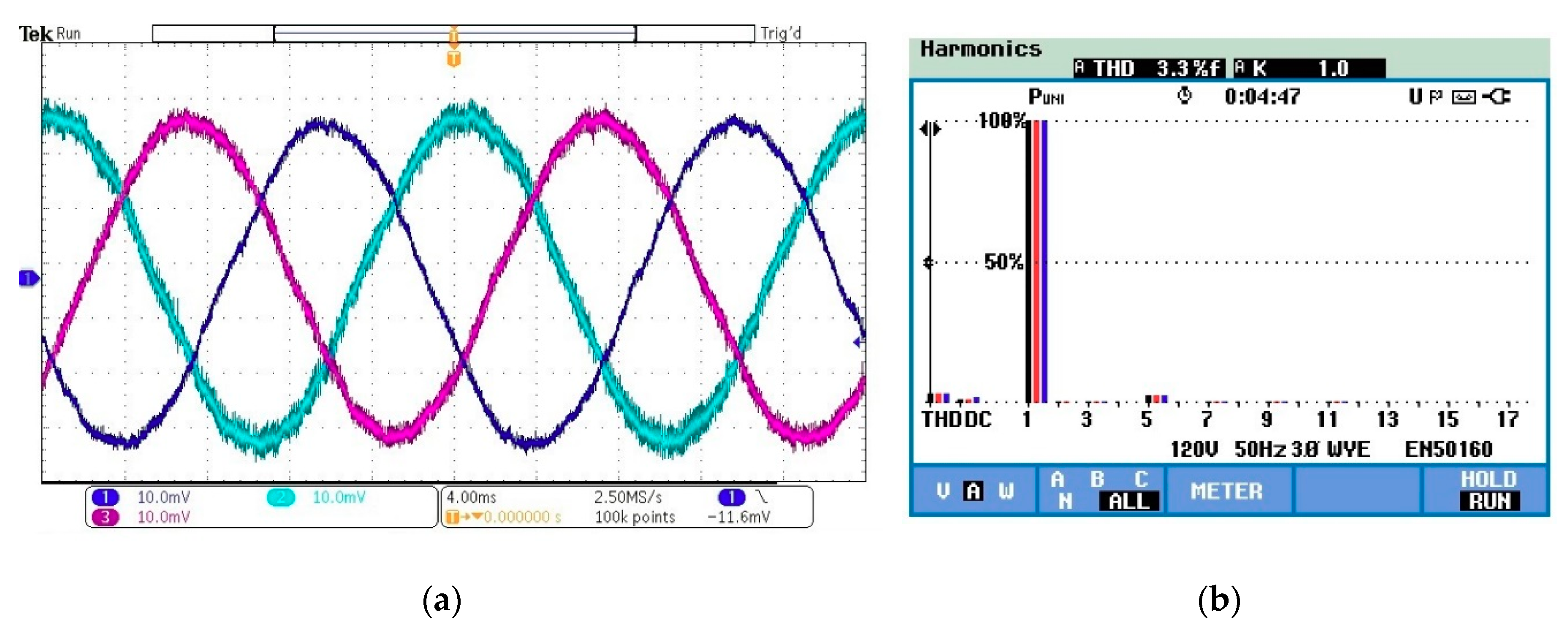
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guo, X.Q.; Wu, W.Y.; Gu, H.R. Modeling and simulation of direct output current control for LCL-interfaced grid-connected inverters with parallel passive damping. Simul. Model. Pract. Theory 2010, 18, 946–956. [Google Scholar] [CrossRef]
- International Standard IEC 61000-3-2:2018 RLV|IEC Webstore|Electromagnetic Compatibility, International Electrotechnical Commission; International Standard IEC: Geneva, Switzerland, 2018.
- Bose, B.K. Modern Power Electronics and AC Drives, 1st ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002; ISBN 978-0130167439. [Google Scholar]
- Mohan, N.; Undeland, T.M.; Robbins, W.P. Power Electronics: Converters, Applications, and Design, 3rd ed.; Wiley Online Library: Hoboken, NJ, USA, 2002; ISBN 978-0-471-22693-2. [Google Scholar]
- Yacoubi, L.; Fnaiech, F.; Dessaint, L.A.; Al-Haddad, K. New nonlinear control of three-phase NPC boost rectifier operating under severe disturbances. In Proceedings of the Mathematics and Computers in Simulation, Vienna, Austria, 5–7 February 2003; Volume 63, pp. 307–320. [Google Scholar]
- Mao, H. Review of high-performance three-phase power-factor correction circuits. IEEE Trans. Ind. Electron. 1997, 44, 437–446. [Google Scholar]
- Cambronne, J.P.; Pierre, X. Synthesis of different synchronous modulators for high power three-phase/single-phase PWM converters. Math. Comput. Simul. 1998, 46, 413–423. [Google Scholar] [CrossRef]
- Kolar, J.W.; Friedli, T. The Essence of Three-Phase PFC Rectifier Systems—Part I—IEEE Journals Magazine. IEEE Trans. Power Electron. 2013, 28, 176–198. [Google Scholar] [CrossRef]
- Yin, B.; Oruganti, R.; Panda, S.K.; Bhat, A.K.S. A simple single-input-single-output (1. Yin, B.; Oruganti, R.; Panda, S.K.; Bhat, A.K.S. A simple single-input-single-output (SISO) model for a three-phase PWM rectifier. IEEE Trans. Power Electron. 2009, 24, 620–631. [Google Scholar] [CrossRef]
- Lee, T.S. Input-output linearization and zero-dynamics control of three-phase AC/DC voltage-source converters. IEEE Trans. Power Electron. 2003, 18, 11–22. [Google Scholar]
- Ang, K.H.; Chong, G.; Li, Y. PID control system analysis, design, and technology. IEEE Trans. Control Syst. Technol. 2005, 13, 559–576. [Google Scholar]
- Cichowlas, M.; Kamierkowski, M.P. Comparison of current control techniques for PWM rectifiers. In Proceedings of the IEEE International Symposium on Industrial Electronics, L’Aquila, Italy, 8–11 July 2002; Volume 4, pp. 1259–1263. [Google Scholar]
- Melício, R.; Mendes, V.M.F.; Catalão, J.P.S. Fractional-order control and simulation of wind energy systems with PMSG/full-power converter topology. Energy Convers. Manag. 2010, 51, 1250–1258. [Google Scholar] [CrossRef]
- Lee, D.C.; Lee, G.M.; Lee, K. Do DC-bus voltage control of three-phase ac/dc PWM converters using feedback linearization. IEEE Trans. Ind. Appl. 2000, 36, 826–833. [Google Scholar]
- Lee, T.-S. Nonlinear state feedback control design for three-phase PWM boost rectifiers using extended linearisation. IEE Proc. Electr. Power Appl. 2003, 150, 554. [Google Scholar] [CrossRef]
- León, A.E.; Solsona, J.A.; Busada, C.; Chiacchiarini, H.; Valla, M.I. High-performance control of a three-phase voltage-source converter including feedforward compensation of the estimated load current. Energy Convers. Manag. 2009, 50, 2000–2008. [Google Scholar] [CrossRef]
- Ye, Y.; Kazerani, M.; Quintana, V.H. Modeling, control and implementation of three-phase PWM converters. IEEE Trans. Power Electron. 2003, 18, 857–864. [Google Scholar]
- Bouafia, A.; Krim, F.; Gaubert, J.P. Design and implementation of high performance direct power control of three-phase PWM rectifier, via fuzzy and PI controller for output voltage regulation. Energy Convers. Manag. 2009, 50, 6–13. [Google Scholar] [CrossRef]
- Aissaoui, A.G.; Tahour, A.; Essounbouli, N.; Nollet, F.; Abid, M.; Chergui, M.I. A Fuzzy-PI control to extract an optimal power from wind turbine. Energy Convers. Manag. 2013, 65, 688–696. [Google Scholar] [CrossRef]
- Lee, T. Lagrangian Modeling and Passivity-Based Control of three-phase AC/DC voltage-source converters. IEEE Trans. Ind. Electron. 2004, 51, 892–902. [Google Scholar] [CrossRef]
- Gensior, A.; Sira-Ramirez, H.; Rudolph, J.; Guldner, H. On some nonlinear current controllers for three-phase boost rectifiers. IEEE Trans. Ind. Electron. 2009, 56, 360–370. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.Y. Decentralized robust adaptive control of nonlinear systems with unmodeled dynamics. IEEE Trans. Automat. Contr. 2002, 47, 848–856. [Google Scholar]
- Landau, I.D. From robust control to adaptive control. Control Eng. Pract. 1999, 7, 1113–1124. [Google Scholar] [CrossRef]
- Sugie, T.; Yoshikawa, T. Adaptive Robust Control of Robot Manipulators—Theory and Experiment. IEEE Trans. Robot. Autom. 1994, 10, 705–710. [Google Scholar]
- Vilathgamuwa, D.M.; Wall, S.R.; Jackson, R.D. Variable structure control of voltage sourced reversible rectifiers. IEEE Proc. Electr. Power Appl. 1996, 143, 18. [Google Scholar] [CrossRef]
- Naouar, M.W.; Ben Hania, B.; Slama-Belkhodja, I.; Monmasson, E.; Naassani, A.A. FPGA-based sliding mode direct control of single phase PWM boost rectifier. Math. Comput. Simul. 2013, 91, 249–261. [Google Scholar] [CrossRef]
- Fernando Silva, J. Sliding-mode control of boost-type unity-power-factor PWM rectifiers. IEEE Trans. Ind. Electron. 1999, 46, 594–603. [Google Scholar] [CrossRef]
- Krstić, M.; Kanellakopoulos, I.; Kokotović, P.V. Nonlinear and Adaptive Control Design; Wiley: New York, NY, USA, 1995; ISBN 9780471127321. [Google Scholar]
- Kokotović, P.V. The Joy of Feedback: Nonlinear and Adaptive. IEEE Control Syst. 1992, 12, 7–17. [Google Scholar]
- Zhang, T.; Ge, S.S.; Hang, C.C. Adaptive neural network control for strict-feedback nonlinear systems using backstepping design. Automatica 2000, 36, 1835–1846. [Google Scholar] [CrossRef]
- Yip, P.P.; Hedrick, J.K. Adaptive dynamic surface control: A simplified algorithm for adaptive backstepping control of nonlinear systems. Int. J. Control 1998, 71, 959–979. [Google Scholar] [CrossRef]
- Vincent, U.E.; Njah, A.N.; Laoye, J.A. Controlling chaos and deterministic directed transport in inertia ratchets using backstepping control. Physica D 2007, 231, 130–136. [Google Scholar] [CrossRef]
- Matouk, A.E.; Agiza, H.N. Bifurcations, chaos and synchronization in ADVP circuit with parallel resistor. J. Math. Anal. Appl. 2008, 341, 259–269. [Google Scholar] [CrossRef]
- Karabacak, M.; Eskikurt, H.I. Design, modelling and simulation of a new nonlinear and full adaptive backstepping speed tracking controller for uncertain PMSM. Appl. Math. Model. 2012, 36, 5199–5213. [Google Scholar] [CrossRef]
- El Magri, A.; Giri, F.; Abouloifa, A.; Chaoui, F.Z. Robust control of synchronous motor through AC/DC/AC converters. Control Eng. Pract. 2010, 18, 540–553. [Google Scholar] [CrossRef]
- Karabacak, M.; Eskikurt, H.I. Speed and current regulation of a permanent magnet synchronous motor via nonlinear and adaptive backstepping control. Math. Comput. Model. 2011, 53, 2015–2030. [Google Scholar] [CrossRef]
- Ting, C.S.; Chang, Y.N. Observer-based backstepping control of linear stepping motor. Control Eng. Pract. 2013, 21, 930–939. [Google Scholar] [CrossRef]
- Traoré, D.; De Leon, J.; Glumineau, A. Sensorless induction motor adaptive observer-backstepping controller: Experimental robustness tests on low frequencies benchmark. IET Control Theory Appl. 2010, 4, 1989–2002. [Google Scholar] [CrossRef]
- Trabelsi, R.; Khedher, A.; Mimouni, M.F.; M’Sahli, F. Backstepping control for an induction motor using an adaptive sliding rotor-flux observer. Electr. Power Syst. Res. 2012, 93, 1–15. [Google Scholar] [CrossRef]
- Xie, Q.; Han, Z.; Kang, H. Adaptive backstepping control for hybrid excitation synchronous machine with uncertain parameters. Expert Syst. Appl. 2010, 37, 7280–7284. [Google Scholar] [CrossRef]
- Mian, A.A.; Wang, D. Modeling and backstepping-based nonlinear control strategy for a 6 DOF quadrotor helicopter. Chin. J. Aeronaut. 2008, 21, 261–268. [Google Scholar] [CrossRef]
- Yang, J.H.; Hsu, W.C. Adaptive backstepping control for electrically driven unmanned helicopter. Control Eng. Pract. 2009, 17, 903–913. [Google Scholar] [CrossRef]
- Roy, T.K.; Mahmud, M.A.; Oo, A.M.T. Robust adaptive backstepping excitation controller design for higher-order models of synchronous generators in multimachine power systems. IEEE Trans. Power Syst. 2019, 34, 40–51. [Google Scholar] [CrossRef]
- Wang, K.; Xin, H.; Gan, D.; Ni, Y. Non-linear robust adaptive excitation controller design in power systems based on a new back-stepping method. IET Control Theory Appl. 2010, 4, 2947–2957. [Google Scholar] [CrossRef]
- Yacoubi, L.; Al-Haddad, K.; Dessaint, L.A.; Fnaiech, F. A DSP-based implementation of a nonlinear model reference adaptive control for a three-phase three-level NPC boost rectifier prototype. IEEE Trans. Power Electron. 2005, 20, 1084–1092. [Google Scholar] [CrossRef]
- El Magri, A.; Giri, F.; Elfadili, A.; Dugard, L. Wind sensorless control of wind energy conversion system with PMS generator. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 2238–2243. [Google Scholar]
- Hadri-Hamida, A.; Allag, A.; Hammoudi, M.Y.; Mimoune, S.M.; Zerouali, S.; Ayad, M.Y.; Becherif, M.; Miliani, E.; Miraoui, A. A nonlinear adaptive backstepping approach applied to a three phase PWM AC-DC converter feeding induction heating. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1515–1525. [Google Scholar] [CrossRef]
- Allag, A.; Hammoudi, M.Y.; Ayad, M.Y. Adaptive Backstepping Voltage Controller Design for an PWM AC-DC Converter. Int. J. Electr. Power Eng. 2007, 1, 62–69. [Google Scholar]
- Levant, A. Sliding order and sliding accuracy in sliding mode control. Int. J. Control 1993, 58, 1247–1263. [Google Scholar] [CrossRef]
- Levant, A. Robust Exact Differentiation via Sliding Mode Technique. Automatica 1998, 34, 379–384. [Google Scholar] [CrossRef]
- Shtessel, Y.; Taleb, M.; Plestan, F. A novel adaptive-gain supertwisting sliding mode controller: Methodology and application. Automatica 2012, 48, 759–769. [Google Scholar] [CrossRef]
- Kale, M.; Akar, F.; Karabacak, M. A SOGI Based Band Stop Filter Approach for a Single-Phase Shunt Active Power Filter. In Proceedings of the 2018 2nd International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Ankara, Turkey, 19–21 October 2018; pp. 1–4. [Google Scholar]
- Dannehl, J.; Wessels, C.; Fuchs, F.W. Limitations of voltage-oriented PI current control of grid-connected PWM rectifiers with LCL filters. IEEE Trans. Ind. Electron. 2009, 56, 380–388. [Google Scholar] [CrossRef]
- Kim, K.-S.; Kim, Y. Robust backstepping control for slew maneuver using nonlinear tracking function. IEEE Trans. Control Syst. Technol. 2003, 11, 822–829. [Google Scholar]
- Ioannou, P.A.; Sun, J. Robust Adaptive Control; Prentice Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]







| Parameter | Value |
|---|---|
| Three phase power (Pn) | 3850 W |
| Single phase power (P1) | 1283 W |
| Grid phase voltage (Vn) | 110 V (rms) |
| DC bus capacitor (Cdc) | 3400 uF |
| Grid frequency (fn) | 50 Hz |
| Maximum value of grid inductance (Lg) | 0.5151 mH |
| Switching frequency (fs, fsw) | 10 kHz |
| DC bus voltage (Vdc) | 350 V |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamal, T.; Karabacak, M.; Kilic, F.; Blaabjerg, F.; Fernández-Ramírez, L.M. Fast Adaptive Robust Differentiator Based Robust-Adaptive Control of Grid-Tied Inverters with a New L Filter Design Method. Energies 2020, 13, 360. https://doi.org/10.3390/en13020360
Kamal T, Karabacak M, Kilic F, Blaabjerg F, Fernández-Ramírez LM. Fast Adaptive Robust Differentiator Based Robust-Adaptive Control of Grid-Tied Inverters with a New L Filter Design Method. Energies. 2020; 13(2):360. https://doi.org/10.3390/en13020360
Chicago/Turabian StyleKamal, Tariq, Murat Karabacak, Fuat Kilic, Frede Blaabjerg, and Luis M. Fernández-Ramírez. 2020. "Fast Adaptive Robust Differentiator Based Robust-Adaptive Control of Grid-Tied Inverters with a New L Filter Design Method" Energies 13, no. 2: 360. https://doi.org/10.3390/en13020360
APA StyleKamal, T., Karabacak, M., Kilic, F., Blaabjerg, F., & Fernández-Ramírez, L. M. (2020). Fast Adaptive Robust Differentiator Based Robust-Adaptive Control of Grid-Tied Inverters with a New L Filter Design Method. Energies, 13(2), 360. https://doi.org/10.3390/en13020360








