Different Conventional and Soft Computing MPPT Techniques for Solar PV Systems with High Step-Up Boost Converters: A Comprehensive Analysis

Abstract

Solar photovoltaic (PV) systems are attracting a huge focus in the current energy scenario. Various maximum power point tracking (MPPT) methods are used in solar PV systems in order to achieve maximum power. In this article, a clear analysis of conventional MPPT techniques such as variable step size perturb and observe (VSS-P&O), modified incremental conductance (MIC), fractional open circuit voltage (FOCV) has been carried out. In addition, the soft computing MPPT techniques such as fixed step size radial basis functional algorithm (FSS-RBFA), variable step size radial basis functional algorithm (VSS-RBFA), adaptive fuzzy logic controller (AFLC), particle swarm optimization (PSO), and cuckoo search (CS) MPPT techniques are presented along with their comparative analysis. The comparative analysis is done under static and dynamic irradiation conditions by considering algorithm complexity, tracking speed, oscillations at MPP, and sensing parameters. The single-diode model PV panel and double-diode model PV panel are also compared in terms of fill factor (FF) and maximum power extraction. Clear insight is presented supporting the suitability of MPPT techniques for different types of converter configurations.

1. Introduction

Due to the depletion of fossil fuels and the increment in energy demand, a new era has begun with a huge welcome for renewable energy sources (RESs) all over the world. RESs, such as solar, tidal, and wind that are free from environmental pollution and with excess availability have become important during recent years [1,2,3]. The worldwide concern about CO₂ reduction has led to RES deployment. A solar photovoltaic (PV) system has become a much more flexible RES due to its availability everywhere on the earth [4]. The installation and operating costs of a PV system are reduced to a greater extent due to the development of semiconductor manufacturing technology [5].

There are three types of PV cell technologies, i.e., mono, poly, and thin film [6]. The mono and polycrystalline PV cells are designed using a microelectronic manufacturing technique and their efficiencies, as per REC solar energy reviews, are 21.7% [7] and 17.8% [8], respectively. Thin film PV cells are designed using CdTe, A-Si, and CuInse₂ semiconductor materials with efficiencies ranging from 15% to 15.8% [9]. Hence, most of the PV system designers are considering high-efficiency monocrystalline silicon technology.

From the literature survey [10,11,12,13], many researchers have used different circuit topologies to model the PV array at different atmospheric conditions. Some researchers have focused on single-diode model PV panel modeling and some other researchers have preferred double-diode model PV panel modeling based on their application. In this article, a single- and double-diode model PV panel-based comparative analysis was carried out in terms of fill factor (FF), maximum power extraction, and efficiency. From the comparison results, a double-diode circuit PV panel was used to assess the maximum power point tracking (MPPT) techniques for controlling the boost converter duty cycle.

Research areas in solar have included PV modeling, MPPT techniques, design of high step-up DC-DC converter, duty cycle control, and efficiency improvement [14]. In this article, PV array modeling, variable step size MPPT controller implementation, and design of high step-up boost converters have been carried out. The main issue of PV power generation is its continuous output power variation. In order to overcome this problem, a boost converter is interfaced to harvest the peak power from a solar PV system. From the literature survey [14,15], the boost converter is interfaced between the PV panel and the DC-load in order to improve the efficiency of a solar PV system. In addition, it provides isolation between the PV power generation system and the load so that the PV array operation is not affected by sudden changes in DC-loads and short circuit faults at the load side.

From the literature survey [16,17,18], different types of conventional DC-DC converters are available to control PV voltage such as Boost [19], Buck-Boost [20], single ended primary inductance converter (SEPIC) [18], and CUK [21]. The Boost converter is used to step up the DC voltage, but it does not have overcurrent protection. In order to overcome this issue, a CUK converter is used in [22] to stabilize the PV output voltage. The drawback of the CUK converter is high complexity of implementation and also it requires two switches, two capacitors, and two inductors. The SEPIC voltage gain is high when compared to boost and CUK converters. The problem of a SEPIC is high magnetic inrush current and that it lacks short circuit faults current protection on the load side [23]. Therefore, most of the conventional boost converters are not suitable for achieving constant output voltage, less current ripples, as well as wide input (i/p) and output (o/p) operations. In this work, recently developed high step-up DC-DC converters are presented, a switched capacitor boost converter (SCBC) [24] and a stackable switching boost converter (SSBC) [25], and they are compared with a conventional boost converter (CBC) [19].

There are so many conventional and evolutionary MPPT techniques illustrated in the literature that are based on the technique of controlling the duty cycle and the output voltage of the boost converter [26,27,28]. The overall publications of MPPT techniques, annually, are given in Figure 1. As shown in Figure 1, it is observed that the number of publications, annually, has continued to increase, which shows that most of the researchers have been working on the development of different advanced MPPT techniques and it is the most popular aspect in solar power generation to improve the performance of a PV system [29]. Among all the conventional techniques, fractional open circuit voltage (FOCV) and fractional short circuit (FSC) current techniques have less complexity for implementation [30]. However, these techniques suffer from MPP tracking that is inaccurate and are suitable only for low power applications. Other conventional MPPT techniques such as perturb and observe (P&O) [31], incremental conductance (IC) [32], hill climb (HC) [33], state flow [34], Kalman filter [35], adaptive IC [36], ripple correlation (RC) [37], (dP/dI) variation of power with respect to current or power/voltage (dP/dV) feedback control [38], slider controller [39] and incremental resistance (INR) [40] are applicable for low, as well as high, power application where higher accuracy in MPP tracking is needed.

In the P&O MPPT method [31], the PV array output voltage is adjusted, and the respective power variation is observed. In this P&O, the operating power point oscillates around the MPP that can be handled through a propositional integral (PI) controller. The drawback is that this method causes power loss at the time of a perturbation and it fails to track the MPP at diverse irradiation and temperature conditions. In order to avoid the difficulties of P&O, while tracking the MPP with rapid changes in atmospheric conditions, an incremental conductance (IC) technique is applied [32]. In addition, in IC, the oscillations across the MPP are much less as compared with P&O. However, the major drawback of the IC technique is the complexity of its implementation.

The hill climbing method works similar to the P&O MPPT method to track MPP [33]. Here, voltage is taken as a control variable, and hence by incrementing the PV voltage, the respective increment in PV power can be observed when the operating point is on the left side of the MPP. If the operating point is located on the right side of the MPP, the voltage is incremented to cause a decrement in power. This process is repeated until the MPP is reached. The state flow MPPT method is easy to implement with accuracy and speed of MPP tracking as compared with the P&O and IC MPPT techniques [34]. The dithering effect increases the signal-noise ratio in the linear state space region of the state flow MPPT technique which can be overcome using the Kalman filter MPPT technique [35]. To track the rapid changes of irradiances and to obtain maximum PV voltage that is nearly equal to the open-circuit voltage (V_oc) of PV, an adaptive IC MPPT technique is applied [36]. The major advantage of this technique is its high intrinsic robustness and negligible uncertainties.

The switching states of the boost converter create voltage and current ripples in a PV system. As a result, the PV array generates ripple power [37]. In RC control, the PV power ripples are used to control and extract the maximum power of a solar PV system. The time derivative of voltage and current components in the RC control consists of mutual relationships that make the power gradient zero. Hence, the operating point of the PV system reaches the true MPP. In [38], the slope of dP/dV or dP/dI is calculated from the I-V (Current against Voltage) characteristics of solar PV system and is given as the feedback to the boost converter through a microcontroller to track the MPP. According to the slope of the sign (+ or −), the boost converter duty value either increases or decreases until the operating point reaches the true MPP. In the slider MPPT technique, the switching function of the boost converter is derived from the I-V and P-V (Power against Voltage) characteristics [39,40]. If the switching function consists of a positive sign, then the MPP of the PV system is considered to be on the left side of the PV curve otherwise it is assumed to be on the right side.

At present, most of the authors have focused on soft computing or evolutionary MPPT techniques to solve the issues of conventional MPPT techniques [41,42,43]. The main features of evolutionary algorithms are nonlinear handling capability, broaden search space, and intelligible expertise. All of the soft computing and biological algorithms are used to optimize the nonlinear behavior of the PV system. The evolutionary algorithms have included neural network (NN) [44], fuzzy logic controller (FLC) [45], artificial neuro fuzzy interface system (ANFIS) [46], cuckoo search [47] and particle swarm optimization (PSO) [48], etc.

The ANN (Artificial Neural Network) method is used in [44] to reduce the steady-state oscillations at the MPP during dynamic irradiation conditions. In article [49], the PV voltage and current or sun irradiation and temperature, or any of the two combinations of data, are used to train the NN. The learning process of ANN has been done by updating the weights. The weight updating is carried out using the backpropagation Levenberg Marquardt method. The performance of ANN is analyzed using the mean square error method and the obtained mean square error of NN to track the MPP at epoch 738 which is 0.010516. The major drawback of the ANN method is that it requires lots of data when the architecture has multiple layers. In article [50], the multilayer perceptron (MLP) type of network is used in the NN to track the MPP. The MLP consist of an input layer, output layer, and hidden layer. In the input layer, one neuron is assigned as sun irradiations and another is assigned as sun temperature in order to extract the maximum power from a solar PV system. The training is done using the standard degradation method and the activation function is sigmoidal.

Article [51] explains that the fuzzy MPPT technique is the most popular technique to track MPP and it does not require any mathematical equation computations to solve the nonlinearity issues. In addition, it works for both precise and imprecise input functions as compared with the ANN systems. The drawbacks of the fuzzy technique are that it cannot be altered once the rules are finalized and the selection of membership function purely depends on the knowledge of the user. Without the proper knowledge, the tracking of MPP in fuzzy technique is inaccurate. In order to overcome the drawbacks of the fuzzy technique, in [52], an adaptive fuzzy logic controller (AFLC) based MPPT technique is used to track the MPP. The adaptive neuro fuzzy inference system (ANFIS) is used in solar PV systems in order to overcome the drawbacks of ANN and fuzzy. The attractive features of ANFIS are fast learning capacity, proficiency of adaptation, and that it does not require an expert knowledge person [53].

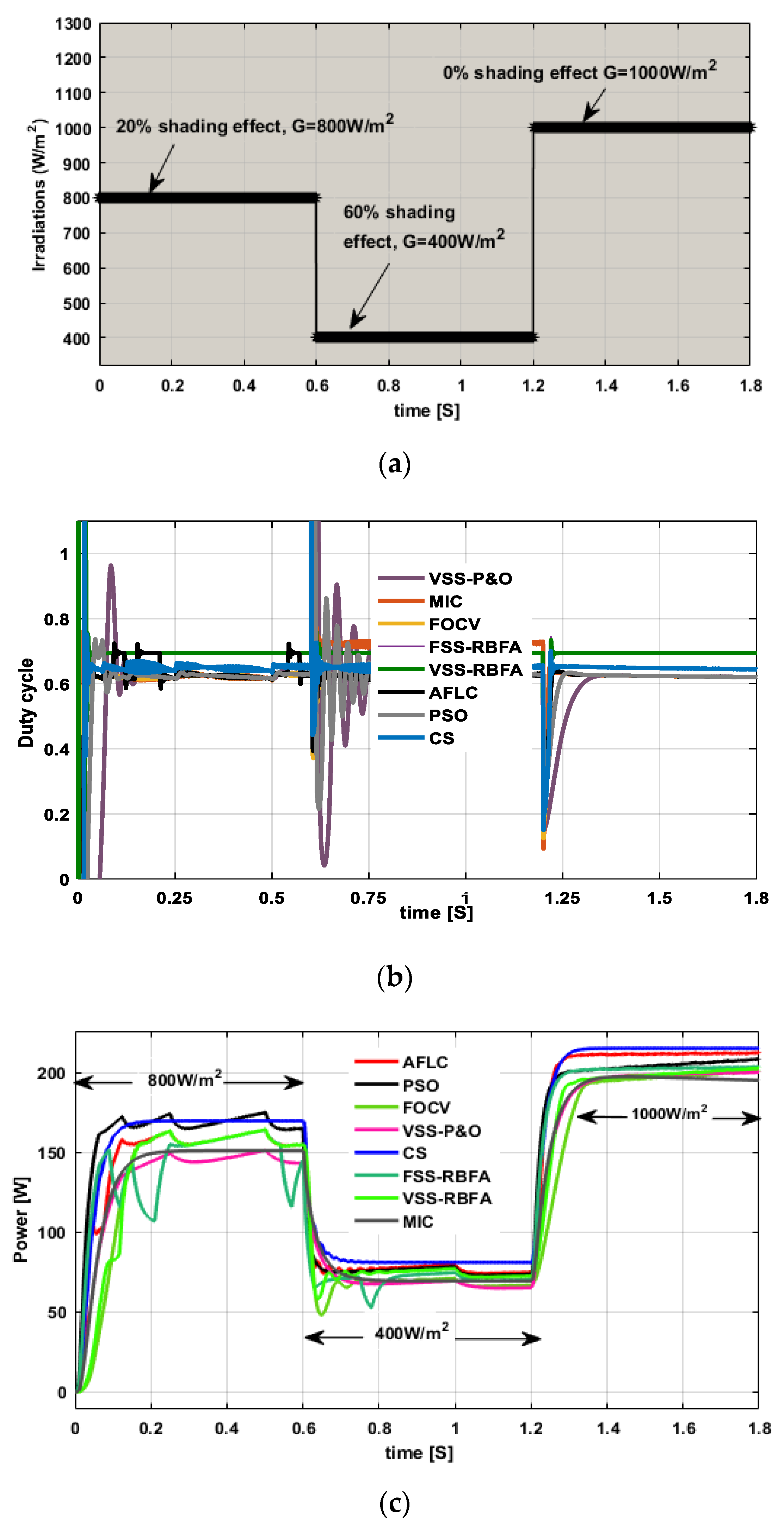
In this article, a comprehensive comparative analysis has been carried out on the recently developed MPPT techniques such as VSS-P&O [54], modified incremental conductance (MIC) [55], FOCV [56], fixed step size radial basis functional algorithm (FSS-RBFA) [57], variable step size radial basis functional algorithm (VSS-RBFA) [58], AFLC [52], PSO [59], and cuckoo search (CS) [60]. The schematic of a PV-fed MPPT controlled boost converter power generation system is illustrated in Figure 2. The rest of this article is organized as follows: In Section 2, the mathematical modeling of the single- and double-diode circuit PV array is presented along with its comparative performance characteristics. In Section 3, the necessity of MPPT technique is explained under different irradiation and load conditions. The explanation about different MPPT techniques and analysis of high step-up DC-DC converters are detailed in Section 4 and Section 5, respectively. The simulated static and dynamic irradiation conditions performance results of PV-fed high step-up boost converters are explained in Section 6. The comparative analysis of MPPT techniques is illustrated in Section 7.

2. Mathematical Modeling of PV Panel

The single-diode PV panel is designed by considering open circuit voltage V_oc, short circuit current, I_sc, maximum peak voltage, V_mpp, and current, I_mpp, at the MPP of the I-V curve [61]. The double-diode PV panel can be modeled by considering two more additional parameters as compared with a single-diode model which are reverse saturation current, I₀, and ideality factor, a, [62]. A few more parameters are also required to model the single- and double-diode models’ PV panels that can be determined by applying different optimization techniques. The equivalent circuits of single-diode circuit PV cell and double-diode circuit PV cell are shown in Figure 3a,b and its comparative analysis has been done using the experimental data of Sun Power systems California [63].

From the single-diode circuit PV cell, the output current (I_i) is derived as,

$$I_i=I_{ph\_i}{N}_{pp\_i}-I_{0\_i}{N}_{pp\_i}\left(exp\left(\frac{V_i+I{R}_{s\_i}\left(\raisebox{1ex}{$N_{ss\_i}$}\!\left/ \!\raisebox{-1ex}{$N_{pp}\_i$}\right.\right)}{a\ast V_{t\_i}\ast N_{ss\_i}}\right)-1\right)-\frac{V_i+I{R}_{s\_i}\left(\raisebox{1ex}{$N_{ss\_i}$}\!\left/ \!\raisebox{-1ex}{$N_{pp\_i}$}\right.\right)}{R_p\ast \left(\raisebox{1ex}{$N_{ss\_i}$}\!\left/ \!\raisebox{-1ex}{$N_{pp\_i}$}\right.\right)}$$

(1)

Similar to the single-diode circuit PV cell, the double circuit output current (I_j) is derived as,

$$I_j=I_{ph-j}{N}_{pp\_j}-I_{{01}_j}{N}_{p{p}_j}\left(exp\left(\frac{V_j+I{R}_{s_j}\left(\raisebox{1ex}{$N_{s{s}_j}$}\!\left/ \!\raisebox{-1ex}{$N_{p{p}_j}$}\right.\right)}{a_1\ast V_{t{1}_j}\ast N_{s{s}_j}}\right)-1\right)-I_x$$

(2)

$$I_x=I_{02\_j}{N}_{pp\_j}\left(exp\left(\frac{V_j+I{R}_{s\_j}\left(\raisebox{1ex}{$N_{ss\_j}$}\!\left/ \!\raisebox{-1ex}{$N_{pp\_j}$}\right.\right)}{a_2\ast V_{t2\_j}\ast N_{ss\_j}}\right)-1\right)-\frac{V_j+I{R}_{s\_j}\left(\raisebox{1ex}{$N_{ss}\_j$}\!\left/ \!\raisebox{-1ex}{$N_{pp\_j}$}\right.\right)}{R_{p\_j}\ast \left(\raisebox{1ex}{$N_{ss\_j}$}\!\left/ \!\raisebox{-1ex}{$N_{pp\_j}$}\right.\right)}$$

(3)

$$I_{p{h}_i,j}=\left(I_{ph\_STC}+k_I\mathsf{\Delta }T\right)\ast \raisebox{1ex}{$G_{i,j}$}\!\left/ \!\raisebox{-1ex}{$G_{ST{C}_i,j}$}\right.$$

(4)

where $\mathsf{\Delta }T$ and $k_{i,j}$ are the change of temperature and current coefficient of the PV panel. The index terms, i and j, indicate the classification of single-diode circuit and double-diode circuit PV module parameters. The nominal irradiance $(G_{ST{C}_i,j})$ and temperature $(T_n)$ of a solar PV system are 1000 W/m² and 25 °C. From Equation (4), we can say that the photovoltaic current is directly proportional to the ratio of instant irradiation with respect to the irradiation at standard test conditions. Whenever the solar irradiations reduce gradually, the PV output voltage decreases because there is a direct proportionality between irradiation and PV power which is given in Figure 4a,b.

$$I_{01\_j}=I_{02\_j}=I_{{01}_{\_i}}=\frac{I_{sc\_STC}+K_i\mathsf{\Delta }T}{exp\left(\left(V_{oc\_STC}+K_v\mathsf{\Delta }T\right)/\left\{\raisebox{1ex}{$a_1+a_2$}\!\left/ \!\raisebox{-1ex}{$p$}\right.\right\}{V}_{t_{i,j}}\right)-1}$$

(5)

where I_01-i, I_01-j, and I_02-j are the reverse saturation currents of single-diode model PV panel and double-diode circuit PV panel. From Equation (6), it can be seen that when the number of PV panel series-connected cells are increased and its equivalent voltage of PV increases [58,64].

$$V_{t\_i}=V_{t1\_\mathrm{j}}=V_{t2\_\mathrm{j}}=\frac{N_s\ast KT}{q}$$

(6)

At MPP, the ratio of derivation photovoltaic power with respect to the derivate voltage is zero which is given in Equation (7).

$${\left(\frac{\mathsf{\Delta }{p}_{pv}}{\mathsf{\Delta }v}\right)}_{V=V_{MPPT}}=0$$

(7)

The shunt resistance of the PV panel at short-circuited current is derived as [64],

$${\left(\frac{\mathsf{\Delta }I}{\mathsf{\Delta }v}\right)}_{I=i_{sc}}=-\frac{1}{R_{sho}}$$

(8)

The single- and double-diode circuit models’ PV panel dynamic characteristics under different irradiation conditions (1000, 800, 600, and 400 W/m²) are shown in Figure 4a,b. From Equation (4), it is observed that the reverse saturation current of the PV panel depends on the operating temperature of the PV system. The PV panel’s I-V and P-V characteristics at different temperature conditions are shown in Figure 5a,b. From Figure 5a,b, it is observed that at static irradiation condition (1000 W/m²), the MPP of the PV panel varies for each operating temperature (25, 35, 45, and 55 °C) condition.

The ratio of maximum peak power with respect to the nominal power is called FF which is used to measure the quality of the PV cell. The single-diode model PV panel and double-diode model PV panel are compared by considering the parameters such as maximum power extraction, FF, and efficiency. From Figure 4a,b, at 1000W/m² the single- and double-diode PV panels’ FF and efficiencies are 0.787, 17.69%, 0.765, and 17.26% respectively. Similarly, from Figure 5a,b, at 25 °C, the single- and double-diode PV panels’ FF and efficiencies are 0.787, 17.69%, 0.782, and 17.2% respectively. Hence, from the above observation, it is concluded that the fill factor and efficiency for a double-diode model is slightly higher than the single-diode model PV panel. Consequently, we can say that the double-diode circuit model PV panel extracts maximum peak power as compared with the single-diode model PV panel.

3. Necessity of the MPPT Technique

To explain the importance of the MPPT technique, the simulated double-diode circuit model PV panel current against voltage characteristics is given in Figure 6. From Figure 6, it is noticed that a unique MPP exists on I-V and P-V curves for every irradiance condition and, conversely, it shifts for different irradiance (1000, 800, 600, and 200 W/m²) conditions. To reduce the cost of PV systems it is necessary to operate the PV power generation system at the MPP. The MPPT controllers are used for continuous MPP tracking and these controllers form an integral part of the PV system [65].

The MPPT controller controls the equivalent resistance of the PV panel to move the operating point closer to the true MPP. For the dynamic loads, different expertise MPPT techniques are applied to vary the duty cycle of the boost converter. The function of MPP in the PV power generation system is evaluated using I-V characteristics, and its load line is shown in Figure 6. If the PV panel is directly connected to a load, the operating point at the resistive load is nothing but the slope of the load line-1 (1/R), which is shown in Figure 6. From Figure 6, when resistance changes from 45 to 50 Ω, the operating point moves from ”a” to ”b”. Similarly, the operating point varies from ”b” to ”b¹ “ when irradiance changes from 1000 to 800 W/m². From Figure 6, it is seen that when the load resistance changes from one level to another level, the corresponding MPP I-V characteristics vary. For the real-time operating conditions, the load resistance and I-V characteristics are not constant. Therefore, to alter the load resistance, a boost converter is placed in between the source and the load.

4. Design and Analysis of MPPT Techniques

Different literature studies have illustrated that the PV panel absorbs 35% to 45% of incident solar energy which is converted to electrical energy [66]. In order to improve the efficiency of the PV power generation system, an MPPT is used to harvest the maximum PV power by finding V_mpp and I_mpp at different atmospheric conditions [66,67]. In this article, the VSS-P&O, MIC, FOCV, FSS-RBFA, VSS-RBFA, AFLC, PSO, and CS-based MPPT techniques are used to track MPP.

4.1. Variable Step Size Perturb and Observe MPPT Technique

Among all the MPPT technologies, the P&O is the most commonly used technique because of its simplicity and accurate steady-state response but the drawback of this method is that it is applicable only at steady-state operating conditions of a solar PV system [28]. In order to overcome the drawback of conventional P&O, a variable step size P& O MPPT technique is used in article [54] to track MPP. At the start, a large step size is used to improve the tracking speed and finally step size is reduced to reduce the oscillations across the MPP. The operational flow chart of the VSS-P&O MPPT technique is shown in Figure 7a.

4.2. Modified IC MPPT Technique

In this MIC MPPT method, the continuous MPP tracking is done by comparing instantaneous conductance with previous conductance. Here, the reference voltage, V_ref, is used to operate the PV panel closer to the MPP and when it reaches the V_MPP point the variation in incremental conductance is stopped. The tracking speed of this method purely depends on the step change of incremental conductance [55].

The MPP tracking speed can be improved by increasing the step size of conductance. In the MIC method, for the first step change in the size of conductance, the operating point of PV panel is close to the MPP and the second time it reaches the MPP of the solar PV system. In this way, the step size continuously varies until achieving the MPP at dynamic irradiation conditions. To properly control the DC-DC converter, the operating point of PV steadily matches with the load line interaction point of the I-V curve and it is directly proportional to the ratio of open-circuit voltage (V_oc) to the short circuit current (I_sc). The duty of a high step-up DC-DC converter is updated using Equation (9).

$$D\left(y\right)=D\left(y-1\right)\pm N\ast \left|\frac{P\left(y\right)-P\left(y-1\right)}{V\left(y\right)-V\left(y-1\right)}\right|$$

(9)

where D is the duty cycle, y is the iteration value, N is the scaling factor, V(y) and P(y) are the PV panel voltage and power, respectively. The operational flow chart of the MIC MPPT technique is shown in Figure 7b.

4.3. Fractional Open Circuit Voltage (FOCV) MPPT Technique

In this technique, there is a direct relation between maximum voltage, V_MPP, and open-circuit voltage, V_oc. The open-circuit voltage of the PV is measured by connecting an additional switch across the PV output terminals. Evaluation of maximum peak voltage is taken from [56].

$$V_{MPP}=k_a{V}_{oc}$$

(10)

where k_a is a proportionality parameter that is calculated from the nonlinear characteristics of the PV panel. The proportionality constant is used to obtain the MPP of the PV panel and its value is between 0.72 to 0.76 for non-uniform irradiation conditions. Once the suitable value of k_a is selected for the PV panel, the maximum peak voltage of PV is calculated using Equation (10).

4.4. Fixed Step Size RBFA Based MPPT Technique

From the literature survey [57], the fixed step size RBFA based NN structure is used in the MPPT controller design to reduce the system cost and size. The NN is an information processing system and it consists of highly interconnected neurons in the form of layers. In this FSS-RBFA technique, three layers are used which are shown in Figure 8. The first layer consist of two neurons and the second layer has twenty neurons. The optimum number of neurons in the output layer is one. In the second layer, the neurons are selected based on the empirical process. The error values of PV voltage (dV) and power (dP) are the inputs to the first layer. The output of NN is a normalized duty cycle which is either zero or one. The adjustment of the duty cycle is mainly dependent on the sign of dP/dV. The working behavior of the technique is shown in

Table 1. Working behavior of the fixed step size radial basis functional algorithm (RBFA) based MPPT technique.

dVPV	dPPV	dPPV/dVPV	Change of Duty Cycle
−1	−1	+1	d (j) = d (j − 1) + Step
+1	−1	−1	d (j) = d (j − 1) − Step
−1	+1	−1	d (j) = d (j − 1) − Step
+1	+1	+1	d (j) = d (j − 1) + Step

.

4.5. Variable Step Size RBFA Based NN MPPT Technique

As discussed previously, the fixed step size RBFA based NN technique gives a good performance. However, the drawbacks of this method are less convergence speed, high steady-state oscillations, and less accuracy for MPP tracking at dynamic irradiation conditions. When the step size is high, the tracking speed of the MPP is high but the drawback is the occurrence of excessive oscillations across the MPP. While the step size is less, the oscillations are reduced but the tracking speed reduces gradually. In order to overcome the dilemma of this condition, a variable step size RBFA based NN MPPT technique is used in [58] to extract the maximum power of a solar PV system at dynamic irradiation conditions.

The training of the RBFA has been done in two stages. In the first stage, the unsupervised learning methodology is used to define the basic factors of the input layer and, in the second stage, the output layer weights are updated. In this RBFA-based NN, there are three layers which are the input, hidden, and output layers, as shown in Figure 8. The instantons PV output voltage and power parameters are the inputs to the VSS-RBFA-based NN MPPT controller which generate the switching pulses to the DC-DC converter. The tracking speed of this MPPT controller depends mainly on the interconnection of weights and the selection of step size. In this method, the duty cycle is updated using Equation (11).

$$D\left(j\right)=D\left(j-1\right)\pm \left(Step+N·dP\right)$$

(11)

where D (j) and D (j − 1) are the duty values at the instant of j and j − 1. The scaling factor, N, is used to adjust the step size of the controller and dP is the variation of PV power.

4.6. Adaptive Fuzzy Logic MPPT Controller

The major drawback of fuzzy is that the rules cannot be updated within the time and expert knowledge is required for the parameter initialization. In order to overcome these drawbacks, an adaptive fuzzy is proposed in [52] to track the MPP, thereby transferring the maximum power from the PV system to the load. The features of the adaptive fuzzy controller are good performance and fast response as compared with P&O and fuzzy controllers. In addition, the adaptive fuzzy itself changes the parameters of fuzzy in order to improve the overall system response. The block diagram of the AFLC is shown in Figure 9a and it consists of two major parts which are the FLC and a learning mechanism. The knowledge-based fuzzy system consists of three parts which are fuzzification, inference engine, and defuzzification. The position of fuzzy sets and its corresponding membership functions are shown in Figure 9b. The value of error $\left(e\right)$ and change of error $\left(\mathsf{\Delta }e\right)$ are standardized by utilizing the scaling factor. The scaling factor range is chosen in between the range of negative one to one. The error and change of error parameters are derived from the maximum power of the solar PV system follows as,

$$e\left(i\right)=\frac{P\left(i\right)-P\left(i-1\right)}{V\left(i\right)-V\left(i-1\right)};\mathsf{\Delta }e\left(k\right)=e\left(k\right)-e\left(k-1\right)$$

(12)

The AFLC rules are shown in

Table 2. Rule-based AFLC for MPPT tracking.

Change in Error (Δe)
Error (e)	NB	NS	Z	PS	PB
PB	NB	NB	NB	ZB	ZB
PS	NS	NS	NS	Z	Z
Z	PS	Z	Z	Z	NS
NS	Z	Z	PS	PS	PS
NB	Z	Z	PB	PB	PB

. In AFLC, the pulse width modulator takes real values to generate the switching pulses to the boost converter. Hence, in the defuzzification process, a height method is used to convert linguistic variables to real values. The rules involved in defuzzification are followed as shown in (13).

$$dx=\frac{C\left(1\right)W_1+C\left(2\right)W_2+C\left(3\right)W_3+C\left(4\right)W_4+\cdots \dots \dots \dots \dots +C\left(n\right)W_n}{W_1+W_2+W_3+W_4+\cdots \dots \dots \dots \dots \dots \dots +W_n}$$

(13)

where $dx$ is changing in output and $W_n$ is the height and maximum output of rule, n.

A learning mechanism is used in the AFLC to learn the rapid change of environmental conditions. According to that, the fuzzy controller parameters are adjusted to operate the operating point of PV at the optimum point. The learning of fuzzy has been done using two methods which are inverse fuzzy system and knowledge-based modifier. In the inverse fuzzy system, the knowledge-based modifier and change of error values are used to modify the FLC parameters in order to optimize the system performance. The learning process of AFLC is given in

Table 3. Learning process of AFLC.

Inverse Fuzzy System		Knowledge-Based Modifier
$\mathbf{Error}\left(\mathit{e}\right)$	$\mathbf{Change}\mathbf{of}\mathbf{Error}\left(\mathsf{\Delta }\mathit{e}\right)$	Membership Peak Value	Scaling Factor
$-\sigma <e\left(n\right)<\sigma$	$-\sigma <\mathsf{\Delta }e\left(n\right)<\sigma$	$c\left(n\right)$	$e\left(n\right)=e\left(n\right)·{\epsilon }_3$
$e\left(n\right)>\sigma$	$\mathsf{\Delta }e\left(n\right)>\sigma$	$c\left(n\right)+{\epsilon }_1$	Unchanged
$e\left(n\right)>\sigma$	$\mathsf{\Delta }e\left(n\right)<-\sigma$	$c\left(n\right)$	$\mathsf{\Delta }e\left(n\right)=e\left(n\right)·{\epsilon }_3$
$e\left(n\right)<-\sigma$	$-\sigma <\mathsf{\Delta }e\left(n\right)<\sigma$	$c\left(n\right)-{\epsilon }_2$	Unchanged
$e\left(n\right)<-\sigma$	$\mathsf{\Delta }e\left(n\right)<-\sigma$	$c\left(n\right)-{\epsilon }_1$	Unchanged
$\sigma$, minimum error and $c\left(n\right)$, maximum peak value

.

4.7. PSO-Based MPPT Technique

In the PSO technique, there are multiple cooperative agents and each agent is considered as one particle. At the first iteration, all the particles move randomly with a velocity, V. After computing the number of iterations, all the particles move towards the main object [55]. The cooperative particles exchange their information in their searching process to obtain the best optimum duty cycle of boost converter [59]. The particle’s velocity and position are obtained using Equations (14) and (15).

$$V^{a+1}=w{V}_i^a+C_1{r}_1\left(P_{best\_i}-x_i^a\right)+C_2{r}_2\left(G_{best\_i}-x_i^a\right)$$

(14)

$$x^{a+1}=x_i^a+V_i^{a+1}$$

(15)

where a indicates the number of iterations and x is a particle position. The acceleration parameters are C₁ and C₂ and random variables are r₁ and r₂. The weight, w, is the inertial weight which is updated continuously based on the number of iterations and P_{best_i} is used to store the best particle position in the first iteration and G_{best_i} is the best particle position among all of the particles after completing “a” number of iterations. The implementation flowchart of the PSO technique is given in Figure 10a.

4.8. Cuckoo Search-Based MPPT Technique

The CS MPPT technique works based on three rules. First, each cuckoo should generate only one egg and, second, the existed egg in the first iteration should be good quality, then, only it will go to the next step. Finally, the host nets are fixed values [60]. The levy function is used in CS to determine the step size of each particle in each and every iteration. The mathematical derivation of Levy is derived as,

$$Lvy\left(\beta eta\right)=L^{-\beta eta};1<\beta eta<3$$

(16)

where L is the length of the step size and βeta is an operating constant. In practical, the βeta is considered as either one or three. The optimizing flight size is α which is a fraction of discharged eggs, Pa. The Levy function is used to update the cuckoos walk which is given in Equation (17).

$$y_m^{k+1}=y_m^k+\alpha \oplus levy\left(\beta eta\right)$$

(17)

where $\alpha ={\alpha }_0\left(y_{best}-y_i\right)$, then, the modified levy function is derived as,

$$l={\alpha }_0\left(y_{best}-y_i\right)\oplus levy\left(\beta eta\right)\approx c\left(\frac{u}{v^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\beta eta$}\right.}}\right)·\left(y_{best}-y_i\right)$$

(18)

The parameters $u$ and $v$ are measured from the nonlinear distribution curves.

$$u\approx n\left(0,{\rho }_u^2\right),v\approx n\left(0,{\rho }_v^2\right)$$

(19)

where ${\rho }_u=\left(\frac{\mathsf{\Gamma }\left(1+\beta \right)·sin\left(\frac{\pi \beta }{2}\right)}{\mathsf{\Gamma }\left(\frac{1+\beta }{2}\right)·\beta ·2^{\frac{\beta -1}{2}}}\right)$ and ${\rho }_v=1$. The flowchart of CSO is given in Figure 10b.

5. Analysis and Comparison of DC-DC Converters

From the literature survey [18,19,20,21,22,23,24,25,26,27], it is evident that there are different types of DC/DC converters used in standalone and grid-connected PV systems to control the load voltage. However, in this article, two high step-up DC-DC converters are discussed which are a SCBC and a SSBC at static and dynamic irradiation conditions and their performance results are compared with CBC.

5.1. Conventional Boost Converter

The conventional boost converter (Figure 11) has been used extensively due to its high reliability and flexibility as compared with other converters [19]. The boost converter operates in two modes of operation which are a conduction mode and a blocking mode. In the conduction mode dT_S, the switch, Q, operates in forward biasing and the diode, D, operates with reverse biased condition. Hence, there is no supply from the source, V_P, to load. Similarly, when the switch is in blocking state (1 − D) ∙ T_S, the diode, D, gets forward biased. Eventually, the energy stored in an inductor, L, is transferred to load.

From Figure 11, the voltage balance equation across the input inductor L is derived as,

$$V_T·d{T}_S+(\left(V_T-V_0\right)·\left(1-d\right)T_S=0$$

(20)

Similar to the inductor property, the average current flowing through the capacitor C is zero.

$$-i_{0}d{T}_S+(\left(I_T-I_0\right)·\left(1-d\right)T_S=0$$

(21)

By solving Equations (20) and (21), the output voltage and current of the boost converter are derived as,

$$V_0=\raisebox{1ex}{$V_T$}\!\left/ \!\raisebox{-1ex}{$\left(1-d\right)$}\right.\mathrm{and},i_0=i_T\left(1-d\right)$$

(22)

5.2. Switched Capacitor Boost Converter

The equivalent resistance across PV terminals can be equalized with the load resistance by varying the duty cycle of the SCBC, and this is shown in Figure 12. The SCBC operates in two modes of operation which are a continuous conduction mode (CCM) and a discontinuous conduction mode (DCM) [24]. The most preferable mode is the CCM because of its continuity of power supply to the load.

In CCM, when the switch, S, is ON, the capacitors, C₁ and C₂, start charging with the constant charge rate and the inductor charging voltage, V_L, is equal to the supply voltage, V_PV. The diodes D_a, D_b, and D₂ operate in reverse biased condition, whereas D₁ and D₃ operate in forward biased condition. The voltage across capacitors is calculated using Equation (23).

$$\{\begin{array}{c}{V}_{PV}=V_L\\ V_{Ca}=V_{C1}+V_{C2}\\ V_{Cb}=V_{Cc}\end{array}$$

(23)

when the switch is OFF, the diodes D_a and D_b are forward biased and the inductor stored energy transfers to the load through diode D₃. The voltage across input inductor, L, and the output voltage of the converter are derived as shown in Equation (24).

$$\{\begin{array}{c}{V}_L=V_{PV}-V_{C1}\\ V_{C1}=V_{C2}\\ V_0=V_{Ca}+V_{Cc}+V_{L0}\end{array}$$

(24)

From Figure 12, at the steady-state operating condition, the inductor property is used to determine the voltage gain of the SCBC. The voltage balance equation across the inductor, L, is derived as,

$$V_{PV}·d{T}_S+(\left(V_{PV}-V_{C1}\right)·\left(1-d\right)T_S=0$$

(25)

The capacitors C₁ and C₂ charge equally and discharges to the load through the capacitors C_a and C_c.

$$\{\begin{array}{c}{V}_C=V_{C1}=V_{C2}=V_{Cb}=V_{Cc}=\frac{1}{\left(1-D\right)}{V}_{PV}\\ V_{Ca}=2V_C=\frac{2}{\left(1-D\right)}{V}_{PV}\\ V_0=V_{C1}+V_{Cb}+V_{Cc}=3V_C=\frac{3}{\left(1-D\right)}{V}_{PV}\end{array}$$

(26)

From Equations (22) and (26), the SCBC voltage gain is high as compared with the conventional boost converter.

5.3. Stackable Switching Boost Converter

The topology of a SSBC is shown in Figure 13. It consists of the single switch (Q), two capacitors (C_a, C_b), three inductors (L_a, L_b, and L₀), and four diodes (d_a, d_b, d_x, and d_y) [25]. When the switch (Q) is ON, the inductor current, i_La, flows through the diode, d_x, and the capacitor C_a gets charged. The stored capacitor and inductor voltages (V_Ca + V_La) are transferred to the load when the diode d_x gets reverse biased. The switching state of the SSBC is derived as,

$$\mathrm{Switch}\mathrm{ON}\mathrm{condition}:\{\begin{array}{c}{L}_a\frac{d{i}_a}{dt}=V_{PV}\\ C_a\frac{d{V}_{Ca}}{dt}=-i_{Lb}-\frac{V_0}{R}\\ L_b\frac{d{i}_b}{dt}=V_{PV}+V_{Ca}\\ C_b\frac{d{V}_{Cb}}{dt}=-\frac{V_0}{R}\end{array}$$

(27)

when the switch is in OFF condition, the diode (d_a) is forward biased and the capacitor C_a starts charging. The inductor (L_a) stored energy is transferred to the load with a slope of V_Ca/L_a. Similarly, the inductor L_b discharges the energy with a slope of V_Cb/L_b. The switching state of the converter when the switch is in OFF condition is given in Equation (28).

$$\mathrm{Switch}\mathrm{OFF}\mathrm{condition}:\{\begin{array}{c}{L}_a\frac{d{i}_a}{dt}=-V_{Ca}\\ C_a\frac{d{V}_{Ca}}{dt}=-i_{La}-\frac{V_0}{R}\\ L_b\frac{d{i}_b}{dt}=-V_{Cb}\\ C_b\frac{d{V}_{Cb}}{dt}=i_{Lb}-\frac{V_0}{R}\end{array}$$

(28)

In both the conditions, the output voltage of the SSBC is the sum of input voltage (V_PV), and the output voltage across the capacitors (V_Ca, V_Cb). From Equations (27) and (28), the voltage gain of the SSBC is derived as,

$$V_0=V_{PV}+V_{Ca}+V_{Cb}=\frac{V_{PV}}{{\left(1-d\right)}^2}$$

(29)

The comparison of the conventional boost converter, the SCBC, and the SSBC was done by considering the parameters such as voltage gain, the voltage stress on switches, and the number of switches used, etc. The comparison of the step-up DC-DC converters is given in

Table 4. Comparison of high step-up voltage DC-DC converters.

Converter	Diodes	Voltage Stress (VD)	Inductors	Voltage Gain	Switches	Capacitors	Voltage Stress (VS)
CBC [19]	1	V0/2	2	1/(1 − D)	1	2	V0/2
IDDBC [23]	-	V0/2	2	2/(1 − D)	4	2	V0/2
SCBC [24]	5	V0/3	2	3/(1 − D)	1	5	V0/3
SSBC [25]	4	V0/2	3	1/(1 − D)2	1	2	V0/3
CUK [29]	1	V0-Vc/2	2	D/(1 − D)	1	2	V0 − VL/2
TBBC [68]	2	V0/2	1	(1 + D)/(1 − D)	2	2	V0/2
ICBC [69]	6	V0/3	1	3/(1 − D)	1	6	V0/3
NHSDC [70]	3	V0/2	1	2/(1 − D)	1	3	V0/2

.

6. Discussion of Simulation Results

In this article, VSS-P&O, MIC, FOCV, FSS-RBFA, VSS-RBFA, AFLC, PSO, and CS MPPT techniques are applied to the PV-fed boost converter to extract the peak power of a solar PV system. The performance of the PV-fed boost converter system is analyzed at static (800 W/m²) and dynamic (800, 400, and 1000 W/m²) irradiation conditions. The operating switching frequency of DC-DC converters is 20 kHz and their design parameters are shown in

Table 5. Design parameters of a high step-up boost converters.

Converters	I/P Inductors	I/P Capacitors	O/P Capacitors	O/P Inductors
CBC [19]	L = 100 mH	Ci = 370$\mathsf{\mu }$F	C = 300$\mathsf{\mu }$F	L0 = 1000 mH
SCBC [24]	L = 100 mH	C1 = C2 = 470$\mathsf{\mu }$F	Ca, b, c = 370$\mathsf{\mu }$F	L0 = 10 mH
SSBC [25]	La = Lb = 100 mH	Ca = Cb = 100$\mathsf{\mu }$F	C0 = 370$\mathsf{\mu }$F	L0 = 90 mH

.

6.1. Static Irradiation Condition

At irradiance of 800 W/m², the MPPT controller takes the instantaneous changes of PV voltage, current, and power variables to extract and transfer the maximum power of a solar PV system. Here, the recently developed MPPT techniques (VSS-P&O, MIC, AFLC, PSO, and CS) use only the PV voltage and current parameters to determine the optimum duty cycle of the DC-DC converter. The FOCV MPPT technique takes only open circuit voltage of PV to track the MPP. The FSS-RBFA and VSS-RBFA-based MPPT techniques take the input parameters based on their application. But here, the change of PV power and voltage variables are considered as inputs to adjust the duty of DC-DC converter based on the change in irradiation conditions.

6.1.1. Conventional Boost Converter at 800 W/m²

The conventional boost converter is designed and simulated by considering the parameters given in Table 5. The simulated duty cycle waveform using different MPPT techniques is given in Figure 14a. From Figure 14a, the maximum duty of the conventional boost converter using the PSO-based MPPT technique is 0.622 and its corresponding converter output power is 158.5 W. Similarly, the duty cycle of the boost converter using CS MPPT technique is 0.59 and its corresponding converter output power is 161.73 W. From Figure 14b, it is observed that the output power of the boost converter is less while we apply the VSS-P&O MPPT technique and its corresponding duty cycle at 800 W/m² is 0.604. The PV power extraction using FSS-RBFA and VSS-RBFA is 155.76 W, 156.5 W, respectively. Hence, from the above observation, it is concluded that the CS MPPT technique is extracting maximum power as compared with VSS-P&O, MIC, FSS-RBFA, VSS-RBFA, AFLC, and PSO-based MPPT techniques.

6.1.2. Switched Capacitor Boost Converter at 800 W/m^2.

Similar to the CBC, the duty cycle waveforms of the SCBC by applying different MPPT techniques is shown in Figure 15a, and its corresponding converter output power is shown in Figure 15b. From Figure 15a, it is observed that the duty of the SCBC using the FOCV MPPT technique is 0.43 and its corresponding converter output power is 170.5W, which is higher than that of the FSS-RBFA, MIC, and VSS-P&O MPPT techniques. However, the drawback is high conduction loss. Moreover, the FOCV MPPT method is an inaccurate method because of its approximation in MPP tracking. The output power of the SCBC using PSO and CS MPPT techniques is 171.8 W and 172.2 W, respectively. From the above observation, it is concluded that the SCBC gives a slightly higher output power by applying the CS MPPT technique as compared with PSO and AFLC techniques. The drawback of the CS technique is high steady-state oscillations. Hence, the PSO-based MPPT technique is used in the PV-fed SCBC system to step-up the PV voltage.

6.1.3. Stackable Switching Boost Converter at 800 W/m²

From Figure 16a, the VSS-RBFA-based MPPT technique extracts the maximum PV power of 169.05 W and its corresponding duty is 0.6. The SSBC steps up the PV voltage using the AFLC MPPT technique and it transfers the maximum power from the source to load of 167.98 W which is nearly equal to the FOCV MPPT technique. The SSBC output power using the MIC MPPT technique is 166 W and its corresponding duty cycle is 0.55. From Figure 16b, it can be observed that the CS MPPT is extracting the maximum power but higher steady-state oscillations. In addition, it takes nearly 0.55 s to come to a steady-state condition. As a result, the conduction losses in the system increase. Hence, it is concluded that the VSS-RBFA-based MPPT technique is suitable for the SSBC application.

6.2. Dynamic Irradiation Condition

At dynamic irradiation conditions, the VSS-P&O, MIC, and FOCV MPPT techniques are compared with FSS-RBFA, VSS-RBFA, AFLC, PSO, and CS MPPT techniques in terms of converter output voltage and power. Here, at dynamic irradiation condition, the irradiations start increasing (0 to 0.6 section) from 0 to 800 W/m². At 0.6 s, the irradiations are stepped down from 800 W/m² to 400 W/m² up to the time duration of 1.2 s. Finally, at 1.2 s, the irradiations are changing from 400 W/m² to 1000 W/m, which is shown in Figure 17a. The high step-up conventional boost converters, SCBC and SSBC, are discussed at dynamic irradiation conditions in the next section.

6.2.1. Conventional Boost Converter at (800, 400, and 1000 W/m²)

The duty cycle variation of the CBC is shown in Figure 17b. At starting (800W/m²), the obtained power using the VSS-P&O MPPT technique is 148.44 W and it is reduced to 77 W when the irradiations are reduced to 50%. At 1000 W/m², the output power of the converter using the FOCV MPPT technique is 197.5 W, which is higher than that of the MIC and VSS-P&O techniques. The output powers of the converter, by applying different MPPT techniques under dynamic irradiation conditions, are shown in Figure 17c and recorded in

Table 6. Performance results of CBC at different irradiation conditions (0.8, 0.4, and 1 kW/m²).

MPPT Method	Performance of Conventional Boost Converter at Different Irradiation Conditions
	800 W/m2 (0 to 0.6 s)				400 W/m2 (0.6 to 1.2 s)				1000 W/m2 (1.2 to 1.8 s)
	VPV (V)	Duty	V0 (V)	P0 (W)	VPV (V)	Duty	V0 (V)	P0 (W)	VPV (V)	Duty	V0 (V)	P0 (W)
VSS-P&O	34	0.604	86	148.44	17	0.711	59	77	38	0.59	94	196.31
MIC	34.3	0.601	86.1	150.7	17.5	0.7	59.6	77.8	39.2	0.58	95.31	197.48
FOCV	33.8	0.62	89	155	17	0.715	59.8	78	39.28	0.59	96	197.5
FSS-RBFA	33	0.627	87	155.76	17.4	0.719	62	79.53	40.1	0.586	96.8	198.78
VSS-RBFA	34.2	0.609	87.5	156.5	18.5	0.72	66.4	79.6	39.8	0.6	100.5	200.2
AFLC	34.8	0.614	90.32	158.2	24	0.64	68	80	45.3	0.56	105	201.8
PSO	34.71	0.622	92	158.5	24.8	0.66	73.7	82	47.07	0.64	132	204.40
CS	37.27	0.59	93.17	161.73	25.76	0.65	73.89	82.2	47.54	0.65	138	205.18

. From Figure 17c, it is observed that the CS-based converter output power at 1000 W/m² is 205.18 W which is higher than the VSS-P&O, MIC, VSS-RBFA, and AFLC MPPT techniques but the drawbacks are high steady-state oscillations and that it takes high conversion time. The drawbacks of the PSO MPPT technique are suppressed using the CS technique.

6.2.2. Switched Capacitor Boost Converter at (800, 400, and 1000 W/m²)

In this converter, at an irradiance of 400 W/m²_, the FOCV MPPT technique is extracting maximum power of the PV system which is nearly equal to the 68.1 W with a duty cycle of 0.35 and this power is increased to 198.5 W when irradiations increase to 1000 W/m² (Figure 18b). The CS MPPT technique-based SCBC transfers the maximum power of 206.29 W at 1000W/m² which is higher than the PSO MPPT technique, but the drawbacks are less MPPT tracking speed and higher steady-state oscillations. Hence, the PSO-based MPPT technique is used for the SCBC to step up the PV voltage. Moreover, its duty cycle is constant at different irradiation conditions, as shown in Figure 18a. The analytical results of the SCBC, applying different MPPT techniques, are shown in

Table 7. Performance results of SCBC at different irradiation conditions (800, 400, and 1000 W/m²).

MPPT Method	Performance of Switched Capacitor Boost Converter at Different Irradiation Conditions
	800 W/m2 (0 to 0.6 s)				400 W/m2 (0.6 to 1.2 s)				1000 W/m2 (1.2 to 1.8 s)
	VPV (V)	Duty	V0 (V)	P0 (W)	VPV (V)	Duty	V0 (V)	P0 (W)	VPV (V)	Duty	V0 (V)	P0 (kW)
VSS-P&O	30.13	0.3	128.57	167.35	14.3	0.33	64.05	78.4	30.2	0.40	151	194.5
MIC	28.5	0.35	131.53	167.5	12.3	0.43	64.73	79.21	32.87	0.38	154.83	196.48
FOCV	27.18	0.43	142.27	170.5	14.3	0.35	68.1	79.4	31.8	0.4	159	198.5
FSS-RBFA	30.31	0.35	138.46	169.5	14.5	0.36	67.96	82.73	35.12	0.34	159.09	198.3
VSS-RBFA	27	0.45	147.27	170.8	14.8	0.35	68.3	85.9	34.89	0.35	161.03	198.9
AFLC	27.04	0.5	162.01	170.21	12.80	0.45	69.81	86.5	35.8	0.35	165.23	201.4
PSO	26.8	0.46	149.22	171.8	12.5	0.5	75.03	86.9	35.2	0.37	167.55	205.7
CS	29.5	0.45	158.43	172.2	12.5	0.515	77.31	87.5	35.28	0.315	153.28	206.29

.

6.2.3. Stackable Switching Boost Converter at (800, 400, and 1000 W/m²)

The operation of a SSBC is similar to a conventional and SCBC but the difference is stackable switching. The operating duty cycle of the SSBC using the MIC MPPT technique is 0.62 which is higher than that of all the other MPPT techniques (Figure 19a), and the extracted power of the PV using the MIC technique is very low. The VSS-RBFA-based MPPT technique varies the duty cycle of the SSBC to transfer the maximum power from the source to load. From Figure 19b, the CS, and PSO-based MPPT techniques are applied to the converter to extract the maximum PV power. The drawbacks of CS and PSO are high steady-state oscillations, large time to convergence, and high conduction losses. The performance parameters of a SSBC at different irradiations are recorded in

Table 8. Performance results of a SSBC at different irradiation conditions (0.8, 0.4, and 1 kW/m²).

MPPT Method	Performance of Switched Capacitor Boost Converter at Different Irradiation Conditions
	800 W/m2 (0 to 0.6 s)				400 W/m2 (0.6 to 1.2 s)				1000 W/m2 (1.2 to 1.8 s)
	VPV (V)	Duty	V0 (V)	P0 (W)	VPV (V)	Duty	V0 (V)	P0 (kW)	VPV (V)	Duty	V0 (V)	P0 (kW)
VSS-P&O	28.2	0.55	139.25	168.2	15.2	0.55	63.30	79.10	31.31	0.55	154.56	196
MIC	28.7	0.55	138.27	166	15.1	0.51	62.47	78.5	28.2	0.62	153.08	195.29
FOCV	28	0.57	151.43	168.7	13.81	0.55	64.19	81.23	31.2	0.55	153.08	196.22
FSS-RBFA	30.22	0.555	153.29	167.31	16.08	0.5	64.10	80.01	35.01	0.52	151.90	195.8
VSS-RBFA	30.42	0.60	154.3	169.05	17.9	0.48	65.82	82.91	35.92	0.525	155.12	200
AFLC	29.5	0.56	152.37	167.98	16.5	0.48	64.05	80.9	35.77	0.53	154.79	199.89
PSO	30.05	0.56	154.84	172.27	16.20	0.51	66.63	83.5	28.8	0.58	158.73	206.5
CS	29.01	0.57	156.84	172.93	17.63	0.54	66.78	83.9	32.5	0.549	159.78	208.27

.

7. Comparison of MPPT Techniques at Different Irradiation Conditions

In order to compare the conventional and soft computing MPPT techniques, the following five parameters are considered: The number of sensors required to sense the PV parameters, the ability to handle multiple MPP under partial shading condition, the tracking speed of the MPPT controllers, and the implementation complexity. However, this is not a final comparison of the MPPT techniques because different researchers have used different parameters for the comprehensive assessment of MPPT techniques at different irradiation and temperature conditions. In this study, different MPPT techniques are compared under dynamic irradiation conditions.

7.1. Sensing Parameters

From the observation of the above results, the MIC, PSO, CS, and VSS-P&O MPPT techniques required one voltage sensor and one current sensor. The FOCV technique required only one voltage sensor. As a result, the cost of the FOCV MPPT controller is much less as compared with other MPPT controllers. The FSS-RBFA, VSS-RBFA, and AFLC-based MPPT techniques used one differentiable voltage sensor and one differentiable power sensor to sense the voltage error and power error. The detailed analysis of the MPPT techniques at different irradiation conditions is given in

Table 9. Comprehensive analysis of different conventional and soft computing MPPT techniques.

Parameters	Types of MPPT Techniques
	VSS-P&O	MIC	FOCV	AFLC	FSS-RBFA	VSS-RBFA	PSO	CS
Sensing variables	I, V	I, V	V	Varies	I, V	Varies	Varies	Varies
Design complexity	Easy	Medium	Easy	Medium	Medium	Medium	Medium	Medium
Tracking speed	0.28 s	0.25 s	0.2 s	0.185 s	0.2 s	0.18 s	0.15 s	0.13 s
Settling time	0.2 s	0.23 s	0.12 s	0.1 s	0.18 s	0.15 s	0.25 s	0.25 s
Operated duty cycle	0.6 to 0.7	0.5 to 0.6	0.6 to 0.7	0.4 to 0.6	0.5 to 0.8	0.3 to 0.7	0.4 to 0.7	0.3 to 0.7
Oscillations at MPP	2%	2.2%	3.5%	1.8%	1.85%	2%	2.5%	2.0%
Is it true MPP	Yes	Yes	No	Yes	Yes	Yes	Yes	Yes
PV panel depends	No	No	Yes	No	Yes	Yes	No	No
Periodic tuning	No	No	Require	No	No	No	Require	Require
Analog or digital	Both	Digital	Both	Both	Both	Both	Both	Both
Error detection accuracy	Medium	Medium	Less	Medium	Medium	High	Medium	High
Dynamic response	Medium	Medium	Less	Medium	Medium	High	Medium	High
Non-linearity	Medium	Moderate	Poor	Good	Good	Good	Good	Good
Hardware complexity	Less	Less	Less	Medium	Medium	Medium	Medium	Medium
Algorithm complexity	Medium	Medium	Less	Medium	Less	Less	Medium	Medium
Efficiency	Medium	Medium	Less	Medium	Medium	High	High	High
Cost	Less	Medium	High	Less	Less	Less	Medium	Medium

.

7.2. Ability to Handle the Multiple MPP

In a static irradiation condition, there is only one MPP with I-V and P-V characteristics but it varies based on the load operating conditions, which is explained in Section 3. In real-time operating conditions, the solar PV system characteristics consist of multiple MPPs and one global MPP which is required to extract the maximum power of a PV system. The tracking of MPP under dynamic irradiation using conventional MPPT techniques is very difficult because it can track the local MPP instead of the global MPP. In order to overcome this problem, the hybrid conventional MPPT techniques are used in article [71] and [72] to track global MPP under partial shading conditions. Among all the soft computing techniques, FSS-RBFA, VSS-RBFA, AFLC, PSO, and CS-based MPPT techniques are the most popular techniques to track MPP because their advantages are fewer oscillations across the MPP and high tracking speed. The FOCV MPPT technique is not an accurate method because of its approximation in MPP tracking.

7.3. Tracking Speed of MPP

In real time, the PV I-V and P-V characteristics vary continuously at diverse environmental conditions. The tracking speed of different conventional MPPT techniques is less because of its fixed step change in the duty cycle. In [73], the optimized P&O MPPT technique is used to track MPP with the convergence time of 1.3 s. The advantage of this method is less oscillations across the MPP (less than 3%). The HC MPPT technique is used in [74] to perturb the duty of boost converter. The tracking speed of this method is 6 s and its incremental step size is 1.5%. However, in order to improve the tracking speed of conventional methods a variable step size P&O MPPT technique is was used to obtain the optimum duty cycle of the boost converter. The convergence speed of VSS-P&O at 800 W/m² is 0.28 s and the oscillations across the MPP are less than 2%. From Figure 18b, at 800 W/m², the convergence speed of AFLC is 0.185 s, which is less than the MIC and FSS-RBFA-based MPPT techniques. The convergence speed of PSO is 0.13 s which is less than the CS-based MPPT controller.

7.4. Implementation Complexity

From the literature survey, the implementation of conventional MPPT techniques is simple. In addition, these methods required less memory. In [75], the authors used dSPACE 1104 software with DSP to implement soft computing-based MPPT techniques. The implementation complexity of VSS-P&O and FOCV was easy as compared with the MIC MPPT techniques and the implementation complexity of PSO and CS was high as compared with FSS-RBFA and VSS-RBFA.

8. Conclusions

Using real-time data, the single- and double-diode models’ PV panels are compared successfully in terms of maximum power extraction, FF, and efficiency. From the comparison results, the double-diode model PV panel harvests maximum PV power with high efficiency as compared to a single-diode model PV panel. The performance evaluation of all conventional and soft computing MPPT techniques was carried out to achieve the optimum duty cycle of the boost converter. From the performance results, it is inferred that the CS MPPT technique is suitable for conventional boost converter applications, and PSO is suitable for SCBC applications at static and dynamic irradiation conditions. The VSS-RBFA-based MPPT technique is suitable for a SSBC due to its high tracking speed and low steady-state oscillations. From the comparison results of DC-DC converters, it is concluded that a SSBC gives high voltage gain, less voltage stress on switches, and required a single switch for wide output voltage applications.