Comparative Analysis of the Mining Cribs Models Filled with Gangue
Abstract
:1. Introduction
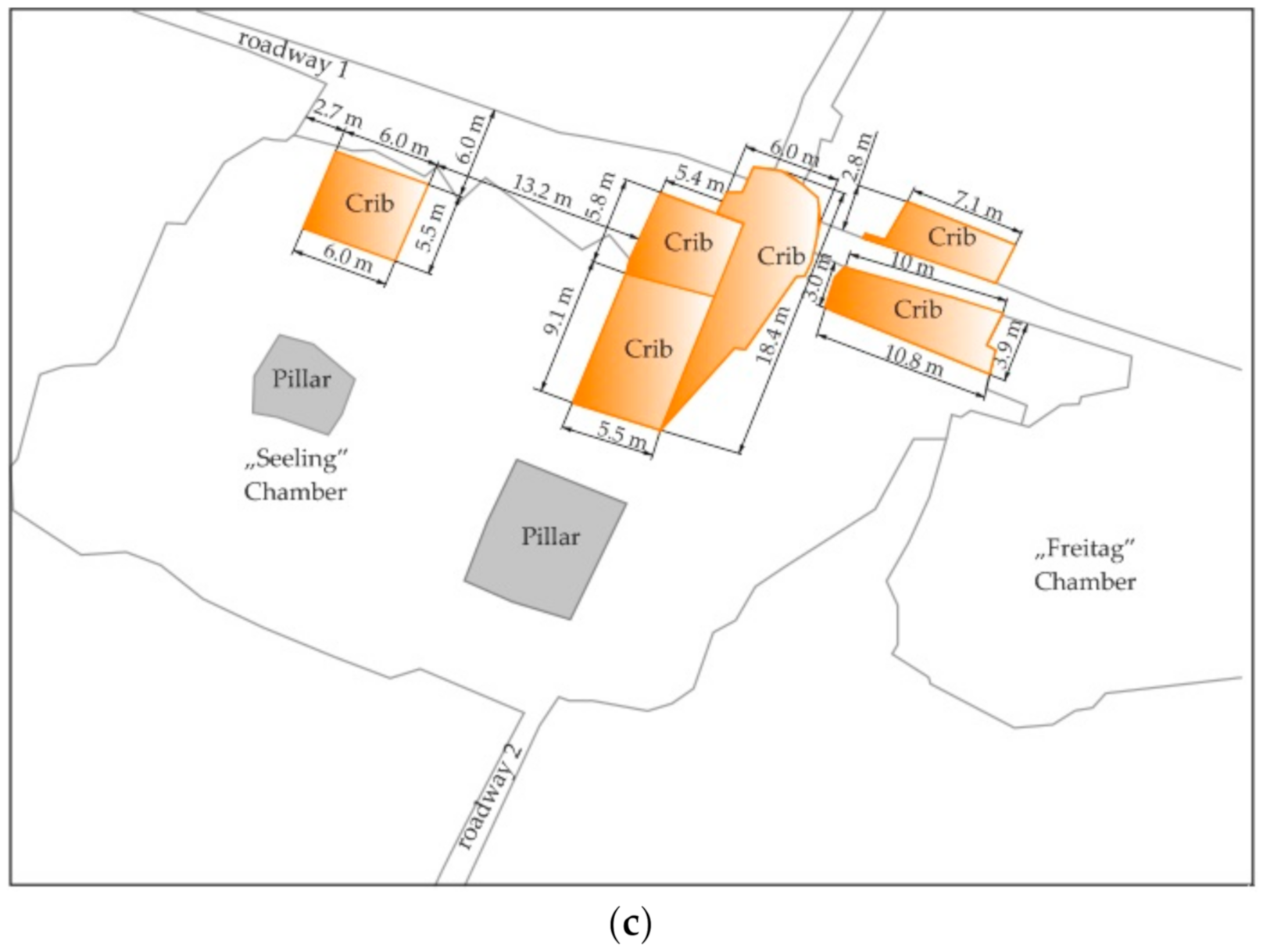
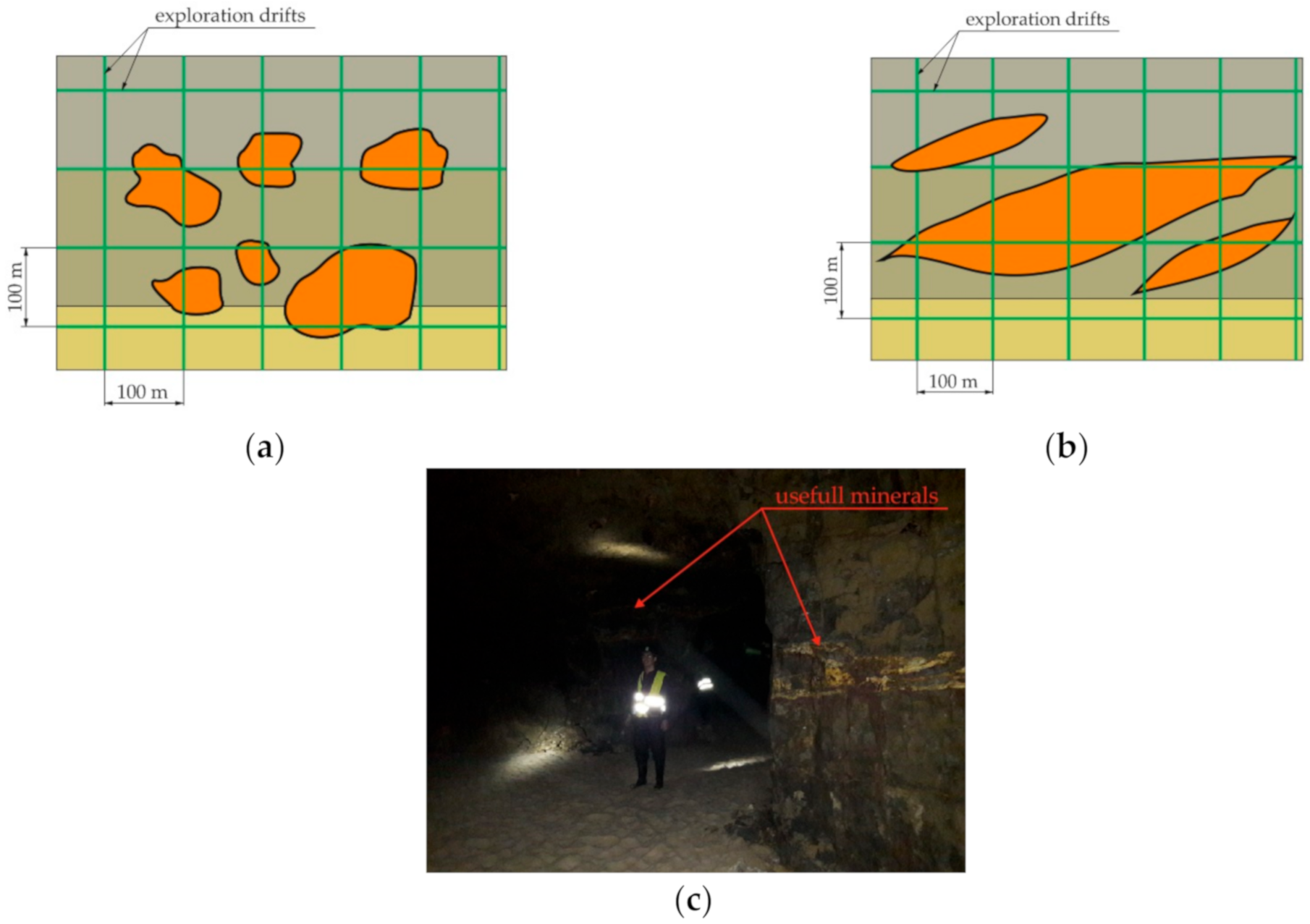
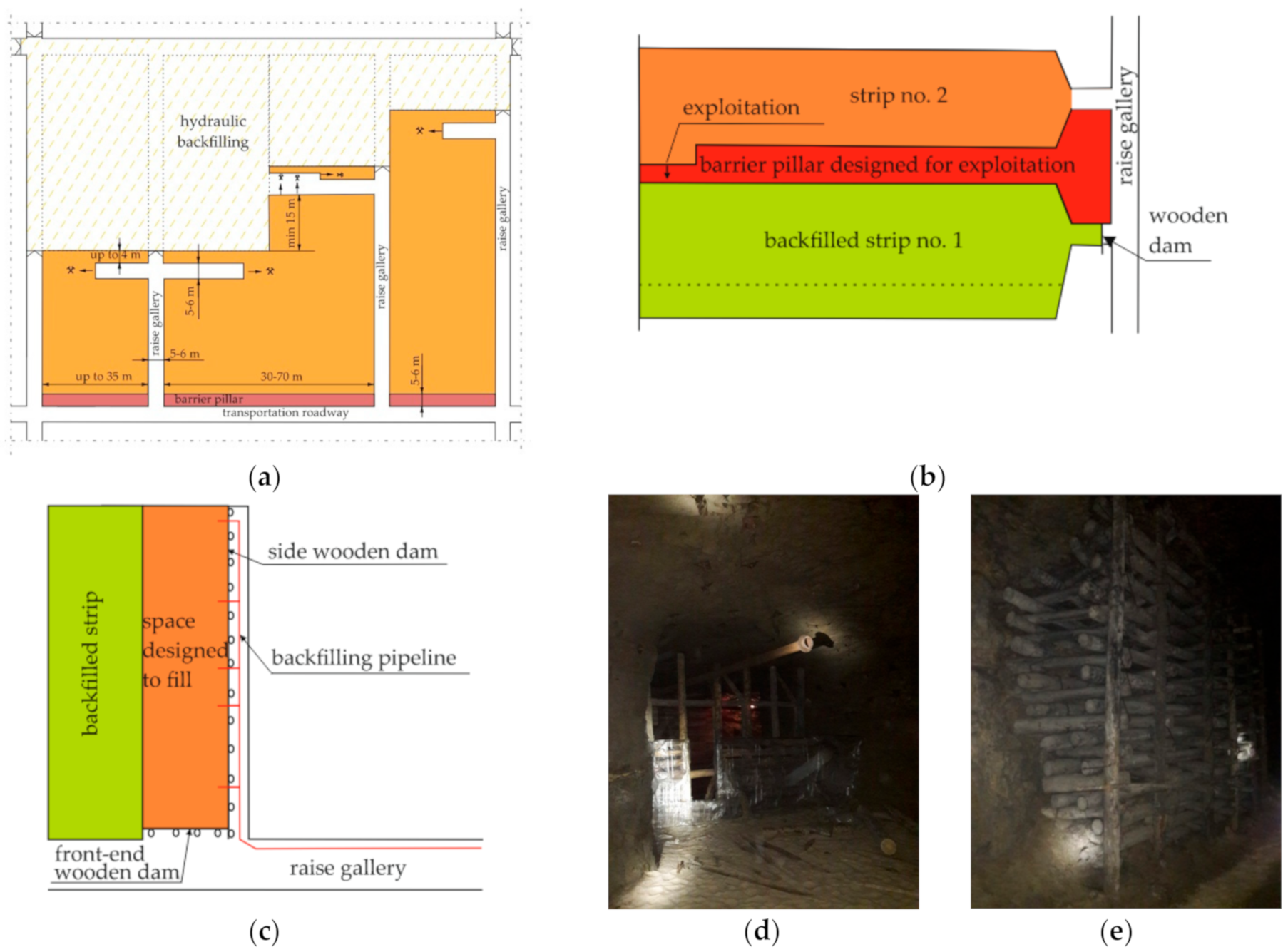
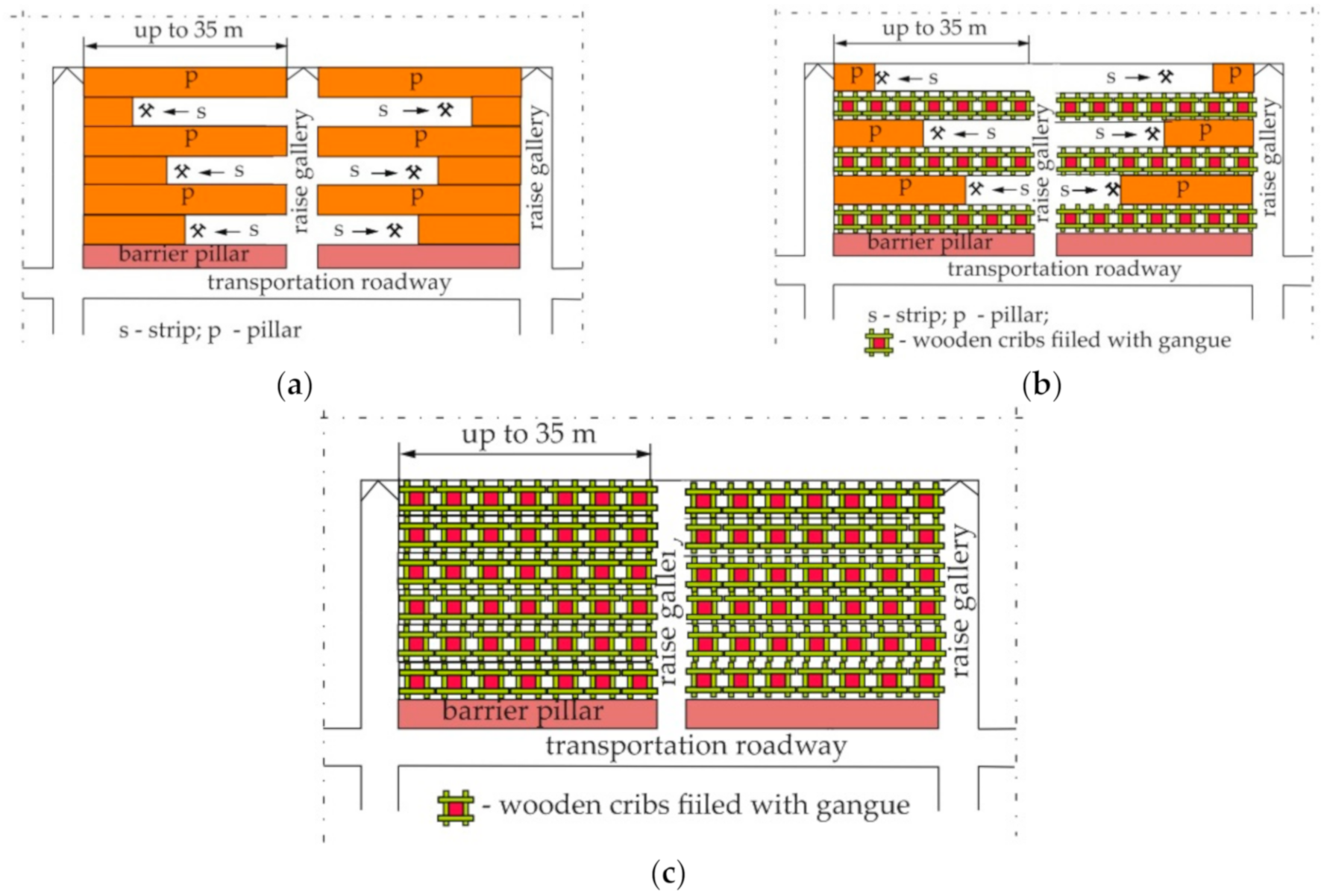
2. Wood and Cribs in Polish Mining
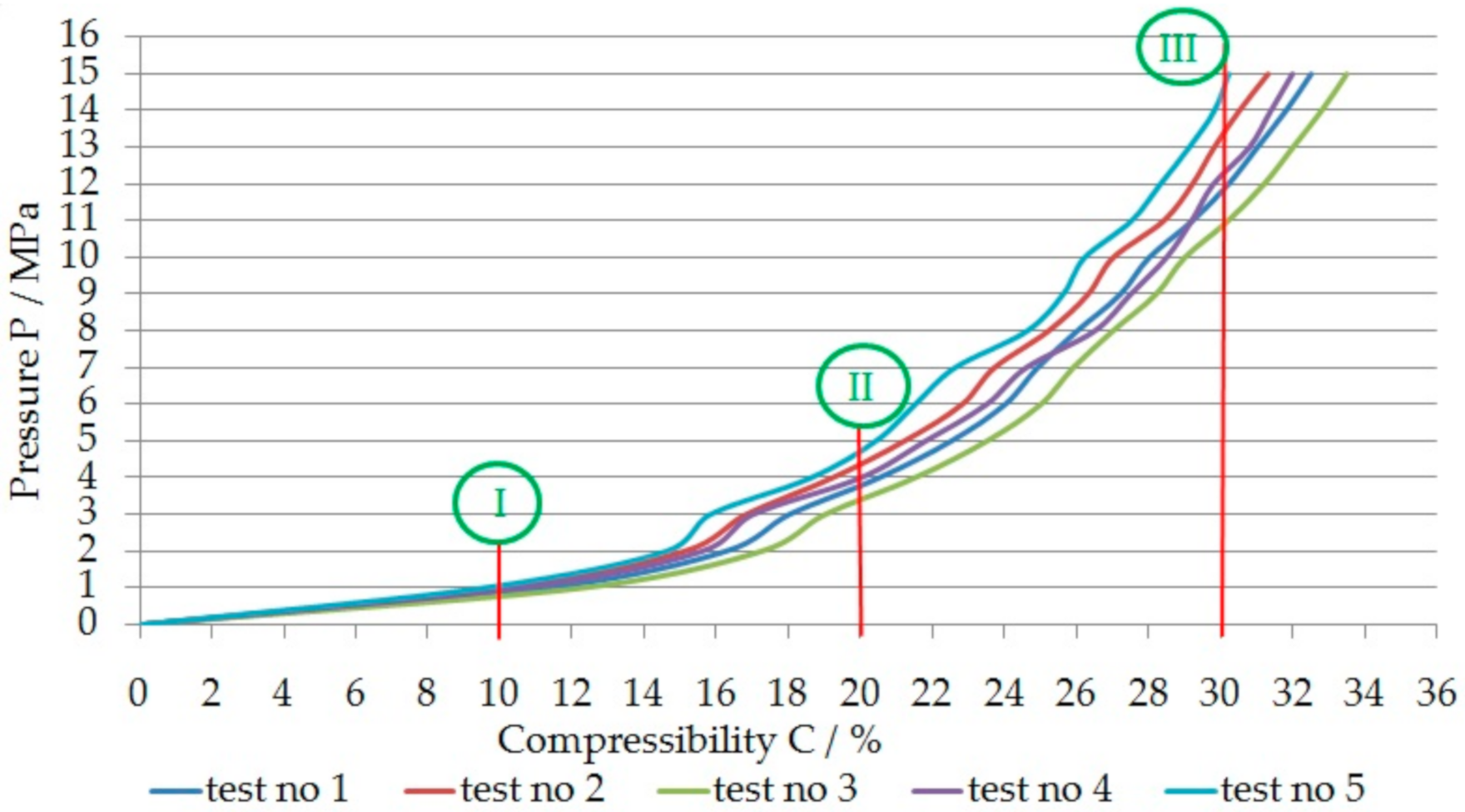
3. Compressibility of the Gangue
- C—compressibility/%,
- hb—height of the gangues in an oedometer before test/mm,
- ha—height of the gangues in an oedometer after test/mm.
4. Laboratory Tests of Wooden Cribs Models
5. Discussion
- R1—predicted compressive strength of the crib filled with gangue on a geometric scale 1:1;
- R0—compressive strength of the four-point wooden crib model filled with gangue;
- V0—volume of the four-point wooden crib model filled with gangue;
- V1—predicted volume of the crib filled with gangue on a geometric scale 1:1;
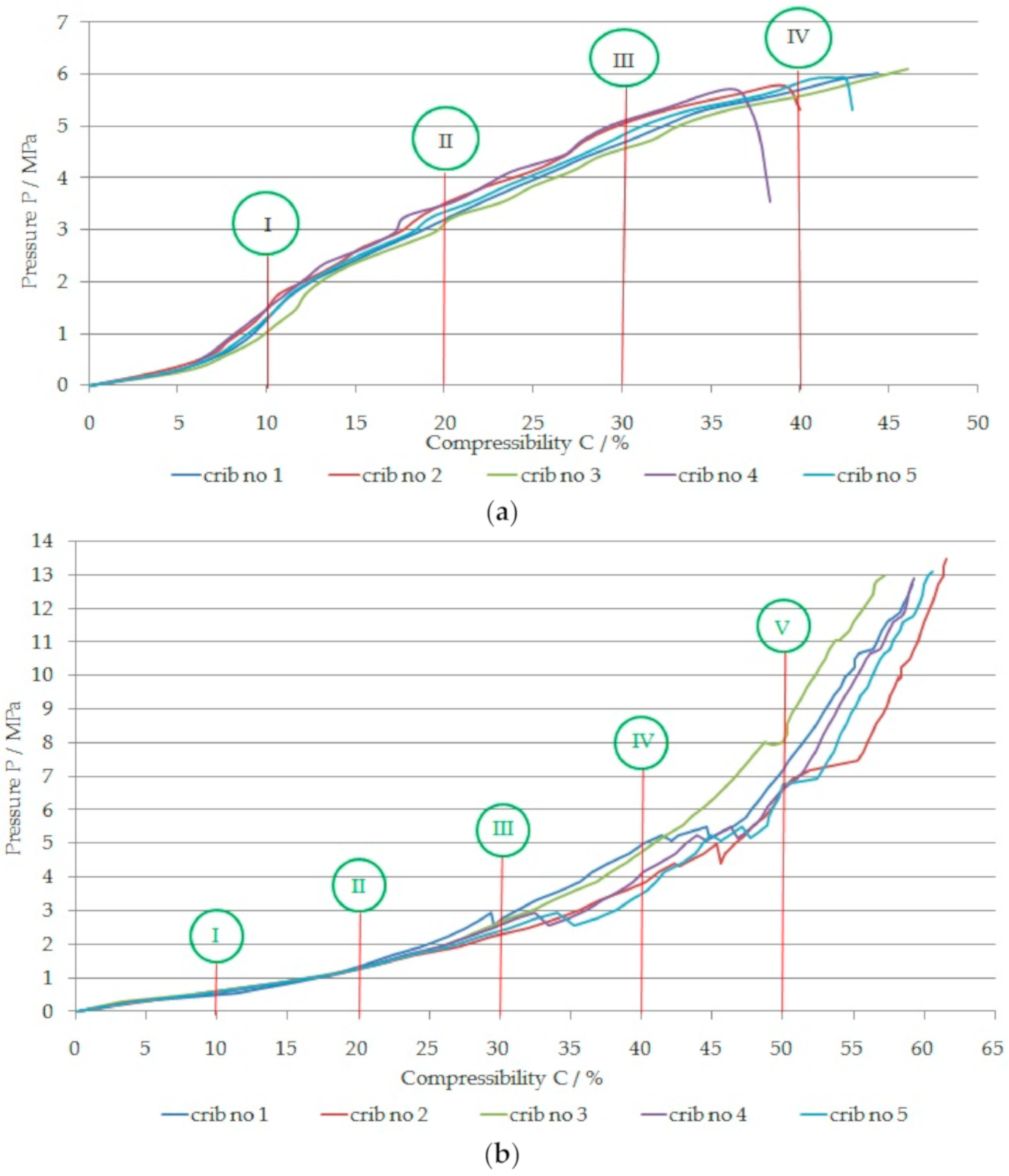
- M—Weibull modulus; it can be estimated from the formula [44]:where Cv is the coefficient of variation of the strength of the material, defined as the ratio of the standard deviation to the average value. It was assumed in this study that the volume of the four-point wooden crib model filled with waste rocks was 0.00150 m3 (Figure 7k–l); the average compressive strength determined experimentally under laboratory conditions for 10%, 20%, 30%, 40%, and 50% of compressibility is equal to 0.6, 1.4, 2.55, 4.25, and 7.31 MPa, respectively (Figure 10b). Taking into account that vertical stress in the mine is about 2.7 MPa, as the convergence of the excavation increases, the compressibility of the wooden cribs will increase, contributing to the improvement of stability conditions. Currently, in the Olkusz-Pomorzany mine, wooden cribs with round beams, as shown in Figure 3e, are used. Due to the fact that the exploitation in the aforementioned mine is carried out at a shallow depth of about 100 m below the ground surface and that there are no tremors or roof fall rocks in the mine (according to the research carried out by an expert for the support of mining excavations, it is possible to leave the rooms and roadways without a rock bolt support [48]), I performed model tests of wooden cribs indicating the possibility of their future consideration for use. The predicted volume of the wooden crib filled with gangue on a geometric scale of 1: 1 will be 205.78 m3, a material strength coefficient of variation (for models of cribs filled with gangue and compressive strength of 0.6, 1.4, 2.55, 4.25, and 7.31 MPa, respectively): Cv = 0.196, 0.084, 0.046, 0.083, 0.064, and Weibull modulus m is equal: 6.122, 14.285, 25.97, 14.45, and 18.75, respectively. Taking into account the above data, the predicted compressive strength of the wooden cribs filled with waste rocks on a geometric scale 1: 1 will be 0.09, 0.61, 1.62, 1.87, and 3.88 MPa for compressibility 10%, 20%, 30%, 40%, and 50%, respectively.
- b1—cost of filling material (sand)/PLN;
- b2—cost of transporting of filling material /PLN;
- b3—material cost of the filling pipeline /PLN;
- b4—cost of the medium (water) transporting filling material /PLN;
- b5—cost of construction the filling dams /PLN;
- b6—energy costs associated with pumping out filling water /PLN;
- b7—cost of building wooden dams with canvas /PLN;
- b8—cost associated with taking the gangue to the surface /PLN;
- b9—cost related to the storage of gangue on the surface /PLN.
- w1—material cost (wood for building cribs: either fresh or obtained from old railway sleepers)/PLN;
- w2—cost of transporting wooden cribs,/PLN;
- w3—costs of building wooden cribs,/PLN;
- w4—costs of transport of gangue from the mining department to the strips,/PLN.
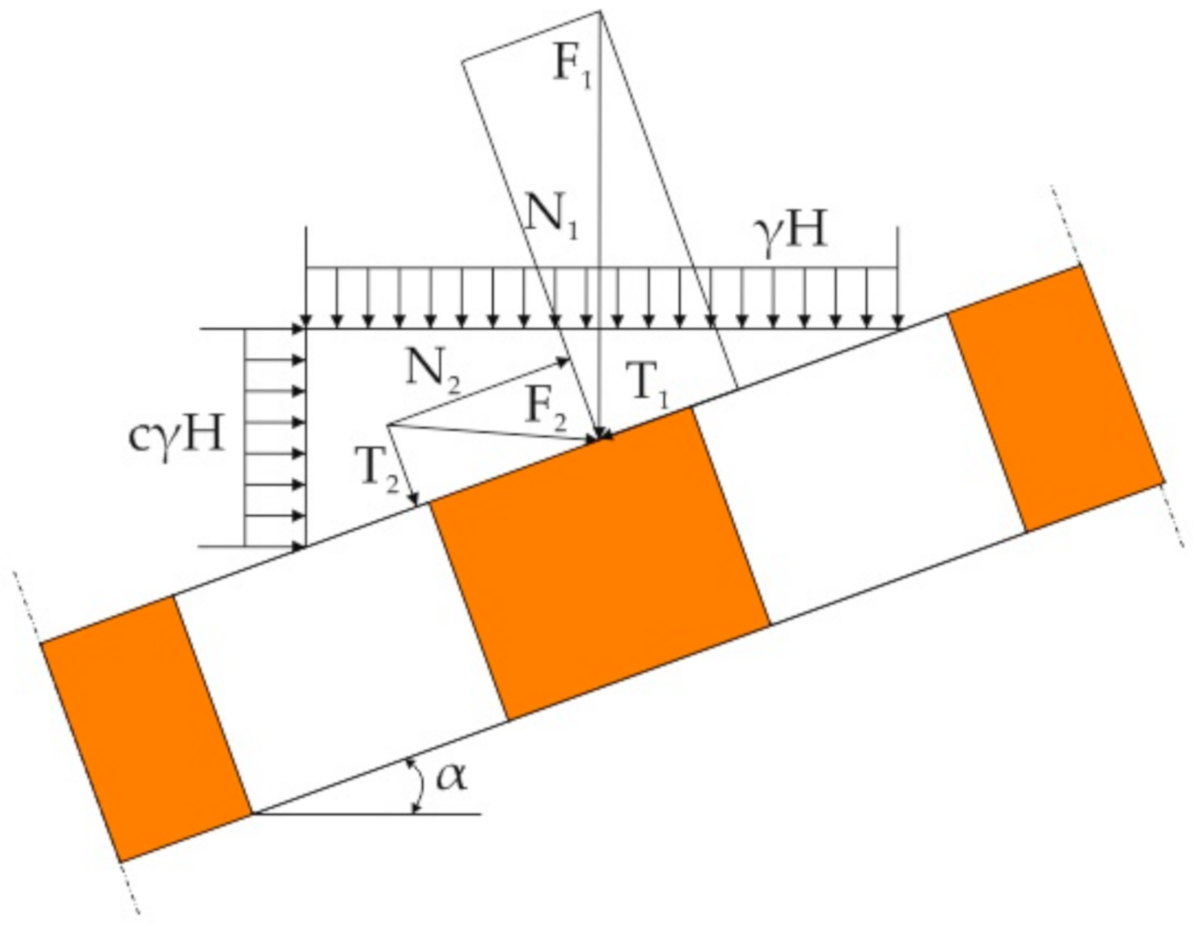
- F1, F2—vertical and horizontal force, respectively/N;
- N1, T1, N2, T2—components of vertical and horizontal forces (normal and shear loads), respectively /N;
- γ—density of adjacent rocks/N/m3;
- H—foundation depth of the crib/m;
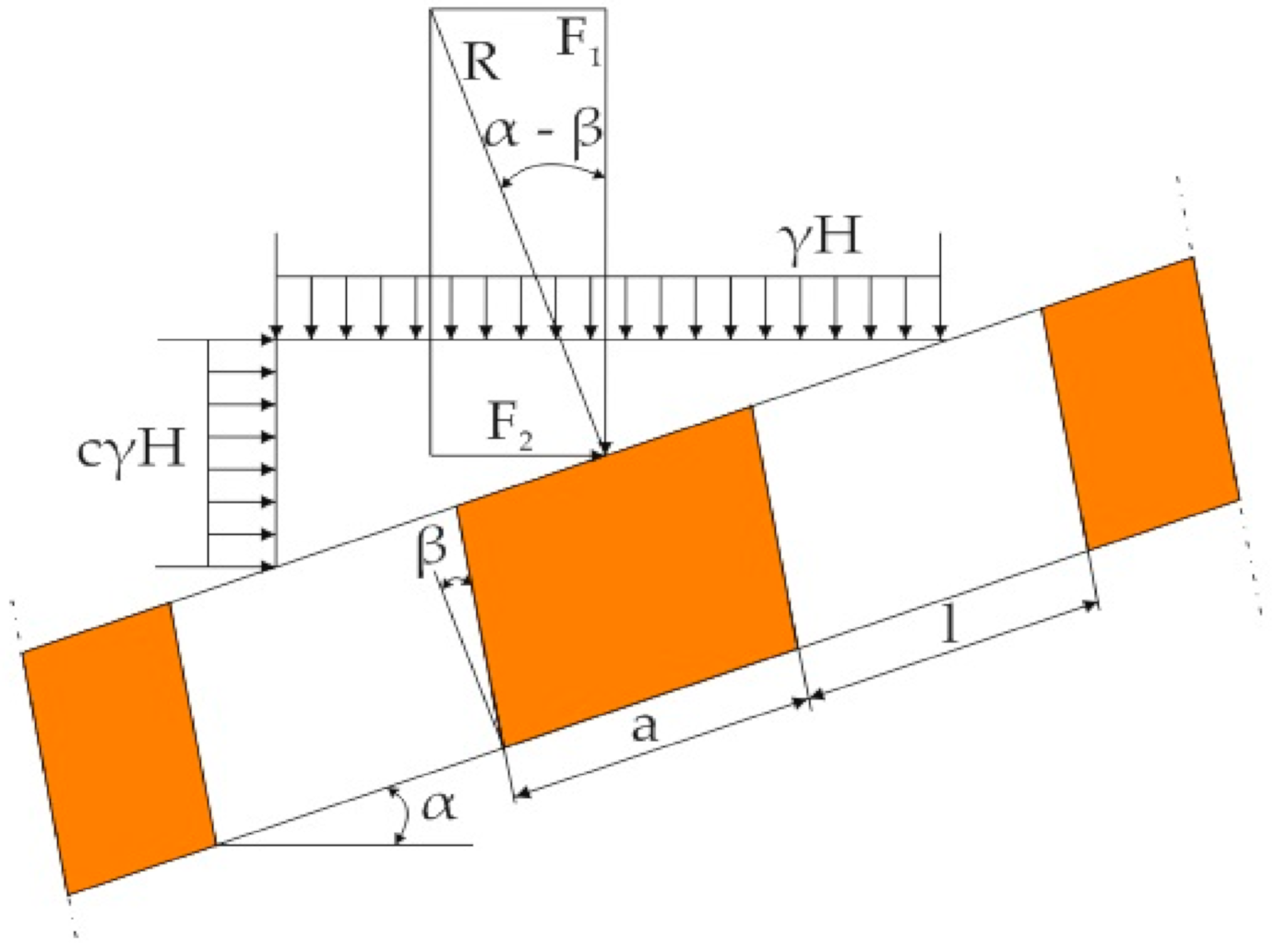
- l—strip width along the dip/m;
- a—crib width along the dip/m;
- l′—strip width along the strike/m;
- b—crib width along the strike/m;
- α—inclination angle of the orebody/°;
- c—horizontal expansion factor (for geological conditions of the Olkusz-Pomorzany mine, c = 0.5).
- S—roof area per crib /m2;
- S—crib surface /m2.
- kc—allowable compressive stress/MPa;
- kt—allowable shear stress/MPa.
- β—optimal angle of deflection (for α = 20°; β = 10°)/°;
- arctg—inverse tangent;
- α—inclination angle of the orebody/°.
- Cs—compressive strength of the crib /MPa.
- kα—factor of orebody inclination (for square cribs along the strike and along the dip, kα is equal 0.97 and 0.94 [50], respectively for α = 20°).
6. Conclusions
- Three-point empty wooden crib models have a higher load capacity of over 30% compared to the four-point crib.
- Filling the three-point crib made of 36 beams filled with gangue increases its load capacity by more than twice.
- Filling the four-point crib made of 20 beams filled with gangue increases its load capacity by over nine times.
- The four-point wooden crib filled with gangue has a load capacity greater by 57% compared to the filled three-point wooden crib.
Funding
Conflicts of Interest
References
- Chang, Q.; Chen, J.; Zhou, H.; Bai, J. Implementation of Paste Backfill Mining Technology in Chinese Coal Mines. Sci. World J. 2014, 2014, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Li, M.; Taheri, A.; Zhang, W.; Wu, Z.; Song, W. Properties and Application of Backfill Materials in Coal Mines in China. Minerals 2019, 9, 53. [Google Scholar] [CrossRef] [Green Version]
- Yildiz, T.D. Waste management costs (WMC) of mining companies in Turkey: Can waste recovery help meeting these costs? Resour. Policy. 2020, 68, 1–17. [Google Scholar] [CrossRef]
- Yang, G.-L.; Yang, R.-S.; Tong, Q.; Huo, C. Coalmine Green Mining with Gangue Backfilling Technique. Procedia Environ. Sci. 2011, 10, 1205–1209. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Guo, G. Surface Subsidence Control Mechanism and Effect Evaluation of Gangue-Backfilling Mining: A Case Study in China. Geofluids 2018, 2018, 1–9. [Google Scholar] [CrossRef]
- Sun, G.; Feng, T.; Liu, J. Survey on roof movement of the gangue backfill working face. J. Vibroeng. 2019, 21, 1107–1115. [Google Scholar] [CrossRef]
- Cao, W.; Wang, X.; Li, P.; Zhang, D.; Sun, C.; Qin, D. Wide Strip Backfill Mining for Surface Subsidence Control and Its Application in Critical Mining Conditions of a Coal Mine. Sustainability 2018, 10, 700. [Google Scholar] [CrossRef] [Green Version]
- Tai, Y.; Han, X.; Huang, P.; An, B. The mining pressure in mixed workface using a gangue backfilling and caving method. J. Geophys. Eng. 2019, 16, 1–15. [Google Scholar] [CrossRef]
- Ran, J.J. Safe mining practices under wide spans in underground non-caving mines—Case studies. Int. J. Min. Sci. Technol. 2019, 29, 535–540. [Google Scholar] [CrossRef]
- Yin, Y.; Zhao, T.; Zhang, Y.; Tan, Y.; Qiu, Y.; Taheri, A.; Jing, Y. An Innovative Method for Placement of Gangue Backfilling Material in Steep Underground Coal Mines. Minerals 2019, 9, 107. [Google Scholar] [CrossRef] [Green Version]
- Skrzypkowski, K. Case Studies of Rock Bolt Support Loads and Rock Mass Monitoring for the Room and Pillar Method in the Legnica-Głogów Copper District in Poland. Energies 2020, 13, 2998. [Google Scholar] [CrossRef]
- Skrzypkowski, K.; Korzeniowski, W.; Zagórski, K.; Zagórska, A. Modified Rock Bolt Support for Mining Method with Controlled Roof Bending. Energies 2020, 13, 1868. [Google Scholar] [CrossRef] [Green Version]
- Lingga, B.A.; Apel, D.B. Shear properties of cemented rockfills. J. Rock Mech. Geotech. Eng. 2018, 10, 635–644. [Google Scholar] [CrossRef]
- Jiang, H.; Fall, M.; Li, Y.; Han, J. An experimental study on compressive behaviour of cemented rockfill. Constr. Build. Mater. 2019, 213, 10–19. [Google Scholar] [CrossRef]
- Skrzypkowski, K.; Korzeniowski, W.; Poborska-Młynarska, K. Binding capability of ashes and dusts from municipal solid waste incineration with salt brine and geotechnical parameters of the cemented samples. Arch. Min. Sci. 2018, 63, 903–918. [Google Scholar] [CrossRef]
- Korzeniowski, W.; Poborska-Młynarska, K. Skrzypkowski, K. The idea of the recovery of municipal solid waste incineration (MSWI) residues in Kłodawa Salt Mine S.A. by filling the excavations with self-solidifying mixtures. Arch. Min. Sci. 2018, 63, 553–565. [Google Scholar] [CrossRef]
- Liu, W.; Xu, J.; Zhu, W.; Wang, S. A novel short-wall caving zone backfilling technique for controlling mining subsidence. Energy Sci. Eng. 2019, 7, 2124–2137. [Google Scholar] [CrossRef] [Green Version]
- Tesarik, D.R.; Seymour, J.B.; Yanske, T.R. Long-term stability of a backfilled room-and-pillar test section at the Buick Mine, Missouri, USA. Int. J. Rock Mech. Min. 2009, 48, 1182–1196. [Google Scholar] [CrossRef]
- Emad, M.Z.; Mitri, H.; Kelly, C. Dynamic model validation using blast vibration monitoring in mine backfill. Int. J. Rock Mech. Min. 2018, 107, 48–54. [Google Scholar] [CrossRef]
- ZGH Bolesław. Available online: https://www.zghboleslaw.pl (accessed on 21 September 2020).
- Timrite. Available online: http://www.timrite.co.za//products (accessed on 29 July 2020).
- Stratawordwide. Available online: https://www.strataworldwide.com/timber-roof-supports (accessed on 29 July 2020).
- Miningproducts. Available online: http://www.miningproducts.co.za/mining-products.html (accessed on 29 July 2020).
- Zhao, H. State-of-the-art of standing supports for gob-side entry retaining technology in China. J. S. Afr. Inst. Min. Metall. 2019, 119, 891–906. [Google Scholar] [CrossRef]
- Skrzypkowski, K. Decreasing mining losses for the room and pillar method by replacing the inter-room pillars by the construction of wooden cribs filled with waste rocks. Energies 2020, 13, 3564. [Google Scholar] [CrossRef]
- Korzeniowski, W.; Skrzypkowski, K.; Szumiński, A.; Zagórski, K. Laboratory investigations of the load capacity and load-strain characteristics of four-point cribs filled with waste rocks. Bull. Inst. Non-Ferrous Metals. 2015, 60, 303–308. [Google Scholar] [CrossRef]
- Skrzypkowski, K. The influence of dimension of mining crib model filled by waste rock on the course of load–displacement characteristic. Bull. Min. Energy Econ. Res. Inst. Pol. Acad. Sci. 2017, 99, 131–141. [Google Scholar]
- Ozbay, M.U.; Ryder, J.A.; Jager, A.J. The design of pillar systems as practiced in shallow hard-rock tabular mines in South Africa. J. S. Afr. Inst. Min. Metall 1995, 1/2, 7–18. [Google Scholar]
- Erasmus, P.N.; Smit, J. Assessment of Precast Cellular Lightweight Concrete (C.L.C.) Support Structures. In Proceedings of the International Symposium on Ground Support; Villaescusa, E., Windsor, C.R., Thompson, A.G., Eds.; Taylor & Francis Group: Kalgoorlie, Australia; Rottedram, The Netherlands, 1999; pp. 349–357. [Google Scholar]
- Pienaar, F.R.P.; Howell, M. The Rapid Loading of Packs. SANIRE Free State Symposium 2007. Redefining the Boundaries Part II; South African National Institute of Rock Engineering: Johannesburg, South Africa, 2007; pp. 1–10. [Google Scholar]
- Skrzypkowski, K. Strengthening the room excavation through the use of additional support in the form of wooden props in underground ore copper mines. Ores Non-Ferr. Met. Recycl. 2017, 5, 10–15. [Google Scholar]
- Brown, C.J. Development process for a higher capacity Propsetter® system. Int. J. Min. Sci. Technol. 2018, 28, 121–126. [Google Scholar] [CrossRef]
- Malan, D.F.; Napier, J.A.L. Rockburst support in shallow-dipping tabular stopes at great depth. Int. J. Rock Mech. Min. 2018, 112, 302–312. [Google Scholar] [CrossRef] [Green Version]
- Klemetti, T.M.; Sears, M.M.; Tulu, I.B. Design concerns of room and pillar retreat panels. Int. J. Min. Sci. Technol. 2017, 27, 29–35. [Google Scholar] [CrossRef]
- Strzelecki, Z. A Material Science Guide for Underground Construction of Mines; Śląsk Publishing House: Bytom, Poland, 1972; p. 21. [Google Scholar]
- Bańkowski, Z. Mechanic’s Guide; First Part; Scientific and Technical Publishers: Warszawa, Poland, 1988; p. 567. [Google Scholar]
- Solis, M.; Silveira, S. Technologies for chemical recycling of household plastics—A technical review and TRL assessment. Waste Manag. 2020, 105, 128–138. [Google Scholar] [CrossRef]
- The Bochnia Salt Mine. Available online: https://bochnia-mine.eu (accessed on 4 September 2020).
- The Wieliczka Salt Mine. Available online: https://www.wieliczka-saltmine.com (accessed on 4 September 2020).
- Li, M.; Zhang, J.; Sun, K.; Zhang, S. Influence of Lateral Loading on Compaction Characteristics of Crushed Waste Rock Used for Backfilling. Minerals 2018, 8, 552. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Y.; Meng, M.; Daouadji, A.; Chen, Q.; Wu, Z.; Jiang, X. Effects of particle size on crushing and deformation behaviors of rockfill materials. Geosci. Front. 2020, 11, 375–388. [Google Scholar] [CrossRef]
- Skrzypkowski, K. Compressibility of materials and backfilling mixtures with addition of solid wastes from flue-gas treatment and fly ashes. E3S Web Conf. 2018, 71, 1–6. [Google Scholar] [CrossRef]
- Skrzypkowski, K. The influence of room and pillar method geometry on the deposit utilization rate and rock bolt load. Energies 2019, 12, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Zweben, C. Designer’s corner. Is there a size effect in composites? Composites 1994, 25, 451–454. [Google Scholar] [CrossRef]
- Korzeniowski, W.; Skrzypkowski, K. Comparative investigations of the load capacity and load-strain characteristics of chocks with different filling. Mining Review. 2012, 68, 36–40. [Google Scholar]
- Korzeniowski, W.; Herezy, Ł.; Krazue, K.; Rak, Z.; Skrzypkowski, K. Rock Mass Monitoring Based on Analysis of Powered Support Response; AGH Publisher: Kraków, Poland, 2013; pp. 153–165. ISBN 978-83-7464-554-6. [Google Scholar]
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar]
- Regulation of the Minister of Energy of November 23, 2016 on detailed requirements for the operation of underground mining plants. Journal of Laws of the Republic of Poland, 9 June 2017; Item 1118.
- Hydrogeological Documentation of the Olkusz-Pomorzany Mine; Mining and Metallurgy Plant: Bukowno, Poland, 2020.
- Piechota, S. Technique of Underground Mining of Deposits; AGH Publisher: Kraków, Poland, 1988; p. 196. [Google Scholar]




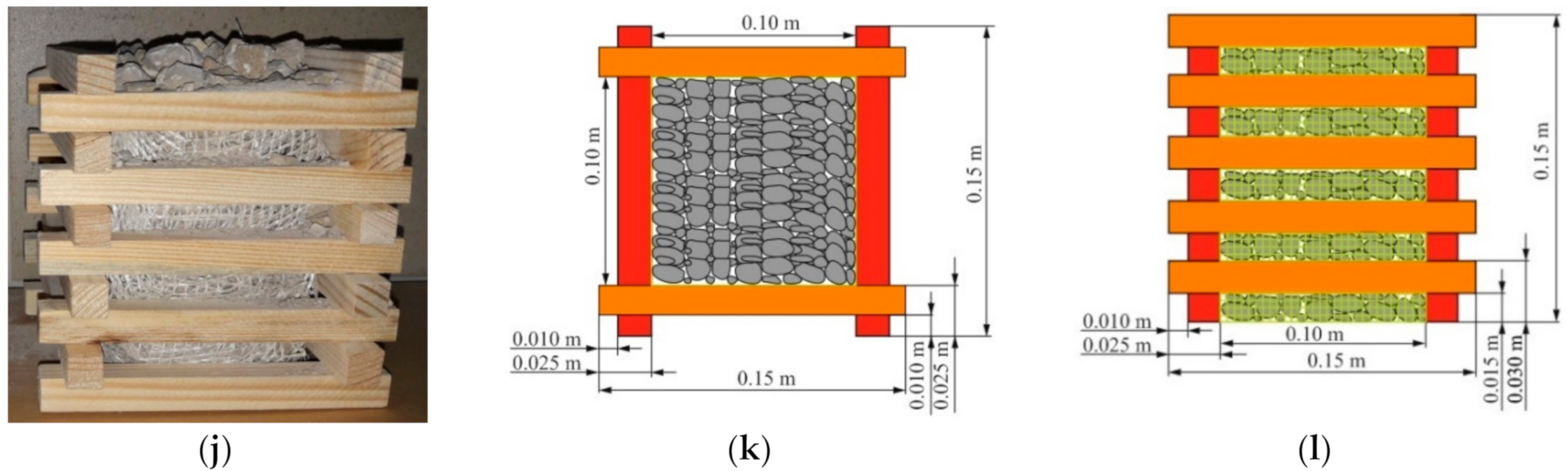

| Type of Wood | Volume Density [kg/m3] | Compressive Strength [MPa] | Tensile Strength [MPa] | Shear Strength [MPa] | |||
|---|---|---|---|---|---|---|---|
| Along the Fibers | Across the Fibers | Along the Fibers | Across the Fibers | Along the Fibers | Across the Fibers | ||
| Pine | 550 | 43.5 | 7.5 | 104 | 3 | 10 | 21 |
| Spruce | 470 | 43 | 6 | 90 | 2.7 | 6.7 | 22 |
| Beech | 730 | 53 | 9 | 135 | 7 | 8 | 29 |
| Oak | 710 | 47 | 11 | 90 | 4 | 7.5 | 27 |
| Fir | 450 | 31 | 4.5 | 84 | 2.3 | 5.1 | 27 |
| Larch | 690 | 42 | 6 | 107 | 2.3 | 9 | 23 |
| Crib Model | Maximal Load F/kN | Vertical Displacement Δl/mm (at Maximal Load) | Average Specific Strain ε/% | ||||
|---|---|---|---|---|---|---|---|
| from | to | Average | from | to | Average | ||
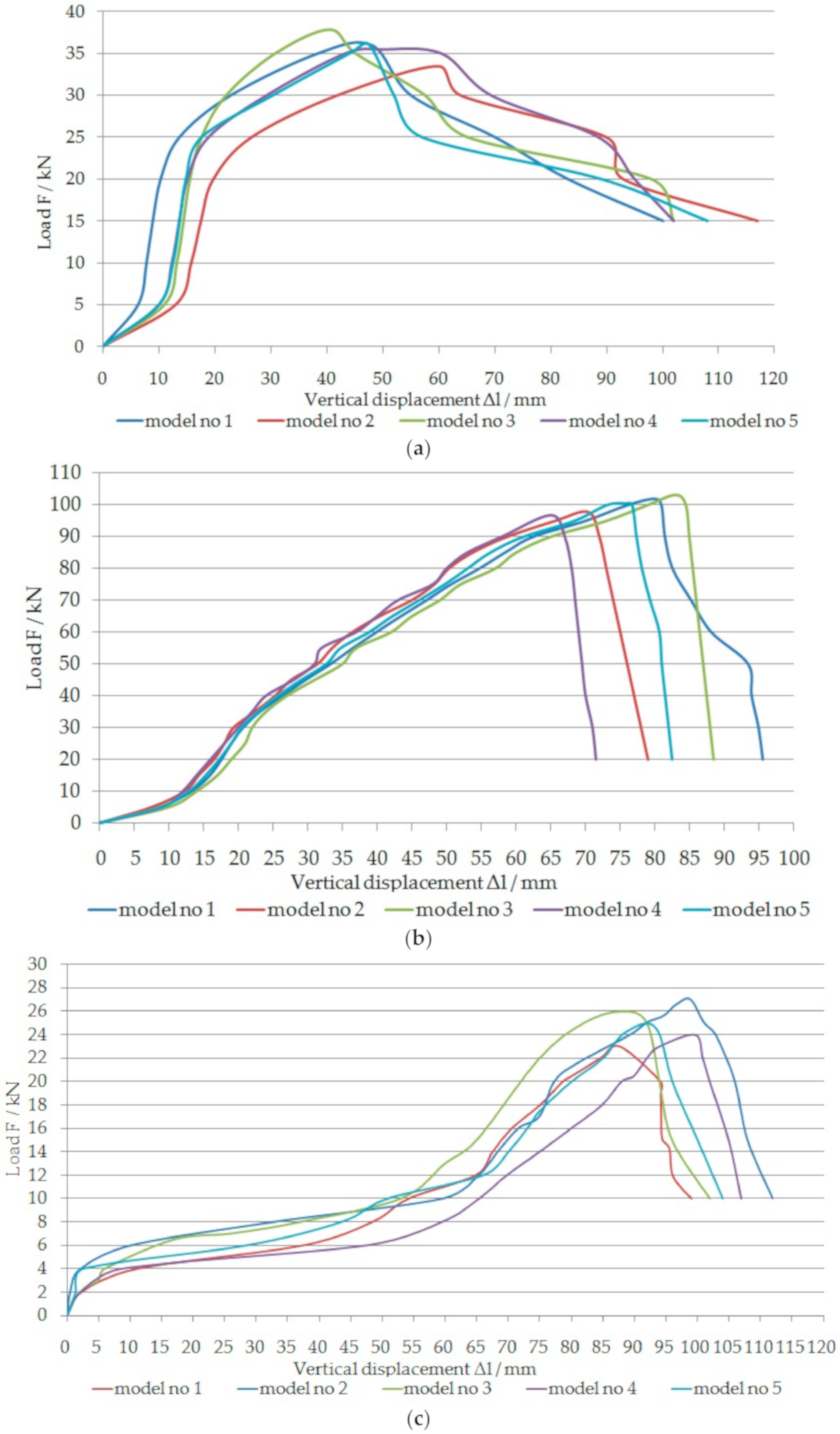
| three-point | 33.5 | 37.9 | 35.79 | 40.5 | 59.9 | 49.18 | 27.32 |
| four-point | 23 | 27 | 25 | 87.7 | 99.7 | 93.26 | 62.17 |
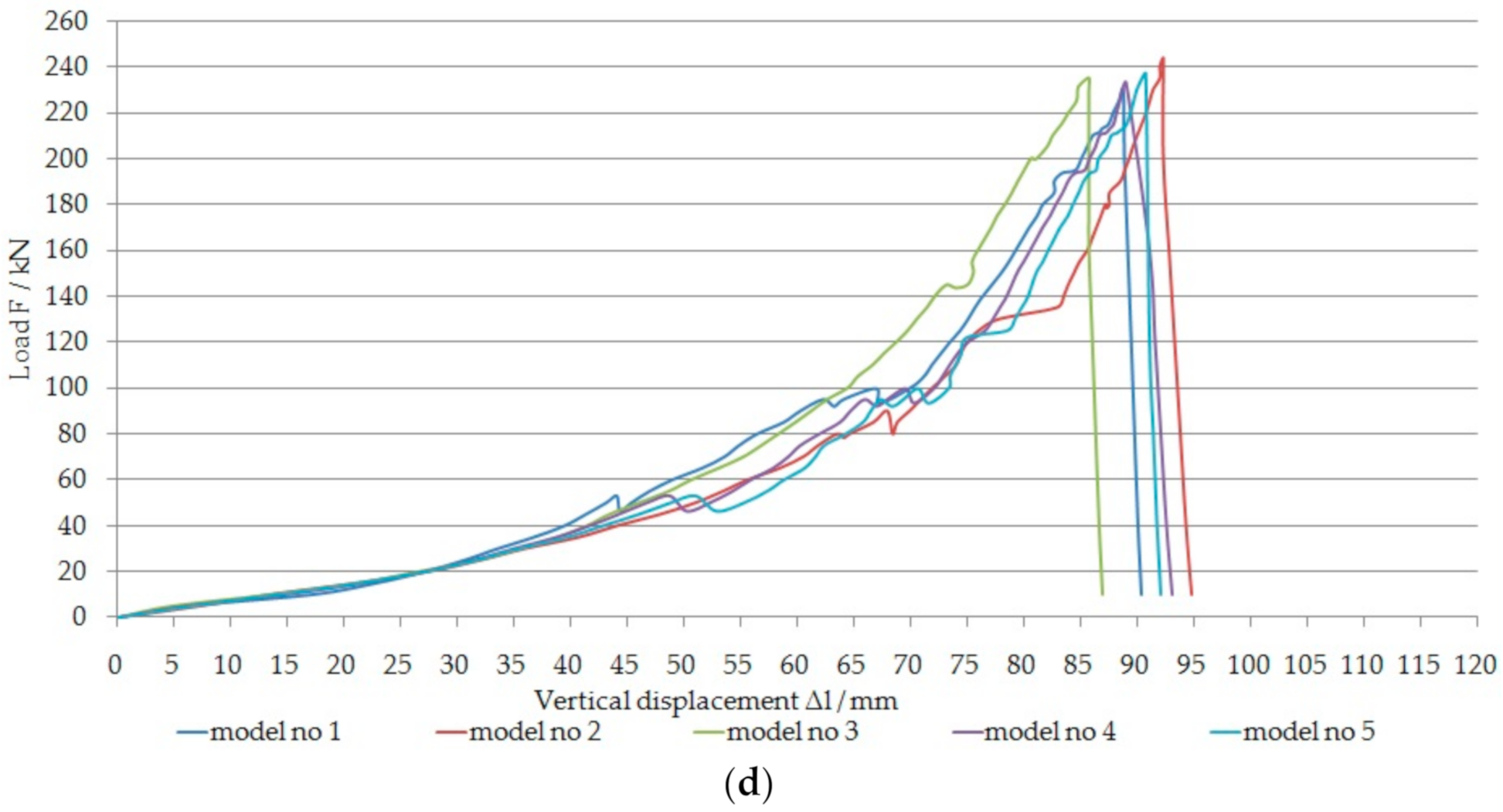
| three-point filled with gangue | 96.7 | 103.2 | 100.04 | 65 | 80 | 74.83 | 41.57 |
| four-point filled with gangue | 230 | 243 | 235.76 | 85.7 | 92.3 | 89.3 | 59.53 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skrzypkowski, K. Comparative Analysis of the Mining Cribs Models Filled with Gangue. Energies 2020, 13, 5290. https://doi.org/10.3390/en13205290
Skrzypkowski K. Comparative Analysis of the Mining Cribs Models Filled with Gangue. Energies. 2020; 13(20):5290. https://doi.org/10.3390/en13205290
Chicago/Turabian StyleSkrzypkowski, Krzysztof. 2020. "Comparative Analysis of the Mining Cribs Models Filled with Gangue" Energies 13, no. 20: 5290. https://doi.org/10.3390/en13205290
APA StyleSkrzypkowski, K. (2020). Comparative Analysis of the Mining Cribs Models Filled with Gangue. Energies, 13(20), 5290. https://doi.org/10.3390/en13205290





