Neutron Activation of Structural Materials of a Dry Storage System for Spent Nuclear Fuel and Implications for Radioactive Waste Management
Abstract
:1. Introduction
2. Methodology
2.1. Selection of Target Spent Nuclear Fuel and Dry Storage System
2.2. Assessment Framework for Neutron Activation of Components in DSSs
2.2.1. General Approach to Estimate Neutron Activation
2.2.2. Calculation of Neutron Source Terms in SNF to Be Stored
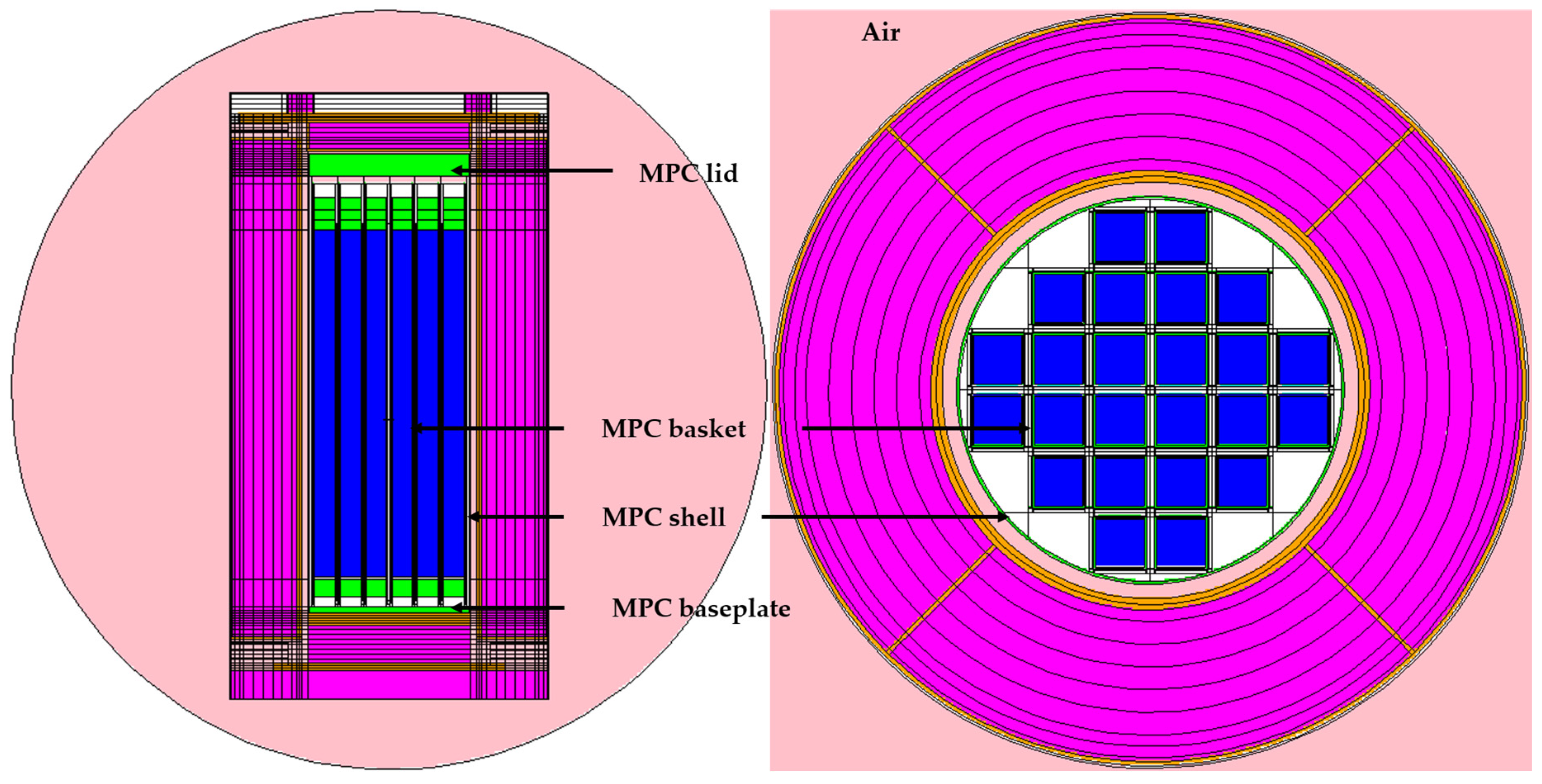
2.2.3. Calculation of Neutron Flux in Components of DSSs
2.2.4. Calculation of Modified Neutron Activation Cross-Section
2.2.5. Material Compositions and Impurity Contents of DSSs
2.2.6. Calculation of Neutron Activation in Components of DSSs
3. Results and Discussion
3.1. Neutron Activation Calculation for the HI-STORM 100 DSS—Reference Case
3.1.1. Calculation of Neutron Source Terms in SNF to Be Stored in the HI-STORM 100
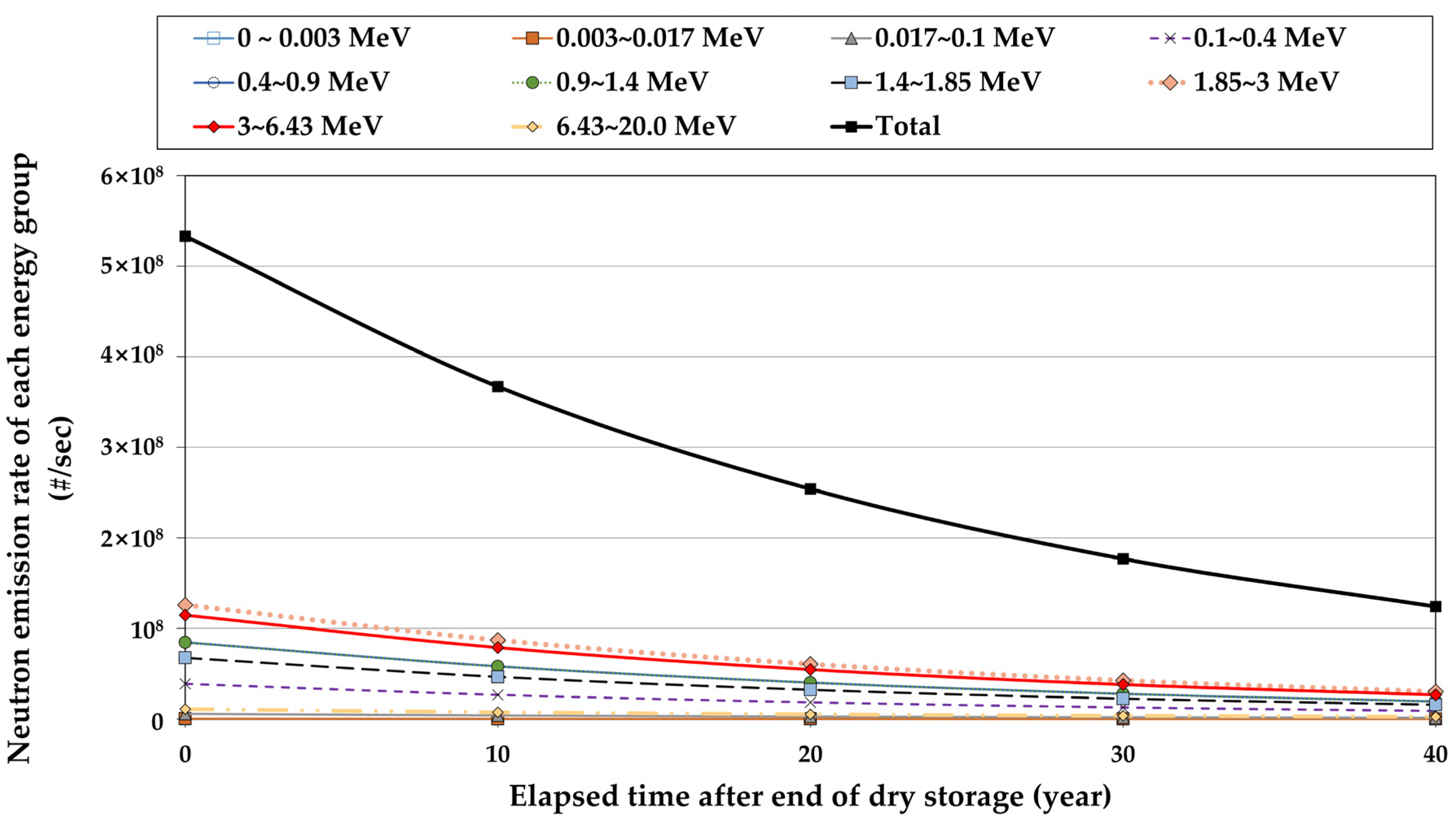
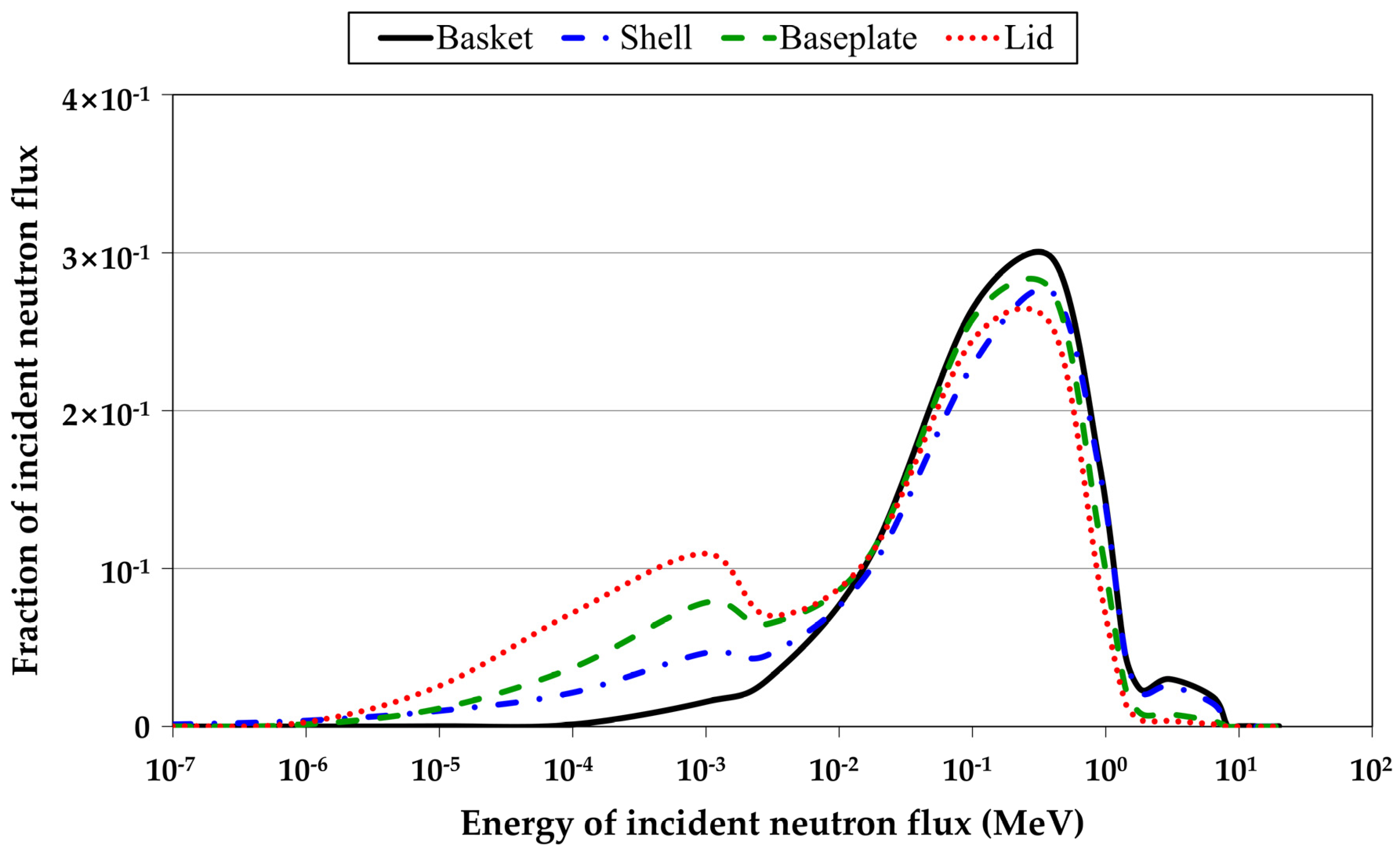
3.1.2. Calculation of Neutron Flux in Components of the HI-STORM 100
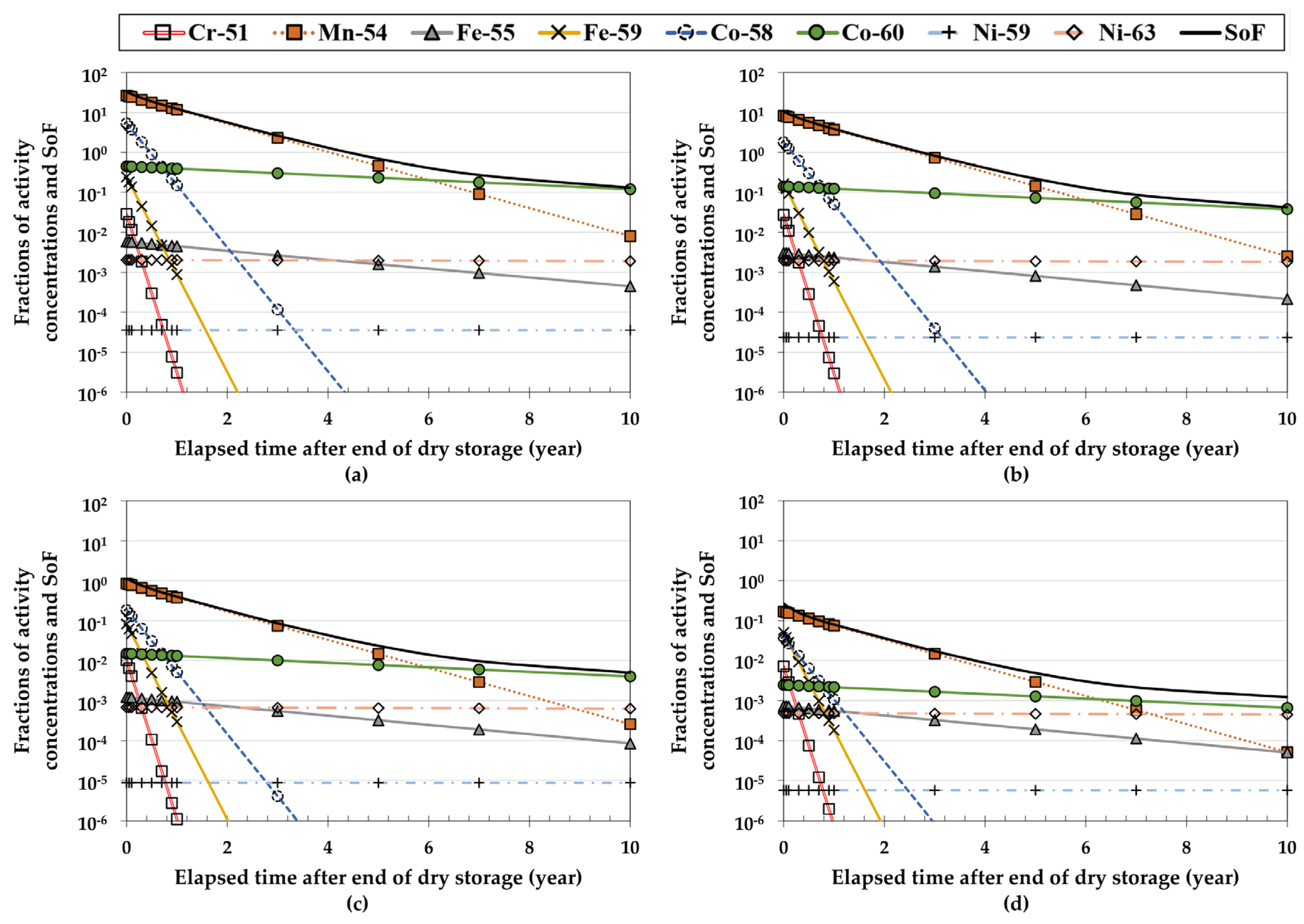
3.1.3. Calculation of Residual Radioactivity Concentration of Each Activation Product in the HI-STORM 100
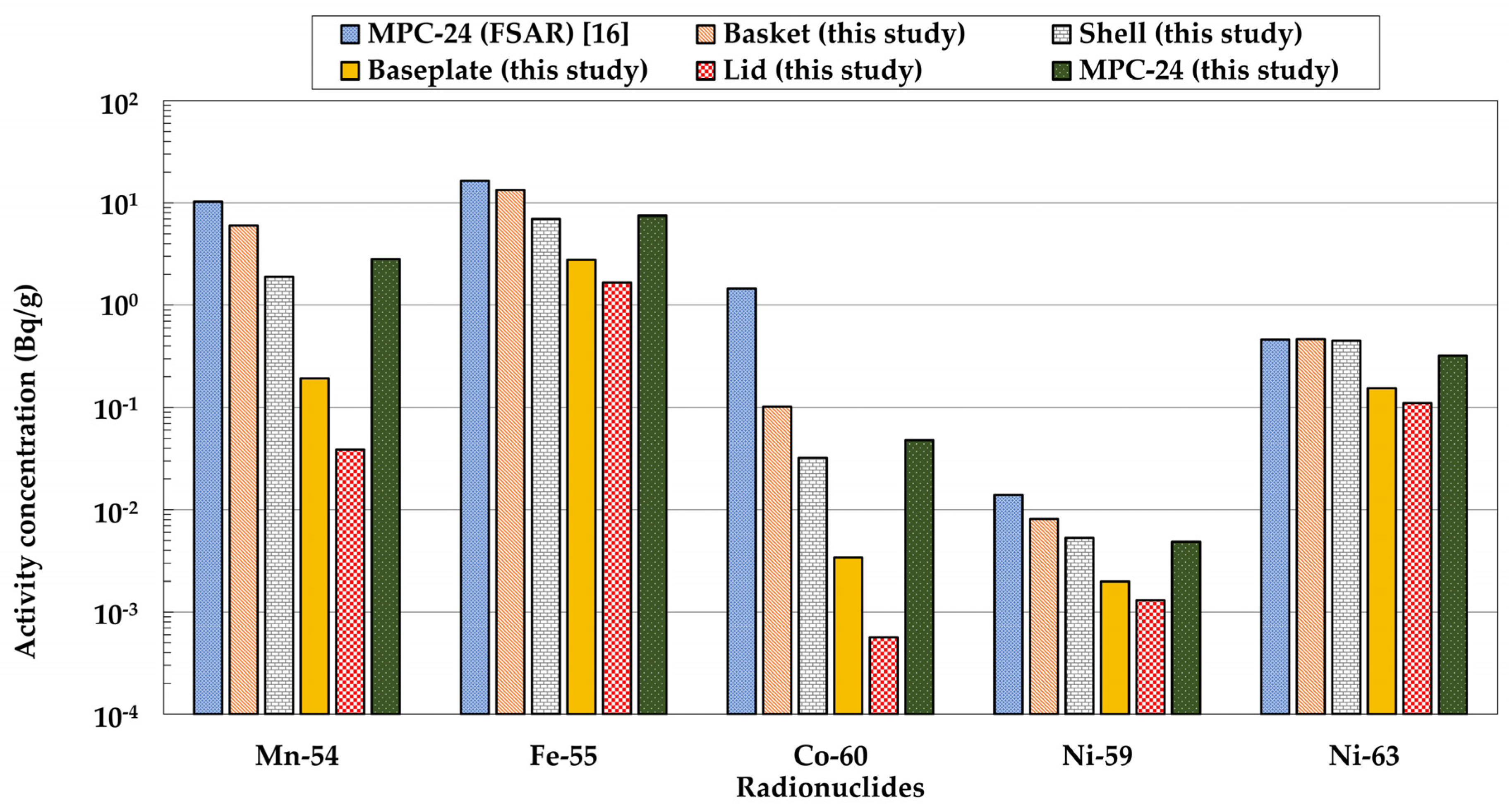
3.2. Application to and Comparison with a Representative Case in the HI-STORM 100 FSAR
3.3. Sensitivity Analysis for Design and/or Operation Parameters
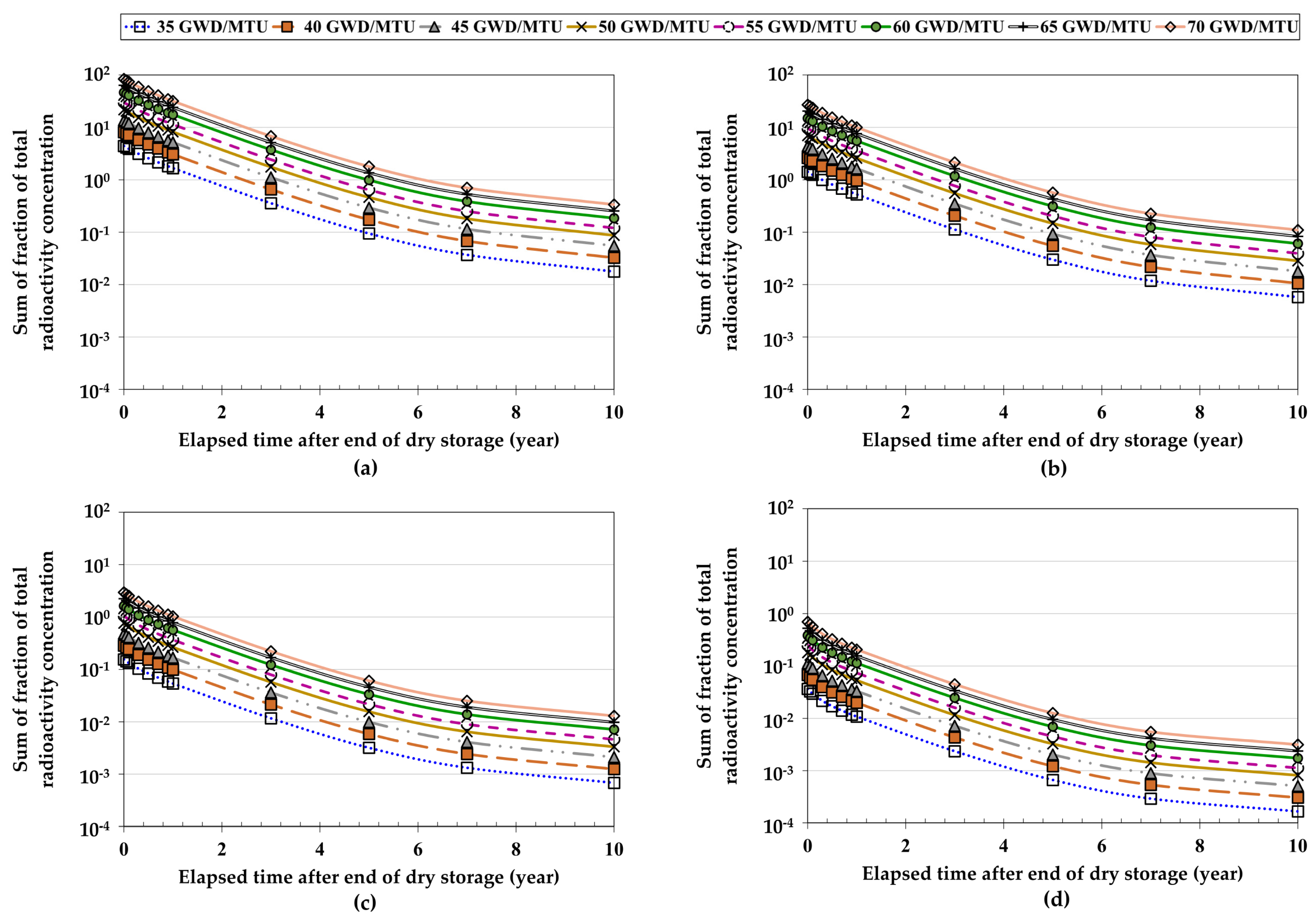
3.3.1. Effect of Fuel Burnup
3.3.2. Effect of Impurity Content
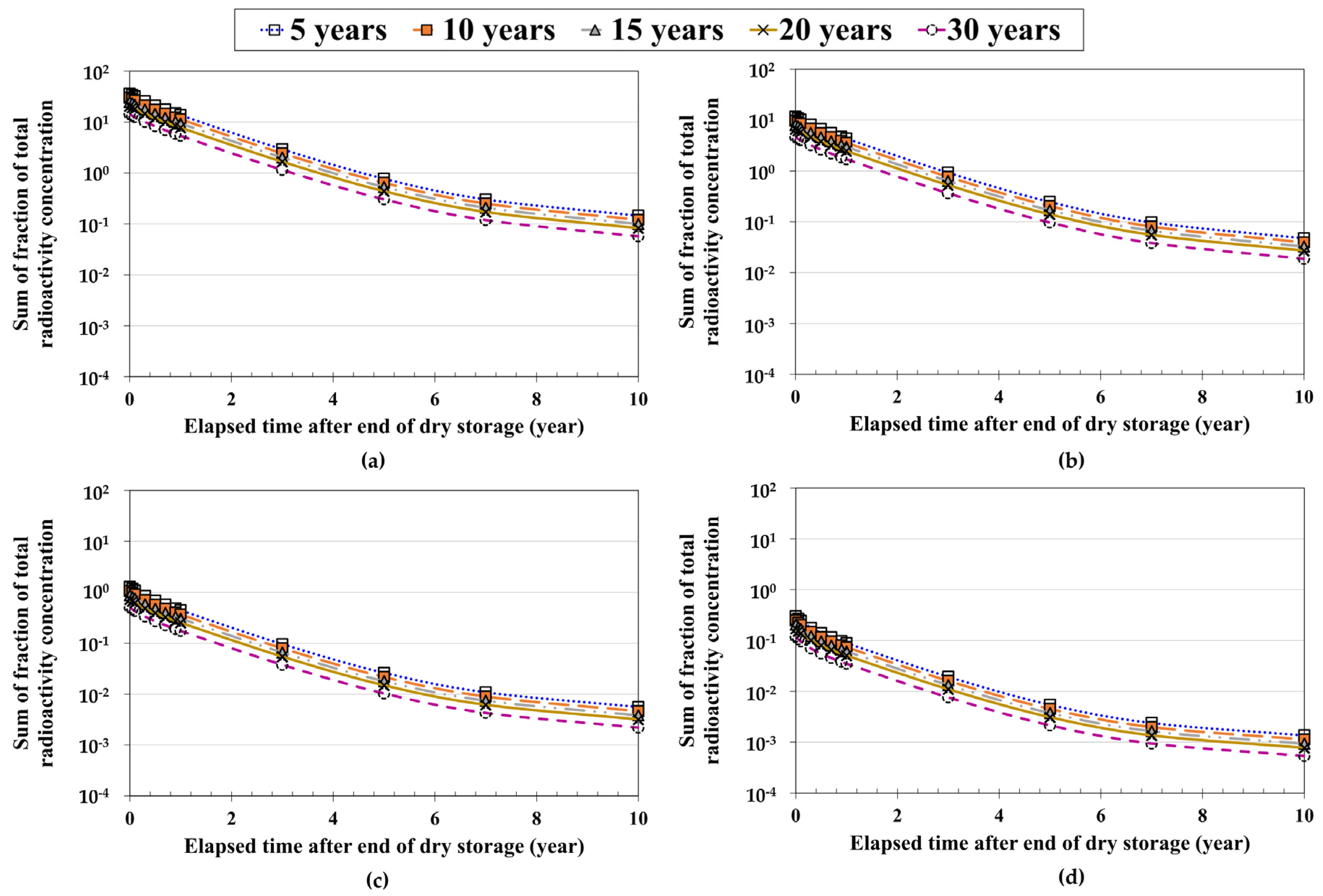
3.3.3. Effect of Fuel Cooling Time after Discharge
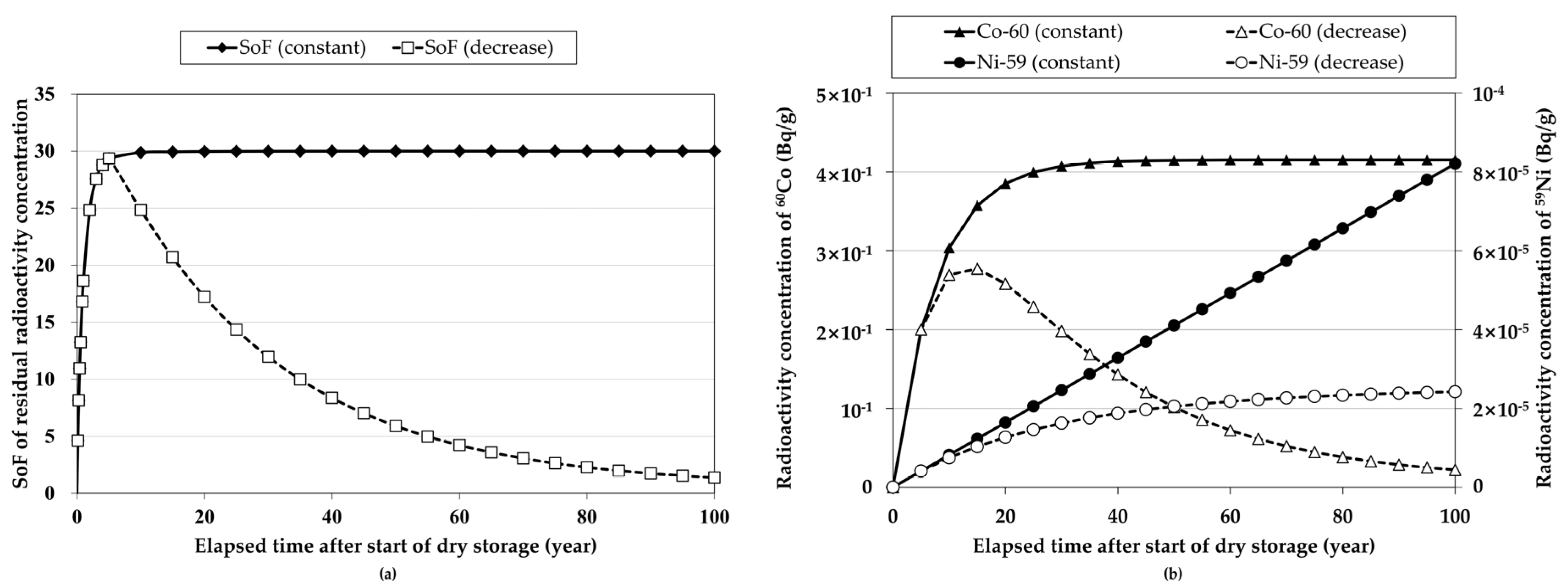
3.3.4. Effect of Dry Storage Time of SNF
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Howard, R.; Van den Akker, B. Consideration for disposition of dry cask storage system materials at end of storage system life. In Proceedings of the Symposium on Recycling of Metals arising from Operation and Decommissioning of Nuclear Facilities, Norrkoping, Sweden, 8–10 April 2014. [Google Scholar]
- United States Government Accountability Office. Spent Nuclear Fuel Accumulating Quantities at Commercial Reactors Present Storage and Other Challenges; United States Government Accountability Office: Washington, DC, USA, 2012.
- Romanato, L.S. Advantages of dry hardened cask storage over wet storage for spent nuclear fuel. In Proceedings of the 2011 International Nuclear Atlantic Conference—INAC 2011, Belo Horizonte, MG, Brazil, 24–28 October 2011. [Google Scholar]
- Pantelias, M.; Volmert, B. Activation neutronics for a swiss pressurized water reactor. Nucl. Technol. 2015, 192, 278–285. [Google Scholar] [CrossRef]
- Cha, G.Y.; Kim, S.Y.; Lee, J.M.; Kim, Y.S. The effects of impurity composition and concentration in reactor structure material on neutron activation inventory in pressurized water reactor. J. Nucl. Fuel Cycle Waste Technol. 2016, 14, 91–100. [Google Scholar] [CrossRef]
- Ahn, J.G.; Lee, M.H.; Ahn, H.C. Analysis of activation source terms of spent nuclear fuel rack for decommissioning of nuclear power plants. In Abstracts of Proceedings of the Korean Radioactive Waste Society Autumn 2013; Korean Radioactive Waste Society: Daejeon-si, Korea, 2013; Volume 11, pp. 135–136. [Google Scholar]
- United States Nuclear Regulatory Commission. Standard Review Plan for Spent Fuel Dry Storage Systems at a General License Facility; NUREG-1536, Revision 1; USNRC: Washington, DC, USA, 2010.
- International Atomic Energy Agency. Spent Fuel Storage and Transport Cask Decontamination and Modification; TECDOC-1081; IAEA: Vienna, Austria, 1999. [Google Scholar]
- United States Nuclear Regulatory Commission. Standard Review Plan for Dry Cask Storage Systems; NUREG-1536, Revision 0; USNRC: Washington, DC, USA, 1997.
- United States Nuclear Regulatory Commission. Standard Format and Content for a Topical Safety Analysis Report for a Spent Fuel Dry Storage Cask; Regulatory Guide 3.61, Revision 1; USNRC: Washington, DC, USA, 2010.
- United States Nuclear Regulatory Commission. Standard Review Plan. for Spent Fuel Dry Storage Facilities; NUREG-1567, Revision 1; USNRC: Washington, DC, USA, 2000.
- TLG Services, Inc. Decommissioning Cost Analysis for the Salem Generation Station; TLG Services, Inc.: Bridgewater, CT, USA, 2015. [Google Scholar]
- Welsch, J.M. 10 CFR 72.30 Diablo Canyon Independent Spent Fuel Storage Installation Decommissioning Cost Estimate. Available online: https://www.nrc.gov/docs/ML1835/ML18351A368.pdf (accessed on 20 June 2020).
- Transnuclear, Inc. TN-32 Final Safety Analysis Report; Transnuclear, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Transnuclear, Inc. Final Safety Analysis Report for the TN-68 Dry Storage Cask; Transnuclear, Inc.: New York, NY, USA, 2000. [Google Scholar]
- Holtec International. Final Safety Analysis Report for the HI-STORM 100 Cask System; Holtec International: Mount Laurel, NJ, USA, 2016. [Google Scholar]
- NAC International. Final Safety Analysis Report for the UMS Universal Storage System; NAC International: Peachtree Corners, GA, USA, 2016. [Google Scholar]
- Kim, T.-M.; Ku, J.-Y.; Dho, H.-S.; Cho, C.-H.; Ko, J.-H. Activation analysis of dual-purpose metal cask after the end of design lifetime for decommissioning. J. Nucl. Fuel Cycle Waste Technol. 2016, 14, 343–356. [Google Scholar] [CrossRef]
- International Atomic Energy Agency. Radiation Protection and Safety of Radiation Sources: International Basic Safety Standards; General Safety Requirements No. GSR Part 3; IAEA: Vienna, Austria, 2014. [Google Scholar]
- International Atomic Energy Agency. Methodologies for Assessing the Induced Activation Source Term for Use in Decommissioning Applications; Safety Reports Series No. 95; IAEA: Vienna, Austria, 2019. [Google Scholar]
- Kruijf, W.J.M.; Janssen, A.J. Detailed Resonance Absorption Calculations with the Monte Carlo Code MCNP and A Collision Probability Version of the Slowing Down Code ROLAIDS; Netherlands Energy Research Foundation ECN: Petten, The Netherlands, 1993. [Google Scholar]
- Sanghwa, S.; Jooho, W. A study on source term assessment of the Kori unit-1 reactor vessel. J. Nucl. Sci. Technol. 2004, 4, 86–89. [Google Scholar]
- Cho, D.-K.; Choi, H.-J.; Ahmed, R.; Heo, G. Radiological characteristics of decommissioning waste from a CANDU reactor. Nucl. Eng. Technol. 2011, 43, 583–592. [Google Scholar] [CrossRef] [Green Version]
- Noh, K.; Hah, C.J. Verification of MCNP/ORIGEN-2 model and preliminary radiation source term evaluation of Wolsung Unit 1. J. Nucl. Fuel Cycle Waste Technol. 2015, 13, 21–34. [Google Scholar]
- Jang, M.; Lim, J.M.; Kim, H.C.; Kim, C.-J. Inventory estimation of 36Cl and 41Ca in concrete of Kori Unit 1. J. Nucl. Fuel Cycle Waste Technol. 2019, 17, 121–126. [Google Scholar]
- Ministry of Trade, Industry & Energy (MoTIE). The Basic Plan on High-Level Radioactive Waste Management; MoTIE: Sejong-si, Korea, 2016.
- Robert, H.J., Jr. Dry Storage Cask Inventory Assessment; SRNL: Jackson, SC, USA, 2016. [Google Scholar]
- Korea Electric Power Corporation (KEPCO); Korea Hydro and Nuclear Power Co. (KHNP), Ltd. APR1400 Design Control Document Tier 2; KHNP: Gyeongju-si, Korea, 2018. [Google Scholar]
- Yuk, D.-S.; An, S.-M.; Jeong, H.-Y.; Lee, H.-J. Analysis of Standardized Data for Spent Fuel in Korea; KOFONS: Seongnam-si, Korea, 2016. [Google Scholar]
- Springman, R. Multi-purpose canisters for long-term interim storage. In Proceedings of the International Conference on Management of Spent Fuel from Nuclear Power Reactors: An Integrated Approach to the Back End of the Fuel Cycle, Vienna, Austria, 15–19 June 2015. [Google Scholar]
- United States Nuclear Regulatory Commission. Neutron Activation and Activation Analysis; NRC/HR-0751-H122; USNRC: Washington, DC, USA, 2011.
- Skutnik, S. ORIGEN-Based Nuclear Fuel Inventory Module for Fuel Cycle Assessment; University of Tennessee-Knoxville: Knoxville, TN, USA, 2017. [Google Scholar]
- Kryuchkov, E.F.; Opalovsky, V.A.; Tikhomirov, G.V. Comparative analysis of radiation characteristics from various types of spent nuclear fuel. In Proceedings of the International Conference on Supercomputing in Nuclear Applications SNA’2003, Paris, France, 22–24 September 2003. [Google Scholar]
- Bowman, S.M.; Gauld, I.C. OrigenArp Primer: How to Perform Isotopic Depletion and Decay Calculations with SCALE/ORIGEN; ORNL: Oak Ridge, TN, USA, 2010.
- Hermann, O.W.; Westfall, R.M. ORIGEN-S: Scale System Module to Calculate Fuel Depletion, Actinide Transmutation, Fission Product Buildup and Decay, and Associated Radiation Source Terms; NUREG/CR-0200, Revision 6; USNRC: Washington, DC, USA, 1998; Volume 2.
- Denise, B. Pelowitz. MCNPXTM User’s Manual Version 2.5.0; LANL: Los Alamos, NM, USA, 2005. [Google Scholar]
- Źerovnik, G.; Podvratnik, M.; Snoj, L. On normalization of fluxes and reaction rates in MCNP criticality calculations. Ann. Nucl. Energy 2014, 63, 126–128. [Google Scholar] [CrossRef]
- Hadd, K.; Nematolahi, M.; Golestani, A. VVER-1000 Cross-section Library Generation for ORIGEN-II based on MCNP Calculations. Int. J. Hydrogen Energy 2015, 40, 15158–15163. [Google Scholar] [CrossRef]
- Syarip, S.; Sutondo, T. Analytical method of atomic density determination of uranyl nitrate solution. J. Phys. Confer. Ser. 2018, 1090, 012036. [Google Scholar] [CrossRef]
- The American Society of Mechanical Engineers. An International Code 2019 ASME Boiler & Pressure Vessel Code Section II: Materials-Part A: Ferrous Material Specifications (Beginning to SA-450); ASME BPVC. II. A-2019; ASME: New York, NY, USA, 2019. [Google Scholar]
- Commission on Isotopic Abundances and Atomic Weights. Available online: https://www.ciaaw.org/atomic-weights.htm (accessed on 28 August 2020).
- Evans, J.C.; Lepel, E.L.; Sanders, R.W.; Wilkerson, C.L.; Silker, W.; Thomas, C.W.; Abel, K.H.; Robertson, D.R. Long-Lived Activation Products in Reactor Material; NUREG/CR-3474; USNRC: Washington, DC, USA, 1984.
- Croff, A.G. A User’s Manual for the ORIGEN2 Computer Code; ORNL: Oak Ridge, TN, USA, 1980.
- Ullah, S.; Awan, S.E.; Mirza, N.M.; Mirza, S.M. Source term evaluation for the upgraded LEU Pakistan research Reactor-1 under severe accidents. Nucl. Eng. Des. 2010, 240, 3740–3750. [Google Scholar] [CrossRef]
- Wagner, J.C.; Dehart, M.D. Review of Axial Burnup Distribution Considerations for Burnup Credit Calculations; ORNL: Oak Ridge, TN, USA, 1999.
- McAlister, D.R. Neutron Shielding Materials Revision 2.1; 1955 University Lane Lisle: Lisle, IL, USA, 2016. [Google Scholar]
- Koning, A.J.; Rochman, D.; Sublet, J.; Dzysiuk, N.; Fleming, M.; Van der Marck, S. TENDL: Complete nuclear data library for innovative nuclear science and technology. Nucl. Data Sheets 2019, 155, 1–55. [Google Scholar] [CrossRef]
- Zhang, T.; Xiong, J.; Liu, X.; Chai, X.; Li, W.; Cheng, X. Conceptual design of an innovative reduced moderation thorium-fueled small modular reactor with heavy-water coolant. Int. J. Energy Res. 2019, 43, 8286–8298. [Google Scholar] [CrossRef]
- Bevard, B.B.; Wagner, J.C.; Parks, C.V.; Aissa, M. Review of Information for Spent Nuclear Fuel Burnup Confirmation; NUREG/CR-6998; USNRC: Washington, DC, USA, 2009.
- Dho, H.-S.; Kim, T.-M.; Cho, C.-H. The evaluation of minimum cooling period for loading of PWR spent nuclear fuel of a dual purpose metal cask. J. Nucl. Fuel Cycle Waste Technol. 2016, 14, 411–422. [Google Scholar]
- Posey, J.C. Curium-244 Isotopic Power Fuel—Chemical Recovery from Commercial Power Reactor Fuels; ORNL: Oak Ridge, TN, USA, 1973.
- The Organisation for Economic Co-Operation and Development Nuclear Energy Agency. Decommissioning Considerations for New Nuclear Power Plants; NEA No.6833; OECD/NEA: Paris, France, 2010. [Google Scholar]
- International Atomic Energy Agency. Managing the Unexpected in Decommissioning; IAEA Nuclear Energy Series No. NW-T-2.8; IAEA: Vienna, Austria, 2016. [Google Scholar]
- TN Americas LLC. NUHOMS® EOS System Final Safety Analysis Report; TN Americas LLC: Columbia, MD, USA, 2017. [Google Scholar]
- Bare, W.C.; Torgerson, L.D.; Kenneally, R.M. Dry Cask Storage Characterization Project-Phase 1: CASTOR V/21 Cask Opening and Examination; NUREC/CR-6745; USNRC: Washington, DC, USA, 2001.
- The Organisation for Economic Co-operation and Development Nuclear Energy Agency. The Safety of Long-Term Interim Storage Facilities in NEA Member Countries; NEA/CSNI/R(2017)4; OECD/NEA: Paris, France, 2017. [Google Scholar]
- Podgoršak, E.B. Activation of nuclides. In Radiation Physics for Medical Physicists, 2nd ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 281–311. [Google Scholar]
- United States Nuclear Regulatory Commission. Generic Environmental Impact Statement for Continued Storage of Spent Nuclear Fuel; NUREG-2157; USNRC: Washington, DC, USA, 2014; Volume 1.
- Korea Radioactive Waste Agency. Development of a National-Level Spent Fuel Management Standardization System; Korea Radioactive Waste Agency: Gyeongju-si, Korea, 2016. [CrossRef]



| Item | Commercial DSSs | Past Study [18] | |||
|---|---|---|---|---|---|
| TN-32 [14] | TN-68 [15] | HI-STORM 100 [16] | NAC UMS [17] | ||
| SNF source term calculation model | SAS2H and ORIGEN-S | SAS2H and ORIGEN-S | SAS2H and ORIGEN-S | SAS2H | ORIGEN-S |
| Neutron transport calculation model | XSDRN-PM | XSDRN-PM | MCNP-4A | N/A | MCNP5 |
| Activation cross-section library | ORIGEN-2 PWRU | ORIGEN-2 BWRU | N/A | N/A 1 | Modified ORIGEN-2 PWRU50 |
| Material of canister | Stainless steel 304 | Stainless steel 304 | Stainless steel 304 | Stainless steel 304 | Stainless steel 304 |
| Target radionuclides | 51Cr, 54Mn, 55Fe, 59Fe, 58Co, 60Co, 59Ni, 63Ni | 51Cr, 54Mn, 55Fe, 59Fe, 58Co, 60Co, 59Ni, 63Ni | 54Mn, 55Fe, 60Co, 59Ni, 63Ni | 54Mn, 55Fe, 60Co, 59Ni, 63Ni | 51Cr, 54Mn, 55Fe, 59Fe, 58Co, 60Co, 59Ni, 63Ni |
| 400 (Basket) | 32 (Basket) | 117 (Canister) | 50 (Canister bottom) | 4.3 (Basket) | |
| Fuel type | PWR 17 × 17 (WH) | BWR 7 × 7 (GE) | PWR 15 × 15 (B&W) | PWR 17 × 17 (WH) | PWR 17 × 17 (WH) |
| Fuel burnup (GWD/MTU) | 45 | 40 | 70 | 40 | 45 |
| Initial enrichment (wt % of 235U) | 3.5 | 3.3 | 4.8 | 3.7 | 4.5 |
| Cooling time (years) | 7 | 10 | 5 | 5 | 10 |
| Element composition | Given | Given | Given | N/A | Given |
| Isotope composition | N/A | N/A | N/A | N/A | N/A |
| Impurities data | N/A | N/A | N/A | N/A | Given |
| Item | Condition | Reference |
|---|---|---|
| Fuel type | PWR 16 × 16 (CE) UO2 | [28] |
| Burnup | 55 GWD/MTU | [29] |
| Initial enrichment | 4.2 wt% of 235U | [29] |
| Refueling intervals | 540 days (18 months) | [28] |
| Cooling time after discharge from reactor core | 10 years | Assumed in this study |
| Component or Object | Dimension 1 (mm) |
|---|---|
| Concrete overpack | 3366 (OD) × 5874 (H) |
| Inner cavity | 1867 (OD) × 4839 (H) |
| MPC | 1737 (OD) × 4839 (H) |
| Shell | 1737 (OD) × 1711 (ID) × 4839 (H) |
| Baseplate | 1711 (OD) × 635 (H) |
| Lid | 1711 (OD) × 2413 (H) |
| Boundary condition 2 | 4000 (from DSS center) |
| Element | Isotope | Isotopic Composition | Element | Isotope | Isotopic Composition |
|---|---|---|---|---|---|
| C | 12C | 7.914 × 10−4 | S | 32S | 2.850 × 10−4 |
| 13C | 8.560 × 10−6 | Mn | 55Mn | 2.000 × 10−2 | |
| N | 14N | 1.000 × 10−3 | Fe | 54Fe | 4.018 × 10−2 |
| Si | 28Si | 6.917 × 10−3 | 56Fe | 6.330 × 10−1 | |
| 29Si | 3.514 × 10−4 | 57Fe | 1.457 × 10−2 | ||
| 30Si | 2.319 × 10−4 | 58Fe | 1.939 × 10−3 | ||
| P | 31P | 4.500 × 10−4 | Ni | 58Ni | 6.297 × 10−2 |
| Cr | 50Cr | 8.256 × 10−3 | 60Ni | 2.426 × 10−2 | |
| 52Cr | 1.592 × 10−1 | 61Ni | 1.054 × 10−3 | ||
| 53Cr | 1.805 × 10−2 | 62Ni | 3.362 × 10−3 | ||
| 54Cr | 4.494 × 10−3 | 64Ni | 8.562 × 10−4 |
| Radionuclide | Half-Life | Major Activation Reaction | Clearance Level [19] |
|---|---|---|---|
| 51Cr | 27.7 days | 50Cr51Cr | |
| 54Mn | 312.3 days | 54Fe54Mn | |
| 55Fe | 2.74 years | 54Fe55Fe | |
| 59Fe | 44.5 days | 58Fe59Fe | |
| 58Co | 70.86 days | 58Ni58Co | |
| 60Co | 5.27 years | 60Ni60Co | |
| 59Ni | 76,000 years | 58Ni59Ni | |
| 63Ni | 100.1 years | 62Ni63Ni |
| Reaction Type | Cross-Section in PWRU50 (Barn) | Modified Cross-Section (Barn) | Ratio of Modified to Built-In Cross-Section | ||
|---|---|---|---|---|---|
| Basket | Lid | Basket | Lid | ||
| 50Cr51Cr | 1.25 | 3.18 × 10−2 | 1.28 × 10−1 | 2.97% | 10.22% |
| 54Fe54Mn | 2.05 × 10−2 | 8.35 × 10−3 | 6.87 × 10−4 | 40.68% | 3.35% |
| 54Fe55Fe | 1.80 × 10−1 | 1.65 × 10=2 | 2.73 × 10−2 | 9.15% | 15.13% |
| 58Fe59Fe | 1.07 × 10−1 | 1.53 × 10−2 | 4.07 × 10−2 | 14.36% | 38.17% |
| 60Ni60Co | 6.21 × 10−4 | 2.49 × 10−4 | 1.76 × 10−5 | 40.07% | 2.83% |
| 58Ni59Ni | 3.60 × 10−1 | 2.18 × 10−2 | 4.43 × 10−2 | 6.04% | 12.30% |
| 58Ni58Co | 2.15 × 10−2 | 1.13 × 10−2 | 1.04 × 10−3 | 52.55% | 4.86% |
| 62Ni63Ni | 1.12 | 3.16 × 10−2 | 9.52 × 10−2 | 2.82% | 8.51% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.G.; Cheong, J.H. Neutron Activation of Structural Materials of a Dry Storage System for Spent Nuclear Fuel and Implications for Radioactive Waste Management. Energies 2020, 13, 5325. https://doi.org/10.3390/en13205325
Lee SG, Cheong JH. Neutron Activation of Structural Materials of a Dry Storage System for Spent Nuclear Fuel and Implications for Radioactive Waste Management. Energies. 2020; 13(20):5325. https://doi.org/10.3390/en13205325
Chicago/Turabian StyleLee, Se Geun, and Jae Hak Cheong. 2020. "Neutron Activation of Structural Materials of a Dry Storage System for Spent Nuclear Fuel and Implications for Radioactive Waste Management" Energies 13, no. 20: 5325. https://doi.org/10.3390/en13205325
APA StyleLee, S. G., & Cheong, J. H. (2020). Neutron Activation of Structural Materials of a Dry Storage System for Spent Nuclear Fuel and Implications for Radioactive Waste Management. Energies, 13(20), 5325. https://doi.org/10.3390/en13205325





