Longitudinal Modelling and Control of In-Wheel-Motor Electric Vehicles as Multi-Agent Systems
Abstract
:1. Introduction
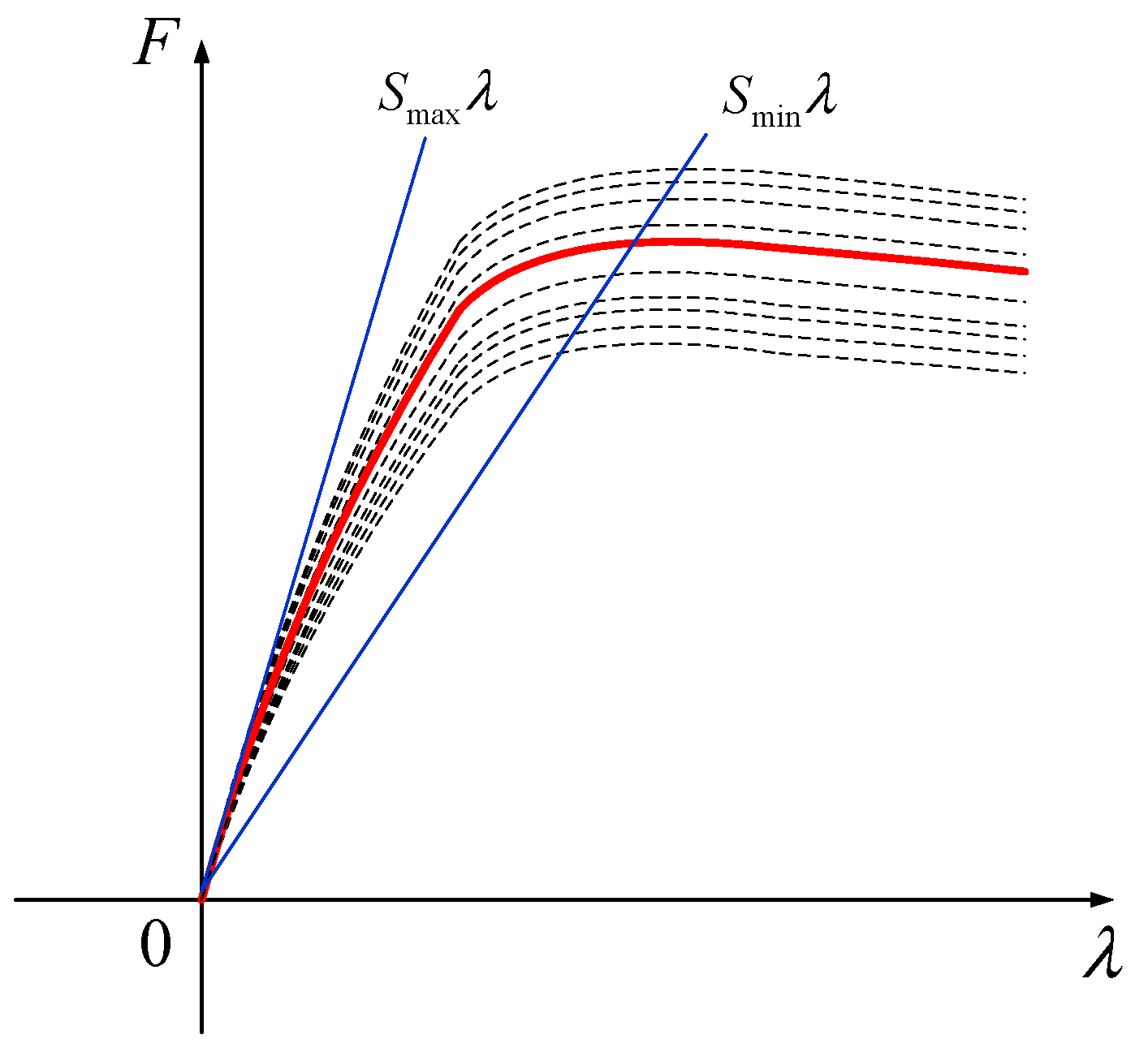
2. Longitudinal Dynamics of Vehicle
3. Motivating Example
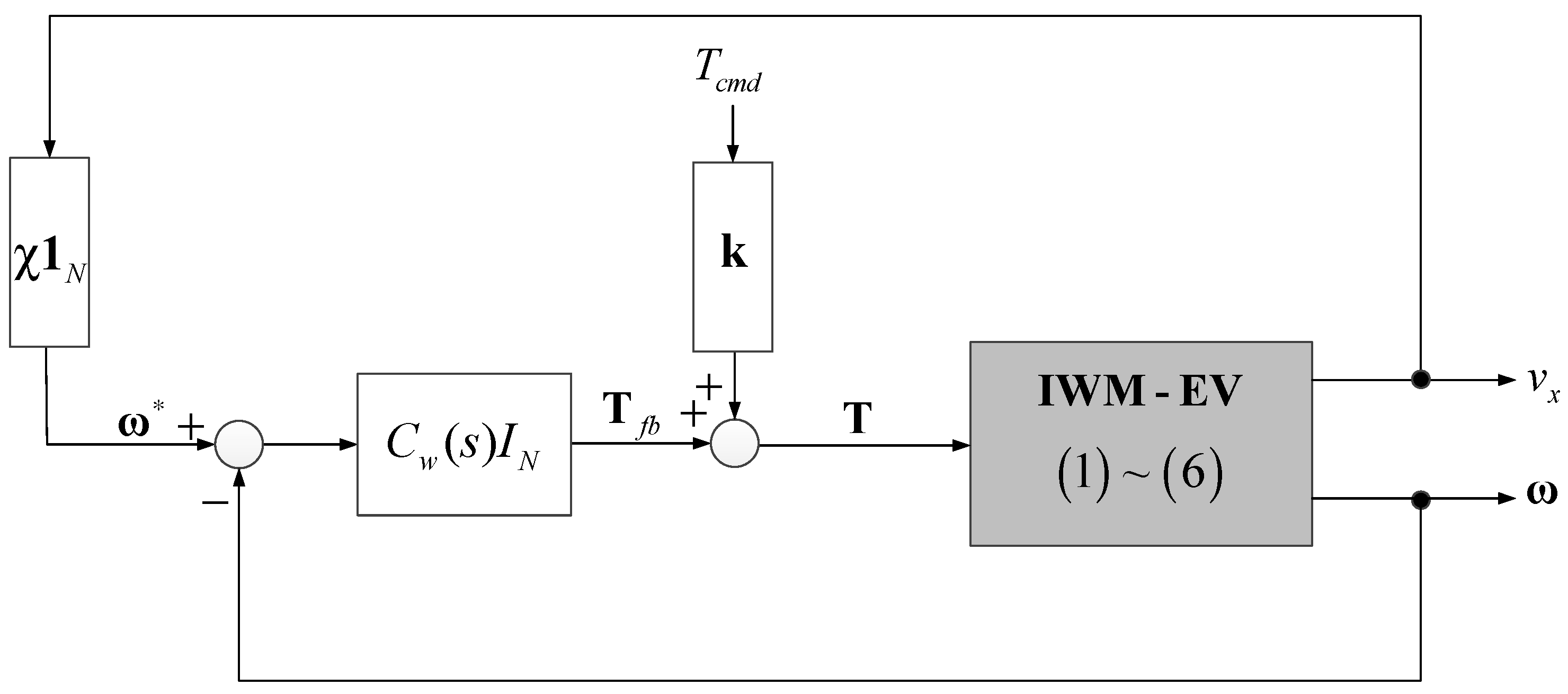
3.1. Anti-Slip Control Based on Wheel Velocity Control
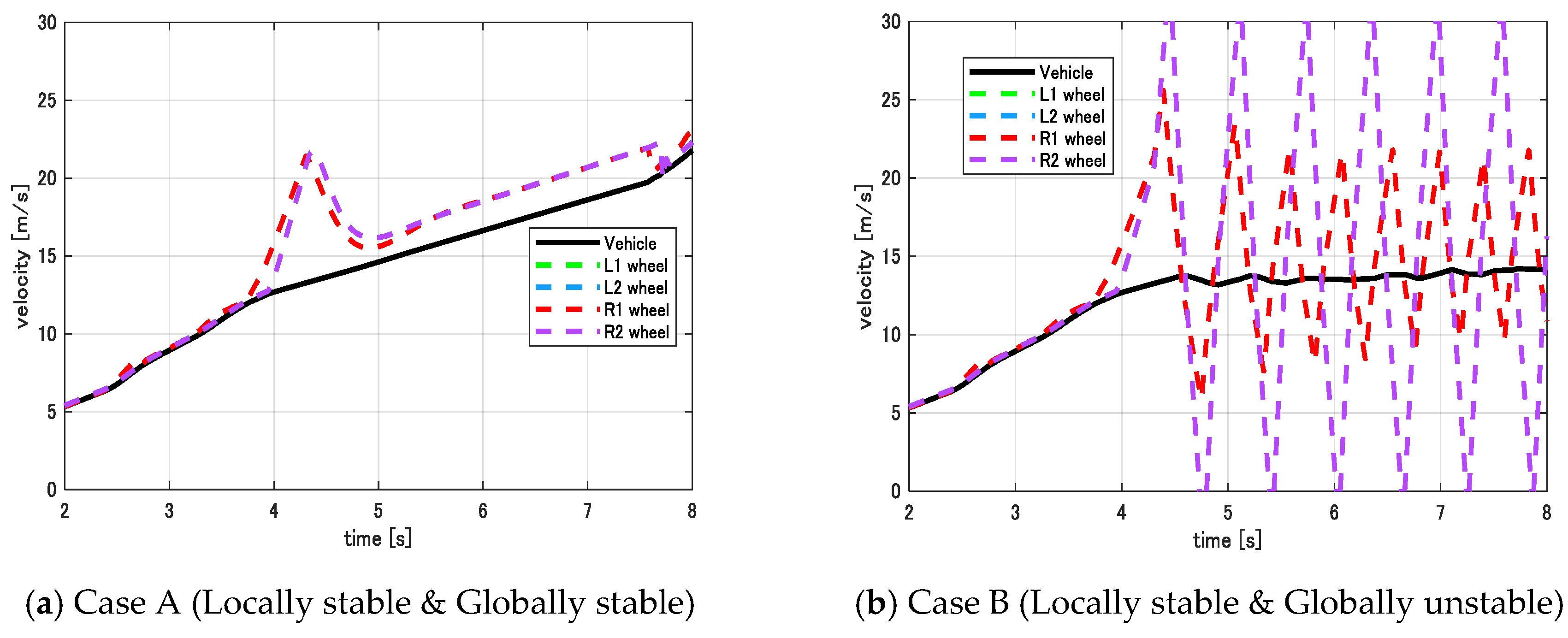
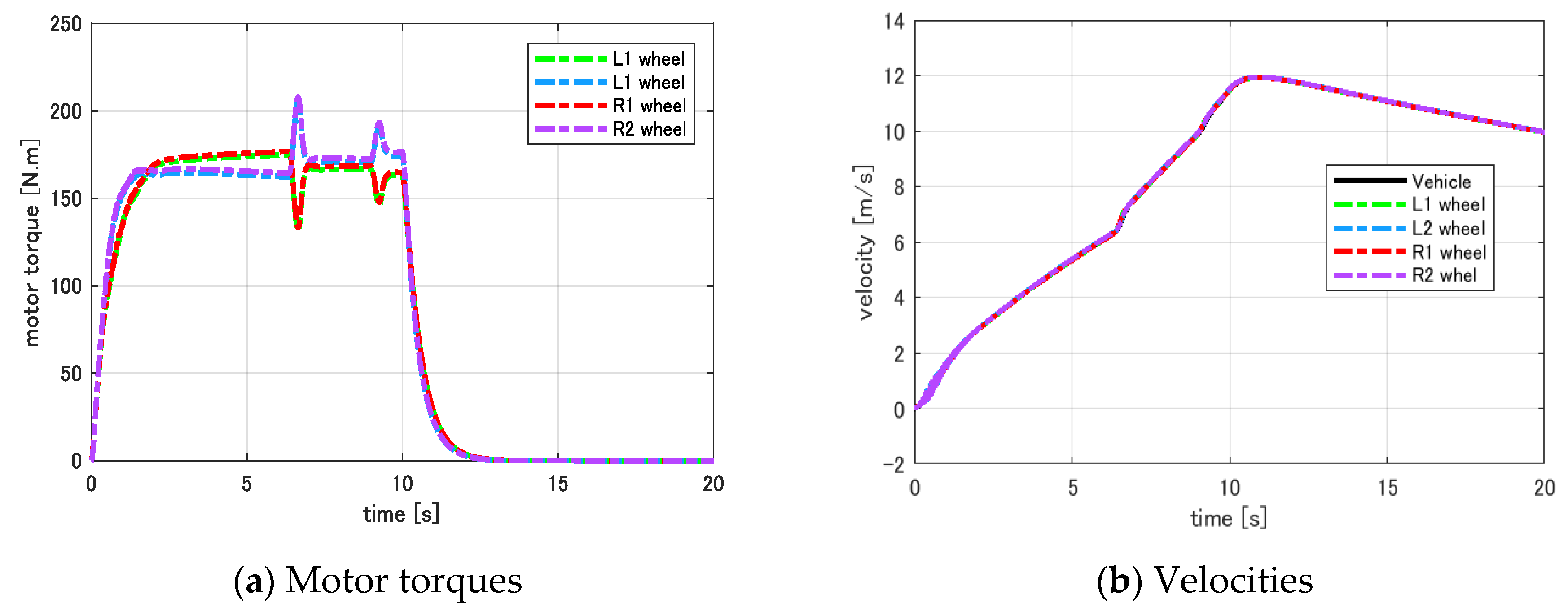
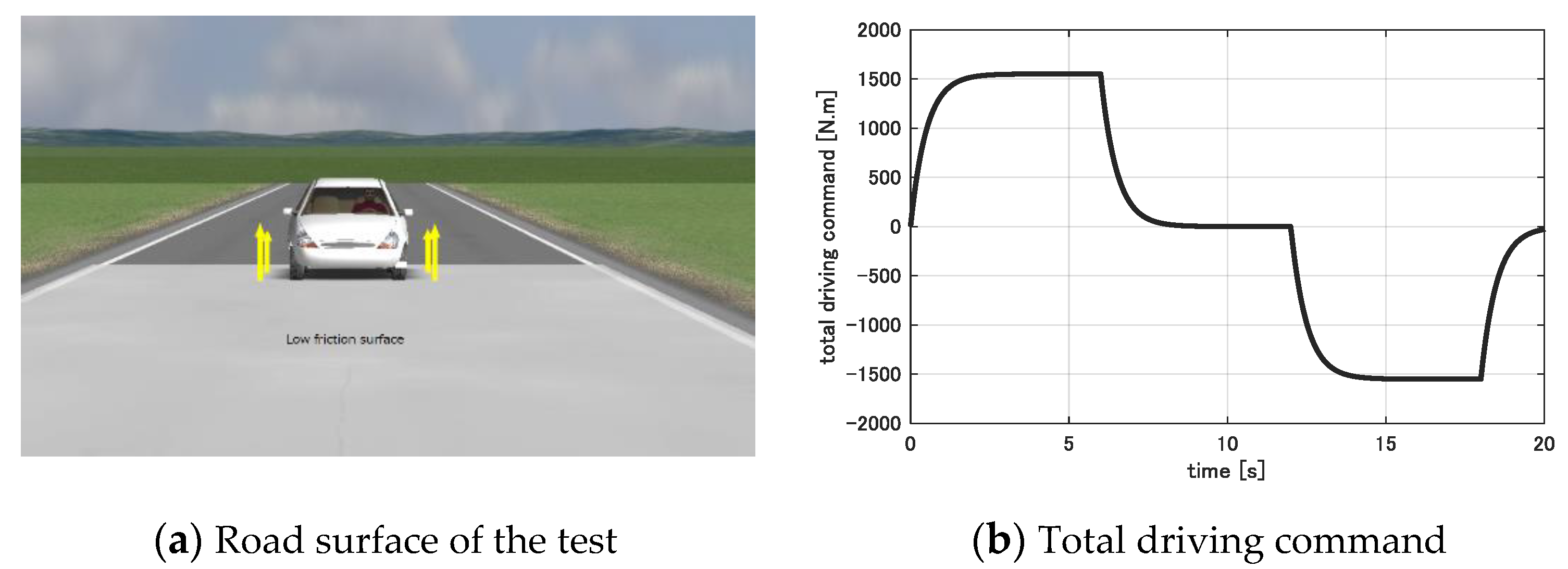
3.2. Simulation and Discussion
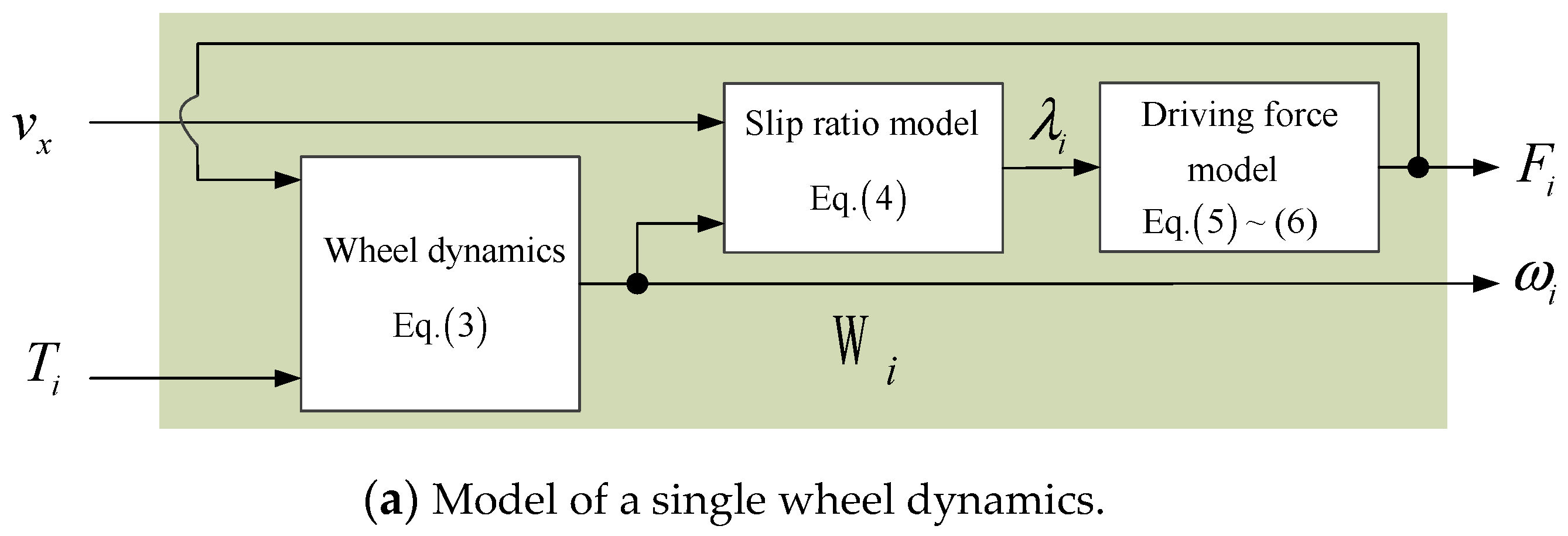
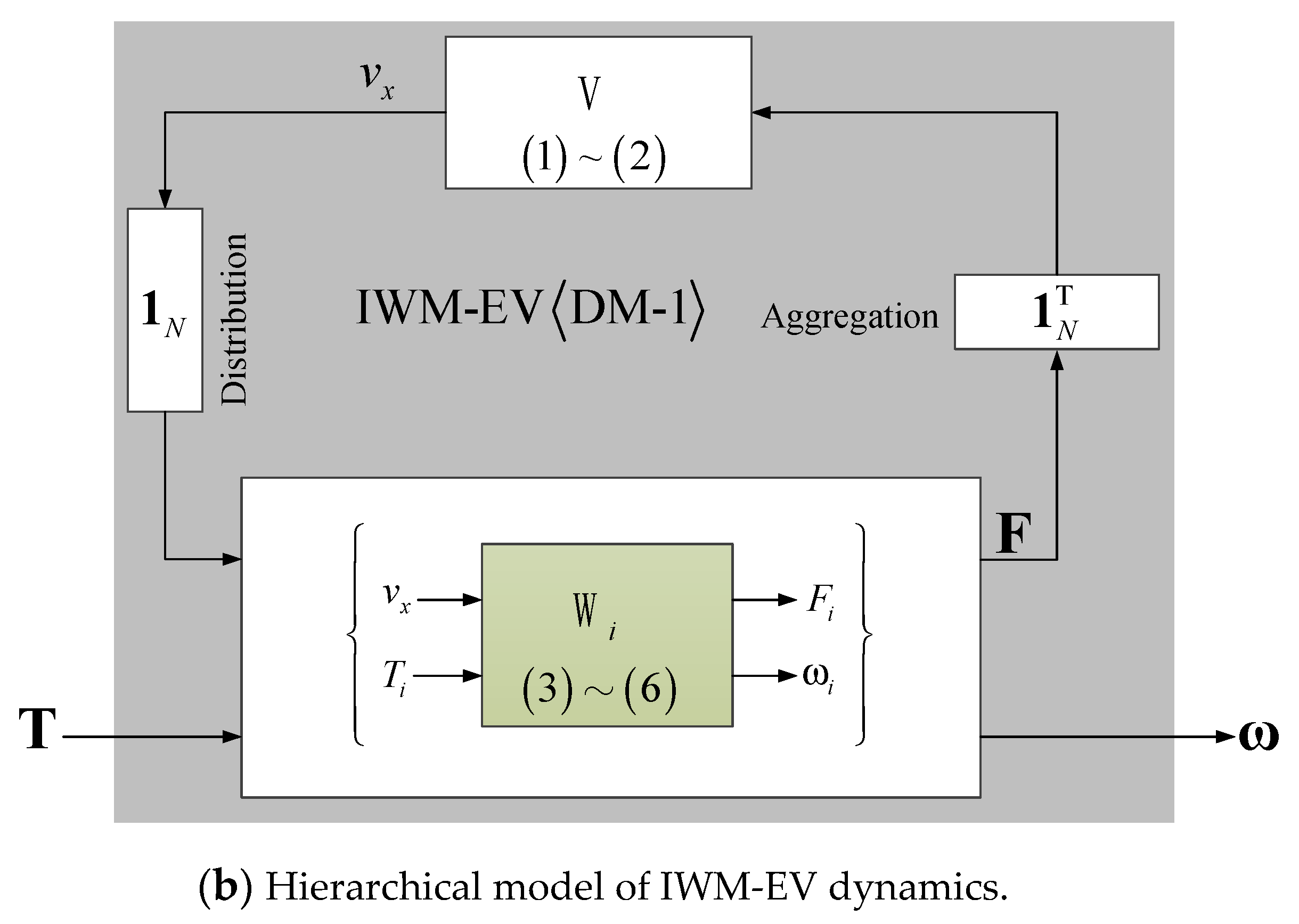
4. DM-1: Nonlinear Model with Hierarchical Structure
4.1. Hierarchical Model of IWM-EV
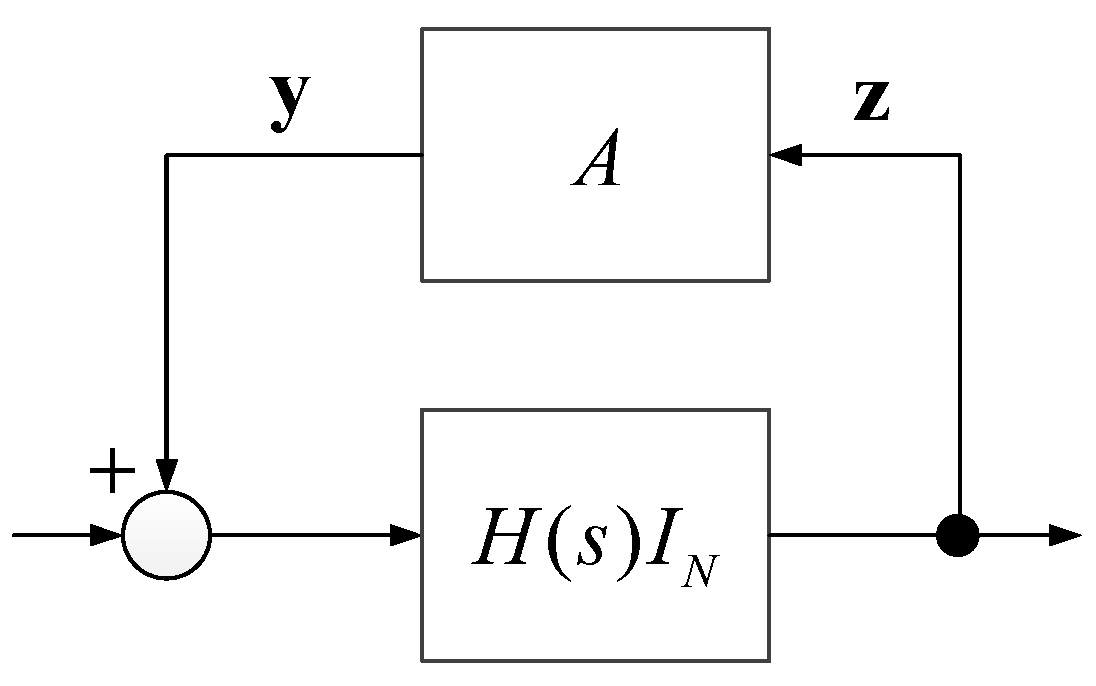
4.2. Passivity Theory and Its Application to DM-1
4.3. Example of DM-1: Passivty Based Anti-Slip Control of IWM-EV
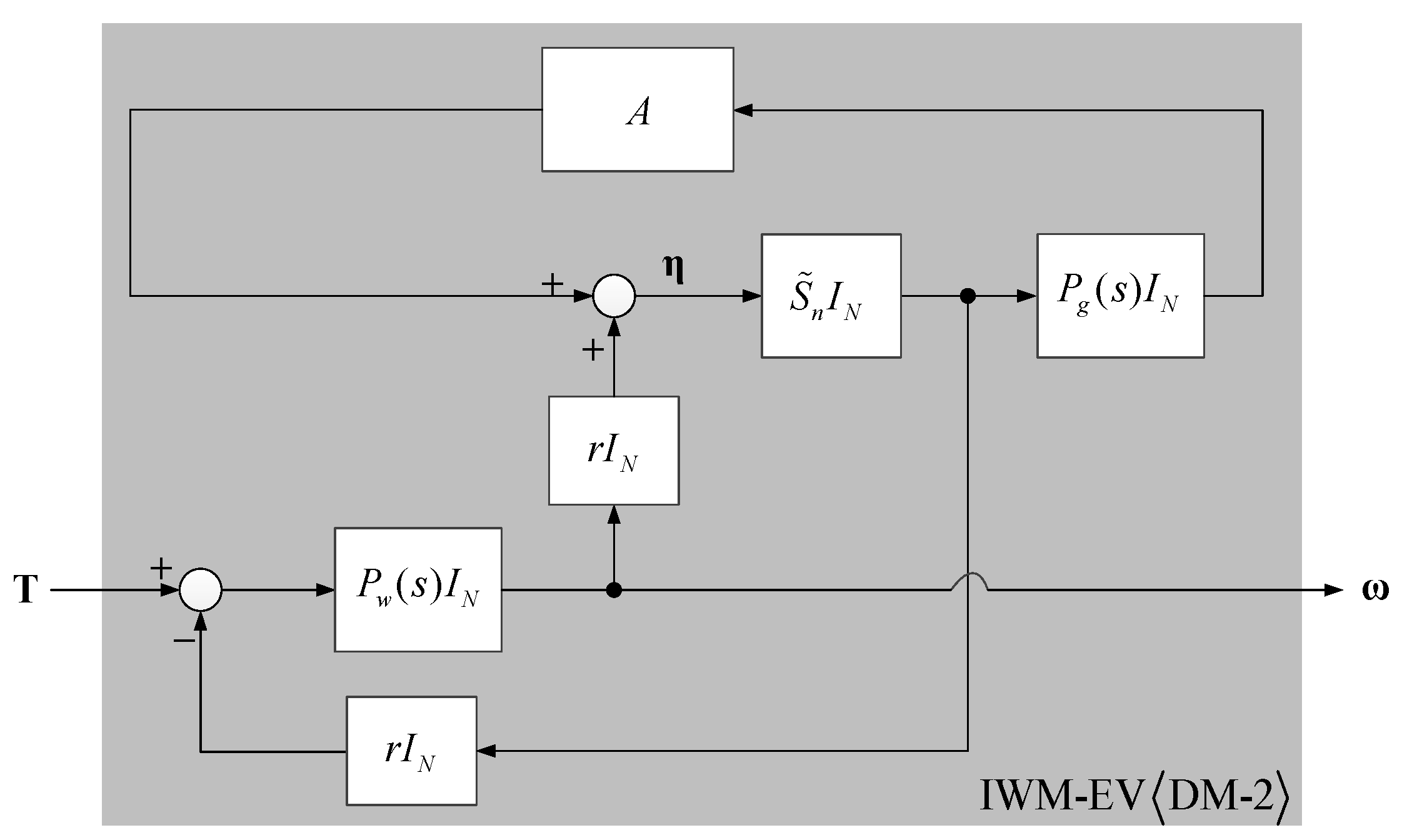
5. DM-2: Linearized Model with Rank-1 Interconnection Matrix
5.1. Linearized Model of IWM-EV
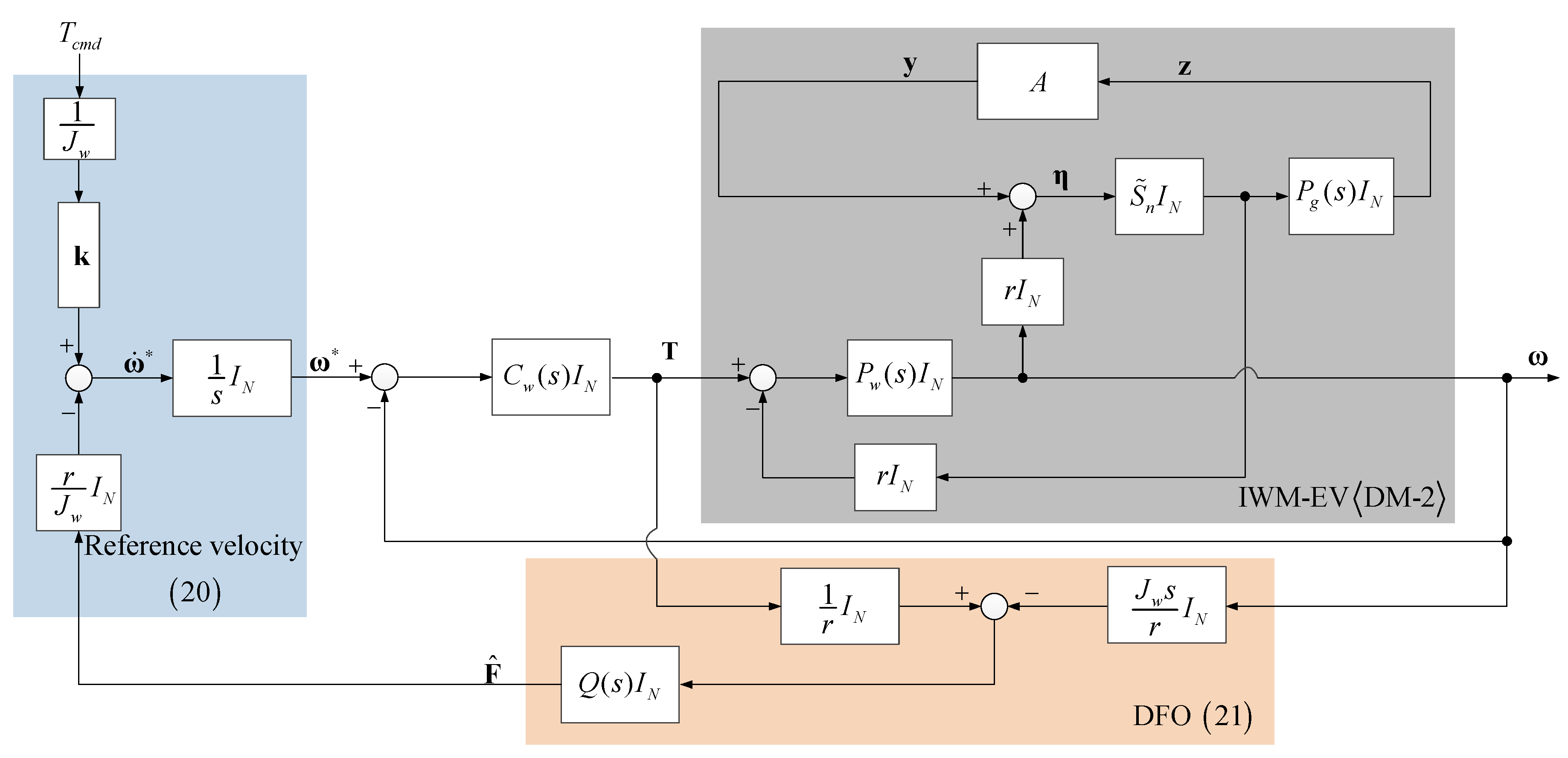
5.2. Example of DM-2: Wheel Velocity Control System and Its Stability Condition
5.3. Stability Test
5.4. Discussion: Possibility of Robust Stability Test
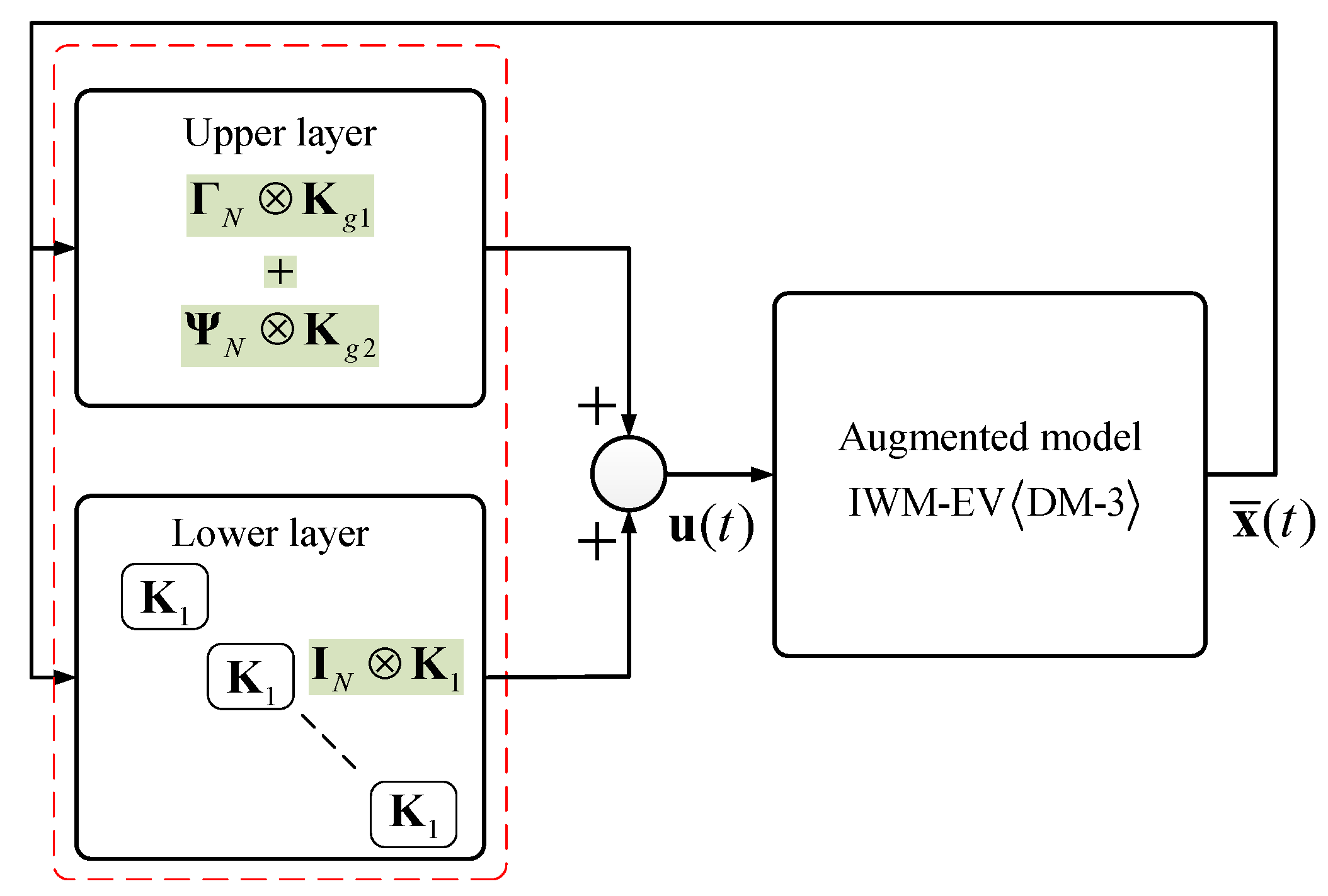
6. DM-3: Time-Varying State-Space Model
6.1. State-Space Model of IWM-EV in the Deceleration Mode
6.2. Example of DM-3: Slip Ratio Control in the Deceleration Mode
7. Evaluation of the Proposed Design Models by Carsim/Matlab Co-Simulator
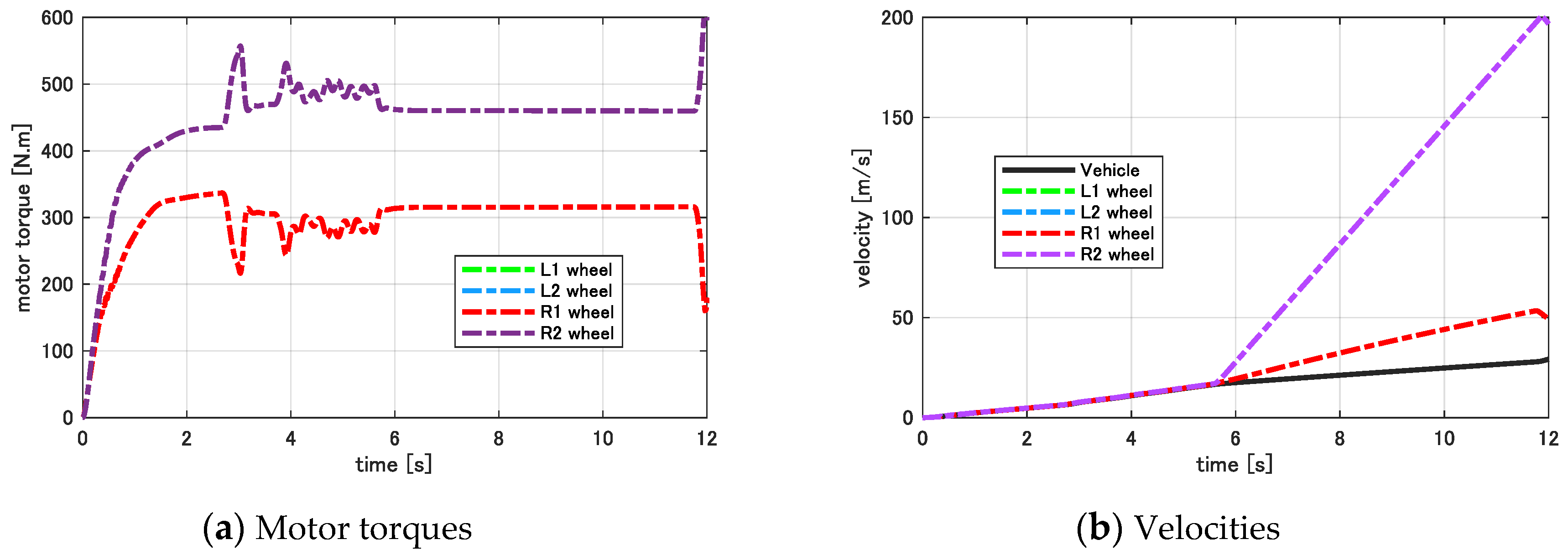
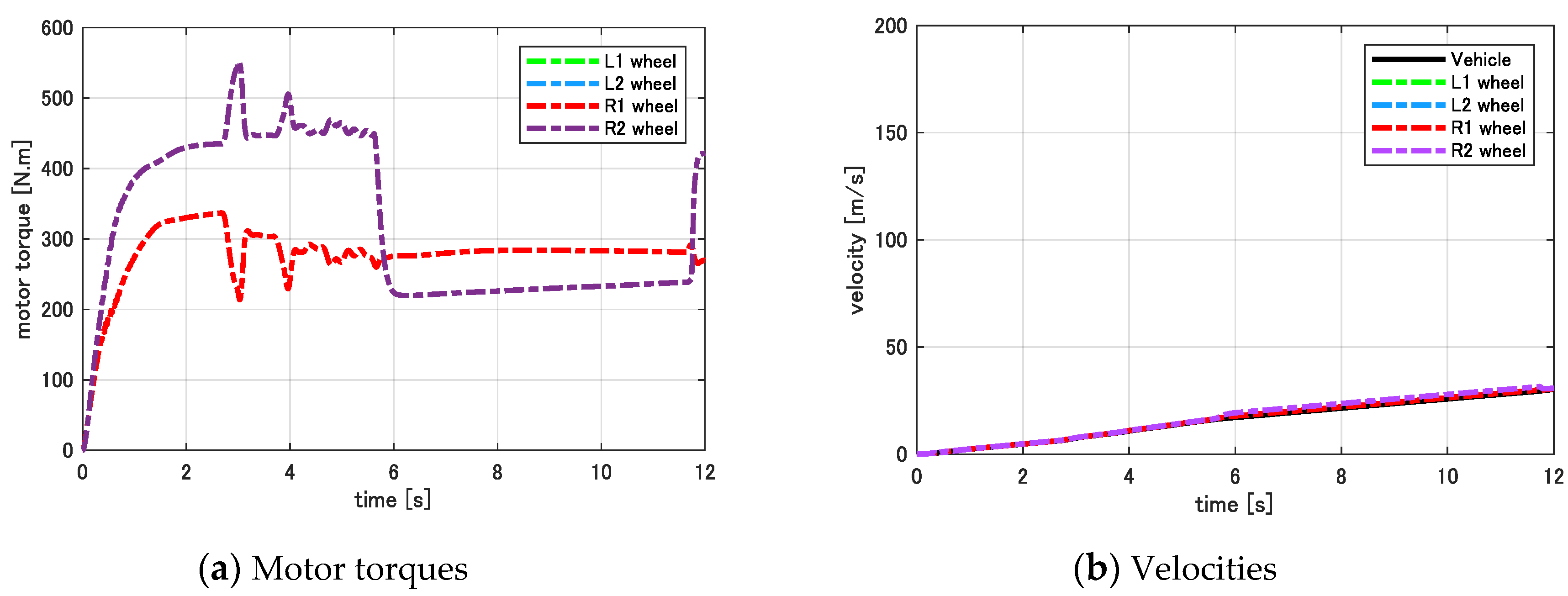
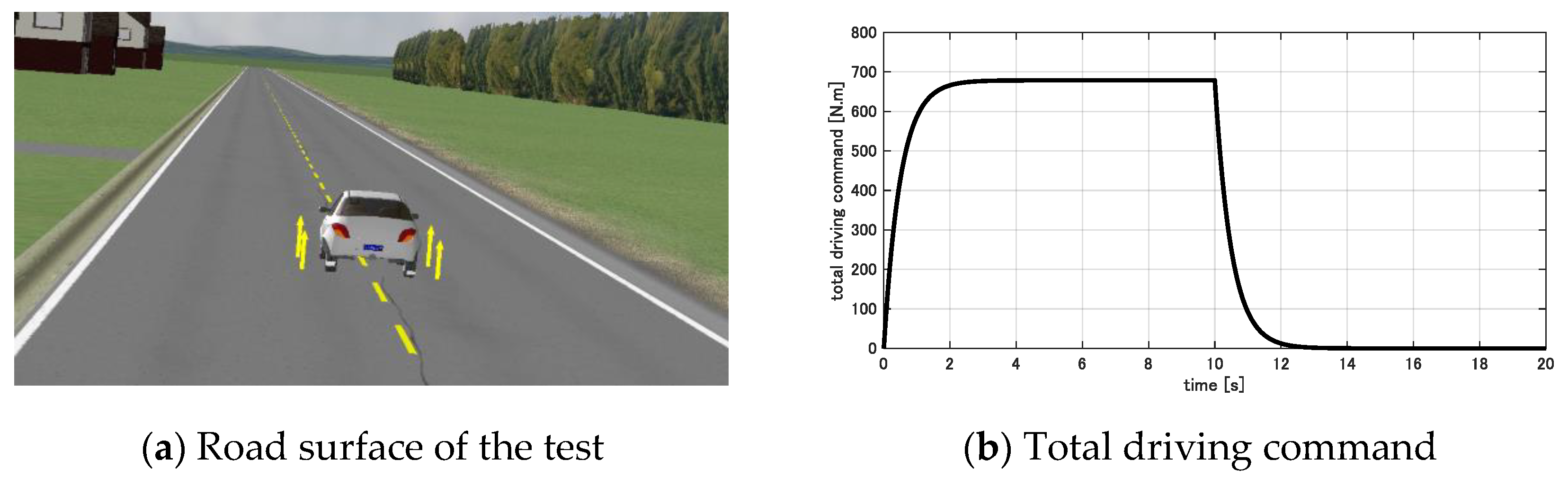
7.1. Evaluation of Passivity Based Anti-Slip Control Using DM-1
7.2. Evaluation of GFV Based Stability Analysis Using DM-2
7.3. Evaluation of LQR-Based Slip-Ratio Control Using DM-3
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Vehicle | |
|---|---|
| Vehicle mass | m = 1080 (kg) |
| Radius of wheel | r = 0.285 (m) |
| Wheel moment of inertia | Jw = 1.25 (kg.m2) |
| Cross-sectional area of vehicle in the air | AF = 2.37 (m2) |
| Drag coefficient | Cd = 0.35 |
| Distance between front axle and rear axle | L = 2.55 (m) |
| Distance from center of gravity to front axle | Lf = 1.45 (m) |
| Distance from center of gravity to rear axle | Lr = 1.10 (m) |
| Height of the center of gravity | Hg = 0.356 (m) |
| Number of wheels | N = 4 |

Appendix B
Appendix C
Appendix D


References
- Hori, Y. Future vehicle driven by electricity and control-Research on 4 wheel motored UOT March II. IEEE Trans. Ind. Electron. 2004, 51, 954–962. [Google Scholar] [CrossRef]
- Geng, C.; Mostefai, L.; Denaï, M.A.; Hori, Y. Direct yaw-moment control of an in-wheel-motored electric vehicle based on body slip angle fuzzy observer. IEEE Trans. Ind. Electron. 2009, 56, 1411–1419. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, B.-M.; Wang, Y.; Fujimoto, H.; Hori, Y. Lateral stability control of electric vehicle based on disturbance accommodating Kalman filter using the integration of single antenna GPS receiver and yaw rate sensor. J. Electr. Eng. Technol. 2013, 8, 899–910. [Google Scholar] [CrossRef] [Green Version]
- Tota, A.; Lenzo, B.; Lu, Q.; Sorniotti, A.; Gruber, P.; Fallah, S.; Velardocchia, M.; Galvagno, E.; De Smet, J. On the experimental analysis of integral sliding modes for yaw rate and sideslip control of an electric vehicle with multiple motors. Int. J. Automot. Technol. 2018, 19, 811–823. [Google Scholar] [CrossRef]
- Nam, K.; Fujimoto, H.; Hori, Y. Lateral stability control of in-wheel-motor-driven electric vehicles based on sideslip angle estimation using lateral tire force sensors. IEEE Trans. Veh. Technol. 2012, 61, 1972–1985. [Google Scholar] [CrossRef]
- Kawashima, K.; Uchida, T.; Hori, Y. Rolling stability control based on electronic stability program for in-wheel-motor electric vehicle. World Electr. Veh. J. 2009, 3, 34–41. [Google Scholar] [CrossRef] [Green Version]
- Fujimoto, H.; Sato, S. Pitching control method based on quick torque response for electric vehicle. In Proceedings of the 2010 International Power Electronics Conference-ECCE ASIA, Sapporo, Japan, 21–24 June 2010; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2010; pp. 801–806. [Google Scholar]
- Kanchwala, H.; Wideberg, J. Pitch reduction and traction enhancement of an EV by real-time brake biasing and in-wheel motor torque control. Int. J. Veh. Syst. Model. Test. 2016, 11, 165. [Google Scholar] [CrossRef]
- Yu, Y.; Xiong, L.; Yu, Z.; Yang, X.; Hou, Y.; Leng, B. Model-based pitch control for distributed drive electric vehicle. SAE Tech. Pap. Ser. 2019. [Google Scholar] [CrossRef]
- He, H.; Peng, J.; Xiong, R.; Fan, H. An acceleration slip regulation strategy for four-wheel drive electric vehicles based on sliding mode control. Energies 2014, 7, 3748–3763. [Google Scholar] [CrossRef] [Green Version]
- Nam, K.; Hori, Y.; Lee, C.-Y. Wheel slip control for improving traction-ability and energy efficiency of a personal electric vehicle. Energies 2015, 8, 6820–6840. [Google Scholar] [CrossRef] [Green Version]
- Savitski, D.; Ivanov, V.; Augsburg, K.; Emmei, T.; Fuse, H.; Fujimoto, H.; Fridman, L.M. Wheel slip control for the electric vehicle with in-wheel motors: Variable structure and sliding mode methods. IEEE Trans. Ind. Electron. 2020, 67, 8535–8544. [Google Scholar] [CrossRef]
- He, L.; Ye, W.; He, Z.; Song, K.; Shi, Q. A combining sliding mode control approach for electric motor anti-lock braking system of battery electric vehicle. Control. Eng. Pr. 2020, 102, 104520. [Google Scholar] [CrossRef]
- Hori, Y.; Toyoda, Y.; Tsuruoka, Y. Traction control of electric vehicle: Basic experimental results using the test EV "UOT electric march". IEEE Trans. Ind. Appl. 1998, 34, 1131–1138. [Google Scholar] [CrossRef]
- Ivanov, V.; Savitski, D.; Augsburg, K.; Barber, P.; Knauder, B.; Zehetner, J. Wheel slip control for all-wheel drive electric vehicle with compensation of road disturbances. J. Terramechanics 2015, 61, 1–10. [Google Scholar] [CrossRef]
- De Pinto, S.; Chatzikomis, C.; Sorniotti, A.; Mantriota, G. Comparison of traction controllers for electric vehicles with on-board drivetrains. IEEE Trans. Veh. Technol. 2017, 66, 6715–6727. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, B.-M.; Hara, S.; Fujimoto, H.; Hori, Y. Slip control for IWM vehicles based on hierarchical LQR. Control. Eng. Pr. 2019, 93, 104179. [Google Scholar] [CrossRef]
- Li, L.; Kodama, S.; Hori, Y. Design of anti-slip controller for an electric vehicle with an adhesion status analyzer based on the ev simulator. Asian J. Control. 2008, 8, 261–267. [Google Scholar] [CrossRef]
- Fujimoto, H.; Saito, T.; Noguchi, T. Motion stabilization control of electric vehicle under snowy conditions based on yaw-moment observer. In Proceedings of the 8th IEEE International Workshop on Advanced Motion Control, Kawasaki, Japan, 28 March 2004; AMC ’04. Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2004. [Google Scholar]
- Yin, D.; Oh, S.; Hori, Y. A novel traction control for ev based on maximum transmissible torque estimation. IEEE Trans. Ind. Electron. 2009, 56, 2086–2094. [Google Scholar] [CrossRef]
- Chiang, W.-P.; Yin, D.; Omae, M.; Shimizu, H. Integrated slip-based torque control of antilock braking system for in-wheel motor electric vehicle. IEEJ J. Ind. Appl. 2014, 3, 318–327. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, T.; Fujimoto, H. Slip ratio estimation and regenerative brake control without detection of vehicle velocity and acceleration for electric vehicle at urgent brake-turning. In Proceedings of the 2010 11th IEEE International Workshop on Advanced Motion Control (AMC), Nagaoka, Japan, 21–24 March 2010; pp. 273–278. [Google Scholar] [CrossRef]
- Amada, J.; Fujimoto, H. Torque based direct driving force control method with driving stiffness estimation for electric vehicle with in-wheel motor. In Proceedings of the IECON 2012–38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2012; pp. 4904–4909. [Google Scholar]
- Maeda, K.; Fujimoto, H.; Hori, Y. Four-wheel driving-force distribution method for instantaneous or split slippery roads for electric vehicle. Automatika 2013, 54, 103–113. [Google Scholar] [CrossRef]
- Maeda, K.; Fujimoto, H.; Hori, Y. Driving force control of electric vehicles with estimation of slip ratio limitation considering tire side slip. Trans. Soc. Instrum. Control. Eng. 2014, 50, 259–265. [Google Scholar] [CrossRef] [Green Version]
- Fuse, H.; Fujimoto, H. Fundamental study on driving force control method for independent-four-wheel-drive electric vehicle considering tire slip angle. In Proceedings of the IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 20–23 October 2018; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2018; pp. 2062–2067. [Google Scholar]
- Boulon, L.; Hissel, D.; Bouscayrol, A.; Pape, O.; Péra, M.-C. Simulation model of a military HEV with a highly redundant architecture. IEEE Trans. Veh. Technol. 2010, 59, 2654–2663. [Google Scholar] [CrossRef]
- Shimizu, H. Multi-purpose electric vehicle “Kaz.”. IATSS Res. 2001, 25, 96–97. [Google Scholar] [CrossRef] [Green Version]
- Sato, M.; Yamamoto, G.; Gunji, D.; Imura, T.; Fujimoto, H. Development of wireless in-wheel motor using magnetic resonance coupling. IEEE Trans. Power Electron. 2015, 31, 5270–5278. [Google Scholar] [CrossRef]
- Hara, S.; Imura, J.-I.; Tsumura, K.; Ishizaki, T.; Sadamoto, T. Glocal (global/local) control synthesis for hierarchical networked systems. In Proceedings of the 2015 IEEE Conference on Control Applications (CCA), Sydney, Australia, 21–23 September 2015; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2015; pp. 107–112. [Google Scholar]
- Kim, T.-H.; Hori, Y.; Hara, S. Robust stability analysis of gene–protein regulatory networks with cyclic activation–repression interconnections. Syst. Control. Lett. 2011, 60, 373–382. [Google Scholar] [CrossRef]
- Khaisongkram, W.; Hara, S. Performance analysis of decentralized cooperative driving under non-symmetric bidirectional information architecture. In Proceedings of the 2011 IEEE International Conference on Control Applications (CCA), Denver, CO, USA, 28–30 September 2011; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2010; pp. 2035–2040. [Google Scholar]
- Nguyen, D.-H.; Hara, S. Hierarchical decentralized controller synthesis for heterogeneous multi-agent dynamical systems by LQR. SICE J. Control. Meas. Syst. Integr. 2015, 8, 295–302. [Google Scholar] [CrossRef] [Green Version]
- Tsumura, K.; Nguyen, B.M.; Wakayama, H.; Hara, S. Distributed stabilization by probability control for deterministic-stochastic large scale systems: Dissipativity approach. In Proceedings of the IEEE Control Decision Conference, Jeju Island, Korea, 14–18 December 2020. [Google Scholar]
- Hara, S.; Tanaka, H.; Iwasaki, T. Stability analysis of systems with generalized frequency variables. IEEE Trans. Autom. Control. 2013, 59, 313–326. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, B.M.; Hara, S.; Fujimoto, H. Stability analysis of tire force distribution for multi-actuator electric vehicles using generalized frequency variable. In Proceedings of the 2016 IEEE Conference on Control Applications (CCA), Buenos Aires, Argentina, 19–22 September 2016; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2016; pp. 91–96. [Google Scholar]
- Liu, K.; Li, K.; Zhang, C. Constrained generalized predictive control of battery charging process based on a coupled thermoeletric model. J. Power Sources 2017, 347, 145–158. [Google Scholar] [CrossRef] [Green Version]
- Ouyang, Q.; Wang, Z.; Liu, K.; Xu, G.; Li, Y. Optimal charging control for lithium-ion battery packs: A distributed average tracking approach. IEEE Trans. Ind. Informatics 2019, 16, 3430–3438. [Google Scholar] [CrossRef]
- Liu, K.; Hu, X.; Wei, Z.; Li, Y.; Jiang, Y. Modified gaussian process regression models for cyclic capacity prediction of lithium-ion batteries. IEEE Trans. Transp. Electrification 2019, 5, 1225–1236. [Google Scholar] [CrossRef]
- Liu, K.; Li, Y.; Hu, X.; Lucu, M.; Widanage, W.D. Gaussian process regression with automatic relevance determination kernel for calendar aging prediction of lithium-ion batteries. IEEE Trans. Ind. Inform. 2019, 16, 3767–3777. [Google Scholar] [CrossRef] [Green Version]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Rajamani, R. Vehicle Dynamics and Control; Springer: Berlin, Germany, 2012. [Google Scholar]
- Pacejka, H.B. Tyre and Vehicle Dynamics; Elsevier BV: Amsterdam, Netherlands, 2006. [Google Scholar]
- Mechanical Simulation Homepage. Available online: https://www.carsim.com/ (accessed on 20 August 2020).
- Ortega, R.; Spong, M.W. Adaptive control of robot manipulators: A tutorial. Automatica 1989, 25, 877–888. [Google Scholar]
- Hatanaka, T.; Chopra, N.; Fujita, M.; Spong, M.W. Passivity-Based Control. and Estimation in Networked Robotics; Springer Science and Business Media LLC: Berlin, Germany, 2015. [Google Scholar]
- Nguyen, B.-M.; Tsumura, K.; Hara, S. Glocal traction control for in-wheel-motor electric vehicles-A passivity approach. In Proceedings of the 1st Virtual IFAC World Congress, Berlin, Germany, 11–17 July 2020. [Google Scholar]
- Wang, Y.; Fujimoto, H.; Hara, S. Torque distribution-based range extension control system for longitudinal motion of electric vehicles by LTI modeling with generalized frequency variable. IEEE/ASME Trans. Mechatron. 2015, 21, 1. [Google Scholar] [CrossRef]
- Harada, S.; Fujimoto, H. Range extension control system for electric vehicles based on optimal-deceleration trajectory and front-rear driving-braking force distribution considering maximization of energy regeneration. In Proceedings of the 2014 IEEE 13th International Workshop on Advanced Motion Control (AMC), Yokohama, Japan, 14–16 March 2014; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2014; pp. 173–178. [Google Scholar]
- Fujimoto, H.; Harada, S. Model-based range extension control system for electric vehicles with front and rear driving–braking force distributions. IEEE Trans. Ind. Electron. 2015, 62, 3245–3254. [Google Scholar] [CrossRef]
- Rill, G. First oder tire dynamics. In Proceedings of the III European Conference on Computational Mechanics Solids, Structures and Coupled Problems in Engineering, Lisbon, Portugal, 5–8 June 2006. [Google Scholar]
- Sado, H.; Sakai, S.; Hori, Y. Road condition estimation for traction control in electric vehicle. In Proceedings of the ISIE ’99 IEEE International Symposium on Industrial Electronics (Cat. No.99TH8465), Bled, Slovenia, 12–16 July 1999; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2003; Volume 2, pp. 973–978. [Google Scholar]
- Fujii, K.; Fujimoto, H. Traction control based on slip ratio estimation without detecting vehicle speed for electric vehicle. In Proceedings of the 2007 Power Conversion Conference, Nagoya, Japan, 2–5 April 2007; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2007; pp. 688–693. [Google Scholar]
- Wilson, D.I. Advanced Control. using MATLAB or Stablising the Unstabilisable; Auckland University of Technology: Auckland, New Zealand, 2015. [Google Scholar]
- Suzuki, Y.; Kano, Y.; Abe, M. A study on tyre force distribution controls for full drive-by-wire electric vehicle. Veh. Syst. Dyn. 2014, 52, 235–250. [Google Scholar] [CrossRef]








| Group | Strategy | Consideration of Physical Interaction (YES/NO) | References |
|---|---|---|---|
| (I) Slip ratio control | Sliding mode control | NO | [10,11,12,13] |
| PI control by linearizing the slip dynamics | NO | [14,15,16] | |
| Optimal control by hierarchical LQR | YES | [17] | |
| (II) Anti-slip control | Zero-slip-model following control | NO | [18,19] |
| Maximum transmissible torque estimation | NO | [20,21] | |
| Direct wheel velocity control | NO | [22] | |
| (III) Driving force control | Direct driving force control | NO | [23] |
| Driving force control based on wheel velocity control and virtual variable control | NO | [24,25,26] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, B.-M.; Nguyen, H.V.; Ta-Cao, M.; Kawanishi, M. Longitudinal Modelling and Control of In-Wheel-Motor Electric Vehicles as Multi-Agent Systems. Energies 2020, 13, 5437. https://doi.org/10.3390/en13205437
Nguyen B-M, Nguyen HV, Ta-Cao M, Kawanishi M. Longitudinal Modelling and Control of In-Wheel-Motor Electric Vehicles as Multi-Agent Systems. Energies. 2020; 13(20):5437. https://doi.org/10.3390/en13205437
Chicago/Turabian StyleNguyen, Binh-Minh, Hung Van Nguyen, Minh Ta-Cao, and Michihiro Kawanishi. 2020. "Longitudinal Modelling and Control of In-Wheel-Motor Electric Vehicles as Multi-Agent Systems" Energies 13, no. 20: 5437. https://doi.org/10.3390/en13205437
APA StyleNguyen, B. -M., Nguyen, H. V., Ta-Cao, M., & Kawanishi, M. (2020). Longitudinal Modelling and Control of In-Wheel-Motor Electric Vehicles as Multi-Agent Systems. Energies, 13(20), 5437. https://doi.org/10.3390/en13205437




