Demand-Based Control Design for Efficient Heat Pump Operation of Electric Vehicles
Abstract
:1. Introduction
1.1. Background and Problem
1.2. Previous Research in the Field
1.3. Current Study Novelties and Focus
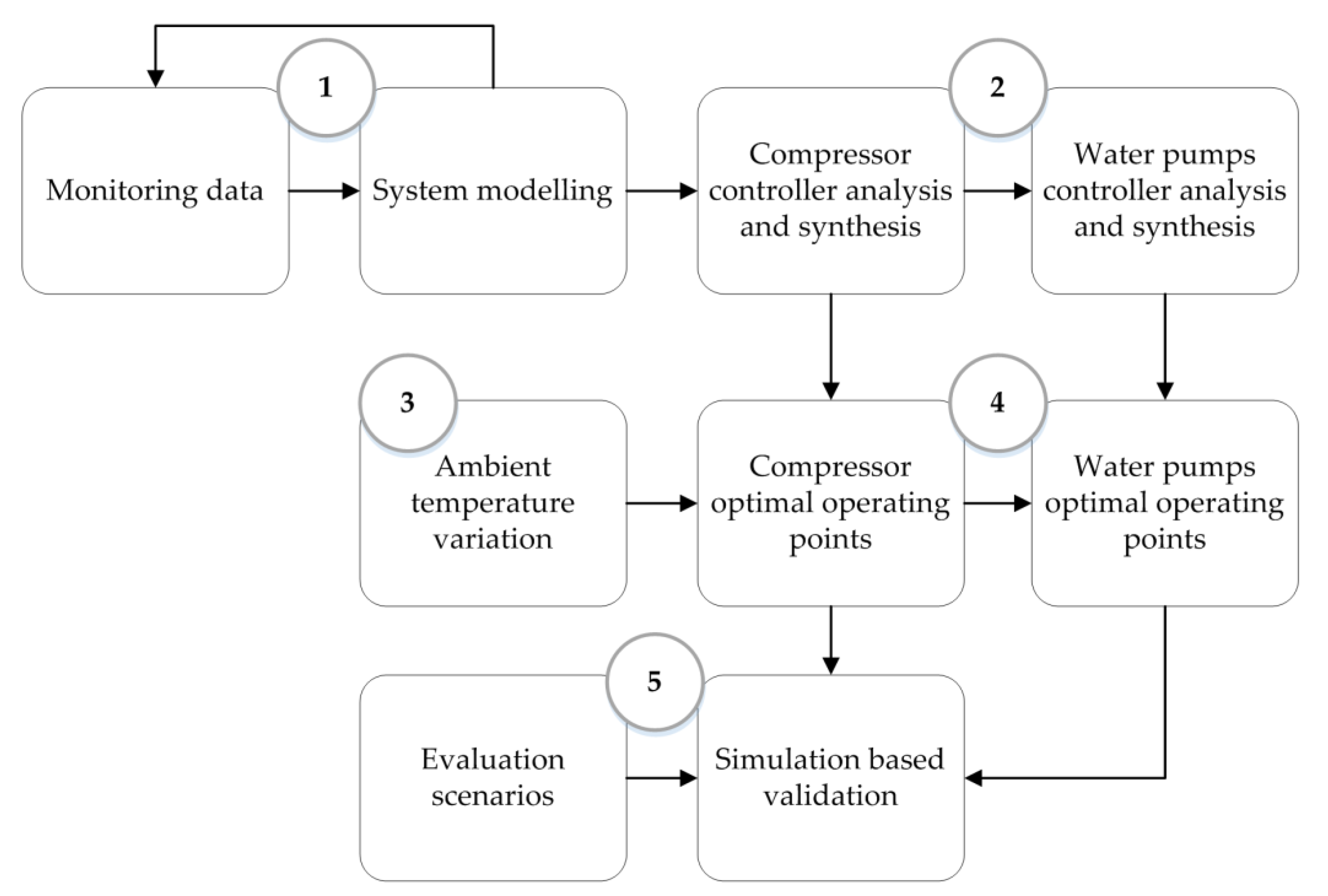
2. Methodology
- Reference scenario (Control Base),
- 1st improvement step: load controlled-compressor scenario with demand-dependent air-outlet-temperature setpoint of the HVAC system (Control Step 1),
- 2nd improvement step: load controlled-water-pumps scenario with demand-dependent speed of the water pumps (Control Step 2),
- 3rd improvement step: combination of steps 1 and 2 (Control Step 3).
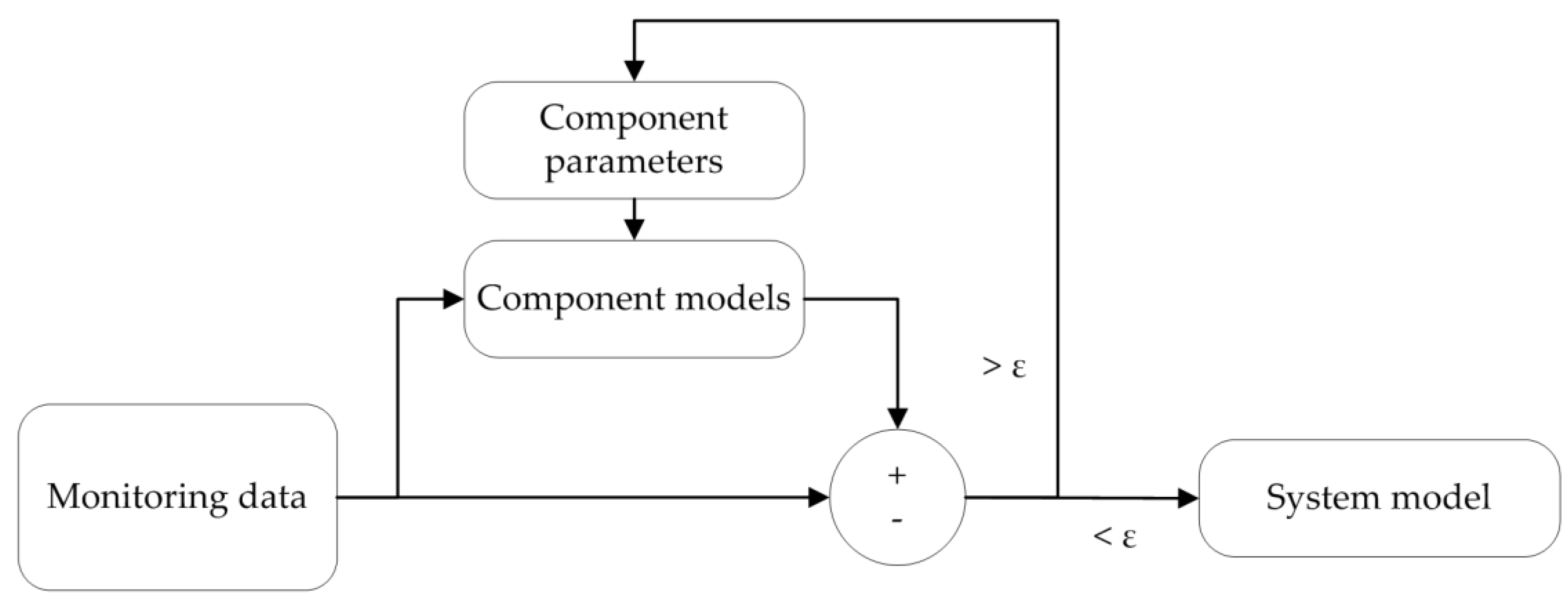
- System identification and modelling in an iterative process: models and measured data from the real-world system have been used for the parametrization;
- HVAC-compressor and water-pumps controller analysis and synthesis: identification of the dynamic characteristics of the system model and definition of an appropriate controller;
- Ambient temperature variation: simulation allows the investigation under various conditions to find the optimal setpoints;
- Determination and extrapolation of the demand-based optimal operating points of the HVAC compressor and the water pumps at various boundary conditions;
- Deployment and validation of the developed component control strategy by quantifying the improvement potentials of the measures.
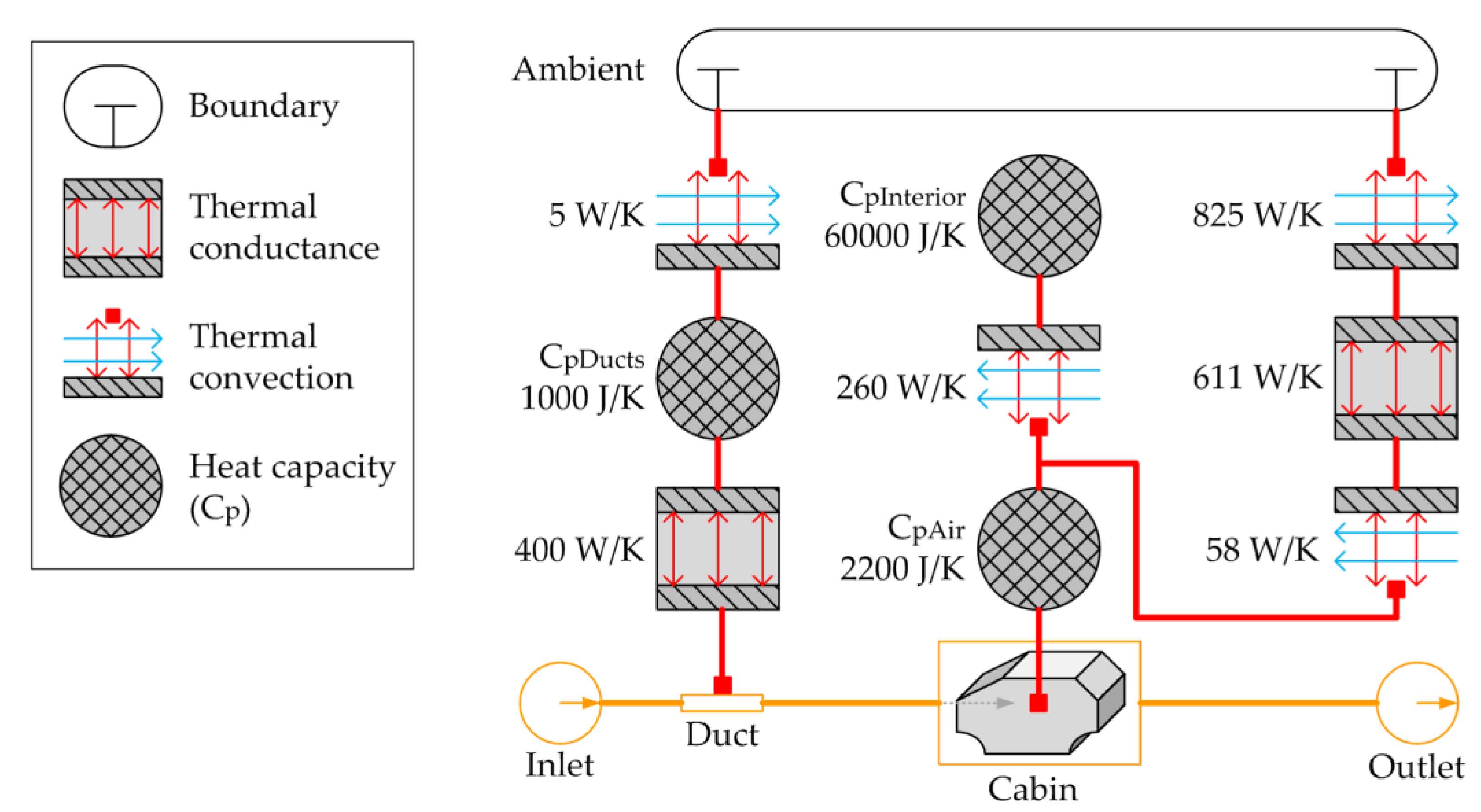
2.1. 1D Thermal Cabin Model
- Qtrans [W], transmission losses through the body of the cabin;
- Qvent [W], ventilation losses through the air leakage of the cabin (depending strongly on the operation mode: fresh air or recirculated air);
- Qrad [W], solar radiation load gain (excluded from the study to reduce the complexity otherwise introduced by a large number of combinations between ambient temperature and solar radiation conditions);
- Qmet [W], metabolic load from the passengers (excluded from the study for the same reason of the solar radiation).
- kcab [W/K.m²], overall heat-loss coefficient of the cabin;
- Acab [m²], overall external area of the cabin;
- Tcab [K], average cabin temperature;
- Tamb [K], ambient temperature;
- min [kg/s], volume flow of the fresh air into the cabin;
- cpAir [J/kg.K], thermal capacity of the air;
- Tvent [K], exhaust air temperature through the air leakages of the cabin.
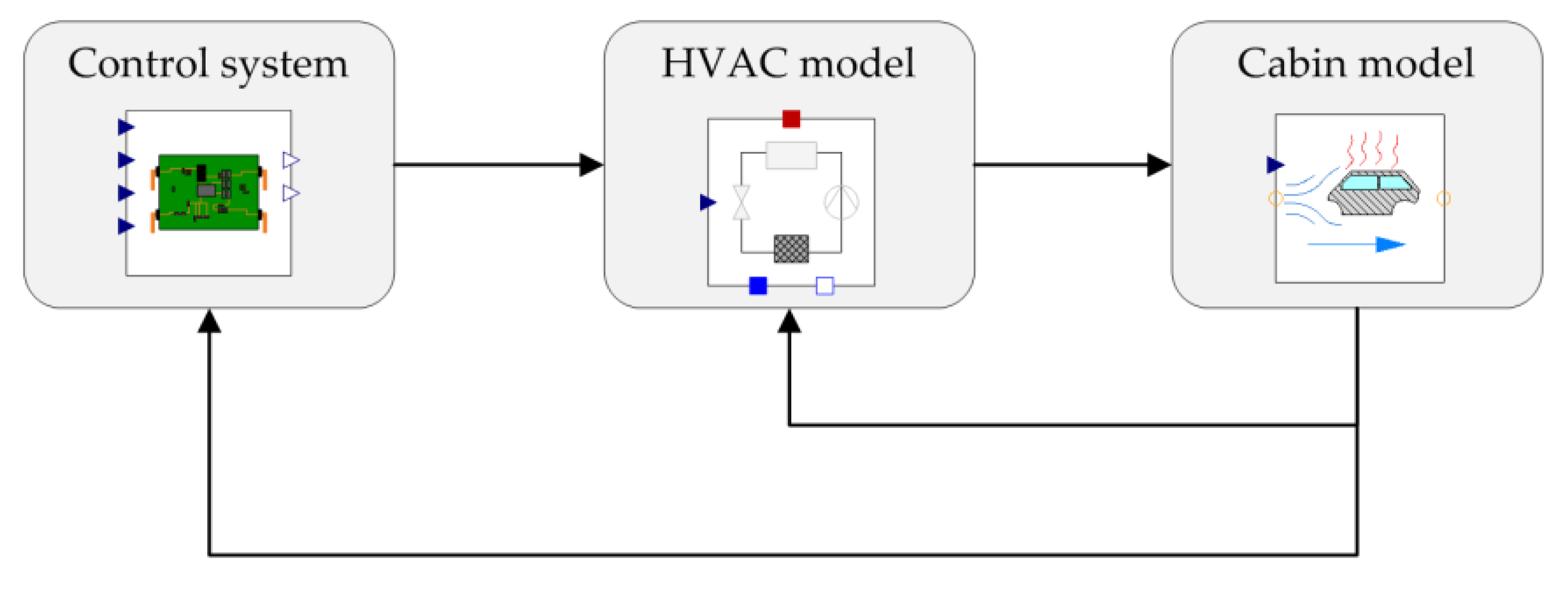
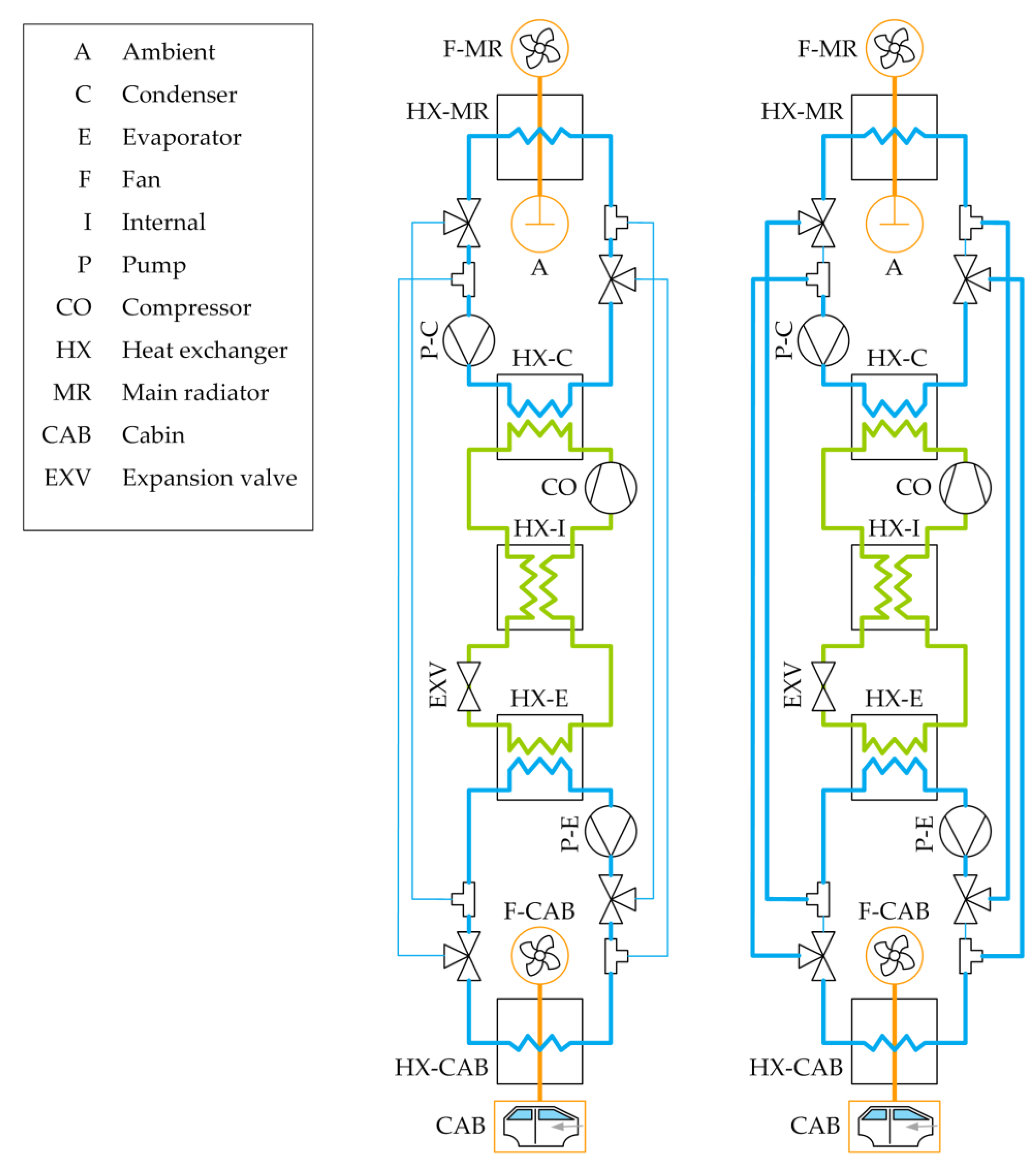
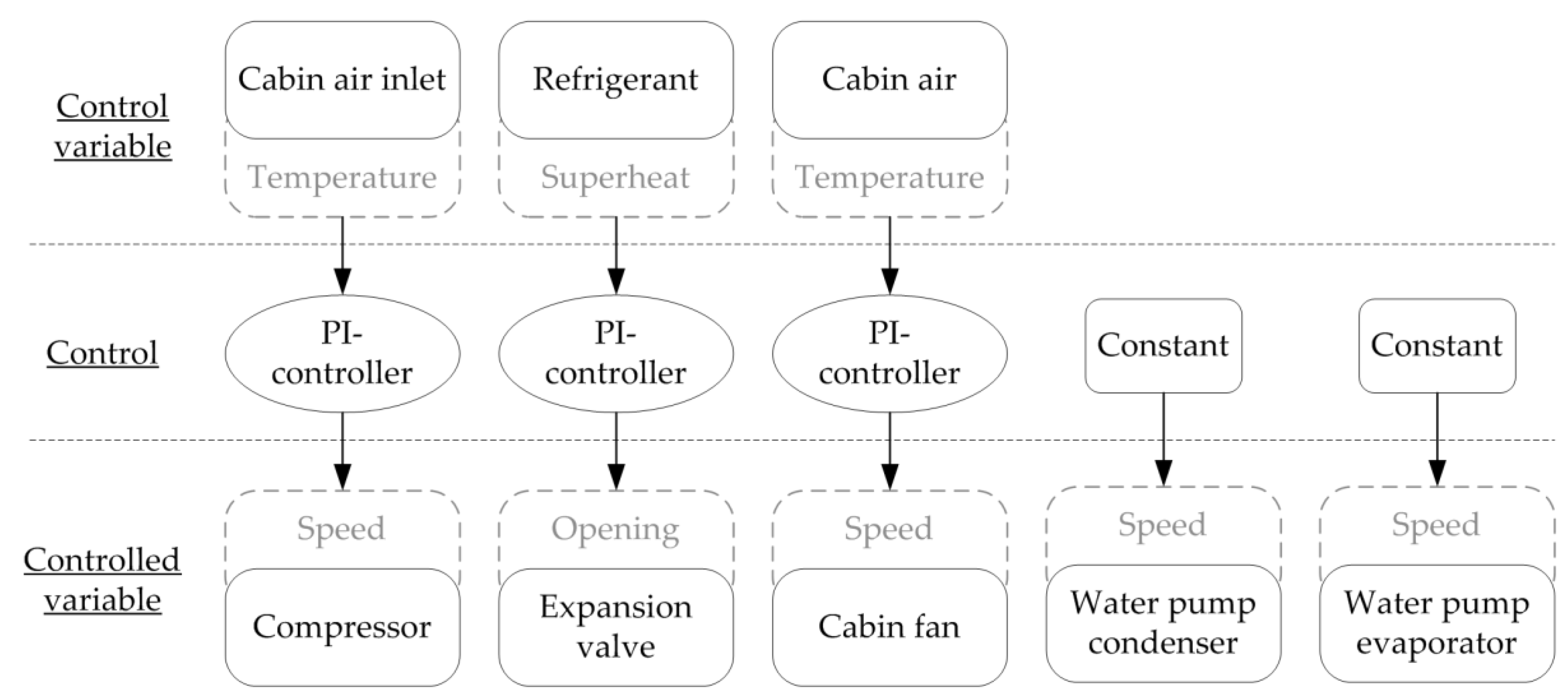
2.2. HVAC System and Control System
- Electrical power consumption PelectricalSys [W], as the electrical energy demand of the entire HVAC system (consisting of compressor, water pumps and cabin fan);
- Average cabin temperature;
- Coefficient of performance (COP and COPsys), related to the heating mode and determined as:
- Qcondenser [W], thermal energy output of the condenser on the refrigerant side;
- Pelectrical [W], the electrical energy of the compressor.
- Compressor: a PI (proportional-integral) controller controls the compressor speed to keep the target air temperature to be supplied by the HVAC system (TinTarget) at a constant value of 70 °C;
- Expansion valve (EXV): a PI controller ensures that no liquid refrigerant is sucked into the compressor by keeping the superheat temperature (Tsh) of the refrigerant after the evaporator at 5 K;
- Cabin fan: a PI controller regulates the air mass flow of the cabin fan via the fan voltage to keep the cabin temperature (Tcab) at a specific target value, which was considered 22 °C in the study;
- Water pumps (condenser and evaporator): constant pump speed on the condenser and evaporator side were set corresponding to the design point at −10 °C.
2.3. Models Parametrization
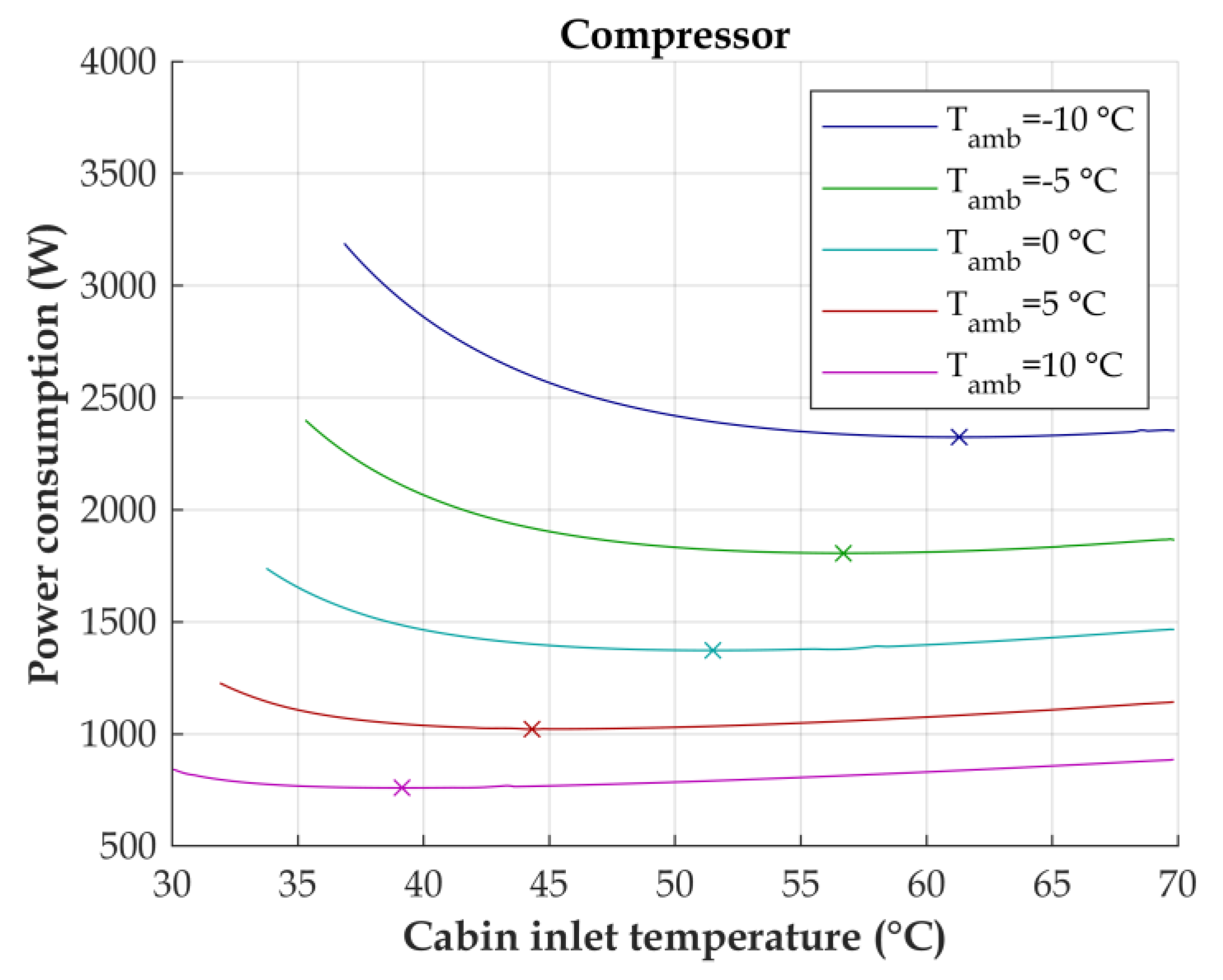
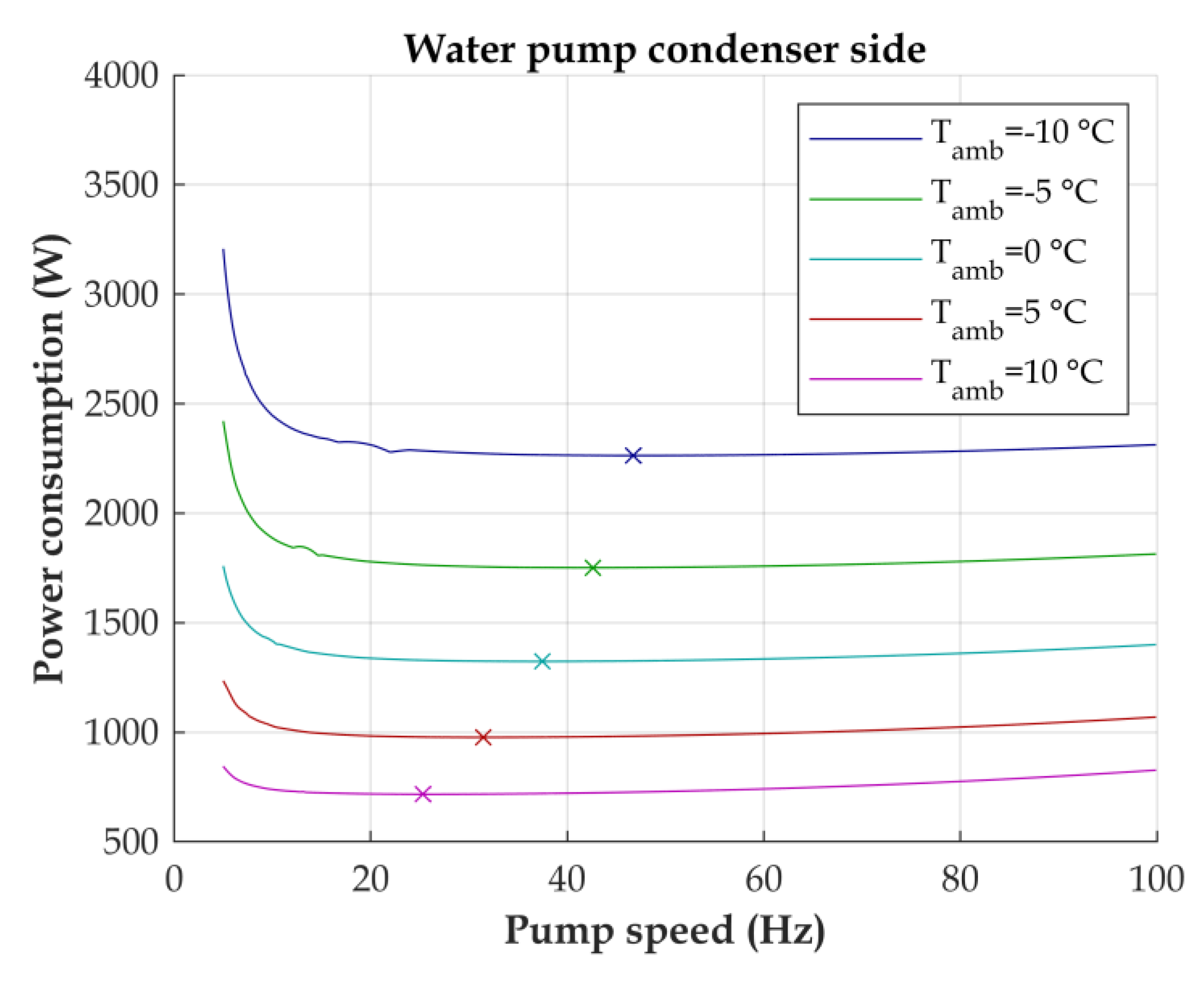
2.4. Demand-Based Control Design
- Control Step 1: compressor,
- Control Step 2: water pump on condenser side, water pump on evaporator side,
- Control Step 3: combination of all measures.
3. Results
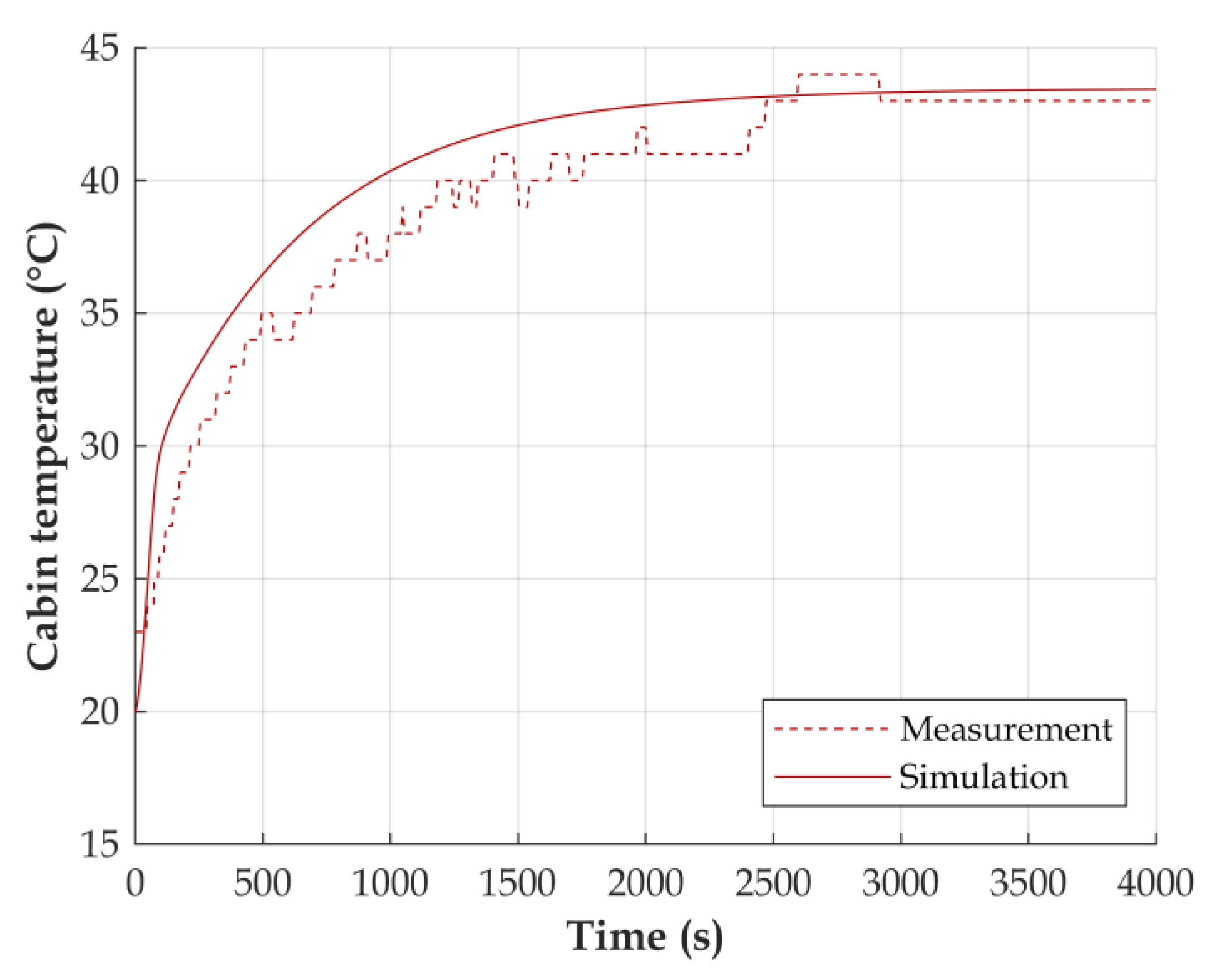
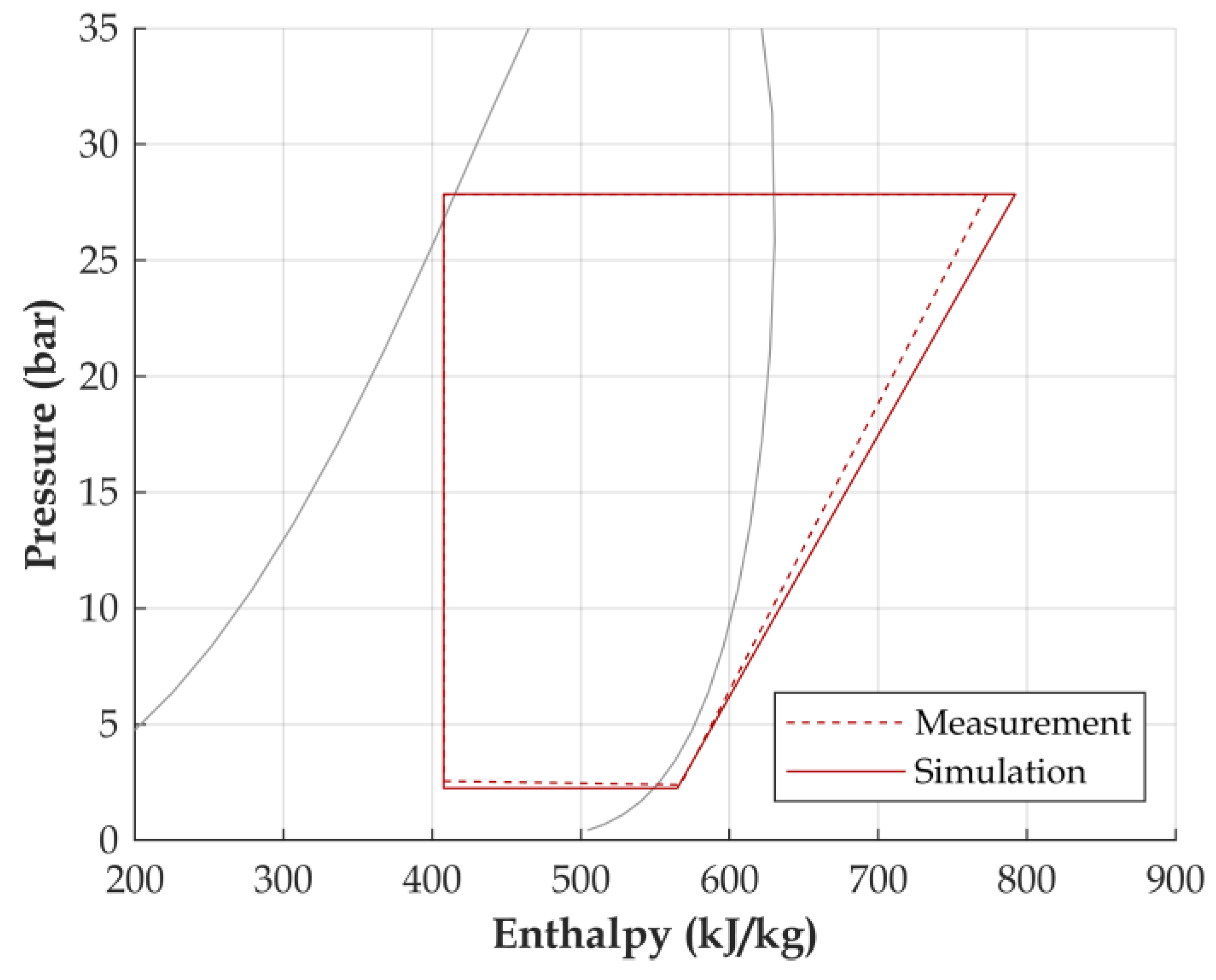
3.1. Models Validation
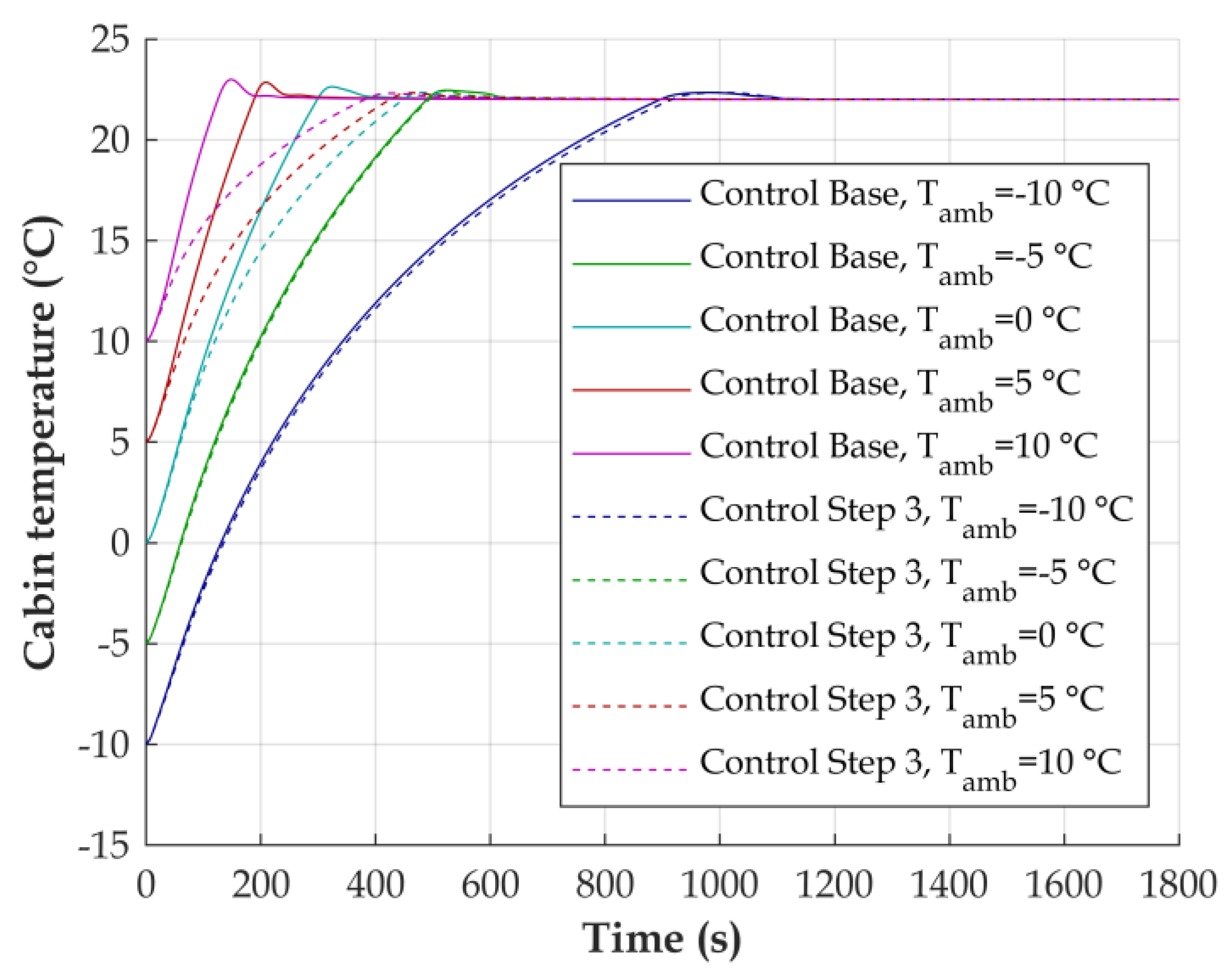
3.2. Demand-Based Control Strategy
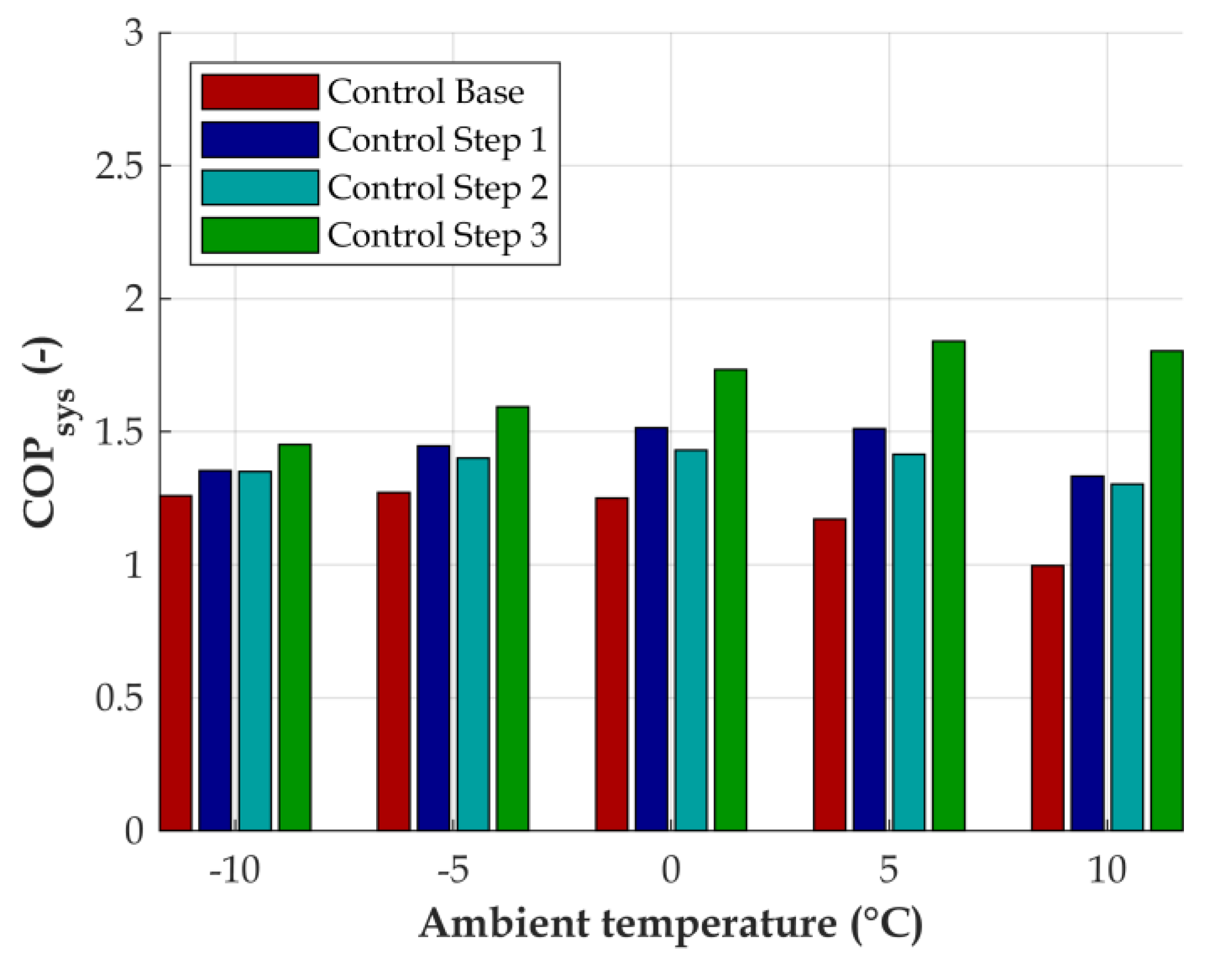
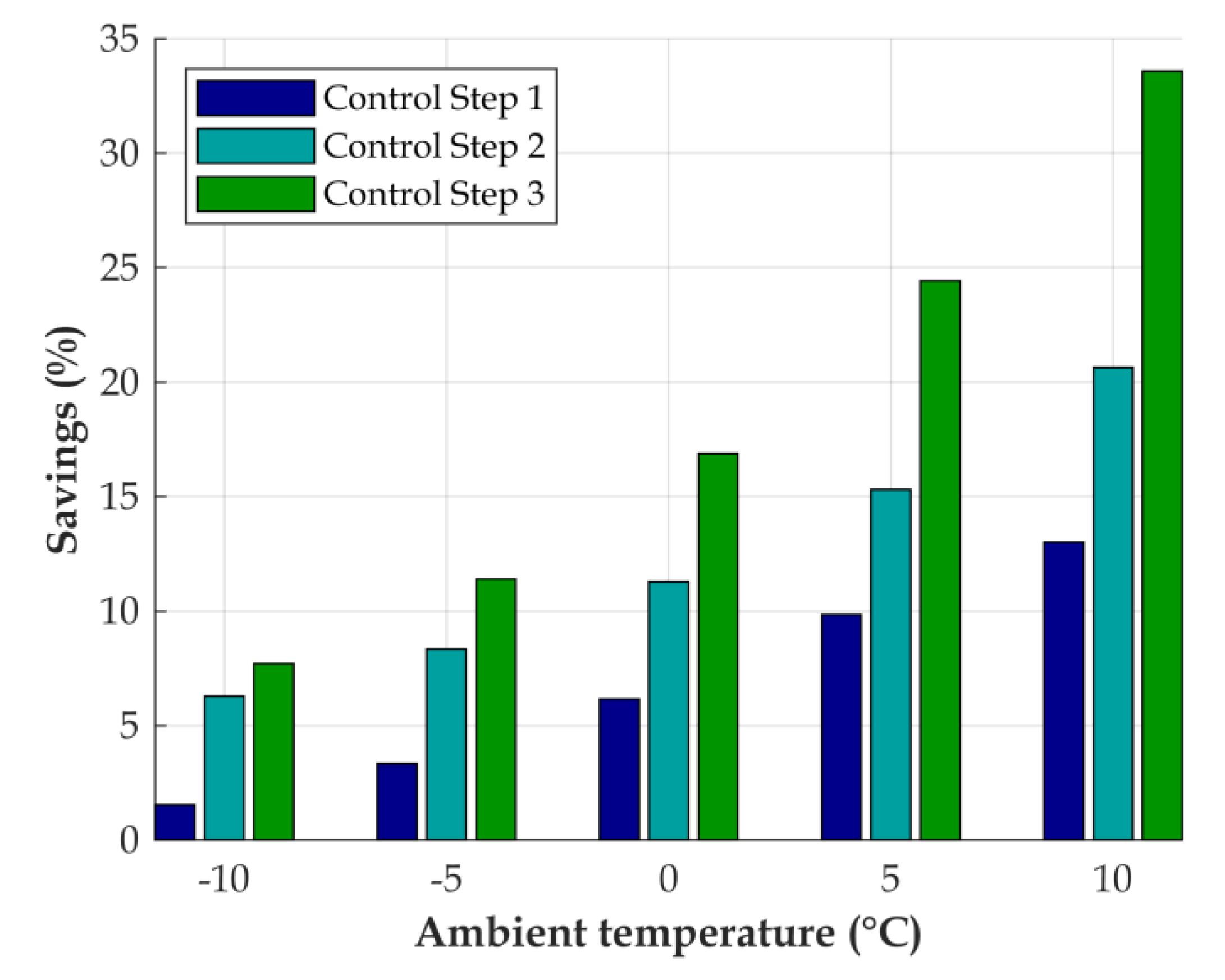
3.3. Use Case Results
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- New Electric Vehicles. Elektro Auto Mobil, Das Magazine für Elektromobilität, Overview BEV & PHEV, February/March 2019. Available online: https://www.elektroautomobil.com (accessed on 16 April 2020).
- ERTRACT. European Roadmap Electrification of Road Transport; ERTRACT: Brussels, Belgium, 2017. [Google Scholar]
- Thomas, C.E. Sustainable Transportation Options for the 21st Century and Beyond; Appendix A Range Limitations of Battery Electric Vehicles; Springer International Publishing: Cham, Switzerland, 2015; p. 119. [Google Scholar] [CrossRef]
- Franke, T.; Rauh, N.; Günther, M.; Trantow, M.; Krems, J.F. Which Factors Can Protect Against Range Stress in Everyday Usage of Battery Electric Vehicles? Toward Enhancing Sustainability of Electric Mobility Systems. Hum. Factors 2015, 58, 13–26. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Basciotti, D.; Dvorak, D.; Gellai, I. A Novel Methodology for Evaluating the Impact of Energy Efficiency Measures on the Cabin Thermal Comfort of Electric Vehicles. Energies 2020, 13, 3872. [Google Scholar] [CrossRef]
- Shete, K. Influence of Automotive Air Conditioning load on Fuel Economy of IC Engine Vehicles. Int. J. Sci. Eng. Res. 2015, 6, 1367–1372. [Google Scholar]
- Farrington, R.; Rugh, J. Impact of Vehicle Air Conditioning on Fuel Economy, Tailpipe Emissions, and Electric Vehicle Range. In Proceedings of the Earth Technologies Forum, Washington, DC, USA, 31 October 2000. [Google Scholar]
- Iora, P.; Tribioli, L. Effect of Ambient Temperature on Electric Vehicles’ Energy Consumption and Range: Model Definition and Sensitivity Analysis Based on Nissan Leaf Data. World Electr. Veh. J. 2019, 10, 2. [Google Scholar] [CrossRef] [Green Version]
- Paffumi, E.; Otura, M.; Centurelli, M.; Casellas, R.; Brenner, A.; Jahn, S. Driving Range and Cabin Temperature Performances at Different Ambient Conditions in Support to the Design of a User-Centric Efficient Electric Vehicle: The QUIET Project. In Proceedings of the 14th Conference on Sustainable Development of Energy, Water and Environment Systems 2019, Dubrovnik, Croatia, 1–6 October 2019. [Google Scholar]
- Park, J.; Lee, M.; Kim, G.; Park, S.; Kim, J. Integrated Approach Based on Dual Extended Kalman Filter and Multivariate Autoregressive Model for Predicting Battery Capacity Using Health Indicator and SOC/SOH. Energies 2020, 13, 2138. [Google Scholar] [CrossRef]
- Maletić, F.; Hrgetić, M.; Deur, J. Dual Nonlinear Kalman Filter-Based SoC and Remaining Capacity Estimation for an Electric Scooter Li-NMC Battery Pack. Energies 2020, 13, 540. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.U.; Zafar, A.; Nengroo, S.H.; Hussain, S.; Park, G.-S.; Kim, H.-J. Online Remaining Useful Life Prediction for Lithium-Ion Batteries Using Partial Discharge Data Features. Energies 2019, 12, 4366. [Google Scholar] [CrossRef] [Green Version]
- Liang, K.; Zhang, Z.; Liu, P.; Wang, Z.; Jiang, S. Data-Driven Ohmic Resistance Estimation of Battery Packs for Electric Vehicles. Energies 2019, 12, 4772. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; He, Y.; Li, Z.; Chen, L. A Combined Multiple Factor Degradation Model and Online Verification for Electric Vehicle Batteries. Energies 2019, 12, 4376. [Google Scholar] [CrossRef] [Green Version]
- Barcellona, S.; Piegari, L. Effect of current on cycle aging of lithium ion batteries. J. Energy Storage 2020, 29, 101310. [Google Scholar] [CrossRef]
- Vatanparvar, K.; Faezi, S.; Burago, I.; Levorato, M.; Al Faruque, M.A. Extended Range Electric Vehicle with Driving Behavior Estimation in Energy Management. IEEE Trans. Smart Grid 2018, 10, 2959–2968. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, W.; Shi, J.; Chen, J. A Study on Electric Vehicle Heat Pump Systems in Cold Climates. Energies 2016, 9, 881. [Google Scholar] [CrossRef] [Green Version]
- Rabl, B. Heat Pump Air Conditioning Systems for Optimized Energy Demand of Electric Vehicles. Comprehensive Energy Management—Safe Adaptation Predictive Control and Thermal Management. In SpringerBriefs in Applied Sciences and Technology; Graz University of Technology: Graz, Austria, 2018; pp. 81–92. [Google Scholar]
- Ozbek, M.; Gyorog, T.; Hunemorder, W.; Kohli, V.; Caldevilla, A.; Savi, A.; Vitali, D.; Biglia, M.; Nakagawa, M. A compact and efficient water-to-water heat-pump system for electric vehicles. In Proceedings of the 1st International FEV Conference: Zero C02 Mobility, Aachen, Germany, 9–10 November 2017. [Google Scholar]
- Lajunen, A. Energy Efficiency and Performance of Cabin Thermal Management in Electric Vehicles. SAE Tech. Pap. 2017. [Google Scholar] [CrossRef]
- Weustenfeld, T.A.; Bauer-Kugelmann, W.; Menken, J.C.; Strasser, K.; Köhler, J. Heat flow rate based thermal management for electric vehicles using a secondary loop heating and cooling system. In Proceedings of the Vehicle Thermal Management Systems Conference and Exhibition, Nottingham, UK, 10–13 May 2015. [Google Scholar]
- Osborne, S.; Kopinsky, J.; Norton, S.; Sutherland, A.; Lancaster, D.; Borgwarner, E.N.; Isenstadt, A.; German, J. Automotive Thermal Management Technology; The International Council on Clean Transportation (ICCT): Washington, DC, USA, 2016. [Google Scholar]
- Suh, I.-S.; Lee, M.; Kim, J.; Oh, S.T.; Won, J.-P. Design and experimental analysis of an efficient hvac (heating ventilation air-conditioning) system on an electric bus with dynamic on-road wireless charging. Energy 2015, 81, 262–273. [Google Scholar] [CrossRef]
- Leighton, D. Combined Fluid Loop Thermal Management for Electric Drive Vehicle Range Improvement. SAE Int. J. Passeng. Cars Mech. Syst. 2015, 8, 711–720. [Google Scholar] [CrossRef] [Green Version]
- Kitanoski, F.; Hofer, A. A contribution to energy optimal thermal management for vehicles. In Proceedings of the IFAC Symposium on Advances in Automotive Control, Munich, Germany, 14 July 2010; pp. 87–92. [Google Scholar]
- Fischer, T.; Götz, F.; Berg, L.F.; Kollmeier, H.-P.; Gauterin, F. Model-based development of a Holistic Thermal Management System for an Electric Car with a High Temperature Fuel Cell Range Extender. In Proceedings of the 11th International Modelica Conference, Versailles, France, 21–23 September 2015; pp. 127–133. [Google Scholar]
- De Nunzio, G.; Sciaretta, A.; Steiner, A.; Mladek, A. Thermal Management Optimization of a Heat-Pump-Based HVAC System for Cabin Conditioning in Electric Vehicles. In Proceedings of the International Conference on Ecological Vehicles and Renewable Energies, Monte-Carlo, Monaco, 10–12 April 2018. [Google Scholar]
- Hosoz, M.; Direk, M. Performance evaluation of an integrated automotive air conditioning and heat pump system. Energy Convers. Manag. 2006, 47, 545–559. [Google Scholar] [CrossRef]
- Al Faruque, M.A.; Vatanparvar, K. Modeling, analysis, and optimization of Electric Vehicle HVAC systems. In Proceedings of the 21st Asia and South Pacific Design Automation Conference (ASP-DAC), Macau, China, 25–28 January 2016. [Google Scholar]
- Hendricks, T.J. Vehicle Transient Air Conditioning Analysis: Model Development & System Optimization Investigations; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2001.
- Lee, H.; Hwang, Y.; Song, I.; Jang, K. Transient thermal model of passenger car’s cabin and implementation to saturation cycle with alternative working fluids. Energy 2015, 90, 1859–1868. [Google Scholar] [CrossRef]
- Modelica Standard Library. Available online: https://www.modelica.org/libraries (accessed on 16 April 2020).
- TIL Suite. Available online: https://www.tlk-thermo.com/index.php/en/software/til-suite (accessed on 16 April 2020).
- QUIET. Available online: http://www.quiet-project.eu (accessed on 16 April 2020).




| Heat Pump Mode | |
|---|---|
| Cabin air inlet temperature [°C] | [22–70] |
| Speed of water pump on condenser side [Hz] | [5–100] |
| Speed of water pump on evaporator side [Hz] | [5–100] |
| Ambient temperature [°C] | [−10, −5, 0, 5, 10] |
| Component | Quantity | Control Base | Control Step 1 | Control Step 2 | |
|---|---|---|---|---|---|
| Target air supply | Temperature | Constant | Ramp | f(Tamb) | f(Tamb) |
| Compressor | Speed | PI = f(Tin) | PI = f(Tin) | PI = f(Tin) | PI = f(Tin) |
| Expansion valve | Opening | PI = f(Tsh) | PI = f(Tsh) | PI = f(Tsh) | PI = f(Tsh) |
| Water pump condenser | Speed | Constant | Constant | Ramp | Constant |
| Water pump evaporator | Speed | Constant | Constant | Constant | Ramp |
| Cabin fan | Speed | PI = f(Tcab) | PI = f(Tcab) | PI = f(Tcab) | PI = f(Tcab) |
| Control Step | Component | Variation Variable | Start Value | End Value | Duration |
|---|---|---|---|---|---|
| 1 | Compressor | TinTarget | 70 °C | 22 °C | 10,000 s |
| 2 | Pump condenser | npumpCond | 100 Hz | 5 Hz | 10,000 s |
| Pump evaporator | npumpEvap | 100 Hz | 5 Hz | 10,000 s |
| Component | Controlled Variable | Control Base | Control Step 3 |
|---|---|---|---|
| Target air supply | Temperature | Constant | f(Tamb) |
| Compressor | Speed | PI = f(Tin) | PI = f(Tin) |
| Expansion valve | Opening | PI = f(Tsh) | PI = f(Tsh) |
| Water pump condenser | Speed | Constant | f(Tamb) |
| Water pump evaporator | Speed | Constant | f(Tamb) |
| Cabin fan | Speed | PI = f(Tcab) | PI = f(Tcab) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dvorak, D.; Basciotti, D.; Gellai, I. Demand-Based Control Design for Efficient Heat Pump Operation of Electric Vehicles. Energies 2020, 13, 5440. https://doi.org/10.3390/en13205440
Dvorak D, Basciotti D, Gellai I. Demand-Based Control Design for Efficient Heat Pump Operation of Electric Vehicles. Energies. 2020; 13(20):5440. https://doi.org/10.3390/en13205440
Chicago/Turabian StyleDvorak, Dominik, Daniele Basciotti, and Imre Gellai. 2020. "Demand-Based Control Design for Efficient Heat Pump Operation of Electric Vehicles" Energies 13, no. 20: 5440. https://doi.org/10.3390/en13205440
APA StyleDvorak, D., Basciotti, D., & Gellai, I. (2020). Demand-Based Control Design for Efficient Heat Pump Operation of Electric Vehicles. Energies, 13(20), 5440. https://doi.org/10.3390/en13205440







