Effects of Fluid Viscosity and Two-Phase Flow on Performance of ESP
Abstract
:1. Introduction
2. Viscous Effects
2.1. Performance Curves
2.2. Flow Mechanism
3. Two-Phase Flow in ESPs
3.1. Erosion Models
3.2. Erosion in ESPs
4. Challenges
4.1. Effects of Viscosity
4.2. Effects of Particles
4.3. Effects of Bubbles
5. Conclusion
Author Contributions
Funding
Conflicts of Interest
References
- Sukarno, P.; Saepudin, D.; Dewi, S.; Soewono, E.; Sidarto, K.A.; Gunawan, A.Y. Optimization of gas injection allocation in a dual gas lift well system. J. Energy Resour. Technol. 2009, 131. [Google Scholar] [CrossRef]
- Robello Samuel, G.; Saveth, K.J. Optimal Design of Progressing Cavity Pumps (PCP). J. Energy Resour. Technol. 2006, 128, 275–279. [Google Scholar] [CrossRef]
- Joel Romero, O.; Hupp, A. Subsea Electrical Submersible Pump Significance in Petroleum Offshore Production. J. Energy Res. Technol. 2013, 136, 012902. [Google Scholar] [CrossRef]
- Takacs, G. Electrical Submersible Pump Manual, Design, Operations and Maintenance; Elsevier: Amsterdam, The Netherlands, 2009; Available online: https://g0.njuu.cf/extdomains/books.google.com.sg/books?hl=zh-CN&lr=&id=isUpDwAAQBAJ&oi=fnd&pg=PP1&dq=Electrical+Submersible+Pump+Manual,+Design,+Operations+and+Maintenance&ots=jvs5sBjmw9&sig=k0pVzQyCg4rMfMLNWiooGpXFLWs#v=onepage&q=Electrical%20Submersible%20Pump%20Manual%2C%20Design%2C%20Operations%20and%20Maintenance&f=false (accessed on 10 February 2020).
- Carvajal Diaz, N. Effects of Sand on the Components and Performance of Electric Submersible Pumps. Master’s Dissertation, Texas A&M University, College Station, TX, USA, 2012. [Google Scholar]
- Yedidiah, S. A study in the use of CFD in the design of centrifugal pumps. Eng. Appl. Comput. Fluid Mech. 2008, 2, 331–343. [Google Scholar] [CrossRef] [Green Version]
- Li, W.-G. Effects of viscosity of fluids on centrifugal pump performance and flow pattern in the impeller. Int. J. Heat Fluid Flow 2000, 21, 207–212. [Google Scholar] [CrossRef]
- Amaral, G.; Estevam, V.; Franca, F.A. On the influence of viscosity on ESP performance. SPE Prod. Oper. 2009, 24, 303–311. [Google Scholar] [CrossRef]
- Stel, H.; Sirino, T.; Ponce, F.J.; Chiva, S.; Morales, R.E.M. Numerical investigation of the flow in a multistage electric submersible pump. J. Pet. Sci. Eng. 2015, 136, 41–54. [Google Scholar] [CrossRef]
- Ofuchi, E.M.; Stel, H.; Sirino, T.; Vieira, T.S.; Ponce, F.J.; Chiva, S.; Morales, R.E.M. Numerical investigation of the effect of viscosity in a multistage electric submersible pump. Eng. Appl. Comput. Fluid Mech. 2017, 11, 258–272. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Banjar, H.; Xia, Z.; Zhang, H.-Q. CFD simulation and experimental study of oil viscosity effect on multi-stage electrical submersible pump (ESP) performance. J. Pet. Sci. Eng. 2016, 146, 735–745. [Google Scholar] [CrossRef]
- Basaran, B. CFD Simulation for the Erosion on Electrical Submersible Pump due to Viscosity and Air presence. Master’s Dissertation, Texas A&M University, College Station, TX, USA, 2017. [Google Scholar]
- Gerald Morrison, Y.; Daniel, S.; Yiming, C.; Changrui, B.; Abhay, P. Effect of Gas Presence on Erosive Wear of Split-Vane Electrical Submersible Pump. In Proceedings of the Turbomachinery and Pump Symposia, Houston, TX, USA, 11–14 December 2017. [Google Scholar]
- Stepanoff, A.J. Centrifugal and Axial Flow Pumps: Theory, Design, and Application. 1957. Available online: https://www.sciencedirect.com/science/article/abs/pii/0016003257900431 (accessed on 10 February 2020).
- Solano, E.A. Viscous Effects on the Performance of Electrical Submersible Pumps (ESPs). Master’s Thesis, University of Tulsa, Tulsa, OK, USA, 2009. [Google Scholar]
- Ofuchi, E.M.; Stel, H.; Vieira, T.S.; Ponce, F.J.; Chiva, S. Morales, Study of the effect of viscosity on the head and flow rate degradation in different multistage electric submersible pumps using dimensional analysis. J. Pet. Sci. Eng. 2017, 156, 442–450. [Google Scholar] [CrossRef]
- Hydraulic, I. Tentative Standards of Hydraulic Institute: Charts for the Determination of Pump Performance When Handling Viscous Liquids; The Institute: NewYork, NY, USA, 1948. [Google Scholar]
- Timár, P. Dimensionless Characteristics of Centrifugal Pump. Chem. Papers-Slovak Acad. Sci. 2005, 59, 500. [Google Scholar]
- Gülich, J.F. Pumping highly viscous fluids with centrifugal pumps—Part 2. World Pumps 1999, 1999, 39–42. [Google Scholar]
- Zhu, J.; Zhu, H.; Cao, G.; Zhang, J.; Peng, J.; Banjar, H.; Zhang, H.-Q. A New Mechanistic Model to Predict Boosting Pressure of Electrical Submersible Pumps Under High-Viscosity Fluid Flow with Validations by Experimental Data. SPE J. 2019. [Google Scholar] [CrossRef]
- Morrison, G.; Yin, W.; Agarwal, R.; Patil, A. Development of Modified Affinity Law for Centrifugal Pump to Predict the Effect of Viscosity. J. Energy Res. Technol. 2018, 140, 092005. [Google Scholar] [CrossRef]
- Patil, A.; Morrison, G. Affinity Law Modified to Predict the Pump Head Performance for Different Viscosities Using the Morrison Number. J. Fluids Eng. 2019, 141, 141. [Google Scholar] [CrossRef]
- Li, W.-G. Mechanism for onset of sudden-rising head effect in centrifugal pump when handling viscous oils. J. Fluids Eng. 2014, 136, 074501. [Google Scholar] [CrossRef]
- Ippen, A.T. The influence of viscosity on centrifugal pump performance. Trans. ASME 1946, 68, 823–848. [Google Scholar]
- Divine, D.L.; Lannom, R.W.; Johnson, R.A. Determining Pump Wear and Remaining Life From Electric Submersible Pump Test Curves. SPE Prod. Facil. 1993, 8, 217–221. [Google Scholar] [CrossRef]
- Sun, D.; Prado, M.G. Single-phase model for electric submersible pump (ESP) head performance. SPE J. 2006, 11, 80–88. [Google Scholar] [CrossRef]
- Vieira, T.S.; Siqueira, J.R.; Bueno, A.D.; Morales, R.E.M.; Estevam, V. Analytical study of pressure losses and fluid viscosity effects on pump performance during monophase flow inside an ESP stage. J. Pet. Sci. Eng. 2015, 127, 245–258. [Google Scholar] [CrossRef]
- Banjar, H.M. Experiments, CFD Simulation and Modeling of Oil Viscosity and Emulsion Effects on ESP Performance. Ph.D. Thesis, The University of Tulsa, Tulsa, OK, USA, 2018. [Google Scholar]
- Gülich, J.F. Pumping highly viscous fluids with centrifugal pumps—Part 1. World Pumps 1999, 1999, 30–34. [Google Scholar] [CrossRef]
- Barrios, L.; Prado, M.G. Experimental visualization of two-phase flow inside an electrical submersible pump stage. J. Energy Resour. Technol. 2011, 133, 042901. [Google Scholar] [CrossRef]
- Noghrehkar, G.; Kawaji, M.; Chan, A.; Nakamura, H.; Kukita, Y. Investigation of Centrifugal Pump Performance under Two-Phase Flow Conditions. J. Fluids Eng. 1995, 117, 129–137. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, J.; Zhu, J.; Rutter, R.; Zhang, H.-Q. A Numerical Study of Turbulence Model and Rebound Model Effect on Erosion Simulations in an Electrical Submersible Pump (ESP). In Proceedings of the ASME-JSME-KSME 2019 8th Joint Fluids Engineering Conference, San Francisco, CA, USA, 28 July–1 August 2019. [Google Scholar]
- Zhu, H.; Zhu, J.; Rutter, R.; Zhang, H.-Q. A Numerical Study on Erosion Model Selection and Effect of Pump Type and Sand Characters in Electrical Submersible Pumps by Sandy Flow. J. Energy Res. Technol. 2019, 141, 1–58. [Google Scholar] [CrossRef]
- Russell, R.; Marsis, E. A state-of-the-art computational fluid dynamics simulation for erosion rates prediction in a bottom hole electrical submersible pump. In Proceedings of the SPE Heavy Oil Conference-Canada, Alberta, Canada, 11–13 June 2013. [Google Scholar]
- King, D.; Traylor, F.; Stewart, R. Abrasion Technology for Electric Submergible Pumps. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Francisco, CA, USA, 5–8 October 1983. [Google Scholar]
- Morrison, G.; Carvajal, N.; Saleh, R.; Bai, C. The Measured Impact of Erosion on the Rotodynamic and Performance Characteristics of a Mixed Flow ESP. In Proceedings of the 31st International Pump Users Symposium, Houston, TX, USA, 14–17 September 2015. [Google Scholar]
- Ahlert, K.R. Effects of Particle Impingement Angle and Surface Wetting on Solid Particle Erosion of AISI 1018 Steel; University of Tulsa: Tulsa, OK, USA, 1994. [Google Scholar]
- Haugen, K.; Kvernvold, O.; Ronold, A.; Sandberg, R. Sand erosion of wear-resistant materials: Erosion in choke valves. Wear 1995, 186, 179–188. [Google Scholar] [CrossRef]
- Oka, Y.; Okamura, K.; Yoshida, T. Practical estimation of erosion damage caused part 2: Mechanical properties of materials directly associated with erosion damage. Wear 2005, 259, 102–109. [Google Scholar] [CrossRef]
- Zhang, Y.; Reuterfors, E.; McLaury, B.S.; Shirazi, S.; Rybicki, E. Comparison of computed and measured particle velocities and erosion in water and air flows. Wear 2007, 263, 330–338. [Google Scholar] [CrossRef]
- Mansouri, A. Development of Erosion Equations for Slurry Flows; Advisory Board Report; Erosion/Corrosion Research Center, the University of Tulsa: Tulsa, OK, USA, 2014. [Google Scholar]
- DNV, G. Recommended Practice–DNVGL-RP-O501–Managing Sand Production and Erosion; DNV GL: Akershus, Norway, 2015; pp. 3–60. [Google Scholar]
- Gülich, J.F. Centrifugal Pumps; Springer: Berlin/Heidelberg, Germany, 2008; Volume 2. [Google Scholar]
- Finnie, I. Erosion of surfaces by solid particles. Wear 1960, 3, 87–103. [Google Scholar] [CrossRef]
- Finnie, I. Some observations on the erosion of ductile metals. Wear 1972, 19, 81–90. [Google Scholar] [CrossRef]
- Bitter, J.G.A. A study of erosion phenomena part I. Wear 1963, 6, 5–21. [Google Scholar] [CrossRef]
- Bitter, J. A study of erosion phenomena: Part II. Wear 1963, 6, 169–190. [Google Scholar] [CrossRef]
- Neilson, J.; Gilchrist, A. Erosion by a stream of solid particles. Wear 1968, 11, 111–122. [Google Scholar] [CrossRef]
- Jianmin, D.; Lyczkowski Robert, W. Three-dimensional kinetic theory modeling of hydrodynamics and erosion in fluidized beds. Powder Technol. 1992, 73, 127–138. [Google Scholar]
- Zhu, H.; Zhu, J.; Rutter, R. Sand Erosion Model Prediction, Selection and Comparison for Electrical Submersible Pump (ESP) Using CFD Method. In Proceedings of the ASME 2018 5th Joint US-European Fluids Engineering Division Summer Meeting, Montreal, QC, Canada, 15–20 July 2018. [Google Scholar]
- Grant, G.; Tabakoff, W. Erosion prediction in turbomachinery resulting from environmental solid particles. J. Aircr. 1975, 12, 471–478. [Google Scholar] [CrossRef]
- Forder, A.; Thew, M.; Harrison, D. A numerical investigation of solid particle erosion experienced within oilfield control valves. Wear 1998, 216, 184–193. [Google Scholar] [CrossRef]
- Lyczkowski, R.W.; Bouillard, J. State-of-the-art review of erosion modeling in fluid/solids systems. Prog. Energy Combust. 2002, 28, 543–602. [Google Scholar] [CrossRef]
- Levy, A.V.; Chik, P. The effects of erodent composition and shape on the erosion of steel. Wear 1983, 89, 151–162. [Google Scholar] [CrossRef] [Green Version]
- Khalid, Y.A.; Sapuan, S.M. Wear analysis of centrifugal slurry pump impellers. Ind. Lubr. Tribol. 2007, 59, 18–28. [Google Scholar] [CrossRef]
- Batalović, V. Erosive Wear Model Slurry Pump Impeller. J. Tribol. 2010, 132, 021602. [Google Scholar] [CrossRef]
- Zhong, Y.; Minemura, K. Measurement of erosion due to particle impingement and numerical prediction of wear in pump casing. Wear 1996, 199, 36–44. [Google Scholar] [CrossRef]
- Krüger, S.; Martin, N.; Dupont, P. Assessment of wear erosion in pump impellers. In Proceedings of the 26th International Pump Users Symposium, Turbomachinery Laboratory, Texas A&M University, College Station, TX, USA, 16–18 March 2010. [Google Scholar]
- Noon, A.A.; Kim, M.-H. Erosion wear on centrifugal pump casing due to slurry flow. Wear 2016, 364–365, 103–111. [Google Scholar]
- Xiao, Y.; Guo, B.; Ahn, S.-H.; Luo, Y.; Wang, Z.; Shi, G.; Li, Y. Slurry Flow and Erosion Prediction in a Centrifugal Pump after Long-Term Operation. Energies 2019, 12, 523. [Google Scholar]
- Pirouzpanah, S.; Patil, A.; Chen, Y.; Morrison, G. Predictive erosion model for mixed flow centrifugal pump. J. Energy Res. Technol. 2019, 141. [Google Scholar] [CrossRef]
- Shojaeefard, M.; Tahani, M.; Ehghaghi, M.; Fallahian, M.; Beglari, M. Numerical study of the effects of some geometric characteristics of a centrifugal pump impeller that pumps a viscous fluid. Comput. Fluids 2012, 60, 61–70. [Google Scholar]
- Shojaeefard, M.; Tahani, M.; Khalkhali, A.; Ehghaghi, M.; Fallah, H.; Beglari, M. A parametric study for improving the centrifugal pump impeller for use in viscous fluid pumping. Heat Mass Transfer. 2013, 49, 197–206. [Google Scholar]
- Duran, J. Pressure Effects on ESP Stages Air-Water Performance; University of Tulsa: Tulsa, OK, USA, 2003. [Google Scholar]
- Minemura, K.; Uchiyama, T. Three-dimensional calculation of air-water two-phase flow in centrifugal pump impeller based on a bubbly flow model. J. Fluids Eng. 1993, 115, 766–771. [Google Scholar]
- Minemura, K.; Uchiyama, T.; Shoda, S.; Egashira, K. Prediction of air-water two-phase flow performance of a centrifugal pump based on one-dimensional two-fluid model. J. Fluids Eng. 1998, 120, 327–334. [Google Scholar]
- Yiming, C.; Abhay, P.; Yi, C.; Changrui, B.; Yintao, W.; Gerald, M. Numerical Study on the First Stage Head Degradation in an Electrical Submersible Pump with Population Balance Model. J. Energy Res. Technol. 2018, 141, 022003. [Google Scholar]
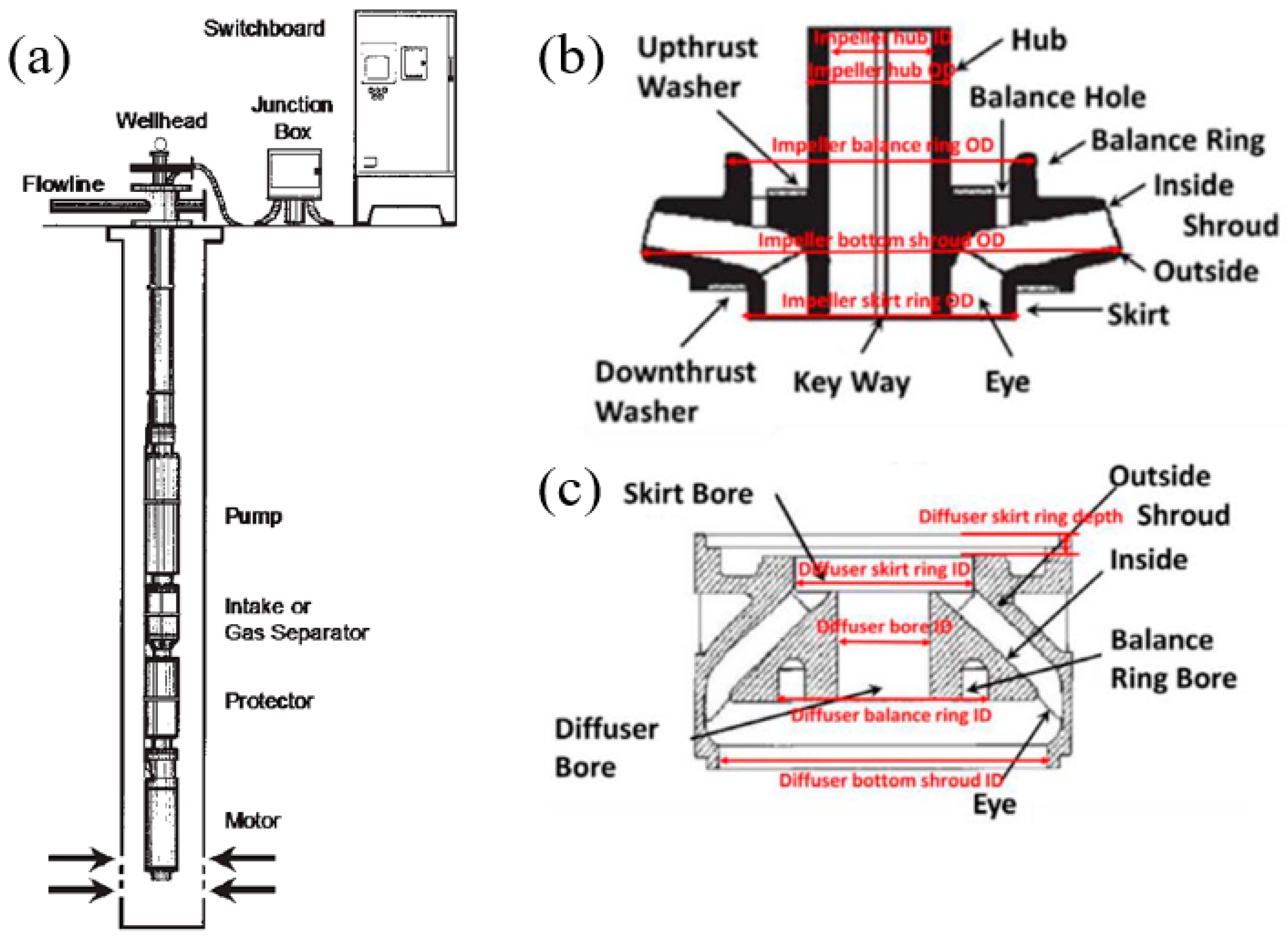
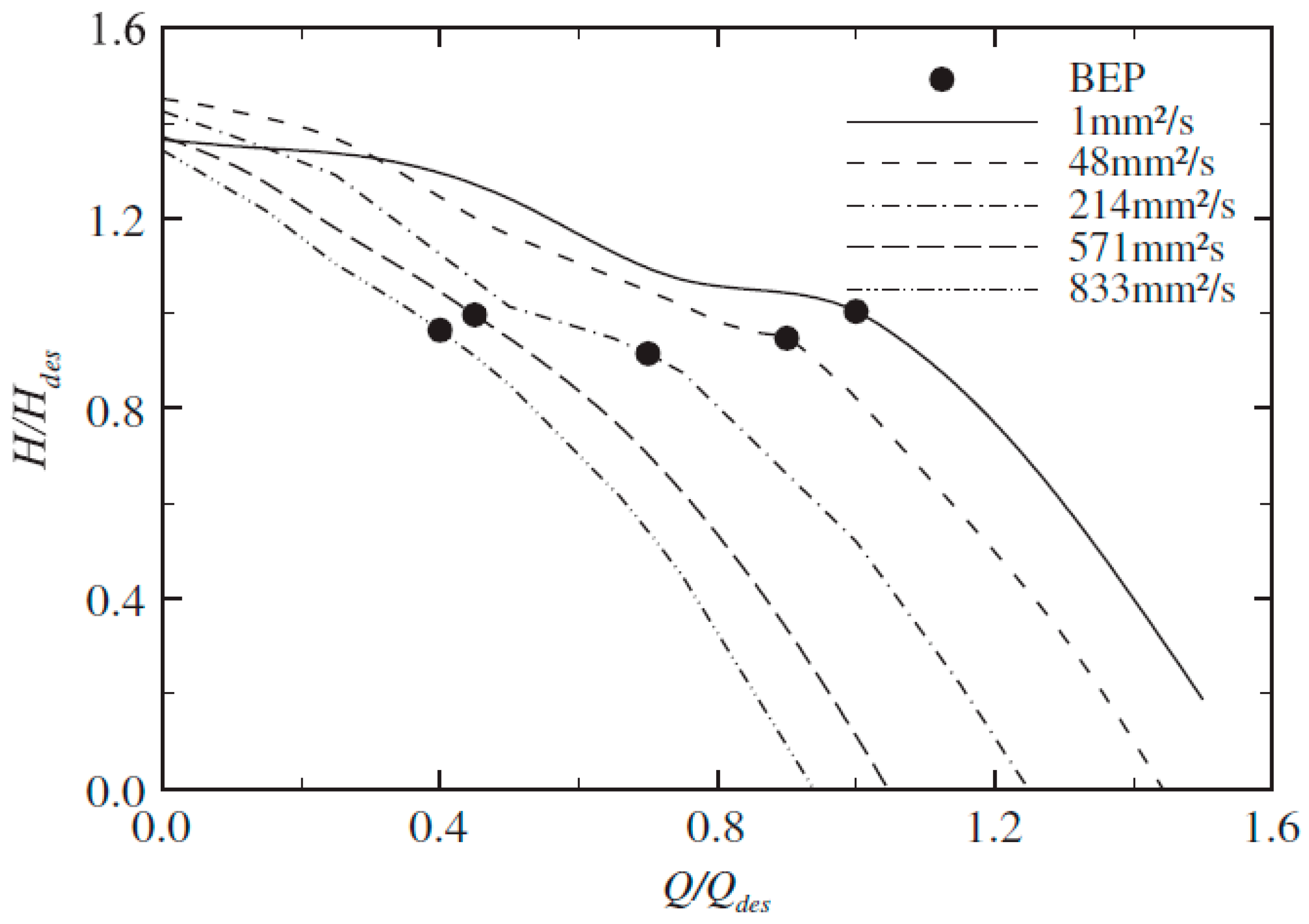
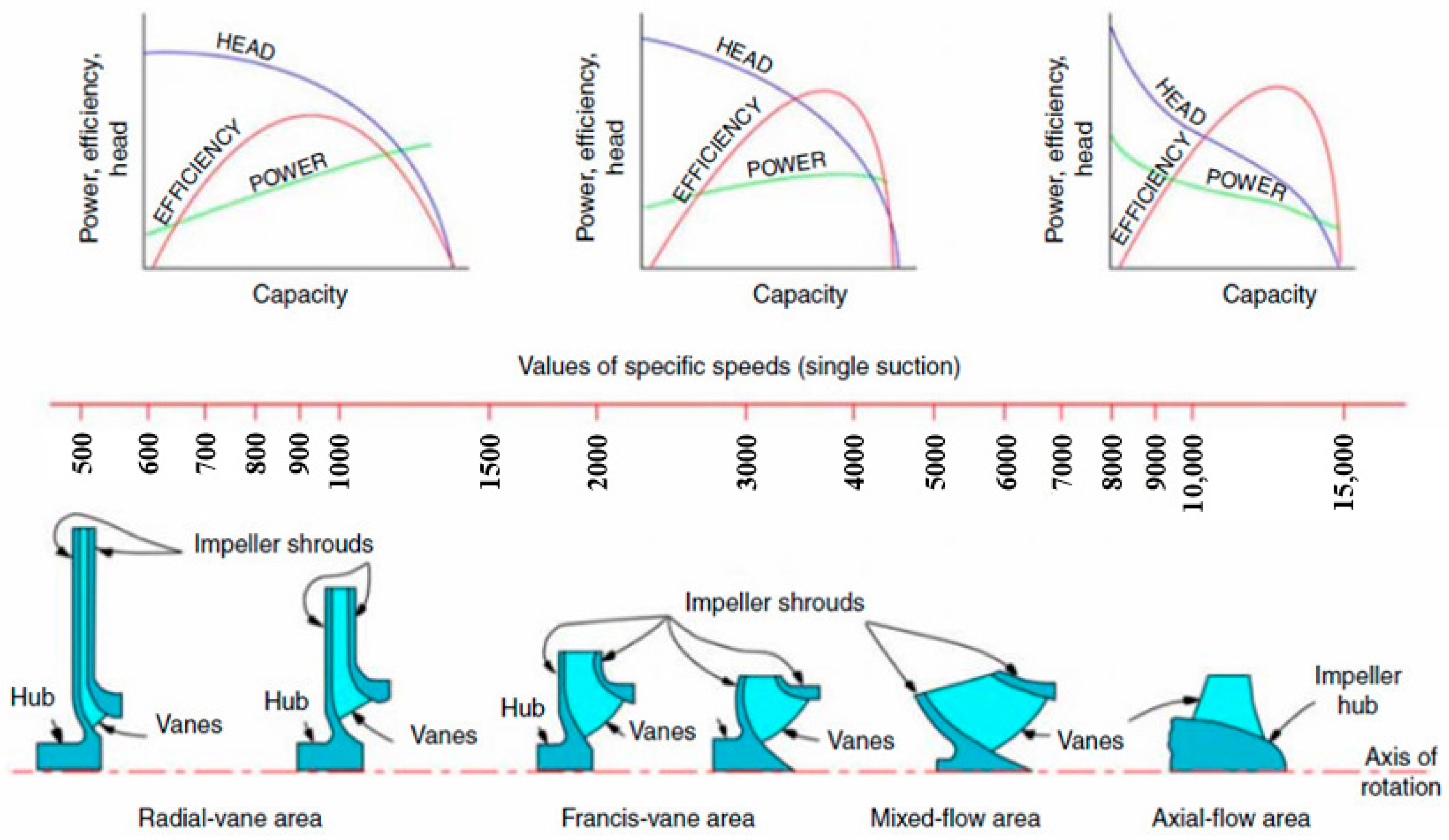

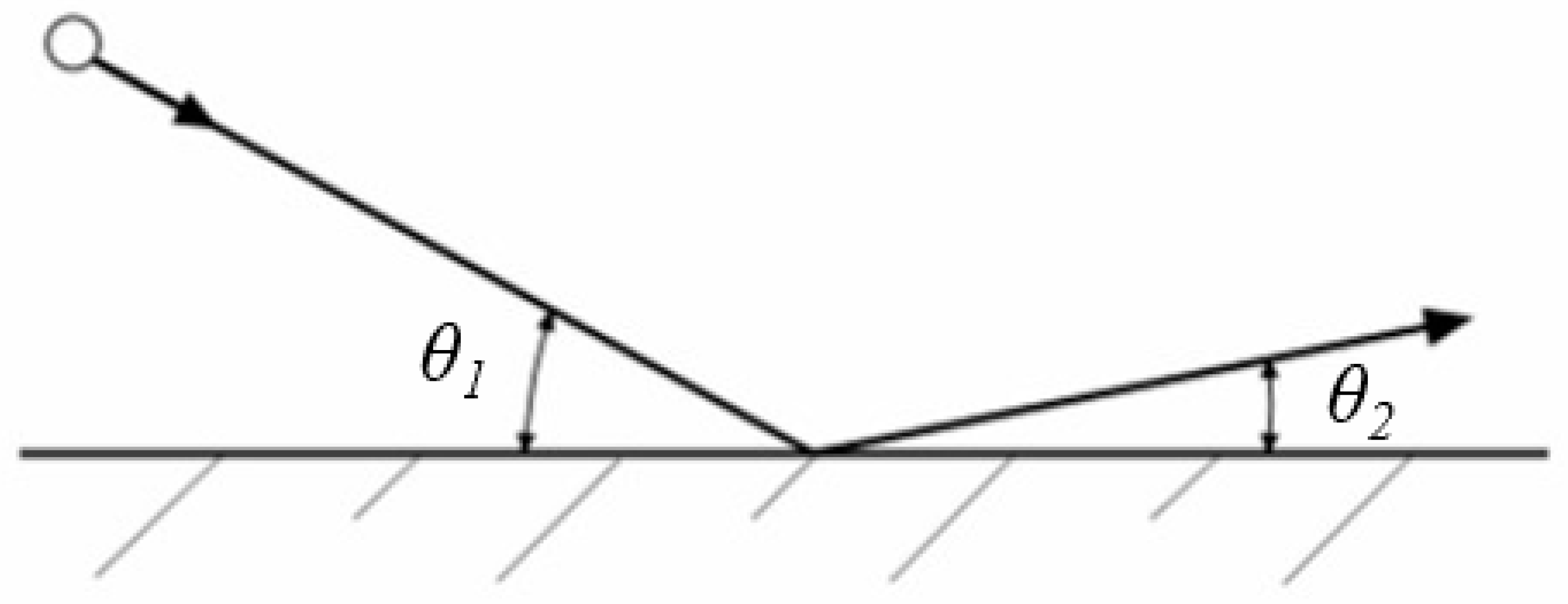
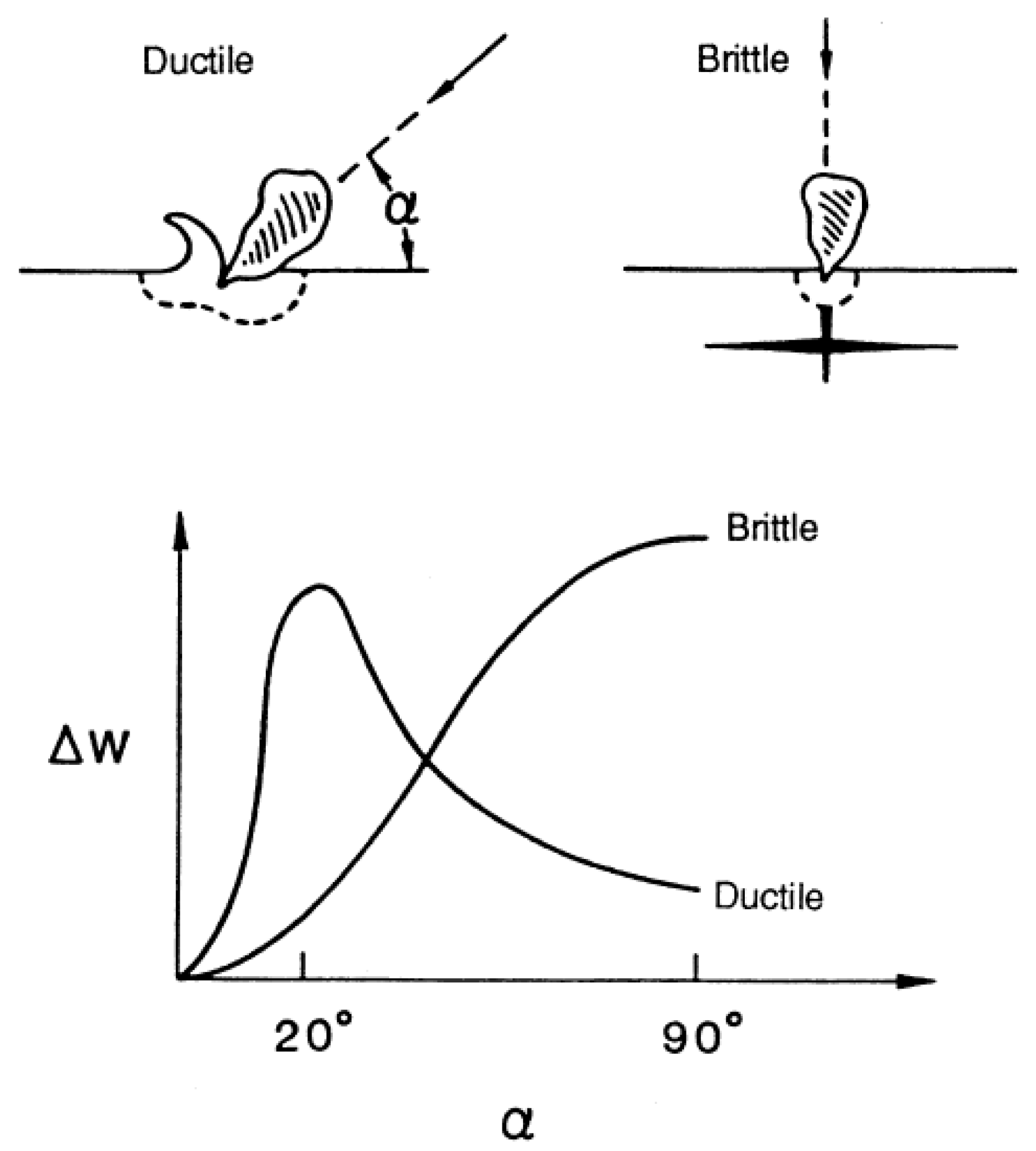
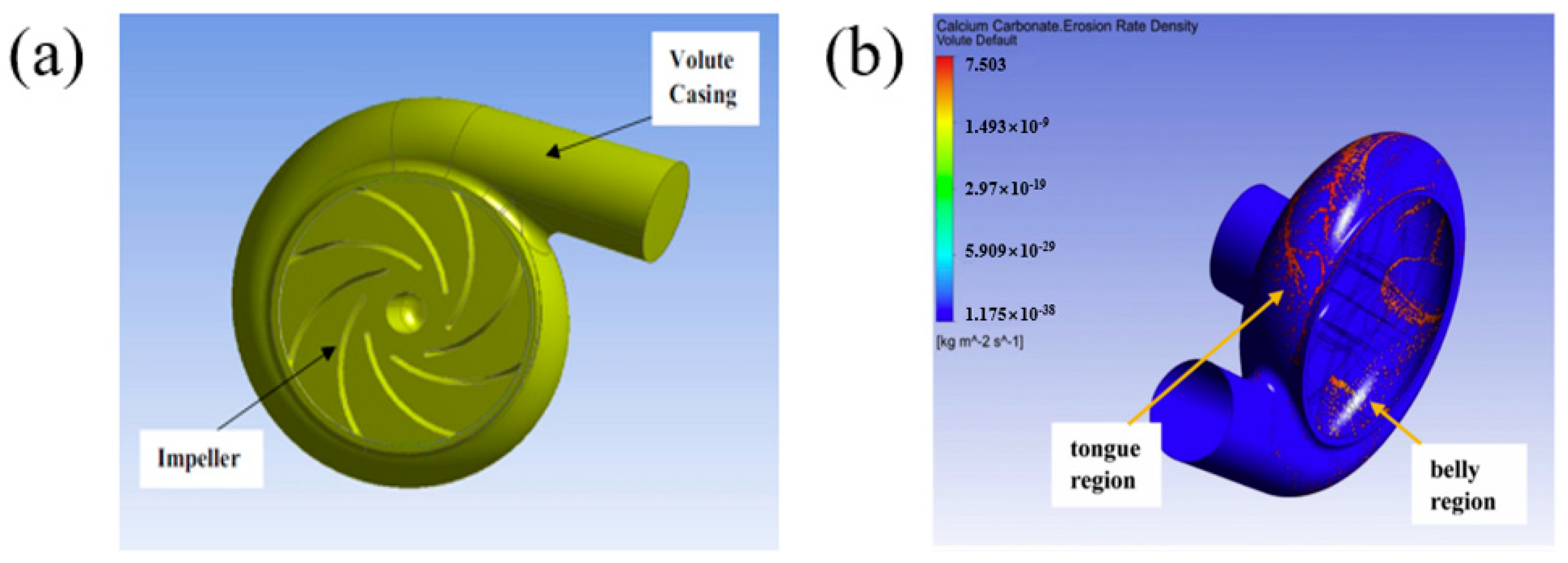
| Approach | Article | Overview |
|---|---|---|
| Empirical correlation | Hydraulic Institute Standards (1948) [17] | Correction coefficients were proposed within a narrow range of specific speeds. |
| Stepanoff (1957) [14] | A new correlation at constant specific speed was proposed. | |
| Experimental tests | Li (2000) [7] | The change in flow pattern was observed through experimental tests. |
| Amaral et al. (2009) [8] | The interaction between impellers and diffusers was proposed to be vital. | |
| CFD simulations | Li (2014) [23] | Skin friction factors were supposed to result in the sudden rising head effect with the standard k-ε turbulence model in Fluent. |
| Stel et al. (2015) [9] | Performance of the first stage was found to be different from that of the following stages with the SST turbulence model in ANSYS CFX 14.5 (ANSYS Inc., Pittsburgh, PA, USA.). | |
| Ofuchi et al. (2017) [10] | Turbulence spread and backflow were used to explain difference between stages with the SST turbulence model in ANSYS CFX 14.5. | |
| Experimental tests and CFD simulations | Zhu et al. (2016) [11] | The flow regime transition was thought to strengthen the recirculation with the SST turbulence model in ANSYS CFX 15. |
| Banjar (2018) [28] | A mechanistic model was proposed with oil–water emulsion effects studied using the SST turbulence model in ANSYS CFX. | |
| Dimensionless analysis | Solano (2009) [15] | Degradation was confirmed at constant specific speed for off-design conditions. |
| Ofuchi et al. (2017) [16] | Normalized specific speeds were proposed to predict performance without geometry. | |
| Morrison et al. (2018) [21] | Morrison’s number was defined to get the relationship between parameters. | |
| Patil and Morrison (2019) [22] | The specific formula to get Morrison’s number was given. | |
| Analytical model | Ippen (1946) [24] | A new analytical model related to Reynolds number was given. |
| Gülich (1999a,1999b) [19,29] | A new analytical procedure was given with all the losses considered. | |
| Sun and Prado (2003) [26] | A one-dimensional analytical model was given with hydraulic friction and shock loss included. | |
| Vieira (2015) [27] | Combinations of pressure losses were proposed to agree with experimental data. | |
| Zhu et al. (2019) [20] | A new mechanistic model was said to be applicable for all pumps. |
| A1 | A2 | A3 | A4 | A5 | A6 | ||
|---|---|---|---|---|---|---|---|
| Tabakoff | eN | 0.993 | −1.76 | 1.56 | −0.49 | - | - |
| eT | 0.988 | −1.66 | 2.11 | −0.67 | - | - | |
| Forder | eN | 0.988 | −0.78 | 0.19 | −0.024 | 0.0027 | - |
| eT | 1 | −0.78 | 0.84 | −0.21 | 0.028 | −0.022 |
| Approach | Article | Overview |
|---|---|---|
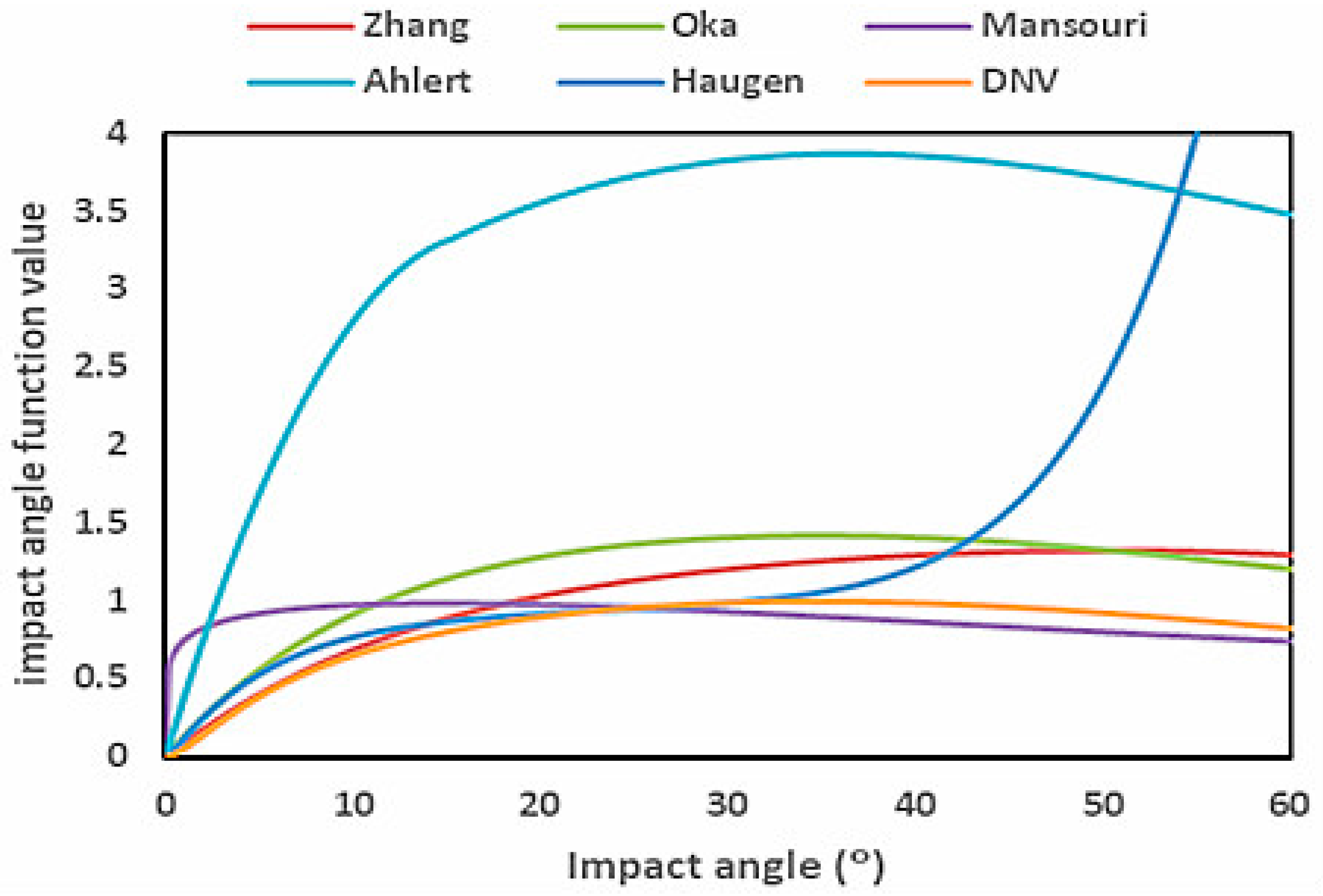
| Empirical model | Ahlert (1994) [37] | The impact angle function was split into two parts. |
| Haugen (1995) [38] | Carbon steel was taken as a brittle material. | |
| Oka (2005) [39] | The erosion rate was calculated with a reference situation. | |
| Zhang (2007) [40] | Ahlert’s model was extended with a polynomial function. | |
| Gülich (2008) [43] | An ESP was divided into several parts according to geometry and flow parameters. | |
| Mansouri (2014) [41] | A trigonometric impact angle function was introduced. | |
| DNV (2015) [42] | Haugen et al.’s model was extended for both brittle and ductile materials. | |
| Mechanistic model | Finnie (1960,1972) [44,45] | A single-particle erosion model for ductile material was proposed. |
| Bitter (1963) [46,47] | A threshold velocity was defined to combine ductile and brittle erosion model. | |
| Neilson (1968) [48] | Bitter’s model was simplified with an empirical constant. | |
| Ding (1992) [49] | Repeated impact of particles was included with the kinetic theory of the granular flow. | |
| Experimental tests | Levy (1983) [54] | Particle hardness could be neglected when it was high enough. |
| Khalid (2007) [55] | Average height loss of the blade was determined to represent the wear content. | |
| Batalović (2010) [56] | A new statistical model was introduced to predict pump working life. | |
| Morrison (2015) [36] | Leakage was believed to cause the decrease in overall head and efficiency. | |
| CFD simulations | Zhong (1996) [57] | Bitter’s model was confirmed, and prediction of pump casing wear was conducted with programming calculation. |
| Kruger (2010) [58] | Erosion processes were split into shock-like and friction-like processes with the Eulerian-Eulerian model. | |
| Noon (2016) [59] | The tongue and belly area were found to be damaged most seriously with Finnie’s model in ANSYS CFX. | |
| Xiao (2019) [60] | The erosion rate was believed to be reduced during the evolution of pump wear with Finnie’s model in ANSYS CFX 17. | |
| Pirouzpanah (2019) [61] | Turbulence kinetic energy was considered the key parameter to predict the erosion rate with the Eulerian–granular model in Fluent. | |
| Zhu (2019) [32,33] | Various turbulence and erosion models were compared with experimental data of erosion with the Eulerian-Lagrangian model in ANSYS Fluent 17.2. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Wang, Y.; Yan, F.; Nie, C.; Ouyang, X.; Xu, J.; Gong, J. Effects of Fluid Viscosity and Two-Phase Flow on Performance of ESP. Energies 2020, 13, 5486. https://doi.org/10.3390/en13205486
Liu P, Wang Y, Yan F, Nie C, Ouyang X, Xu J, Gong J. Effects of Fluid Viscosity and Two-Phase Flow on Performance of ESP. Energies. 2020; 13(20):5486. https://doi.org/10.3390/en13205486
Chicago/Turabian StyleLiu, Peng, Yumo Wang, Feng Yan, Chaofei Nie, Xin Ouyang, Jiashuang Xu, and Jing Gong. 2020. "Effects of Fluid Viscosity and Two-Phase Flow on Performance of ESP" Energies 13, no. 20: 5486. https://doi.org/10.3390/en13205486
APA StyleLiu, P., Wang, Y., Yan, F., Nie, C., Ouyang, X., Xu, J., & Gong, J. (2020). Effects of Fluid Viscosity and Two-Phase Flow on Performance of ESP. Energies, 13(20), 5486. https://doi.org/10.3390/en13205486





