Thermophysical Properties of 1,1,1,3,3,3-hexafluoro-2-methoxypropane (HFE-356mmz) in the Vapor Phase Measured by Using an Acoustic-Microwave Resonance Technique
Abstract
:1. Introduction
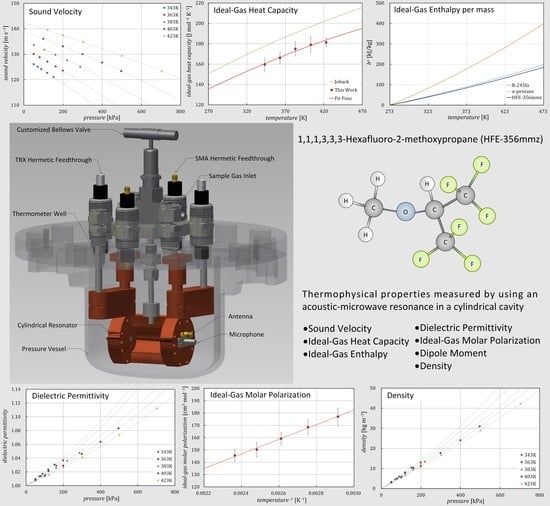
2. Experimental Setup
3. Measurement Results
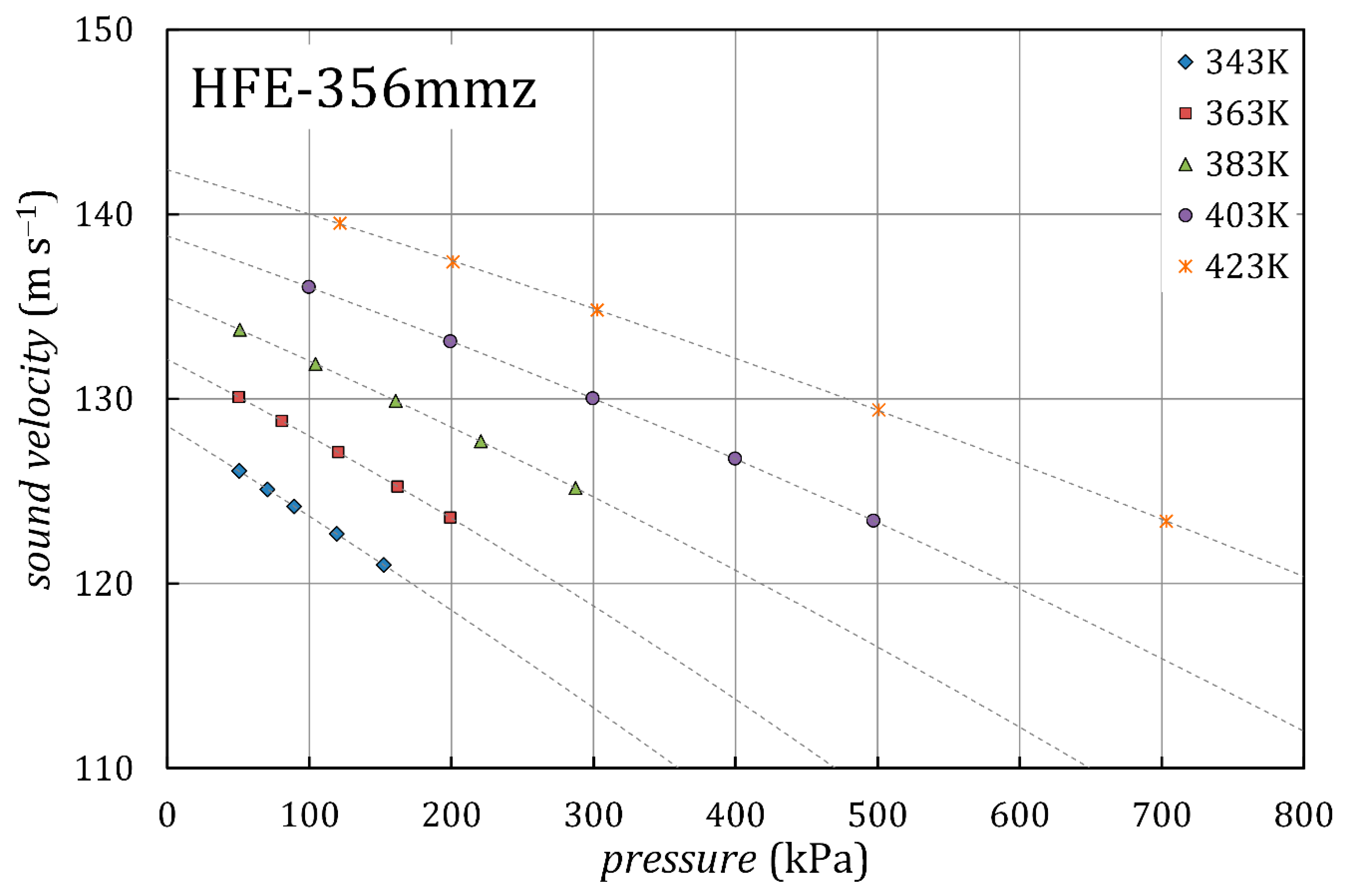
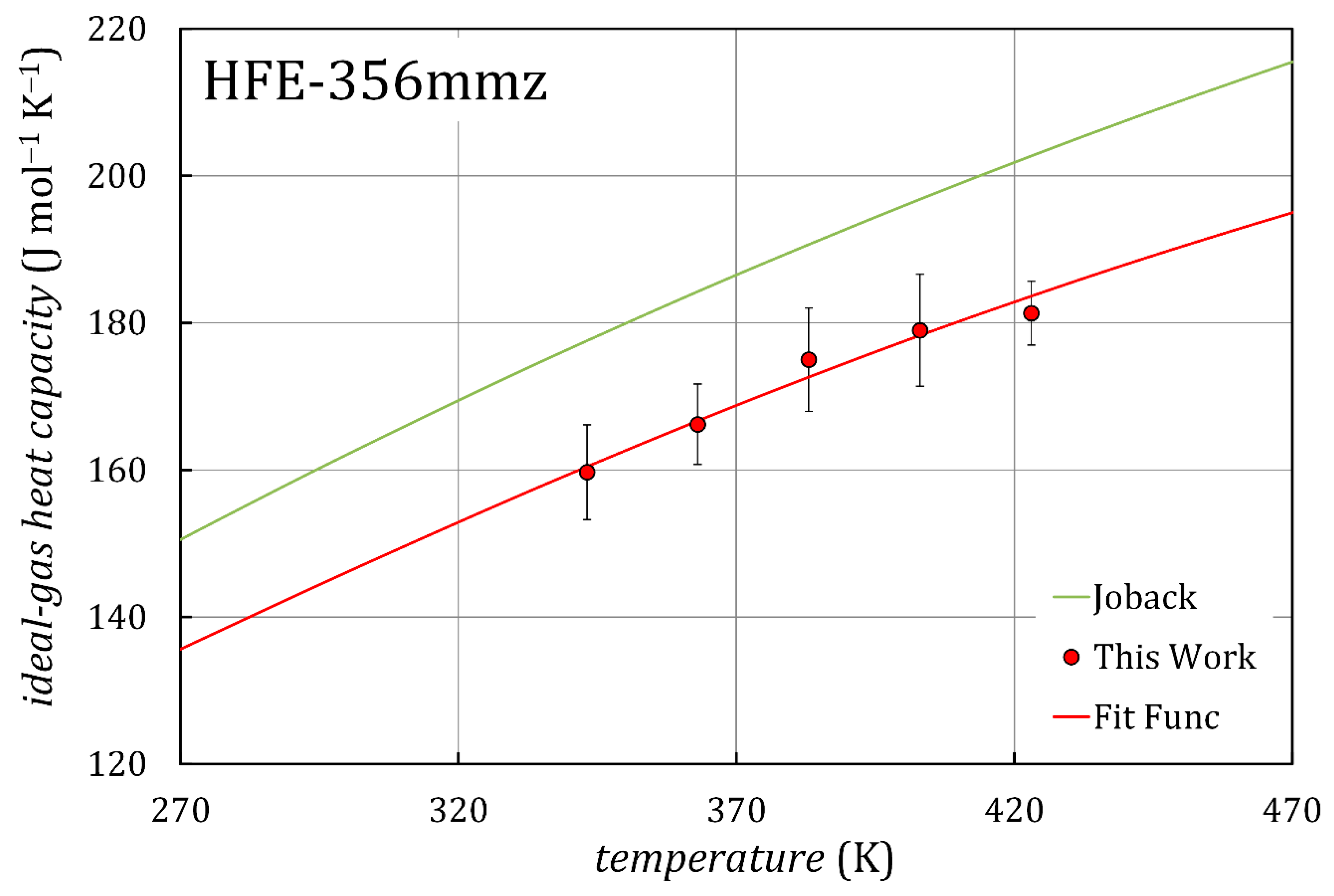
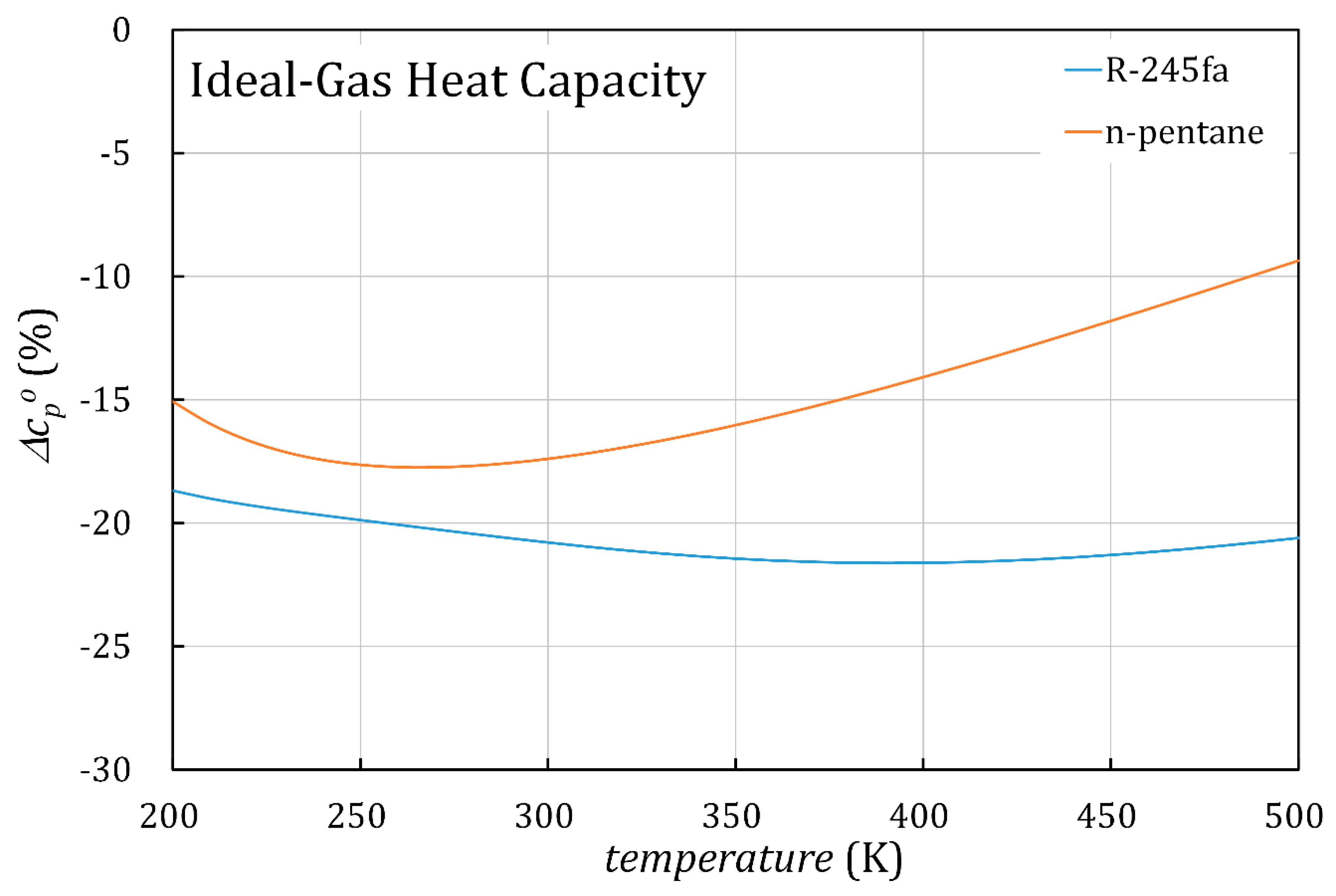
3.1. Sound Velocity and Ideal-Gas Heat Capacity
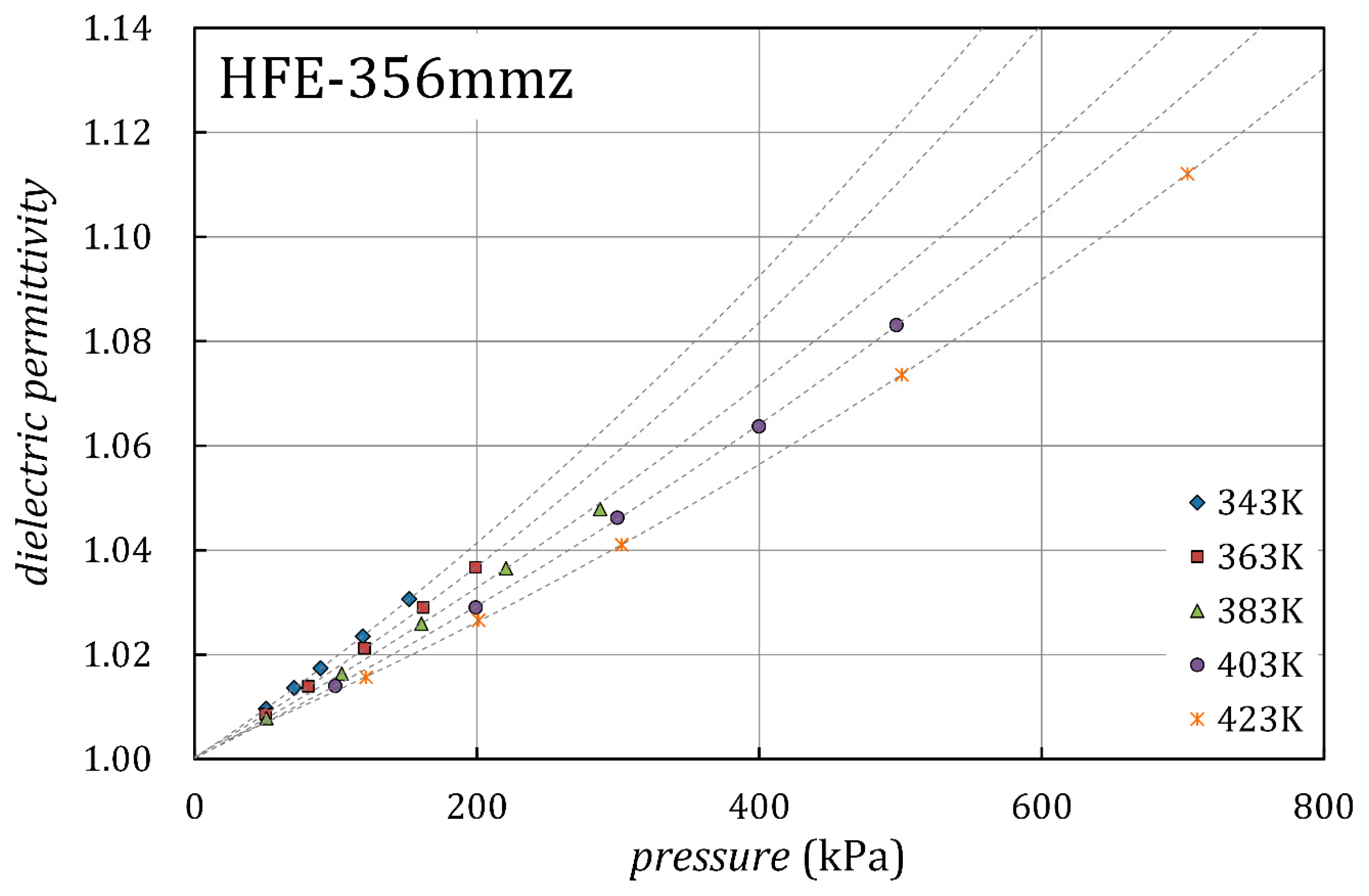
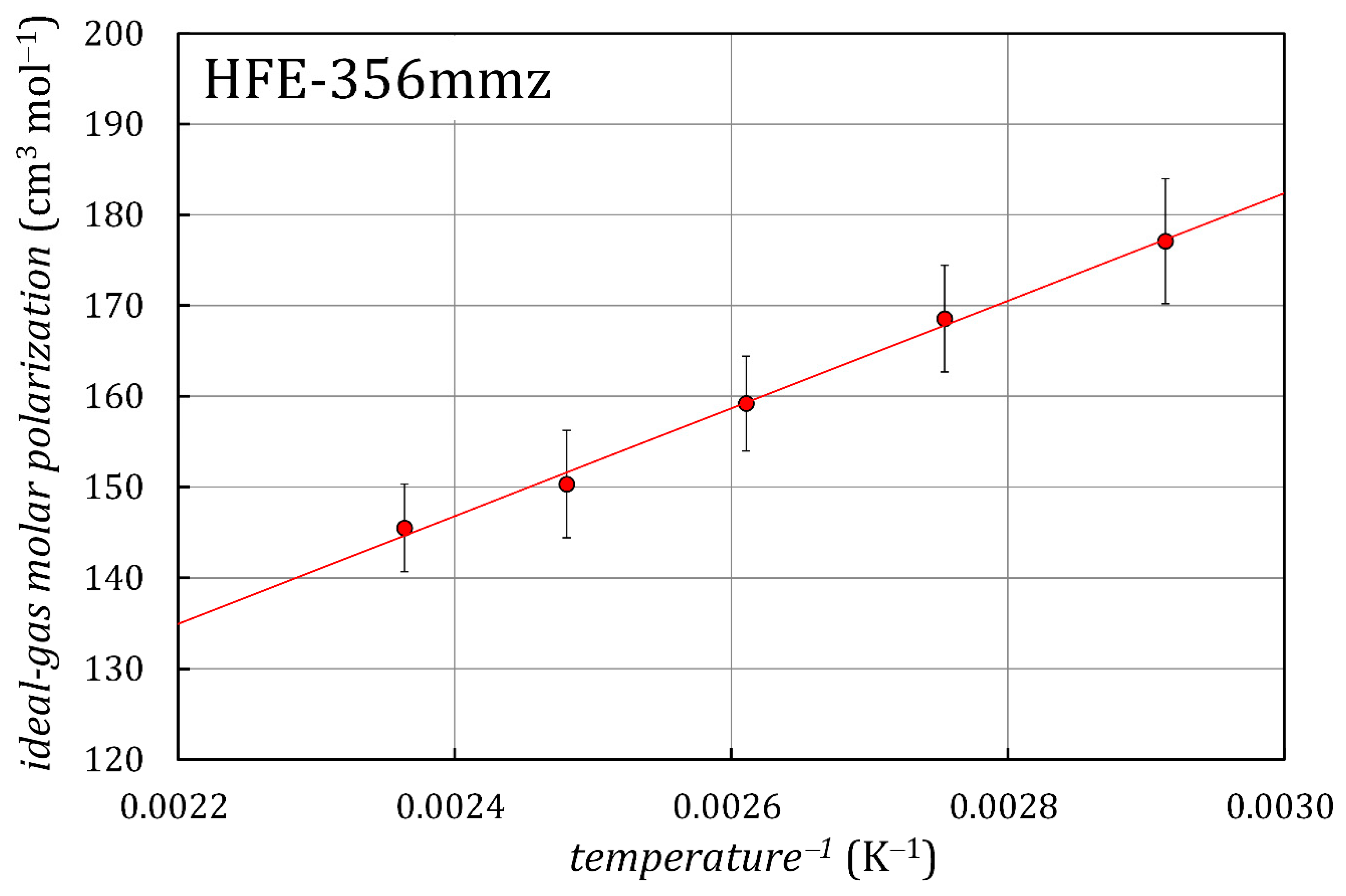
3.2. Dielectric Permittivity and Ideal-Gas Molar Polarization
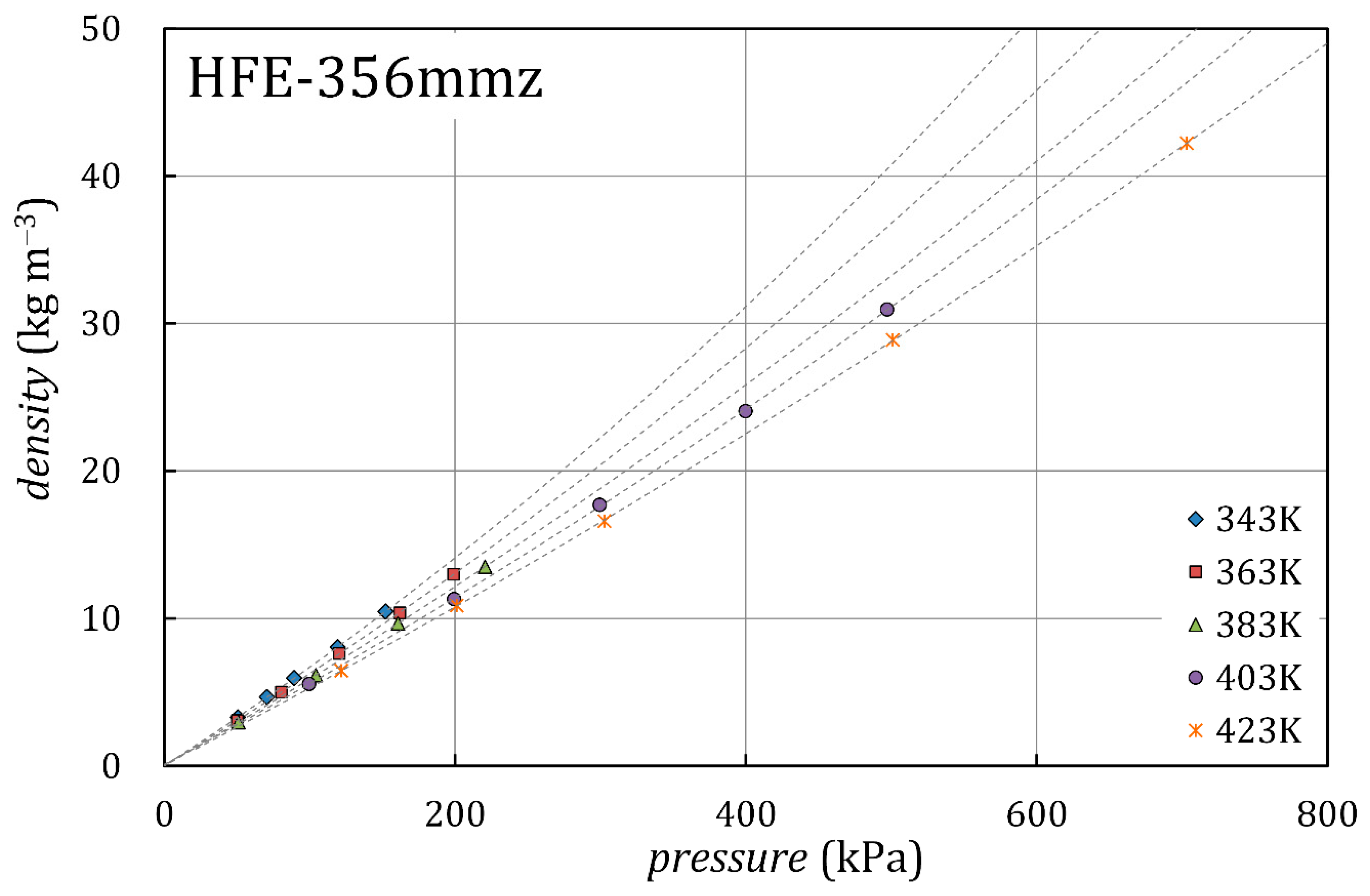
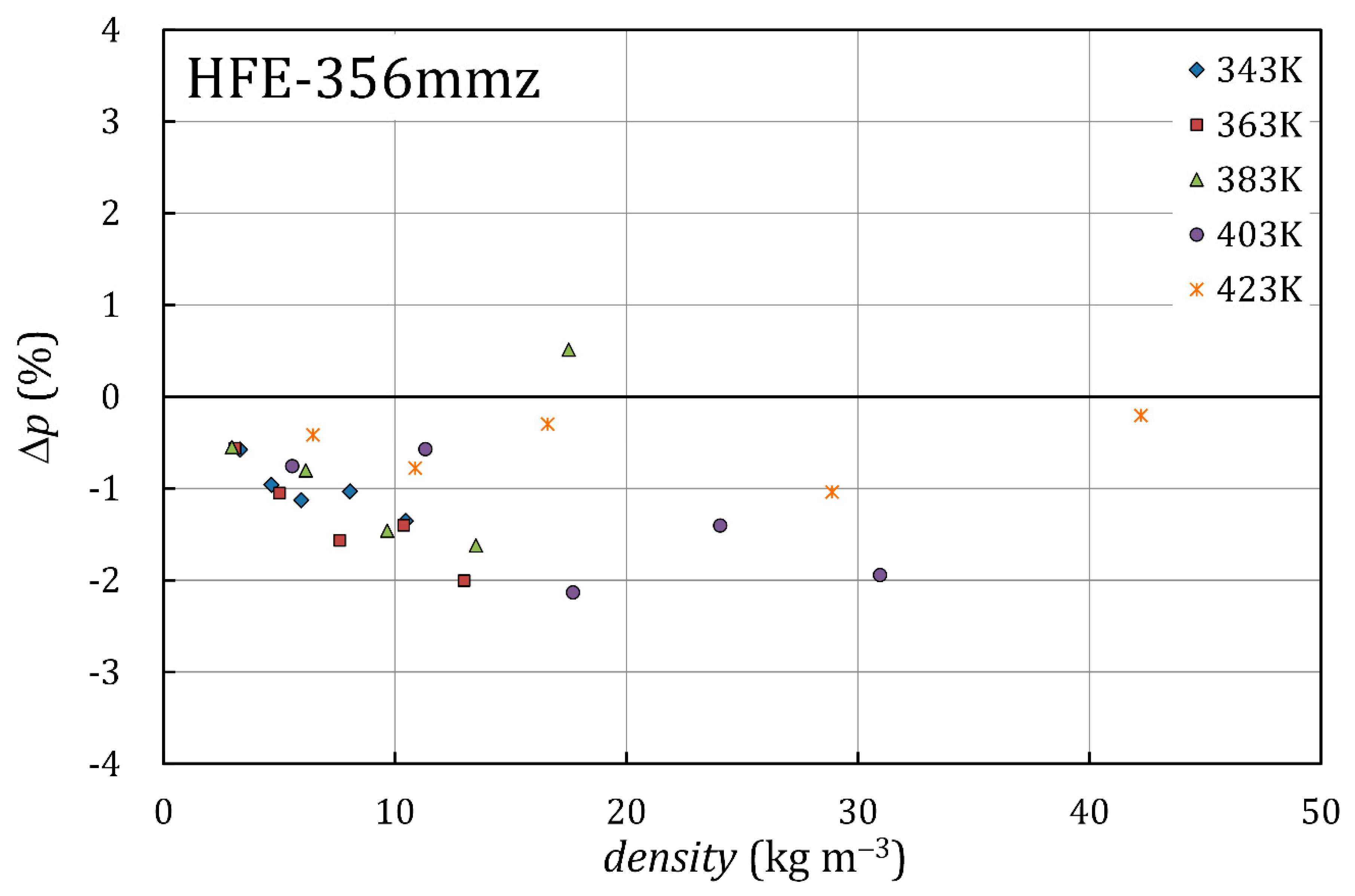
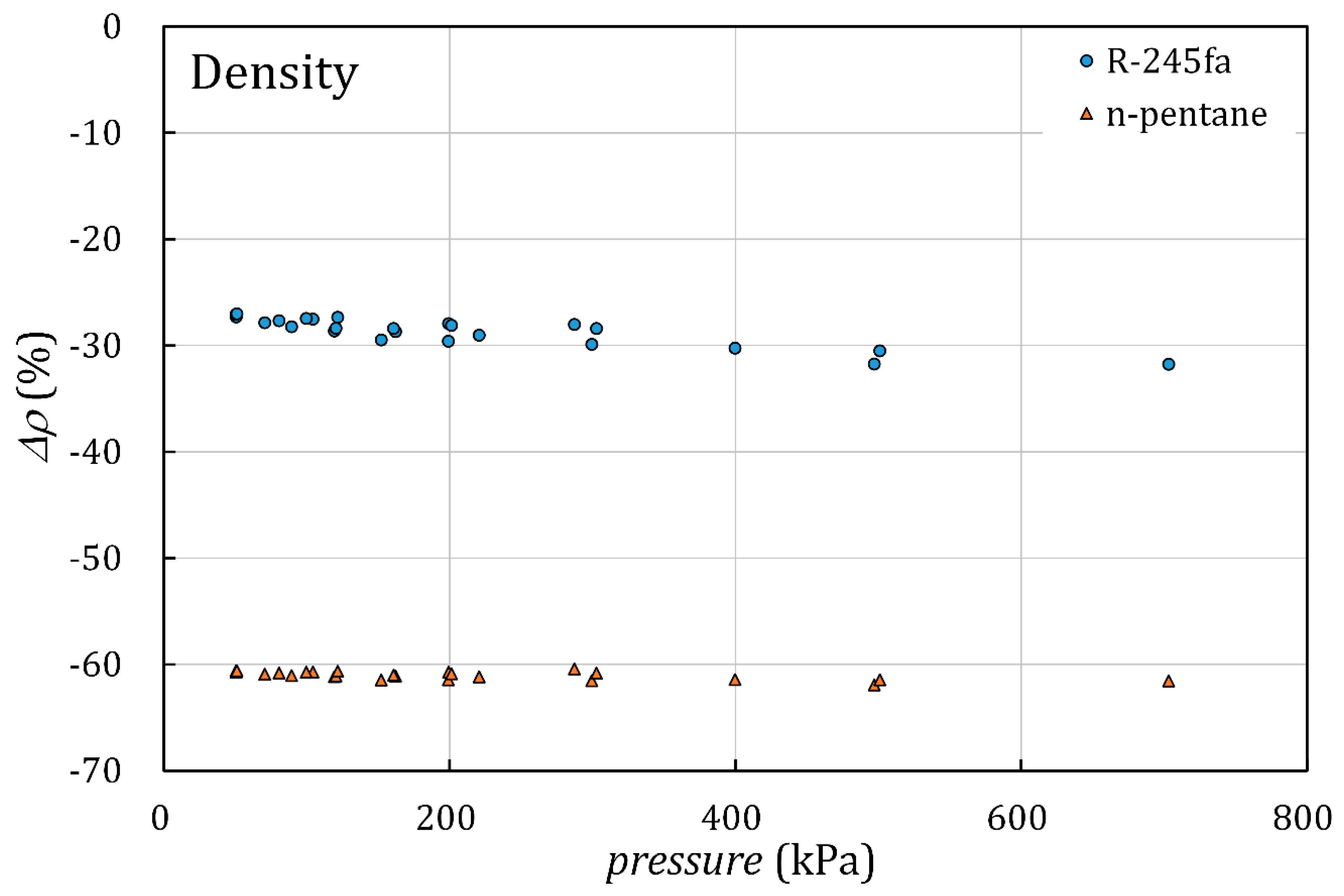
3.3. Dipole Moment and Density
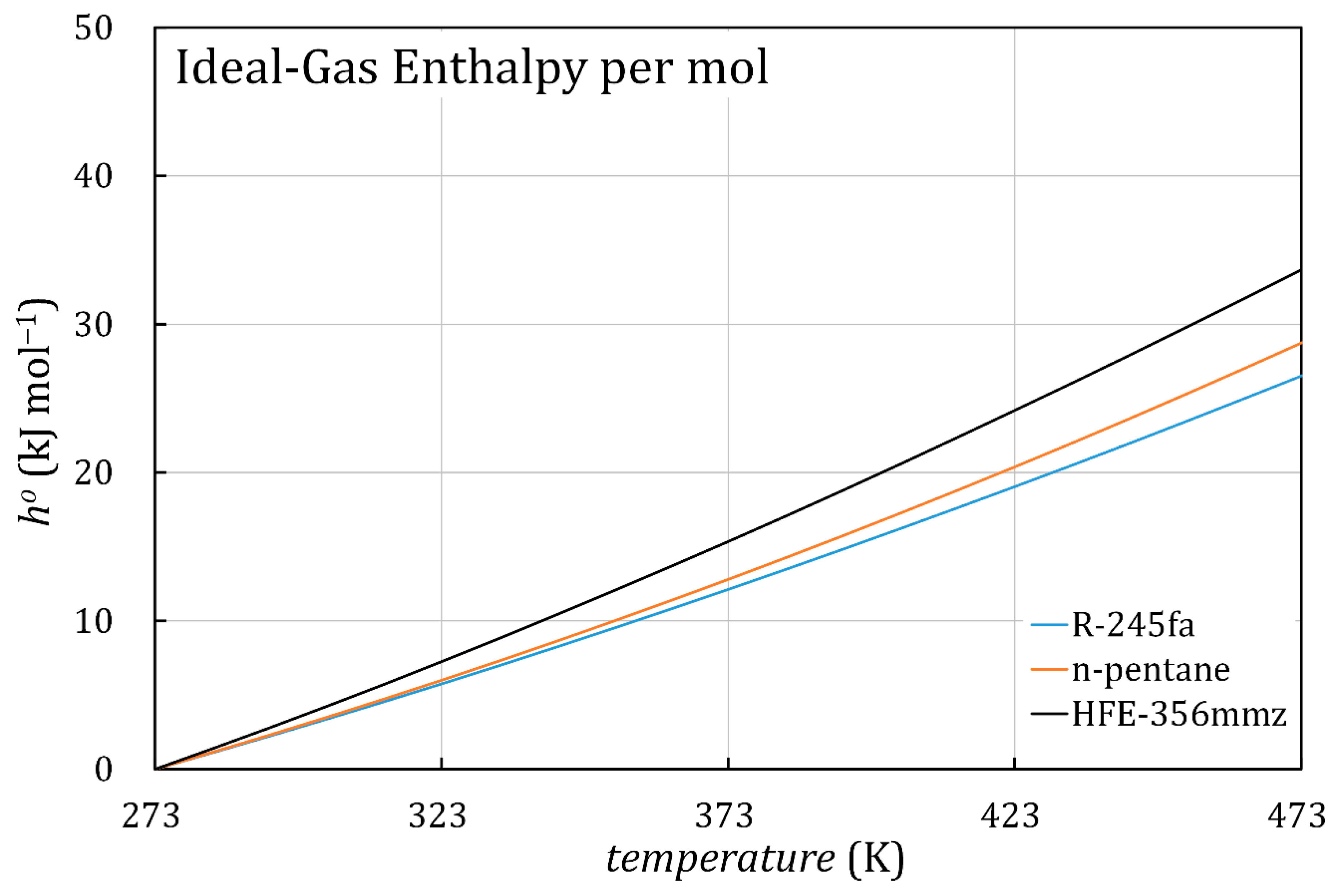
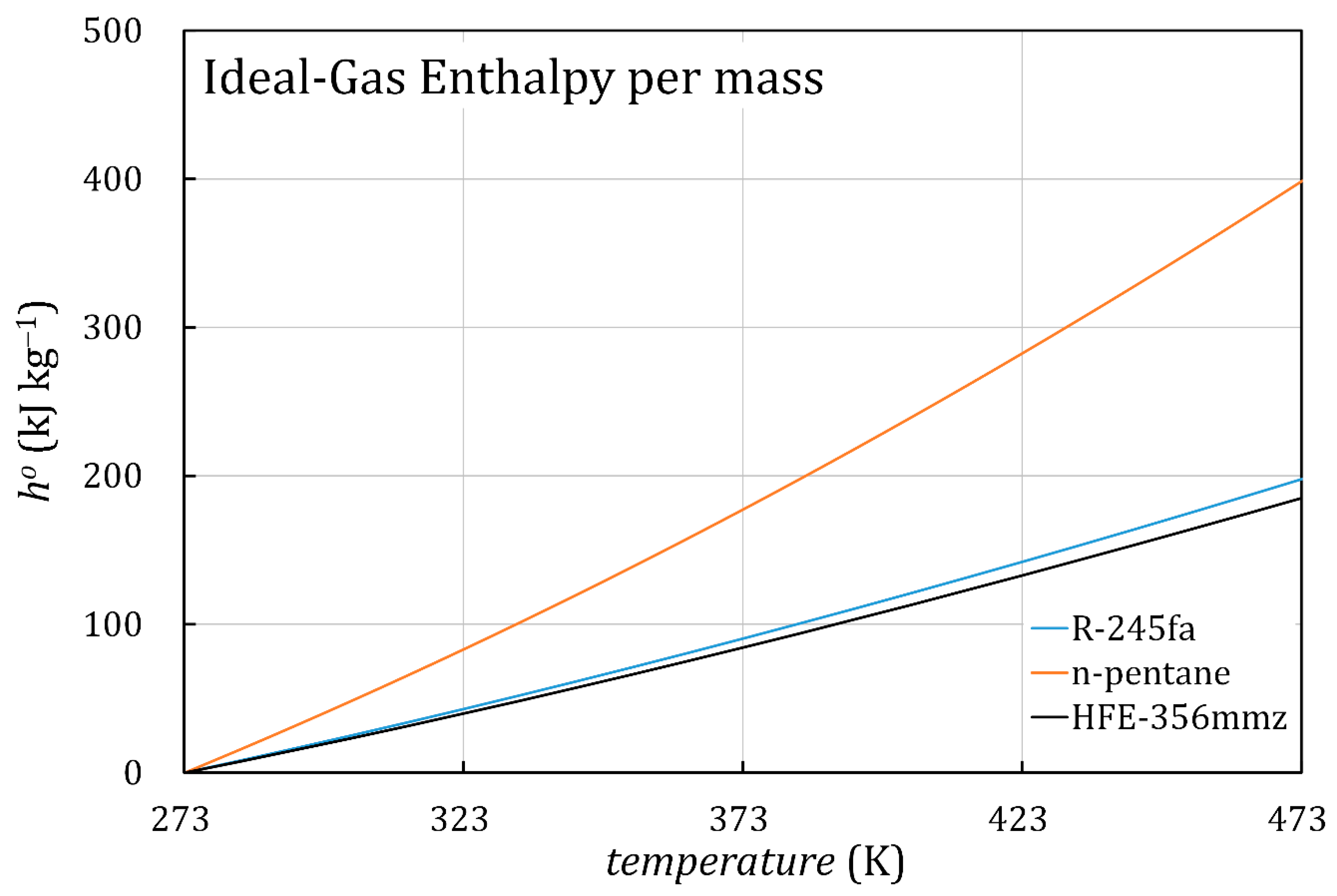
4. Discussion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Myhre, G.; Shindell, D.; Bréon, F.-M.; Collins, W.; Fuglestvedt, J.; Huang, J.; Koch, D.; Lamarque, J.-F.; Lee, D.; Mendoza, B.; et al. Anthropogenic and Natural Radiative Forcing. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 659–740. [Google Scholar]
- Heath, E.A. Amendment to the Montreal Protocol on Substances that Deplete the Ozone Layer (Kigali Amendment). Int. Leg. Mater. 2017, 56, 193–205. [Google Scholar] [CrossRef] [Green Version]
- Sekiya, A.; Misaki, S. The potential of hydrofluoroethers to replace CFCs, HCFCs and PFCs. J. Fluor. Chem. 2000, 101, 215–221. [Google Scholar] [CrossRef]
- Kondo, S.; Urano, Y.; Takizawa, K.; Takahashi, A.; Tokuhashi, K.; Sekiya, A. Flammability limits of multi-fluorinated compounds. Fire Saf. J. 2006, 41, 46–56. [Google Scholar] [CrossRef]
- Sako, T.; Yasumoto, M.; Sato, M.; Kitao, O.; Ishiguro, K.; Kato, M. Measurement of critical properties of fluorinated ethers and amines. Fluid Phase Equilib. 1998, 144, 113–117. [Google Scholar] [CrossRef]
- Alam, J.M.; Kariya, K.; Yamaguchi, K.; Hori, Y.; Miyara, A. Measurement of thermal conductivity and kinematic viscosity of 1,1,1,3,3,3-hexafluoro-2-methoxypropane (HFE-356mmz). Int. J. Refrig. 2019, 103, 1–8. [Google Scholar] [CrossRef]
- Chen, Q.; Gao, R.; Guan, X.; Du, L.; Chen, G.; Tang, L. Measurement and correlation of gaseous pvt property for 1,1,1,3,3,3-hexafluoro-2-methoxypropane (HFE-356mmz). J. Chem. Eng. Data 2020, 65, 4230–4235. [Google Scholar] [CrossRef]
- Meng, L.; Duan, Y.Y.; Li, L. Correlations for second and third virial coefficients of pure fluids. Fluid Phase Equilib. 2004, 226, 109–120. [Google Scholar] [CrossRef]
- Kano, Y.; Kayukawa, Y.; Fujita, Y. Dipole moment and heat capacity in the ideal gas state derived from relative permittivity and speed of sound measurements for HFO-1123 and HCFO-1224yd(Z). Int. J. Refrig. 2020, 118, 354–364. [Google Scholar] [CrossRef]
- Kano, Y. Multi-property evaluation for a gas sample based on the acoustic and electromagnetic resonances measurement in a cylindrical cavity. J. Chem. Thermodyn. 2020. submitted for publication. [Google Scholar]
- Joback, K.G.; Reid, R.C. Estimation of pure-component properties from group-contributions. Chem. Eng. Commun. 1987, 57, 233–243. [Google Scholar] [CrossRef]
- Richter, M.; McLinden, M.O.; Lemmon, E.W. Thermodynamic properties of 2,3,3,3-tetrafluoroprop-1-ene (R1234yf): Vapor pressure and p-r-T measurements and an equation of state. J. Chem. Eng. Data 2011, 56, 3254–3264. [Google Scholar] [CrossRef]
- St-Arnaud, J.M.; Hourri, A.; Okambawa, R.; Belanger, M. Determination of the density in the gas phase with a computer-controlled measuring system of the dielectric constant. Rev. Sci. Instrum. 1995, 66, 5311–5316. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Bell, I.H.; Huber, M.H.; McLinden, M.O. REFPROP—NIST Standard Reference Database 23. Version 10.0; National Institute of Standard and Technology: Boulder, CO, USA, 2018.
- Lemmon, E.W.; Span, R. Short fundamental equations of state for 20 industrial fluids. J. Chem. Eng. Data 2006, 51, 785–850. [Google Scholar] [CrossRef]


| Factor of Uncertainty | (2, 0) Mode | (3, 0) Mode | (4, 0) Mode | (5, 0) Mode |
|---|---|---|---|---|
| Acoustic resonance frequency, | 0.001% | 0.001% | 0.001% | 0.001% |
| Frequency correction, | 0.057% | 0.020% | 0.021% | 0.026% |
| Cavity length, | 0.011% | 0.011% | 0.011% | 0.011% |
| Elastic compliance, | 9 × 10−7% | 9 × 10−7% | 9 × 10−7% | 9 × 10−7% |
| Sample gas pressure, | 5 × 10−8% | 5 × 10−8% | 5 × 10−8% | 5 × 10−8% |
| Covariance between & | 0.011% | 0.007% | 0.007% | 0.008% |
| Single mode result, | 0.059% | 0.024% | 0.025% | 0.030% |
| Standard deviation of the four modes | 0.006% | |||
| Weighted mean of the four modes, | 0.016% | |||
| Factor of Uncertainty | TM010 Mode | TM011 Mode | TM012 Mode | TM013 Mode |
|---|---|---|---|---|
| Microwave resonance frequency in gas, | 0.001% | 0.001% | 0.001% | 0.003% |
| Microwave resonance frequency in vacuum, | 2 × 10−5% | 2 × 10−5% | 3 × 10−5% | 5 × 10−5% |
| Frequency correction in gas, | 0.178% | 0.188% | 0.204% | 0.215% |
| Frequency correction in vacuum, | 0.016% | 0.034% | 0.033% | 0.046% |
| Elastic compliance, | 2 × 10−6% | 2 × 10−6% | 2 × 10−6% | 2 × 10−6% |
| Sample gas pressure, | 1 × 10−7% | 1 × 10−7% | 1 × 10−7% | 1 × 10−7% |
| Covariance between & | −2 × 10−4% | −2 × 10−4% | −2 × 10−4% | −6 × 10−4% |
| Covariance between & | 0.014% | 0.014% | 0.020% | 0.037% |
| Covariance between & | −0.004% | −0.006% | −0.008% | −0.017% |
| Covariance between & | −0.003% | −0.003% | −0.003% | −0.005% |
| Covariance between & | 0.001% | 0.001% | 0.001% | 0.002% |
| Covariance between & | −0.076% | −0.114% | −0.116% | −0.141% |
| Single mode result, | 0.162% | 0.155% | 0.172% | 0.172% |
| Standard deviation of the four modes | 0.012% | |||
| Weighted mean of the four modes, | 0.083% | |||
| , K | , kPa | , m/s | |
|---|---|---|---|
| 343.15 | 50.6 | 126.10 | 0.02 |
| 343.15 | 70.6 | 125.10 | 0.02 |
| 343.15 | 89.3 | 124.17 | 0.02 |
| 343.15 | 119.3 | 122.68 | 0.02 |
| 343.15 | 152.4 | 120.99 | 0.02 |
| 363.06 | 50.3 | 130.09 | 0.03 |
| 363.06 | 80.5 | 128.80 | 0.03 |
| 363.06 | 120.4 | 127.11 | 0.03 |
| 363.06 | 162.0 | 125.24 | 0.03 |
| 363.05 | 199.1 | 123.56 | 0.03 |
| 383.02 | 51.0 | 133.75 | 0.02 |
| 383.02 | 104.4 | 131.89 | 0.02 |
| 383.02 | 160.7 | 129.88 | 0.02 |
| 383.03 | 220.7 | 127.69 | 0.02 |
| 383.03 | 287.4 | 125.15 | 0.02 |
| 403.03 | 99.6 | 136.08 | 0.02 |
| 403.03 | 199.2 | 133.10 | 0.02 |
| 403.03 | 299.3 | 130.01 | 0.02 |
| 403.04 | 399.6 | 126.74 | 0.02 |
| 403.04 | 497.0 | 123.37 | 0.02 |
| 423.05 | 121.6 | 139.51 | 0.02 |
| 423.05 | 201.1 | 137.42 | 0.02 |
| 423.05 | 302.6 | 134.81 | 0.02 |
| 423.06 | 500.8 | 129.40 | 0.02 |
| 423.05 | 703.1 | 123.37 | 0.02 |
| , K | ||
|---|---|---|
| 343.15 | 159.7 | 6.5 |
| 363.06 | 166.2 | 5.5 |
| 383.03 | 175.0 | 7.0 |
| 403.04 | 179.0 | 7.6 |
| 423.05 | 181.3 | 4.3 |
| Coefficient | Value |
|---|---|
| 139.302 | |
| 103.482 | |
| 1474.761 | |
| 424.514 |
| , K | , kPa | ||
|---|---|---|---|
| 343.15 | 50.6 | 1.00964 | 0.00021 |
| 343.15 | 70.6 | 1.01360 | 0.00031 |
| 343.15 | 89.3 | 1.01737 | 0.00046 |
| 343.15 | 119.3 | 1.02351 | 0.00064 |
| 343.15 | 152.1 | 1.03062 | 0.00086 |
| 363.06 | 50.4 | 1.00858 | 0.00018 |
| 363.06 | 80.6 | 1.01390 | 0.00032 |
| 363.06 | 120.4 | 1.02119 | 0.00054 |
| 363.06 | 162.0 | 1.02904 | 0.00079 |
| 363.05 | 199.0 | 1.03673 | 0.00102 |
| 383.03 | 51.1 | 1.00783 | 0.00016 |
| 383.02 | 104.4 | 1.01636 | 0.00042 |
| 383.03 | 160.7 | 1.02591 | 0.00073 |
| 383.02 | 220.7 | 1.03654 | 0.00104 |
| 383.03 | 287.3 | 1.04787 | 0.00132 |
| 403.04 | 99.7 | 1.01403 | 0.00034 |
| 403.03 | 199.3 | 1.02905 | 0.00080 |
| 403.03 | 299.4 | 1.04621 | 0.00121 |
| 403.03 | 399.7 | 1.06374 | 0.00152 |
| 403.04 | 497.1 | 1.08313 | 0.00190 |
| 423.05 | 121.7 | 1.01566 | 0.00039 |
| 423.04 | 201.2 | 1.02658 | 0.00069 |
| 423.04 | 302.7 | 1.04104 | 0.00121 |
| 423.05 | 501.0 | 1.07358 | 0.00160 |
| 423.05 | 703.2 | 1.11209 | 0.00211 |
| , K | ||
|---|---|---|
| 343.15 | 177.1 | 6.9 |
| 363.06 | 168.6 | 5.9 |
| 383.03 | 159.2 | 5.2 |
| 403.03 | 150.3 | 5.9 |
| 423.04 | 145.5 | 4.8 |
| , K | , kPa | , kg/m3 | |
|---|---|---|---|
| 343.15 | 50.6 | 3.31 | 0.15 |
| 343.15 | 70.6 | 4.67 | 0.21 |
| 343.15 | 89.3 | 5.96 | 0.28 |
| 343.15 | 119.3 | 8.06 | 0.38 |
| 343.15 | 152.1 | 10.47 | 0.50 |
| 363.06 | 50.4 | 3.10 | 0.13 |
| 363.06 | 80.6 | 5.02 | 0.21 |
| 363.06 | 120.4 | 7.62 | 0.33 |
| 363.06 | 162.0 | 10.38 | 0.45 |
| 363.05 | 199.0 | 13.00 | 0.55 |
| 383.03 | 51.1 | 2.97 | 0.11 |
| 383.02 | 104.4 | 6.15 | 0.25 |
| 383.03 | 160.7 | 9.66 | 0.41 |
| 383.02 | 220.7 | 13.50 | 0.57 |
| 383.03 | 287.3 | 17.51 | 0.72 |
| 403.04 | 99.7 | 5.56 | 0.25 |
| 403.03 | 199.3 | 11.32 | 0.52 |
| 403.03 | 299.4 | 17.70 | 0.80 |
| 403.03 | 399.7 | 24.05 | 1.06 |
| 403.04 | 497.1 | 30.95 | 1.37 |
| 423.05 | 121.7 | 6.46 | 0.26 |
| 423.04 | 201.2 | 10.88 | 0.45 |
| 423.04 | 302.7 | 16.60 | 0.71 |
| 423.05 | 501.0 | 28.88 | 1.07 |
| 423.05 | 703.2 | 42.22 | 1.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kano, Y. Thermophysical Properties of 1,1,1,3,3,3-hexafluoro-2-methoxypropane (HFE-356mmz) in the Vapor Phase Measured by Using an Acoustic-Microwave Resonance Technique. Energies 2020, 13, 5525. https://doi.org/10.3390/en13205525
Kano Y. Thermophysical Properties of 1,1,1,3,3,3-hexafluoro-2-methoxypropane (HFE-356mmz) in the Vapor Phase Measured by Using an Acoustic-Microwave Resonance Technique. Energies. 2020; 13(20):5525. https://doi.org/10.3390/en13205525
Chicago/Turabian StyleKano, Yuya. 2020. "Thermophysical Properties of 1,1,1,3,3,3-hexafluoro-2-methoxypropane (HFE-356mmz) in the Vapor Phase Measured by Using an Acoustic-Microwave Resonance Technique" Energies 13, no. 20: 5525. https://doi.org/10.3390/en13205525
APA StyleKano, Y. (2020). Thermophysical Properties of 1,1,1,3,3,3-hexafluoro-2-methoxypropane (HFE-356mmz) in the Vapor Phase Measured by Using an Acoustic-Microwave Resonance Technique. Energies, 13(20), 5525. https://doi.org/10.3390/en13205525