Local Carrier PWM for Modular Multilevel Converters with Distributed PV Cells and Circulating Current Reduction

Abstract

A new topology has been recently proposed for grid-connected photovoltaic (PV) systems, using modular multilevel converters (MMCs) and distributing PV panels throughout the MMC cells. This topology has two main advantages: it reduces the power losses related to moving the energy into the MMC capacitors from an external source, and it removes the losses and costs related to the DC to DC converters used to track the maximum power point on string converters or central converters, because that task is delegated to MMC cells. However, traditional pulse width modulation (PWM) techniques have many problems when dealing with this application: the distortion at the output increases to unacceptable values when MMC cells target different voltages. This paper proposes a new modulation technique for MMCs with different cell voltages, taking into account the measured cell voltages to generate switching sequences with more accurate timing. It also adapts the modulator sampling period to improve the transitions from level to level, an important issue to reduce the internal circulating currents. The proposed modulation has been validated using simulations that show a consistent behavior in the output distortion throughout a wide operation range, and it also reduces the circulating currents and cuts the conduction losses by half. The behavior of this new topology and this new modulation has been compared to the mainstream topology with external PV panels and also to a fixed carrier modulation.

1. Introduction

Photovoltaic installations are growing throughout the world, nearly according to Moore’s law, duplicating the cumulative installed PV capacity roughly every two years: about 2 GWp were installed in 2002, 40 GWp were available in 2010 and more than 480 GWp operated all over the world in 2018 [1,2]. Moreover, in the last 40 years, photovoltaic modules have decreased in cost at an average rate of about 10% per year [2]. As long as this trend continues, efficiency and performance are the most important features of power converters used to manage PV energy.

Grid-connected PV systems usually consist of a series of PV panels or strings, and as shown in Figure 1, they are frequently configured by a couple of serially connected power converters, first a DC–DC converter that gets the maximum energy from the panels and then a DC–AC inverter that transfers all the available power to the grid [3]. Central inverters are normally used in three-phase grid-connected PV plants larger than tens of KWp [4,5,6,7], with a market share of about 44% [1,7]. This technology generally achieves high productivity with a lower cost, yet it requires high-voltage DC cables [5] and uniform irradiance. Besides, the power mismatch issue is significant in this structure due to its low immunity to hotspots and partial shading, leading to a lower PV utilization. In contrast, the maximum power point tracking (MPPT) control is applied on each string of string/multi-string PV inverter, leading to a better total energy production [3]; nowadays, they represent a market share of 52% [1]. However, this topology requires more power electronic converters and reactors, resulting in increasing costs and losses, and there are still mismatches in the PV panels at each string. For low-power PV applications, module PV inverters are generally used, allowing module-level monitoring and diagnostics [8]. This topology also minimizes the effects of partial shadowing and power mismatch because the module converter optimizes a single PV panel with an individual MPPT control. Nevertheless, the overall efficiency is smaller when compared to central and string converters [8].

Considering the above issues, spreading the PV panels over the sub-modules (SMs) of a modular multilevel converter (MMC) by integrating PV strings directly on converter cells has been recently proposed in [9,10]. This topology, shown later in Figure 3, has nearly the same installation cost than central inverters, achieving better performance, it gets mostly the same power optimization as string converters at a lower cost and it may work in a wider power and voltage range with fewer losses than all previous topologies due to removing DC–DC converters.

MMCs were introduced in 2003 [11] and they have attracted significant research interest in medium-voltage [12] and high-voltage applications [13]. Modular converters, such as the MMC, reach any number of voltage levels by increasing or decreasing the number of SMs, and they offer various advantages over other multilevel topologies such as fault tolerant operation, easy to achieve capacitor voltage balance, low harmonic distortion and elimination of the bulky DC-link capacitor [13,14]. Therefore, they have seen rapid growth in a broad field of applications, including DC transmission, solid-state transformers and renewable energy integration.

When using MMCs for renewable energies, specifically for PV applications, the mainstream is the topology shown in Figure 2, used in [15,16], where PV panels are connected to the grid or load by the MMC through a DC link. In contrast, recently, a new topology has been proposed in [9,17], as shown in Figure 3. These papers focus on the latter due to important advantages: on the one hand, the optimization function of string converters is performed at no additional cost by the MMC cells, reducing the costs and losses related to the intermediate booster converters; on the other hand, with an appropriate control, placing the PV panels inside the MMC may lead to smaller circulating currents that mean smaller power losses, increasing the converter efficiency. However, this topology has an important drawback: the voltage of each SM depends on the irradiance and temperature of its PV panels, and the output distortion increases when MMC cells target different voltages and traditional PWMs are used, reducing the operation range. The new modulation proposed in this paper will solve this problem and, at the same time, it will reduce the MMC internal circulating currents with important savings for the semiconductor power rating and also for the conduction power losses.

The modulation method has a significant influence on MMC performance, such as the switching losses, capacitor voltage balancing and output voltage harmonic content [18,19]. A wide variety of modulation techniques have been applied to the MMC, essentially relying upon the number of SMs. The most usual methods for a low number of SMs are carrier-based PWM (CB-PWM) [20], either phase-shifted PWM (PS-PWM) [21,22] or level-shifted PWM (LS-PWM) [22,23]. As a result of its better harmonic performance, PS-PWM is usually the preferred choice among CB-PWM techniques in MMCs.

Due to their two-arm configuration, MMCs can generate two different numbers of voltage levels using the same number of SMs per arm [22]. The most straightforward method of gaining these additional levels is interleaving upper and lower carriers [24] while maintaining the effective switching frequency of each SM constant, but at the cost of increased internal currents and losses. This article will focus on non-interleaving.

An additional feature of MMCs is that capacitor voltages must be balanced to keep the average cell voltage at a given reference value. The usual technique used to perform capacitor voltage balance is based on sorting capacitor voltage values and thus the SMs to be activated or deactivated are selected using the sign of the arm current [25]. Moreover, voltage balancing can also be achieved, saving the cost of the measures of the cell voltages by means of integrating the current at each capacitor when they are inserted [26].

Probably the most important variable of the MMC is the internal circulating current that affects the semiconductor rating because of the arm peak current and capacitor voltage ripple [27]. In fact, it may also have an effect on the operating range of the MMC under balanced conditions [27,28,29,30,31].

Circulating currents typically have a DC component when energy is transferred from phase to phase or from an external energy source at the DC side to the MMC phases [32]. Afterwards, that energy is sent to the AC side by means of the output AC current. In addition, circulating currents may have a 50 Hz component that can be used by the controller to transfer energy from the upper arm to the lower arm or back [17]. The main drawback of the MMC is that an additional 100 Hz negative-sequence component arises in the circulating current when using traditional modulators, and, under unbalanced AC grid conditions, they may also include a 100 Hz positive-sequence and even a zero-sequence component [33].

As long as those 100 Hz components at the circulating current are a source of losses with no real contribution to the MMC control, a few techniques have traditionally been used to remove or at least reduce them: proportional integral (PI) controllers are used in the dq synchronous rotating frame [33], a set of proportional-resonant controllers in the αβ reference frame have also been proposed [34,35] and other authors have tried a few repetitive control schemes [36,37]. Those uncontrolled components of circulating current may also have an additional side effect on the capacitor voltage ripples, so further techniques have been proposed to minimize that undesired effect: adding a second harmonic to the circulating current has shown that the capacitor voltage variations can be reduced [38,39], and the addition of a second and a fourth harmonic has been proposed, targeting the same result [40]. All of these undesired effects, that become more critical on unbalanced grids, usually have an important impact on the operating regions of the MMC, so this issue has been analyzed for different circulating current control methods [27].

In order to expand the application of MMCs to medium-voltage and high-voltage renewable energy applications, this paper proposes a new modulation method, named local carrier pulse width modulation (LC-PWM), to deal with different voltages in the MMC cells, and the higher precision of this technique reduces the resulting circulating currents and the output distortion throughout a wider operational range. The implementation of LC-PWM will be discussed and validated through simulation, and the performance of this new modulation will be compared to conventional PS-PWM on isolated loads to remove any possible interaction related to the grid or its controllers. The feasibility of proposed LC-PWM will be evaluated through a study of the circulating currents, the corresponding converter power losses, the performance of the MMC converter on this application and the total harmonic distortion (THD) under different scenarios.

The paper is structured as follows. The MMC topology and modeling are introduced in Section 2. The proposed LC-PWM method is presented in detail in Section 3, followed by Section 4 where the performance of the proposed modulation is validated and compared to alternate conventional methods. Conclusions are summarized in Section 5.

2. MMC Converter

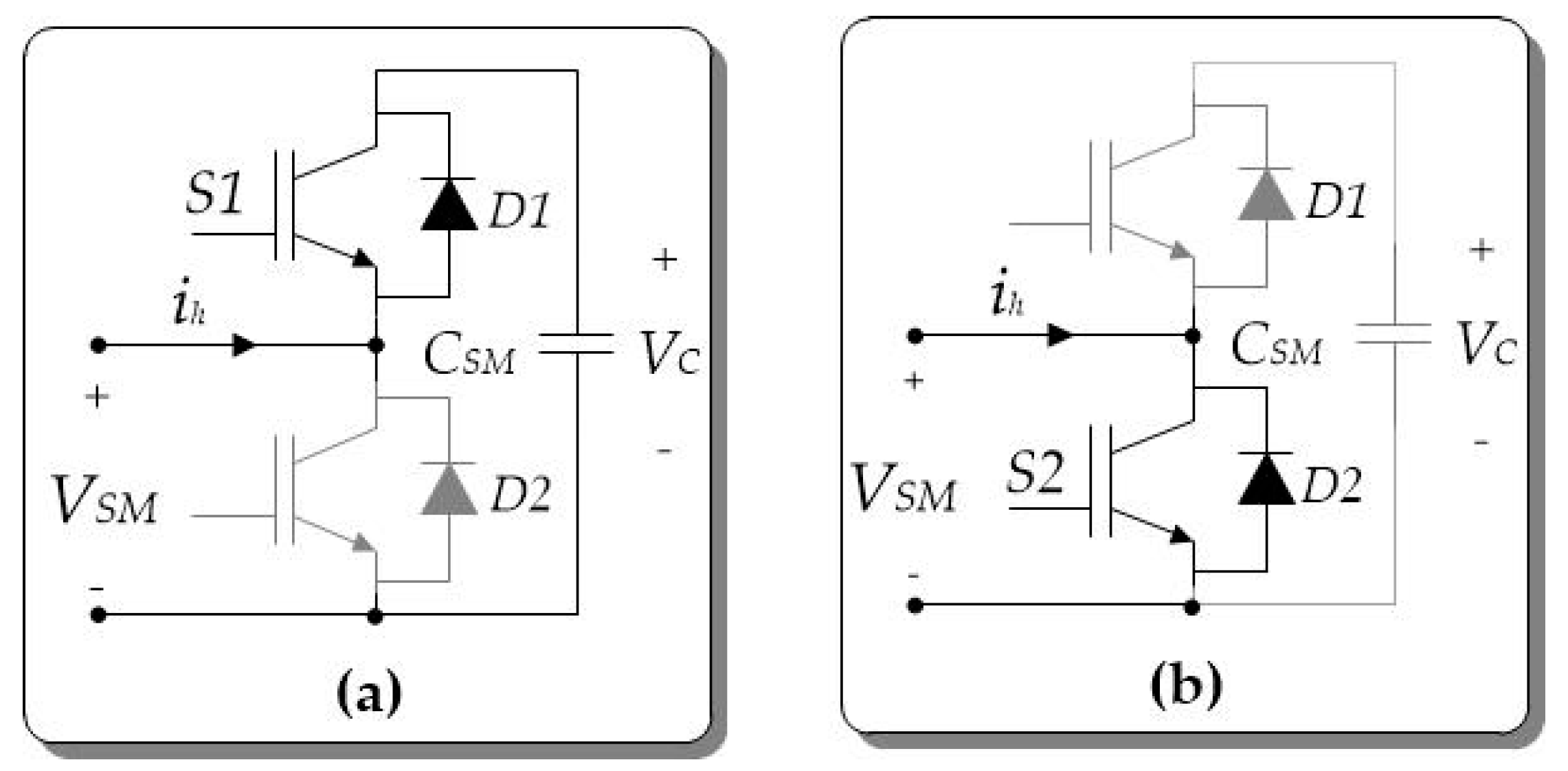
The conventional structure of a three-phase MMC is shown in Figure 2, which usually makes up a series of SMs based on the half-bridge circuit with a capacitor (C_SM) as a DC voltage source (V_C) in each SM. Each phase-leg consists of two arms, upper and lower, with a number (N) of SMs per arm connected in series with the arm inductor (L_arm). The function of the arm reactor is to limit the phase circulating current (i_za) and the DC fault current within the phase-leg of the MMC. It also enables control of the circulating current within the converter.

Table 1. Switching states for SM.

SM States	S1	S2	VSM
ON	ON	OFF	VC
OFF	OFF	ON	0

shows the possible switch states for a half-bridge SM. The switches are usually built using an insulated gate bipolar transistor (IGBT) and a freewheeling diode (FWD). The two switches (S1 and S2) at each SM operate in a complementary manner, meaning that when S1 is ON, S2 must be OFF, and vice versa. Based on the state of the two switches, the SM is either inserted or bypassed, adding to the arm a voltage V_SM, equal to either V_C or zero, respectively [36]. This operation of the SM is illustrated in Figure 4. When an SM is bypassed (OFF state), its capacitor voltage remains constant, but inserted capacitors will charge or discharge depending on the sign of the arm current.

Taking phase “a” as an example, the voltages of the upper and lower arms of the MMC can be expressed as:

$$\frac{1}{2}{V}_{\mathit{dc}}-v_{\mathit{ua}}-L_{\mathit{arm}}\frac{{\mathit{di}}_{\mathit{ua}}}{\mathit{dt}}-v_{\mathit{oa}}=\mathit{0}$$

(1)

$$\frac{1}{2}{V}_{\mathit{dc}} -v_{\mathit{la}}-L_{\mathit{arm}}\frac{{\mathit{di}}_{\mathit{la}}}{\mathit{dt}}+v_{\mathit{oa}}=\mathit{0}$$

(2)

where v_ua and v_la are the total voltages of the cascaded SMs in the upper and lower arms for phase “a”, respectively. Meanwhile, i_ua and i_la are the currents of the upper and lower arms, respectively, and v_oa is the output voltage from phase “a” to DC middle point “m”.

Adding (1) and (2) leads to (3), expressed as (5) using the circulating current defined in (4):

$$V_{\mathit{dc}}=v_{\mathit{ua}}+v_{\mathit{la}}+L_{\mathit{arm}}\frac{{\mathit{di}}_{\mathit{ua}}}{\mathit{dt}}+L_{\mathit{arm}}\frac{{\mathit{di}}_{\mathit{la}}}{\mathit{dt}}$$

(3)

$$i_{\mathit{za}}\equiv \frac{i_{\mathit{ua}}+i_{\mathit{la}}}{2}$$

(4)

$$(V_{\mathit{dc}}-v_{\mathit{ua}})-v_{\mathit{la}}={2L}_{\mathit{arm}}\frac{{\mathit{di}}_{\mathit{za}}}{\mathit{dt}}$$

(5)

where v_la is the voltage of the inserted cells at the lower arm, and it is also the value of the converter voltage referring to point “n” through the MMC lower arm, while (V_dc − v_ua) represents the converter voltage referring to point “n” through the upper arm, which usually is enforced to be equal to v_la.

Equation (4) defines the circulating current in phase “a”, named i_za. As previously pointed out, the DC component of this current is responsible of the energy sent or received by this phase to or from other phases or from a common DC network [32]; its 50 Hz component can be used to move energy from the upper arm to the lower arm or back [17]. The circulating current may have other uncontrolled components, usually at 100 Hz [33]. The behavior of the circulating current is described in (5), and this equation will be used later, in (20), for the design of an appropriate controller.

At the same time, subtracting (1) from (2) leads to (6), and applying (7) it will lead to (8):

$$v_{\mathit{la}} -v_{\mathit{ua}}=L_{\mathit{arm}}\frac{{\mathit{di}}_{\mathit{ua}}}{\mathit{dt}} -L_{\mathit{arm}}\frac{{\mathit{di}}_{\mathit{la}}}{\mathit{dt}}+{2v}_{\mathit{oa}}$$

(6)

$$i_{\mathit{oa}}=i_{\mathit{ua}} -i_{\mathit{la}}$$

(7)

$$\frac{v_{\mathit{la}} -v_{\mathit{ua}}}{2}=v_{\mathit{oa}}+\frac{1}{2}{L}_{\mathit{arm}}\frac{{\mathit{di}}_{\mathit{oa}}}{\mathit{dt}}$$

(8)

where i_oa represents the output current according to Kirchhoff’s current law at point “a”, and v_oa represents again the converter voltage in phase “a” referring to point “m”.

Connecting the converter to grids, the output voltage at each phase is related to the grid voltage by the output inductor, as stated in (9):

$$v_{\mathit{oa}}=L_o\frac{{\mathit{di}}_{\mathit{oa}}}{\mathit{dt}}+v_{\mathit{ac}\_a}+v_{\mathit{gm}}$$

(9)

where v_{ac_a} is the ac voltage at phase “a” related to a neutral point named “g”, and v_gm is the voltage between that AC neutral point and the DC middle point “m”. The latter voltage, v_gm, could be neglected for output current controllers as long as there is no path for the zero-sequence components of those currents. Thus, an equivalent inductor L_eq can be defined in (10) to get (11), an equation usually applied to PI or deadbeat controllers to manage the active and reactive power transferred to the grid.

$$L_{\mathit{eq}}\equiv \frac{1}{2}{L}_{\mathit{arm}}+L_o$$

(10)

$$\frac{v_{\mathit{la}} -v_{\mathit{ua}}}{2}\cong v_{\mathit{ac}\_a}+L_{\mathit{eq}}\frac{{\mathit{di}}_{\mathit{oa}}}{\mathit{dt}}$$

(11)

As stated in (11), output currents depend on the voltages generated by the upper and lower arms, that rely on the switching states of the SMs and the modulation technique applied to the converter.

3. Proposed LC-PWM

In order to control the MMC under the more demanding situations found when variable voltage power sources like PV panels are moved into the MMC, spreading them throughout all the switching modules, a new adaptive modulation technique is proposed. This modulation does not use a fixed carrier frame where modulator waves find the switching times; it uses a private local carrier created for each modulator in every switching period using the measured cell voltages, generating more accurate switching times. In addition, the modulator also introduces small changes in switching periods to anticipate each change in the number of cells used to modulate the output to reduce distortion: incorrect decisions when crossing from level to level generate fast transients on circulating currents that must be avoided to reduce conduction losses.

Actually, using capacitor voltage information on MMC modulators causes no additional overheads, because those voltages are measured and used in the sorting algorithm in order to keep those capacitors balanced. Using that information on modulation improves the timing of the switching sequence, generates more accurate voltages at the output of the converter and helps to remove the annoying 100 Hz component on circulating currents [8]. Thus, in order to compute a precise duty cycle for each sampling period, the LC-PWM produces a specific local carrier for each MMC arm, as illustrated in Figure 5.

Referring to the lower arm of phase “a”, Figure 5 explains the proposed modulation in more detail. When using four SMs per arm, available voltages for this arm are voltages near [0, ¼V_dc, ½V_dc, ¾V_dc, V_dc], but actually arm voltages will be a few volts above or below those levels, not only because of voltage fluctuations on MMC capacitors due to their charge and discharge processes, but also because of MPPT on PV panels that will target different voltages for cells due to differences in irradiance and/or temperature. Regardless of these difficulties, the LC-PWM method generates an accurate output voltage by calculating a local carrier for the lower arm in each sampling period using the previous and target voltages of this arm, as stated in (12) and (14), and a separated carrier is developed for the upper arm using (13) and (15). Previous voltages are known from the previous sampling period, and target voltages at the end of the sampling period can be estimated after a decision on inserting or bypassing the most appropriate SM is made for each arm.

$$v_{\mathit{la}}\left(t\right)={\displaystyle \sum }_{j=1}^N{\mathit{Vcl}}_j\left(t\right)·{\mathit{Sl}}_j\left(t\right)$$

(12)

$$v_{\mathit{ua}}\left(t\right)={\displaystyle \sum }_{j=1}^N{\mathit{Vcu}}_j\left(t\right)·{\mathit{Su}}_j\left(t\right)$$

(13)

$$v_{\mathit{la}}{(t+T}_{\mathit{sa}})\cong {\displaystyle \sum }_{j=1}^N{\mathit{Vcl}}_j\left(t\right)·{\mathit{Sl}}_j{(t+T}_{\mathit{sa}})$$

(14)

$$v_{\mathit{ua}}\left({t+T}_{\mathit{sa}}\right)\cong {\displaystyle \sum }_{j=1}^N{\mathit{Vcu}}_j\left(t\right)·{\mathit{Su}}_j\left({t+T}_{\mathit{sa}}\right)$$

(15)

In these equations, Vcu_j and Vcl_j represent the SM voltages for the upper and lower arms, whereas Su_j and Sl_j are the switch statuses on the upper and lower SMs at the beginning or at the end of the switching period.

Figure 6 shows in detail the LC-PWM strategy for each sampling period T_sa in phase “a”. The intersection of two separated carriers with the two output references, v*_la and (V_dc − v*_ua), generates an upper arm voltage and a lower arm voltage that exactly match the desired voltage for each arm during that period.

Therefore, the desired duty cycles d_ua for the upper arm and d_la for the lower arm are computed using (16) and (17) for the current sampling period:

$$d_{\mathit{ua}}=\frac{T_{\mathit{ua}}}{T_{\mathit{sa}}}=\left|\frac{v^{*}{}_{\mathit{ua}}\left(t\right)-v_{\mathit{ua}}\left({t+T}_{\mathit{sa}}\right)}{v_{\mathit{ua}}\left(t\right)-v_{\mathit{ua}}\left({t+T}_{\mathit{sa}}\right)}\right|$$

(16)

$$d_{\mathit{la}}=\frac{T_{\mathit{la}}}{T_{\mathit{sa}}}=\left|\frac{v^{*}{}_{\mathit{la}}\left(t\right)-v_{\mathit{la}}\left({t+T}_{\mathit{sa}}\right)}{v_{\mathit{la}}\left(t\right)-v_{\mathit{la}}\left({t+T}_{\mathit{sa}}\right)}\right|$$

(17)

where T_ua and T_la are the exact timing when an SM must be inserted or bypassed, and v*_ua and v*_la are the reference voltages for the upper arm and the lower arm, as described below. In fact, an important contribution of the proposed method is that LC-PWM accurately finds the precise time to change from one state level to the next level, allowing full control of the generated voltages.

Equations (18) and (19) describe the reference voltage for the upper and lower arm, respectively,

$$v_{\mathit{ua}}^{*}=\frac{1}{2}{V}_{\mathit{dc}}-v_{\mathit{oa}}^{*}-v_{\mathit{za}}^{*}$$

(18)

$$v_{\mathit{la}}^{*}=\frac{1}{2}{V}_{\mathit{dc}}+v_{\mathit{oa}}^{*}-v_{\mathit{za}}^{*}$$

(19)

where v*_oa is the alternating reference for the output voltage in phase “a”. The value of v*_za is used to control the evolution of the circulating current; a simple deadbeat controller based on (5) can be used to keep the circulating current near the desired value i*_za:

$$v_{\mathit{za}}^{*}=\frac{L_{\mathit{arm}}}{T_{\mathit{sa}}}(i_{\mathit{za}}^{*} -i_{\mathit{za}})$$

(20)

As shown in Figure 6, v*_za introduces a small differential voltage, forcing the circulating current to follow the given reference for each phase. Actually, this controller plays an important role in the overall behavior of the MMC when using this modulation, and must be carefully used to drive any energy imbalance on the MMC, but for the sake of simplicity and to remain focused on the modulation, this paper will discuss the converter behavior only under balanced scenarios, so the reference for this circulating current controller can be set to zero in the steady state.

In order to apply (14) and (15), the appropriate SMs that are going to be inserted or bypassed during the current switching period must be selected. Traditional MMC topologies with external energy sources look for the greatest or the lowest capacitor voltage at each arm to keep the cell capacitors balanced, but when using internal energy sources, the distance to the reference voltage for each cell must be used instead. As usual [17], only one SM status is changed in each sampling period to decrease switching losses, and this decision usually simplifies the sorting task, reduced to one run over the arm voltages to find the location of the appropriate SM.

Nonetheless, LC-PWM will require a full sorting of all arm voltages, as seen immediately in (21) to (23), and this issue usually becomes overwhelming when the number of SMs increases. The difference in this application, with energy sources distributed throughout the MMC cells that targeted different voltages, is that capacitor voltage evolves up and down in a coordinated fashion, thus they can actually be sorted in a few one-pass steps throughout a few sampling periods: the relative locations of all cells are continuously updated in each sampling period and they are kept sorted in a list. Therefore, the computational effort of sorting is mostly equal when energy sources are in or out of the MMC.

As seen later in Section 4, using capacitor voltage information on LC-PWM duty cycle computation, generated switching sequences greatly reduce the root mean square (RMS) value of circulating currents by removing the 100 Hz component, but an important source of noise remains on those internal currents: in a few situations, when the converter changes the number of cells used to modulate the output, for example, when it alternates using one or two cells and starts using two or three cells, in those switching periods it is possible that the voltage given as reference cannot be reached by just inserting or bypassing one cell, and then an important transient alters the circulating current, seriously affecting its RMS value. Thus, LC-PWM must anticipate all those events, adapting the duration of a few sampling periods just before each crossing point in such a way that it guarantees the converter will have the appropriate number of active cells when arriving at all crossing points. In the given example, the converter must have exactly two active cells in every sampling period when the converter changes from using one or two active cells to two or three cells.

The first step for this task is to anticipate the voltage for the following crossing level, as shown in Figure 7. Depending on selected cells, upper and lower arms have many different options to generate a voltage near the targeted crossing voltage; as a compromise, valid for the upper and lower arms, the modulator will use the midpoint between the greatest and the lowest of all those options as an estimation for the following crossing voltage. To do so, upper and lower cell voltages are always kept sorted in linked lists, as described above, and in each sampling period, a few cells are selected from the beginning and from the end of those lists, and those voltages are added to compute four values, named v_{max_up_a}, v_{min_up_a}, v_{max_lw_a} and v_{min_lw_a}. For each phase, the estimated voltage for the following crossing is then computed using (23) as the average of the maximum v_{max_a} and the minimum v_{min_a} of those four values.

v_{max_a} = max(v_{max_up_a}, v_{max_lw_a})

(21)

v_{min_a} = min(v_{min_up_a}, v_{min_lw_a})

(22)

$${\widehat{v}}_{level\_a}=\frac{v_{\mathit{max}\_a}+v_{\mathit{min}\_a}}{2}$$

(23)

The second step to achieve clean crossings defines the modulator state as “even” or “odd”. When an arm voltage is near to the next crossing voltage, the value previously computed as ${\widehat{v}}_{level\_a}$ for the first phase, the arm is said to be in an “even” state, because next crossing will be cleaner if the modulator executes an even number of steps before the transition. The opposite situation is found when the arm voltage is far from the crossing level, where an odd number of steps is then desired.

The third step, described in (24) to (26), computes the length for the PWM period using the remembered time for the next crossing point t_{next_cross_a} and the registered time t_current during the grid cycle. In this case, a central value of 250 microseconds is used for a nominal switching frequency of 2 KHz, and this value is changed to 225 or 275 microseconds to consistently reach the following crossing point in an “even” state, which guarantees the correct switching decision to remove undesired transients from the circulating current of each phase.

$$t_{\mathit{cross}\_a}=t_{\mathit{next}\_\mathit{cross}\_a}-t_{\mathit{current}}$$

(24)

When modulator is in an “even” state, it applies (25) to get the next sampling time, in “odd” states, it applies (26):

$$T_{\mathit{sa}}=250+25·\mathit{sign}\left(t_{\mathit{cross}\_a} -500·(\lfloor t_{\mathit{cross}\_a}/500+0.5\rfloor )\right)$$

(25)

$$T_{\mathit{sa}}=250+25·\mathit{sign}\left(t_{\mathit{cross}\_a} -500·(\lfloor t_{\mathit{cross}\_a}/500\rfloor +0.5)\right)$$

(26)

where all times including the sampling period “T_sa” for phase “a” are measured in microseconds and $\lfloor x\rfloor$ represents the lower bounded integer of “x”.

The final step for this task detects the exact time when the MMC crosses from one level to the next one in order to remember that point for the next cycle. It is not difficult to detect each crossing by comparing the reference voltage and the estimated voltage for the next crossing:

$$\Delta v_a(t)={\widehat{v}}_{level\_a}-v_{\mathit{la}}^{*}(t)$$

(27)

$$\Delta v_a(t-T_{\mathit{sa}})={\widehat{v}}_{level\_a}-v_{\mathit{la}}^{*}(t-T_{\mathit{sa}})$$

(28)

At each crossing, the current and previous voltage differences computed by (27) and (28) have different signs. In those sampling periods, assuming a smooth evolution of capacitor voltages, the time deviation of the crossing point from the middle of the sampling period is estimated using (29). Later on, this information is used in (30) to accurately locate the current crossing point, and the location of the following crossing point is recovered from an appropriate store using (32):

$$∆t_{\mathit{cross}\_a}=\frac{T_{\mathit{sa}}}{2}·\frac{\left|∆v_a\left(t\right)\right| -\left|∆v_a(t-T_{\mathit{sa}})\right|}{\left|∆v_a\left(t\right)\right|+\left|∆v_a(t-T_{\mathit{sa}})\right|}$$

(29)

$${\mathit{crossings}}_a\left[i_a\right]=t_{\mathit{current}} -∆t_{\mathit{cross}\_a}$$

(30)

$$i_a={(i}_a+1)\mathit{mod}6$$

(31)

$$t_{\mathit{next}\_\mathit{cross}\_a}={\mathit{crossings}}_a\left[i_a\right]$$

(32)

where “i_a” is an integer that identifies the crossing point. This index is updated in (31) to have a value ranging from 0 to 5, as long as an MMC with four SMs per arm may have up to six crossing points.

4. Simulation Results

In order to evaluate the proposed modulation, a few simulations were performed using a MATLAB/Simulink model for the three-phase MMC with internal or external PV cells, as shown in Figure 2 and Figure 3. A 169 KW photovoltaic system was set up using 528 Suntech STP320-24/Ve PV cells, described in

Table 2. Parameters of Suntech STP320-24/Ve PV panels.

Parameters	Value
Maximum power (Pmax)	320 W
Maximum power voltage (Vmax)	36.7 V
Maximum power current (Imax)	8.72 A
Open circuit voltage (Voc)	45.6 V
Short circuit current (Isc)	9.07 A
Shunt resistance (Rsh)	4.24 Ω
Series resistance (Rs)	0.03 Ω
Ideal factor of diode (m)	1.1238

, and connected to an isolated load using the parameters described in

Table 3. Parameters of the three-phase MMC.

Parameters	Value
Active power (P)	169 KW
DC link voltage (Vdc)	3200 V
Switching frequency (fs)	2000 Hz
SM capacitance (CSM)	3000 µF
SM capacitor voltage (VSM)	807.4 V
Arm inductor (Larm)	340 µH
Output inductor (Lo)	680 µH
Output capacitor (Co)	187 µF
Nominal load resistor (R)	13 Ω

. The PV panel behavior was modeled as a voltage-controlled current source, using a fifth-order polynomial approximation that guarantees the correct power and slope at the maximum power point and other relevant points, such as open circuit and short circuit. A full set of polynomials was developed for different irradiance values ranging from 100 W/m² to 1000 W/m², with steps of 50 W/m². In the simulations, a discrete 0.25-microsecond sampling period was used for the plant and the converter, with Tustin integration. Switching signals were generated with a resolution of 1 microsecond. For the controller simulation, a constant 250-microsecond period was used when using PS-PWM; a 25-microsecond period was used for LC-PWM in order to switch one SM in each phase every 225, 250 or 275 microseconds.

PV panels were distributed as an array of 6 × 88 cells when connected externally to the MMC, giving a nominal DC voltage of 3200 V, or as 24 strings of 22 panels serially connected to each one of the 24 SMs of a five-level three-phase MMC, giving 807.4 V at their maximum power point. As this research was focused on the features of the proposed modulation, an open-loop isolated load was preferred rather than a grid-connected system to remove any possible interaction related to the grid or its controllers.

Simulations covered different irradiance situations to validate the consistent behavior of the proposed modulation when MMC cells target different voltages, and also to assess the distortion that arises at the output of the MMC when traditional modulations are used in this application. Traditional PS-PWM and newly proposed LC-PWMs were tested using external and internal PV panels.

A behavioral description of LC-PWM compared to PS-PWM is shown in Figure 8. One of the MMC phase voltages is shown above, the second row displays the voltages of the upper and lower capacitors and the last row shows the circulating current in one phase, demonstrating a clean and controlled behavior when using LC-PWM.

4.1. Scenario 1: PS-PWM-Controlled MMC

An MMC with four SMs per arm is connected to external or internal PV panels and to a three-phase resistive load, with 13 Ω per phase when irradiance is 100%, but 130 Ω when irradiance decreases to 10%. The target phase voltage on the outputs is the required to get steady conditions, and it is almost constant in all irradiance situations to replicate the behavior of a grid connection.

4.1.1. Case 1: PV Panels Located Externally to the MMC Converter

In this case, PV panels are connected as a central converter using an array of 88 panels in series and six strings in parallel, and all of them receive the same irradiance. The performance of the MMC was measured under different irradiance levels evolving from 100% (situation 1) to 10% (situation 7), increasing the load resistors accordingly in order to keep the output voltage constant.

Table 4. Simulation results of the MMC modulated using PS-PWM with external PV panels.

Situation	Irradiance [W/m2]	LHD [%]	THDC [%]	THDO [%]	dc(iz) [A]	rms(iz) [A]	rms[iz–dc(iz)] [A]
1	1000	0.32	23.9	1.10	17.6	46.0	42.5
2	850	0.32	23.8	1.10	15.3	41.5	38.6
3	700	0.31	23.8	1.13	12.3	38.3	36.3
4	550	0.30	23.8	1.10	9.7	35.0	33.6
5	400	0.30	23.7	1.05	7.1	32.3	31.5
6	250	0.30	23.7	1.10	4.5	30.2	29.9
7	100	0.30	23.8	1.16	1.9	28.6	28.5

illustrates the results of these simulations including a measure of the low harmonic distortion (LHD) from the 2nd to the 19th harmonic, the total harmonic distortion at converter output voltage (THD_C), the total harmonic distortion at the load voltage (THD_O), the DC and RMS components of the circulating current and the RMS value of the circulating current when removing its DC component.

4.1.2. Case 2: PV Panels Distributed throughout the MMC Cells

In this case, strings with 22 PV panels in series were integrated directly into each SM of the MMC, as shown in Figure 3, and the DC link was removed. Identical solar panels were used in all SMs, but the irradiance changes at different SMs, as described in

Table 5. Irradiance received at PV string located on SMs in the simulated situations.

Situation	SM1 Irr. [%]	SM2 Irr. [%]	SM3 Irr. [%]	SM4 Irr. [%]	Average Irr. [%]
1	100	100	100	100	100
2	100	90	80	70	85
3	100	80	60	40	70
4	100	70	40	10	55
5	70	50	30	10	40
6	40	30	20	10	25
7	10	10	10	10	10

. However, the scope of this paper is not to deal with unbalanced situations, so all six arms of the MMC received the same average irradiance, thus there was no energy transferred from phase to phase or from arm to arm. Therefore, situations 1 to 7 of this case are mostly equivalent to those situations described for the previous case.

Table 6. Simulation results of the MMC modulated using PS-PWM with distributed PV panels.

Situation	LHD [%]	THDC [%]	THDO [%]	dc(iz) [A]	rms(iz) [A]	rms[iz–dc(iz)] [A]
1	0.32	23.9	1.1	−0.01	47.7	47.7
2	0.36	23.8	1.1	−0.01	43.2	43.2
3	0.30	23.8	1.2	0.00	38.3	38.3
4	0.98	23.6	2.7	0.16	38.0	38.0
5	0.88	23.6	3.7	0.08	36.6	36.6
6	0.86	23.8	4.3	0.06	34.3	34.3
7	0.31	23.8	1.2	0.00	28.7	28.7

shows the results generated from these simulations.

These results, also included in Figure 9, clearly show the ability of PS-PWM to manage an external array of PV panels even with different irradiances, but they also demonstrate the problems that arise when trying to deal with different irradiance levels of different PV cells when they are distributed throughout the MMC cells. In such a case, target voltages are different due to MPPT, and fixed PWM carriers do not adapt to those changes, thus LHD and THD_O distortion increase beyond tolerable levels; this issue is more evident in situations 4 to 6.

When using PS-PWM, external PV panels are a better option not only because of a wider operation range, as demonstrated above, but also because the achieved performance is greater. Table 4 clearly shows that the DC component of the circulating current is proportional to the power supplied by the external PV panels, and Table 6 shows that this DC component is completely removed when moving PV panels into the MMC. However, the RMS value of the circulating current remains mostly constant when moving the PV panels into the MMC, and when removing the DC component from the circulating current, an increase of about 10% is observed.

This issue reflects the lack of control of circulating currents when using PS-PWM and it must have an effect on the conduction power losses of the MMC.

Table 7. Converter power losses, converter efficiency and application performance using PS-PWM.

PV Panel Connection	Situation	Power Losses [W]	Efficiency [%]	Performance [%]
External PV	1	2791	98.3	98.1
	2	2304	98.2	98.1
	3	1933	98.2	98.1
	4	1618	98.1	97.9
	5	1371	97.8	97.6
	6	1199	97.1	97.0
	7	1071	93.6	93.4
Internal PV	1	2912	98.1	97.6
	2	2391	98.2	97.7
	3	1930	98.2	97.8
	4	1881	97.9	97.5
	5	1609	97.6	97.2
	6	1320	96.6	96.3
	7	1075	93.6	93.3

shows the results of these simulations where conduction power losses (P_losses) have been estimated using a simplified but representative model for the semiconductors: a 30 mΩ resistance (R_on) for each IGBT and FWD when they are active. As long as four semiconductors are always active at each MMC arm, and conduction power losses can be roughly estimated using (33) throughout a period (T) of 20 milliseconds for a 50 Hz system.

$$P_{\mathit{losses}}=\frac{1}{T}{\displaystyle \int }{4R}_{\mathit{on}}{(i}_{\mathit{ua}}^2+i_{\mathit{ub}}^2+ i_{\mathit{uc}}^2+ i_{\mathit{la}}^2+i_{\mathit{lb}}^2+ i_{\mathit{lc}}^2)\mathit{dt}$$

(33)

Then, the efficiency of the MMC and the performance of the application can be computed using (34) and (35), where P_{PV_MPP} represents the maximum power that can be extracted from PV panels at their maximum power point under different situations of irradiance, P_{MMC_IN} represents the measured power at the input of the MMC and P_{MMC_OUT} is computed by subtracting the power losses from P_{MMC_IN}, a value that is quite similar to the power measured at the resistive load.

$$\mathit{Efficiency}=\frac{P_{\mathit{MMC}\_\mathit{OUT}}}{P_{\mathit{MMC}\_\mathit{IN}}}·100\%$$

(34)

$$\mathit{Performance}=\frac{P_{\mathit{MMC}\_\mathit{OUT}}}{P_{\mathit{PV}\_\mathit{MPP}}}·100\%$$

(35)

As can be seen in Table 7, conduction losses and converter efficiency are mostly equal when using internal or external PV panels, because the RMS value of the uncontrolled circulating currents remain constant. Moreover, the application performance when using internal PV panels is even smaller than the corresponding value seen with external panels because MPPT controllers are less accurate: when using internal panels, each SM has its own MPPT, but only the summation of all the MMC voltage cells can be regulated by the active power controller, while the whole PV array voltage, the DC link voltage, is directly measured and regulated when using external PV panels. In this case, moving PV panels into the MMC gives no advantage.

4.2. Scenario 2: LC-PWM-Controlled MMC Converter

The proposed LC-PWM was simulated in the same situations as PS-PWM and using the same parameters described in Table 2 and Table 3. A uniform averaged irradiance was used again on the external PV array, and different irradiances were used for different MMC cells when using internal PV panels, following the same situations described in Table 5.

4.2.1. Case 1: PV Panels Located Externally to the MMC

Again, a 6 × 88 PV array is connected at the DC side of a five-level MMC that feeds a resistive load, but in this case, the newly proposed LC-PWM is applied. The distortion results shown in

Table 8. Simulation results of the MMC modulated using LC-PWM with external PV panels.

Situation	Irradiance [W/m2]	LHD [%]	THDC [%]	THDO [%]	dc(iz) [A]	rms(iz) [A]	rms[iz–dc(iz)] [A]
1	1000	0.34	26.6	1.31	17.4	19.0	7.6
2	850	0.33	26.8	1.35	14.8	16.1	6.3
3	700	0.34	26.8	1.33	12.2	13.6	6.0
4	550	0.33	27.2	1.37	9.6	10.7	4.7
5	400	0.35	27.3	1.36	7.0	8.3	4.5
6	250	0.32	27.1	1.39	4.4	5.9	3.9
7	100	0.38	25.7	1.39	1.7	4.2	3.8

are consistent in a wide operation range (irradiance from 100% to 10%) and were moderate when compared to those results shown for PS-PWM in Table 4. The main difference is that the circulating current is mostly limited to the function of moving energy from external PV panels to internal capacitors.

4.2.2. Case 2: PV Panels Distributed throughout the MMC

PV panels are spread for a second time throughout the MMC cells, placing a string of 22 serially connected PV panels on each SM. As above, all panels on each SM receive the same irradiance, but different cells receive different irradiances, as described in Table 5.

Table 9. Simulation results of the MMC modulated using LC-PWM with distributed PV panels.

Situation	LHD [%]	THDC [%]	THDO [%]	dc(iz) [A]	rms(iz) [A]	rms[iz–dc(iz)] [A]
1	0.30	27.4	1.31	−0.02	6.27	6.27
2	0.30	27.3	1.30	−0.05	5.89	5.89
3	0.29	27.2	1.30	−0.04	5.15	5.15
4	0.31	26.4	1.32	−0.01	5.32	5.32
5	0.33	26.9	1.36	0.02	4.99	4.99
6	0.26	26.6	1.33	−0.02	4.64	4.64
7	0.36	25.9	1.32	0.04	3.95	3.95

shows the results generated in these simulations. Now, the voltage differences between different cells are compensated by LC-PWM and as a result the output distortion is under control in the whole operation range for this application, from 100% irradiance to 10%, even with variable irradiance at different MMC cells. In addition, the DC component of the circulating current was removed because PV panels generate energy directly to MMC capacitors, and the RMS value of the circulating current reflects only the ripple on the arm currents due to switching. Figure 10 clearly shows that LC-PWM can keep distortion within acceptable levels for any irradiance situation when using external and also internal PV panels.

The power loss analysis, shown in

Table 10. Converter power losses, converter efficiency and application performance using LC-PWM.

PV Panel Connection	Situation	Power Losses [W]	Efficiency [%]	Performance [%]
External PV	1	1600	99.1	99.1
	2	1314	99.1	99.1
	3	1073	99.1	99.1
	4	882	99.1	99.1
	5	736	98.9	98.9
	6	631	98.5	98.5
	7	599	96.4	96.4
Internal PV	1	1353	99.2	98.5
	2	1136	99.2	98.6
	3	953	99.2	98.7
	4	805	99.1	98.7
	5	693	99.0	98.6
	6	615	98.5	98.3
	7	551	96.7	96.4

, confirms the improvement achieved by LC-PWM, an optimized modulation that takes into account the measured voltages of the MMC cells and synchronizes each level to level transition to remove all transients in the circulating current. Figure 11 clearly shows that the proposed LC-PWM may cut the conduction losses of the MMC converter by half when compared to traditional PS-PWM, and this feature translates immediately to the converter efficiency. Moreover, using the proposed modulation reduces power losses further, up to 15%, when moving PV panels into the MMC converter, as seen in Table 10.

The performance analysis for this application is shown in Figure 12. Both LC-PWM and PS-PWMs are applied first to a set-up with external PV panels and uniform irradiance, and then to a second set-up with internal PV panels and variable irradiance. A third set-up, represented using dashed lines, shows the application performance when PV panels are connected externally to the MMC and 99% efficient boosters are used on each PV string to deal with variable irradiances. The best performance results were achieved when using LC-PWM and external panels, with no boosters, because of the accuracy of its global and direct MPPT; however, this set-up can only be used when uniform irradiance is expected in the application and a unique and global MPPT can be applied. For applications where variable irradiance throughout the PV field is an important issue or frequent situations of partial shadowing are expected, then the best performance results were obtained using LC-PWM and PV panels spread throughout the MMC, a topology that uses the switches of the MMC cells to apply an MPPT to each PV string.

5. Conclusions

A new modulation method, named local carrier PWM, has been proposed to manage MMCs with PV panels distributed throughout their cells. In this application, each SM is connected to a PV string and it applies an MPPT that targets a voltage not related to other cells. These variable voltages at MMC cells generate an unacceptable distortion at the output voltage when using traditional modulations, as seen in a few simulations, and they also increase the internal circulating currents with an undesirable effect on converter losses.

The proposed LC-PWM uses the available cell voltage information to generate more accurate voltages at the MMC arms that reduce to a great extent the internal circulating currents and maintain the output distortion in moderate values for a wide operation range. Furthermore, the modulator sampling period is slightly lengthened or shortened to reach each level to level transition with the correct number of inserted cells, removing undesired fast transients from circulating currents.

A few simulations of different irradiance situations were used to validate this development. They demonstrate the consistency and improved behavior of the proposed LC-PWM that greatly reduces the circulating currents and they also demonstrate that conduction power losses of PV applications can be cut by half when using MMCs with distributed PV panels.