Conventional and Advanced Exergy and Exergoeconomic Analysis of a Spray Drying System: A Case Study of an Instant Coffee Factory in Ecuador
Abstract
:1. Introduction
2. Materials and Methods
2.1. System Description
- The process was at a steady state condition.
- The coffee extract was modeled as a solution with a constant concentration of soluble solids from Coffea arabica beans.
- The heat losses from the components were neglected.
- The pressure losses in the pipes, heat exchangers, bag filter, and spray dryer were neglected.
- The properties of the incoming air were considered as constants.
2.2. Exergy Analysis
2.3. Advanced Exergy Analysis
2.4. Exergoeconomic Analysis
2.5. Advanced Exergoeconomic Analysis
3. Results and Discussions
3.1. Conventional Exergy Analysis
3.2. Advanced Exergy Analysis
3.3. Conventional Exergoeconomic Analysis
3.4. Advanced Exergoeconomic Analysis
4. Conclusions
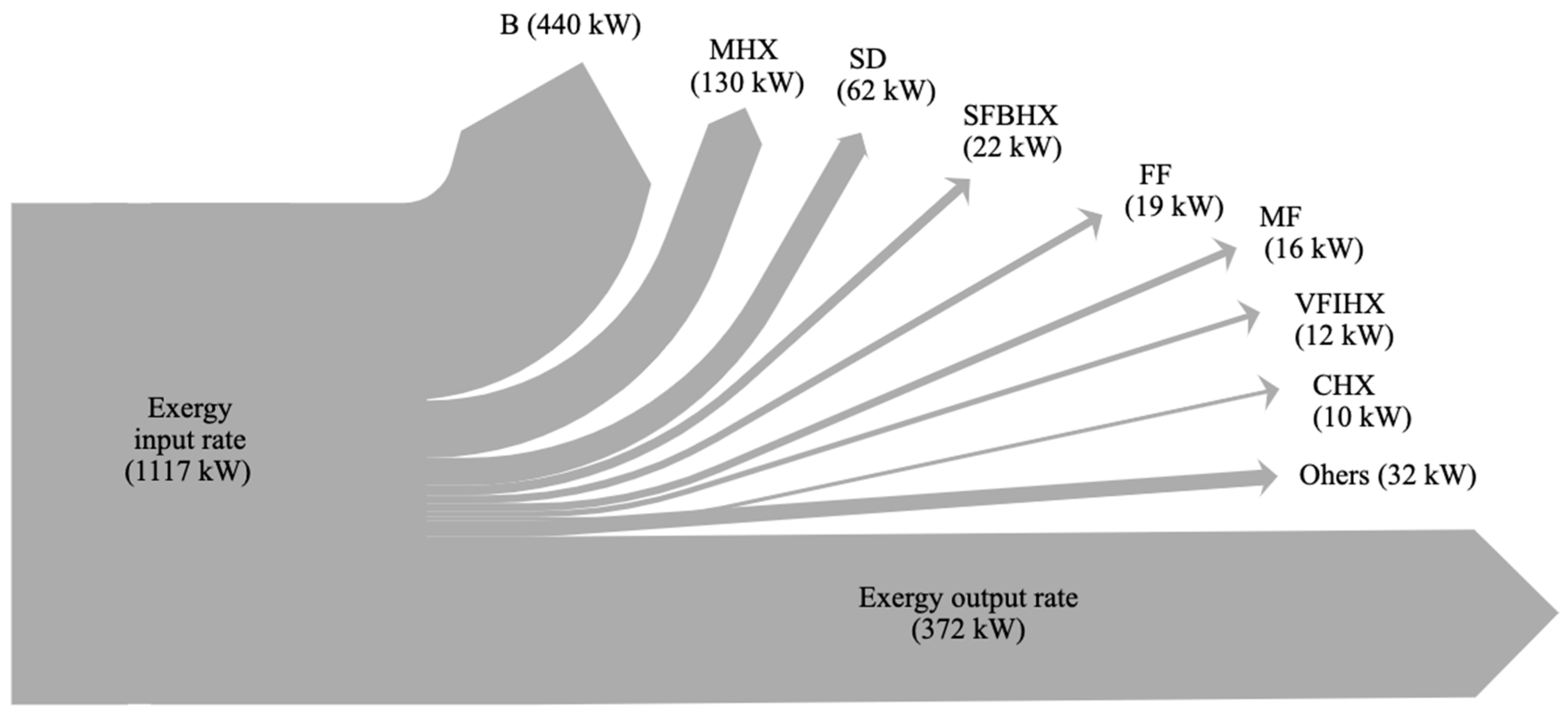
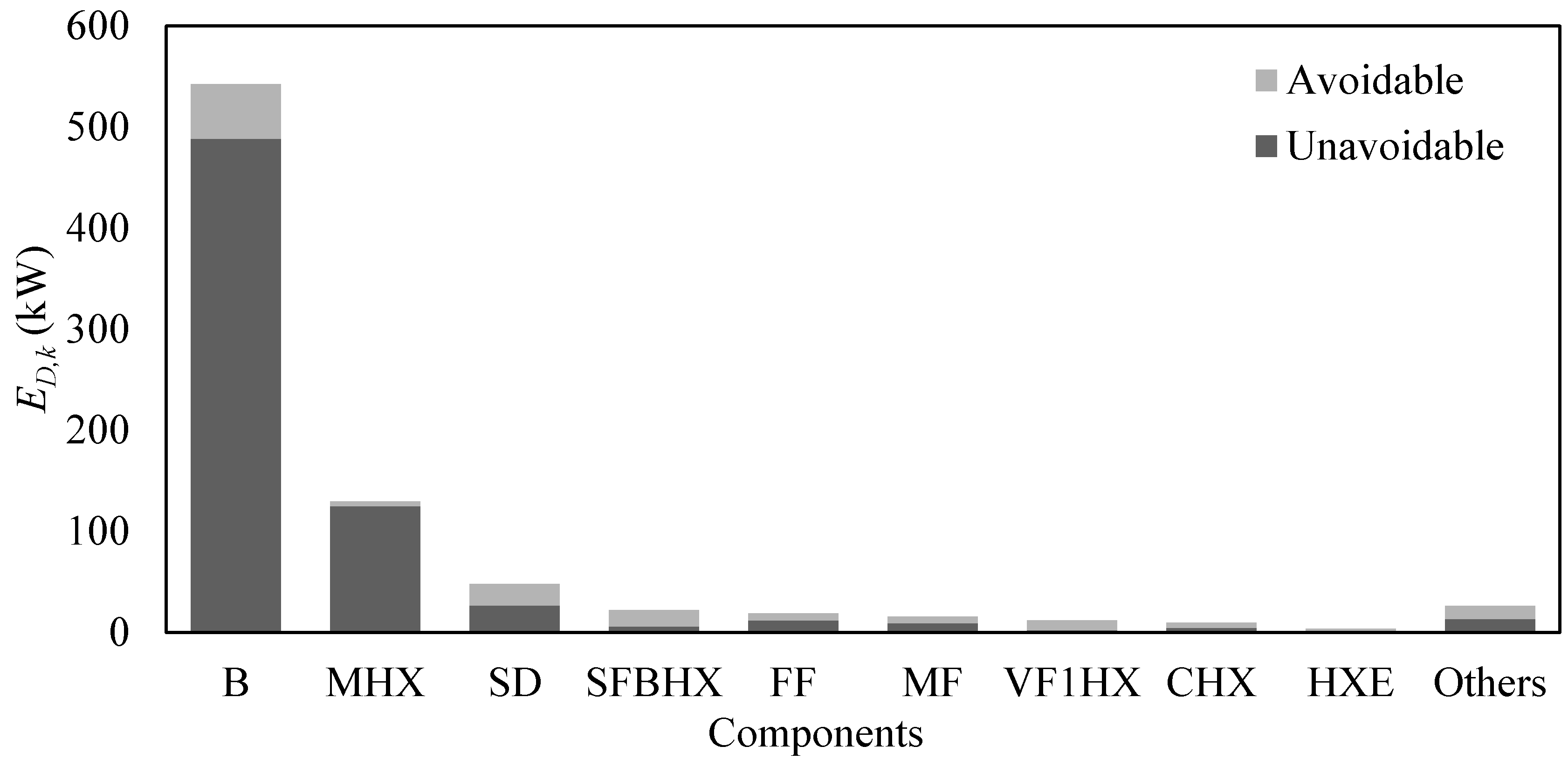
- The overall energy and exergy efficiencies of the spray drying system were calculated as 71% and 33% respectively, where the B had the highest exergy destruction rate, but most of it (90%) was unavoidable exergy destruction.
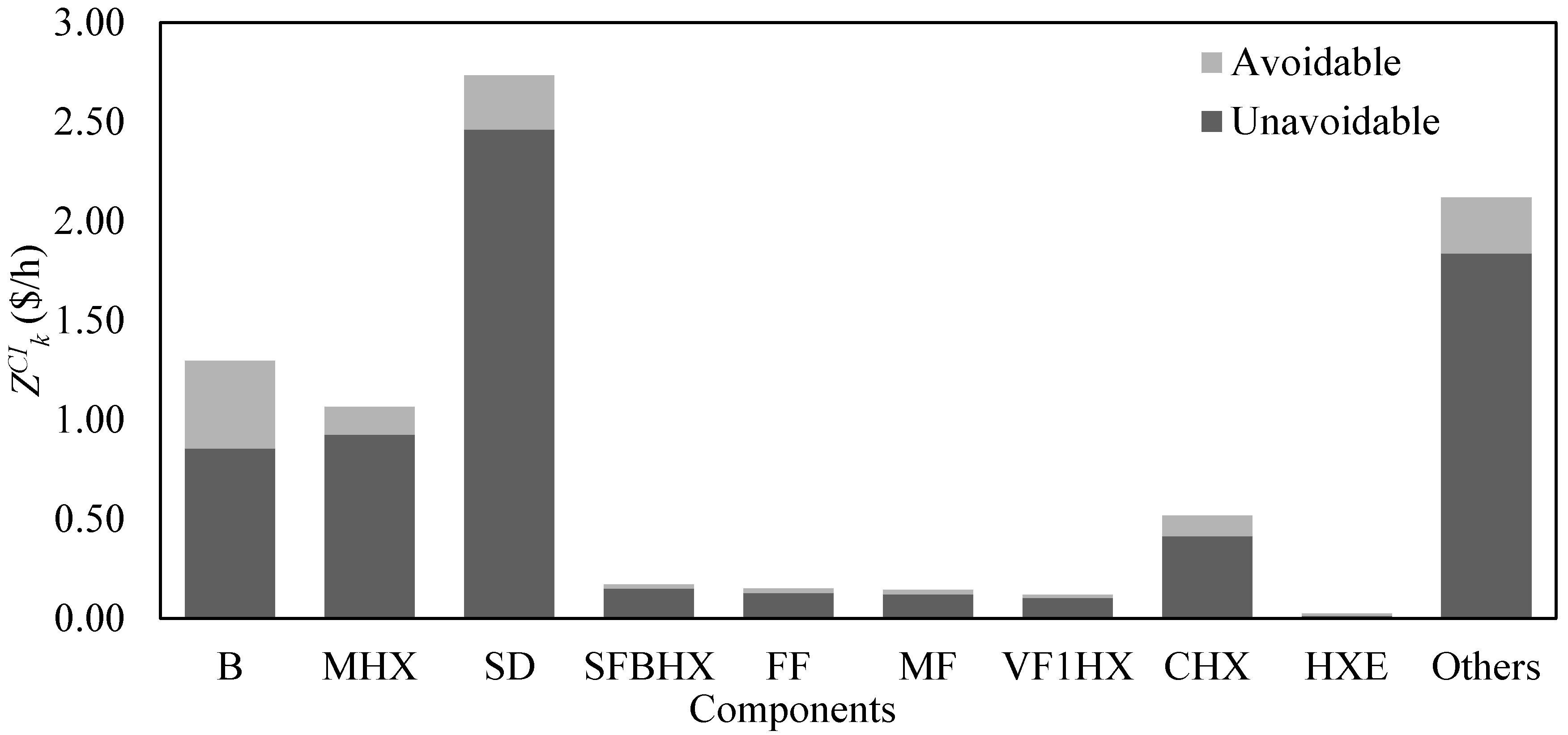
- The conventional exergoeconomic analysis allows for the quantification of the overall operational cost rate ($207.9/h); more than 70% of that cost rate was due to the SD and the MHX.
- The exergoeconomic factor allowed for the identification of the SD and MHX as the sources with the highest cost rate. More than 97% of the operating cost rate of the SD and the MHX were due to a high exergy destruction rate; of all the components in the studied system, these components were the most exergy destructive. The cost rates of the exergy destruction for the SD and the MHX were 106.9 $/h and 60.5$/h, respectively.
- The advanced exergoeconomic analysis revealed that 33% of the exergy destruction cost rate of the overall system was avoidable. Additionally, it established that 70% of the avoidable exergy destruction cost rate was located in the SD, demonstrating that this was the component with the highest improvement potential.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| cost rate associated with an exergy stream ($/h) | |
| y | destruction rate |
| exergy rate (kJ/h) | |
| f | exergy rate (kJ/h) |
| i | interest rate |
| heat capacity (kJ/K*kg) | |
| heat flow rate (kJ/h) | |
| R | ideal gas constant (kJ/kmol*K) |
| investment cost rate ($/h) | |
| mass flow rate (kg/h) | |
| n | life time of the system |
| P | pressure (kPa) |
| r | relative cost difference |
| y* | relative irreversibility |
| h | specific enthalpy (kJ/kg) |
| s | specific entropy (kJ/kg) |
| e | specific exergy rate (kJ/kg) |
| T | temperature (°C) |
| c | unit exergy cost ($/kJ) |
| mole fraction of water vapor | |
| power (kJ/h) | |
| x | mole fraction |
| Greek letters | |
| Δ | difference |
| γ | specific heat ratio |
| ɳ | efficiency |
| air density (kg/m3) | |
| τ | annual operating hours (h) |
| Abbreviations | |
| B | boiler |
| BT | belt |
| CHX | cooler heat exchanger |
| HXE | extract heat exchanger |
| RFF | fine returns fan |
| SFBF | fluidized bed fan |
| SFBHX | fluidized bed heat exchanger |
| HP | high pressure pump |
| LP | low pressure pump |
| MF | main fan |
| MHX | main heat exchanger |
| N | nozzle |
| PEC | purchased equipment cost |
| SD | spray dryer |
| FF | vacuum pump |
| VF1F | vf1 fan |
| VF1HX | vf1 heat exchanger |
| VF2F | vf2 fan |
| VF2HX | vf2 heat exchanger |
| S | vibrating screen |
| Subscripts | |
| con | conversion |
| D | exergy destruction |
| elec | electric |
| en | energy |
| ex | exergy |
| F | fuel exergy |
| in | inflow |
| is | isentropic |
| k | kth component |
| mech | mechanical |
| min | minimum |
| mix | mixture |
| out | outflow |
| P | product exergy |
| L | loss |
| tot | overall system |
| o | thermodynamic environment |
| Superscripts | |
| AV | avoidable |
| CH | chemical |
| CI | capital investment |
| KN | kinetic |
| OM | operating and maintenance |
| PH | physical |
| PT | potential |
| UN | unavoidable |
References
- Statista Consumer Market Outlook for Instant Coffee. 2020. Available online: https://www.statista.com/outlook/30010200/100/instant-coffee/worldwide (accessed on 20 May 2020).
- Svilaas, A.; Sakhi, A.K.; Andersen, L.F.; Svilaas, T.; Ström, E.C.; Jacobs, D.R.; Ose, L.; Blomhoff, R. Intakes of Antioxidants in Coffee, Wine, and Vegetables Are Correlated with Plasma Carotenoids in Humans. J. Nutr. 2004, 134, 562–567. [Google Scholar] [CrossRef]
- Gebhardt, S.; Lemar, L.; Haytowitz, D.; Pehrsson, P.; Nickle, M.; Showell, B.; Holden, J. USDA National Nutrient Database for Standard Reference, Release 21; United States Department of Agriculture Agricultural Research Service: Washington, DC, USA, 2008.
- Lucas, M.; Mirzaei, F.; Pan, A.; Okereke, O.I.; Willett, W.C.; O’Reilly, É.J.; Koenen, K.; Ascherio, A. Coffee, Caffeine, and Risk of Depression Among Women. Arch. Intern. Med. 2011, 171, 1571–1578. [Google Scholar] [CrossRef] [Green Version]
- Market, A. Global Industry Analysis, Size, Share, Growth, Trends and Forecast 2019–2025. 2019. Available online: https://www.transparencymarketresearch.com/logistics-market.html (accessed on 20 May 2020).
- Bhandari, B. Handbook of Industrial Drying; Mujumdar, A.S., Ed.; CRC Press: Boca Raton, FL, USA, 2015; ISBN 978-1-4665-9665-8. [Google Scholar]
- Aghbashlo, M.; Mobli, H.; Rafiee, S.; Madadlou, A. A review on exergy analysis of drying processes and systems. Renew. Sustain. Energy Rev. 2013, 22, 1–22. [Google Scholar] [CrossRef]
- Johnson, W.P.; Langrish, A.T. Interpreting exergy analysis as applied to spray drying systems. Int. J. Exergy 2020, 31, 120–149. [Google Scholar] [CrossRef]
- Johnson, P.W.; Langrish, T.A.G. Exergy analysis of a spray dryer: Methods and interpretations. Dry. Technol. 2017, 36, 578–596. [Google Scholar] [CrossRef]
- Erbay, Z.; Koca, N. Energetic, Exergetic, and Exergoeconomic Analyses of Spray-Drying Process during White Cheese Powder Production. Dry. Technol. 2012, 30, 435–444. [Google Scholar] [CrossRef]
- Saygı, G.; Erbay, Z.; Koca, N.; Pazir, F. Energy and exergy analyses of spray drying of a fruit puree (cornelian cherry puree). Int. J. Exergy 2015, 16, 315. [Google Scholar] [CrossRef]
- Çay, A.; Kumbasar, E.P.A.; Morsunbul, S. Exergy analysis of encapsulation of photochromic dye by spray drying. IOP Conf. Ser. Mater. Sci. Eng. 2017, 254, 22003. [Google Scholar] [CrossRef]
- Aghbashlo, M.; Mobli, H.; Madadlou, A.; Rafiee, S. Influence of spray dryer parameters on exergetic performance of microencapsulation processs. Int. J. Exergy 2012, 10, 267. [Google Scholar] [CrossRef]
- Bühler, F.; Nguyen, T.-V.; Jensen, J.K.; Holm, F.M.; Elmegaard, B. Energy, exergy and advanced exergy analysis of a milk processing factory. Energy 2018, 162, 576–592. [Google Scholar] [CrossRef] [Green Version]
- Camci, M. Thermodynamic analysis of a novel integration of a spray dryer and solar collectors: A case study of a milk powder drying system. Dry. Technol. 2019, 38, 350–360. [Google Scholar] [CrossRef]
- Tsatsaronis, G. Definitions and nomenclature in exergy analysis and exergoeconomics. Energy 2007, 32, 249–253. [Google Scholar] [CrossRef]
- Bejan, A.; Tsatsaronis, G.; Michael, M. Thermal Design and Optimization; John Wiley & Sons: New York, NY, USA, 1996; Volume 21, ISBN 0471584673. [Google Scholar]
- Tsatsaronis, G. Thermoeconomic analysis and optimization of energy systems. Prog. Energy Combust. Sci. 1993, 19, 227–257. [Google Scholar] [CrossRef]
- Ozgener, L. Exergoeconomic analysis of small industrial pasta drying systems. Proc. Inst. Mech. Eng. Part A J. Power Energy 2007, 221, 899–906. [Google Scholar] [CrossRef]
- Ozturk, M.; Dincer, I. Exergoeconomic analysis of a solar assisted tea drying system. Dry. Technol. 2019, 38, 655–662. [Google Scholar] [CrossRef]
- Erbay, Z.; Koca, N. Exergoeconomic performance assessment of a pilot-scale spray dryer using the specific exergy costing method. Biosyst. Eng. 2014, 122, 127–138. [Google Scholar] [CrossRef]
- Walmsley, T.G.; Walmsley, M.R.; Atkins, M.J.; Neale, J.R.; Tarighaleslami, A.H. Thermo-economic optimisation of industrial milk spray dryer exhaust to inlet air heat recovery. Energy 2015, 90, 95–104. [Google Scholar] [CrossRef]
- Walmsley, T.G.; Walmsley, M.R.W.; Atkins, M.J.; Neale, J.R. Thermo-Economic assessment tool for industrial milk spray dryer exhaust heat recovery systems with particulate fouling. Chem. Eng. Trans. 2014, 39, 1459–1464. [Google Scholar] [CrossRef]
- Petrakopoulou, F.; Tsatsaronis, G.; Morosuk, T.; Carassai, A. Advanced Exergoeconomic Analysis Applied to a Complex Energy Conversion System. J. Eng. Gas Turbines Power 2011, 134, 031801. [Google Scholar] [CrossRef]
- Burmester, K.; Fehr, H.; Eggers, R. A Comprehensive Study on Thermophysical Material Properties for an Innovative Coffee Drying Process. Dry. Technol. 2011, 29, 1562–1570. [Google Scholar] [CrossRef]
- Clément, Y.B.Y.; Benjamin, Y.N.; Roger, K.B.; Clement, A.D.; Kablan, T. Moisture Adsorption Isotherms Characteristic of Coffee (Arabusta) Powder at Various Fitting Models. Int. J. Curr. Res. Biosci. Plant Biol. 2018, 5, 26–35. [Google Scholar] [CrossRef]
- Wepfer, W.J.; Gaggioli, R.A.; Obert, E.F. Proper evaluation of available energy for HVAC. ASHRAE Trans. 1979, 85, 214–230. [Google Scholar]
- Lazzaretto, A.; Tsatsaronis, G. SPECO: A systematic and general methodology for calculating efficiencies and costs in thermal systems. Energy 2006, 31, 1257–1289. [Google Scholar] [CrossRef]
- Tsatsaronis, G.; Park, M.-H. On avoidable and unavoidable exergy destructions and investment costs in thermal systems. Energy Convers. Manag. 2002, 43, 1259–1270. [Google Scholar] [CrossRef]
- Vučković, G.D.; Stojiljković, M.M.; Vukić, M.V.; Stefanović, G.M.; Dedeić, E.M. Advanced exergy analysis and exergoeconomic performance evaluation of thermal processes in an existing industrial plant. Energy Convers. Manag. 2014, 85, 655–662. [Google Scholar] [CrossRef]
- Cziesla, F.; Tsatsaronis, G.; Gao, Z. Avoidable thermodynamic inefficiencies and costs in an externally fired combined cycle power plant. Energy 2006, 31, 1472–1489. [Google Scholar] [CrossRef]
- Petroecuador, E.P. Precios de Venta a Nivel de Terminal para las Comercializadoras Calificadas y Autorizadas a Nivel Nacional. Ep Petroecuador Gerencia de Comericalización Nacional. 2019. Available online: http://bit.ly/2XeM8Zq (accessed on 20 March 2020).
- Interagua. Informe Anual 2018–2019; International Water Services (Guayaquil) Interagua C. Ltda: Guayaquil, Ecuador, 2019. [Google Scholar]
- Apak. Energy exergy analyses, Turkey (Supervisor: Prof. Dr. Ramazan K€OSE). In A Ceramic Factory, Mechanical Engineering Branche; Engineering Faculty, Dumlupınar University: Kütahya, Turkey, 2007; p. 110. (In Turkish) [Google Scholar]
- Utlu, Z.; Hepbasli, A.; Hepbaşlı, A. Exergoeconomic analysis of energy utilization of drying process in a ceramic production. Appl. Therm. Eng. 2014, 70, 748–762. [Google Scholar] [CrossRef]
- Kurozawa, L.E.; Park, K.J.; Hubinger, M.D. Spray Drying of Chicken Meat Protein Hydrolysate: Influence of Process Conditions on Powder Property and Dryer Performance. Dry. Technol. 2011, 29, 163–173. [Google Scholar] [CrossRef]
- Mohammadi, A.; Ahmadi, M.H.; Bidi, M.; Joda, F.; Valero, A.; Uson, S. Exergy analysis of a Combined Cooling, Heating and Power system integrated with wind turbine and compressed air energy storage system. Energy Convers. Manag. 2017, 131, 69–78. [Google Scholar] [CrossRef]
- Jokandan, M.J.; Aghbashlo, M.; Mohtasebi, S.S. Comprehensive exergy analysis of an industrial-scale yogurt production plant. Energy 2015, 93, 1832–1851. [Google Scholar] [CrossRef]
- Singh, G.; Singh, P.; Tyagi, V.; Barnwal, P.; Pandey, A. Exergy and thermo-economic analysis of ghee production plant in dairy industry. Energy 2019, 167, 602–618. [Google Scholar] [CrossRef]
- Yildirim, N.; Genc, S. Energy and exergy analysis of a milk powder production system. Energy Convers. Manag. 2017, 149, 698–705. [Google Scholar] [CrossRef]
- Li, B.; Li, C.; Huang, J.; Li, C. Exergoeconomic Analysis of Corn Drying in a Novel Industrial Drying System. Entropy 2020, 22, 689. [Google Scholar] [CrossRef]
- Gungor, A.; Erbay, Z.; Hepbasli, A. Exergoeconomic (Thermoeconomic) Analysis and Performance Assessment of a Gas Engine–Driven Heat Pump Drying System Based on Experimental Data. Dry. Technol. 2012, 30, 52–62. [Google Scholar] [CrossRef]
- Erbay, Z.; Hepbasli, A. Exergoeconomic evaluation of a ground-source heat pump food dryer at varying dead state temperatures. J. Clean. Prod. 2017, 142, 1425–1435. [Google Scholar] [CrossRef]
- Erbay, Z.; Hepbasli, A. Advanced exergoeconomic evaluation of a heat pump food dryer. Biosyst. Eng. 2014, 124, 29–39. [Google Scholar] [CrossRef]
- Gungor, A.; Tsatsaronis, G.; Gunerhan, H.; Hepbasli, A. Advanced exergoeconomic analysis of a gas engine heat pump (GEHP) for food drying processes. Energy Convers. Manag. 2015, 91, 132–139. [Google Scholar] [CrossRef]
- Wang, L.; Fu, P.; Yang, Z.; Lin, T.-E.; Yang, Y.; Tsatsaronis, G. Advanced Exergoeconomic Evaluation of Large-Scale Coal-Fired Power Plant. J. Energy Eng. 2020, 146, 04019032. [Google Scholar] [CrossRef]
- Erbay, Z.; Hepbasli, A. Assessment of cost sources and improvement potentials of a ground-source heat pump food drying system through advanced exergoeconomic analysis method. Energy 2017, 127, 502–515. [Google Scholar] [CrossRef]
- Hamdy, S.; Morosuk, T.; Tsatsaronis, G. Exergoeconomic optimization of an adiabatic cryogenics-based energy storage system. Energy 2019, 183, 812–824. [Google Scholar] [CrossRef]


| State | Description | Soluble Solids (kg/kg) | Water (kg/kg) | Dried Air (kg/kg) |
|---|---|---|---|---|
| 2 | Coffee extract | 0.440 | 0.560 | - |
| 23 | Soluble Coffee powder | 0.970 | 0.030 | - |
| 24 | Mixture BT | 0.001 | 0.009 | 0.990 |
| 29 | Mixture SD | 0.004 | 0.040 | 0.955 |
| 33 | Mixture S | 0.038 | 0.008 | 0.954 |
| 34 | Mixture FF | 0.117 | 0.001 | 0.882 |
| Component | ||
|---|---|---|
| LP | ||
| HP | ||
| HXE | ||
| MHX | ||
| SFBHX | ||
| VF1HX | ||
| VF2HX | ||
| MF | ||
| SFBF | ||
| VF1F | ||
| VF2F | ||
| RFF | ||
| FF | ||
| SD | ||
| BT | ||
| S | ||
| B | ||
| CHX |
| Component | RC | RTI | UIC |
|---|---|---|---|
| Heat Exchangers | ΔTmin, HXE = 51 | ΔTmin, HXE = 30 | ΔTmin, HXE = 60 |
| ΔTmin, MHX = 12 | ΔTmin, MHX = 10 | ΔTmin, MHX = 20 | |
| ΔTmin, SFBHX = 69 | ΔTmin, SFBHX, VFIHX = 20 | ΔTmin, SFBHX = 80 | |
| ΔTmin, VF1HX = 80 | ΔTmin, VF2HX = 80 | ΔTmin, VF1HX = 90 | |
| ΔTmin, VF2HX = 139 | ΔTmin, CHX = 4 | ΔTmin, VF2HX = 145 | |
| ΔTmin, CHX = 9 | ΔTmin, CHX = 15 | ||
| Pumps | ɳis = 60% | ɳis = 86% | ɳis = 65% |
| F | ɳis = 60% | ɳis = 90% | 0.85 |
| S | ɳelec = 78% | ɳelec = 90% | ɳelec = 78% |
| BT | ɳelec = 60% | ɳelec = 85% | ɳelec = 60% |
| B | ɳcon = 90% | ɳcon = 95% | 0.66 |
| SD | AP-Ratio = 18.8 | AP-Ratio = 8.6 | 0.90 |
| Component | Fuel Cost Expression | Product Cost Expression | Auxiliary Equations |
|---|---|---|---|
| LP | - | ||
| HP | |||
| HXE | |||
| MHX | |||
| SFBHX | |||
| VF1HX | |||
| VF2HX | |||
| MF | |||
| SFBF | - | ||
| VF1F | - | ||
| VF2F | |||
| RFF | |||
| FF | |||
| SD | |||
| BT | |||
| S | ; | ||
| B | ; | ||
| CHX | ; |
| State | (kg/h) | T (°C) | P (kPa) | (kJ/kg) | (kJ/kg) | (kJ/kg) | (kJ/h) |
|---|---|---|---|---|---|---|---|
| 1 | 7.4 | 12 | 101 | 322 | 0.22 | 0.0 | 2383 |
| 2 | 528 | 14 | 101 | 2.25 | 10.8 | 0.0 | 6891 |
| 3 | 528 | 15 | 750 | 2.25 | 9.70 | 0.5 | 6593 |
| 4 | 528 | 16 | 750 | 1.56 | 8.84 | 0.5 | 5776 |
| 5 | 528 | 18 | 5400 | 1.56 | 4.73 | 4.0 | 5470 |
| 6 | 528 | 39 | 5400 | 1.56 | 13.4 | 4.0 | 10,045 |
| 7 | 9922 | 28 | 101 | 0.00 | 0.00 | 0.0 | 0 |
| 8 | 9922 | 28 | 105 | 0.01 | 0.00 | 1.0 | 10,286 |
| 9 | 9922 | 178 | 105 | 0.01 | 29.9 | 1.0 | 307,205 |
| 10 | 4002 | 28 | 101 | 0.00 | 0.00 | 0.0 | 0 |
| 11 | 1626 | 15 | 101 | 0.002 | 0.27 | 0.0 | 436 |
| 12 | 1626 | 15 | 105 | 0.012 | 0.27 | 1.0 | 2126 |
| 13 | 1626 | 96 | 105 | 0.012 | 6.97 | 1.0 | 13,031 |
| 14 | 1100 | 15 | 101 | 0.002 | 0.27 | 0.0 | 295 |
| 15 | 1100 | 15 | 105 | 0.012 | 0.27 | 1.0 | 1438 |
| 16 | 1100 | 85 | 105 | 0.012 | 5.02 | 1.0 | 6665 |
| 17 | 1276 | 15 | 101 | 0.002 | 0.27 | 0.0 | 342 |
| 18 | 1276 | 26 | 101 | 0.002 | 0.00 | 0.0 | 6 |
| 19 | 1101 | 26 | 101 | 0.002 | 0.00 | 0.0 | 6 |
| 20 | 1101 | 27 | 105 | 0.012 | 0.00 | 1.0 | 1146 |
| 21 | 175 | 26 | 101 | 0.002 | 0.00 | 0.0 | 1 |
| 22 | 175 | 27 | 105 | 0.012 | 0.00 | 1.0 | 182 |
| 23 | 209 | 80 | 101 | 5.80 | 8.24 | 6.0 | 4202 |
| 24 | 2203 | 58 | 101 | 0.002 | 1.49 | 0.0 | 3298 |
| 25 | 207 | 35 | 101 | 5.80 | 0.18 | 1.0 | 1450 |
| 27 | 0.04 | 30 | 101 | 4.18 | 0.07 | 0.0 | 0.04 |
| 26 | 200 | 30 | 101 | 5.80 | 0.02 | 0.0 | 1163 |
| 28 | 6.96 | 30 | 101 | 5.80 | 0.02 | 0.0 | 40 |
| 29 | 12,065 | 96 | 100 | 0.001 | 7.45 | 2.1 | 114,790 |
| 30 | 14,268 | 94 | 100 | 0.003 | 6.94 | 0.0 | 99,094 |
| 31 | 14,252 | 94 | 105 | 0.003 | 6.94 | 0.9 | 111,685 |
| 32 | 16 | 94 | 100 | 1647 | 11.2 | 0.0 | 26,942 |
| 33 | 182 | 30 | 101 | 1647 | 0.01 | 0.0 | 26,763 |
| 34 | 198 | 40 | 101 | 1647 | 0.26 | 0.9 | 27,009 |
| 35 | 20 | 90 | 70 | 480 | 418 | 0.0 | 18,231 |
| 36 | 20 | 90 | 70 | 2.50 | 23.9 | 0.0 | 537 |
| 37 | 806 | 190 | 1250 | 480 | 499 | 0.0 | 789,231 |
| 38 | 806 | 190 | 1250 | 2.50 | 29.0 | 0.0 | 25,387 |
| 39 | 80 | 165 | 700 | 480 | 753 | 0.0 | 98,620 |
| 40 | 80 | 165 | 700 | 2.50 | 104 | 0.0 | 8507 |
| 41 | 43 | 165 | 700 | 480 | 753 | 0.0 | 53,008 |
| 42 | 43 | 165 | 700 | 2.50 | 104 | 0.0 | 4581 |
| 43 | 10 | 165 | 700 | 480 | 753 | 0.0 | 12,328 |
| 44 | 10 | 165 | 700 | 2.50 | 104 | 0.0 | 1063 |
| 45 | 25,438 | 2 | 500 | 2.50 | 5.13 | 0.0 | 194,111 |
| 46 | 25,438 | 6 | 500 | 2.50 | 3.71 | 0.0 | 157,878 |
| 47 | 959 | 190 | 1250 | 480 | 499 | 0.0 | 938,861 |
| 48 | 959 | 104 | 1250 | 2.50 | 39.3 | 0.0 | 40,075 |
| 49 | 2217 | 28 | 101 | 0.00 | 0.00 | 0.0 | 0 |
| 50 | 77 | 28 | 101 | 43,293 | 0.00 | 0.0 | 3,332,277 |
| 51 | 2294 | 650 | 101 | 26.0 | 331 | 0.0 | 817,815 |
| Component | (kJ/h) | (kJ/h) | (%) | (%) | ||
|---|---|---|---|---|---|---|
| SD | 205,446 | 32,852 | 16.0 | 93.9 | 0.058 | 0.040 |
| LP | 7920 | 298 | 3.8 | 27.2 | 0.003 | 0.002 |
| HP | 19,800 | 307 | 1.5 | 34.2 | 0.007 | 0.005 |
| HXE | 17,694 | 4576 | 25.9 | 76.4 | 0.005 | 0.003 |
| MHX | 763,844 | 296,918 | 38.9 | 79.4 | 0.174 | 0.116 |
| SFBHX | 90,114 | 10,906 | 12.1 | 81.4 | 0.030 | 0.020 |
| VF1HX | 48,427 | 5227 | 10.8 | 88.6 | 0.016 | 0.011 |
| VF2HX | 11,264 | 336 | 3.0 | 69.2 | 0.004 | 0.003 |
| MF | 66,600 | 10,286 | 15.4 | 46.3 | 0.021 | 0.014 |
| SFBF | 19,800 | 1690 | 8.5 | 24.0 | 0.007 | 0.005 |
| VF1F | 14,400 | 1143 | 7.9 | 22.4 | 0.005 | 0.003 |
| VF2F | 14,400 | 1140 | 7.9 | 23.3 | 0.005 | 0.003 |
| RFF | 1980 | 181 | 9.2 | 29.4 | 0.001 | 0.001 |
| FF | 108,000 | 39,534 | 36.6 | 51.5 | 0.026 | 0.017 |
| CHX | 36,233 | 1072 | 3.0 | 27.8 | 0.013 | 0.009 |
| B | 2,514,427 | 898,786 | 35.7 | 73.3 | 0.611 | 0.374 |
| BT | 7920 | 546 | 6.9 | 69.9 | 0.003 | 0.002 |
| S | 3600 | 247 | 6.9 | n/a | 0.001 | 0.001 |
| Component | cF ($/kJ) | ($/h) | ($/h) | fk (%) | |
|---|---|---|---|---|---|
| SD | 6.2 × 10−4 | 106.8 | 109.6 | 0.02 | 2.50 |
| MHX | 1.3 × 10−4 | 60.5 | 61.6 | 0.01 | 1.73 |
| B | 6.7 × 10−6 | 13.1 | 14.4 | 0.07 | 9.03 |
| SFBHX | 1.0 × 10−4 | 8.2 | 8.3 | 0.02 | 2.06 |
| VF1HX | 1.0 × 10−4 | 4.4 | 4.6 | 0.02 | 2.61 |
| BT | 5.7 × 10−4 | 4.2 | 4.5 | 0.06 | 5.71 |
| CHX | 7.0 × 10−5 | 2.4 | 3.0 | 0.20 | 17.43 |
| HXE | 1.4 × 10−4 | 1.9 | 1.9 | 0.01 | 1.37 |
| VF2HX | 1.0 × 10−4 | 1.1 | 1.2 | 0.03 | 3.17 |
| FF | 2.6 × 10−5 | 1.8 | 1.9 | 0.05 | 7.83 |
| MF | 2.6 × 10−5 | 1.5 | 1.6 | 0.08 | 9.00 |
| HP | 2.6 × 10−5 | 0.5 | 1.1 | 1.14 | 53.73 |
| RTF | 2.6 × 10−5 | 0.05 | 0.2 | 3.30 | 78.42 |
| SFBF | 2.6 × 10−5 | 0.5 | 0.6 | 0.33 | 26.52 |
| VF2F | 2.6 × 10−5 | 0.3 | 0.5 | 0.45 | 33.02 |
| VF1F | 2.6 × 10−5 | 0.3 | 0.5 | 0.45 | 33.03 |
| LP | 2.6 × 10−5 | 0.2 | 0.4 | 1.21 | 55.73 |
| S | 2.6 × 10−5 | 0.1 | 0.4 | 8.16 | 78.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tinoco-Caicedo, D.L.; Lozano-Medina, A.; Blanco-Marigorta, A.M. Conventional and Advanced Exergy and Exergoeconomic Analysis of a Spray Drying System: A Case Study of an Instant Coffee Factory in Ecuador. Energies 2020, 13, 5622. https://doi.org/10.3390/en13215622
Tinoco-Caicedo DL, Lozano-Medina A, Blanco-Marigorta AM. Conventional and Advanced Exergy and Exergoeconomic Analysis of a Spray Drying System: A Case Study of an Instant Coffee Factory in Ecuador. Energies. 2020; 13(21):5622. https://doi.org/10.3390/en13215622
Chicago/Turabian StyleTinoco-Caicedo, Diana L., Alexis Lozano-Medina, and Ana M. Blanco-Marigorta. 2020. "Conventional and Advanced Exergy and Exergoeconomic Analysis of a Spray Drying System: A Case Study of an Instant Coffee Factory in Ecuador" Energies 13, no. 21: 5622. https://doi.org/10.3390/en13215622
APA StyleTinoco-Caicedo, D. L., Lozano-Medina, A., & Blanco-Marigorta, A. M. (2020). Conventional and Advanced Exergy and Exergoeconomic Analysis of a Spray Drying System: A Case Study of an Instant Coffee Factory in Ecuador. Energies, 13(21), 5622. https://doi.org/10.3390/en13215622





