An Efficient Mine Ventilation Solution Method Based on Minimum Independent Closed Loops

Abstract

In this paper, according to the analysis of optimum circuits, we present an efficient ventilation network solution based on minimum independent closed loops. Our main contribution is optimizing the circuit dividing strategy to improve the iteration convergence and the efficiency of a single iteration. In contrast to a traditional circuit, a minimum closed loop may contain one or more co-tree branches but fewer high-resistance branches and fan branches. It is helpful in solving the problem of divergence or slow convergence for complex ventilation networks. Moreover, we analyze the dividing rules of closed loops and improve the dividing algorithm of minimum independent closed loops. Compared with the traditional Hardy Cross iteration method, the improved solution method has better iteration convergence and computation efficiency. The experimental results of real-world mine ventilation networks show that the improved solution method converges rapidly within a small number of iterations. We also investigate the influence of network complexity, iterative precision, and initial airflow on the iteration convergence.

1. Introduction

The effect of mine ventilation mainly depends on the airflow distribution in the ventilation networks. Measuring and computing the natural distribution of airflow is the basis of ventilation regulation optimization [1,2,3,4,5] and the key technology of the real-time ventilation network solution [6,7,8].

The ventilation network simulation is the basis of ventilation system optimization, and it represents, in essence, the solution to a set of large-scale nonlinear equations. A novel and more effective algorithm must be developed to solve the large-scale nonlinear problem of airflow distribution in complex ventilation networks. Another common approach is to convert the nonlinear equations into linear equations and then solve the linear equations iteratively. At present, there are many kinds of ventilation network calculation methods, including the airflow-based methods and the air pressure-based methods. However, each kind of calculation method has its own advantages and disadvantages. Finding a calculation method with fast and stable convergence is of great significance for the real-time solution and disaster ventilation solution in a large-scale complex ventilation network.

The iterative methods solve the equations formulated from several basic ventilation network laws iteratively. As a representative of early solution algorithms, the Hardy Cross iteration method [9,10,11,12] (also known as the Scott Hinsley iteration method) is the most widely used in computer programs for ventilation network analysis. The method implements an iteration process to correct the airflow until the estimation error lies within a given precision. However, because of a variety of factors (including the circuits dividing, the iterative precision, the network complexity and the initial airflow), the traditional solution methods may converge slowly or tend to diverge in complex ventilation networks [13,14,15,16]. To improve the convergence of iteration, it is necessary to find a fast and effective solution method [17,18].

Among the influence factors of convergence, we mainly focus on the strategy of circuit dividing in the process of iteration. The airflow of each branch is corrected by constructing a set of independent circuits. The independent circuits have a great impact on the iteration convergence and the efficiency of a single iteration. To improve the process of iteration, the minimum independent closed loops (MICL) [19] are used to divide circuits with better convergence.

Similar to the dividing strategy of independent circuits, the minimum independent closed loops can be divided using the searching algorithm based on the spanning tree [20]. In contrast to a traditional circuit, a minimum closed loop may contain one or more co-tree branches but fewer high-resistance branches and fan branches. In this case, the independence of closed loops should be checked to ensure the reliability of the searching results. As an available approach, we define a set of conflicting co-tree branches to ensure the independence of closed loops. Firstly, add the repeated co-tree branches in the process of searching the conflicting co-tree branches by judging the relationship between a minimum closed loop and a circuit. Then, define the order of adding co-tree branches set to improve the searching efficiency of the minimum closed loops.

In this paper, we improve the algorithm of minimum independent closed loops and present an efficient ventilation network solution based on minimum independent closed loops. The basic idea of this method is to construct independent circuits with more than one co-tree branches. Compared with the traditional Hardy Cross iteration method, the improved solution method has better iteration convergence and computation efficiency. Mine ventilation software (iVent) is developed using the improved Hardy Cross iteration method for the calculation of airflow distribution.

2. Problem Formulation

The Hardy Cross iteration method was developed from the Newton–Raphson iteration method by the secondary simplification of the Jacobi matrix. The method is an iterative method. It selects an initial value for each branch and then corrects the value iteratively until the calculation error is less than or equal to a required accuracy.

One of the essential conditions is that the value of the non-main diagonal elements is small enough for the Hardy Cross iteration solution. The larger the absolute value of the non-main diagonal elements, the greater the effect. Different independent circuits have different effects of simplification, which will influence the convergence of iteration. Therefore, the convergence of the Hardy Cross iteration solution is influenced enormously by the selection of independent circuits. The traditional approach is to create the spanning tree by the weight of air resistance. However, the truncation error of the Hardy Cross iteration method is not necessarily related to the minimum spanning tree. In fact, it depends on the optimal circuits. For the traditional method of dividing circuits, some studies show that the method of creating a minimum spanning tree cannot improve the convergence speed and instead reduces the convergence speed in some cases.

The method of dividing circuits by creating a minimum spanning tree only increases the weight of the main diagonal elements and ignores the processing of non-main diagonal elements, which does not achieve the purpose of making the main diagonal elements dominant. Therefore, the minimum spanning tree is not a necessary condition for reducing the truncation error and improving the convergence speed.

From the above analysis, it can be found that in order to achieve the condition in which the non-main diagonal elements are far less than the main diagonal elements, the optimal circuits should have the following characteristics:

(1)

Increase the weight of the main diagonal elements.

(2)

Reduce the number of non-main diagonal elements.

(3)

Minimize the weight of the non-main diagonal elements.

(4)

Minimize the number of branches sharing a circuit to avoid mutual interference between the circuits.

For the complex ventilation networks, an obvious disadvantage of the traditional circuits is that it tends to form a circuit with too many branches. It may result in thousands or even millions of accumulation errors, which are nearly impossible to reduce in a limited amount of time. Therefore, selecting the optimum circuits is one of the keys to improve the iteration convergence.

A good approach is to reduce the truncation error to improve the convergence speed. If a circuit contains fewer branches and shared branches, it is beneficial to avoid mutual interference between the circuits. When the number of branches in a circuit decreases, the number of equations in the iterative formula will be reduced, and the calculation of the relevant parameters of each circuit will also be reduced.

3. Algorithm

3.1. MICL

From the perspective of graph theory [21,22], a mine ventilation system can be simplified as a ventilation network. The ventilation network can be viewed as a connected graph with a number of branches (airways), including general branches, fix branches and fan branches. The network focuses on the topological relationship of branches instead of the spatial geometry position [4,5,6]. To facilitate this research, some related concepts should be cleared:

Spanning tree: a tree subgraph containing all of the nodes and a minimum possible number of branches in the ventilation network. In general, there are several spanning trees in a connected graph.

Tree branch: a branch that is contained in the given spanning tree. The tree branches of a spanning tree create no circuits.

Co-tree branch (basic branch): a branch contained in the connected graph but not in the given spanning tree. The branches in a connected graph can be split into two categories: tree branch and co-tree branch.

Minimum closed loop: a closed loop (circuit) with minimum weight of branches in the ventilation network. To improve the convergence of iteration, the weight of a branch is constructed by the characteristics of optimal circuits.

Minimum independent closed loops: a set of minimum closed loops that satisfy the conditions of the closed loops being linearly independent. This means that any one of the loops in the set cannot be defined as a linear combination of the others. To ensure the whole network is converged, we must find a maximum set of minimum independent closed loops.

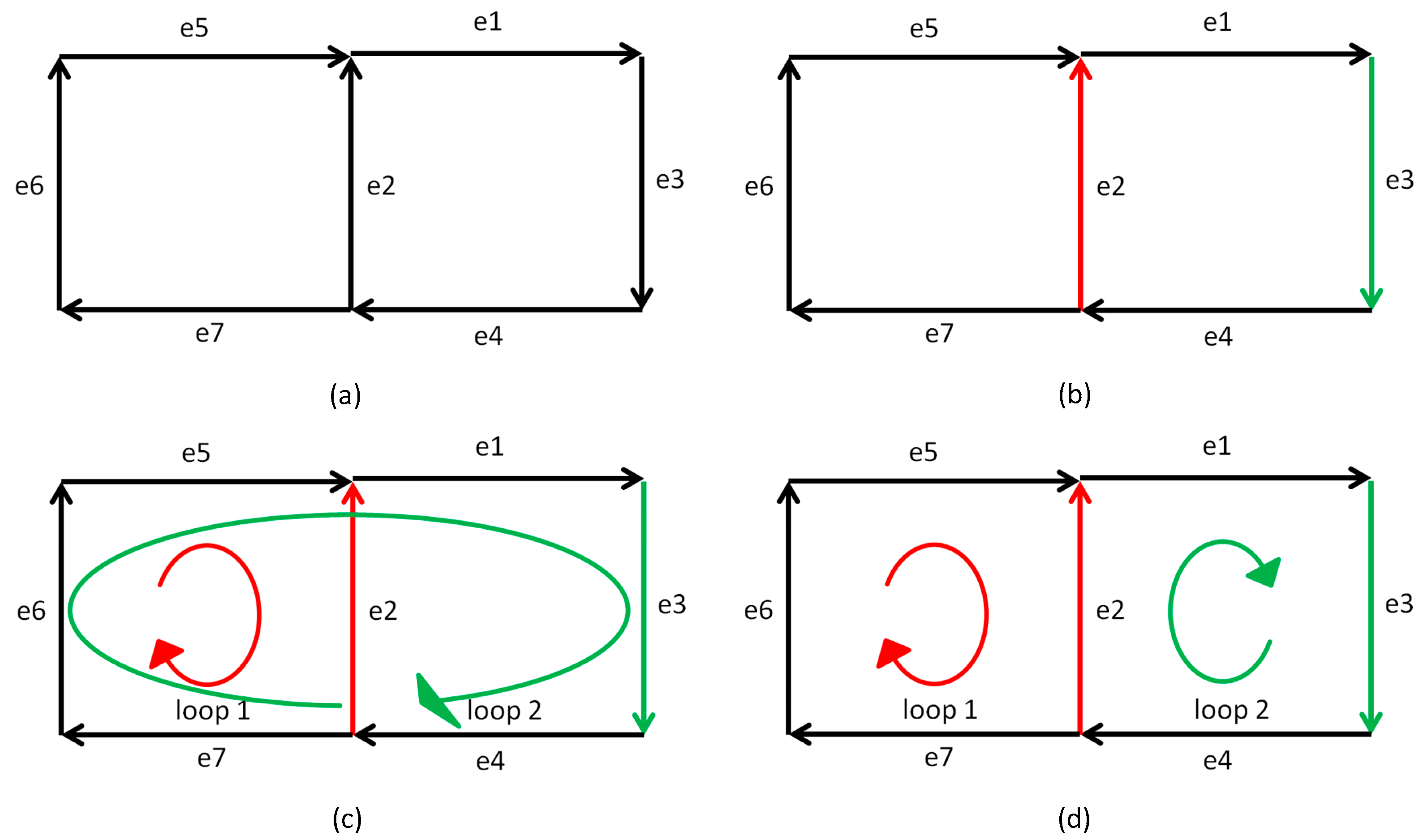
The Hardy Cross iteration method requires constructing a set of independent circuits. Considering the fact that adding a co-tree branch in the corresponding spanning tree creates a circuit, the traditional approach is to construct a spanning tree and to create circuits by adding the co-tree branches in the corresponding spanning tree. This kind of circuits satisfies the condition that a circuit contains one and only one co-tree branch. There is a different branch between any two loops, which ensures the independence of circuits. As shown in Figure 1, Figure 1b shows a spanning tree (black edges) and the corresponding co-tree branches (red and green edges). The traditional divided loops are e2-e5-e6-e7 (loop one in Figure 1c) and e3-e1-e5-e6-e7-e4 (loop two in Figure 1c). In this case, to avoid the co-tree branch e2, loop two creates a long path.

Differing from the traditional circuit, a minimum closed loop may contain one or more co-tree branches, which makes the construction of closed loops more flexible. Therefore, the minimum closed loops can reduce the number of branches and the total weight of non-co-tree branches in a loop. Taking the same spanning tree in Figure 1b as an example, the divided minimum closed loops are e2-e5-e6-e7 (loop one in Figure 1d) and e3-e1-e2-e4 (loop two in Figure 1d). In this case, loop two creates a short path using the co-tree branch e2.

Note that a minimum closed loop is not necessarily the shortest path between its start and end nodes. The number of branches in a loop depends on the weight of a branch. For the ventilation network, to ensure the minimum closed loops satisfy the characteristics of optimal circuits, the weight of a branch is determined by both the air resistance of branch and the type of branch. Among the three types of branches, the fix branches have the largest weight, and the general branches have the smallest weight. For example, the fan branches are distributed in different closed loops as much as possible to make the fan branches converge, as shown in Figure 2. It is useful for the calculation of the ventilation network with multiple fans. In this case, a minimum closed loop contains fewer high-resistance branches and fan branches. Furthermore, the number of branches in a loop is small.

3.2. MICL Searching Algorithm

3.2.1. Basic Principles

As mentioned, the most important difference between the MICL and the traditional independent circuits is that the latter does not allow containing two or more co-tree branches in a circuit, while the former may contain more than one co-tree branches in a closed loop. The key of the MICL method is to control the independence of the closed loops and to avoid duplication or omission of loops.

Principle 1:

With regard to a connected graph$G\left(V,E\right)$with$N$branches and$J$nodes, it is possible to create a spanning tree. One more closed loop could be generated for each adding of a co-tree branch. The number of the independent closed loops is$M=N-J+1$

In the connected graph $G$, there are $J-1$ tree branches and $N-\left(J-1\right)$ co-tree branches through creating a spanning tree. One more closed loop could be generated for each adding of a co-tree branch. In the process of adding, each loop contains at least one branch, such as the co-tree branch, which is not in the other loops added previously; therefore, the loops are mutually independent.

Principle 2:

Concerning a series of closed loops added in proper sequence, if each of them contains at least one branch that does not exist in the closed loops ahead, these closed loops are mutually independent.

In a connected graph $G\left(V,E\right)$ with $N$ branches and $J$ nodes, after getting $M$ minimum closed loops, we can express the closed loop $C_i$ as: $C_i={\left(b_{ij}\right)}_{i\times N}$.

According to the above analysis, M independent closed loops can be formed into a $M\times N$ matrix. If we remove the columns of non-co-tree branches, we can get a $M\times M$ matrix. The matrix can be converted to an up-triangle matrix by matrix transformation. The rank of the matrix is $M$.

The searching method based on the spanning tree using the above two principles ensures the independence of the closed loops by defining the order, in which the co-tree branches are added to the spanning tree, and the minimality of the closed loops use the Dijkstra algorithm to search the shortest path. The basic idea is to create a spanning tree based on the weight of the branches, obtain branches of the co-tree and back substitute the branches one by one so as to add them to the current tree graph. A set of closed loops will be created for each adding of a co-tree branch. The shortest path algorithm, based on the weight of the branches, is adopted to obtain the shortest distance between the two points of a co-tree branch. At the same time, compared with the shortest distance of all the added co-tree branches, select the minimum distance of the shortest distance and add to the current tree graph preferentially, until all the co-tree branches are added. Finally, we can obtain a set of minimum independent closed loops [19].

To avoid duplication or omission of the closed loops when searching, we need to check their independence. Typically, the mutual independent closed loops that contain all the branches are not necessarily $M$ and the $M$ closed loops that contain all the branches are not necessarily independent, so the independence inspection of the closed loops is extremely important.

With regard to the searched loops, judge the number of loops firstly, if $M=N-J+1$, then consist a determinant $\left|C\right|$ according to the matrix of loops. If $\left|C\right|=0$, the closed loops are repeated; otherwise, the $M$ closed loops are mutually independent.

3.2.2. MICL Method

Every ventilation network graph can be separated into two sets: a spanning tree and its chords. It is often feasible to select the minimum shortest path as a minimum closed loop by comparing all the shortest paths of the co-tree branches.

For a series of closed loops added in proper sequence, if each of them contains at least one branch that does not exist in the closed loops in the early stages, the closed loops are mutually independent. Our method based on a spanning tree ensures the independence of the closed loops by defining the order of the co-tree branches added to the spanning tree and the minimum weights of the closed loops by using the Dijkstra algorithm to search for the shortest path [19,20]. The basic procedures of a search method based on a spanning tree are as follows:

Step 1: Initialize the detailed data relevant to the algorithm. Then, check the connectivity of the network graph and build the topology relationship between the nodes and branches.

Step 2: Obtain a spanning tree and the corresponding co-tree branches in the given network.

Step 3: Try to add the co-tree branches to the spanning tree graph. Once a co-tree branch is added, disconnect it and search for the shortest path from its beginning point to its end point with the Dijkstra algorithm. In all of the shortest paths, select the corresponding co-tree branch with minimum length preferentially in the closed loop and add it to the current tree graph. The selected closed loop is used as the current minimum closed loop.

Step 4: After adding the first co-tree branch, try to add the remaining co-tree branches to the current tree graph. Similarly, select the corresponding co-tree branch with minimum length preferentially and add it to the current tree graph. The selected closed loop is used as the current minimum closed loop.

Step 5: Repeat the process until all of the co-tree branches are added to the current tree graph. Finally, we can obtain a group of MICL.

Step 6: Check the independence of the closed loops.

Step 7: Output the search results and then exit.

The search method based on the spanning tree can search all of the minimal closed loops satisfying independence, but it is much more computationally expensive to search for the shortest path of all the remaining co-tree branches.

Strict MICL are not necessary for a ventilation network. We can search for the shortest path of a co-tree branch directly with no comparison, which is helpful for improving the search efficiency. In this case, the number of shortest path searches is reduced from $M$ to $M\times \left(M+1\right)/2$.

3.2.3. Conflicting Rules

To simplify the process of multiple comparisons, firstly, search the shortest path of the complete network graph. If it has nothing to do with the other co-tree branches, we can use the shortest path to divide the corresponding minimum closed loop directly.

Principlen 3:

When adding a co-tree branch in the given graph$G$, if the divided closed loop only has one co-tree branch, it is an independent one.

If the divided closed loop only has a co-tree branch, it is an independent one. Figure 3 shows the division of the minimum closed loops based on different spanning trees and the corresponding co-tree branches. If a closed loop only contains one co-tree branch by shortest path searching, it can be viewed as one of the minimum independent closed loops directly, as shown in Figure 3a,b. Therefore, we just need to pay attention to the closed loops containing more than one co-tree branches. In this case, some dividing rules should be defined to avoid repeated loops, as shown in Figure 3c,d.

For a closed loop containing more than one co-tree branches, traverse the other co-tree branches in this closed loop preferentially. If one of the co-tree branches has divided a corresponding closed loop, then find the next co-tree branch in this closed loop; otherwise, process recursively in the same way. If all the other closed loops in this closed loop have been designated, divide this closed loop finally.

There are three kinds of cases in accordance with the above way of dividing the closed loops recursively. Firstly, the divided closed loop has only one co-tree branch, as shown in Figure 4a,b. Secondly, the divided closed loop has a number of co-tree branches, while the other co-tree branches have their own corresponding divided closed loops, as shown in Figure 4d. Thirdly, the divided closed loop has several co-tree branches, and at least one of the corresponding closed loops is repeated, as shown in Figure 4c.

According to the third principle, the two former cases can ensure the independence of the closed loops, while the third case may lead to the omission of the independent closed loops for the repeated loops and the co-tree branch of the corresponding minimum closed loop cannot be determined. In this case, conflicting rules of co-tree branches should be defined to deal with this problem. The basic idea is to convert the third case into the second one. Firstly, construct a set of conflicting co-tree branches and add the repeated closed loops to the set. Secondly, the corresponding loops of the conflicting co-tree branches are determined in sequence to ensure the independence of the closed loops. In the process of dividing, the type of co-tree branch is marked to distinguish the type of its corresponding loop.

3.2.4. Improved MICL Method

Based on the above analysis and basic principles, an improved MICL algorithm was proposed, the implementation procedure of which can be shown as Figure 5. The detailed procedure can be described as follows.

Step 1: Initialize the detailed data relevant to the algorithm. Then, check the connectivity of the graph.

Step 2: Create a spanning tree by the improved Breadth First Search (BFS) method and obtain the corresponding tree branches and co-tree branches.

Step 3: Traversing the co-tree branches, obtain the corresponding minimum closed loop of a co-tree branch by the shortest path algorithm based on the Depth First Search (DFS) method.

Step 4: According to the conflicting rules of co-tree branches, obtain the set of the conflicting co-tree branches. Then, divide the closed loops directly by the other co-tree branches without conflict, and add them to the current tree graph.

Step 5: With regard to the conflicting co-tree branches, once adding one in sequence, disconnect it and search the shortest path from its beginning point to end point with the Dijkstra algorithm. In all the shortest paths, select the corresponding co-tree branch with minimum length preferentially in the closed loop, and add it to the current tree graph. The selected closed loop is used as the current minimum closed loop.

Step 6: Similarly, try to add the remaining conflicting co-tree branches to the current tree graph, respectively, in sequence.

Step 7: Repeat the process until all of the co-tree branches are added to the current tree graph. Finally, get a group of minimum independent closed loops.

Step 8: Check the independence of the closed loops.

Step 9: Output the searching results, and then exit.

3.3. Dividing Rules of Closed Loops

Theoretically, according to the analysis of the Hardy Cross iteration method, the iteration calculation based on MICL has a better iterative effect. However, considering the restriction of the network solution and the improved speed of dividing MICL, the closed loops are not strict MICL. Actually, there is no need to adopt strict MICL in the iteration. Therefore, some dividing rules of closed loops are defined.

The branch resistance is selected as the weight of the minimum closed loop. In the solution process, the branches are classified into three categories: fixed airflow branches, fan branches and general branches. As the fan branches have a great influence on the calculation results, they are distributed in the different closed loops as far as possible. To reduce the emergence of fans in a number of closed loops, we can increase the weight of fan branches to reduce the repeated searching of fan branches in a complex multi-fan ventilation network.

As the fixed airflow loop cannot be involved in the iterative calculation, to ensure the independence of the loop, a closed loop is not allowed to contain a number of fixed airflow branches.

At the same time, with regard to a non-fixed airflow co-tree branch, in the process of the closed loop search, the fixed airflow branches cannot be searched, as this process would increase the fixed airflow closed loops, which cannot participate in the iterative calculation.

Figure 6 shows a spanning tree (black edges) and the corresponding co-tree branches (red edges). To adjust the airflow of e2, e2 is set as a fixed airflow branch. Assuming that the closed loops are e2-e7-e6-e5 and e2-e4-e3-e1, the two closed loops are fixed airflow closed loops, which cannot participate in the iterative calculation, resulting in the failure of the network solution. Therefore, a fixed airflow branch is only allowed to be contained in a closed loop.

3.4. Improved Solution Algorithm

The improved closed loop search method was used to search for MICL to improve the division speed. Based on MICL, the improved closed loop solution was proposed to make the solution converge quickly in a complex network. As shown in Figure 7, the basic steps of the improved closed loop solution are as follows:

Step 1: In a given graph with $N$ branches and $J$ nodes, initialize the parameters and construct the topology between branches and nodes.

Step 2: Classify the $N$ branches according to the branch types, such as general branches, fan branches and fixed airflow branches. Then, sort the branches by the selected weight.

Step 3: Create the minimum spanning tree with the Prim algorithm and divide the MICL by the type of co-tree branches (fixed airflow branches, fan branches, general branches). According to the division rules of a closed loop, search the shortest path of both sides of the co-tree branch directly. Finally, the number of closed loops is $M=N-J+1$.

Step 4: Initialize the airflow of the co-tree branches and then calculate the airflow of the corresponding tree branches. Correct abnormal airflow with reasonable airflow.

Step 5: Calculate the iterative airflow $\left\{\Delta Q_i\right\}$, and then correct the airflow of each circuit by traversing the M independent closed loops. Correct abnormal airflow with reasonable airflow.

Step 6: Return to Step 5 until the condition $\max \left\{\Delta Q_i\right\}>Tol$ is satisfied.

Step 7: As the fixed airflow closed loops do not participate in the iterative calculation, we should only calculate the airflow of branches that are in the fixed airflow closed loops.

Step 8: With regard to the solution for demand, the unbalanced pressure of the fixed airflow branches should be calculated to ensure the pressure balance.

Step 9: Fixing the direction of the branches, output the solution results, and then exit.

4. Results and Discussion

4.1. Solution Examples

Based on the iVent mine ventilation software, 3D ventilation network models of four actual mines—ShiZiShan Copper Mine, PuLang Copper Mine, BeiMingHe Iron Mine, and DaHongShan Copper Mine—were established, as shown in Figure 8.

In this paper, the improved closed loop solution was achieved by secondary development via iVent and the C++ programming language. The speed of running a network depends on the solution method and the type of microprocessor. The running environment was Windows 7, and the CPU was a 3.2 GHz Intel(R) Core(TM)i5-3470. The results of iteration are shown in

Table 1. Solution results of four actual mines, including the network and convergence parameters.

	Mines	ShiZiShan Copper Mine	PuLang Copper Mine	BeiMingHe Iron Mine	DaHongShan Copper Mine
Parameters
Branches		272	594	660	908
Nodes		215	443	482	671
Fans		8	24	3	69
Independent loops		58	152	179	238
Iterative number		19	51	67	78
Iterative time (ms)		49	150	180	276
Iterative airflow error (m3/s)		0.0001	0.0001	0.0001	0.0001
Iterative pressure error (Pa)		0.01814	0.00451	0.00401	0.00561
Loops dividing time (ms)		160	300	360	690
Total solution time (ms)		270	490	610	1060

, and the solution convergence is shown in Figure 9 and Figure 10. Note that the iterative time is the time of the iteration process excluding the loops dividing time (the same below). The total solution time is the time of the whole process.

According to the solution convergence graph, the convergence effect of the improved closed loop solution is better. In the practice of solution, the method also tends to converge quickly in the multi-stage fan station ventilation network, which can satisfy the fast solution requirement of a large-scale complex mine ventilation network.

With the increase in network complexity, the iterative time exhibits an approximately linear growth trend. Therefore, it can be considered that the Hardy Cross iteration method based on MICL has good convergence and stability.

There are many influencing factors in the actual ventilation network solution, and the convergence and stability of the improved closed loop solution algorithm still need to be further analyzed. This paper analyzes the influence factors of the solving convergence through numerical experiments.

4.2. Convergence Analysis

There are numerous factors affecting the iterative number in the course of the ventilation network solution, such as the iterative precision, the network complexity, and the initial airflow. To investigate the influence factors, some random complex networks were constructed. The main numerical test results are described as follows [23].

4.2.1. Network Complexity

Some complex networks were randomly constructed to clarify the influence of network complexity on convergence. To compare all the characteristics of the experimental results, all parameters in the numerical test were given the same value. Under the given conditions (the iterative precision was 0.01 m³/s, and the initial airflow was 0 m³/s), the computation results are as listed in

Table 2. Comparison of the iterative number for ventilation networks with different branches using the traditional Hardy Cross solution method with the improved closed loop solution method.

	Circuits (Branches)	9 (24)	36 (84)	121 (264)	264 (562)	528 (1112)
Solution Method
Traditional Hardy Cross solution		19	56	157	744	843
Improved closed loop solution		20	45	108	163	202

and

Table 3. Comparison of the iterative time (ms) for ventilation networks with different branches using the traditional Hardy Cross solution method with the improved closed loop solution method.

	Circuits (Branches)	9 (24)	36 (84)	121 (264)	264 (562)	528 (1112)
Solution Method
Traditional Hardy Cross solution		47	218	3603	6381	18,860
Improved closed loop solution		52	118	318	527	780

.

By analyzing the data in Table 2 and Table 3, we can draw the conclusion that the improved closed loop solution, unlike the traditional Hardy Cross solution, shows substantially linear or close to linear convergence.

With the increase in network complexity, compared with the traditional Hardy Cross solution, the improved closed loop solution shows obvious advantages in terms of the increasing number of mutually influenced circuits. In the complex network, if a circuit contains excessive branches, it may lead to thousands of iterative errors in the first iteration. A single iteration error greatly deviates from the actual value, so the iterative error cannot be gradually reduced, and the solution process exhibits an obviously divergent trend.

4.2.2. Iterative Precision

Some complex networks were randomly constructed to clarify the influence of iterative precision on convergence. To compare all characteristics of the experimental results, all parameters in the numerical test were given the same value. Under the given conditions (the network complexity was 528(1112), and the initial airflow was 0 m³/s), the computation results are as listed in

Table 4. Comparison of the iterative number for different specified iterative precisions (m³/s) using the traditional Hardy Cross solution method with the improved closed loop solution method.

	Iterative Precision	1.0	0.1	0.01	0.001	0.0001
Solution Method
Traditional Hardy Cross solution		28	199	843	4012	6147
Improved closed loop solution		13	85	202	320	453

and

Table 5. Comparison of the iterative time (ms) for different specified iterative precisions (m³/s) using the traditional Hardy Cross solution method with the improved closed loop solution method.

	Iterative Precision	1.0	0.1	0.01	0.001	0.0001
Solution Method
Traditional Hardy Cross solution		2184	13,650	18,860	33,072	42,525
Improved closed loop solution		47	328	780	1233	1685

.

By analyzing the data in Table 4 and Table 5, we can draw the conclusion that if the required precision is not too strict, the solution converges quickly, and the curve is close to linear in the range of low precision. If the required iterative accuracy is higher, the number of iterations increases sharply, and the solution converges slowly or tends to diverge. Taking into account the cumulative error, the suggested airflow iteration precision is 0.01 m³/s, which can satisfy the actual need and ensure the running efficiency.

4.2.3. Initial Airflow

The iterative process is not the same for different solution methods. The requirement of the algorithm for the initial value is the characteristic of the nonlinear problem. Due to the existence of multiple solutions of nonlinear functions, when the initial value is not suitable, any solution method may not converge or may lead to a false convergence.

Some complex networks were randomly constructed to clarify the influence of initial airflow on convergence. To compare all characteristics of the experimental results, all parameters in the numerical test were given the same value. Under the given conditions (the network complexity was 528(1112), and the iterative precision was 0.01 m³/s), the computation results are as listed in

Table 6. Comparison of the iterative number for different specified initial airflows (m³/s) using the traditional Hardy Cross solution method with the improved closed loop solution method.

	Initial Airflow	0	10	50	100	200	500	1000
Solution Method
Traditional Hardy Cross solution		843	2830	3212	3465	-	-	-
Improved closed loop solution		202	240	314	332	346	482	495

and

Table 7. Comparison of the iterative time (ms) for different specified initial airflows (m³/s) using the traditional Hardy Cross solution method with the improved closed loop solution method.

	Initial Airflow	0	10	50	100	200	500	1000
Solution Method
Traditional Hardy Cross solution		18,860	54,601	68,782	85,316	-	-	-
Improved closed loop solution		780	936	1248	1295	1342	1887	1934

.

The selection of the initial airflow has a great influence on the solution convergence. If the initial airflow is close to the actual value, the solution converges quickly. An unreasonable initial airflow will not only influence the iterative convergence speed but may also lead to the solution of non-convergence or false convergence.

By analyzing the data in Table 6 and Table 7, we can draw the conclusion that the procedure converges towards a balanced solution even when early values of $\Delta Q$ are large. One of the most important reasons is that the tendency towards unstable divergence is inhibited by limiting the reasonable range. Obviously, the improved solution based on MICL is remarkably tolerant to poorly estimated initial airflow.

5. Conclusions

Considering that the truncation error of the Hardy Cross iteration method is not necessarily related to the minimum spanning tree, we propose an improved MICL search algorithm to find the optimum circuits in a given minimum spanning tree. The algorithm can be applied in different complex networks, such as a water network, survey control network, wind network and other relevant networks to find a group of minimum independent closed loops.

Our main contribution is optimizing the circuit dividing strategy to improve the iteration convergence and the efficiency of a single iteration. In contrast to a traditional independent circuit, an independent closed loop may contain one or more co-tree branches but fewer high-resistance branches and fan branches. It is helpful in solving the problem of divergence or slow convergence for complex ventilation networks.

The improved solution method can be used to calculate the problem of airflow distribution for large-scale ventilation networks with multiple fans. The experimental results of real-world mine ventilation networks show that the improved solution method converges rapidly within a small number of iterations.