Thermo-Mechanical Stress Comparison of a GaN and SiC MOSFET for Photovoltaic Applications
Abstract
1. Introduction
- Less space will be needed for the installation of PV panels.
- Less installation and repair costs are required.
- Lower distribution and transmission losses, because the electricity generated by the BIPV system will be consumed locally.
- Lower heat transfer coefficients between different building partitions, which improves the building energy efficiency.
2. Electro-Thermal Modeling of a Wide-Bandgap Based String Inverter
2.1. Electro-Thermal Model Construction
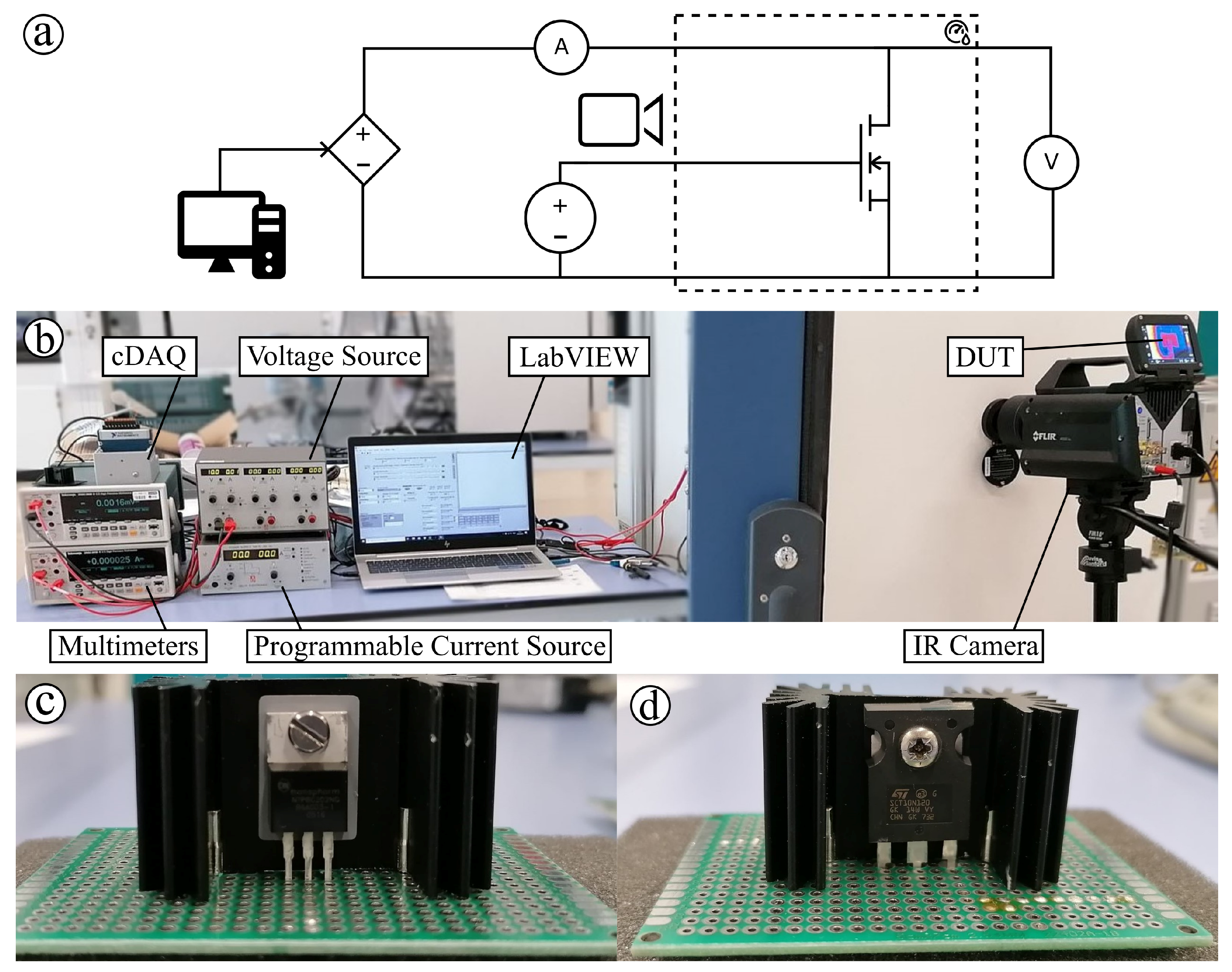
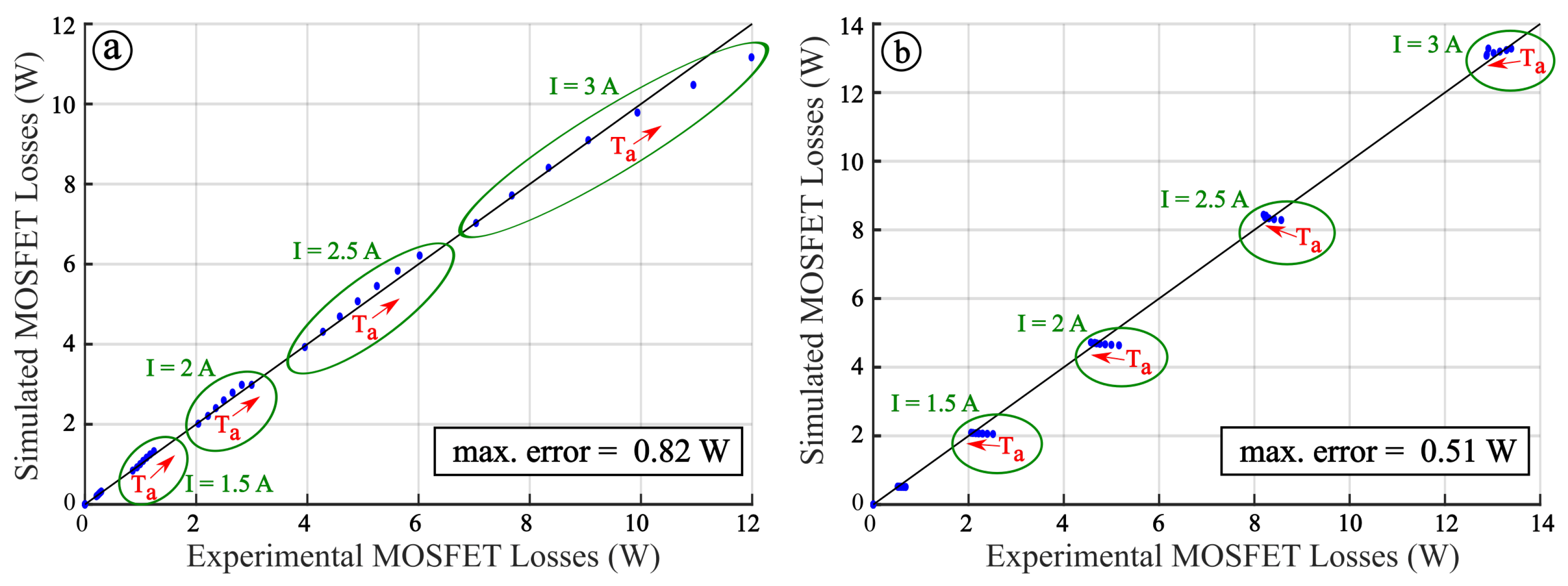
2.2. MOSFET Losses Electrical Model Validation
3. Reverse Engineering Wide-Bandgap Devices
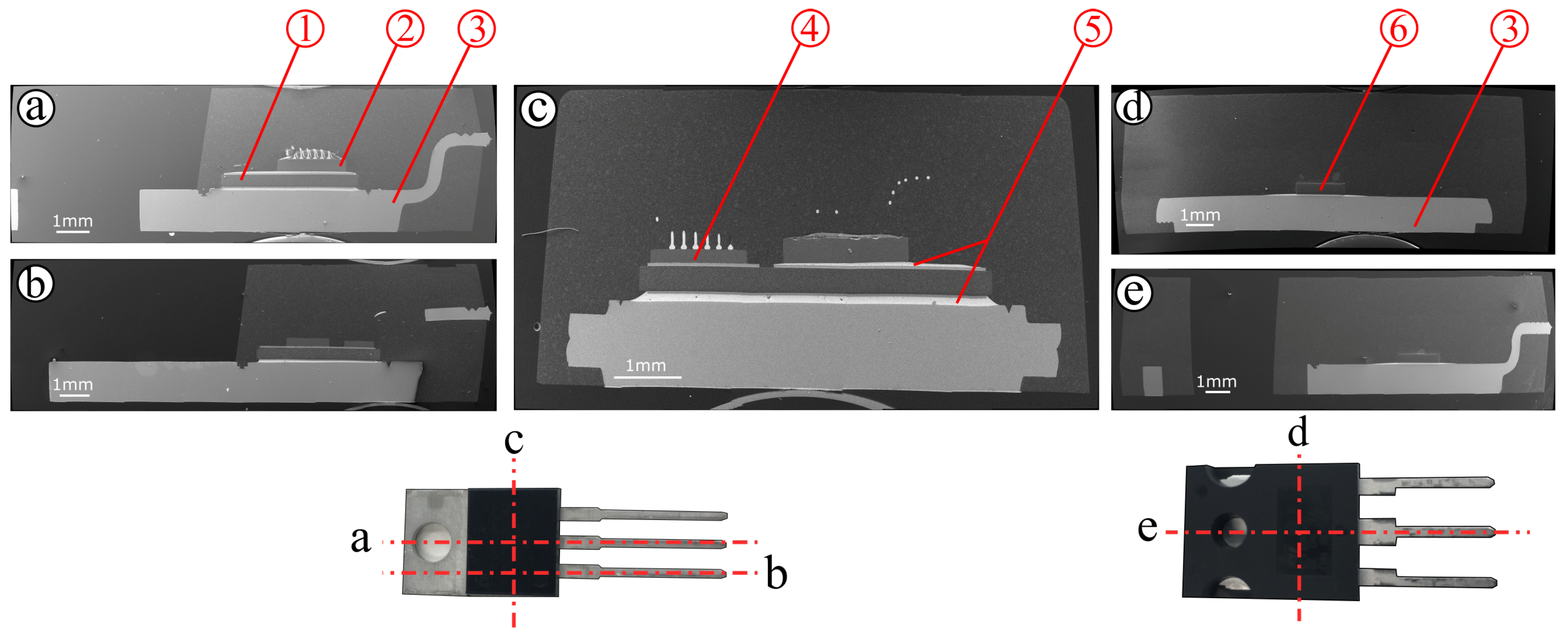
3.1. X-ray Imaging
3.2. Scanning Electronic Microscopy and Energy-Dispersive X-Ray Spectroscopy
4. Finite Element Method Modeling of Wide-Bandgap Devices
4.1. FEM MOSFET Model Construction
4.2. MOSFET Losses Thermal Model Validation
5. Mission-Profile Based Thermo-Mechanical FEM Simulations of Wide-Bandgap Devices
5.1. Mission-Profile Translation
5.2. Thermo-Mechanical FEM Simulation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Breyer, C.; Bogdanov, D.; Aghahosseini, A.; Gulagi, A.; Child, M.; Oyewo, A.S.; Farfan, J.; Sadovskaia, K.; Vainikka, P. Solar photovoltaics demand for the global energy transition in the power sector. Prog. Photovolt. Res. Appl. 2018, 26, 505–523. [Google Scholar] [CrossRef]
- Rakhshani, E.; Rouzbehi, K.; del Pozo Fernandez, A.J.S.; Cabrera-Tobar, A.; Pouresmaeil, E. Integration of Large Scale PV-Based Generation into Power Systems: A Survey. Energies 2019, 12, 1425. [Google Scholar] [CrossRef]
- Apostoleris, H.; Sgouridis, S.; Stefancich, M.; Chiesa, M. Utility solar prices will continue to drop all over the world even without subsidies. Nat. Energy 2019, 4, 833–834. [Google Scholar] [CrossRef]
- Mehravaran, A.; Derhem, A.; Nassereddine, M. Building-Integrated Photovoltaics (BIPV) for Residential and Industrial Properties. In Proceedings of the 2019 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, UAE, 26 March–10 April 2019; IEEE: Dubai, UAE, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Sarkar, D.; Kumar, A.; Sadhu, P.K. A Survey on Development and Recent Trends of Renewable Energy Generation from BIPV Systems. IETE Tech. Rev. 2020, 37, 258–280. [Google Scholar] [CrossRef]
- Quintana, S.; Huang, P.; Saini, P.; Zhang, X. A preliminary techno-economic study of a building integrated photovoltaic (BIPV) system for a residential building cluster in Sweden by the integrated toolkit of BIM and PVSITES. Intell. Build. Int. 2020, 1–19. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, G.; Wu, Y.; Liu, C. Optimal planning of building integrated photovoltaic system in urban energy internet. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017; IEEE: Beijing, China, 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Dobrzycki, A.; Kurz, D.; Mikulski, S.; Wodnicki, G. Analysis of the Impact of Building Integrated Photovoltaics (BIPV) on Reducing the Demand for Electricity and Heat in Buildings Located in Poland. Energies 2020, 13, 2549. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, M.; Yang, H. A Review of the Energy Performance and Life-Cycle Assessment of Building-Integrated Photovoltaic (BIPV) Systems. Energies 2018, 11, 3157. [Google Scholar] [CrossRef]
- Arai, J.; Iba, K.; Funabashi, T.; Nakanishi, Y.; Koyanagi, K.; Yokoyama, R. Power electronics and its applications to renewable energy in Japan. IEEE Circuits Syst. Mag. 2008, 8, 52–66. [Google Scholar] [CrossRef]
- Chakraborty, S.; Simões, M.G.; Kramer, W.E. (Eds.) Power Electronics for Renewable and Distributed Energy Systems: A Sourcebook of Topologies, Control and Integration; Green Energy and Technology; Springer: London, UK, 2013; OCLC: 855561950. [Google Scholar]
- Rezk, H.; Eltamaly, A.M. A comprehensive comparison of different MPPT techniques for photovoltaic systems. Sol. Energy 2015, 112, 1–11. [Google Scholar] [CrossRef]
- Falck, J.; Felgemacher, C.; Rojko, A.; Liserre, M.; Zacharias, P. Reliability of Power Electronic Systems: An Industry Perspective. IEEE Ind. Electron. Mag. 2018, 12, 24–35. [Google Scholar] [CrossRef]
- De León-Aldaco, S.E.; Calleja, H.; Chan, F.; Jiménez-Grajales, H.R. Effect of the Mission Profile on the Reliability of a Power Converter Aimed at Photovoltaic Applications—A Case Study. IEEE Trans. Power Electron. 2013, 28, 2998–3007. [Google Scholar] [CrossRef]
- Petrone, G.; Spagnuolo, G.; Teodorescu, R.; Veerachary, M.; Vitelli, M. Reliability Issues in Photovoltaic Power Processing Systems. IEEE Trans. Ind. Electron. 2008, 55, 2569–2580. [Google Scholar] [CrossRef]
- Sintamarean, C.; Eni, E.; Blaabjerg, F.; Teodorescu, R.; Wang, H. Wide-band gap devices in PV systems—Opportunities and challenges. In Proceedings of the 2014 International Power Electronics Conference (IPEC-Hiroshima 2014-ECCE ASIA), Hiroshima, Japan, 18–21 May 2014; IEEE: Hiroshima, Japan, 2014; pp. 1912–1919. [Google Scholar] [CrossRef]
- Singh, R. Reliability and performance limitations in SiC power devices. Microelectron. Reliab. 2006, 46, 713–730. [Google Scholar] [CrossRef]
- Roccaforte, F.; Fiorenza, P.; Greco, G.; Lo Nigro, R.; Giannazzo, F.; Iucolano, F.; Saggio, M. Emerging trends in wide band gap semiconductors (SiC and GaN) technology for power devices. Microelectron. Eng. 2018, 187–188, 66–77. [Google Scholar] [CrossRef]
- She, X.; Huang, A.Q.; Lucia, O.; Ozpineci, B. Review of Silicon Carbide Power Devices and Their Applications. IEEE Trans. Ind. Electron. 2017, 64, 8193–8205. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, X. Review and analysis of SiC MOSFETs’ ruggedness and reliability. IET Power Electron. 2020, 13, 445–455. [Google Scholar] [CrossRef]
- Ceccarelli, L.; Kotecha, R.M.; Bahman, A.S.; Iannuzzo, F.; Mantooth, H.A. Mission-Profile-Based Lifetime Prediction for a SiC mosfet Power Module Using a Multi-Step Condition-Mapping Simulation Strategy. IEEE Trans. Power Electron. 2019, 34, 9698–9708. [Google Scholar] [CrossRef]
- Sintamarean, N.; Wang, H.; Blaabjerg, F.; Rimmen, P.P. A design tool to study the impact of mission-profile on the reliability of SiC-based PV-inverter devices. Microelectron. Reliab. 2014, 54, 1655–1660. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Zhou, D.; Sangwongwanich, A.; Wang, H. Design for reliability in renewable energy systems. In Proceedings of the 2017 International Symposium on Power Electronics (Ee), Novi Sad, Serbia, 19–21 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Graovac, D.; Pürschel, M.; Kiep, A. MOSFET Power Losses Calculation Using the Data-Sheet Parameters; Technical Report; Newark element14; Infineon Technologies AG: Chicago, IL, USA, 2006. [Google Scholar]
- Van De Sande, W.; Ravyts, S.; Alavi, O.; Nivelle, P.; Driesen, J.; Daenen, M. The Sensitivity of an Electro-Thermal Photovoltaic DC–DC Converter Model to the Temperature Dependence of the Electrical Variables for Reliability Analyses. Energies 2020, 13, 2865. [Google Scholar] [CrossRef]
- Novelline, R.A.; Squire, L.F. Squire’s Fundamentals of Radiology, 5th ed.; Harvard University Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Goldstein, J. (Ed.) Scanning Electron Microscopy and X-ray Microanalysis, 3rd ed.; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2003. [Google Scholar]
- Li, T.; Zhao, B.; Lu, X.; Xu, H.; Zou, D. A Comparative Study on Johnson Cook, Modified Zerilli–Armstrong, and Arrhenius-Type Constitutive Models to Predict Compression Flow Behavior of SnSbCu Alloy. Materials 2019, 12, 1726. [Google Scholar] [CrossRef]
- Zein, H.; Irfan, O. Surface Roughness Investigation and Stress Modeling by Finite Element on Orthogonal Cutting of Copper. Metals 2018, 8, 418. [Google Scholar] [CrossRef]
- Hu, Y.; Kumar, P.; Xu, R.; Zhao, K.; Cheng, G.J. Ultrafast direct fabrication of flexible substrate-supported designer plasmonic nanoarrays. Nanoscale 2016, 8, 172–182. [Google Scholar] [CrossRef] [PubMed]
- Manikam, V.R.; Cheong, K.Y. Die Attach Materials for High Temperature Applications: A Review. IEEE Trans. Compon. Packag. Manuf. Technol. 2011, 1, 457–478. [Google Scholar] [CrossRef]
- Bressan, J.D.; Lopez, K. New constitutive equation for plasticity in high speed torsion tests of metals. Int. J. Mater. Form. 2008, 1, 213–216. [Google Scholar] [CrossRef]
- Khatibi, G.; Betzwar Kotas, A.; Lederer, M. Effect of aging on mechanical properties of high temperature Pb-rich solder joints. Microelectron. Reliab. 2018, 85, 1–11. [Google Scholar] [CrossRef]
- Long, X.; Chen, Z.; Wang, W.; Fu, Y.; Wu, Y. Parameterized Anand constitutive model under a wide range of temperature and strain rate: Experimental and theoretical studies. J. Mater. Sci. 2020, 55, 10811–10823. [Google Scholar] [CrossRef]
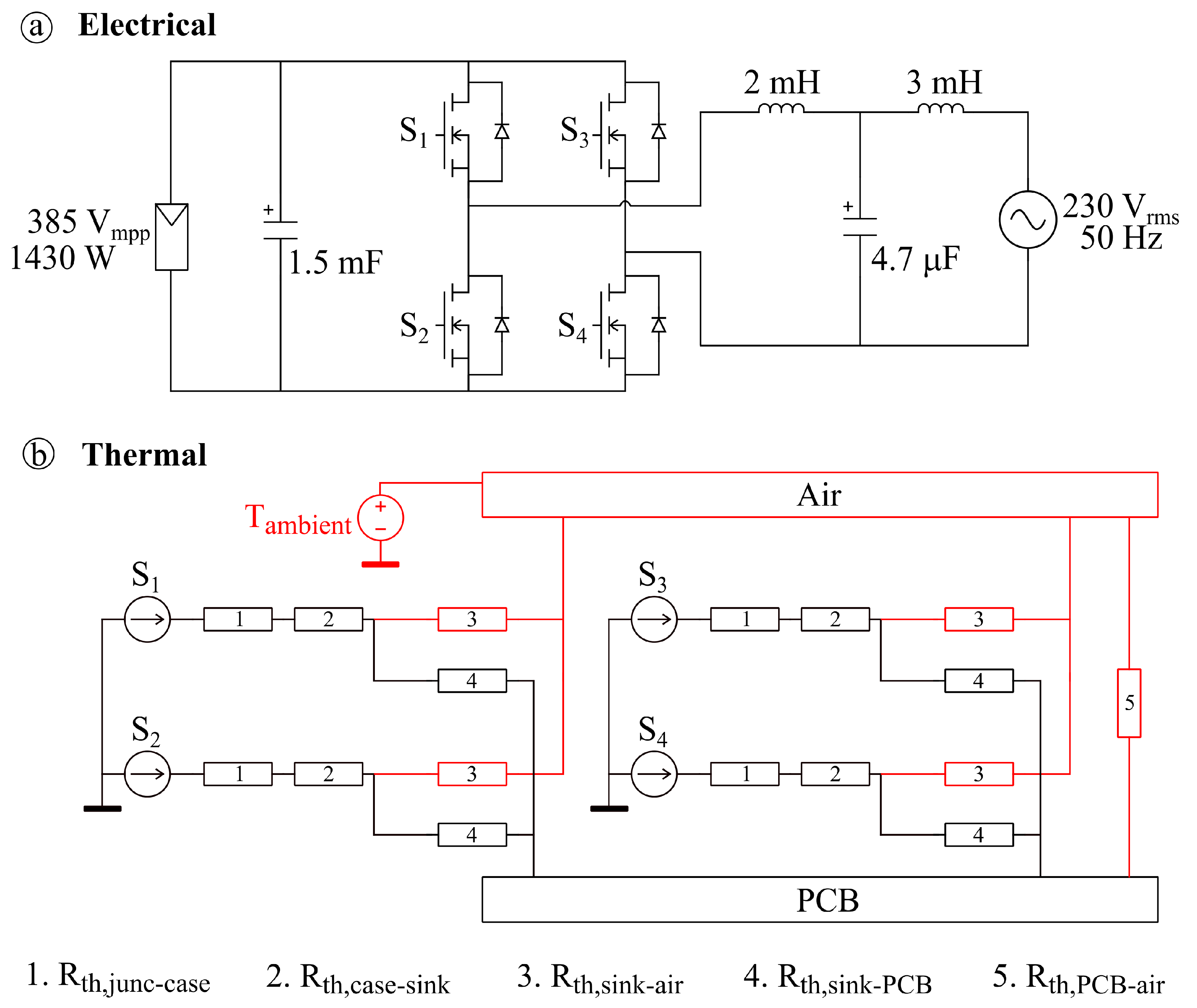




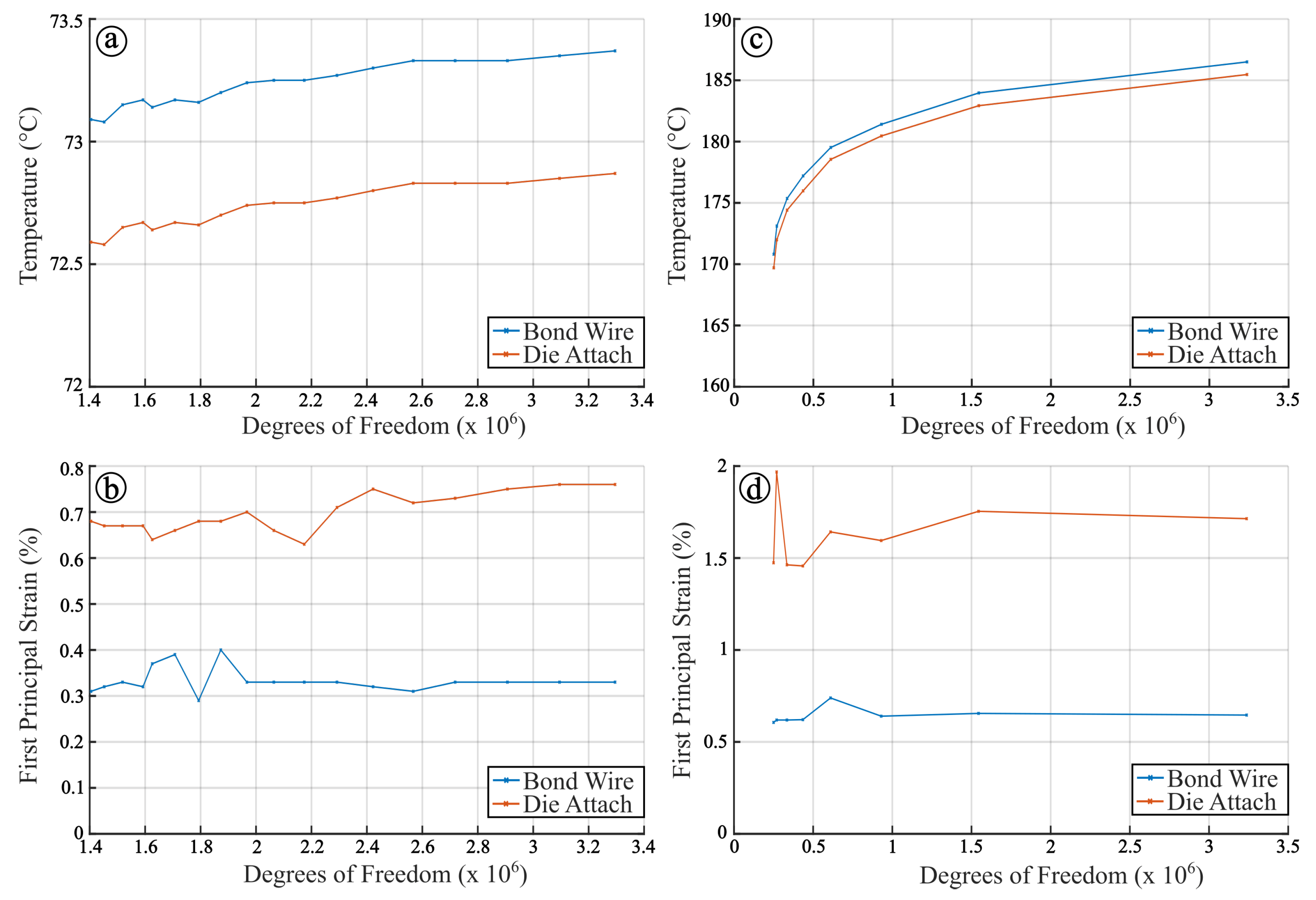

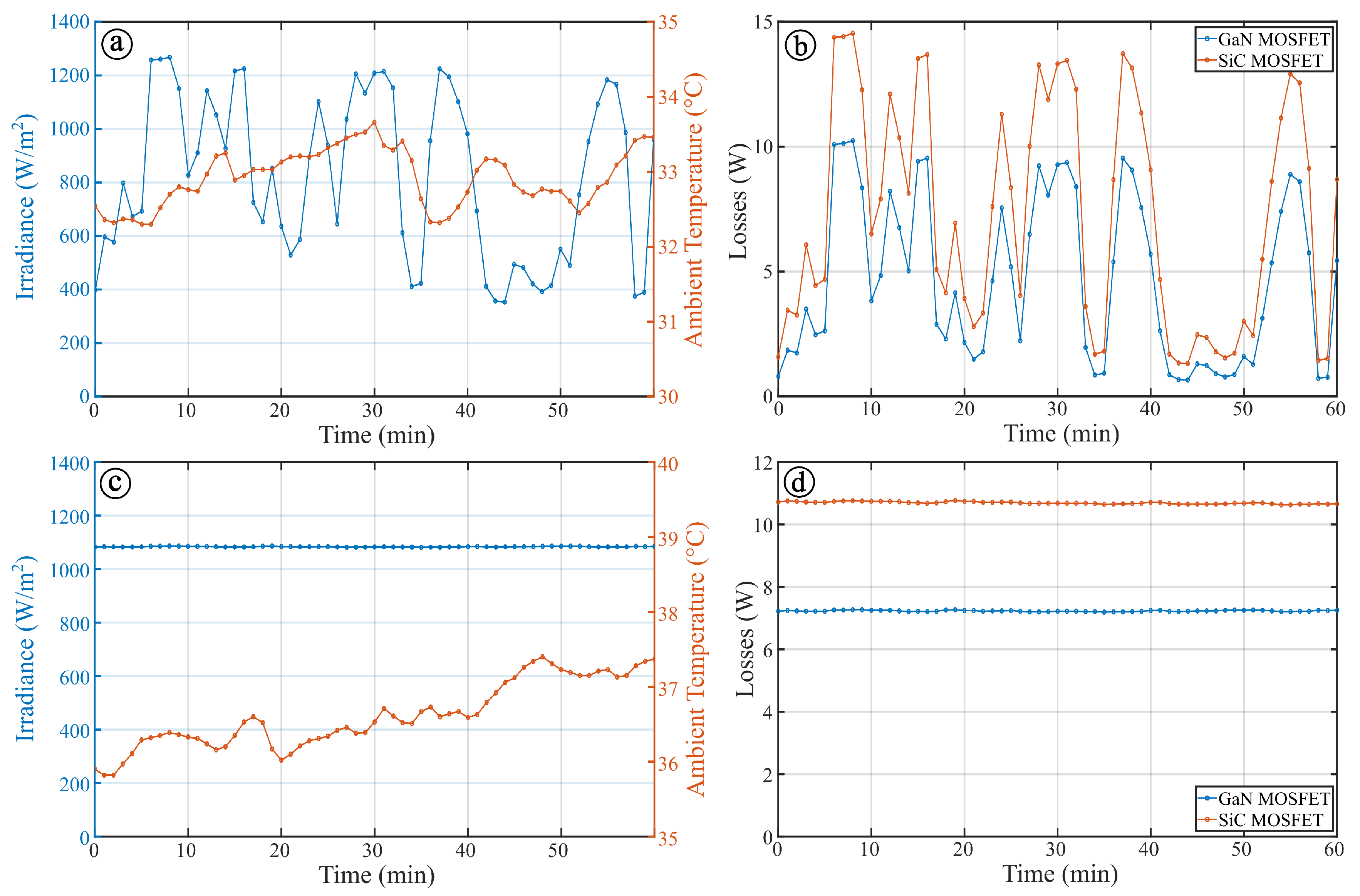
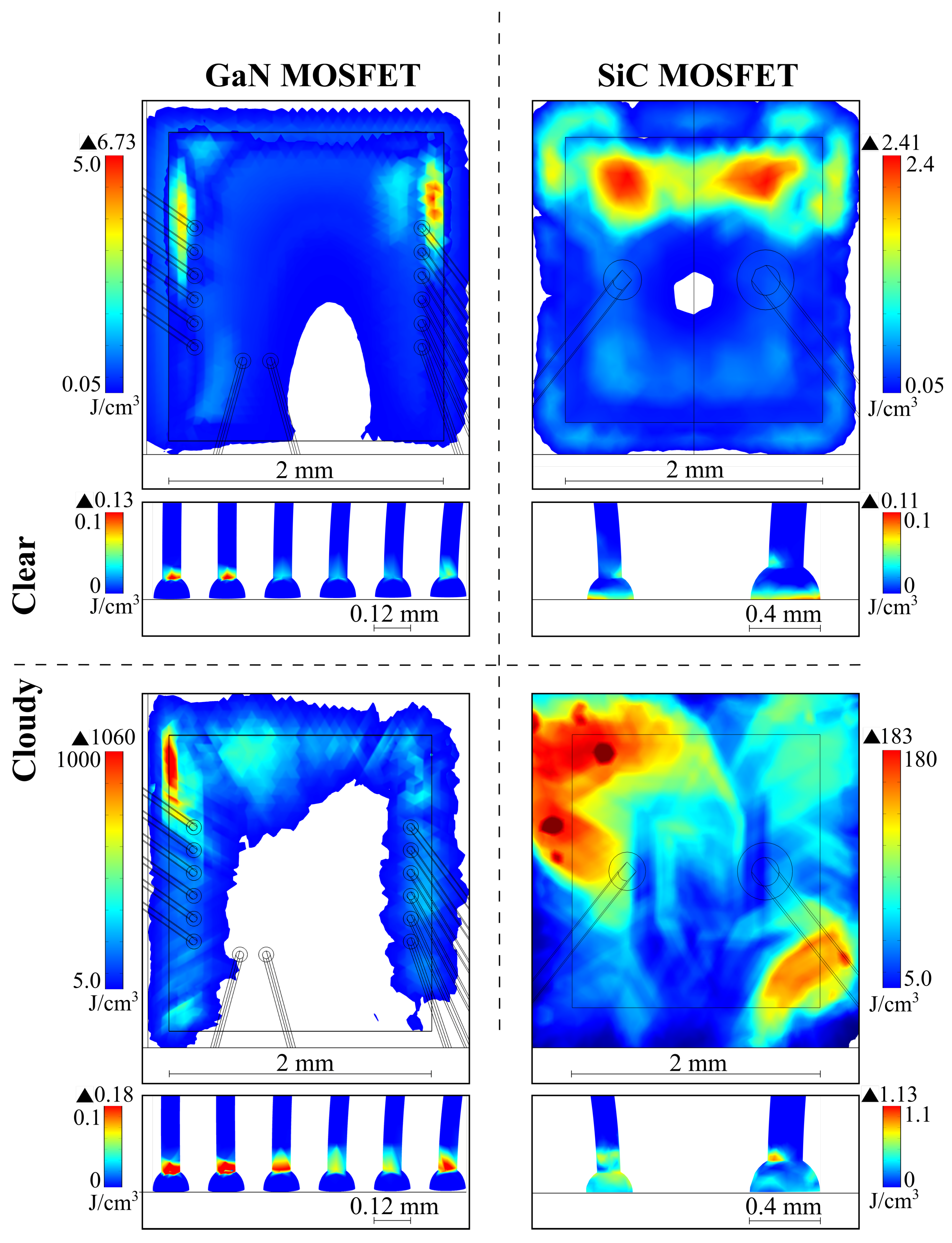
| Number | Thermal Resistance | GaN Cascode MOSFET | SiC MOSFET |
|---|---|---|---|
| 1 | Junction-to-Case (Rth,junc-case) | 2.3 K/W | 1.17 K/W |
| 2 | Case-to-Heatsink (Rth,case-sink) | 0.69 K/W | |
| 3 | Heatsink-to-Air (Rth,sink-air) | 3.06 K/W | |
| 4 | Heatsink-to-PCB (Rth,sink-PCB) | 13.25 K/W | |
| 5 | PCB-to-Air (Rth,PCB-air) | 9.5 K/W | |
| GaN Cascode MOSFET | SiC MOSFET | |
|---|---|---|
| Manufacturer | ON Semiconductor | STMicroelectronics |
| Code | NTP8G202N | SCT10N120 |
| Package | TO-220 | HiP247TM |
| On-resistance at Tj = 25 °C | 0.290 Ω | 0.520 Ω |
| On-resistance at Tj = 150 °C | 0.580 Ω | 0.533 Ω |
| Max. junction operating temperature | 150 °C | 200 °C |
| Drain-source voltage | 600 V | 1200 V |
| Drain current at Tc = 25 °C | 9 A | 12 A |
| Reverse recovery charge | 29 nC | 107 nC |
| Material | Young’s Modulus (GPa) | Poisson’s Ratio | Thermal Conductivity (W/m·K) | Coefficient of Thermal Expansion (K−1) | Heat Capacity at Constant Pressure (J/kg·K) |
|---|---|---|---|---|---|
| Epoxy resin (SiO2 fill) | 13 | 0.34 | 0.6 | 23 × 10−6 | 1.3 × 103 |
| Si | 160 | 0.27 | 130 | 2.6 × 10−6 | 700 |
| AlN | 320 | 0.26 | 120 | 5.3 × 10−6 | 800 |
| 95Pb-5Sn | 15 | 0.44 | 36 | 28.6 × 10−6 | 140 |
| GaN (Wurtzite) | 295 | 0.23 | 130 | 3.2 × 10−6 | 490 |
| Au | 78 | 0.42 | 315 | 14 × 10−6 | 130 |
| SiC | 410 | 0.2 | 370 | 3.5 × 10−6 | 690 |
| Cu | 110 | 0.35 | 400 | 17 × 10−6 | 385 |
| Al | 70 | 0.35 | 237 | 23.1 × 10−6 | 904 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van De Sande, W.; Alavi, O.; Nivelle, P.; D’Haen, J.; Daenen, M. Thermo-Mechanical Stress Comparison of a GaN and SiC MOSFET for Photovoltaic Applications. Energies 2020, 13, 5900. https://doi.org/10.3390/en13225900
Van De Sande W, Alavi O, Nivelle P, D’Haen J, Daenen M. Thermo-Mechanical Stress Comparison of a GaN and SiC MOSFET for Photovoltaic Applications. Energies. 2020; 13(22):5900. https://doi.org/10.3390/en13225900
Chicago/Turabian StyleVan De Sande, Wieland, Omid Alavi, Philippe Nivelle, Jan D’Haen, and Michaël Daenen. 2020. "Thermo-Mechanical Stress Comparison of a GaN and SiC MOSFET for Photovoltaic Applications" Energies 13, no. 22: 5900. https://doi.org/10.3390/en13225900
APA StyleVan De Sande, W., Alavi, O., Nivelle, P., D’Haen, J., & Daenen, M. (2020). Thermo-Mechanical Stress Comparison of a GaN and SiC MOSFET for Photovoltaic Applications. Energies, 13(22), 5900. https://doi.org/10.3390/en13225900





