Fractional Time Derivative Seismic Wave Equation Modeling for Natural Gas Hydrate
Abstract
:1. Introduction
2. Materials and Methods
2.1. Definitions of Fractional Derivatives
2.1.1. Grunwald–Letnikov Fractional-Order Derivative
2.1.2. Riemann–Liouville Fractional-Order Derivative
2.1.3. Caputo’s Fractional-Order Derivative
2.1.4. The Riesz Fractional-Order Derivative
2.1.5. Relations between the above Fractional-Order Derivatives
2.2. Establishing Velocity and Quality Factor Model of Hydrate Layer
2.3. Viscoacoustic Wave Equation
2.4. Methods
2.4.1. Fractional-Order Derivatives Approximation
2.4.2. Finite Difference Method for Integer-Order Derivatives
2.4.3. Fractional Differencing Scheme
2.5. Proposition
3. Results
3.1. Different Q Media
3.2. Layered Model
3.3. Simulations on Velocity and Quality Factor Model of Hydrate Layer
3.4. Layered NGH Model
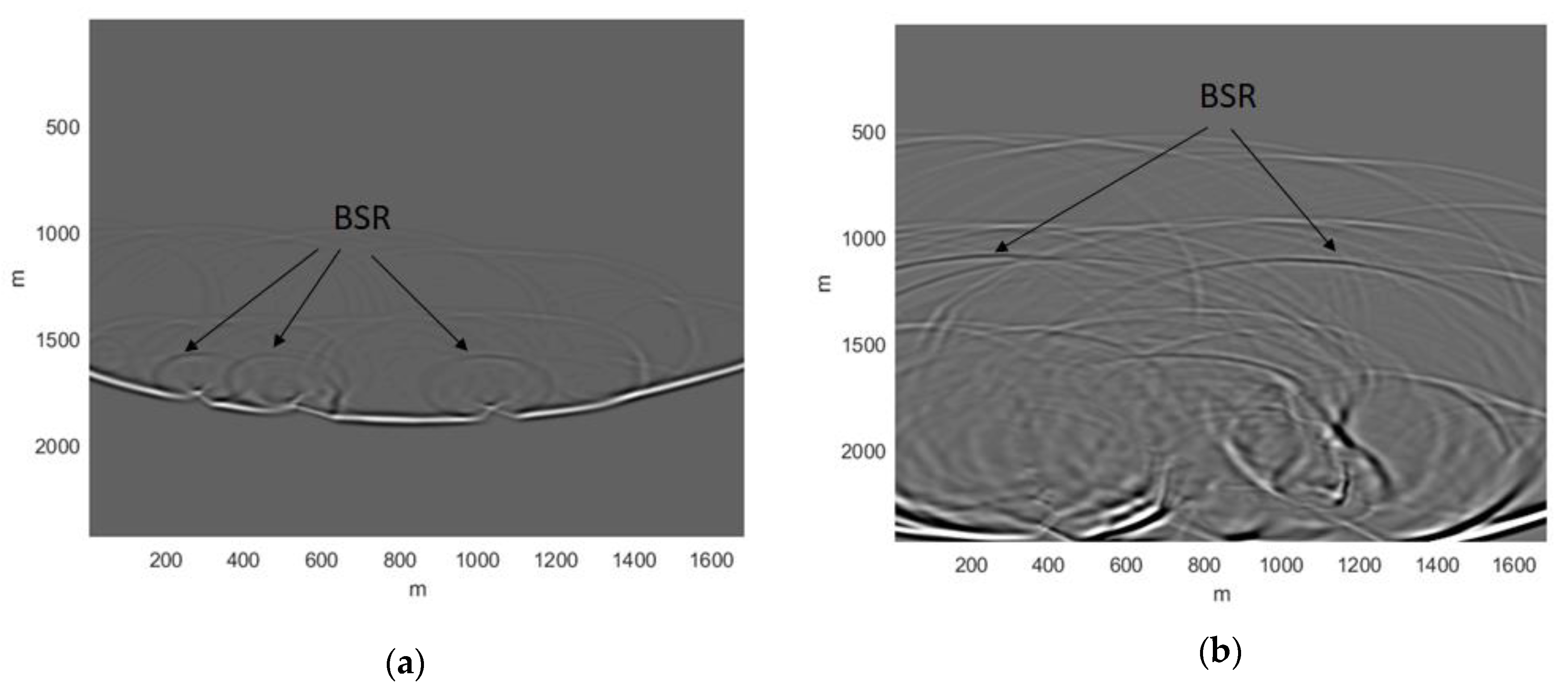
3.5. Complex Seabed NGH Model
4. Discussion and Future Research
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guo, P.; Mcmechan, G.A. Evaluation of three first-order isotropic viscoelastic formulations based on the generalized standard linear solid. J. Seism. Explor. 2017, 26, 199–226. [Google Scholar]
- Kang, I.B.; McMechan, G.A. Separation of intrinsic and scattering Q based on frequency-dependent amplitude ratios of transmitted waves. J. Geophys. Res. 1994, 99, 23875–23885. [Google Scholar] [CrossRef]
- Zhu, T.; Harris, J.M. Modeling acoustic wave propagation in heterogeneous attenuating media using decoupled fractional Laplacians. Geophysics 2014, 79, T105–T116. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Fomel, S.; Zhu, T.; Hu, J. Q-compensated least-squares reverse time migration using low-rank one-step wave extrapolation. Geophysics 2016, 81, S271–S279. [Google Scholar] [CrossRef]
- Carcione, J.M. Wave Fields in Real Media: Wave Propagation in Anisotropic, Anelastic, Porous and Electromagnetic Media; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Štekl, I.; Pratt, R.G. Accurate viscoelastic modeling by frequency-domain finite differences using rotated operators. Geophysics 1998, 63, 1779–1794. [Google Scholar] [CrossRef]
- Zhu, T.; Carcione, J.M.; Harris, J.M. Approximating constant-Q seismic propagation in the time domain. Geophys. Prospect. 2013, 61, 931–940. [Google Scholar] [CrossRef]
- Aki, K.; Richards, P.G. Quantitative Seismology: Theory and Methods; W. H. Freeman: San Franccisco, CA, USA, 1980; Volume 1. [Google Scholar]
- Blanch, J.O.; Robertsson, J.O.A.; Symes, W.W. Modeling of a constant Q: Methodology and algorithm for an efficient and optimally inexpensive viscoelastic technique. Geophysics 1995, 60, 176–184. [Google Scholar] [CrossRef] [Green Version]
- Blanch, J.O.; Symes, W.W. Efficient iterative viscoacoustic linearized inversion. In SEG Technical Program Expanded Abstracts 1995; Society of Exploration Geophysicists: Houston, TX, USA, 1995; pp. 627–630. [Google Scholar] [CrossRef]
- Robertsson, J.O.; Blanch, J.O.; Symes, W.W. Viscoacoustic finite-difference modeling. Geophysics 1994, 59, 1444–1456. [Google Scholar] [CrossRef] [Green Version]
- Carcione, J.M.; Cavallini, F.; Mainardi, F.; Hanyga, A. Time-domain seismic modeling of constant-Q wave propagation using fractional derivatives. Pure Appl. Geophys. 2002, 159, 1719–1736. [Google Scholar] [CrossRef]
- Kjartansson, E. Constant Q-wave propagation and attenuation. J. Geophys. Res. Space Phys. 1979, 84, 4737–4748. [Google Scholar] [CrossRef] [Green Version]
- Caputo, M.; Mainardi, F. A new dissipation model based on memory mechanism. Pure Appl. Geophys. 1971, 91, 134–147. [Google Scholar] [CrossRef]
- Carcione, J.M. Theory and modeling of constant-Q P- and S-waves using fractional time derivatives. Geophysics 2009, 74, T1–T11. [Google Scholar] [CrossRef]
- Chen, W.; Holm, S. Fractional Laplacian time-space models for linear and nonlinear lossy media exhibiting arbitrary frequency power-law dependency. J. Acoust. Soc. Am. 2004, 115, 1424–1430. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carcione, J.M. A generalization of the Fourier pseudospectral method. Geophysics 2010, 75, A53–A56. [Google Scholar] [CrossRef]
- Song, G.; Zhang, X.; Wang, Z.; Chen, Y.; Chen, P. The asymptotic local finite-difference method of the fractional wave equation and its viscous seismic wavefield simulation. Geophysics 2020, 85, T179–T189. [Google Scholar] [CrossRef]
- Sun, J.; Zhu, T.; Fomel, S. Viscoacoustic modeling and imaging using low-rank approximation. Geophysics 2015, 80, A103–A108. [Google Scholar] [CrossRef] [Green Version]
- Fomel, S.; Ying, L.; Song, X. Seismic wave extrapolation using low rank symbol approximation. Geophys. Prospect. 2013, 61, 526–536. [Google Scholar] [CrossRef]
- Sun, J.; Fomel, S. Low-rank one-step wave extrapolation. SEG Tech. Program Expand. Abstr. 2013, 2013, 3905–3910. [Google Scholar] [CrossRef]
- Yao, J.; Zhu, T.; Hussain, F.; Kouri, D.J. Locally solving fractional Laplacian viscoacoustic wave equation using Hermite distributed approximating functional method. Geophysics 2017, 82, T59–T67. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Zhu, T.; Zhou, H.; Chen, H.; Zhao, X.; Tian, Y. Fractional Laplacians viscoacoustic wavefield modeling with k-space-based time-stepping error compensating scheme. Geophysics 2020, 85, T1–T13. [Google Scholar] [CrossRef]
- Xu, Y.; Li, J.-Y.; Chen, X.; Pang, G. Solving fractional Laplacian visco-acoustic wave equations on complex-geometry domains using Grünwald-formula based radial basis collocation method. Comput. Math. Appl. 2020, 79, 2153–2167. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Youssri, Y.H. A Novel Operational Matrix of Caputo Fractional Derivatives of Fibonacci Polynomials: Spectral Solutions of Fractional Differential Equations. Entropy 2016, 18, 345. [Google Scholar] [CrossRef]
- Youssri, Y.H.; Abd-Elhameed, W.M. Numerical spectral Legendre-Galerkin algorithm for solving time fractional telegraph equation. Rom. J. Phys. 2018, 63, 3–4. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: Mathematics in Science and Engineering; Academic Press: Cambridge, MA, USA, 1999; Volume 198. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, D.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Philadelphia, PA, USA, 1993. [Google Scholar]
- White, J.E. Computed seismic speeds and attenuation in rocks with partial gas saturation. Geophysics 1975, 40, 224–232. [Google Scholar] [CrossRef]
- Shapiro, S.A.; Müller, T.M. Seismic signatures of permeability in heterogeneous porous media. Geophysics 1999, 64, 99–103. [Google Scholar] [CrossRef]
- Helgerud, M.B.; Dvorkin, J.; Nur, A.; Sakai, A.; Collett, T. Elastic-wave velocity in marine sediments with gas hydrates: Effective medium modeling. Geophys. Res. Lett. 1999, 26, 2021–2024. [Google Scholar] [CrossRef]
- Carcione, J.M.; Helle, H.B.; Pham, N.H. White’s model for wave propagation in partially saturated rocks: Comparison with poroelastic numerical experiments. Geophysics 2003, 68, 1389–1398. [Google Scholar] [CrossRef]
- Sumelka, W.; Voyiadjis, G.Z. A hyperelastic fractional damage material model with memory. Int. J. Solids Struct. 2017, 124, 151–160. [Google Scholar] [CrossRef]
- Jia, X.; Li, G. Numerical simulation and parameters inversion for non-symmetric two-sided fractional advection-dispersion equations. J. Inverse Ill Posed Probl. 2016, 24, 29–39. [Google Scholar] [CrossRef]
- Priest, J.A.; Best, A.I.; Clayton, C.R.I. Attenuation of seismic waves in methane gas hydrate-bearing sand. Geophys. J. Int. 2006, 164, 149–159. [Google Scholar] [CrossRef] [Green Version]
- Geng, Z.; Wang, Y. Automated design of a convolutional neural network with multi-scale filters for cost-efficient seismic data classification. Nat. Commun. 2020, 11, 3311. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Wang, Y. Reparameterized full waveform inversion using deep neural networks. Geophysics 2020. [Google Scholar] [CrossRef]
- Wang, Y.F.; Volkov, V.T.; Yagola, A.G. Basic Theory of Inverse Problems: Variational Analysis and Geoscientific Applications, 1st ed.; Science Press: Beijing, China, 2020; in press. [Google Scholar]
- Zhu, T.; Harris, J.M.; Biondi, B.L. Q-compensated reverse-time migration. Geophysics 2014, 79, S77–S87. [Google Scholar] [CrossRef] [Green Version]


























| Memory Lengths | L = 9 | L = 14 | L = 24 | L = 34 | L = 44 | |
|---|---|---|---|---|---|---|
| CPU Time (s) | Original method | 286 | 440 | 760 | 1097 | 1413 |
| New method | 57 | 88 | 152 | 219 | 282 | |
| Rock Parameters | Values |
|---|---|
| Clay bulk modulus (Pa) | 20.9 × 109 |
| Clay shear modulus (Pa) | 6.85 × 109 |
| Clay density (kg/m3) | 2580 |
| Quartz bulk modulus (Pa) | 36.6 × 109 |
| Quartz shear modulus (Pa) | 45 × 109 |
| Quartz density (kg/m3) | 2650 |
| Sea water bulk modulus (Pa) | 2.55 × 109 |
| Density of sea water (kg/m3) | 1050 |
| Seawater viscosity coefficient (Pa·s) | 0.0018 |
| Methane bulk modulus (Pa) | 0.01 × 109 |
| Methane gas density (kg/m3) | 100 |
| Methane viscosity coefficient (Pa·s) | 0.00002 |
| Hydrate bulk modulus (Pa) | 5.6 × 109 |
| Hydrate shear modulus (Pa) | 2.4 × 109 |
| Hydrate density (kg/m3) | 920 |
| Permeability (m2) | 100 × 10−14 |
| Interparticle connection coefficient | 9 |
| Stratum Serial Number | Depth (m) | Porosity | Hydrate Saturation | Gas Saturation |
|---|---|---|---|---|
| 1 (Seawater) | 1300 | - | - | - |
| 2 (General sediment) | 200 | 0.5 | 0 | 0 |
| 3 (Hydrate) | 50 | 0.5 | 0.4 | 0 |
| 4 (Hydrate) | 50 | 0.45 | 0.36 | 0 |
| 5 (Hydrate) | 50 | 0.4 | 0.32 | 0 |
| 6 (Hydrate) | 50 | 0.35 | 0.28 | 0 |
| 7 (Hydrate) | 50 | 0.35 | 0.28 | 0 |
| 8 (Free gas) | 100 | 0.42 | 0 | 0.01 |
| 9 (General sediment) | 200 | 0.42 | 0 | 0 |
| Stratum Serial Number | Depth (m) | Porosity | Hydrate Saturation | Gas Saturation |
|---|---|---|---|---|
| 1 (Seawater) | 1300 | - | - | - |
| 2 (General sediment) | 200 | 0.5 | 0 | 0 |
| 3 (Hydrate) | 50 | 0.5 | 0.1429 | 0 |
| 4 (Hydrate) | 50 | 0.45 | 0.1286 | 0 |
| 5 (Hydrate) | 50 | 0.4 | 0.114 | 0 |
| 6 (Hydrate) | 50 | 0.35 | 0.1 | 0 |
| 7 (Hydrate) | 50 | 0.35 | 0.1 | 0 |
| 8 (Free gas) | 100 | 0.42 | 0 | 0.01 |
| 9 (General sediment) | 200 | 0.42 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Ning, Y.; Wang, Y. Fractional Time Derivative Seismic Wave Equation Modeling for Natural Gas Hydrate. Energies 2020, 13, 5901. https://doi.org/10.3390/en13225901
Wang Y, Ning Y, Wang Y. Fractional Time Derivative Seismic Wave Equation Modeling for Natural Gas Hydrate. Energies. 2020; 13(22):5901. https://doi.org/10.3390/en13225901
Chicago/Turabian StyleWang, Yanfei, Yaxin Ning, and Yibo Wang. 2020. "Fractional Time Derivative Seismic Wave Equation Modeling for Natural Gas Hydrate" Energies 13, no. 22: 5901. https://doi.org/10.3390/en13225901




