Optimization of Spatial Configuration of Multistrand Cable Lines
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Determination of Current Asymmetry for Single-Phase Systems
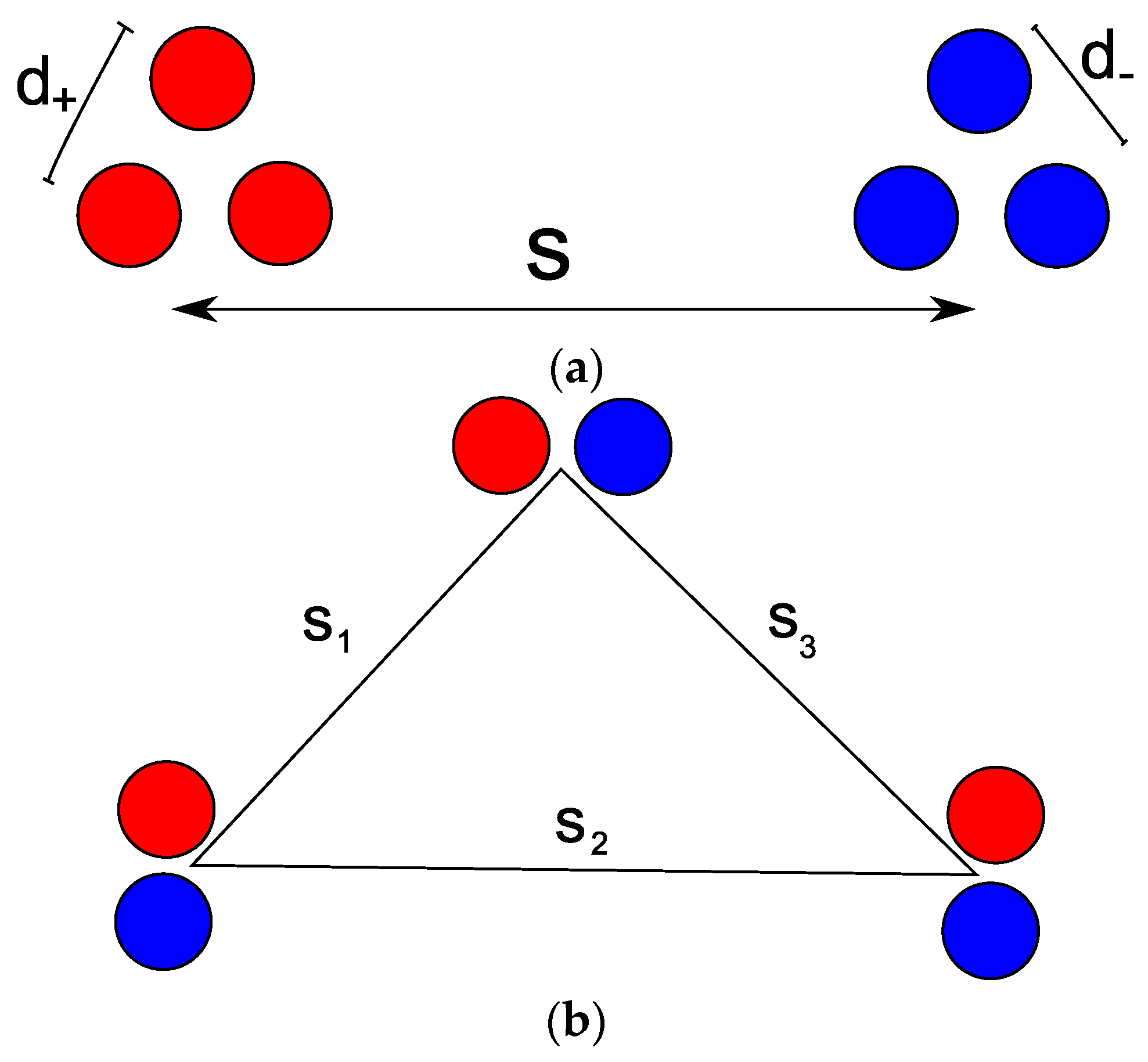
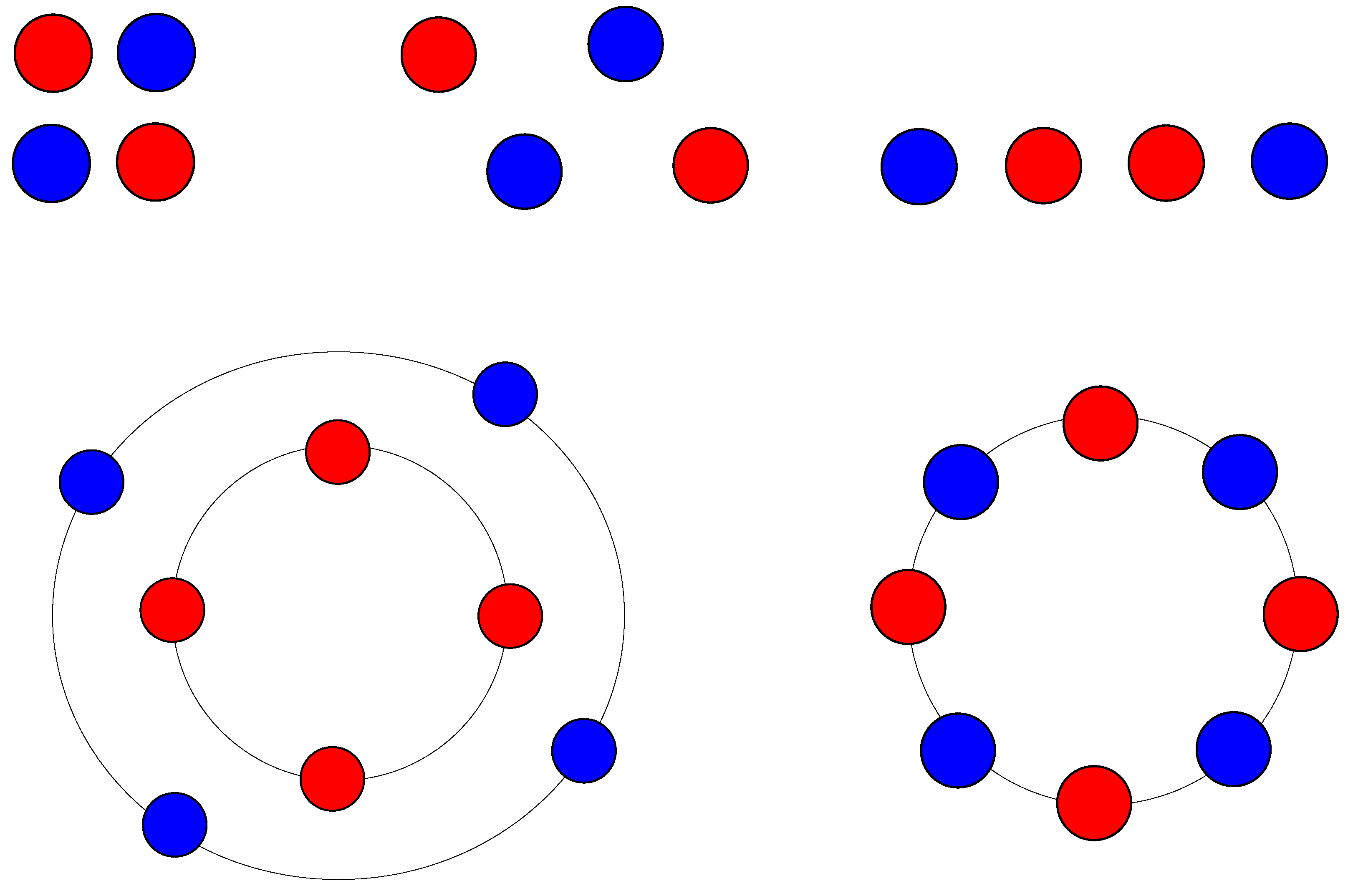
2.2. Distance-Based Criterion
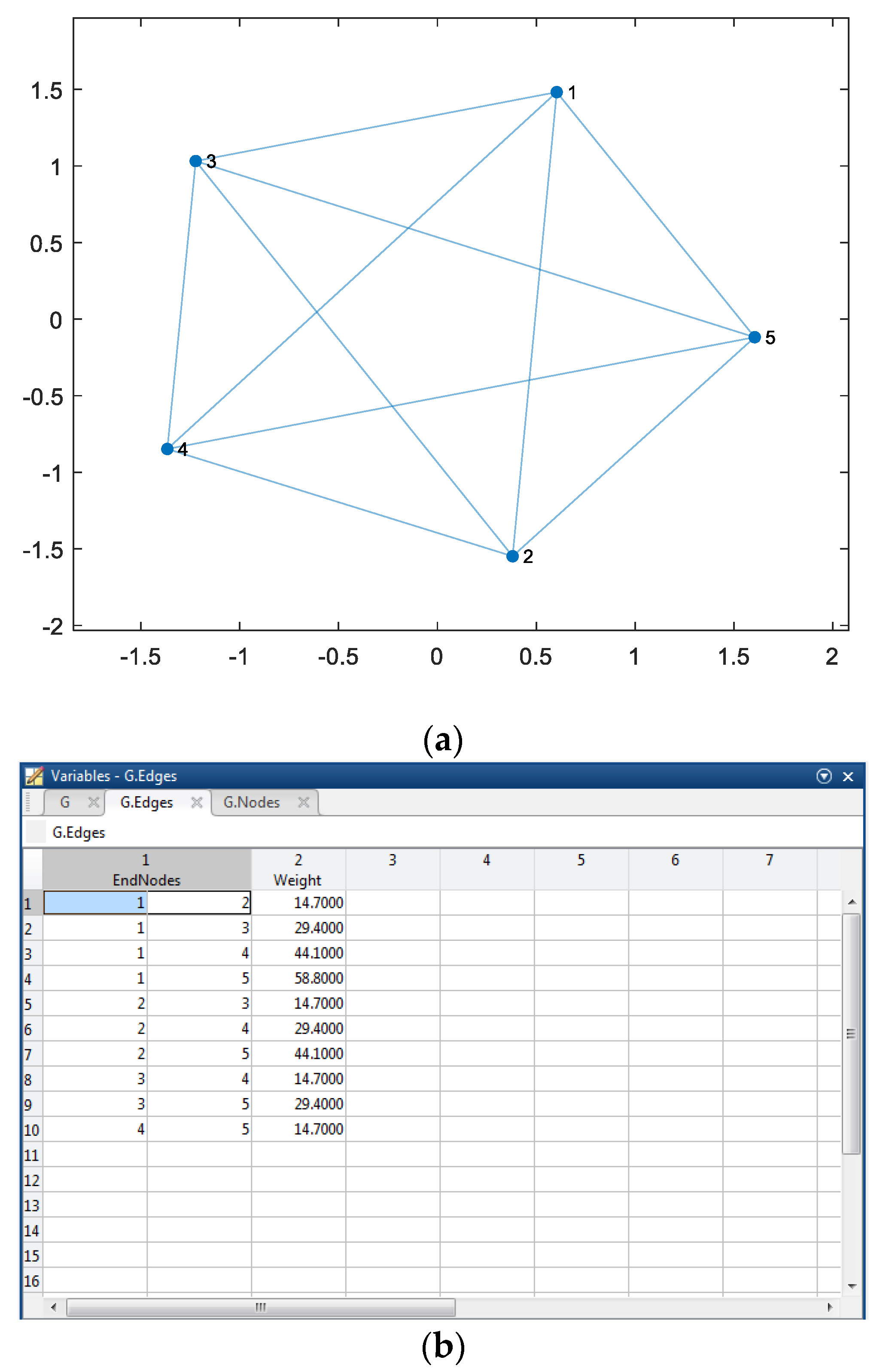
- points = [points_x points_y]; % node coordinates
- distances = squareform(pdist(points));
- G = graph(distances); G.Nodes.x=points(:,1); G.Nodes.y=points(:,2);
- A = full(adjacency(G, G.Edges.Dist));
- Currents = zeros(length(points_x),1);
- for i = 1:length(Currents) Currents(i)=sum(A(i,:)); end
- Currents = Currents./sum(sum(A));
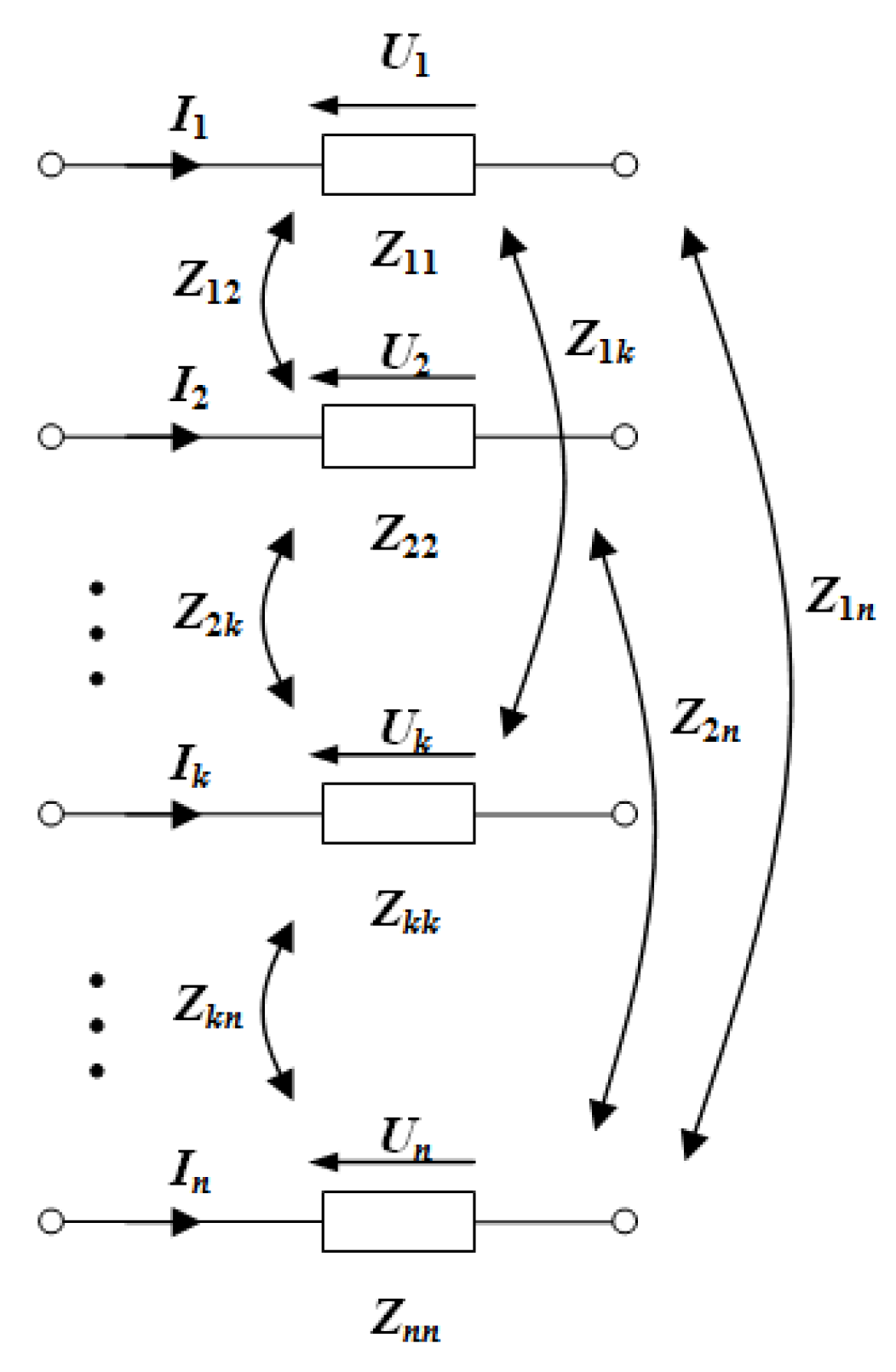
2.3. Barycenter-Based Criterion
3. Relevant Case Studies from Literature
- adding series resistance (not recommended, due to increased losses)
- adding series reactance (enhances the self-inductance/mutual inductance ratio. In this way, the effect of asymmetries in mutual inductance values is diminished. The method is not recommended for circuits operating at higher frequencies).
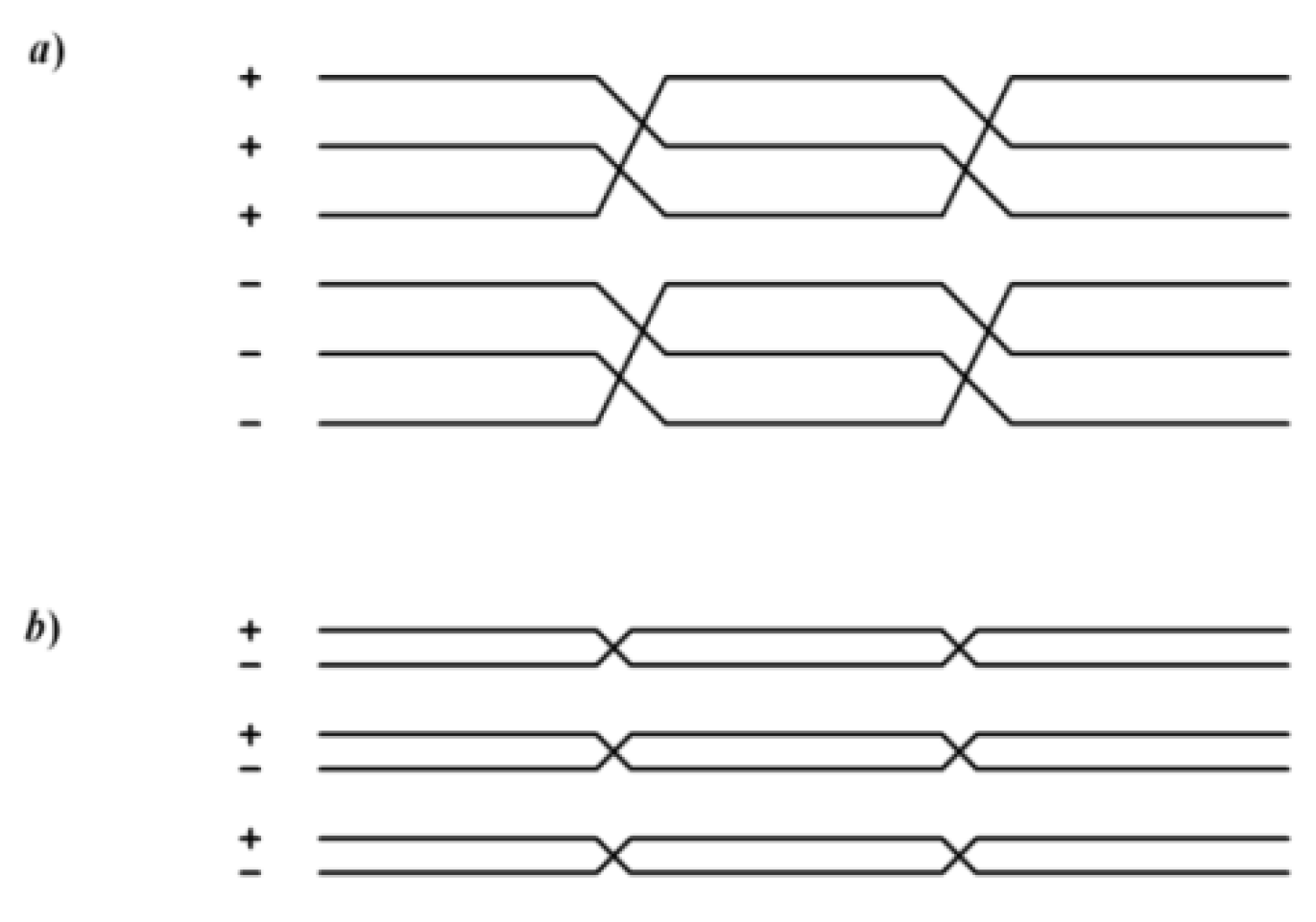
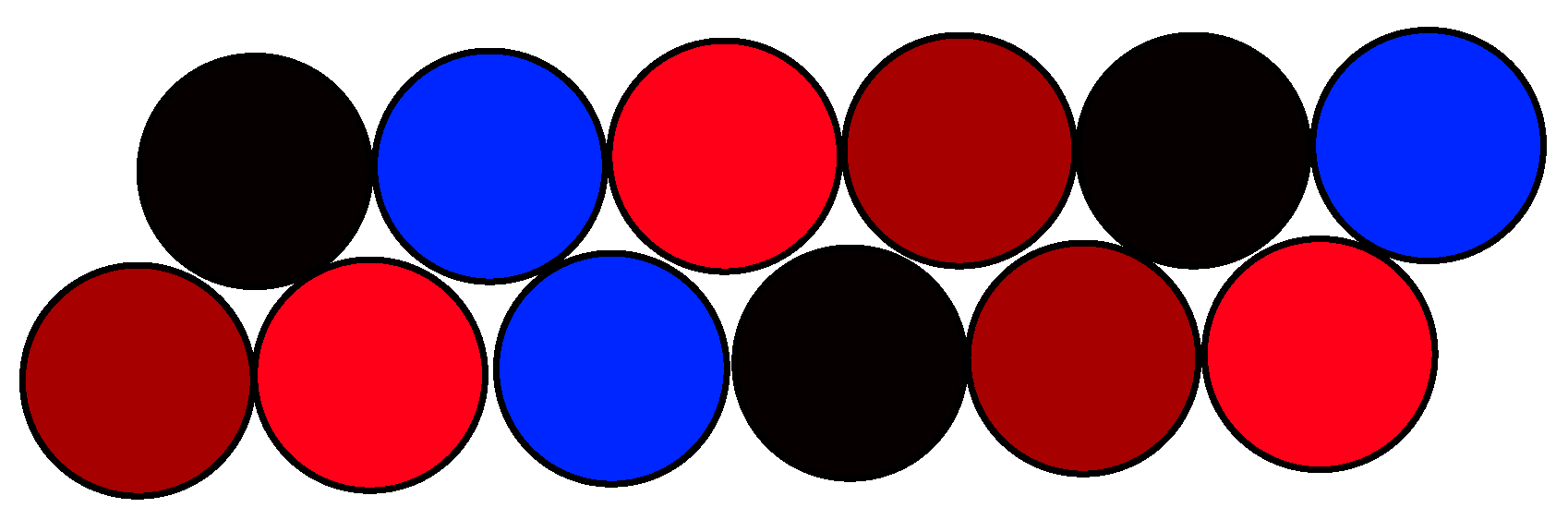
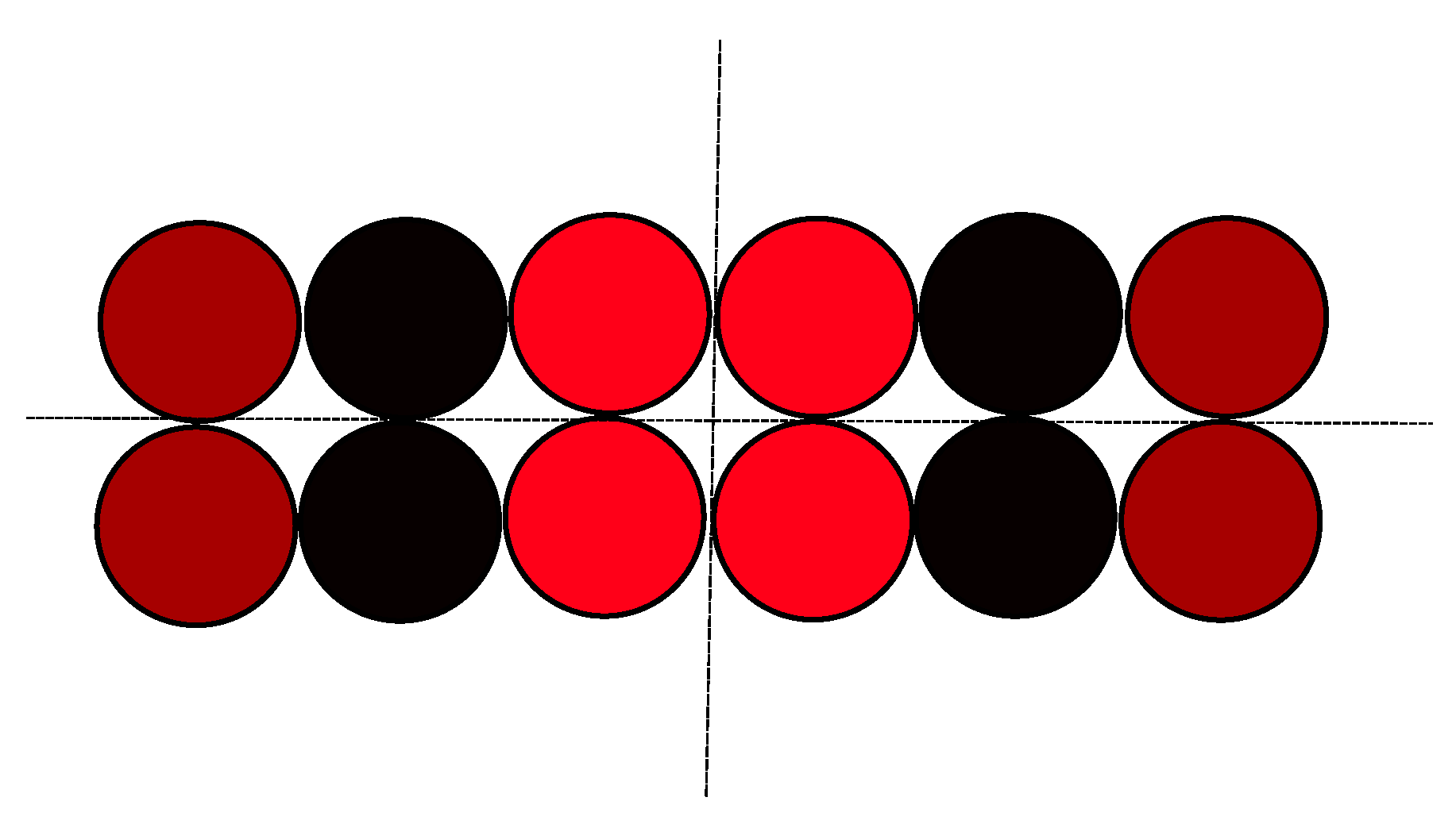
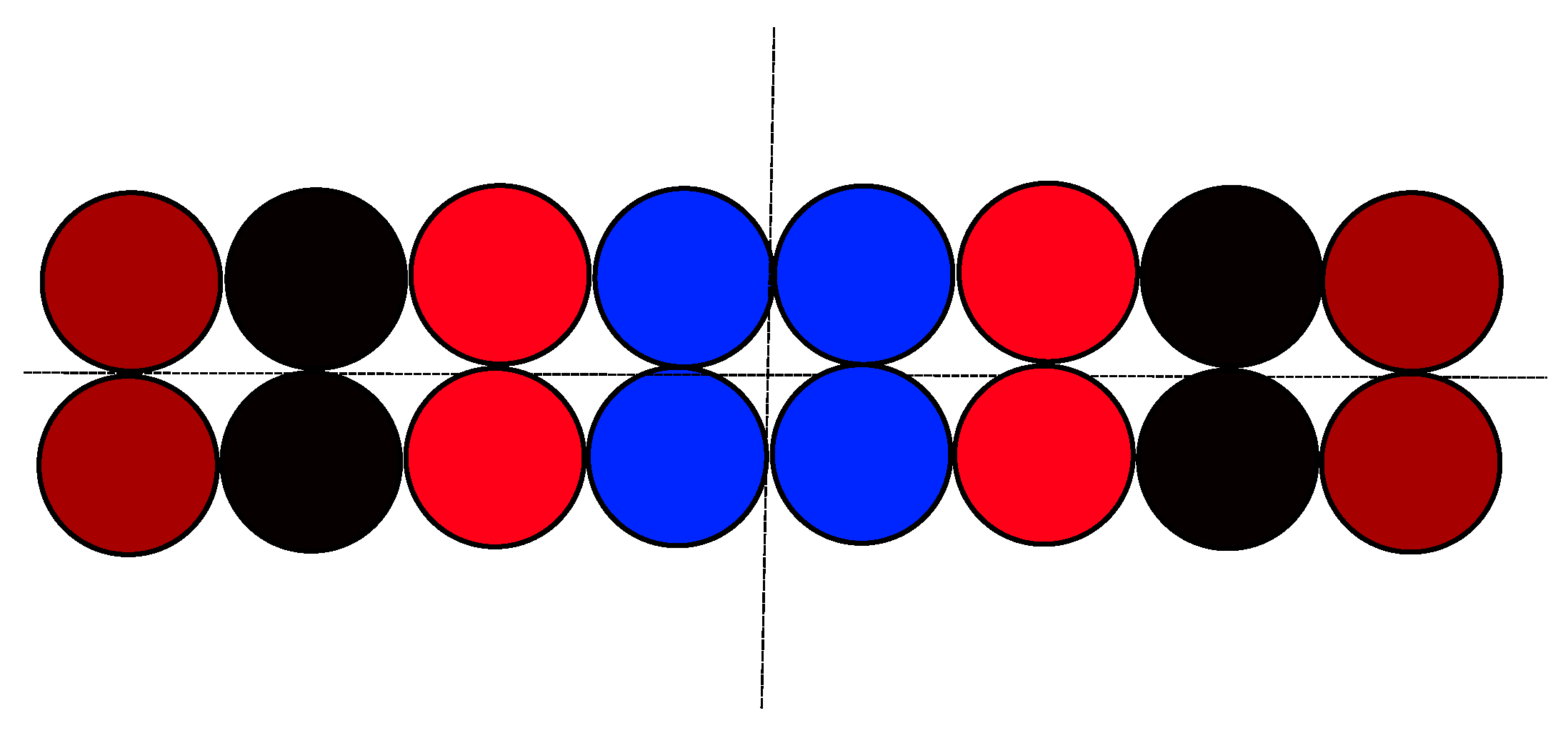
- separation of cables with complementary polarizations or of groups of cable pairs (Figure 7). Red circle—“hot” (phase) wire, blue circle—return wire.
- -
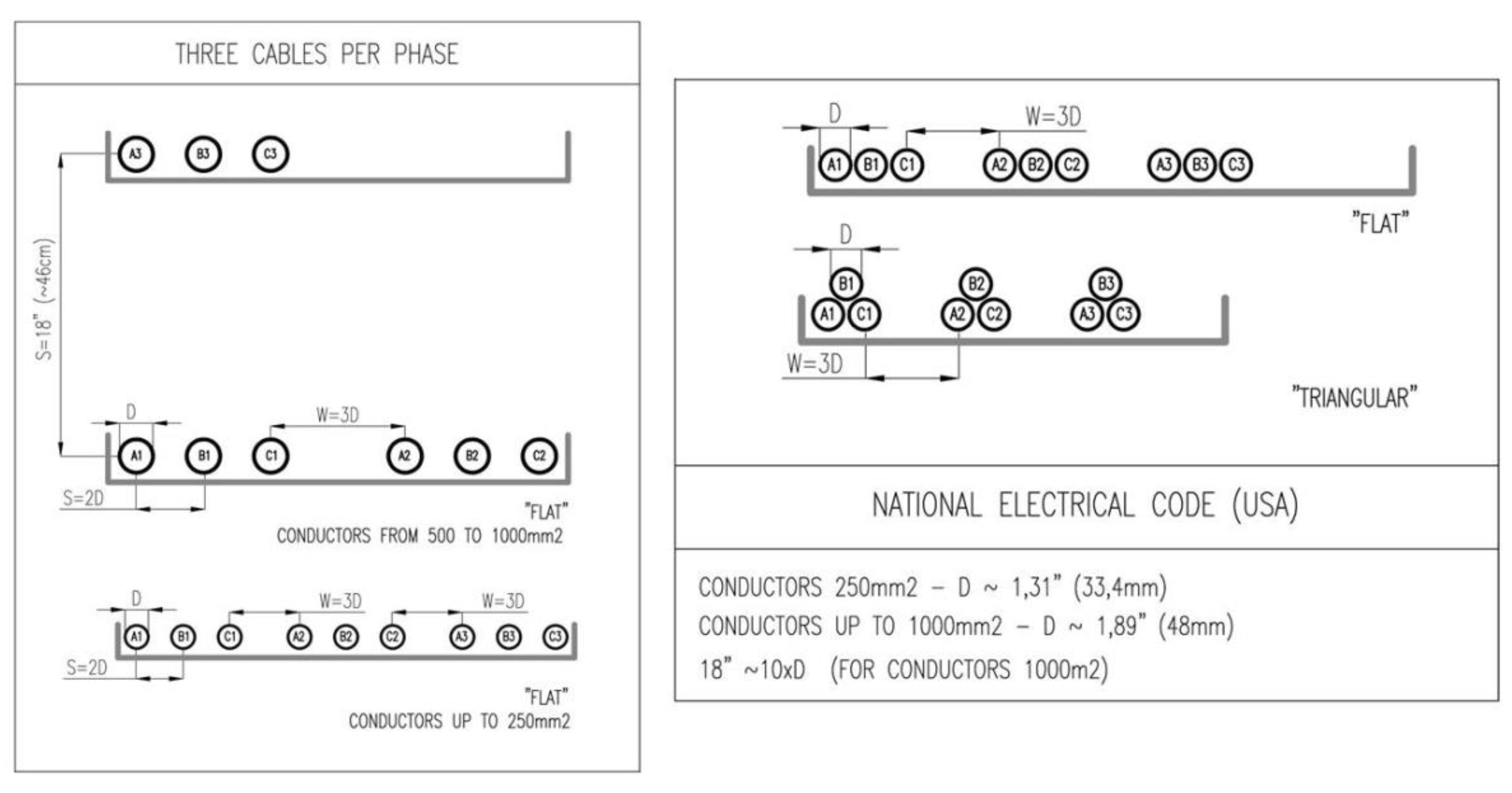
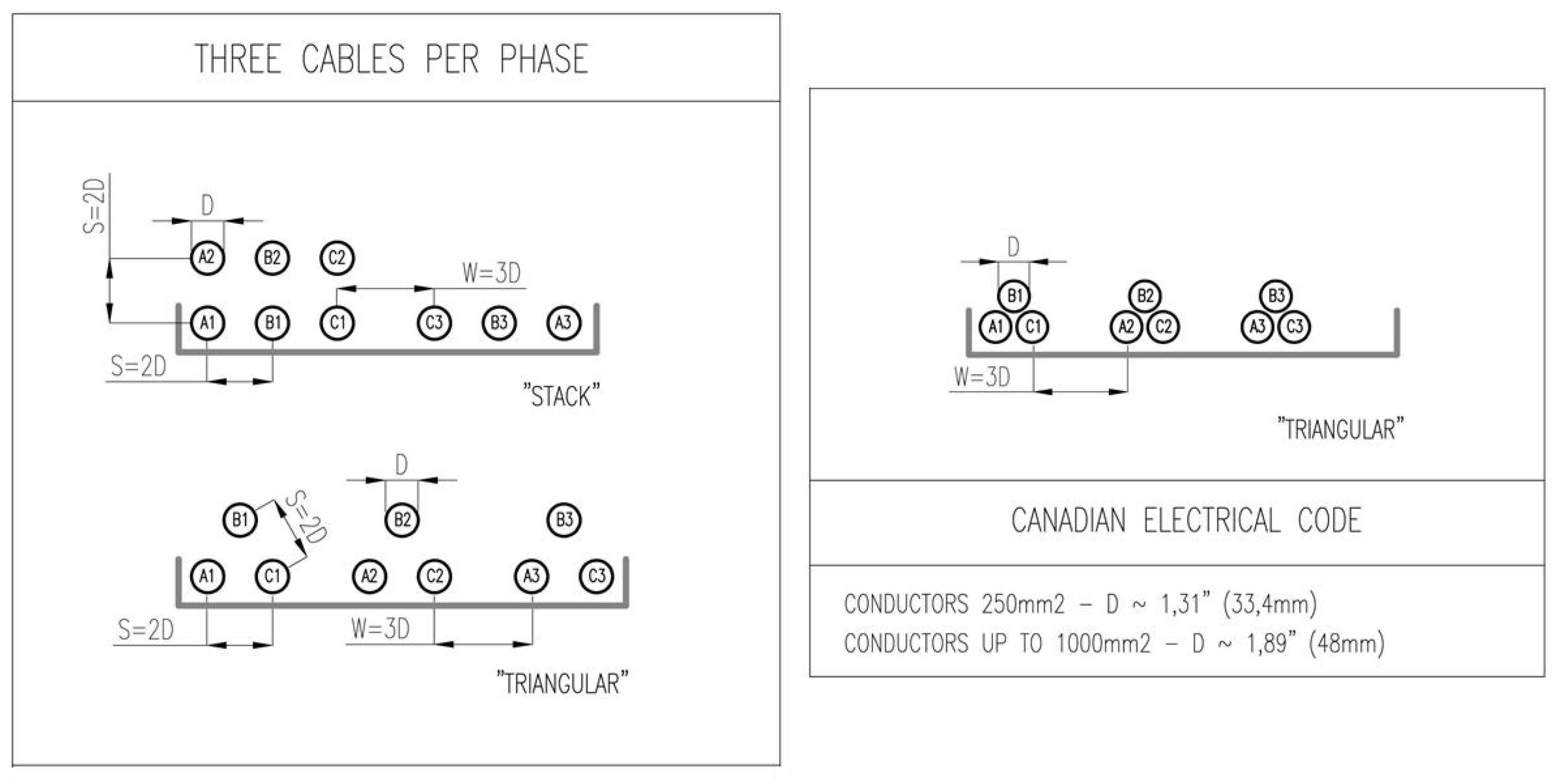
- Three strands per phase
- -
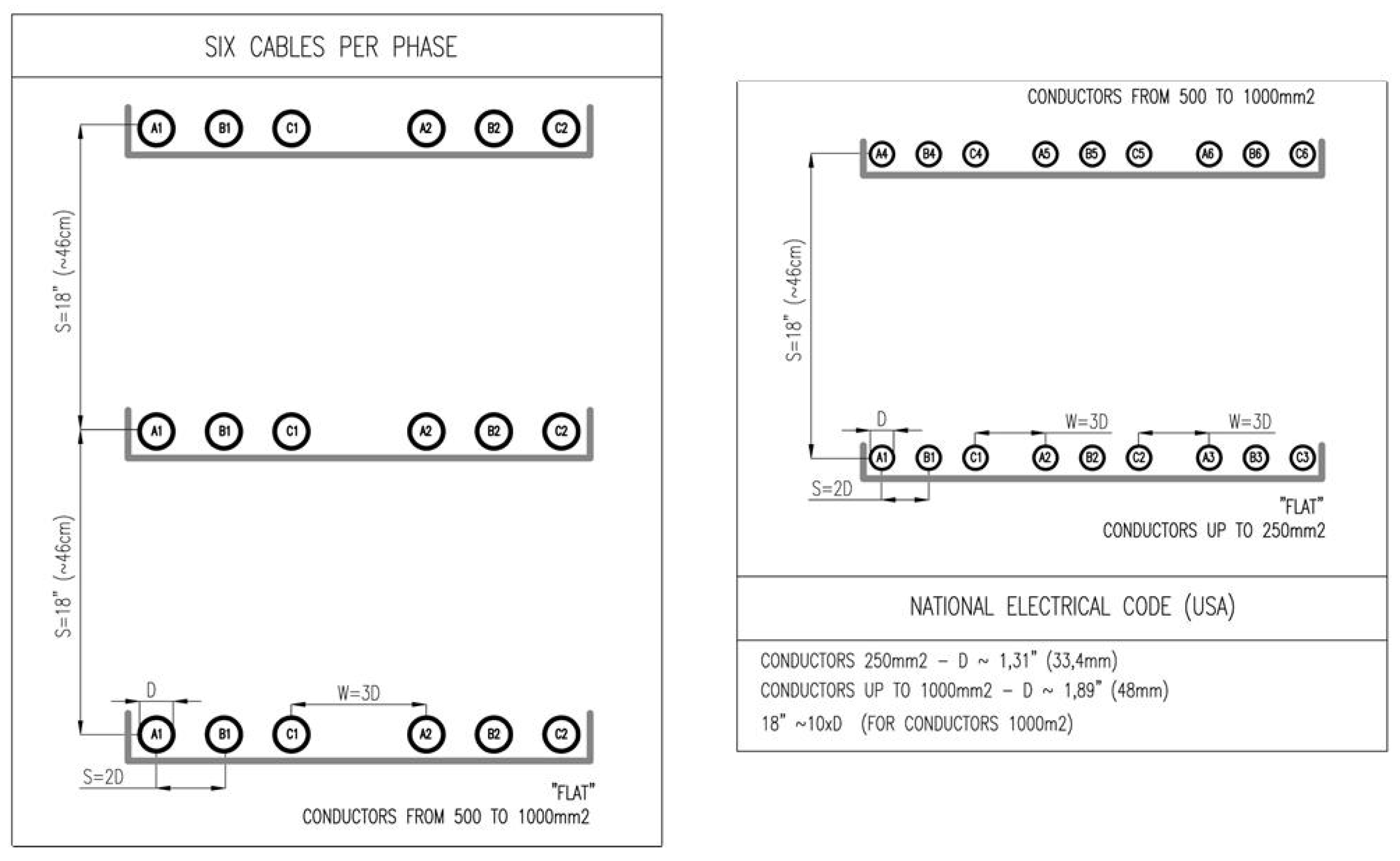
- Fours strands per phase
- -
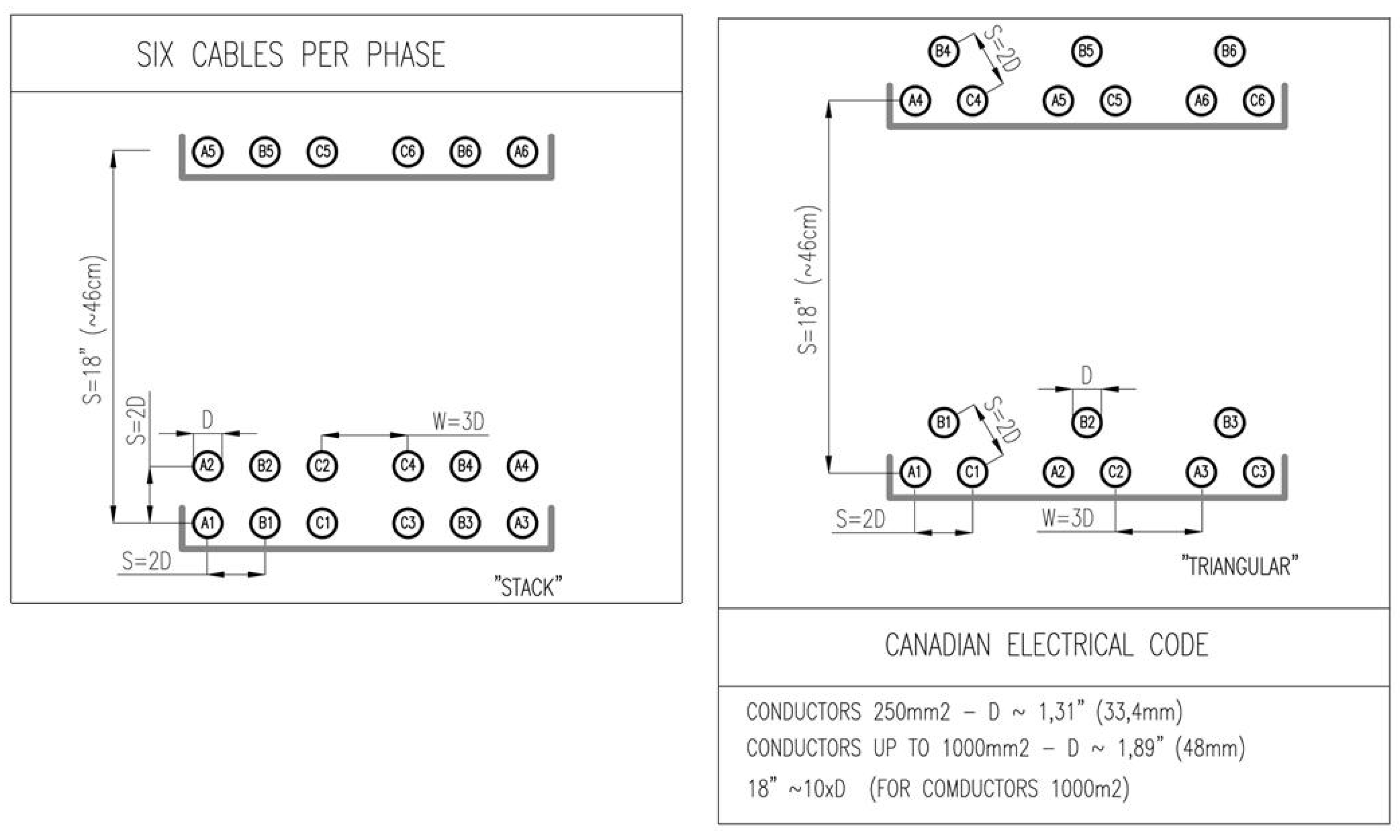
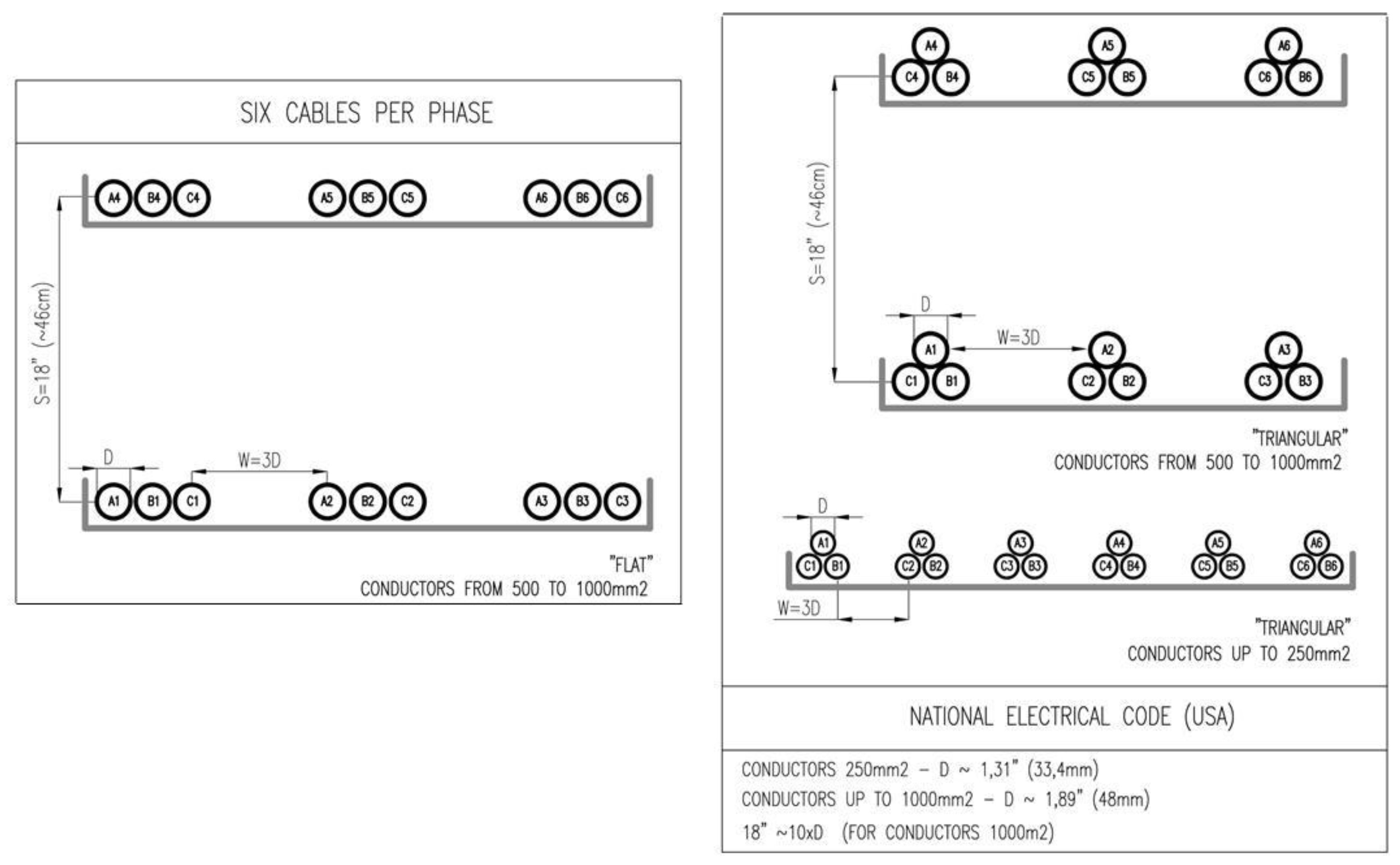
- Recommendations concerning spatial layouts in the North American and the Canadian standards
- the U.S. standards include flat configurations; such solutions are not used in Canada;
- the lumped triangular layout is used both in the U.S. and in Canada;
- the layout with strands lumped within a group (three phases close to each other, either in the flat or in the triangular configuration) may be perceived as three-phase equivalents of the recommended DC layouts, discussed previously;
- interesting conclusions may be arrived at when one analyzes the results illustrating the current nonuniformity for the lumped and dispersed triangular layouts (Table X in [20]). Setting the cables apart is used in practice in order to improve the heat exchange conditions. From the point of geometry, both layouts are equivalent, however, Wu has noticed that, paradoxically, the geometry with dispersed cables is worse, since the indicator takes a higher value (1.59 for the dispersed cables, 1.31 for the lumped cables). It is remarkable that phase C features the highest current asymmetry in both cases, which is most probably due to an additional effect related to phase rotation sequence;
- for six strands per phase, there are some layouts recommended by the U.S. standards, which are not in use in Canada (the cables dispersed in a nonuniform manner, placed on three shelves for wire diameter in the range of 500–1000 mm2, on two shelves for wire diameter up to 250 mm2). The first aforementioned configuration features a very balanced current distribution (Tables XI and XII in [20]). The values of nonuniformity indicator do not exceed 1.04.
- -
- Other cases of interest analyzed in the literature
- the case of supply of a textile factory in Greece [21]
- phase A
- phase B
- phase C
- phase A
- phase B
- phase C
- The case of Teatro Regio in Turin, Italy [15]
- Canova et al. have considered the optimal layout of cables using the Vector Immune System algorithm [22]. The case considered was six strands per phase, lack of neutral wire. The configuration indicated by the authors as the optimal one, featuring both the most uniform current partition and the lowest value of magnetic induction, was:BCAACBBCAACBBCAACB
- Lee has considered a similar case (six wires per phase, two shelves), but with neutral wires [18]. Let us assume that the origin of the coordinate system was placed in the center of the leftmost downward wire (phase A) and that the distance was equal to unity.ABCNNCBANABCABCNNCBANABC
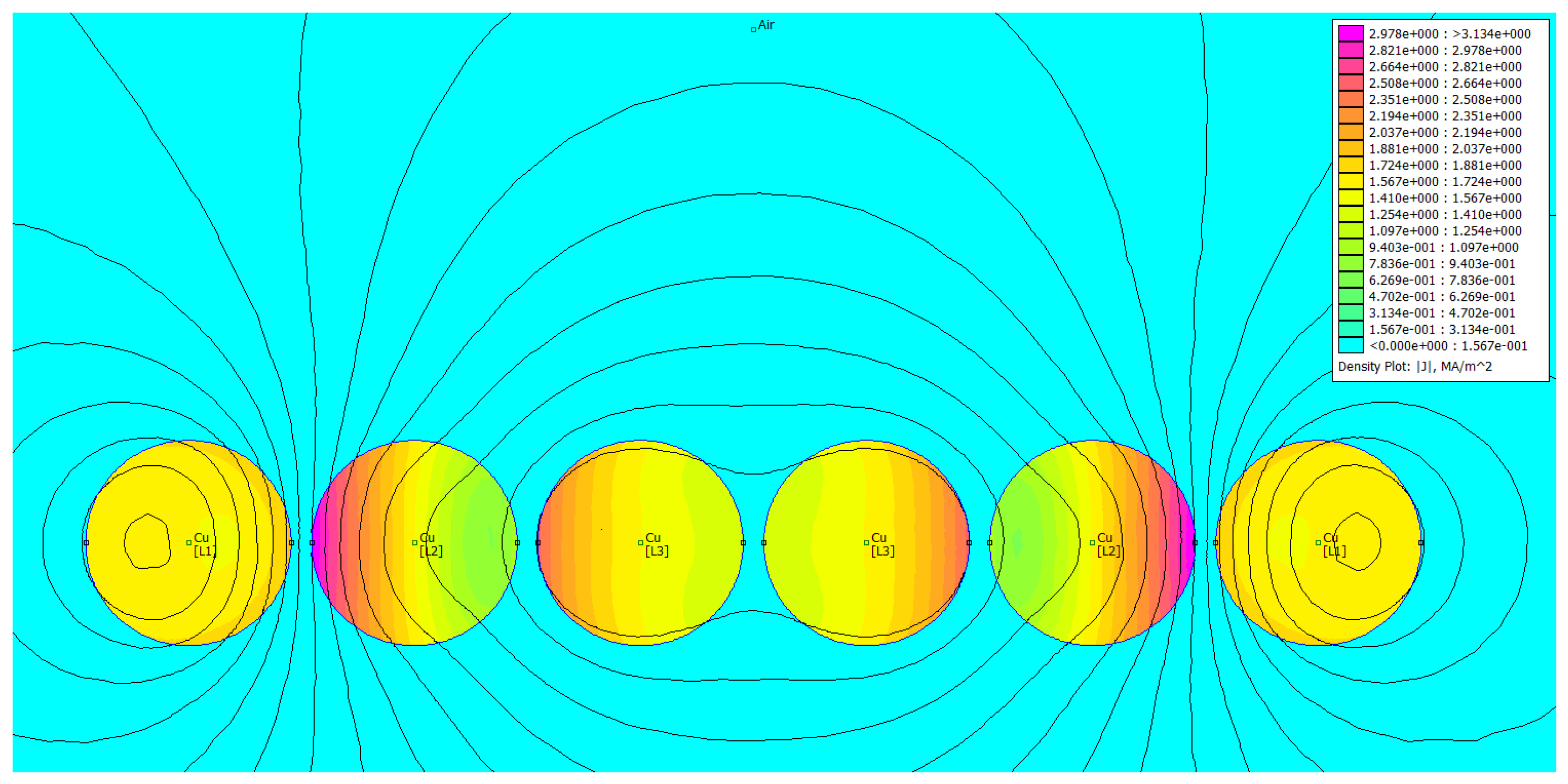
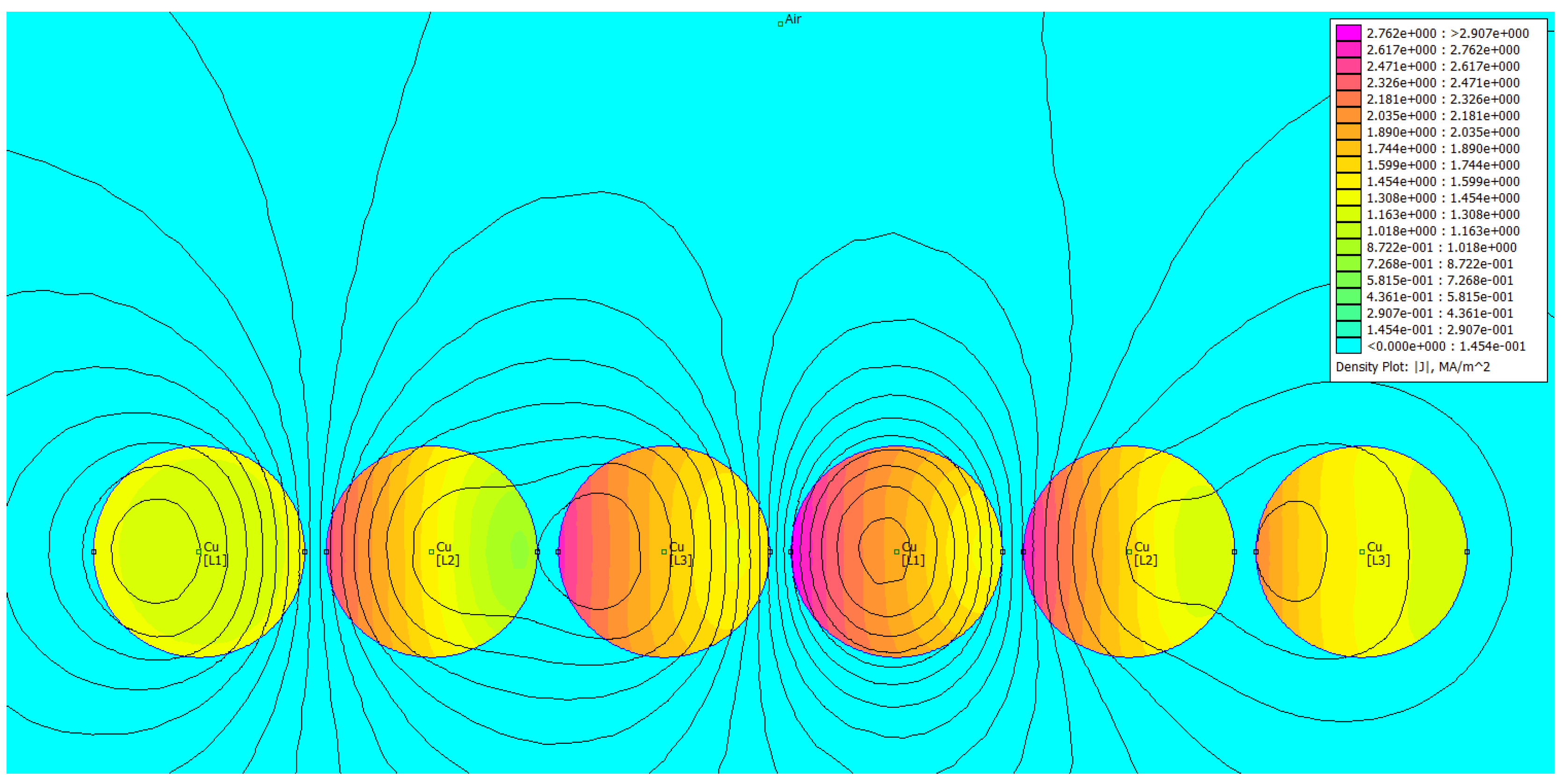
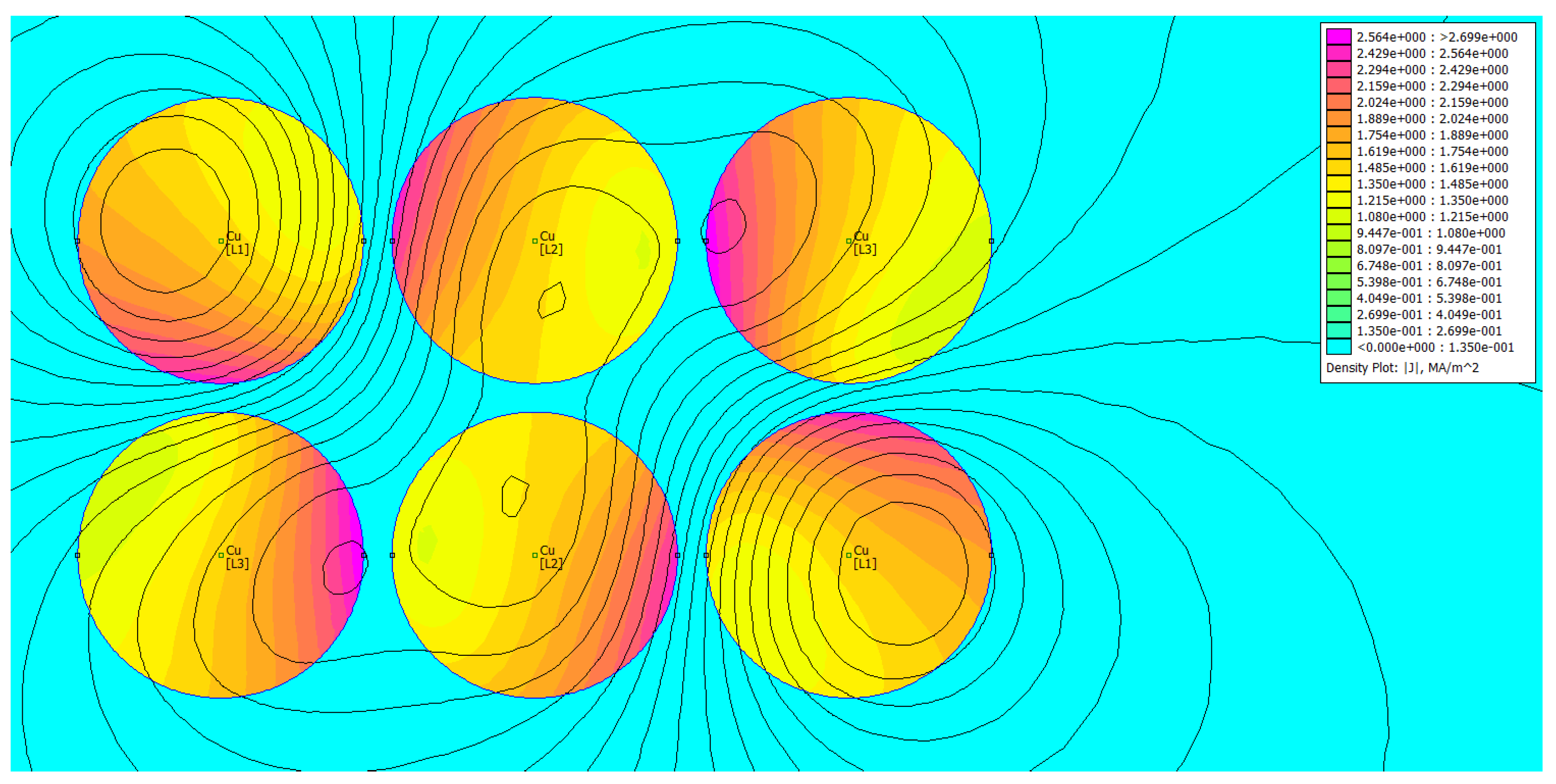
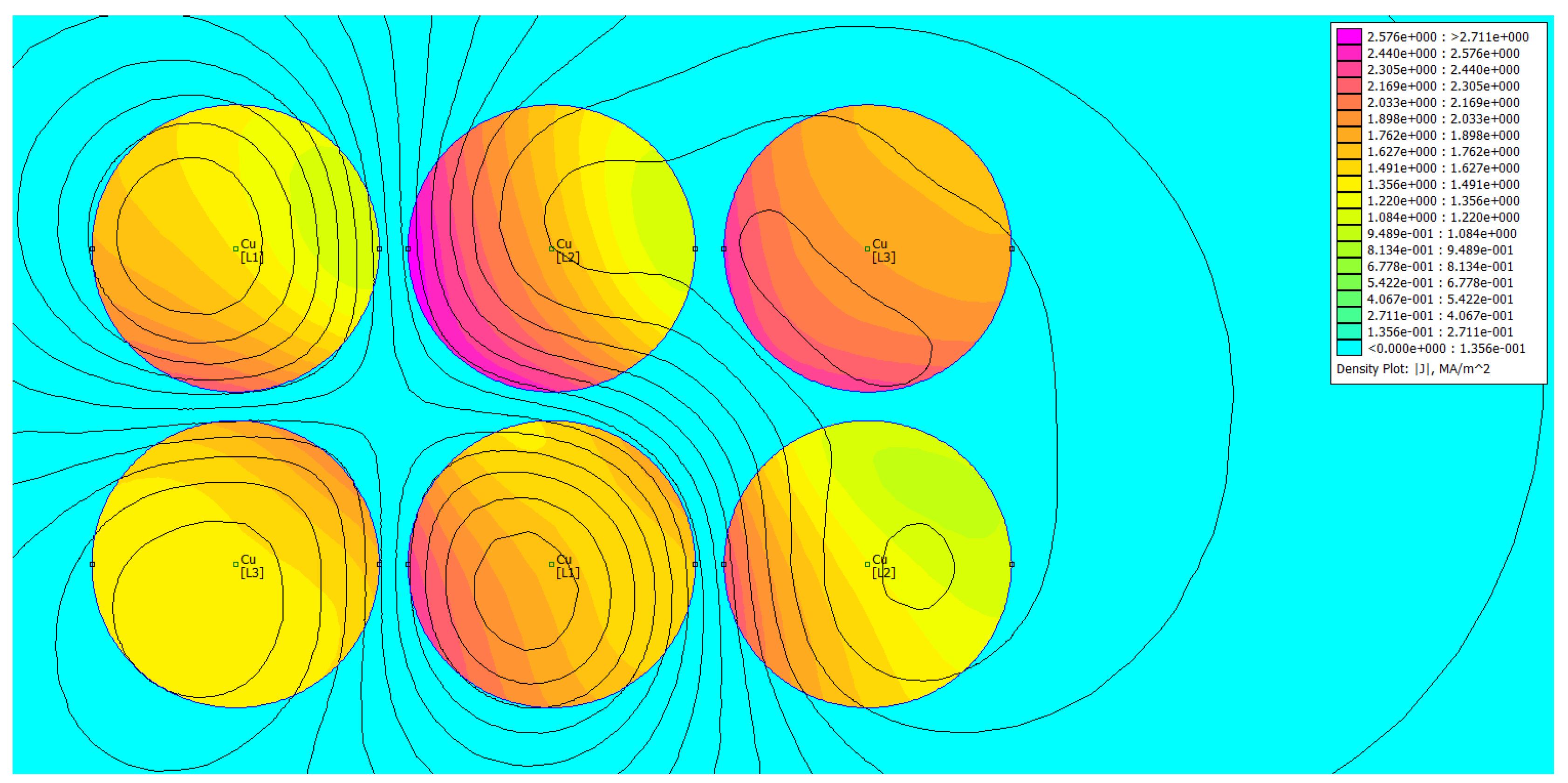
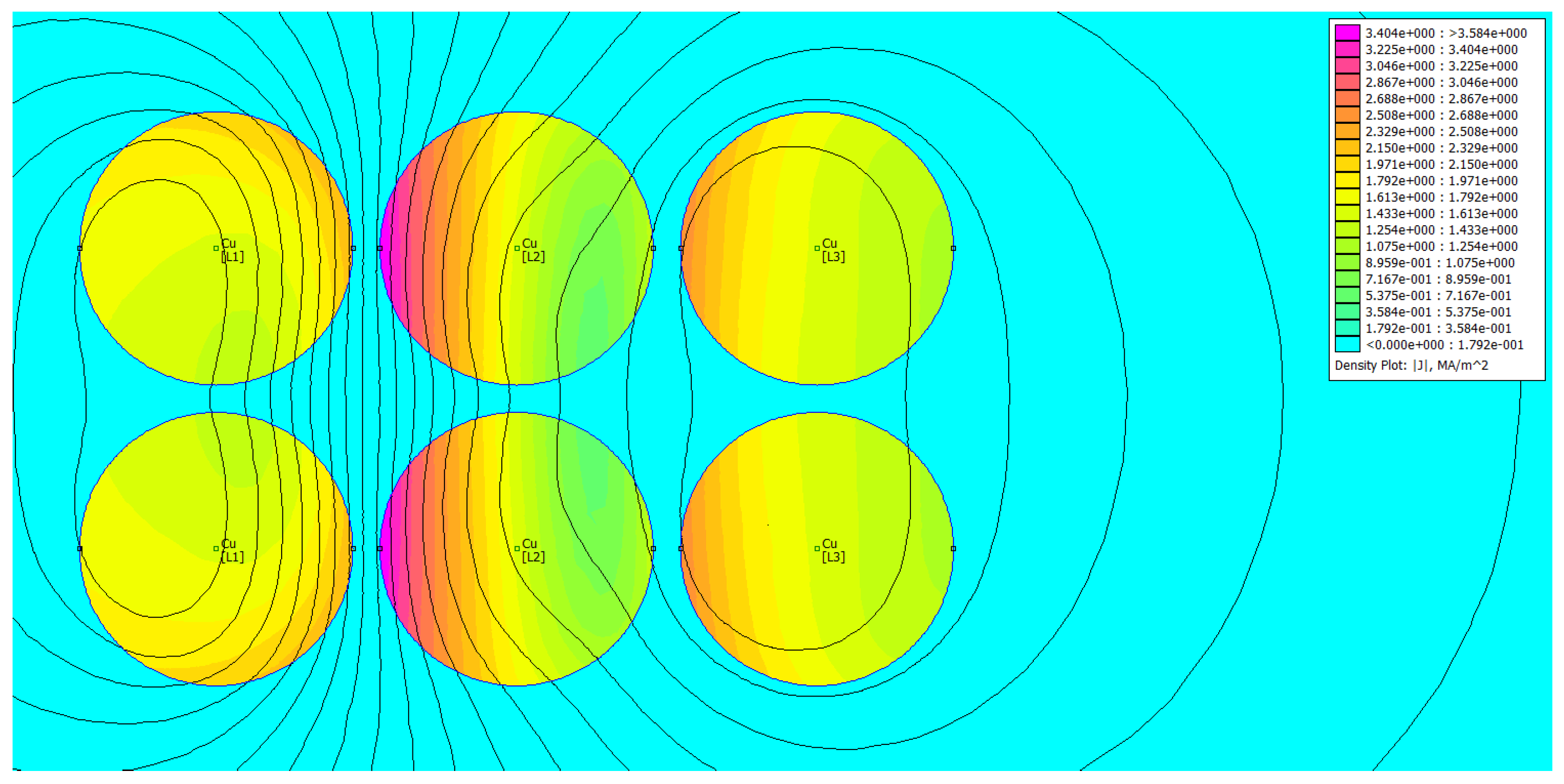
4. Verification of the Proposed Criterion for Optimal Current Distribution Using FEM
5. Conclusions
- for the single-phase excitation case, a description of experimental stand was presented and several cable configurations were considered;
- we suggested to avail of MATLAB routines related to nonoriented graphs, in particular the adjacency function, in order to simplify the analysis;
- a simplified relationship for determination of current distribution based on the distance of the cable to its neighbors was proposed;
- several practical solutions found in the literature, including recommendations of the National U.S. Code and Canadian standard, were analyzed;
- a common feature of all optimal configurations was found, namely the barycenter locations for individual phases should overlap in order to provide uniform current distribution in the strands;
- a FEM-based verification of the proposed criterion was carried out for simple cases using the freeware FEMM software.
Author Contributions
Funding
Conflicts of Interest
References
- Neher, J.; McGrath, M. The calculation of the temperature rise and load capability of cable systems. AIEE Trans. Part III 1957, 76, 752–757. [Google Scholar] [CrossRef]
- Murgatroyd, P.N. Calculation of proximity losses in multistranded conductor bunches. IEE Proc. 1989, 126, 115–120. [Google Scholar] [CrossRef]
- Dawson, F.P.; Jain, P.K. A simplified approach to calculating current distribution in paralleled power buses. IEEE Trans. Magn. 1990, 26, 971–974. [Google Scholar] [CrossRef]
- Petty, K.A. Calculation of current division in parallel single-conductor power cables for generating station applications. IEEE Trans. Power. Deliv. 1991, 6, 479–483. [Google Scholar] [CrossRef]
- Ghandakly, A.A.; Curran, R.L.; Collins, G.B. Ampacity ratings of bundled cables for heavy current applications. IEEE Trans. Ind. Appl. 1994, 30, 233–238. [Google Scholar] [CrossRef]
- Sellers, S.M.; Black, W.Z. Refinements to the Neher-McGrath model for calculating the ampacity of underground cables. IEEE Trans. Power Del. 1996, 11, 12–30. [Google Scholar] [CrossRef]
- Du, Y.; Burnett, J. Current distribution in single-core cables connected in parallel. IEE Proc.-Gener. Transm. Distrib. 2001, 148, 406–412. [Google Scholar] [CrossRef]
- Anders, G.J. Rating of Electric Power Cables in Unfavorable Thermal Environment; J. Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Xiong, L.; Chen, Y.; Jiao, Y.; Wang, J.; Hu, X. Study on the Effect of Cable Group Laying Mode on Temperature Field Distribution and Cable Ampacity. Energies 2019, 12, 3397. [Google Scholar] [CrossRef]
- Zhu, W.W.; Zhao, Y.F.; Han, Z.Z.; Wang, X.B.; Wang, Y.F.; Liu, G.; Xie, Y.; Zhu, N.X. Thermal Effect of Different Laying Modes on Cross-Linked Polyethylene (XLPE) Insulation and a New Estimation on Cable Ampacity. Energies 2019, 12, 2994. [Google Scholar] [CrossRef]
- Rasoulpoor, M.; Mirzaie, M.; Mirimani, S.M. Calculation of losses and ampacity derating in medium-voltage cables under harmonic load currents using finite element method. Int. Trans. Electr. Energ. Syst. 2017, 27, e2267. [Google Scholar] [CrossRef]
- Jabłoński, P.; Szczegielniak, T.; Kusiak, D.; Piątek, Z. Analytical–Numerical Solution for the Skin and Proximity Effects in Two Parallel Round Conductors. Energies 2019, 12, 3584. [Google Scholar] [CrossRef]
- Čiegis, R.; Jankevičiūtė, G.; Bugajev, A.; Tumanova, N. Numerical simulation of heat transfer in underground electrical cables. In Progress in Industrial Mathematics at ECMI 2014, Mathematics in Industry 22; Russo, G., Vincenzo, C., Giuseppe, N., Vittorio, R., Eds.; Spring Nature: Cham, Switzerland, 2014; pp. 1111–1119. [Google Scholar] [CrossRef]
- Desmet, J.; Vanalme, G.; Belmans, R.; Van Dommelen, D. Simulation of Losses in LV Cables due to Nonlinear Loads. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; Volumes 1–10, pp. 785–3182683. Available online: http://hdl.handle.net/1854/LU-3182683 (accessed on 1 September 2020).
- Freschi, F.; Tartaglia, M. Power lines made of many parallel single-core cables: A case study. IEEE Trans. Ind. Appl. 2013, 49, 1744–1750. [Google Scholar] [CrossRef]
- Borowik, L.; Cywiński, A. Current-carrying capacity parallel single-core LV cable. Przegl. Elektrotechn. 2016, 1, 71–74. [Google Scholar] [CrossRef][Green Version]
- Mathworks. MATLAB Toolbox for Graph and Network Algorithms; Mathworks: Natick, MA, USA, 2015. [Google Scholar]
- Lee, S.-Y. A cable configuration technique for the balance of current distribution in parallel cables. J. Marine Sci. Techn. 2010, 18, 290–297. [Google Scholar]
- Jabłoński, P.; Kusiak, D.; Szczegielniak, T.; Piątek, Z. Reduction of impedance matrices of power busducts. Przegl. Elektrotechn. 2016, 12, 49–52. [Google Scholar] [CrossRef]
- Wu, A. Single-conductor cables in parallel. IEEE Trans. Ind. Appl. 1984, 20, 377–395. [Google Scholar] [CrossRef]
- Gouramanis, K.; Demoulias, C.; Labridis, D.; Dokopoulos, P. Distribution of non-sinusoidal currents in parallel conductors used in three-phase four-wire networks. Electr. Power Syst. Res. 2009, 79, 766–780. [Google Scholar] [CrossRef]
- Canova, A.; Freschi, F.; Tartaglia, M. Multiobjective optimization of parallel cable layout. IEEE Trans. Magn. 2007, 43, 3914–3920. [Google Scholar] [CrossRef]
- Meeker, D. Available online: http://www.femm.info (accessed on 1 September 2020).


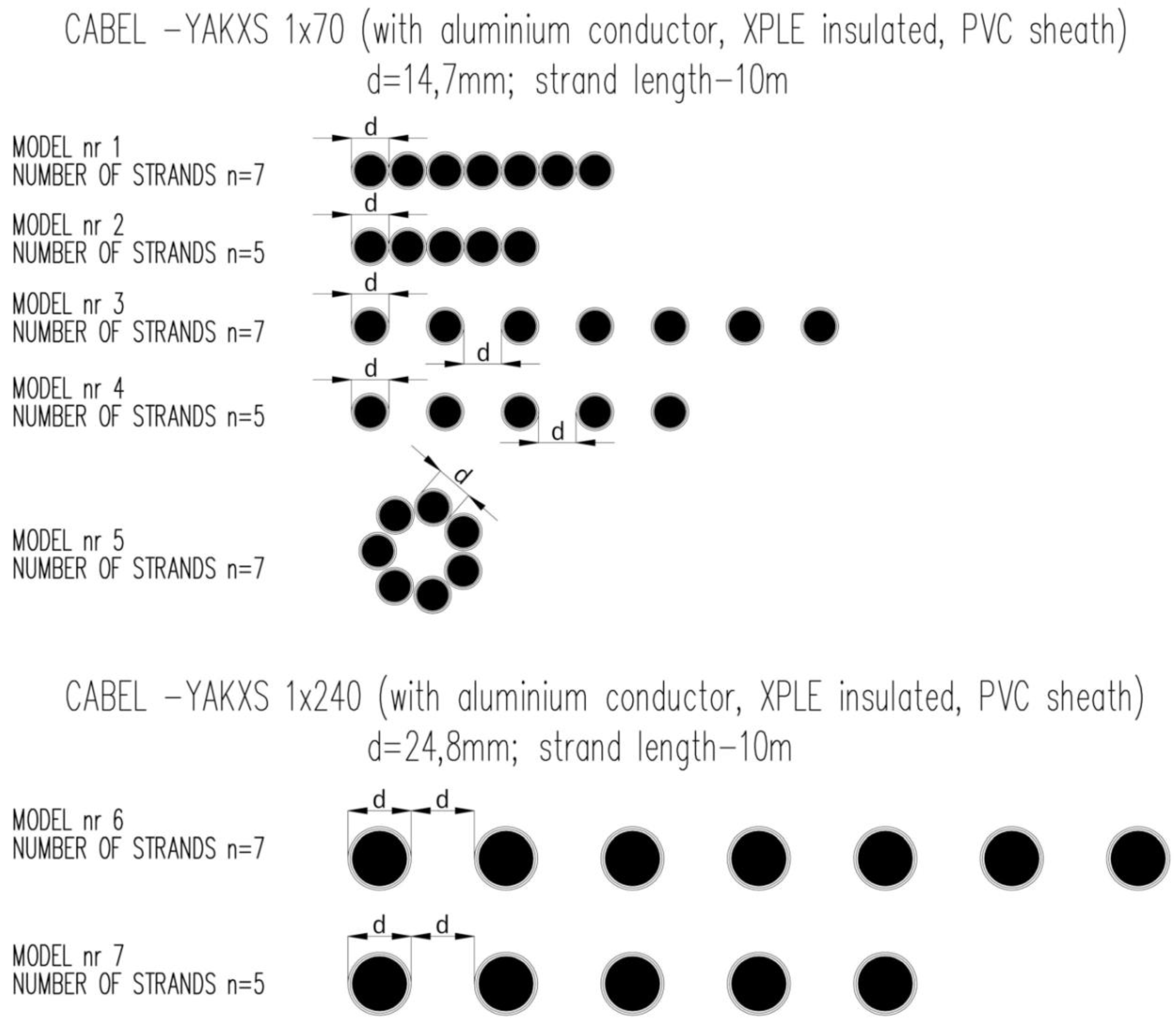












| YAKY 1 × 70 | YAKY 1 × 240 | ||||||
|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M4 | M5 | M6 | M7 | |
| S1 | 116 A | 138 A | 94 A | 104 A | 66 A | 128 A | 148 A |
| S2 | 104 A | 128 A | 84 A | 94 A | 66 A | 106 A | 126 A |
| S3 | 98 A | 126 A | 76 A | 86 A | 66 A | 76 A | 86 A |
| S4 | 92 A | 128 A | 70 A | 92 A | 66 A | 67 A | 122 A |
| S5 | 98 A | 140 A | 72 A | 104 A | 66 A | 76 A | 146 A |
| S6 | 102 A | 84 A | 68 A | 108 A | |||
| S7 | 116 A | 106 A | 66 A | 128 A | |||
| EXCITATION | 726 A | 660 A | 586 A | 480 A | 465 A | 689 A | 628 A |
| PHYSICAL MODEL | |||||||
|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M4 | M5 | M6 | M7 | |
| CAS | 1.26 | 1.11 | 1.51 | 1.20 | 1.00 | 1.91 | 1.69 |
| CAS for 200 A | 1.28 | 1.13 | 1.50 | 1.13 | 1.00 | 1.50 | 1.50 |
| Configuration | Percentage Error for Current | ||||||
|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | |
| M1 | 17.2 | 2.0 | −10.7 | −14.3 | −10.7 | 2.0 | 17.2 |
| M2 | 19.0 | −7.9 | −21.0 | −10.3 | 16.3 | ||
| M3 | −16.9 | −0.3 | −10.5 | −10.3 | −5.5 | −0.3 | 3.7 |
| M4 | 19.0 | −7.9 | −21.0 | −10.3 | 16.3 | ||
| M5 | 0 | 0 | 0 | 0 | 0 | −3.0 | 0 |
| M6 | 0.9 | −7.2 | 5.2 | 10.2 | 5.2 | −8.9 | 0.9 |
| M7 | 6.0 | −12.8 | 9.5 | −9.9 | 7.5 | ||
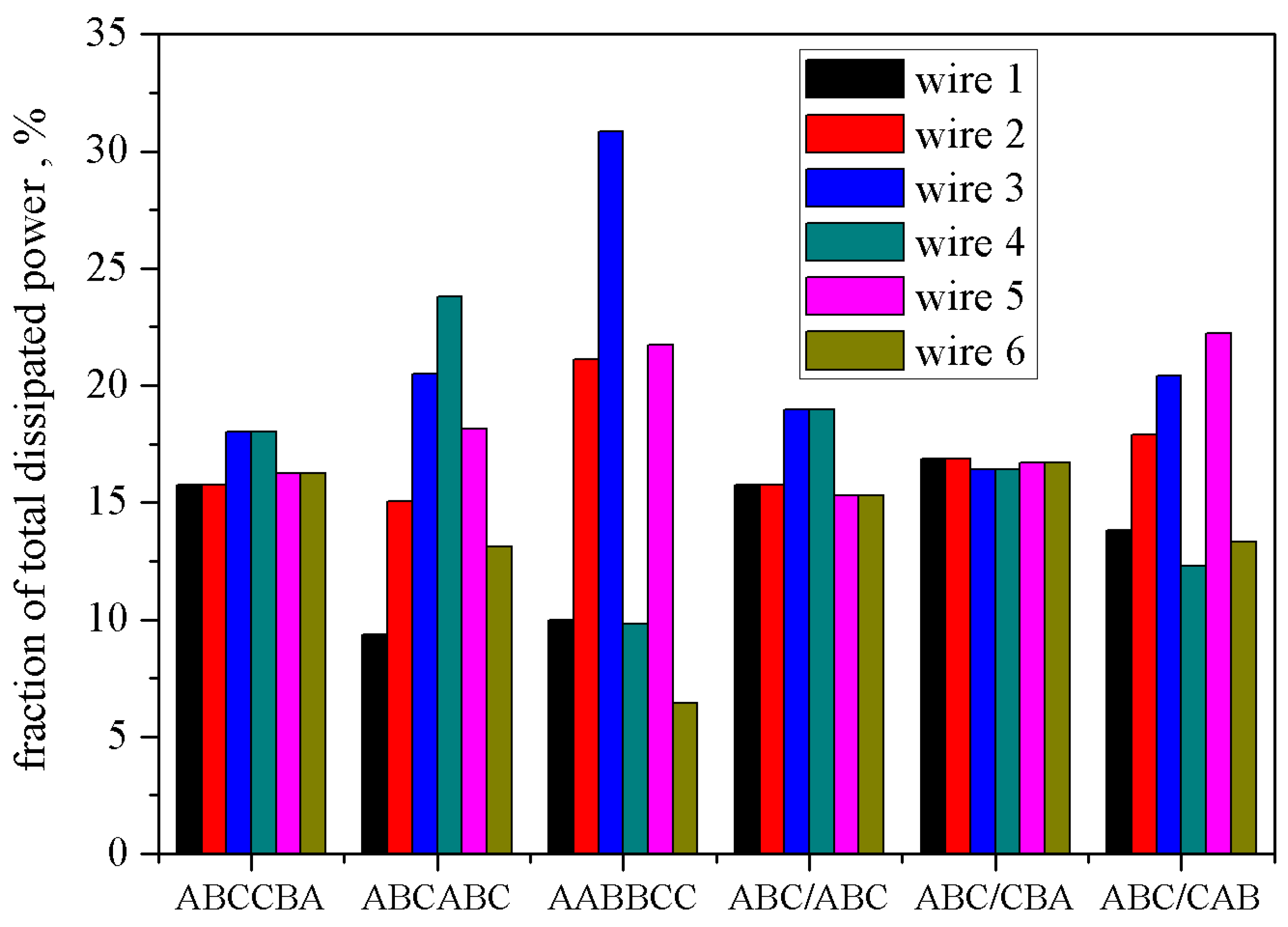
| Configuration | Phase A | Phase B | Phase C | |||
|---|---|---|---|---|---|---|
| A1 | A2 | B1 | B2 | C1 | C2 | |
| ABCCBA | 50% | 50% | 50% | 50% | 50% | 50% |
| ABCABC | 38% | 62% | 48% | 53% | 57% | 46% |
| AABBCC | 46% | 61% | 78% | 37% | 64% | 36% |
| Configuration | Phase A | Phase B | Phase C | |||
|---|---|---|---|---|---|---|
| A1 | A2 | B1 | B2 | C1 | C2 | |
| ABC/ABC | 50% | 50% | 50% | 50% | 50% | 50% |
| ABC/CBA | 50% | 50% | 50% | 50% | 50% | 50% |
| ABC/CAB | 47% | 54% | 57% | 43% | 60% | 46% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cywiński, A.; Chwastek, K.; Kusiak, D.; Jabłoński, P. Optimization of Spatial Configuration of Multistrand Cable Lines. Energies 2020, 13, 5923. https://doi.org/10.3390/en13225923
Cywiński A, Chwastek K, Kusiak D, Jabłoński P. Optimization of Spatial Configuration of Multistrand Cable Lines. Energies. 2020; 13(22):5923. https://doi.org/10.3390/en13225923
Chicago/Turabian StyleCywiński, Artur, Krzysztof Chwastek, Dariusz Kusiak, and Paweł Jabłoński. 2020. "Optimization of Spatial Configuration of Multistrand Cable Lines" Energies 13, no. 22: 5923. https://doi.org/10.3390/en13225923
APA StyleCywiński, A., Chwastek, K., Kusiak, D., & Jabłoński, P. (2020). Optimization of Spatial Configuration of Multistrand Cable Lines. Energies, 13(22), 5923. https://doi.org/10.3390/en13225923








