Estimation for Battery State of Charge Based on Temperature Effect and Fractional Extended Kalman Filter
Abstract
:1. Introduction
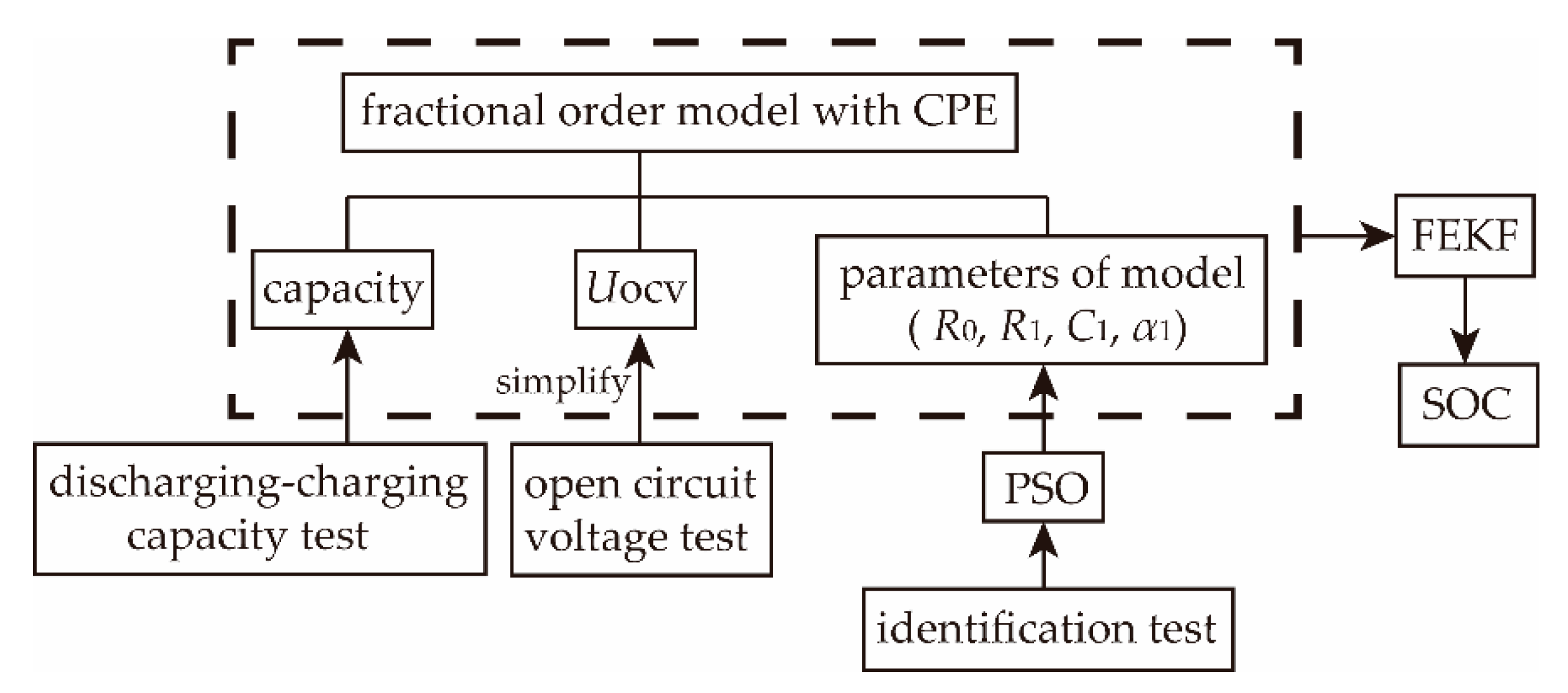
2. Fractional Order Model
2.1. Fractional Order Theory
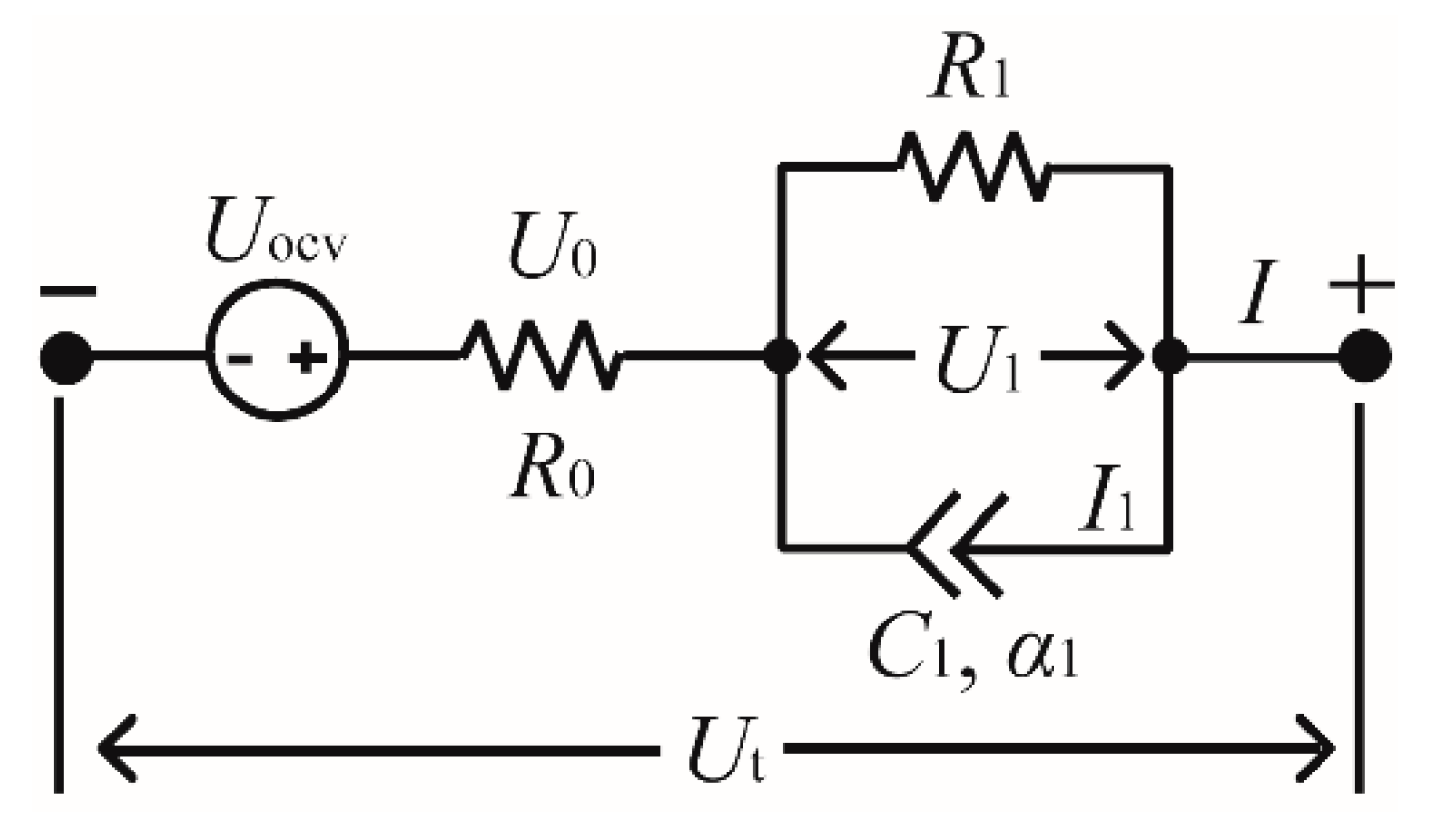
2.2. Fractional Equivalent Circuit Model
- ; ;
- ; ; ;
- ; ;
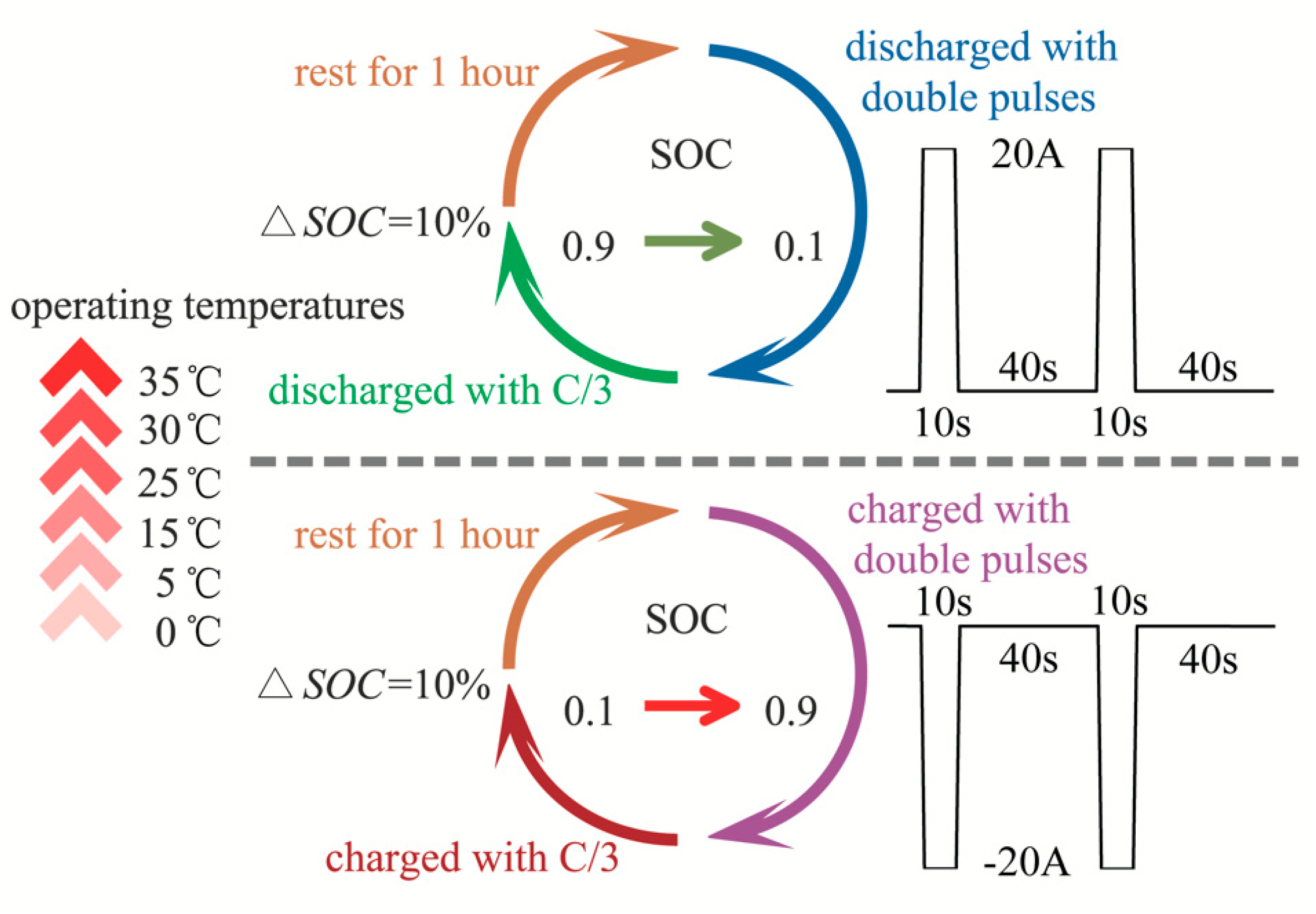
3. Battery Characteristics under Different Influential Factors
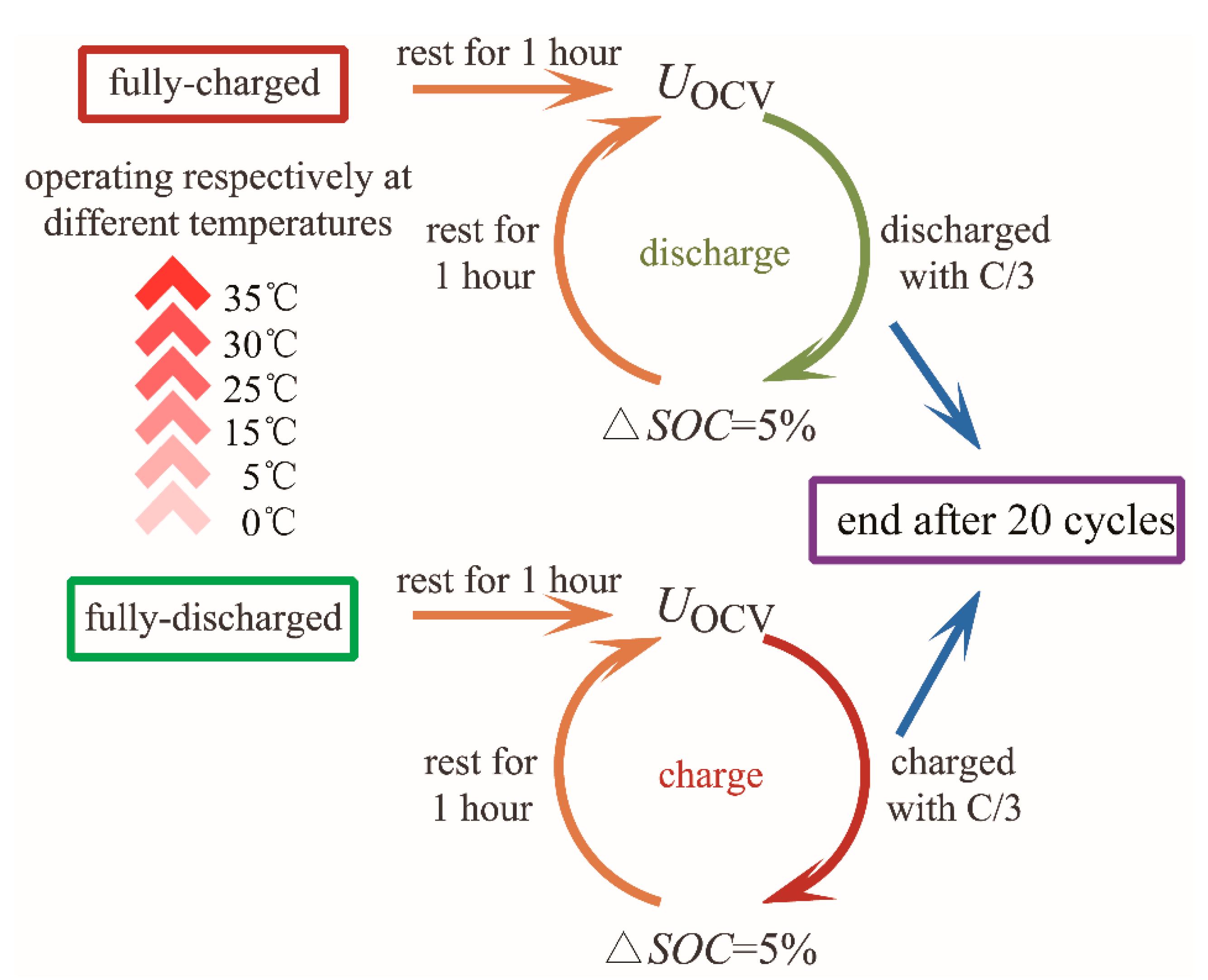
3.1. Characteristics of Battery Capacity
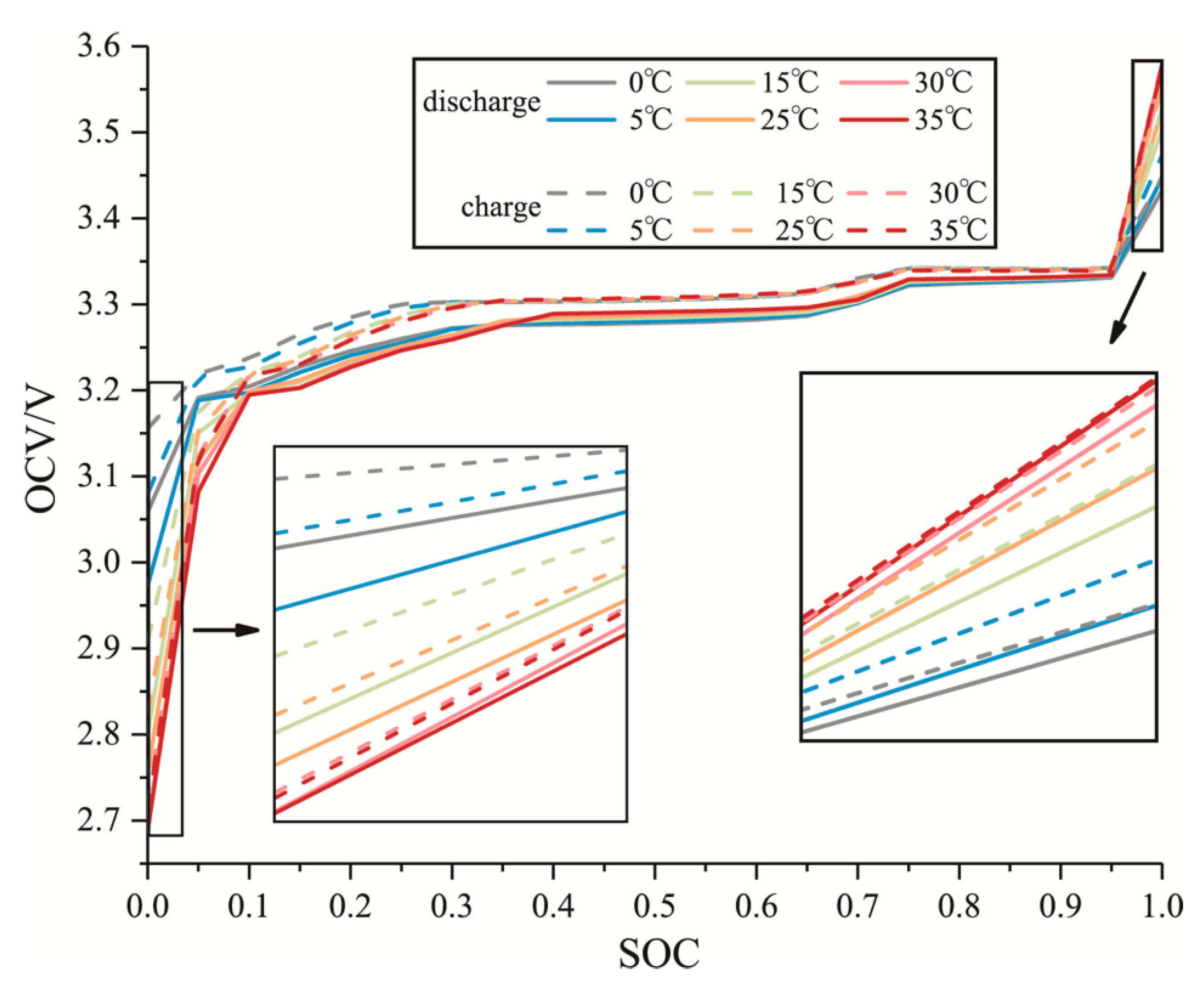
3.2. Characteristics of Open Circuit Voltage
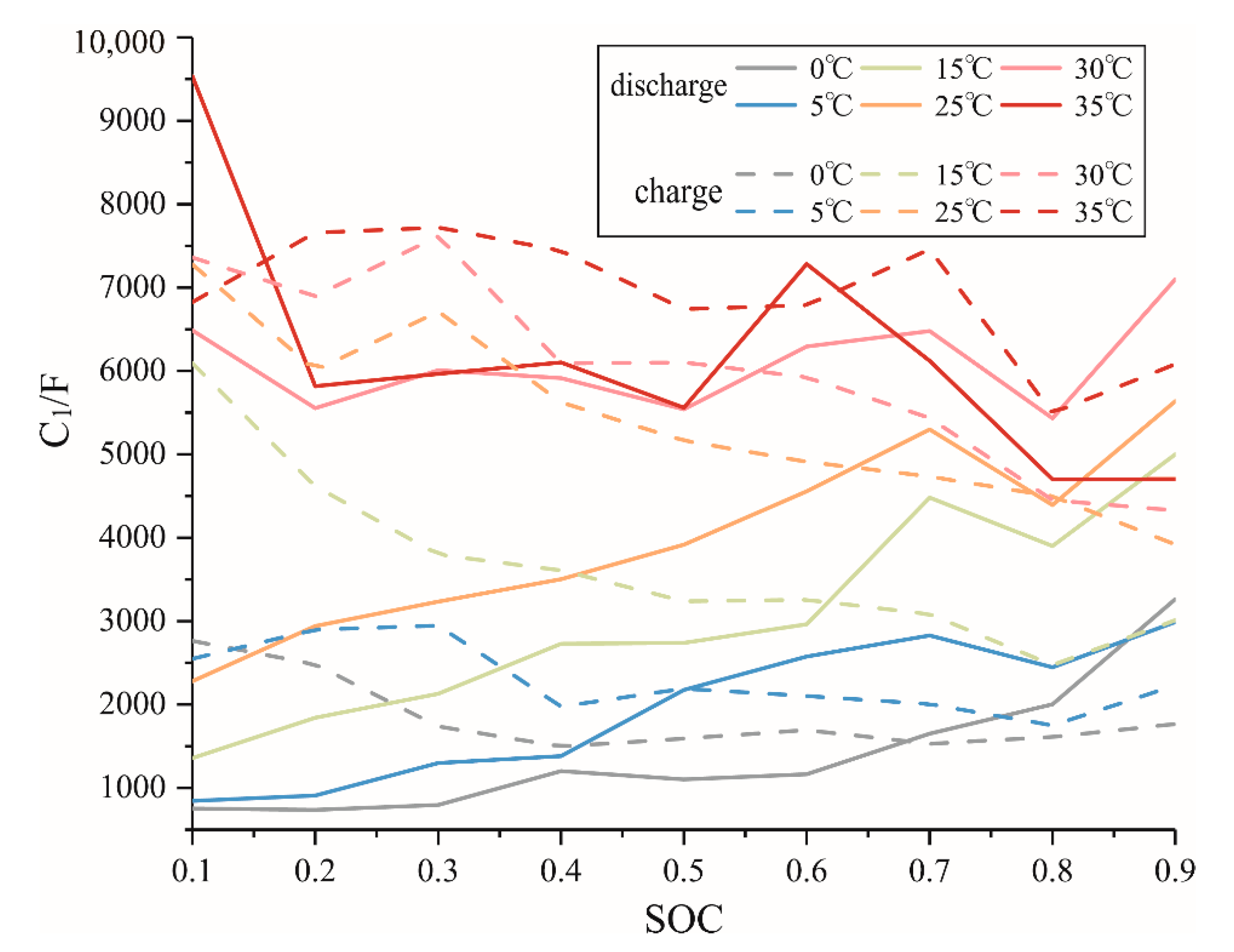
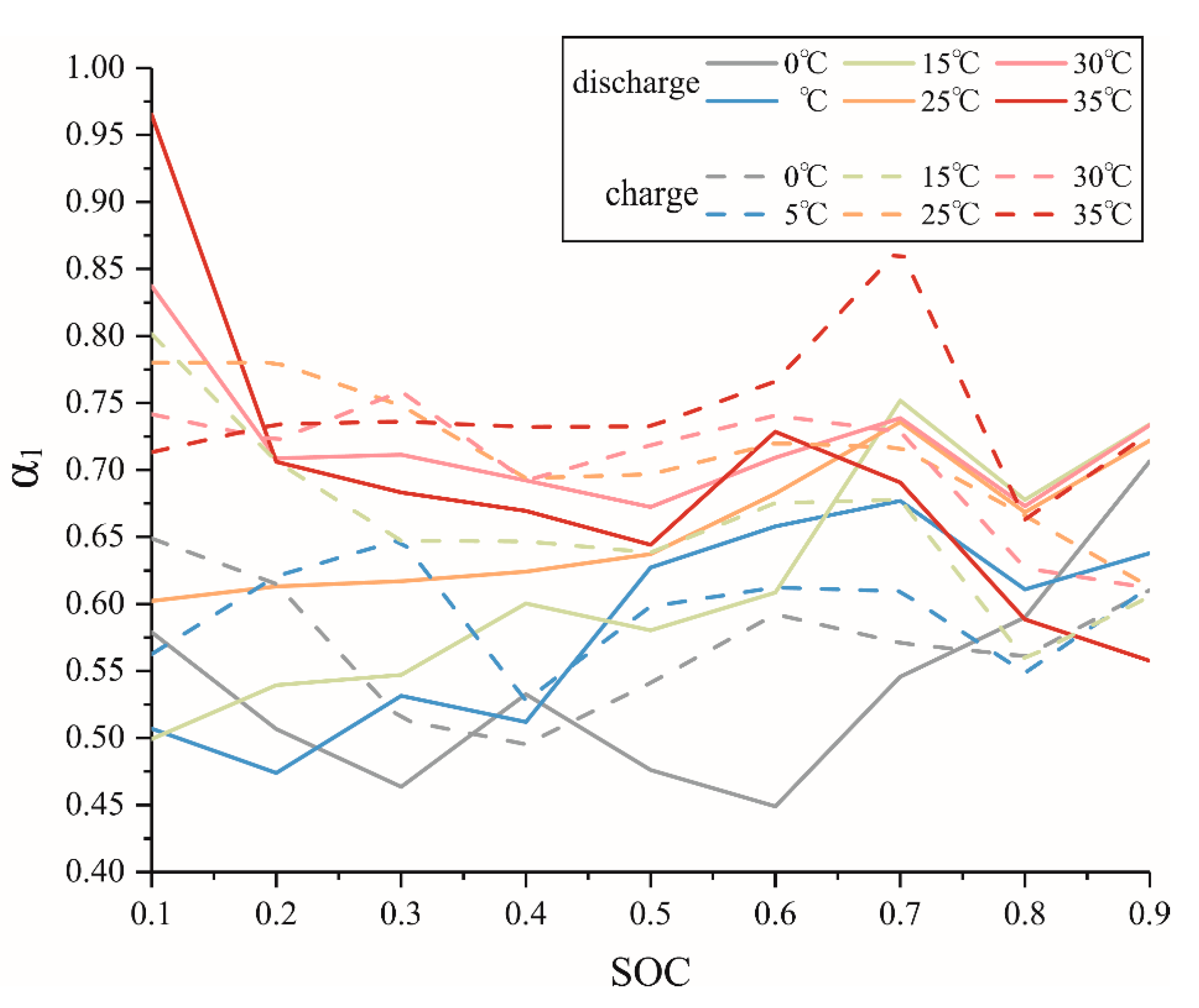
4. Parameter Identification of Fractional Equivalent Circuit Model Based on Particle Swarm Optimization (PSO)
4.1. Identification with PSO Algorithm
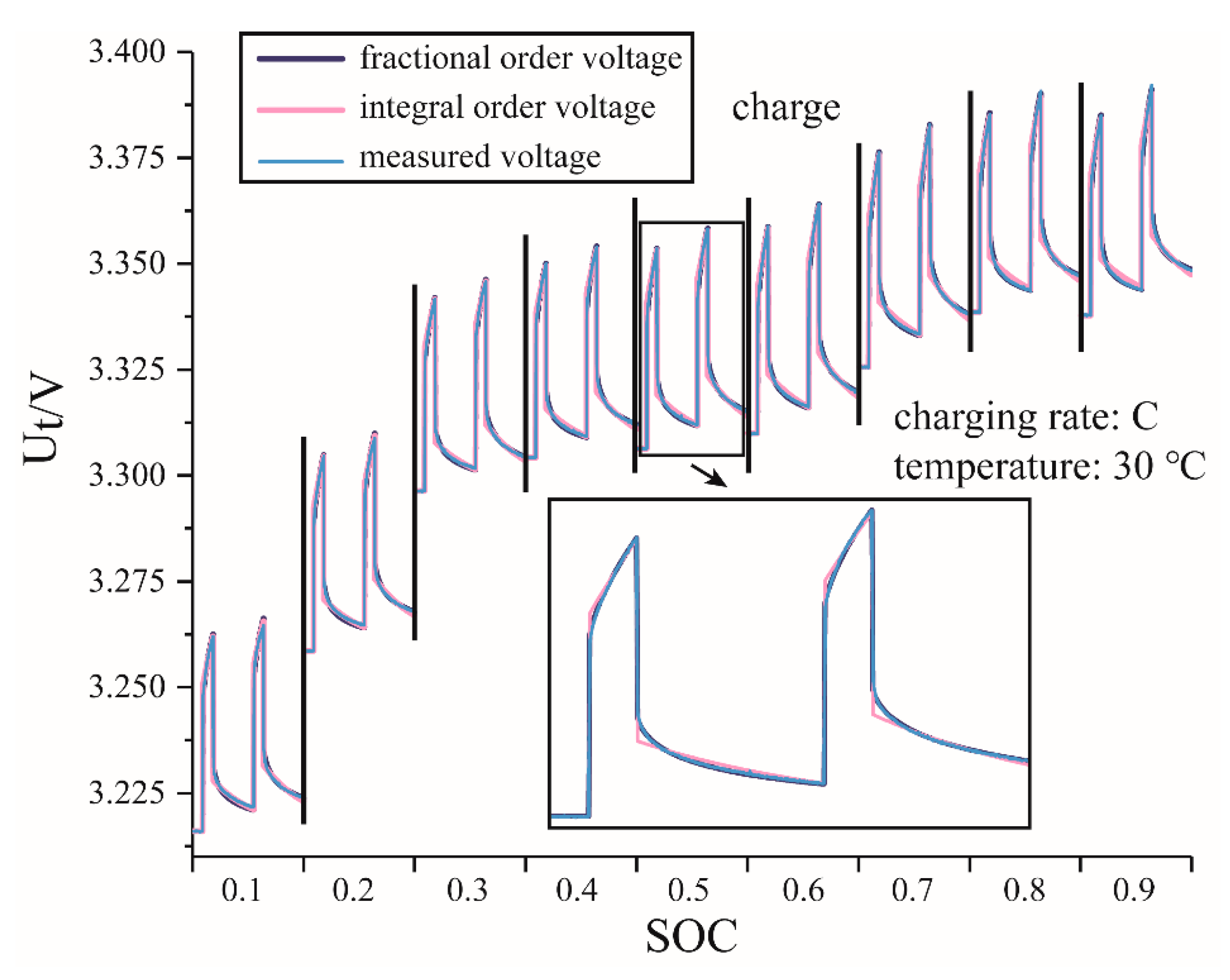
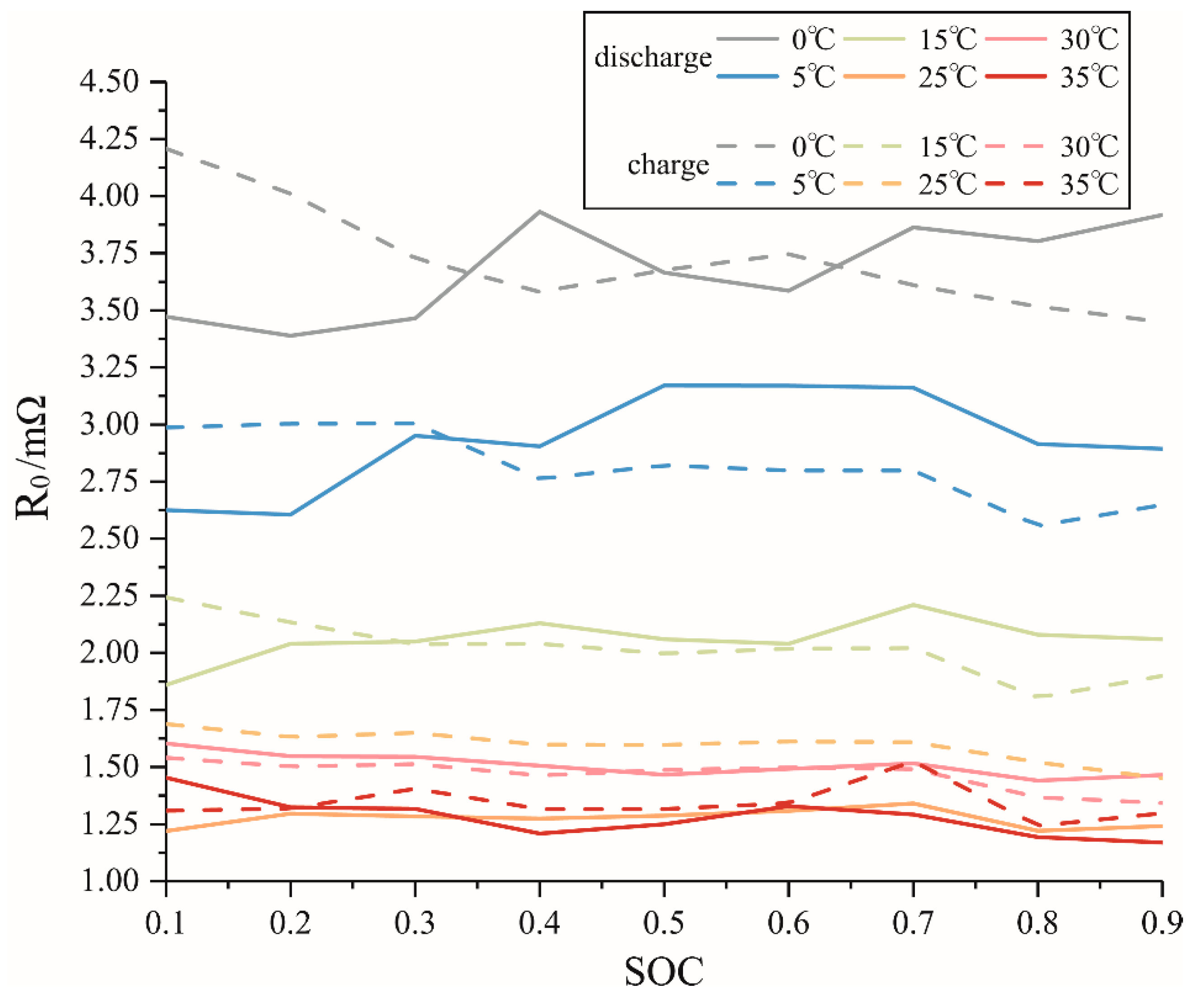
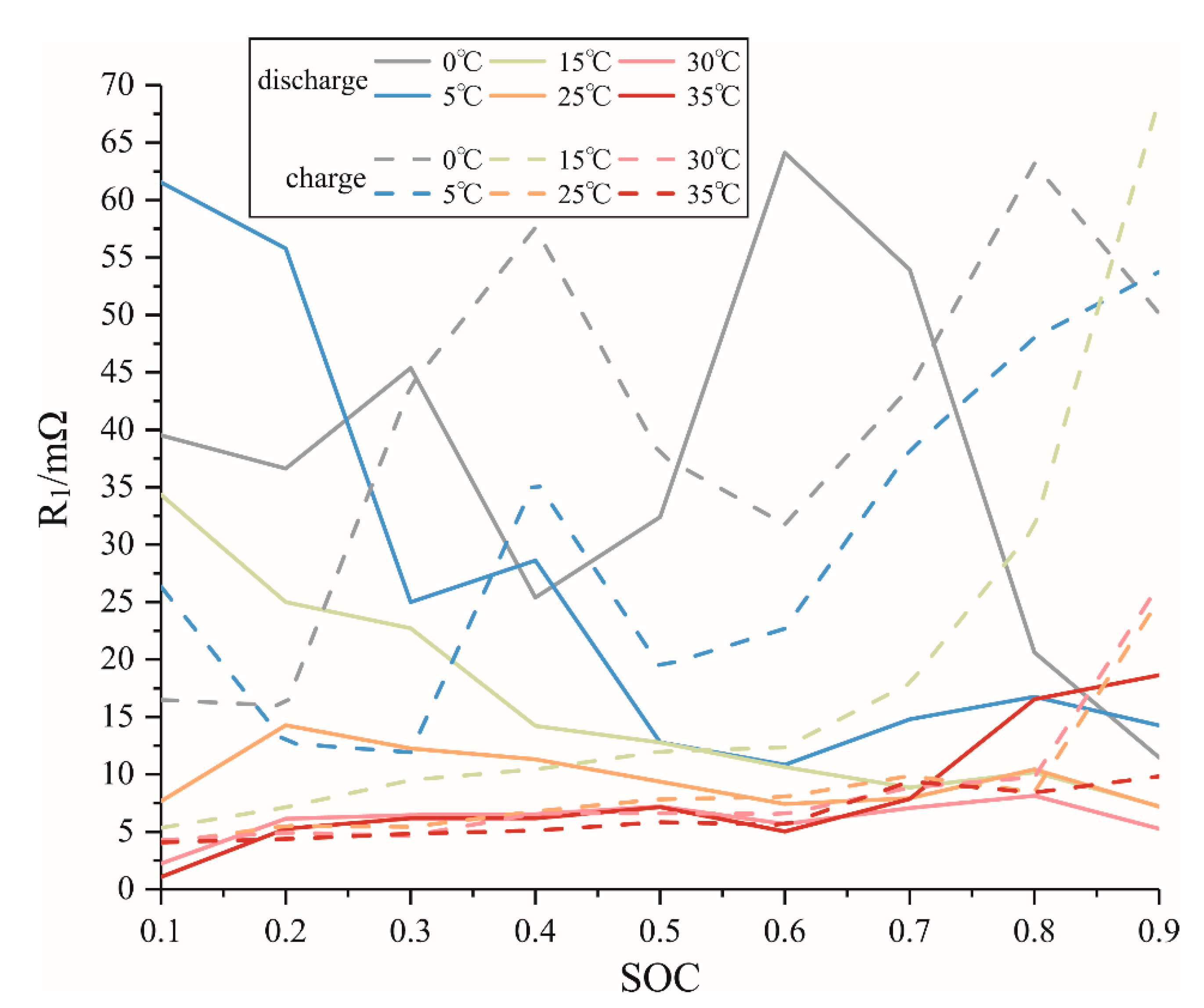
4.2. Identification Test and Results
4.3. Verification of Identification Results
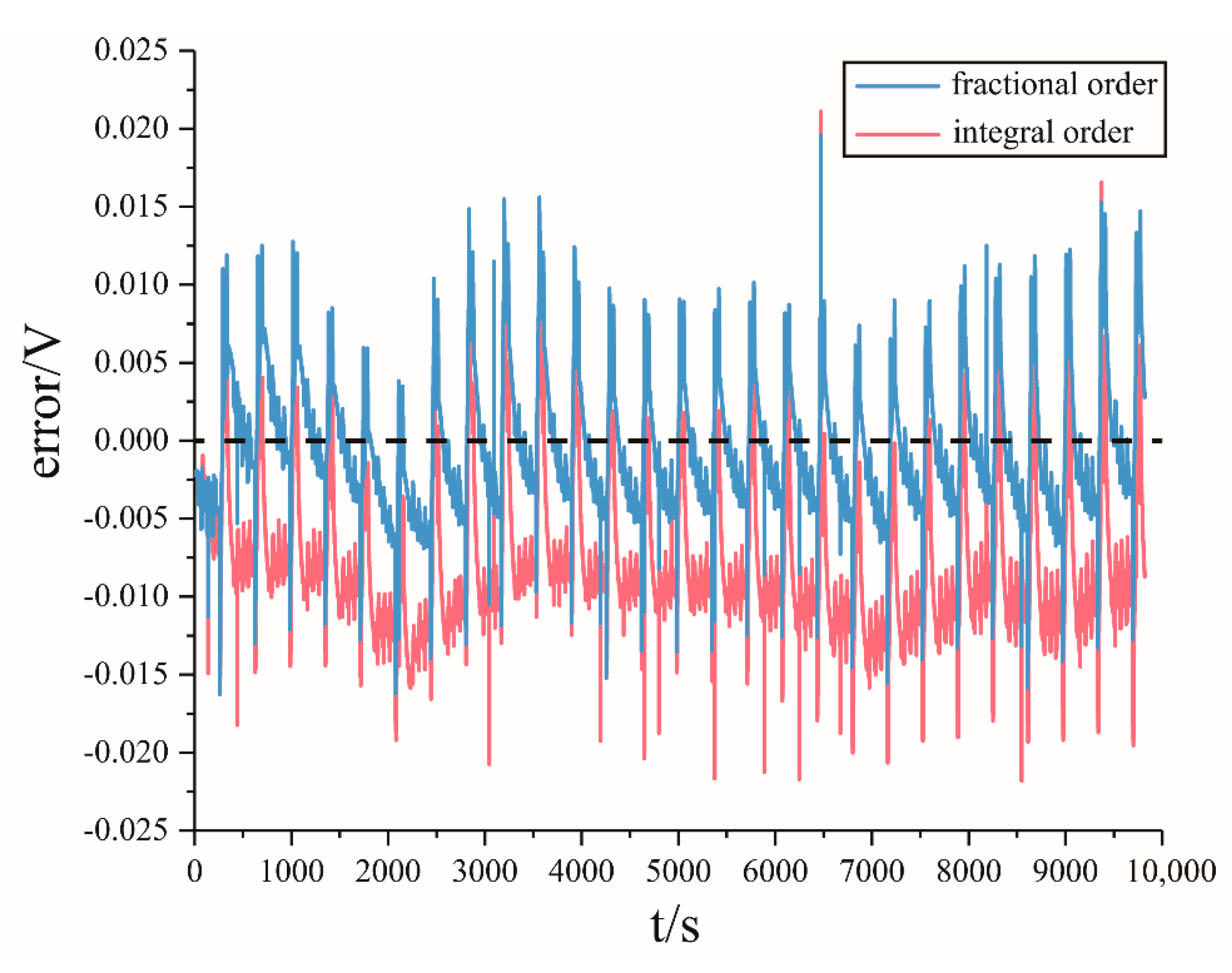
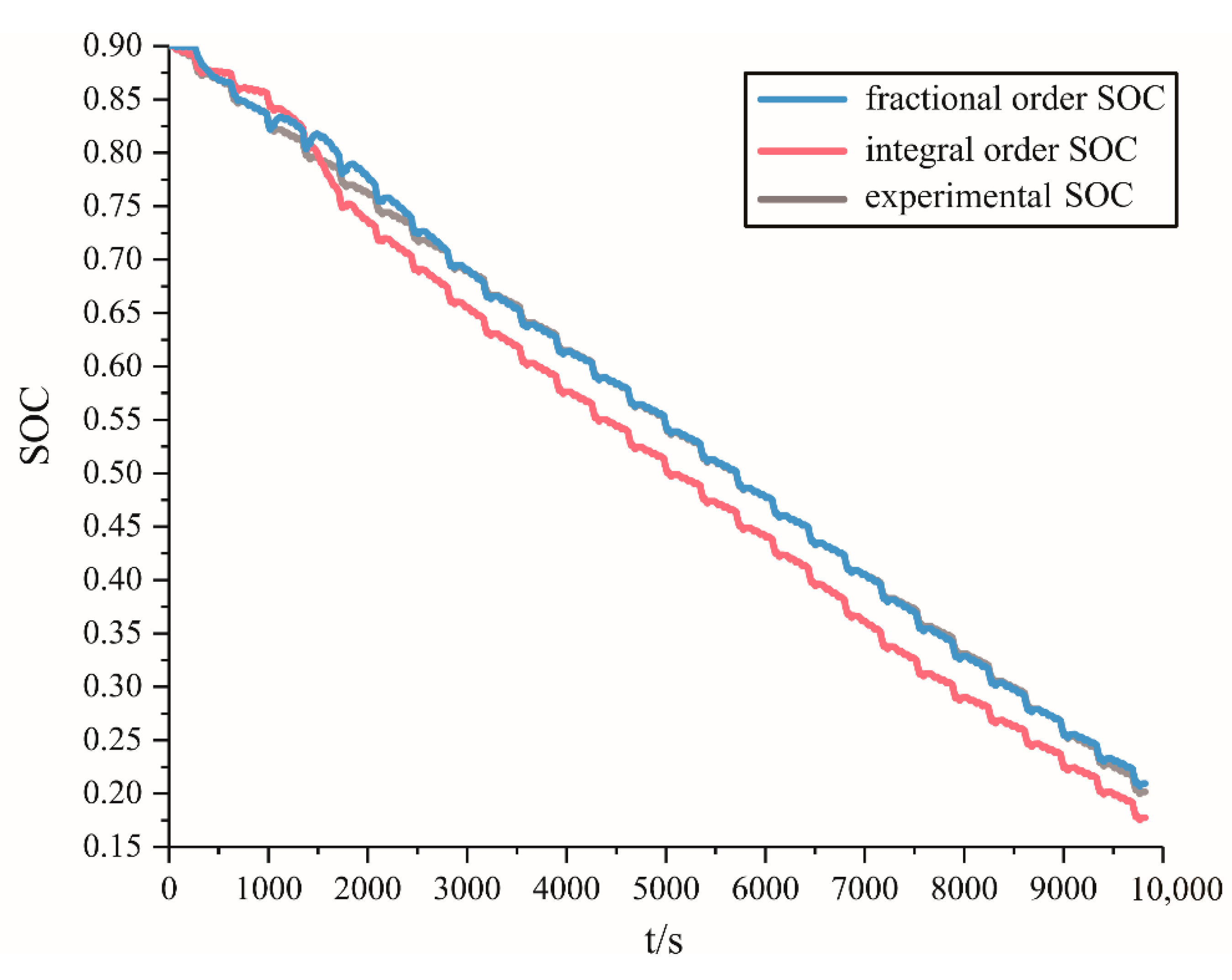
5. Estimation for SOC Based on Fractional Extended Kalman Filter (FEKF)
5.1. Iterative Formula of FEKF
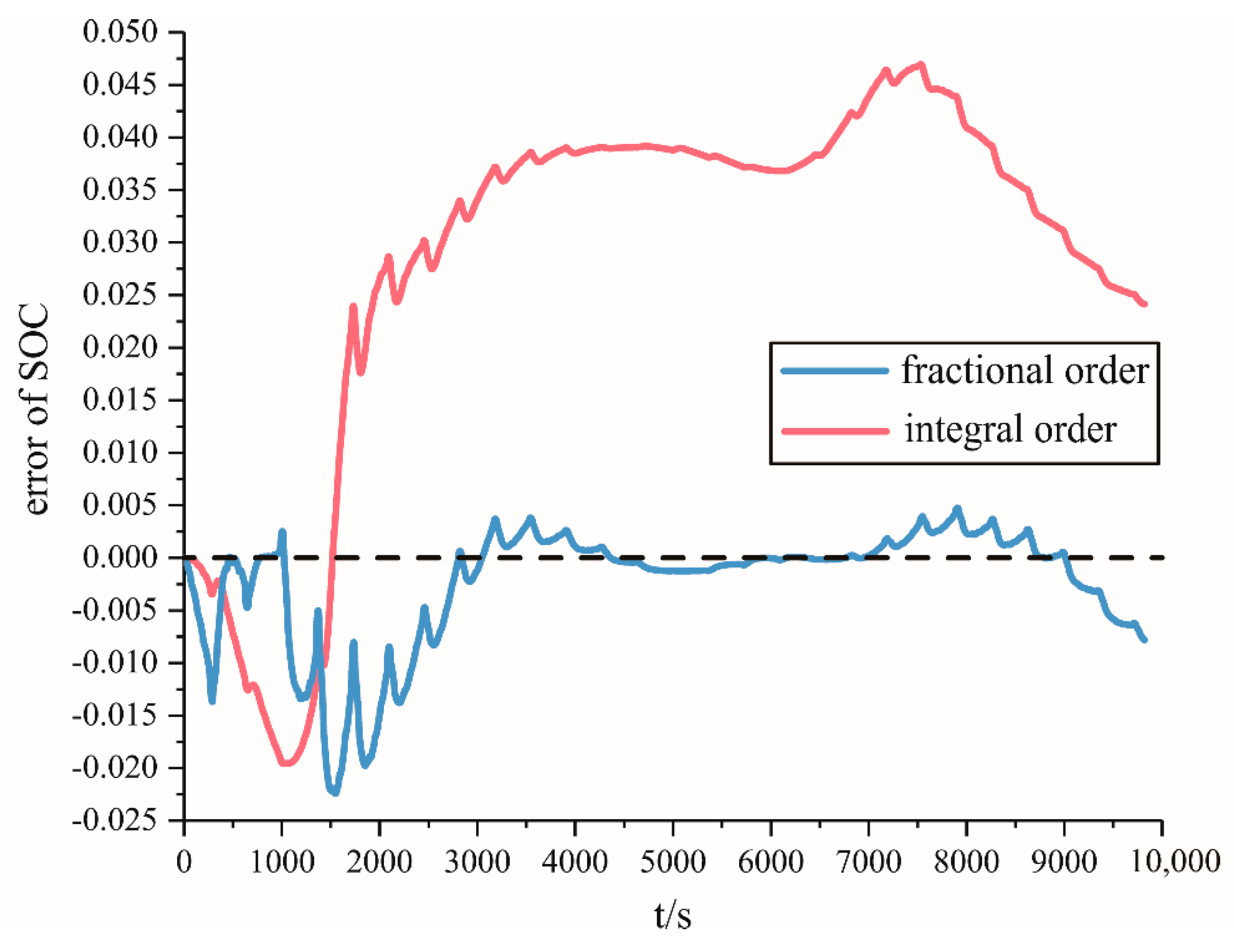
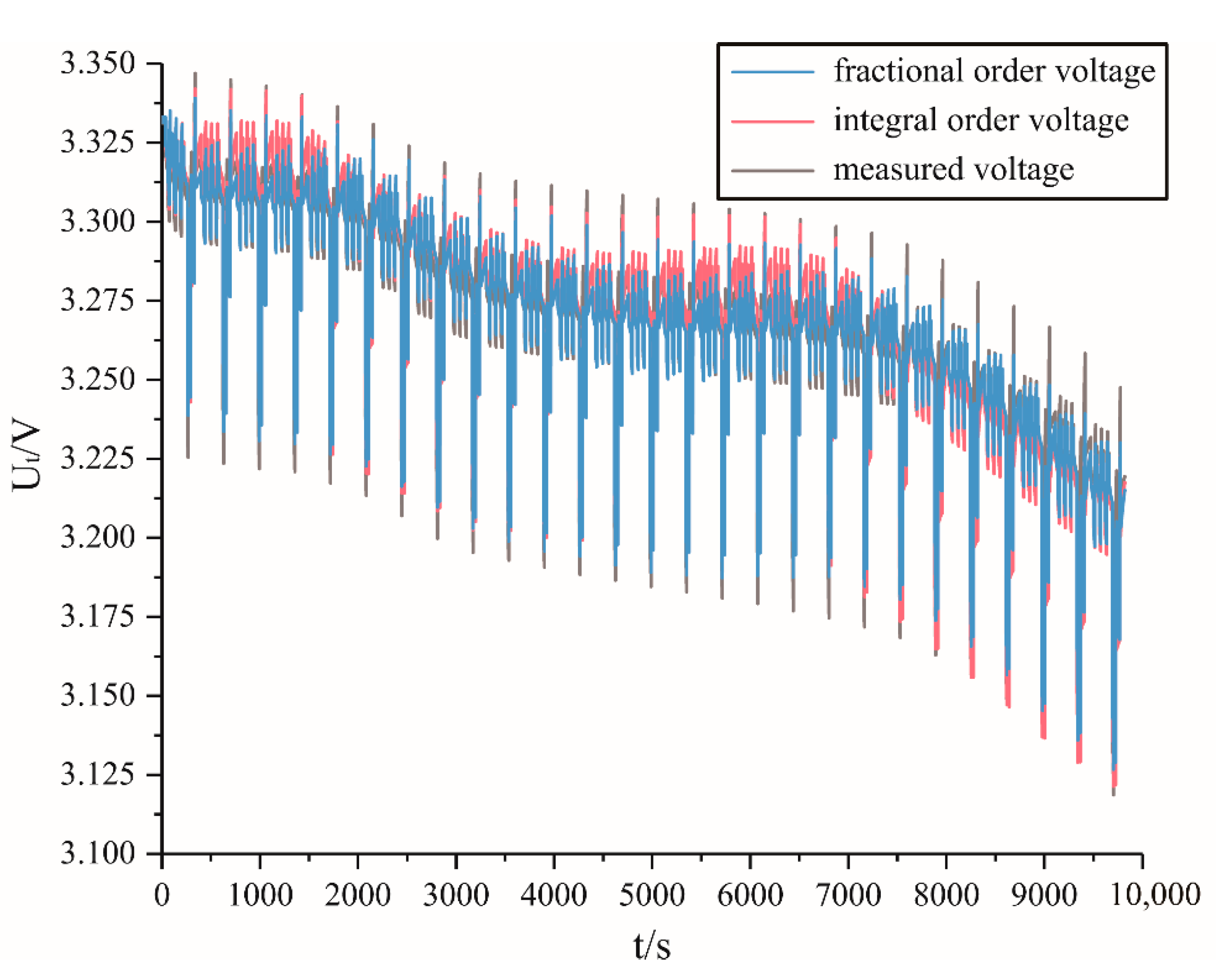
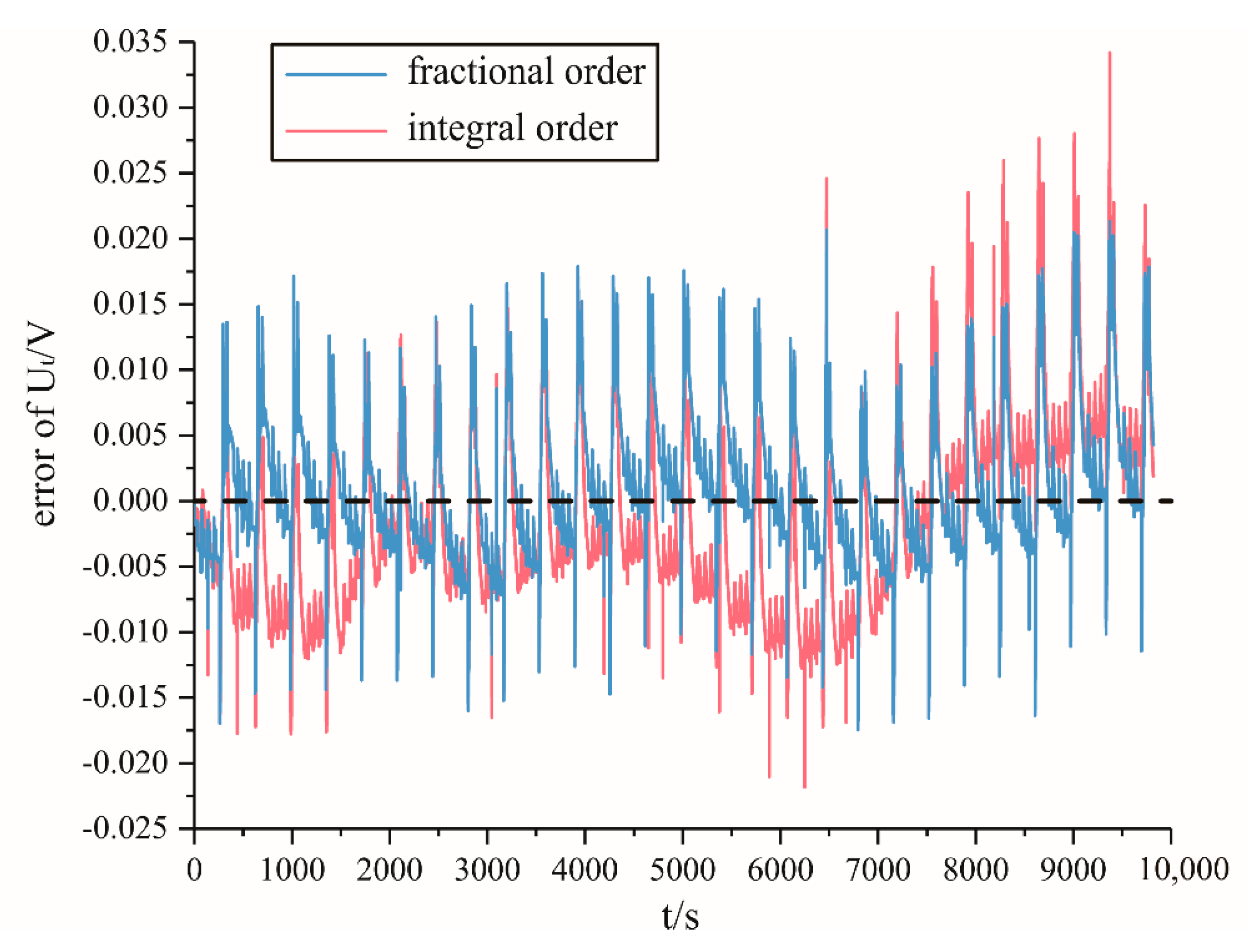
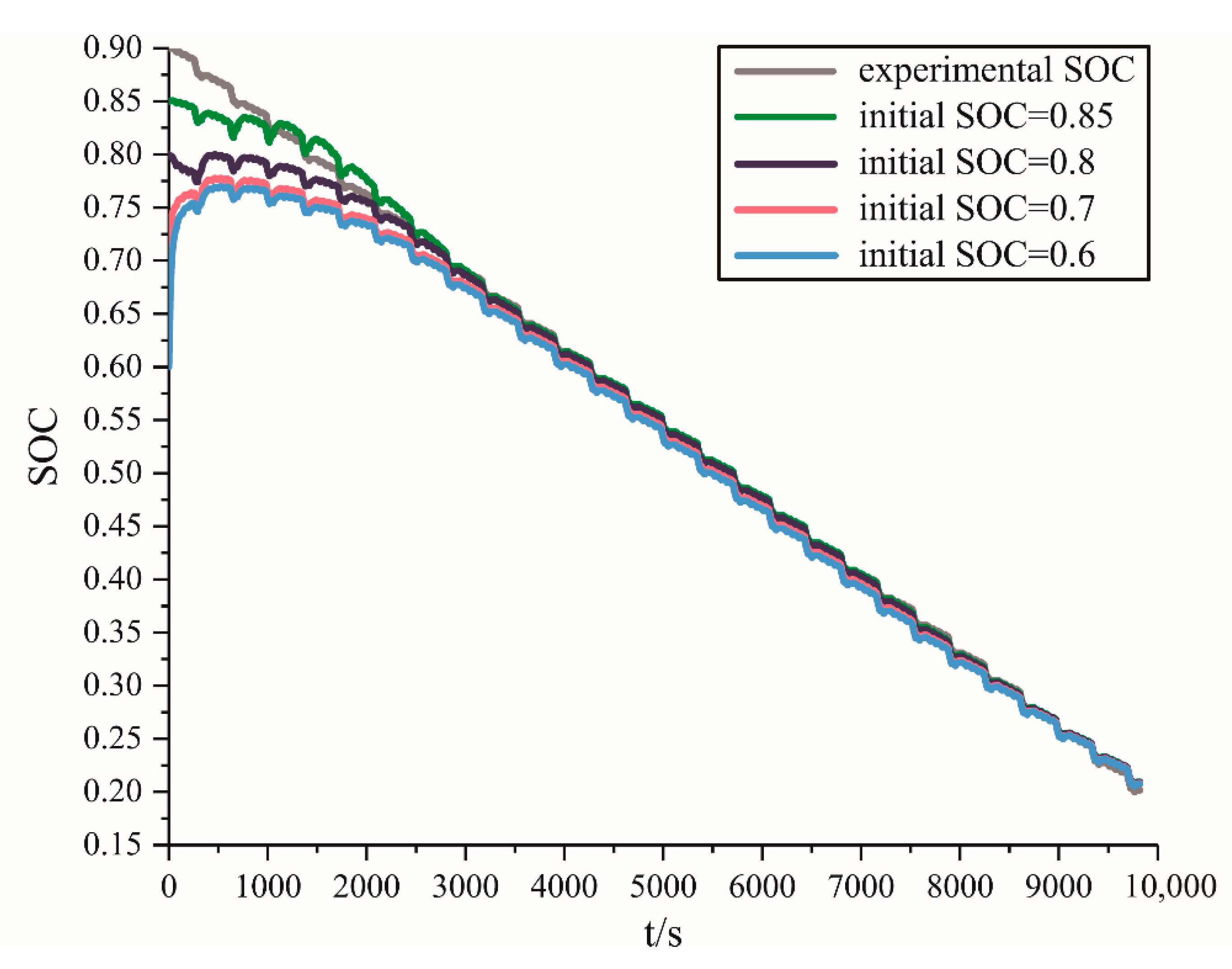
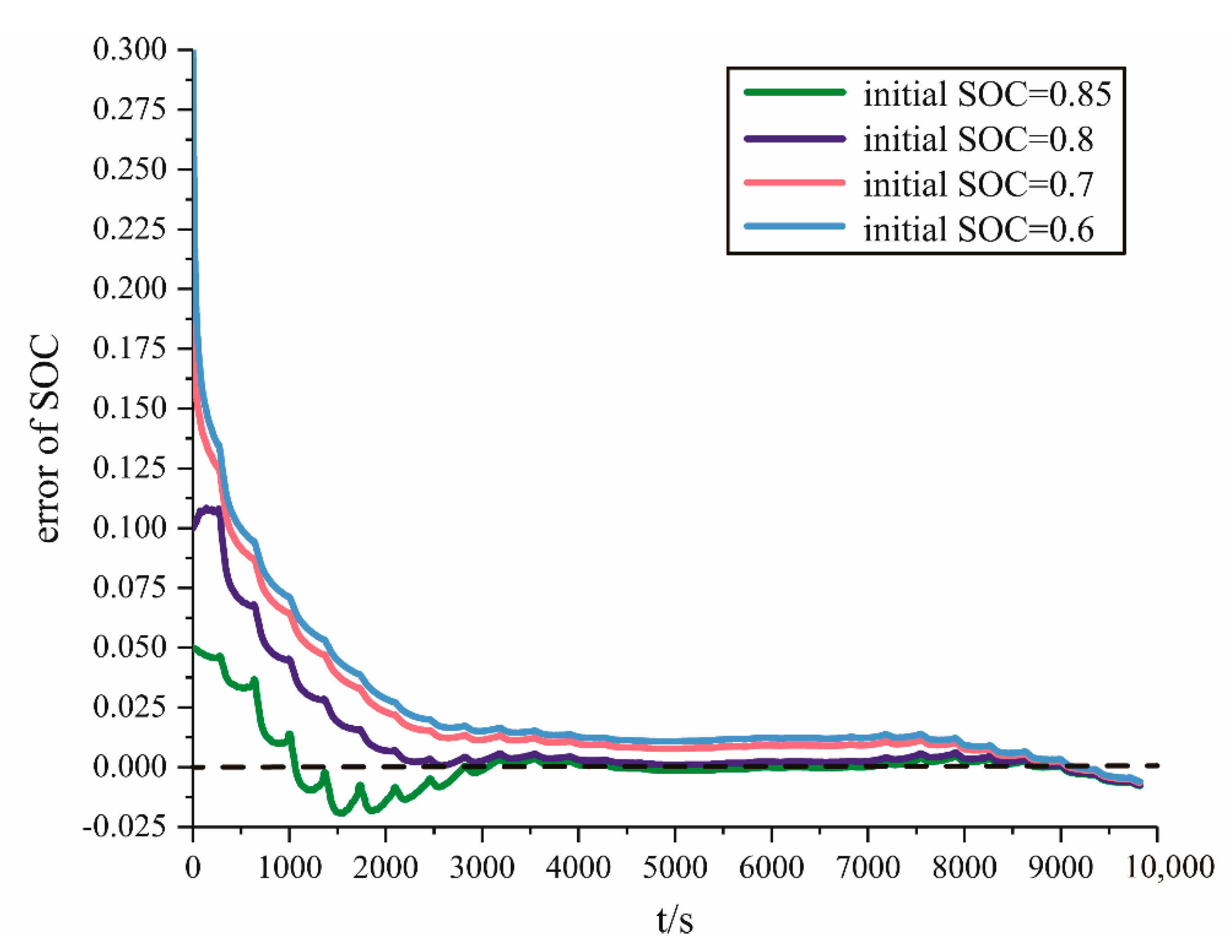
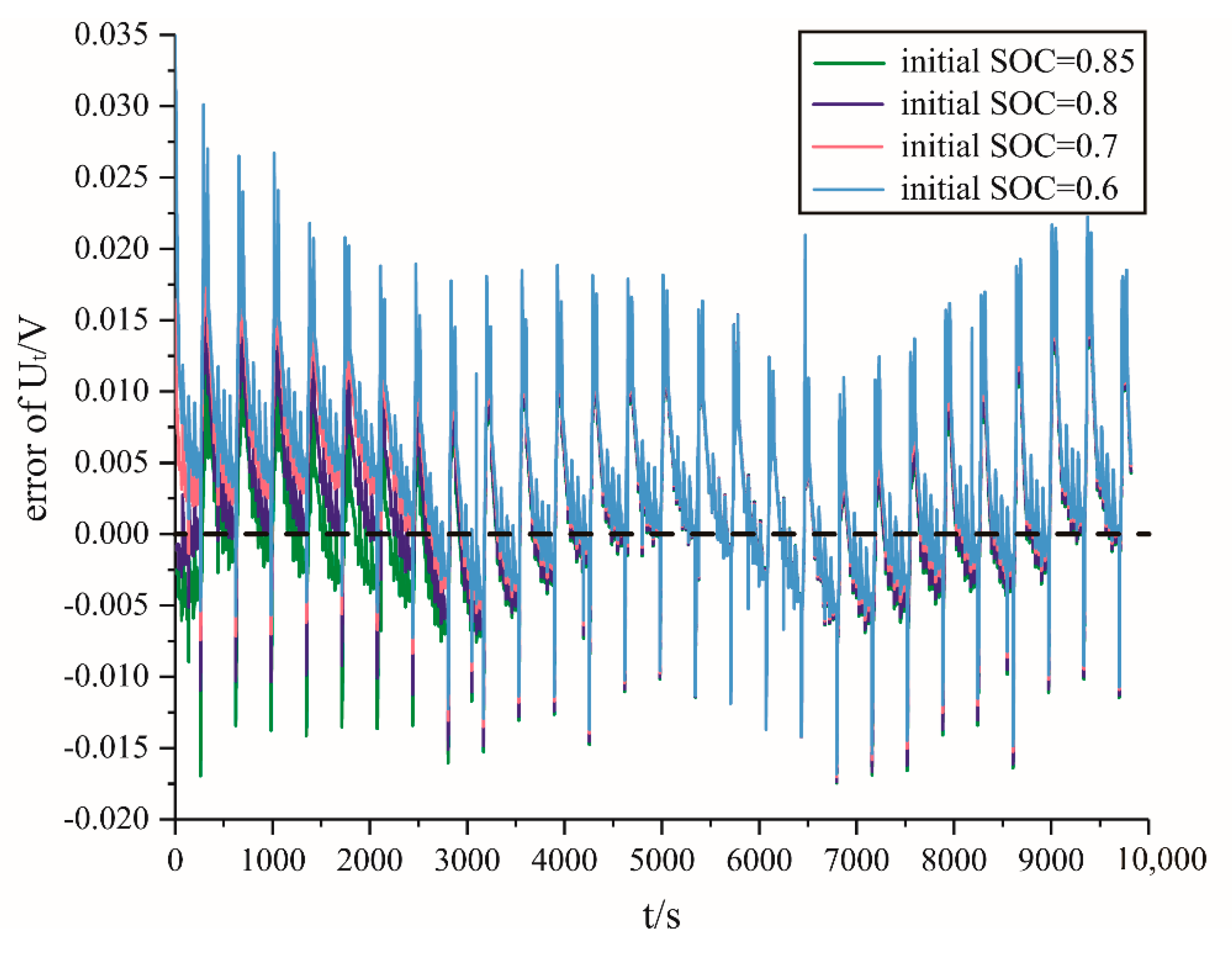
5.2. Verification of Estimation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, A.C.; Zhang, Y.; Zuo, H.F. Assessing the Performance Degradation of Lithium-Ion Batteries Using an Approach Based on Fusion of Multiple Feature Parameters. Math. Probl. Eng. 2019, 7, 1–12. [Google Scholar] [CrossRef]
- Tian, J.; Wang, Q.; Ding, J.; Wang, Y.Q.; Ma, Z.S. Integrated Control with, D.Y.C and, D.S.S for 4WID Electric Vehicles. IEEE Access 2019, 7, 124077–124086. [Google Scholar] [CrossRef]
- Cheng, K.W.E.; Divakar, B.P.; Wu, H.J.; Ding, K.; Ho, H.F. Battery-Management System (BMS) and, S.O.C Development for Electrical Vehicles. IEEE Trans. Veh. Technol. 2011, 60, 76–88. [Google Scholar] [CrossRef]
- Guo, J.G.; Dong, H.X.; Sheng, W.H.; Tu, C. Optimum control strategy of regenerative braking energy for electric vehicle. J. Jiangsu Univ. (Nat. Sci. Ed.) 2018, 39, 132–138. [Google Scholar] [CrossRef]
- Dai, H.F.; Wei, X.Z.; Sun, Z.C.; Wang, J.Y.; Gu, W.J. Online cell, S.O.C estimation of Li-ion battery packs using a dual time-scale Kalman filtering for, E.V. applications. Appl. Energy 2012, 95, 227–237. [Google Scholar] [CrossRef]
- Wang, S.Q.; Verbrugge, M.; Wang, J.S.; Liu, P. Multi-parameter battery state estimator based on adaptive and direct solution of the governing differential equations. J. Power Sources 2011, 196, 8735–8741. [Google Scholar] [CrossRef]
- Hu, Y.; Yurkovich, S. Battery cell state-of-charge estimation using linear parameter varying system techniques. J. Power Sources 2012, 198, 338–350. [Google Scholar] [CrossRef]
- Tian, Y.; Xia, B.Z.; Sun, W.; Xu, Z.H.; Zheng, W.W. A modified model based state of charge estimation of power lithium-ion batteries using unscented Kalman filter. J. Power Sources 2014, 270, 619–626. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Ahmed, R.; Emadi, A. Long Short-Term Memory Networks for Accurate State-of-Charge Estimation of Li-ion Batteries. IEEE Trans. Ind. Electron. 2018, 65, 6730–6739. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Ahmed, R.; Emadi, A. State-of-charge estimation of Li-ion batteries using deep neural networks: A machine learning approach. J. Power Sources 2018, 400, 242–255. [Google Scholar] [CrossRef]
- Xia, B.Z.; Cui, D.Y.; Sun, Z.; Lao, Z.Z.; Zhang, R.F.; Wang, W.; Sun, W.; Lai, Y. State of charge estimation of lithium-ion batteries using optimized Levenberg-Marquardt wavelet neural network. Energy 2018, 153, 694–705. [Google Scholar] [CrossRef]
- Tian, Y.; Li, D.; Tian, J.D.; Xia, B.Z. State of charge estimation of lithium-ion batteries using an optimal adaptive gain nonlinear observer. Electrochim. Acta 2017, 225, 225–234. [Google Scholar] [CrossRef]
- Rivera-Barrera, J.P.; Muñoz-Galeano, N.; Sarmiento-Maldonado, H.O. SoC Estimation for Lithium-ion Batteries: Review and Future Challenges. Electronics 2017, 6, 102. [Google Scholar] [CrossRef] [Green Version]
- Awadallah, M.A.; Venkatesh, B. Accuracy improvement of, S.O.C estimation in lithium-ion batteries. J. Energy Store 2016, 6, 95–104. [Google Scholar] [CrossRef]
- Huang, K.; Guo, Y.F.; Li, Z.G. Review of state of charge estimation methods for power lithium-ion battery. Chin. J. Power Sources 2018, 42, 1395–1401. Available online: http://kns.cnki.net/KCMS/detail/detail.aspx?FileName=DYJS201809051&DbName=CJFQ2018 (accessed on 11 November 2020).
- Jiang, C.Y.; Wang, W.C.; Yang, X.P. Modeling and, S.O.C calculations of hybrid electrical vehicles (HEV) powered by lithium iron phosphate batteries. Energy Storage Sci. Technol. 2018, 7, 897–901. [Google Scholar] [CrossRef]
- Tong, S.J.; Lacap, J.H.; Park, J.W. Battery state of charge estimation using a load-classifying neural network. J. Energy Storage 2016, 7, 236–243. [Google Scholar] [CrossRef]
- Sheikhan, M.; Pardis, R.; Gharavian, D. State of charge neural computational models for high energy density batteries in electric vehicles. Neural Comput. Appl. 2013, 22, 1171–1180. [Google Scholar] [CrossRef]
- Álvarez Antón, J.C.; García Nieto, P.J.; de Cos Juez, F.J.; Sánchez Lasheras, F.; González Vega, M.; Roqueñí Gutiérrez, M.N. Battery state-of-charge estimator using the, S.V.M technique. Appl. Math. Model. 2013, 37, 6244–6253. [Google Scholar] [CrossRef]
- Charkhgard, M.; Farrokhi, M. State-of-Charge Estimation for Lithium-Ion Batteries Using Neural Networks and, E.K.F. IEEE Trans. Ind. Electron. 2010, 57, 4178–4187. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Chen, C.C.; Pecht, M. State of charge estimation for Li-ion batteries using neural network modeling and unscented Kalman filter-based error cancellation. Int. J. Electr. Power Energy Syst. 2014, 62, 783–791. [Google Scholar] [CrossRef]
- Du, S.Y.; Tang, Z.; Chen, D. Research on, S.O.C estimation methods for lead-acid batteries based on fuzzy control. Power Electron. 2017, 51, 95–97. Available online: http://kns.cnki.net/KCMS/detail/detail.aspx?FileName=DLDZ201712030&DbName=CJFQ2017 (accessed on 11 November 2020).
- Sheng, H.M.; Xiao, J. Electric vehicle state of charge estimation: Nonlinear correlation and fuzzy support vector machine. J. Power Sources 2015, 281, 131–137. [Google Scholar] [CrossRef]
- Dong, G.Z.; Chen, Z.H.; Wei, J.W.; Zhang, C.B.; Wang, P. An online model-based method for state of energy estimation of lithium-ion batteries using dual filters. J. Power Sources 2016, 301, 277–286. [Google Scholar] [CrossRef]
- Liu, C.Z.; Liu, W.Q.; Wang, L.Y.; Hu, G.D.; Ma, L.P.; Ren, B.Y. A new method of modeling and state of charge estimation of the battery. J. Power Sources 2016, 320, 1–12. [Google Scholar] [CrossRef]
- Lu, X.; Li, H.; Xu, J.; Chen, S.Y.; Chen, N. Rapid Estimation Method for State of Charge of Lithium-Ion Battery Based on Fractional Continual Variable Order Model. Energies 2018, 11, 714. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.J.; Li, S.B.E.; Peng, H.; Liu, Z.Y. Fractional-order modeling and parameter identification for lithium-ion batteries. J. Power Sources 2015, 293, 151–161. [Google Scholar] [CrossRef]
- He, Y.; Qin, S.X.; Liu, X.T.; Zheng, X.X.; Zeng, G.J. Power Battery, S.O.C Estimation Based on Fractional Unscented Particle Filter. Automob. Technol. 2018, 5, 6–11. [Google Scholar] [CrossRef]
- Wang, Y.J.; Zhang, C.B.; Chen, Z.H. An adaptive remaining energy prediction approach for lithium-ion batteries in electric vehicles. J. Power Sources 2016, 305, 80–88. [Google Scholar] [CrossRef]
- Sun, F.C.; Xiong, R.; He, H.W. Estimation of state-of-charge and state-of-power capability of lithium-ion battery considering varying health conditions. J. Power Sources 2014, 259, 166–176. [Google Scholar] [CrossRef]
- Xiong, R.; Zhang, X.W.; Sun, F.C.; Fan, J.X. State-of-Charge Estimation of the Lithium-Ion Battery Using an Adaptive Extended Kalman Filter Based on an Improved Thevenin Model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar] [CrossRef]
- Cheng, Z.; Lv, J.K.; Liu, J.G.; Wang, L. Application of equivalent hysteresis model in estimation of state of charge of lithium-ion battery. J. Hunan Univ. (Nat. Sci.) 2015, 42, 63–70. [Google Scholar] [CrossRef]
- Ou, Y.J. The Research for Lithium Ion Power Battery, S.O.C Estimation and, S.O.F Evaluation of Electric Vehicles. Ph.D. Thesis, South China University of Technology, Guangzhou, China, 2016. Available online: http://kns.cnki.net/KCMS/detail/detail.aspx?FileName=1016737137.nh&DbName=CDFD2017 (accessed on 11 November 2020).
- Lee, S.; Kim, J.; Lee, J.; Cho, B.H. State-of-charge and capacity estimation of lithium-ion battery using a new open-circuit voltage versus state-of-charge. J. Power Sources 2008, 185, 1367–1373. [Google Scholar] [CrossRef]
- Wei, J.W.; Dong, G.Z.; Chen, Z.H. On-board adaptive model for state of charge estimation of lithium-ion batteries based on Kalman filter with proportional integral-based error adjustment. J. Power Sources 2017, 365, 308–319. [Google Scholar] [CrossRef]
- Wang, B.J. Modeling and State Estimation for Lithium-Ion Batteries Based on Fractional Calculus. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2016. [Google Scholar]
- Weng, C.H.; Sun, J.; Peng, H. A unified open-circuit-voltage model of lithium-ion batteries for state-of-charge estimation and state-of-health monitoring. J. Power Sources 2014, 258, 228–237. [Google Scholar] [CrossRef]
- Kalman, R.E. On the general theory of control systems. Ifac Proc. Vol. 1960, 1, 491–502. [Google Scholar] [CrossRef]






| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 |
|---|---|---|---|---|---|---|---|---|
| −218.825 | 1017.918 | −1958.44 | 2013.781 | −1194.95 | 413.3511 | −80.8272 | 8.4897 | 2.8423 |
| Order | Current I/A | Duration/s | Order | Current I/A | Duration/s |
|---|---|---|---|---|---|
| 1 | 0 | 16 | 11 | 10 | 12 |
| 2 | 5 | 28 | 12 | −5 | 8 |
| 3 | 10 | 12 | 13 | 0 | 16 |
| 4 | −5 | 8 | 14 | 5 | 36 |
| 5 | 0 | 16 | 15 | 40 | 8 |
| 6 | 5 | 24 | 16 | 25 | 24 |
| 7 | 10 | 12 | 17 | −10 | 8 |
| 8 | −5 | 8 | 18 | 10 | 32 |
| 9 | 0 | 16 | 19 | −17 | 8 |
| 10 | 5 | 24 | 20 | 0 | 44 |
| Method | Average Error | Relative Error |
|---|---|---|
| FEKF | 0.0036 | 0.52% |
| EKF | 0.0224 | 3.2% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, C.; Zheng, Y.; Yu, Y. Estimation for Battery State of Charge Based on Temperature Effect and Fractional Extended Kalman Filter. Energies 2020, 13, 5947. https://doi.org/10.3390/en13225947
Chang C, Zheng Y, Yu Y. Estimation for Battery State of Charge Based on Temperature Effect and Fractional Extended Kalman Filter. Energies. 2020; 13(22):5947. https://doi.org/10.3390/en13225947
Chicago/Turabian StyleChang, Chengcheng, Yanping Zheng, and Yang Yu. 2020. "Estimation for Battery State of Charge Based on Temperature Effect and Fractional Extended Kalman Filter" Energies 13, no. 22: 5947. https://doi.org/10.3390/en13225947
APA StyleChang, C., Zheng, Y., & Yu, Y. (2020). Estimation for Battery State of Charge Based on Temperature Effect and Fractional Extended Kalman Filter. Energies, 13(22), 5947. https://doi.org/10.3390/en13225947






