Research on Multi-Attribute Decision-Making in Condition-Based Maintenance for Power Transformers Based on Cloud and Kernel Vector Space Models
Abstract
:1. Introduction
2. Establishment of the Transformer Condition Maintenance Evaluation System
2.1. Comprehensive Evaluation Index System
2.2. Cloud Model
3. Determination of Evaluation Index Weight
3.1. Grey Correlation Analysis
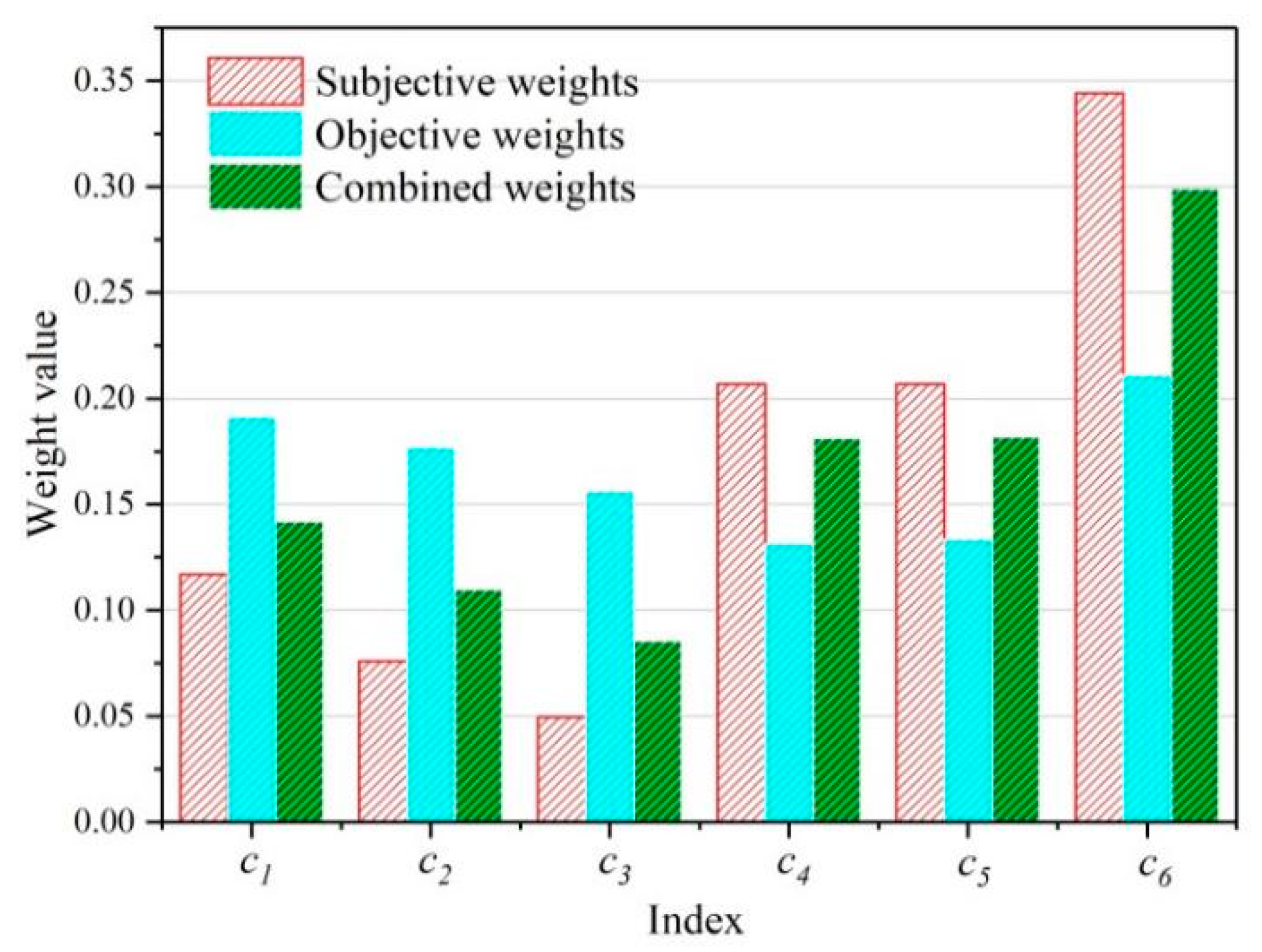
3.2. Determination of the Comprehensive Index Weight
4. Kernel Vector Space Model
5. Case Analysis
- (1)
- Based on the influence of maintenance in power transformers, the expected results of qualitative index c2 were calculated using Equation (6), as follows:
- (2)
- The expected results of qualitative indicators c1 and c3 to c6 were calculated using Equation (7), as follows:
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lösch, A.; Schneider, C. Transforming power/knowledge apparatuses: The smart grid in the German energy transition. Innov. Eur. J. Soc. Sci. 2016, 29, 262–284. [Google Scholar] [CrossRef]
- Fofana, I.; Hemmatjou, H.; Meghnefi, F. Effect of thermal transient on the polarization and depolarization current measurements. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 513–520. [Google Scholar] [CrossRef]
- Wada, J.; Ueta, G.; Okabe, S. Method to evaluate the degradation condition of transformer insulating oil-establishment of the evaluation method and application to field transformer oil. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 1266–1274. [Google Scholar] [CrossRef]
- Abu-Siada, A.; Lai, S.P.; Islam, S.M. A novel fuzzy-logic approach for furan estimation in transformer oil. IEEE Trans. Power Deliv. 2012, 27, 469–474. [Google Scholar] [CrossRef]
- Shintemirov, A.; Tang, W.; Wu, Q.H. Power transformer fault classification based on dissolved gas analysis by implementing bootstrap and genetic programming. IEEE Trans.Syst. Man Cybern. Part C 2008, 39, 69–79. [Google Scholar] [CrossRef]
- Singh, J. The influence of service aging on transformer insulating oil parameters. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 421–426. [Google Scholar] [CrossRef]
- Sim, S.H.; Endrenyi, J. A failure-repair model with minimal and major maintenance. IEEE Trans. Reliab. 1993, 42, 134–140. [Google Scholar] [CrossRef]
- Huynh, K.T.; Grall, A. A condition-based maintenance model with past-dependent imperfect preventive repairs for continuously deteriorating systems. J. Risk Reliab. 2020, 234, 333–358. [Google Scholar] [CrossRef]
- Hinow, M.; Mevissen, M. Substation maintenance strategy adaptation for life-cycle cost reduction using genetic algorithm. IEEE Trans. Power Deliv. 2010, 26, 197–204. [Google Scholar] [CrossRef]
- Tang, W.H.; Spurgeon, K.; Wu, Q.H. An evidential reasoning approach to transformer condition assessments. IEEE Trans. Power Deliv. 2004, 19, 1696–1703. [Google Scholar] [CrossRef]
- Li, D. A fuzzy closeness approach to fuzzy multi-attribute decision making. Fuzzy Optim. Decis. Mak. 2007, 6, 237–254. [Google Scholar] [CrossRef]
- Bisoi, R.; Chakravorti, T.; Nayak, N.R. A hybrid Hilbert Huang transform and improved fuzzy decision tree classifier for assessment of power quality disturbances in a grid connected distributed generation system. Int. J. Power Energy Convers. 2020, 11, 60–81. [Google Scholar] [CrossRef]
- Sivaperumal, P.; Subranhsu-Sekhar, D.; Saravanan, K. Enhancing the power of quality issues using superconducting magnetic storage devices—Based dynamic voltage restorer—Aided switched coupled inductor inverter with space vector pulse width modulation techniques. Meas. Control. 2019, 52, 1329–1343. [Google Scholar] [CrossRef]
- Xiang, Z.; Ji, V.; Hai, Z.; Jie, D.; Fang, C.; Xin, Z. Very short-term prediction model for photovoltaic power based on improving the total sky cloud image recognition. J. Eng. 2017, 2017, 1947–1952. [Google Scholar] [CrossRef]
- Yang, J.B.; Singh, M.G. An evidential reasoning approach for multiple-attribute decision making with uncertainty. IEEE Trans. Syst. Man Cybern. 2002, 24, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez, R.M.; Martinez, L.; Herrera, F. Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. Fuzzy Syst. 2012, 20, 109–119. [Google Scholar] [CrossRef]
- Bovea, M.D.; Wang, B. Identifying environmental improvement options by combining life cycle assessment and fuzzy set theory. Int. J. Prod. Res. 2003, 41, 593–609. [Google Scholar] [CrossRef]
- Dixit, V.; Chaudhuri, A.; Srivastava, R.K. Assessing value of customer involvement in engineered-to-order shipbuilding projects using fuzzy set and rough set theories. Int. J. Prod. Res. 2019, 57, 6943–6962. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Liu, C.; Gan, W. A new cognitive model: Cloud model. Int. J. Intell. Syst. 2009, 24, 357–375. [Google Scholar] [CrossRef]
- Lv, P.; Yuan, L.; Zhang, J. Cloud theory-based simulated annealing algorithm and application. Eng. Appl. Artif. Intell. 2009, 22, 742–749. [Google Scholar] [CrossRef]
- Li, W.; Zhao, J.; Xiao, B. Multimodal medical image fusion by cloud model theory. Signal Image Video Process 2018, 12, 437–444. [Google Scholar] [CrossRef]
- Shi, Y.; Zhou, H. Research on monthly flow uncertain reasoning model based on cloud theory. Sci. China Technol. Sci. 2010, 53, 2408–2413. [Google Scholar] [CrossRef]
- Wang, J.Q.; Wang, P.; Wang, J. Atanassov’s interval-valued intuitionistic linguistic multicriteria group decision-making method based on the trapezium cloud model. IEEE Trans. Fuzzy Syst. 2015, 23, 542–554. [Google Scholar] [CrossRef]
- Gleue, C.; Eilers, D. Decision support for the automotive industry: Forecasting residual values using artificial neural networks. Wirtschaftsinformatik 2019, 61, 385–397. [Google Scholar] [CrossRef]
- Zhao, B.; Chen, S. Maintenance decision methodology of petrochemical plant based on fuzzy curvelet neural network. Appl. Soft Comput. 2018, 69, 203–212. [Google Scholar] [CrossRef]
- Saeed, Y.; Ahmed, K.; Zareei, M. In-vehicle cognitive route decision using fuzzy modeling and artificial neural network. IEEE Access 2019, 7, 20262–20272. [Google Scholar] [CrossRef]
- Tan, Y.; Niu, C.; Tian, H. A one-class SVM based approach for condition-based maintenance of a naval propulsion plant with limited labeled data. Ocean Eng. 2019, 193, 106592.1–106592.12. [Google Scholar] [CrossRef]
- Nie, F.; Zhu, W.; Li, X. Decision tree SVM: An extension of linear SVM for non-linear classification. Neurocomputing 2019, 11, 153–159. [Google Scholar] [CrossRef]
- Liu, Q.; Lu, H.; Ma, S. Improving kernel Fisher discriminant analysis for face recognition. IEEE Press 2004, 14, 42–49. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Q.; Wei, H. Functional analysis model for selecting leading industry under grey information. Kybernetes Int. J. Syst. Cybern. 2013, 41, 851–859. [Google Scholar] [CrossRef]
- Javanmardi, E.; Liu, S. Exploring grey systems theory-based methods and applications in analyzing socio-economic systems. Sustainability 2019, 11, 4192. [Google Scholar] [CrossRef] [Green Version]
- Tsai, M.S.; Hsu, F.Y. Application of grey correlation analysis in evolutionary programming for distribution system feeder reconfiguration. IEEE Trans. Power Syst. 2010, 25, 1126–1133. [Google Scholar] [CrossRef]
- Liu, S.; Guan, Y.; Song, D. Correlation analysis of bearing track using grey system theory. Kybernetes 2012, 41, 945–952. [Google Scholar]
- Yang, L.J.; Xiong, X.F.; Zhang, Y. Research on condition-based maintenance policy of electric power equipment based on grey correlation degree and TOPSIS. Power Syst. Prot. Control 2009, 18, 74–78. [Google Scholar]
- Yuan, Z.; Sun, C.; Li, A. Assessment on condition based maintenance policy of transformer using fuzzy multiple attribute decision making. High Volt. Eng. 2004, 30, 33–35. [Google Scholar]

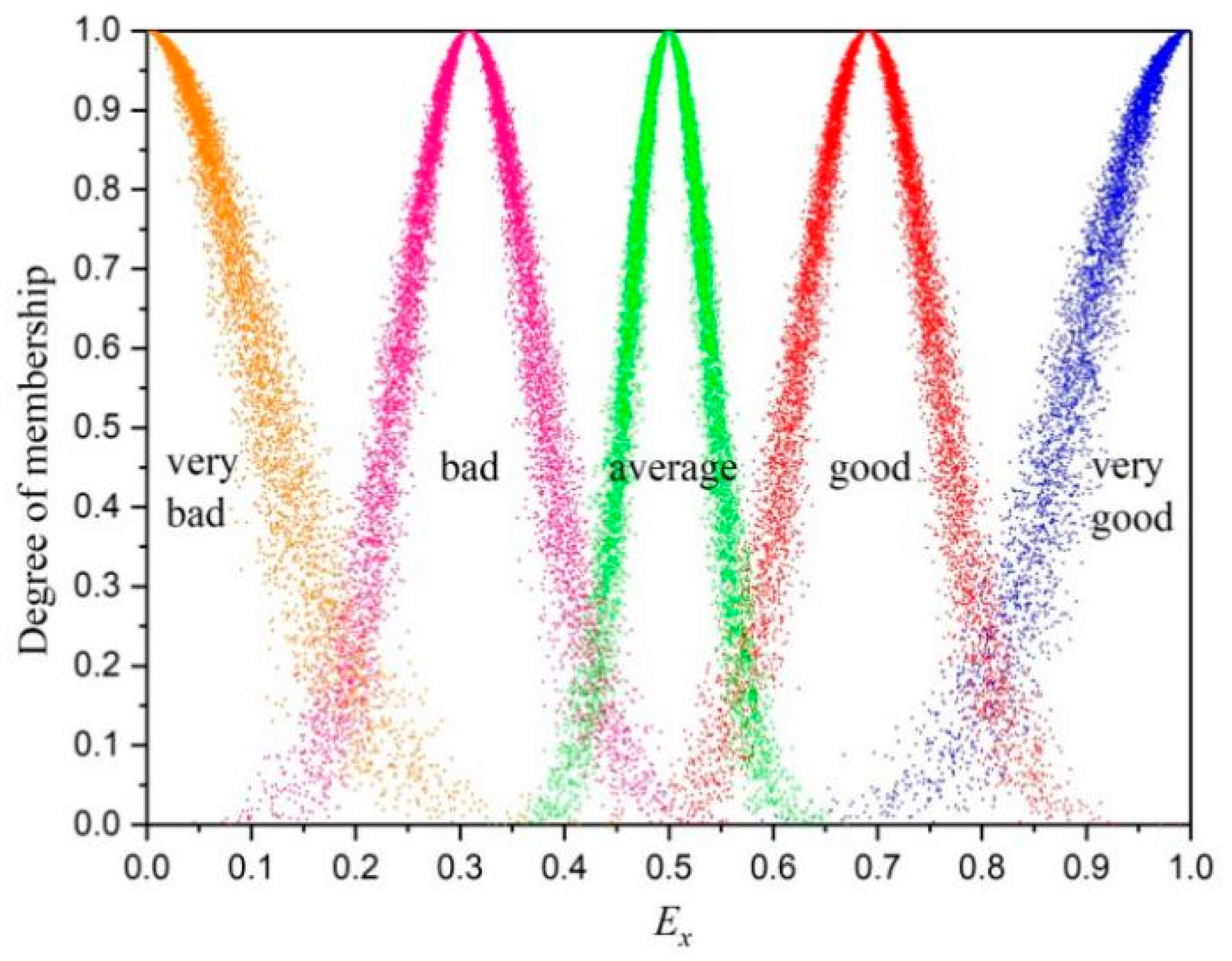
| c1, c3 | c2 | c4–c6 | Cloud Model |
|---|---|---|---|
| Lower | Very Good | Smaller | C(1, 0.104, 0.015) |
| Low | Good | Small | C(0.691, 0.064, 0.009) |
| Average | Average | Average | C(0.5, 0.039, 0.006) |
| High | Bad | Big | C(0.309, 0.064, 0.009) |
| Higher | Very Bad | Bigger | C(0, 0.104, 0.015) |
| Strategy | c1 | c2 | c3 | c4 | c5 | c6 |
|---|---|---|---|---|---|---|
| M1 | High | Very Good | Higher | Bigger | Bigger | Bigger |
| Higher | Very Good | Higher | Bigger | Bigger | Bigger | |
| High | Very Good | Higher | Big | Bigger | Big | |
| Higher | Good | Higher | Bigger | Big | Big | |
| M2 | High | Good | High | Medium | Big | Bigger |
| Low | Very Good | Average | Big | Big | Bigger | |
| High | Very Good | Average | Medium | Big | Big | |
| Average | Good | Good | Small | Big | Bigger | |
| M3 | Average | Very Bad | Low | Small | Smaller | Bigger Bigger |
| Average | Bad | Low | Smaller | Smaller | Bigger | |
| High | Very Bad | Low | Smaller | Small | Bigger | |
| High | Bad | Average | Medium | Small |
| Index | Subjective Weights | Objective Weights | Combined Weights |
|---|---|---|---|
| c1 | |||
| c2 | |||
| c3 | |||
| c4 | |||
| c5 | |||
| c6 |
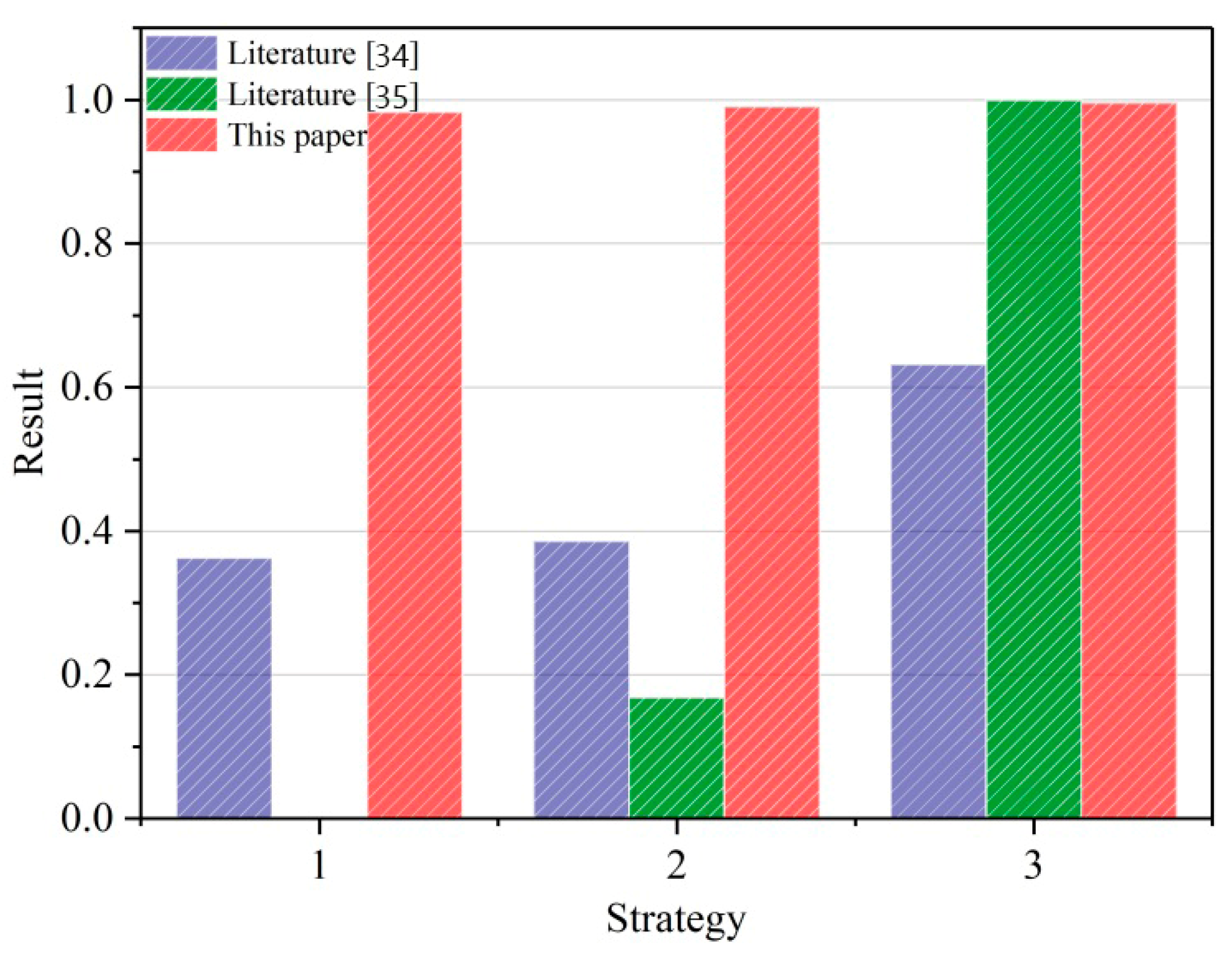
| Maintenance Strategy | Proximity |
|---|---|
| M1 | 0.9836 |
| M2 | 0.9906 |
| M3 | 0.9963 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, R.; Li, S.; Peng, W. Research on Multi-Attribute Decision-Making in Condition-Based Maintenance for Power Transformers Based on Cloud and Kernel Vector Space Models. Energies 2020, 13, 5948. https://doi.org/10.3390/en13225948
Gong R, Li S, Peng W. Research on Multi-Attribute Decision-Making in Condition-Based Maintenance for Power Transformers Based on Cloud and Kernel Vector Space Models. Energies. 2020; 13(22):5948. https://doi.org/10.3390/en13225948
Chicago/Turabian StyleGong, Renxi, Siqiang Li, and Weiyu Peng. 2020. "Research on Multi-Attribute Decision-Making in Condition-Based Maintenance for Power Transformers Based on Cloud and Kernel Vector Space Models" Energies 13, no. 22: 5948. https://doi.org/10.3390/en13225948
APA StyleGong, R., Li, S., & Peng, W. (2020). Research on Multi-Attribute Decision-Making in Condition-Based Maintenance for Power Transformers Based on Cloud and Kernel Vector Space Models. Energies, 13(22), 5948. https://doi.org/10.3390/en13225948




