Numerical Investigation of the Rotor-Rotor Aerodynamic Interaction for eVTOL Aircraft Configurations

Abstract

The rotor-rotor aerodynamic interaction is one of the key phenomena that characterise the flow and the performance of most of the new urban air mobility vehicles (eVTOLs) developed in the recent years. The present article describes a numerical activity that aimed to the systematic study of the rotor-rotor aerodynamic interaction with application to the flight conditions typical of eVTOL aircraft. The activity considers the use of a novel mid-fidelity aerodynamic solver based on vortex particle method. In particular, numerical simulations were performed when considering two propellers both in side-by-side and tandem configuration with different separation distances. The results of numerical simulations showed a slight reduction of the propellers performance in side-by-side configuration, while a remarkable loss of thrust in the order of 40% and a reduction of about 20% of the propulsive efficiency were found in tandem configuration, particularly when the propeller disks are completely overlapped. Moreover, the flow field analysis enabled providing a detailed insight regarding the flow physics involved in such aerodynamic interactions.

1. Introduction

In recent years, a great interest and development effort has been devoted towards the design of unconventional VTOL aircraft based on electric distributed propulsion (eVTOLs) with the aim to create a novel concept of urban air mobility to be considered as an effective alternative to ground transportation in overcrowded metropolitan areas [1]. The development of these new aircraft architectures combining in a single vehicle aerodynamic elements typical of different classical configurations, such as fixed lifting surfaces, lifting rotors, and thrusting propellers, pose unprecedented challenges to engineers in several areas. In particular, even if the aircraft architectures that are designed by the companies are rather diverse, the rotor-rotor interaction represents, from an aerodynamic standpoint, one of the novel key phenomena that characterise the flow around most eVTOLs as well as their performance, handling qualities, and noise. Indeed, the common feature that characterises eVTOLs design is the use of multiple propellers, as illustrated by the layout of few examples of eVTOLs aircraft developed in the last years shown in Figure 1. The multiple propellers mounted on wings are typically close to each other, as can be observed from the layout of the novel aircraft designed by Archer that is shown in Figure 1a and by the Vahana aircraft architecture designed by A³ by Airbus LLC [2] shown in Figure 1b. Moreover, the propellers are often arranged on two lifting surfaces with different longitudinal separation distance and typically present a certain region of overlapping between the rotor disks, as can be observed from the layout of the Bell-Nexus 6HX designed by Bell shown in Figure 1c and by the S4 aircraft that were designed by Joby Aviation shown in Figure 1d. Therefore, two main types of rotor-rotor aerodynamic interaction can be outlined as the more interesting for eVTOL applications, i.e., with the propellers in side-by-side and tandem configurations.

In the recent years, the investigation of these kinds of rotor-rotor aerodynamic interaction has begun to gather interest in the scientific community both in experimental and numerical field, in particular for applications of multirotor drones. For instance, the experimental work by Zhou et al. [3] investigated the interactional effect of the distance between two small UAV propellers in side-by-side configuration for hover conditions. This work shows that a negligible reduction of the interacting propellers performance is obtained in such test conditions, while a high level of unsteady load fluctuations is achieved, decreasing the lateral distance between the rotor disks. A similar test configuration, when considering a side-by-side configuration of two mini-drone rotors in hover, was investigated in the experimental work by Shukla and Komerath [4]. This work shows, by means of stereo Particle Image Velocimetry (PIV) measurements, an increase of the rotor wake interactions decreasing the rotor spacing and Reynolds number. Concerning the investigation of the aerodynamic interaction of rotors in tandem the majority of the works dealt with coaxial rotors configuration. For instance, wind tunnel tests were performed by Shukla et al. [5] in order to study the aerodynamic interaction of two coaxial rotors considering particularly the effects of Reynolds number and of advance ratio. In particular, this work showed that, for low Reynolds, the upper rotor provides a higher figure of merit due to swirl recovery. Moreover, Brazinskas et al. [6] investigated, by means of loads and torque measurements, the performance of two co-axial rotors when also considering partially overlapped conditions between the rotors disks, but with longitudinal distance below a rotor radius.

Despite this effort, there is a certain lack in literature of a systematic study aimed in order to obtain parametric data on the different types of rotor-rotor interactions occurring in flight conditions typical of the eVTOL vehicles. In particular, there is a limited effort in the scientific literature regarding the investigation of aerodynamic interaction between rotors in tandem characterised by large longitudinal distance and a different degree of overlapping region between rotors that are typical characteristics of several eVTOL architectures. Moreover, there is a lack concerning research works that aimed to analyse the aerodynamic interaction of rotors in both tandem and side-by-side configurations for cruise flight conditions that are typical of eVTOLs aircraft.

Computational fluid dynamics (CFD) simulations represent a valuable tool for the investigation of this complex aerodynamic interactions. Indeed, high-fidelity CFD simulations were used in the work by Yoon et al. [7] to investigate the the performance and efficiency of multi-rotor systems with particular effort on the study of the effects of the separation distance between rotors, fuselage, and wings. Nevertheless, time-accurate URANS simulations of multi-rotor configurations still require a huge computational effort. Consequently, high-fidelity CFD simulations can not be considered to be the suitable tool for a systematic study of the different kinds of rotor-rotor interactions involved in eVTOLs aerodynamics. On the other hand, a mid-fidelity numerical approach combining different models and characterised by a low computational effort represents the best option for providing parametric data on the different types of rotor-rotor interactions and exploring a comprehensive range of space parameters. Several mid-fidelity aerodynamic solvers were developed in recent years with successful application to the study of rotary wing aerodynamics. To cite an example, DLR developed UPM code [8], an unsteady panel, and free-wake code originally intended for aeroacoustic simulations of helicopters but recently applied on arbitrary complex configurations as compound rotorcraft [9]. In particular, the use of vortex particle method (VPM) [10,11] for wake modelling enabled obtaining a better representation of the rotor aerodynamic characteristics and to capture the aerodynamic interactions between several bodies. Indeed, recent literature shows several works employing the VPM for the simulations of rotorcraft applications [12,13,14,15]. Concerning rotor-rotor interactions, Alvarez and Ning [16] used a mid-fidelity aerodynamic code based on VPM in order to simulate the side-by-side configuration of two propellers in hover investigated by Zhou et al. [3], finding good agreement with experiments for both the rotor performance and for the representation of the interacting flow fields.

A novel medium fidelity aerodynamic open-source software, called DUST (https://www.dust-project.org/), has been recently developed by Politecnico di Milano as the result of a collaboration with A³ by Airbus LLC. The code was thoroughly validated against experiments and high fidelity CFD on different rotorcraft configurations from simpler rotor-wing test cases to a full eVTOL vehicle. In particular, a recent work [17] showed that DUST simulations provide a quite good representation of both the performance and flow physics of a half-span tiltwing vehicle. These results were found when comparing the DUST simulations results with both wind tunnel data and high-fidelity CFD results. DUST was also used in a recent work [18] in order to simulate the aerodynamics of the full Vahana vehicle developed by A³ by Airbus LLC characterised by two rows of four rotors in tandem configuration. A quite good agreement between DUST simulations results and both flight test data and high-fidelity CFD results was found in this work for the full Vahana vehicle flight performance, particularly for cruise conditions. Thus, the results obtained confirm the suitability of mid-fidelity simulations performed with DUST for the study of the complex aerodynamic interactions that characterise multi-rotors aircraft configuration as eVTOLs. Consequently, DUST can be considered in a mature state to be used for the investigation of the rotor-rotor aerodynamic interactions that is the object of the present work.

Indeed, the present work aimed to provide a comprehensive analysis of the rotor-rotor aerodynamic interaction by means of mid-fidelity numerical simulations performed with DUST. In particular, the numerical simulations investigated the aerodynamic interactions between two propellers both in side-by-side and in tandem configuration. The low computational effort that is required by the mid-fidelity solver used in this activity enabled to study several tandem configurations characterised by both low and large longitudinal distances between the propellers and several degrees of overlapping between the rotor disks. In particular, the present numerical activity was focused on the cruise flight condition of an eVTOL aircraft.

The paper is organized, as follows. A brief outline of the numerical approach implemented in DUST is presented in Section 2 with a particular insight on the description of the lifting line elements used for blade modelling and of the VPM implemented for wake modelling. Section 3 provides the validation of the parameters used for DUST simulations by means of comparison of the numerical results with experimental data available in literature for a propeller model test case in forward flight conditions. Section 4 describes the numerical model that was implemented for the study of the interacting propellers and the test cases analysed in the numerical activity. Section 5 presents the discussion of the main results obtained by mid-fidelity simulations in terms of propeller performance and flow physics involved in the problem. Conclusions are drawn in Section 6.

2. Numerical Approach Implemented in DUST

DUST was developed in order to obtain a fast, flexible, and accurate numerical solver that is suitable to perform aerodynamic simulations of complex aircraft configurations capable to provide a reliable representation of interactional aerodynamic phenomena. DUST is a flexible aerodynamics tool allowing for simulating models with different levels of accuracy. In particular, the solver integrates thick surface panels, thin vortex lattices and lifting lines to model solid bodies, while panels and vortex particles can be used to model the wake. The vortex particles wake is accelerated while using a Fast Multipole Method (FMM) [19] that was developed to obtain a robust and accurate model to simulate interactional aerodynamics phenomena, particularly for multiple wake interactions or for interactions of wakes with solid bodies. The implementation of DUST employed the use of the Object Oriented paradigms of the latest Fortran standards in order to obtain a high level of flexibility to model a complex aircraft configuration made of several components and to describe their motion. The aerodynamic solver is based on the Helmholtz decomposition of the velocity field, $\overrightarrow{u}={\overrightarrow{u}}_{\phi }+{\overrightarrow{u}}_{\psi }$, where ${\overrightarrow{u}}_{\phi }$ and ${\overrightarrow{u}}_{\psi }$ are, respectively, the irrotational and solenoidal contributions. A time-stepping algorithm alternating the solution of a three-dimensional boundary element method for ${\overrightarrow{u}}_{\phi }$ and the Lagrangian time evolution of the rotational contribution of the velocity ${\overrightarrow{u}}_{\psi }$ is implemented for the solution advancing in time. In order to run the simulation the surface mesh only of the investigated object is required. Depending on the level of fidelity required, different aerodynamic elements can be used to discretise the model, in particular, lifting line elements, zero-thickness lifting surfaces, and surface panels. Surface panels are implemented while using a piecewise-uniform distribution of doublets and sources, according to a formulation for the velocity potential defined by Morino [20]. Moreover, zero-thickness surfaces of vortex lattice elements can be used in order to model thin lifting bodies. The result of the mixed potential-velocity formulation for the boundary element problem is a linear system where the unknowns are the doublet distribution intensity on the surface panels and the equivalent doublet intensity of the vortex lattice elements. In the following, a more detailed description of the lifting line elements used in the present work for the propeller blades modelling and of the implemented VPM used for rotor wake modelling is provided. A more detailed description of the numerical approach that was implemented in DUST is provided in [17,18].

2.1. Lifting Line Elements

The lifting bodies with high aspect ratio, as, for instance, rotor blades are properly modelled by one-dimensional lifting line elements. These elements naturally include viscous effects modelling, since they rely on tabulated aerodynamic performance of the two-dimensional sections of the modelled body. In particular, the aerodynamic tables are constituted by lift, drag and pitching moment coefficients as functions of the relative velocity direction and magnitude. Each lifting line element is constituted by a vortex ring along with its trailing vortices and the last line vortex are released in the wake aligned to the spanwise direction. The intensity Γ of the vortex ring, and therefore of the lifting line, is calculated through a fixed point algorithm that solves a nonlinear problem, connecting the lifting line elements intensity to the tabulated aerodynamic coefficients of the lifting sections. With this aim, DUST formulation implements both a loosely-coupled Γ-method [21] and a α-method [22] solver. The first method is based on the equivalence of the semi-empirical equation for the sectional lift with its analytical expression from the Kutta-Joukowski theorem,

$${\displaystyle \frac{1}{2}}\rho |U_{rel,i}{|}^2{c}_i{c}_{\ell ,i}\left({\mathbf{\alpha }}_i\left({\Gamma }_k\right)\right)=-\mathbf{\rho }\left|U_{rel,i}\right|{\Gamma }_i,$$

(1)

where $c_i$ is the $i^{th}$ section chord, $c_{\ell ,i}\left({\mathbf{\alpha }}_i\right)$ its lift curve, with ${\alpha }_i$ and $U_{rel,i}$ being the incidence angle and the relative velocity calculated at the control point of the $i^{th}$ lifting line. When considering that the lifting line element is positioned at $1/4$ of the chord, the control point is evaluated at $3/4$ of the chord [21,22]. In the latter method, the incidence angle resulting from the velocity field that is induced by all of the wake elements, including the particles and all the different lifting line elements constituting the model is considered as the input to find the corresponding aerodynamic coefficients in the two-dimensional tabulated aerodynamic data,

$${\alpha }_i=\mathrm{atan}2(U_{rel,i}\left({\mathbf{\alpha }}_k\right)·{\widehat{n}}_i,U_{rel,i}\left({\mathbf{\alpha }}_k\right)·{\widehat{t}}_i).$$

(2)

The nonlinear problem of computing the loads on lifting lines is solved through an iterative procedure that considers their mutual interference by means of the use of the Kutta–Joukowski theorem in order to evaluate the circulations of the elements from their lift.

2.2. Vortex Particle Method

The wake shed from the trailing edges by lifting bodies can be represented by vortex particles. The vortex particle [10,11] numerical modelling of the wake was introduced in order to provide a more robust representation of the interactional aerodynamics of both rotorcraft and complex aircraft configurations. The vortex particles method (VPM) is a Lagrangian grid-free method describing the wake evolution through the rotational component of the velocity field ${\overrightarrow{u}}_{\psi }$ by means of material vortex particles used to obtain the approximate vorticity field, as follows,

$${\displaystyle {\overrightarrow{\omega }}^h(\overrightarrow{r},t)=\sum _{p=1}^{N_p}{\overrightarrow{\alpha }}_p\left(t\right)\zeta \left(\overrightarrow{r}-{\overrightarrow{r}}_p\left(t\right);R_p\right),}$$

(3)

where ${\overrightarrow{r}}_p\left(t\right)$ is the position, ${\overrightarrow{\alpha }}_p\left(t\right)$ the intensity, and $R_p$ the radius of the p-th vortex particle, while $\zeta \left(r\right)$ is the cut-off function considering the vorticity distribution induced by each particle. By substituting (3) in the equation of the dynamics of vorticity,

$$\frac{D\overrightarrow{\omega }}{Dt}=\overrightarrow{\omega }·\nabla \overrightarrow{u}+\nu {\nabla }^2\overrightarrow{\omega },$$

(4)

the dynamical equations for the intensity ${\overrightarrow{\alpha }}_p\left(t\right)$ and position ${\overrightarrow{r}}_p\left(t\right)$ of all the material vortex particles to be integrated in time can be obtained, as follows,

$$\left\{\begin{array}{c}{\displaystyle \frac{d{\overrightarrow{\alpha }}_p}{dt}}={\overrightarrow{\alpha }}_p·\nabla \overrightarrow{u}({\overrightarrow{r}}_p\left(t\right),t)+\nu ″{\nabla }^2{\overrightarrow{\alpha }}_p″\hfill \\ {\displaystyle \frac{d{\overrightarrow{r}}_p}{dt}}=\overrightarrow{u}({\overrightarrow{r}}_p\left(t\right),t).\hfill \end{array}\right.$$

(5)

The viscosity diffusion term “${\nabla }^2{\overrightarrow{\alpha }}_p$” is calculated using the particle strength exchange method (PSE) that approximates the Laplacian operator acting on the vorticity field with an integral operator, as was described in [11].

The mathematical formulation used in the solver relies on the Helmholtz decomposition of the velocity field $\overrightarrow{u}={\overrightarrow{u}}_{\phi }+{\overrightarrow{u}}_{\psi }$. The irrotational velocity ${\overrightarrow{u}}_{\phi }$ is induced by the free stream velocity, by the singularity distributions of the source and doublet on the body surface and by the wake panels, while the rotational velocity ${\overrightarrow{u}}_{\psi }$ is induced by the vortex particles. Moreover, the solenoidal constraint on the rotational velocity, $\nabla \times {\overrightarrow{u}}_{\psi }=\overrightarrow{0}$, is used in order to define the vector potential $\overrightarrow{\psi }$, s.t. ${\overrightarrow{u}}_{\psi }=\overrightarrow{\nabla }\times \overrightarrow{\psi }$. Consequently, the Poisson’s equation is obtained for $\overrightarrow{\psi }$,

$$-{\nabla }^2\overrightarrow{\psi }=\overrightarrow{\omega },$$

(6)

considering the gauge condition $\nabla ·\overrightarrow{\psi }=0$, the vorticity field definition $\overrightarrow{\omega }=\nabla \times \overrightarrow{u}$ and the vector identity $\nabla \times {\overrightarrow{u}}_{\phi }=\nabla \times \nabla \phi =0$. The Poisson’s equation solution (6) reads

$$\overrightarrow{\psi }(\overrightarrow{r},t)={\int }_{V_0}G(\overrightarrow{r},{\overrightarrow{r}}_0)\overrightarrow{\omega }({\overrightarrow{r}}_0,t)d{V}_0,$$

(7)

$${\overrightarrow{u}}_{\psi }(\overrightarrow{r},t)={\int }_{V_0}\overrightarrow{K}(\overrightarrow{r},{\overrightarrow{r}}_0)\times \overrightarrow{\omega }({\overrightarrow{r}}_0,t)d{V}_0$$

(8)

where $G(\overrightarrow{r},{\overrightarrow{r}}_0)$ is the Green’s function of the Laplace equation and $\overrightarrow{K}(\overrightarrow{r},{\overrightarrow{r}}_0)$ represents its gradient with respect to the first argument.

Substituting the definition of the discretized vorticity field of the particles (3) into Equation (8), the contribution of velocity induced by the particles can be obtained, as follows,

$${\displaystyle {\overrightarrow{u}}_{\psi }^h(\overrightarrow{r},t)=\sum _{p=1}^{N_p}{\overrightarrow{K}}^h(\overrightarrow{r}-{\overrightarrow{r}}_p\left(t\right))\times {\overrightarrow{\alpha }}_p\left(t\right).}$$

(9)

The discrete kernel ${\overrightarrow{K}}^h(\overrightarrow{r}-{\overrightarrow{r}}_p\left(t\right))$ have to be consistent with the selected cutoff function $\zeta$. The cutoff function in the singular vortex particle method is a Dirac delta function and the Biot–Savart kernel is retrieved. In DUST implementation the selected cutoff function $\zeta$ leads to the Rosenhead-Moore kernel,

$${\overrightarrow{K}}^h(\overrightarrow{x},\overrightarrow{y})=-{\displaystyle \frac{1}{4\pi }}{\displaystyle \frac{\overrightarrow{x}-\overrightarrow{y}}{\left(\right|\overrightarrow{x}-\overrightarrow{y}{{|}^2+R_v^2)}^{3/2}}},$$

(10)

a regular kernel fitting naturally in the Cartesian fast multipole method (FMM) [19,23]. The induced rotational velocity ${\overrightarrow{u}}_{\psi }$ have to be accounted in the material objects convection and in the right-hand side of the linear system of equations for the potential velocity. Moreover, the velocity field gradient is calculated in order to evaluate the vortex stretching-tilting term with the FMM. Indeed, this term is a function of both the vortex intensities and particles distance in particle-to-particle interactions [11].

3. Validation of the DUST Simulations Parameters for a Propeller Test Case in Forward Flight Conditions

A validation study was performed by comparison with experimental data regarding a propeller model in forward flight in order to validate the DUST simulations parameters to be used for the simulation of the interacting propellers. The considered experimental data were obtained by McCrink and Gregory [24] for the APC thin-electric $10\times 7$ propeller in forward-flight conditions. A numerical model of the APC $10\times 7$ propeller was built for DUST simulations considering the airfoil geometry and the chord and twist distributions that were provided in the work by McCrink and Gregory [24]. Each of the two blades of the propeller was modelled using lifting lines elements, naturally including the viscosity contributions to aerodynamic loads through tabulated sectional aerodynamic data. The tabulated data of the blade airfoils were computed by XFOIL simulations [25], before stall angle of attack, while the Viterna method [26] was used in order to obtain the post-stall behaviour of the two-dimensional aerodynamic loads coefficients curves to cover the range $\pm {180}^{\circ }$ of angle of attack. DUST simulations reproduce a sweep of advance ratio J, defined as $J=V_{\infty }/\left(nD\right)$, where $V_{\infty }$ is the free-stream velocity, $n=RPM/60$ is the propeller rotational velocity, and D is the propeller diameter of 0.254 m. The rotational speed of the propeller was fixed to 9200 RPM corresponding to a tip Mach number ($M_t$) of 0.36 and a Reynolds number $R{e}_D=1.5·{10}^6$, where $R{e}_D=V_{70\%}D/\nu$ and $V_{70\%}$ is the effective velocity at 70% blade span. The propeller thrust (T) coefficient $C_T$, the torque (Q) coefficient $C_Q$, the power (P) coefficient $C_P$, and the propulsive efficiency $\eta$ considered throughout the paper for the results discussion are defined as

$$C_T=\frac{T}{\rho n^2{D}^4},\hspace{1em}\hspace{1em}{C}_Q=\frac{Q}{\rho n^2{D}^5},\hspace{1em}\hspace{1em}{C}_P=\frac{P}{\rho n^3{D}^5},\hspace{1em}\hspace{1em}\eta =J\frac{C_T}{C_P}.$$

(11)

A dependence study was performed for this test case due to the availability of experimental data in order to evaluate the optimal spatial and temporal discretization parameters for the propeller simulations. The full description of this study is reported in [27]. With this aim, numerical simulations were performed for $J=0.6$ fixing the spatial discretization to 20 lifting line elements for each blade and changing the time step throughout a simulation length of 10 rotor revolutions ($N_{rev}$). A minimum error of the computed $C_T$ with respect to the experimental value was found for a time discretization that corresponds to $5^{\circ }$ of blade azimuthal angle for each rotor revolution. Halving the time-step to $2.5^{\circ }$ the variation of the $C_T$ error was negligible. Subsequently, simulations were repeated fixing the time-step to $5^{\circ }$ of blade azimuthal angle for each rotor revolution and increasing the number of lifting line elements to model the blades. A minimum error of the computed $C_T$ with respect to the experimental value was found while using 40 lifting line elements. Consequently, numerical simulations for a sweep of J were performed while using the optimal parameters found from the spatial and temporal dependence study. In particular, simulations were advanced in time with a discretization of $5^{\circ }$ of blade azimuthal angle for each rotor revolution, while each blade was modelled using 40 lifting line elements.

Figure 2a shows the time histories of the thrust coefficient $C_T$ calculated by DUST throughout a simulation length of 10 rotor revolutions ($N_{rev}$) for the APC $10\times 7$ propeller at different advance ratios J. The curves behaviour shows that after five rotor revolutions the computed thrust coefficients reach a steady value for all of the advance ratio J, thus confirming that the number of rotor revolutions used for the simulations is quite enough to reproduce a fully developed wake of the propeller and obtain converged values of the propeller performance coefficients.

Figure 2b–d show the comparison of DUST simulations results with the experimental data from McCrink and Gregory [24] and the numerical results from Alvarez and Ning [16] obtained on the same test case with a VPM-based code. The DUST simulations results were obtained by averaging the $C_T$ and $C_P$ that were calculated over the last two rotor revolution.

The behaviour of the $C_T$, $C_Q$, and propulsive efficiency $\eta$ curves computed by DUST simulations is in quite good agreement with the experimental data. In particular, the DUST simulations showed a higher accuracy with respect to the results obtained by a similar VPM-based solver [16] for the evaluation of $C_T$ in the range of advance ratio between $J=0.4$ and $J=0.65$ and at low advance ratios (see Figure 2b). Concerning $C_Q$ evaluation, DUST showed the same quite good matching with experimental data for almost the whole range of advance ratios tested, with some discrepancies only observed at high advance ratios (see Figure 2c). The quite good agreement with experimental and numerical data available in literature observed in Figure 2d for the propulsive efficiency confirms that the parameters used to build the numerical model and run the simulations in DUST can be considered to be suitable for the study of a propeller model performance in forward-flight conditions. Therefore, the same parameters that were used for the APC propeller simulations in terms of time and space discretisations were used for the numerical study of the interacting propellers.

4. Numerical Model of the Interacting Propellers

The model used for the study of the rotor-rotor aerodynamic interactions is a three-bladed propeller equipped with a Varioprop 12C blade with a rotor radius R of 0.15 m. This hobby-grade model propeller was selected for this study, because is commercially available and provides dimensions that are suitable for performing experiments in a medium size wind tunnel for a thorough validation of the numerical investigation. The blade geometry was digitally created by 3D scanning of the blade model. CAD software was used in order to manage the generation of the blade geometry from the surfaces provided by the scanning system. Figure 3a shows the geometry of the blade where the coloured bar indicates an error below 0.1 mm between the reconstructed CAD geometry and the surfaces that were provided by the 3D scanner.

Figure 4 shows the twist, dihedral angle, and chord distributions along the blade radial coordinate (r). The propeller model used for this study is completed by a nacelle equipped with a 65 mm diameter spinner in order to reproduce the geometry of a eVTOL aircraft propeller. The airfoil sections and the nacelle geometry will be provided by request to the authors.

For DUST simulations, the propeller blades were modelled while using 40 lifting lines elements each and the tabulated aerodynamic coefficients before stall were provided by XFOIL simulations [25] that were computed on the airfoil sections provided by the three-dimensional (3D) scanning along the span. The Viterna method [26] was used to obtain the post-stall behaviour of the sectional aerodynamic loads coefficients to cover the range between $\pm {180}^{\circ }$ of angle of attack. The spinner-nacelle surface was modeled with 1212 surface panel elements. The layout of the numerical model, including the reference system used throughout the results discussion, is shown in Figure 3b. The origin (O) of the reference system $x-y-z$ is positioned on the center of the propeller disk, while the x axis is directed downstream and it is aligned with the free-stream velocity vector. In all of the simulations, the longitudinal axis of the nacelle is aligned with free-stream velocity vector.

Description of the Analysed Interacting Propellers Configurations

The numerical activity was focused on the study of two propellers in both tandem and side-by-side configurations in forward flight, with particular attention on the typical cruise flight velocity of eVTOL urban air mobility vehicles that can be considered in the order of 100 km per hour (i.e., $V_{\infty }$ = 28 m/s). In all of the simulations, the rotational speed of both the propellers was fixed to 7000 RPM to reproduce the full-scale tip Mach number ($M_t=0.32$) of a eVTOL aircraft in cruise [2]. The Reynolds number calculated on the base of the propeller disk diameter and on the rotational velocity evaluated at 70% R is $R{e}_D=1.93\times {10}^6$. The blade pitch angle at 75% of the rotor radius was fixed to $\theta =25.5^{\circ }$ for both the interacting propellers. In order to reproduce cruise flight conditions of eVTOLs, the simulations were performed with the propellers aligned to the freestream velocity vector. In the following, the longitudinal distance along x axis between the rotor disks planes is defined as $L_x$, while the lateral distance between the propellers shaft axis is defined as $L_y$, as shown in the layout of the interacting configurations presented in Figure 5.

A preliminary simulation of the single propeller was performed in order to obtain the reference performance for comparison with the interacting configurations results.

The investigation of the side-by-side propellers interaction was focused on the advance ratio $J=0.8$ that corresponds to a freestream velocity of $V_{\infty }$ = 28 m/s, considered the target cruise velocity for eVTOLs. In particular, numerical simulations were performed for two counter-rotating propellers with rotor disks lying on the same $y-z$ plane ($L_x=0$) at different lateral separation distances that range from $L_y=2.05R$ (blade tips distance equal to 0.05R) to $L_y=4R$.

The tandem interaction was investigated when considering two co-rotating propellers positioned with two different longitudinal distances between the rotor disks. In particular, simulations were performed with a longitudinal distance of 6 rotor radii ($L_x=6R$) between the tandem propellers disks in order to reproduce the configuration of a Vahana-like aircraft (see Figure 1b). Moreover, in order to evaluate the effect of the longitudinal distance on the rotor-rotor interaction, simulations were performed also with $L_x=2.5R$ reproducing the configuration of a more compact propulsive system that characterise for instance the Bell-Nexus 6HX aircraft architecture (see Figure 1c). A sweep along y axis was considered to evaluate the effect of the interaction due to a different overlapping area between the tandem propellers disks. In particular, the simulations reproduce a lateral sweep that ranges from the configuration where the propellers disks are completely ($L_y=0$) to a separation distance between the propellers shaft axis of two rotor radii ($L_y=2R$). Becasue of the low computational effort of the mid-fidelity approach, all of the tandem simulations were performed for a sweep of advance ratios J between 0.4 and 0.9 with a step of 0.1.

Table 1. Summary of the configurations analysed by DUST simulations.

	$\mathit{RPM}$	${\mathit{\theta }}_{75\%\mathit{R}}$	J	${\mathit{L}}_{\mathit{x}}$ [R]	${\mathit{L}}_{\mathit{y}}$ [R]
Single Prop	7000	$25.5^{\circ }$	[0.4, 0.5, 0.6, 0.7, 0.8, 0.9]	-	-
Side-by-side Props	7000	$25.5^{\circ }$	0.8	0	[2.05, 2.15, 2.25, 2.4, 2.5, 2.7, 3, 3.3, 3.5, 4]
Tandem Props	7000	$25.5^{\circ }$	[0.4, 0.5, 0.6, 0.7, 0.8, 0.9]	[2.5, 6]	[0, 0.25, 0.5, 1, 1.5, 2]

summarises the configuration parameters of the DUST simulations performed in this numerical activity. In particular, as done for the APC propeller numerical analysis, the interacting propellers simulations were performed for a length of 10 rotors revolutions with a time discretisation of $5^{\circ }$ of blade azimuthal angle. A fully developed wake for the interacting propellers test cases consisted of around one million vortex particles. The computational time of the simulation of a single interacting configuration while using a workstation with a 18 cores processor was approximately 40 min for both the tandem and side-by-side test conditions.

5. Results and Discussion

5.1. Side-by-Side Propellers Configuration

In this section, the results that were obtained for the side-by-side propellers simulations are presented. In particular, the effect of the lateral distance between the rotor disks is discussed by means of comparison of the performance coefficients and by means of the analysis of the interacting flow field.

Figure 6a shows the time histories of the thrust coefficient $C_T$ calculated for the counter-clockwise rotating propeller in side-by-side configuration (upper propeller of Figure 5a) at some different lateral distances $L_y$ as compared to the results that were obtained from the single propeller simulation.

The $C_T$ curves behaviour shows that after a transient of four revolutions, the results that were obtained for the side-by-side propellers simulations reach a periodic behaviour, while the single propeller simulation reaches a converged steady state value. The periodic behaviour obtained for the side-by-side simulations reflects the physics of the aerodynamic interaction between the propellers that is the object of this study, thus confirming the suitability of the numerical model considered to investigate this problem. The periodicity of the $C_T$ curves is particularly evident in the last three revolutions of the simulations, thus the load coefficients considered in the following discussion were obtained as the averaged values that were calculated over this time interval.

Figure 6b shows the averaged thrust coefficient $C_T$, power coefficient $C_P$ and propulsive efficiency $\eta$ computed for the propeller in side-by-side configuration normalized with respect to the corresponding parameters evaluated from the single rotor simulation. The average performance of the propellers in side-by-side configuration are negligibly affected by the aerodynamic interaction, as can be observed in Figure 6b. Indeed, a loss of performance lower than 1% of the single propeller is observed for both thrust, power and propulsive efficiency when the propellers hubs are at a lateral distance $L_y=2.05R$. Increasing the lateral distance $L_y$, the propeller resumes the performance of the single propeller configuration. The amount of thrust loss that was calculated in the present activity at high advance ratio is slightly lower than the outcomes of the works by Zhou et al. [3] and by Alvarez et al. [16] for side-by-side propellers at similar separation distance but in hover condition. Even if the effects on the average performance of the propellers can be considered negligible, an interesting effect of the aerodynamic interaction between the propellers is the fluctuation of the loads occurring during a rotor revolution. An indication of the loads fluctuations amplitude is provided by the standard deviation of the $C_T$ and $C_P$ computed over the last three revolutions plotted as errorbars in Figure 6c,d. This representation shows that the amplitude of the loads fluctuations is quite high when the lateral separation distance between the propellers is small. Indeed, when the distance between the propellers blades tips are equal to 0.05, a robust interaction between the tip vortices is expected, as will be discussed in the following analysis of the instantaneous flow fields. As the separation distance increases, the thrust and power coefficients for the side-by-side propellers approach the values of the single propeller configuration, while the load fluctuations amplitude decreases.

In order to provide a more detailed analysis of the local performance of the propeller blades at $L_y=2.05R$, Figure 7 shows the difference of the sectional lift coefficient $C_l$ and the effective angle of attack ${\alpha }_{eff}$ experienced by a propeller blade in side-by-side configuration with respect to the single rotor configuration that was computed during the last revolution.

The polar plot of the effective angle of attack variation $\Delta {\alpha }_{eff}$ indicates that around $\psi =0^{\circ }$, corresponding to the azimuthal angle where the tip-to-tip distance of the side-by-side blades is 0.05R, the blade experiences a slight increase of angle of attack at the tip region with respect to the single propeller condition (see Figure 7a). Consequently, the loads that act on the blade tip region increase along the azimuthal range of the rotor revolution, where the side-by-side propeller blades approach each other. Consequently, an increase of the sectional $C_l$ with respect to the single propeller configuration is observed at the blade tip region around $\psi =0^{\circ }$ (see Figure 7b). On the other hand, a slight decrease of the effective angle of attack is experienced by almost all the blade sections in the range of azimuthal angle between ${300}^{\circ }<\psi <{330}^{\circ }$ with a consequent decrease of the blade loading. The local behaviour of these quantities along the blade revolution reflects the fluctuations that were observed in the computed time history of the side-by side propeller thrust shown in Figure 6a.

Detailed insight regarding the flow physics involved in the side-by-side aerodynamic interaction is provided by the analysis of the propellers wake computed for the configuration characterised by the greatest interaction ($L_y=2.05R$) when compared to the single propeller condition. In particular, Figure 8 shows the contours of the average freestream velocity component (u) calculated over the last rotor revolution on the $x-y$ plane for the single propeller and side-by-side propellers with lateral separation distance $L_y=2.05R$.

Figure 8 shows that the propeller wake in side-by-side configuration slightly expands, starting from a distance of 0.5R downstream the rotor disk. Consequently, a merging of the propellers wakes occurs at about 3.5R, thus producing an increase of the resulting flow speed in this region, if compared to the single propeller case. These features were also observed in the experiments by Zhou et al. [3] performed in hover conditions, but occurring further upstream with respect to the present case. Further details of the flow physics of the side-by-side interaction are obtained analysing the instantaneous flow field calculated at $\psi =0^{\circ }$, corresponding to the azimuthal angle along rotor revolution where the interacting blades axis are aligned and the tip-to-tip distance is equal to 0.05R. Figure 9 shows the iso-surface of the instantaneous vorticity magnitude calculated at $\psi =0^{\circ }$ for the side-by-side configuration with $L_y=2.05$. This flow representation clearly shows the interaction between the vortices that are released by the tips of the counter-rotating propellers that leads to the merging of the iso-vorticity tubes in the region of the wake between the propellers.

A more detailed analysis of this vortex interaction can be provided by the comparison of the contours of the in-plane vorticity shown on $x-y$ plane in Figure 9. The single propeller wake is characterised by the periodic shed of counter-rotating tip vortices that are dragged downstream by the freestream velocity and conserve their relative distance showing a slow rate of dissipation throughout the entire area of investigation, as can be observed in Figure 10a. For the side-by-side interaction case, the tip vortices were found to merge starting from the distance $X/R=0.5R$ downstream the propellers disks and dissipate much faster with respect to the single propeller case. Indeed, starting from a distance of $X/R=1R$ downstream the propellers disks, the vortices loose their coherent structures and they are nearly unrecognizable in the region of the wake between the propellers.

5.2. Tandem Propellers Configuration

In this section, the results that were obtained for the tandem propellers simulations are presented. In particular, the effect of the longitudinal distance between the propellers and the effect of the different degree of overlapping between the rotor disks is discussed by means of comparison of the computed performance coefficients and the analysis of the interacting flow field.

Figure 11 shows the time histories of the thrust coefficient $C_T$ computed for the rear propeller (right propeller of Figure 5b) in tandem configuration with different lateral distances $L_y$ and advance ratio $J=0.8$. In particular, the thrust time histories are shown for both the two longitudinal distances $L_x$ considered in the numerical activity and compared with the results that were obtained for the single propeller.

The $C_T$ curves behaviour clearly reflects that the rear propeller is invested by the wake of the front one at different time instances due to the different longitudinal distance between the propellers disks. In particular, the rear propeller thrust coefficient reaches a periodic behaviour after almost two and four rotor revolutions, respectively, for the longitudinal distance $L_x=2.5R$ and $L_x=6R$. This periodic behaviour of the computed thrust reflects the beginning of the aerodynamic interaction between the tandem propellers wakes. In particular, the aerodynamic interaction becomes stronger when the rotor disks are partially overlapped, as clearly shown by the large amplitude of the $C_T$ fluctuations computed for $L_y=0.5R$ and $L_y=1R$. On the other hand, the thrust fluctuations are almost negligible when the rotor disks are completely overlapped ($L_y=0$). As the periodicity of the loads is particularly evident over the last three revolutions of the simulations, in the following discussion the load coefficients were obtained as the averaged values calculated over this time interval.

Figure 12 shows the averaged thrust coefficient $C_T$, power coefficient $C_P$, and propulsive efficiency $\eta$ of the rear propeller as function of the advance ratio J for both the considered longitudinal distances $L_x$ and the different lateral distances $L_y$ between the propellers disks. As can be observed from the comparison of the curves that are shown in Figure 12, the performance of the rear propeller strongly decrease when the lateral separation of the two propellers is reduced. This behaviour is apparent in the whole range of advance ratio investigated in this activity. In particular, for both the longitudinal distances $L_x$ the highest loss of performance is obtained when the two propeller disks are completely overlapped ($L_y=0$). By increasing the lateral distance between the propellers, the loss of the rear propeller performance decreases, as for lateral distance $L_y=2R$ the performance curves resume the behaviour of the single rotor ones, thus confirming that, for this lateral separation, the interactional aerodynamic effects are almost negligible due to the fact that the rear rotor is unaffected by the front rotor slipstream. Moreover, the behaviour of the propulsive efficiency curves shows that the occurrence of their peaks is not affected by the tandem interaction. Indeed, for both the longitudinal distances $L_x$, the peak of the rear propeller propulsive efficiency $\eta$ remains at $J=0.8$ for all of the analysed lateral distances $L_y$.

A more detailed analysis of the rear propeller performance in tandem configuration is provided in the following for $J=0.8$, the advance ratio corresponding to the freestream velocity considered as the target cruise velocity of urban air mobility eVTOL aircraft. In particular, Figure 13a shows the normalised thrust coefficient $C_T$, power coefficient $C_P$, and propulsive efficiency $\eta$ of the rear propeller with respect to the corresponding parameters that were evaluated from the single rotor simulation. The effect of the rotor-rotor interaction on rear propeller performance is further when the degree of overlapping between the rotor disks increases, while the interactional effects become negligible when the lateral separation distance is equal to the propeller diameter ($L_y=2R$). In particular, the higher loss of performance due to the interaction is observed when the propeller disks are completely overlapped ($L_y=0$), where a decrease of about 45% and of more than 30%, respectively, of the thrust and power coefficients is observed for the rear propeller at $L_x=6R$ with respect to the single propeller case. These losses lead to a reduction of about 20% of the propulsive efficiency of the rear propeller in the same tandem configuration. The effect of a lower longitudinal separation distance between the propellers is a slight decrease of the performance loss in the order of few percents of both the thrust and power coefficients of the single propeller. Indeed, for the tandem configuration with $L_x=2.5R$, a reduction of 15% of the propulsive efficiency is observed. Moreover, Figure 13a shows that, for both the longitudinal distances between the propellers, the gradient of the performance loss is higher in the spatial range between $L_y=0$ and $L_y=1R$.

In order to analyse the effect of this aerodynamic interaction on the behaviour of the rear propeller loads over a rotor revolution, Figure 13b,c show the averaged $C_T$ and $C_P$ curves calculated at $J=0.8$ for both the longitudinal distances $L_x$ with errorbars representing the standard deviation of the coefficients computed over the last three revolutions. The amplitude of the loads fluctuations is higher when the lateral separation distance between the propellers is $L_y=1R$, as can be observed from these figures. In particular, for this tandem configuration, the loads fluctuation amplitude is an order of magnitude higher than the largest value that was observed in the side-by-side configuration. The loads fluctuations level of the $C_T$ and $C_P$ decreases when the degree of overlapping between the propellers disks increases and become negligible when the propellers disks are completely overlapped. Moreover, for lateral separation distances higher than $L_y=1R$, the thrust and power coefficients of the rear propeller in tandem approach the values of the single propeller configuration, while the loads fluctuations amplitude decreases.

A better insight of the effects of the aerodynamic interaction on the propeller performance already discussed is provided by Figure 14 and Figure 15, showing the distributions of the differences of the axial velocity $u_a$, tangential velocity $u_t$, effective angle of attack ${\alpha }_{eff}$, and sectional lift coefficient $C_l$ of a rear propeller blade in tandem configuration with respect to the single rotor configuration computed during the last revolution. In particular, this analysis was performed for the test cases with lateral distances $L_y=0,0.5R,1R$, showing the greatest interaction effects on the rear propeller aerodynamic performance, as shown in Figure 13.

For the test configuration with the propeller disks completely overlapped ($L_y=0$) and longitudinal distance $L_x=2.5R$, the rear propeller blade experiences an increase of the axial velocity component with respect to freestream velocity due to the ingestion of the front propeller slipstream. This effect is particularly apparent in the outer spanwise region of the propeller blade, where the variation of the axial velocity component with respect to the single propeller reaches a value of about 5 m/s (see Figure 14a). The interaction with the front propeller slipstream also provides a slight negative variation of the tangential velocity experienced by the rear propeller blade in tandem with respect to the single propeller condition (see Figure 14d). These combined effects produce a reduction of the local effective angle of attack seen by a large region of the rear propeller blade along span (see Figure 14g). Consequently, a large reduction of the sectional lift coefficient is observed in the same spanwise region of the rear blade (see Figure 14j), thus reflecting the large loss of the average thrust calculated for this tandem configuration, as shown in Figure 13a. In particular, the axial-symmetrical behaviour that was observed for $\Delta C_l$ along propeller azimuthal angle explains the negligible amount of the loads fluctuation calculated for this tandem configuration. Similar behaviours of these variable distributions are observed for this configuration at $L_x=6R$. In particular, due to the larger longitudinal distance between the propellers, the rear blade experiences a slightly larger increase of the axial velocity with respect to the test case with $L_x=2.5R$ as the front propeller slipstream is further developed. This effect provides a slight higher decrease of the effective angle of attack seen by the rear propeller blade at $L_x=6R$ and a consequent slight increase of the rear propeller performance loss with respect to the configuration with lower longitudinal distance ($L_x=2.5R$), as shown by the average loads coefficients comparison in Figure 13.

For the test configuration with $L_y=0.5R$, the polar plots that are shown in Figure 5 and Figure 15 loose their axial-symmetrical behaviour, as the rear propeller disk in partially invested by the front propeller slipstream. For both the longitudinal distances tested, a conspicuous increase of the axial velocity component with respect to freestream component is observed along almost the whole blade span, particularly in the azimuthal region of the rotor revolution between $\psi ={190}^{\circ }$ and $\psi ={230}^{\circ }$.

This effect is due to the local acceleration of the front propeller slipstream that was provided by cambered shape of the nacelle-spinner, as will be shown later in the flow visualization of Figure 19. On the other hand, a small reduction of the axial velocity is observed on the outer blade span region in the range between $\psi =0^{\circ }$ and $\psi ={180}^{\circ }$ (see Figure 14b and Figure 15b), where the effect of the front propeller slipstream is negligible due to the relative position of the rotor disks. The effect of the front propeller wake interaction does not provide an apparent modification of the tangential velocity on the rear propeller blade with the exception of a smaller spanwise area of the blade that is interested by the ingestion of the outer region of the front propeller slipstream characterised by high swirl. In particular, due to the lower distance between the propellers, the rear propeller blade at $L_x=2.5R$ experiences higher peaks of tangential velocity variations with respect to the tandem configuration with $L_x=6R$ (see Figure 14e and Figure 15e). The more apparent effect of the combination of the axial and tangential velocity distributions is a reduction of the effective angle of attack seen by the almost all of the rear blade sections in the azimuthal angle ranges ${190}^{\circ }<\psi <{230}^{\circ }$ and ${330}^{\circ }<\psi <{360}^{\circ }$ (see Figure 14h and Figure 15h). Consequently, a quite large negative variation of the rear blade sectional lift coefficient distributions is observed in these regions with respect to the single propeller configuration (see Figure 14k and Figure 15k), thus reflecting the remarkable amount of the loads fluctuation amplitude calculated for this tandem configuration (see Figure 13). The small difference between the average thrust losses that were calculated for the different longitudinal distances at $L_y=0.5R$ is justified by the quite similar local behaviour observed for the spanwise sectional lift coefficient. Indeed, for this lateral distance the effect of the longitudinal distance between the propellers on the slipstream velocity components ingested by the rear propeller blade is quite small.

For the test configuration with $L_y=1R$, the effects of the front propeller slipstream on the rear propeller blade is smaller with respect to the previous analysed configuration due to the lower degree of overlapping between the propellers disks in tandem. In particular, the most evident effects of this interaction is observed in the azimuthal angle range of the rotor revolution between $\psi ={180}^{\circ }$ and $\psi ={360}^{\circ }$. For both of the longitudinal distances tested, the axial velocity component behaviour shows a concentrated increase in this azimuthal angle range due to the local acceleration of the front propeller slipstream in this areaprovided by the curvature of the nacelle-spinner surface (see Figure 14c and Figure 15c), as will be shown later in the flow visualization of Figure 22. In the same region, the interaction of the front propeller slipstream provides a large increase of the tangential velocity (see Figure 14f and Figure 15f), thus the combination of these velocity components variations provides a remarkable decrease of the effective angle of attack seen by the rear blade sections in the ranges ${210}^{\circ }<\psi <{240}^{\circ }$ and ${300}^{\circ }<\psi <{330}^{\circ }$ (see Figure 14i and Figure 15i) and a consequent high variation of the sectional lift in the same areas. The behaviour of the sectional lift variation reflects the larger amplitude of the loads fluctuations observed for this tandem configuration (see Figure 13). Additionally, for this lateral distance, a quite low effect due to the longitudinal distance is observed from the representations of the analysed local quantities reflecting the results comparison in terms of the average rear propeller performance.

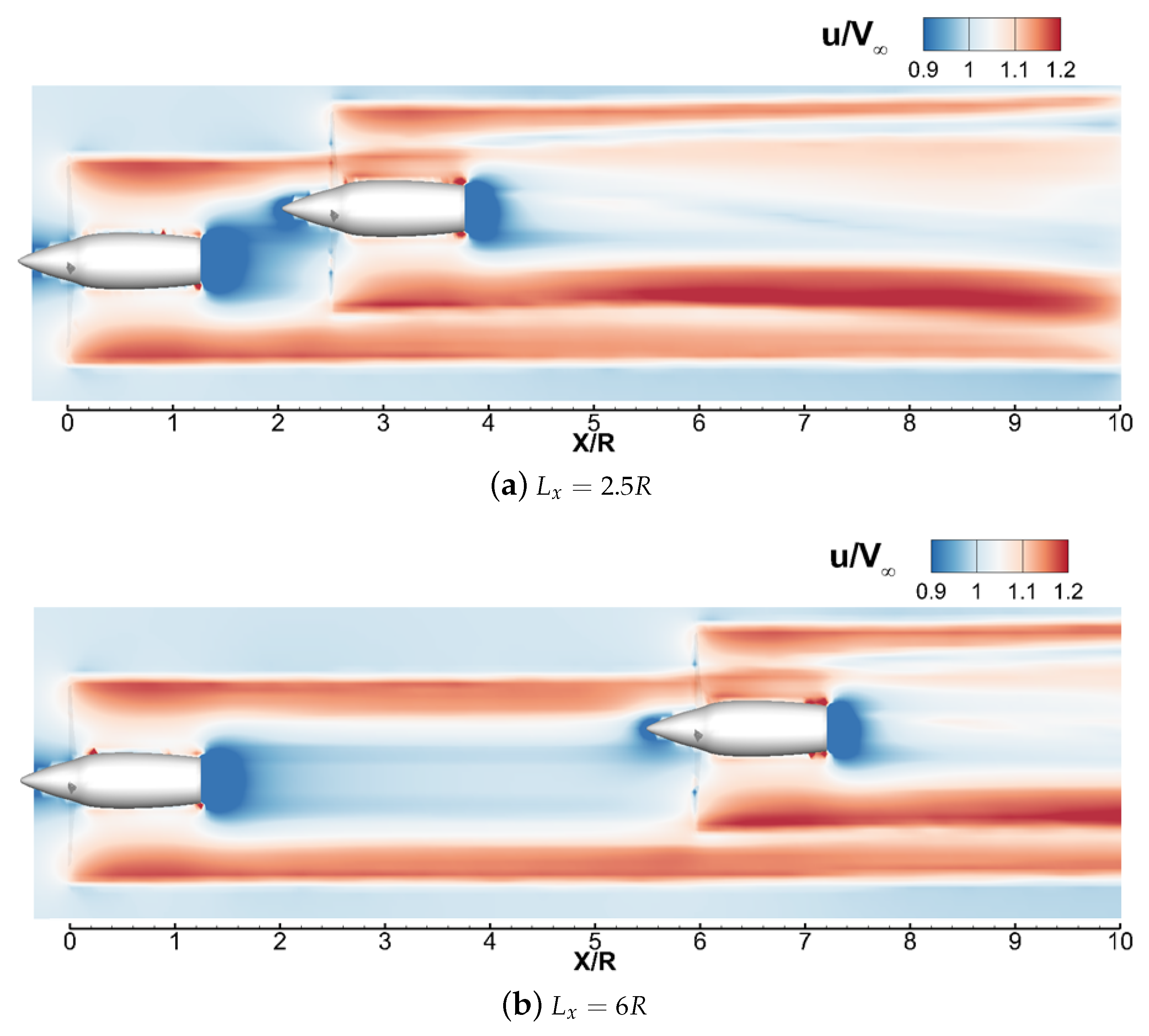
Global insight regarding the flow physics that are involved in the aerodynamic interaction for the investigated tandem configurations is provided by the following analysis of the propellers wakes computed at $J=0.8$ for the same lateral distances $L_y=0,0.5R,1R$ discussed before. For the test configuration with the propeller disks completely overlapped ($L_y=0$), Figure 16 shows the contours of the average freestream velocity component (u) calculated over the last rotor revolution on the $x-y$ plane. The averaged flow fields clearly show that, for both the longitudinal distances $L_x$, the wake of the rear propeller is quite faster at the tip region of the rotor disk with respect to the front propeller one. Indeed, the co-axial configuration of the two propellers provides a combination of the accelerated flow regions passing through the outer regions of the propeller disks.

A more detailed understanding of the flow physics that are involved in the wakes interaction is obtained by the instantaneous flow field shown for the azimuthal angle $\psi =0^{\circ }$ in Figure 17 by means of the iso-surfaces of the instantaneous vorticity magnitude. This flow representation clearly shows that, for both of the considered distances $L_x$, the interaction between the propellers wakes does not affect the coherence of the helical structure of vorticity released by the rear propeller. In particular, an increase of the iso-vorticity tubes is observed downstream the rear propeller due to the coalescence of the vortical structures that are released by the two co-axial propellers in tandem.

Figure 18 shows more details of the aerodynamic interaction by means of the contours of the in-plane vorticity calculated on the $x-y$ from the instantaneous flow field at $\psi =0^{\circ }$.

Because, in the present simulations, the blades of the propellers in tandem are co-rotating and synchronised, the tip vortices shed by the front propeller blades interact with the ones released by the rear propeller providing downstream the rotor disk co-rotating vortical structures that are characterised by higher vorticity and larger core. This feature is observed for both the longitudinal distances analysed, but for $L_x=2.5R$ the resulting vortical structures show a higher level of vorticity with respect to the configuration with $L_x=6R$. Indeed, the vortices released by the front propeller blades are less dissipated when they interact with the ones released by the rear propeller, due to the lower longitudinal distance between the propellers. This feature is highlighted by the higher intensity of red that characterise the representation of the vortex investing the tip region of the rear propeller blade for $L_x=2.5R$ with respect to the test configuration with $L_x=6R$ (see Figure 18a,b).

For the tandem configuration with lateral distance $L_y=0.5$, the averaged flow fields that are presented in Figure 19 show an asymmetrical behaviour of the rear propeller wake with respect to the longitudinal axis due to the interaction with the front propeller slipstream. Indeed, for this configuration the rear propeller disk is only partially invested by the front propeller slipstream, thus the lower region of the rear propeller wake is accelerated by the effect of the front propeller wake. This effect is particularly evident for the lower longitudinal distance $L_x=2.5R$. Moreover, the upper region of the front propeller slipstream is dragged upward and locally accelerated by the the cambered shape of the nacelle-spinner surface.

The three-dimensional representation of the instantaneous flow field provided by the iso-surfaces of vorticity in Figure 20 shows, for this configuration ($L_y=0.5R$), a stronger interaction between the vortical structures released the propeller blades with respect to the test case where the propeller disks are completely overlapped ($L_y=0$). Indeed, for both the longitudinal distances between the propellers the helical structures of vorticity released by the rear propeller blades loose their coherence due to the interaction.

More details regarding the interaction of the propellers wakes is provided by the representation of the in-plane vorticity contours that are shown in Figure 21. A relevant effect of the interaction is that the upper region of the front propeller wake diverges upward due to the presence of the rear propeller nacelle. Therefore, in the upper region past, the rear propeller disk the vortices that are released by the front propeller blades are dragged toward the ones released by the rear propeller, thus producing a pairing of the co-rotating vortices that provides the winding of the shear layer into a series of counter-rotating vortices. This feature is observed for both the longitudinal distances of the propellers in tandem.

For the tandem configuration with lateral distance $L_y=1R$, the averaged flow field presented in Figure 22 shows an asymmetrical behaviour of the rear propeller wake similarly to what was found for $L_y=0.5R$. In particular, for this test case, due to the higher degree of overlapping between the propeller disks, the upper region of the front propeller slipstream is dragged downward and locally accelerated by the presence of the rear propeller nacelle. Thus, an increase of the area of accelerated flow can be observed in the lower region of the rear propeller wake. This effect is more pronounced for the tandem configuration with $L_x=2.5R$.

The instantaneous flow representation that is provided by the iso-surfaces of vorticity shows, similarly to the test case with $L_y=0.5R$, that the wakes interaction produces a break of the coherent helical structures released by the rear propeller blades (see Figure 23. In particular, the in-plane vorticity field presented in Figure 24 shows that for this lateral distance ($L_y=1R$) the tip vortices shed by the front propeller blades dissipate once they impinge the rear propeller nacelle nose. Indeed, the trace of these vortices is negligible downstream the rear propeller disk.

6. Conclusions

A numerical activity was performed in order to investigate the rotor-rotor aerodynamic interaction that is typical of the novel architectures of eVTOL aircraft designed for urban air mobility. With this aim, a systematic study of the aerodynamic interaction of two propellers both in side-side and tandem configurations was performed while using a mid-fidelity aerodynamic solver. The low computational effort required by the solver enabled to simulate a comprehensive set of propellers configurations at different advance ratios, thus providing a comprehensive numerical database to eVTOL research community to be used to drive the design of new unconventional aircraft configurations. In particular, the numerical simulations enabled investigating the effects of these kinds of aerodynamic interactions both on propellers performance and flow physics involved. The discussion was particularly focused on the results that were obtained for the propellers advance ratio corresponding to the target cruise velocity of a eVTOL aircraft in urban areas.

The main results that were obtained from the side-by-side simulations showed that the greatest effect of the aerodynamic interaction on the propellers performance is reached at the lowest lateral separation distance between them. In particular, a slight reduction of the average propeller thrust and propulsive efficiency below 1% was found for the interacting case with respect to the single propeller configuration. On the other hand, a high amplitude of load fluctuations is observed for this test condition that could provide a drawback for aeroacoustic issues. Moreover, the visualizations of the instantaneous flow field illustrate the strong interaction between the tip vortices that were released by the two side propellers.

A more comprehensive investigation was performed for the tandem configuration that aimed to evaluate the different effect of the aerodynamic interaction due to the longitudinal and lateral distance between the propellers at several advance ratios. The results analysis, focused on the advance ratio corresponding to the target cruise speed of eVTOLs, showed that a remarkable decrease of the rear propeller performance is observed due to this aerodynamic interaction. In particular, a loss of the average thrust of the rear propeller in tandem in the order of 40% with respect to the single propeller and a reduction of about 20% of the propulsive efficiency was found when the propellers disks are completely overlapped. In particular, the effect of a lower longitudinal distance between the propellers is a slight reduction of the performance losses on the rear propeller. The performance losses that were evaluated on the rear propeller in tandem were discussed, analysing the axial and tangential velocity components of the slipstream investing the rear propeller blade during a rotor revolution and the consequent distributions of the effective angle of attack seen by the blade propeller sections and the sectional loads. The analysis of the local loads acting on the rear propeller blade shows that a partial overlapping between the propellers in tandem provides a lower effect on the average loads, but a larger amplitude of loads fluctuation along a rotor revolution with respect to the co-axial configuration. Moreover, a deeper insight regarding the flow physics that are involved in the interaction between the wakes of the two propellers in tandem was provided by means of the analysis of the averaged and instantaneous flow fields for the three lateral separation distances between the propellers characterised by the highest effects on the rear propeller performance. The flow fields analysis illustrated how the front propeller slipstream interacts with the wake of the rear propeller, showing, in particular, the pairing between the tip vortices that are released by the two propellers that occur when the rotor disks are co-axial or present a low degree of overlapping.