The Allocation of Carbon Intensity Reduction Target by 2030 among Cities in China
Abstract
1. Introduction
2. Literature Review
2.1. Research Progress on Carbon Emissions at the City Level
2.2. Carbon Reduction Target Allocation Method
2.3. Contribution of this Article
3. Materials and Methods
3.1. Technical Route of the Research
3.2. Construction of a Carbon Intensity Reduction Target Allocation Index System
3.2.1. Economic Factors
3.2.2. Population Factors
3.2.3. Energy Factors
3.2.4. Technological Factors
3.3. Construction of Total Allocation Method
3.3.1. Entropy Method
3.3.2. Improved Equal-Proportion Distribution Method
3.4. Data Source and Processing
4. Results
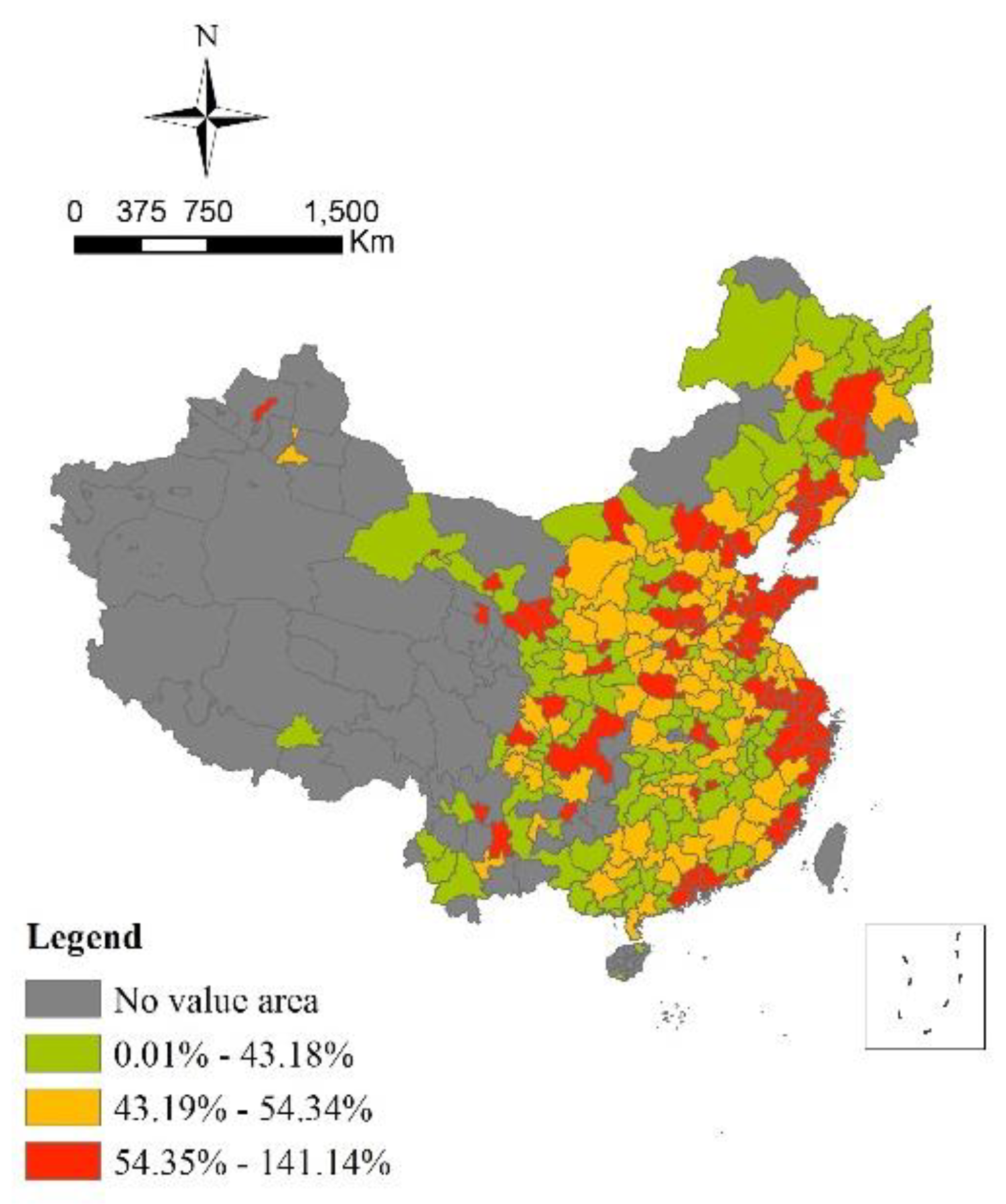
4.1. CITRR in Each City
4.2. Spatial Correlation Analysis of CITRR of Each City
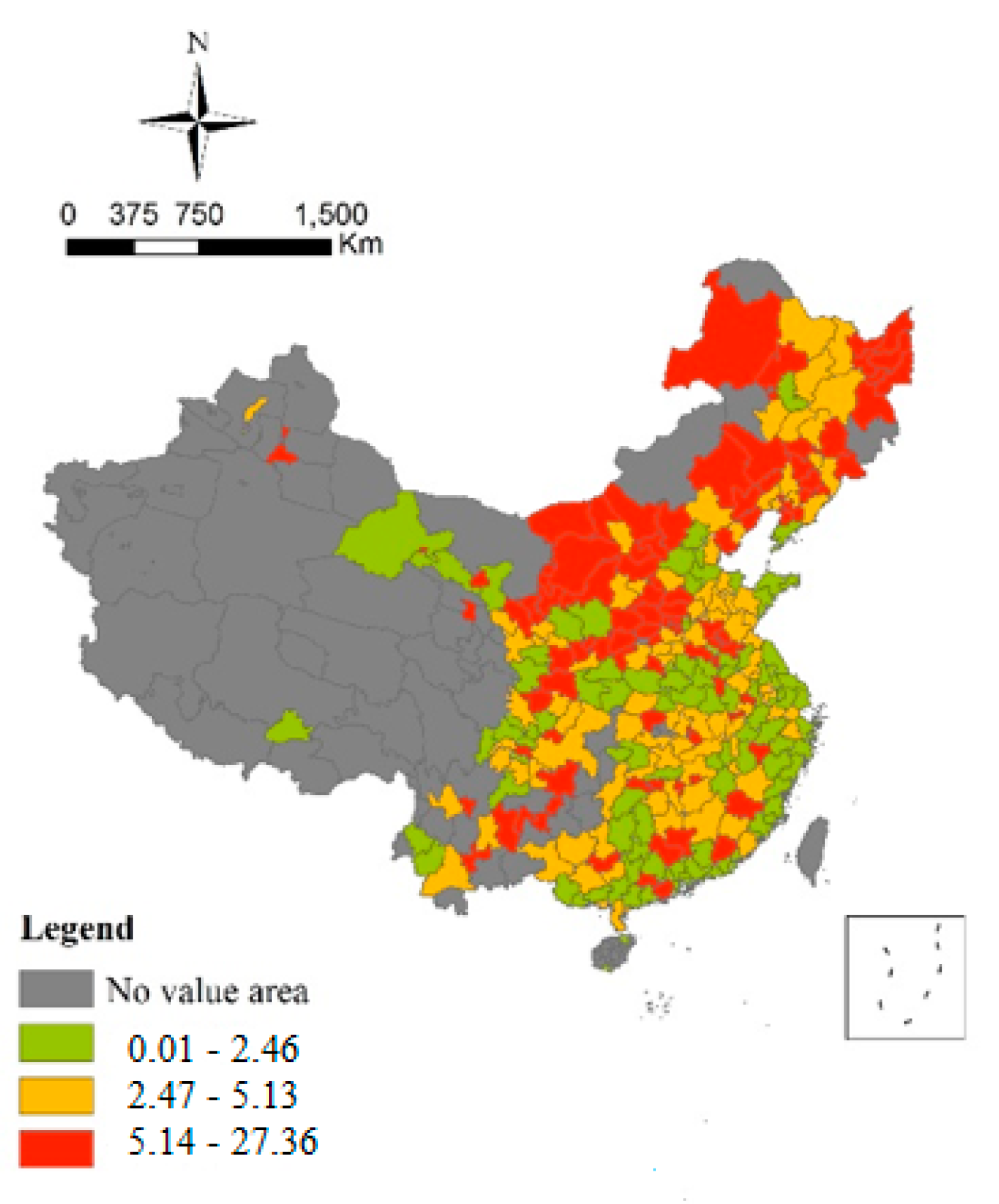
4.3. The Relationship between Carbon Intensity and CITRR
5. Discussion
5.1. Non-Proportional Allocation
5.2. CITRR and Economic Development
5.3. Spatial Correlation
5.4. Method Deficiencies
6. Conclusions
- The range of changes in the CITRR is relatively large across the nation. The southeast coast is an area with developed economy and technological capabilities and a high-level CITRR. North China is a resource-rich economy that develops rapidly and has a high-level carbon intensity and a low-level CITRR. Cities should choose differentiated low-carbon development paths combining their resource endowments, industrial structure, economic foundation, and other aspects of heterogeneous characteristics.
- The CITRR of city presents significant spatial positive correlation. When formulating carbon emission reduction policies, the spatial effects of carbon emissions in each city should be fully considered. In addition to considering the city’s own carbon emission reduction, the carbon emission reduction situation of neighboring cities should be comprehensively considered, for mobilizing the demonstration and leadership of economically developed regions in emission reduction are conducive to the steady advancement of carbon emission reduction.
- In summary, the allocation method considers fairness and efficiency, reflects the difference between cities, and the allocation result is more easily accepted by all parties. Meanwhile, this method breaks the limitation of data and is likely to be implemented in practical operation, providing a new way for the allocation of carbon emission reduction targets.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Noah, S.D. Changes in ecologically critical terrestrial climate conditions. Science 2013, 341, 486–492. [Google Scholar]
- Rogelj, J.; Elzen, M.D.; Höhne, N.; Fransen, T.; Fekete, N.H.H.; Winkler, H.; Schaeffer, R.; Sha, F.; Riahi, J.R.K.; Meinshausen, M. Paris Agreement climate proposals need a boost to keep warming well below 2 °C. Nat. Cell Biol. 2016, 534, 631–639. [Google Scholar] [CrossRef] [PubMed]
- Global Carbon Atlas. CO2 Emissions Data. Available online: http://www.globalcarbonatlas.org/en/CO2-emissions (accessed on 4 October 2020).
- Gallagher, K.S.; Zhang, F.; Orvis, R.; Rissman, J.; Liu, Q. Assessing the Policy gaps for achieving China’s climate targets in the Paris Agreement. Nat. Commun. 2019, 10, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Elzen, M.D.; Fekete, H.; Höhne, N.; Admiraal, A.; Forsell, N.; Hof, A.F.; Olivier, J.G.; Roelfsema, M.; Van Soest, H. Greenhouse gas emissions from current and enhanced policies of China until 2030: Can emissions peak before 2030? Energy Policy 2016, 89, 224–236. [Google Scholar] [CrossRef]
- Liu, C.; Cai, B.; Chen, C.; Wang, H.; Li, Z.; Beijing Municipal Research Institute of Environmental Protection; Center for Climate and Environmental Policy, Chinese Academy for Environmental Planning. Review of Carbon Mitigation Targets Allocation in China. Sci. Geogr. Sin. 2013, 33, 9. (In Chinese) [Google Scholar]
- Kong, Y.; Zhao, T.; Yuan, R.; Chen, C. Allocation of carbon emission quotas in Chinese provinces based on equality and efficiency principles. J. Clean. Prod. 2019, 211, 222–232. [Google Scholar] [CrossRef]
- Liang, S.; Zhao, J.; He, S.; Xu, Q.; Ma, X. Spatial econometric analysis of carbon emission intensity in Chinese provinces from the perspective of innovation-driven. Environ. Sci. Pollut. Res. 2019, 26, 13878–13895. [Google Scholar] [CrossRef]
- Gu, C.; Tan, Z.; Liu, W.; Yu, T.; Han, Q.; Liu, H.; Dai, Y.; Liu, Z.; Zheng, S. Study on Climate Change, Carbon Emissions and Low-carbon City Planning. Urban Plan. Forum 2009, 3, 38–45. (In Chinese) [Google Scholar]
- He, Y. Chinese Energy Carbon Dioxide Emissions Control Objectives and Geographical Distribution Statistics; Southwestern University of Finance and Economics: Chengdu, China, 2013. (In Chinese) [Google Scholar]
- Jotzo, F.; Pezzey, J.C.V. Optimal intensity targets for greenhouse gas emissions trading under uncertainty. Environ. Resour. Econ. 2007, 38, 259–284. [Google Scholar] [CrossRef]
- Zheng, B.; Zhang, Q.; Davis, S.J.; Ciais, P.; Hong, C.; Li, M.; Liu, F.; Tong, D.; Li, H.; He, K. Infrastructure Shapes Differences in the Carbon Intensities of Chinese Cities. Environ. Sci. Technol. 2018, 52, 6032–6041. [Google Scholar] [CrossRef]
- Shan, Y.; Guan, D.; Hubacek, K.; Zheng, B.; Davis, S.J.; Jia, L.; Liu, J.; Liu, Z.; Fromer, N.; Mi, Z.; et al. City-level climate change mitigation in China. Sci. Adv. 2018, 4, eaaq0390. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Liu, X. China’s city-level energy-related CO2 emissions: Spatiotemporal patterns and driving forces. Appl. Energy 2017, 200, 204–214. [Google Scholar] [CrossRef]
- Wang, S.; Huang, Y.; Zhou, Y. Spatial spillover effect and driving forces of carbon emission intensity at the city level in China. J. Geogr. Sci. 2019, 29, 231–252. [Google Scholar] [CrossRef]
- Li, S. Accounting for the Overall Carbon Emission Allowance and Its Cross-Administraive Regional Allocation: A Case of Zhejiang Province; Zhejiang University: Hangzhou, China, 2019. (In Chinese) [Google Scholar]
- Chang, K.; Chang, H. Cutting CO2 intensity targets of interprovincial emissions trading in China. Appl. Energy 2016, 163, 211–221. [Google Scholar] [CrossRef]
- Qin, Q.; Liu, Y.; Li, X.; Li, H. A multi-criteria decision analysis model for carbon emission quota allocation in China’s east coastal areas: Efficiency and equity. J. Clean. Prod. 2017, 168, 410–419. [Google Scholar] [CrossRef]
- Feng, Z.; Tang, W.; Niu, Z.; Wu, Q. Bi-level allocation of carbon emission permits based on clustering analysis and weighted voting: A case study in China. Appl. Energy 2018, 228, 1122–1135. [Google Scholar] [CrossRef]
- Zhang, Y.-J.; Wang, A.-D.; Da, Y.-B. Regional allocation of carbon emission quotas in China: Evidence from the Shapley value method. Energy Policy 2014, 74, 454–464. [Google Scholar] [CrossRef]
- Zhang, J.; Hao, J.-F. Carbon emission quota allocation among China’s industrial sectors based on the equity and efficiency principles. Ann. Oper. Res. 2016, 255, 117–140. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, Q. Pollutant Reduction Alloction Based on Regional Differences—COD Reduction Allocation Between Provinces as a Case. Resour. Environ. Yangtze Basin 2012, 21, 512–517. (In Chinese) [Google Scholar]
- Wang, Q.; Zhao, X. Allocation of carbon dioxide emission reduction targets in China based on the improved equal proportion distribution. J. Arid Land Resour. Environ. 2019, 33, 1–8. (In Chinese) [Google Scholar]
- Zhao, R.; Min, N.; Geng, Y.; He, Y. Allocation of carbon emissions among industries/sectors: An emissions intensity reduction constrained approach. J. Clean. Prod. 2017, 142, 3083–3094. [Google Scholar] [CrossRef]
- Grossman, G.M.; Krueger, A.B. Environmental Impacts of a North American Free Trade Agreement; National Bureau of Economic Research: Cambridge, MA, USA, 1991. [Google Scholar]
- Magazzino, C.; Cerulli, G. The determinants of CO2 emissions in MENA countries: A responsiveness scores approach. Int. J. Sustain. Dev. World Ecol. 2019, 26, 522–534. [Google Scholar] [CrossRef]
- Ang, B.; Liu, N. A cross-country analysis of aggregate energy and carbon intensities. Energy Policy 2006, 34, 2398–2404. [Google Scholar] [CrossRef]
- Sustainable Development Strategy Study Group Chinese Academy of Sciences. China Sustainable Development Strategy Report 2009—China’s Approach towards a Low Carbon Future; Science Press: Beijing, China, 2009. (In Chinese) [Google Scholar]
- Chang, N. Changing industrial structure to reduce carbon dioxide emissions: A Chinese application. J. Clean. Prod. 2015, 103, 40–48. [Google Scholar] [CrossRef]
- Huang, J. Investigating the driving forces of China’s carbon intensity based on a dynamic spatial model. Environ. Sci. Pollut. Res. 2018, 25, 21833–21843. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, B.; Liu, T. Empirical analysis on the factors influencing national and regional carbon intensity in China. Renew. Sustain. Energy Rev. 2016, 55, 34–42. [Google Scholar] [CrossRef]
- Li, J.; Huang, X.; Yang, H.; Chuai, X.; Wu, C. Convergence of carbon intensity in the Yangtze River Delta, China. Habitat Int. 2017, 60, 58–68. [Google Scholar] [CrossRef]
- Zhao, X.; Burnett, J.W.; Fletcher, J.J. Spatial analysis of China province-level CO2 emission intensity. Renew. Sustain. Energy Rev. 2014, 33, 1–10. [Google Scholar] [CrossRef]
- Hao, Y.; Liao, H.; Wei, Y.-M. Is China’s carbon reduction target allocation reasonable? An analysis based on carbon intensity convergence. Appl. Energy 2015, 142, 229–239. [Google Scholar] [CrossRef]
- Dong, F.; Long, R.; Li, Z.; Dai, Y. Analysis of carbon emission intensity, urbanization and energy mix: Evidence from China. Nat. Hazards 2016, 82, 1375–1391. [Google Scholar] [CrossRef]
- Zhu, B.; Ye, S.; Jiang, M.; Wang, P.; Wu, Z.; Xie, R.; Chevallier, J.; Wei, Y.-M. Achieving the carbon intensity target of China: A least squares support vector machine with mixture kernel function approach. Appl. Energy 2019, 233, 196–207. [Google Scholar] [CrossRef]
- Soimakallio, S.; Saikku, L. CO2 emissions attributed to annual average electricity consumption in OECD (the Organisation for Economic Co-operation and Development) countries. Energy 2012, 38, 13–20. [Google Scholar] [CrossRef]
- Zhang, H. Effects of electricity consumption on carbon intensity across Chinese manufacturing sectors. Environ. Sci. Pollut. Res. 2019, 26, 27414–27434. [Google Scholar] [CrossRef] [PubMed]
- Jaffe, A.B.; Newell, R.G.; Stavins, R.N. A tale of two market failures: Technology and environmental policy. Ecol. Econ. 2005, 54, 164–174. [Google Scholar] [CrossRef]
- Vollebergh, H.R.; Kemfert, C. The role of technological change for a sustainable development. Ecol. Econ. 2005, 54, 133–147. [Google Scholar] [CrossRef]
- Apergis, N.; Eleftheriou, S.; Payne, J.E. The relationship between international financial reporting standards, carbon emissions, and R&D expenditures: Evidence from European manufacturing firms. Ecol. Econ. 2013, 88, 57–66. [Google Scholar] [CrossRef]
- Berkhout, P.H.; Muskens, J.C.; Velthuijsen, J.W. Defining the rebound effect. Energy Policy 2000, 28, 425–432. [Google Scholar] [CrossRef]
- China City Greenhouse Gas Working Group. China City CO2 Emissions Dataset (2005); China Environment Publishing Group: Beijing, China, 2020. (In Chinese) [Google Scholar]
- Poo, M.-M. Scientific leap-forward in the critical period: The thirteenth Five-Year Plan of the Chinese Academy of Sciences (CAS). Natl. Sci. Rev. 2016, 3, 393. [Google Scholar] [CrossRef][Green Version]
- The World Bank; Development Research Center of the State Council PRC. China 2030: Building a Modern, Harmonious, and Creative Society; World Bank Publications: Beijing, China, 2013. [Google Scholar]
- Qian, Y.; Sun, L.; Qiu, Q.; Tang, L.; Shang, X.; Lu, C. Analysis of CO2 Drivers and Emissions Forecast in a Typical Industry-Oriented County: Changxing County, China. Energies 2020, 13, 1212. [Google Scholar] [CrossRef]
- Pan, W.; Zhang, R.; Pan, Y. CO2 emissions in coastal and inland regions in China:Perspectives based on the final products. J. Tsinghua Univ. Sci. Technol. 2016, 56, 417–423. (In Chinese) [Google Scholar]
- Wang, K.; Lu, M.; Wang, Q. The impact of the COVID-19 epidemic on China’s CO2 emissions. J. Beijing Inst. Technol. Soc. Sci. Ed. 2020, 4, 11–16. (In Chinese) [Google Scholar]
- Le Quéré, C.; Jackson, R.B.; Jones, M.W.; Smith, A.J.P.; Abernethy, S.; Andrew, R.; De-Gol, A.J.; Willis, D.R.; Shan, Y.; Canadell, J.G.; et al. Temporary reduction in daily global CO2 emissions during the COVID-19 forced confinement. Nat. Clim. Chang. 2020, 10, 647–653. [Google Scholar] [CrossRef]
- Smith, L.V.; Tarui, N.; Yamagata, T. Assessing the Impact of COVID-19 on Global Fossil Fuel Consumption and CO2 Emissions. SSRN Electron. J. 2020. [Google Scholar] [CrossRef]
- Xu, J.; Xu, Y. Analysis of Chinese Regional Carbon Emissions Based on Spatial Panel Data. Ecol. Econ. 2015, 31, 32–36. (In Chinese) [Google Scholar]
- Hou, L.; Tang, L.; Qian, Y.; Chen, H.; Wang, L. Study of county-level low-carbon standards in China based on carbon emissions per capita. Int. J. Sustain. Dev. World Ecol. 2019, 26, 698–707. [Google Scholar] [CrossRef]

| Method | Principle | Advantage | Disadvantage | |
|---|---|---|---|---|
| Index Method | Single index method | Select a certain index for quantitative allocation. | Much easier to understand and operate, the results are intuitive. | It is one-sided and only reflect one factor of carbon emission right, which easily to produce extreme results. |
| Multi-index method | Two or more indexes are selected for quantitative allocation. | It is widely used and takes into account the multiple factors of carbon emission rights allocation. | The index weight and its dynamic adjustment have direct influence on the final allocation result. | |
| Game Theory | The allocation weight is determined according to the contribution of each emission subject to the overall. | Consider the contribution and demand differences of each subject. | The operation is complex, transparency and feasibility is questionable. | |
| DEA Method | Estimate the relative efficiency based on the input and output factors of different emission subjects. | The allocation result can achieve the highest overall allocation efficiency. | Excessive emphasis on the maximization of distributive efficiency, the results may lack fairness and rationality, which may to be questioned by people. | |
| Improved Equal-Proportion Distribution Method | Make adjustments based on differences between regions and the overall average reduction, so that the emission reduction tasks undertaken by each region match its own conditions. | Considering the objective difference of each region, it is easy to implement in practice. | It is impossible to measure the potential contribution of specific policy measures to achieving the carbon intensity target. | |
| Integrated | Multiple methods or models are used for allocation. | gather the advantages of a variety of methods. | The process is complex, the operation is difficult, each link may exist deviation, high uncertainty. | |
| Factors Affecting Carbon Strength | Index | Index Connotation | Index Attribute |
|---|---|---|---|
| Economic Factors | GDP Per-capita | Reflect the level of economic development | + |
| Proportion of secondary industry | Reflect industrial structure | + | |
| Population Factors | Total population | Reflect the total population | + |
| Agricultural/ Non-agricultural population | Reflect demographic structure | − | |
| Energy Factors | Ten thousand yuan of gross output power consumption | Reflect energy consumption | + |
| Technological Factors | Scientific financial expenditure/local financial general budget expenditure | Reflect investment in scientific research | + |
| Index | Weight |
|---|---|
| GDP per-capita | 0.253 |
| Proportion of secondary industry | 0.047 |
| Total population | 0.172 |
| Agricultural/Non-agricultural population | 0.042 |
| Ten thousand yuan of gross output power consumption | 0.285 |
| Scientific financial expenditure/ local financial general budget expenditure | 0.200 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, L.; Yang, F.; Gao, L. The Allocation of Carbon Intensity Reduction Target by 2030 among Cities in China. Energies 2020, 13, 6006. https://doi.org/10.3390/en13226006
Shi L, Yang F, Gao L. The Allocation of Carbon Intensity Reduction Target by 2030 among Cities in China. Energies. 2020; 13(22):6006. https://doi.org/10.3390/en13226006
Chicago/Turabian StyleShi, Longyu, Fengmei Yang, and Lijie Gao. 2020. "The Allocation of Carbon Intensity Reduction Target by 2030 among Cities in China" Energies 13, no. 22: 6006. https://doi.org/10.3390/en13226006
APA StyleShi, L., Yang, F., & Gao, L. (2020). The Allocation of Carbon Intensity Reduction Target by 2030 among Cities in China. Energies, 13(22), 6006. https://doi.org/10.3390/en13226006




