Experimental and Artificial Intelligence Modelling Study of Oil Palm Trunk Sap Fermentation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation and Mechanical Pretreatment of the Oil Palm Trunk
2.2. Chemical Experiments and Analysis
2.3. Artificial Intelligence Model
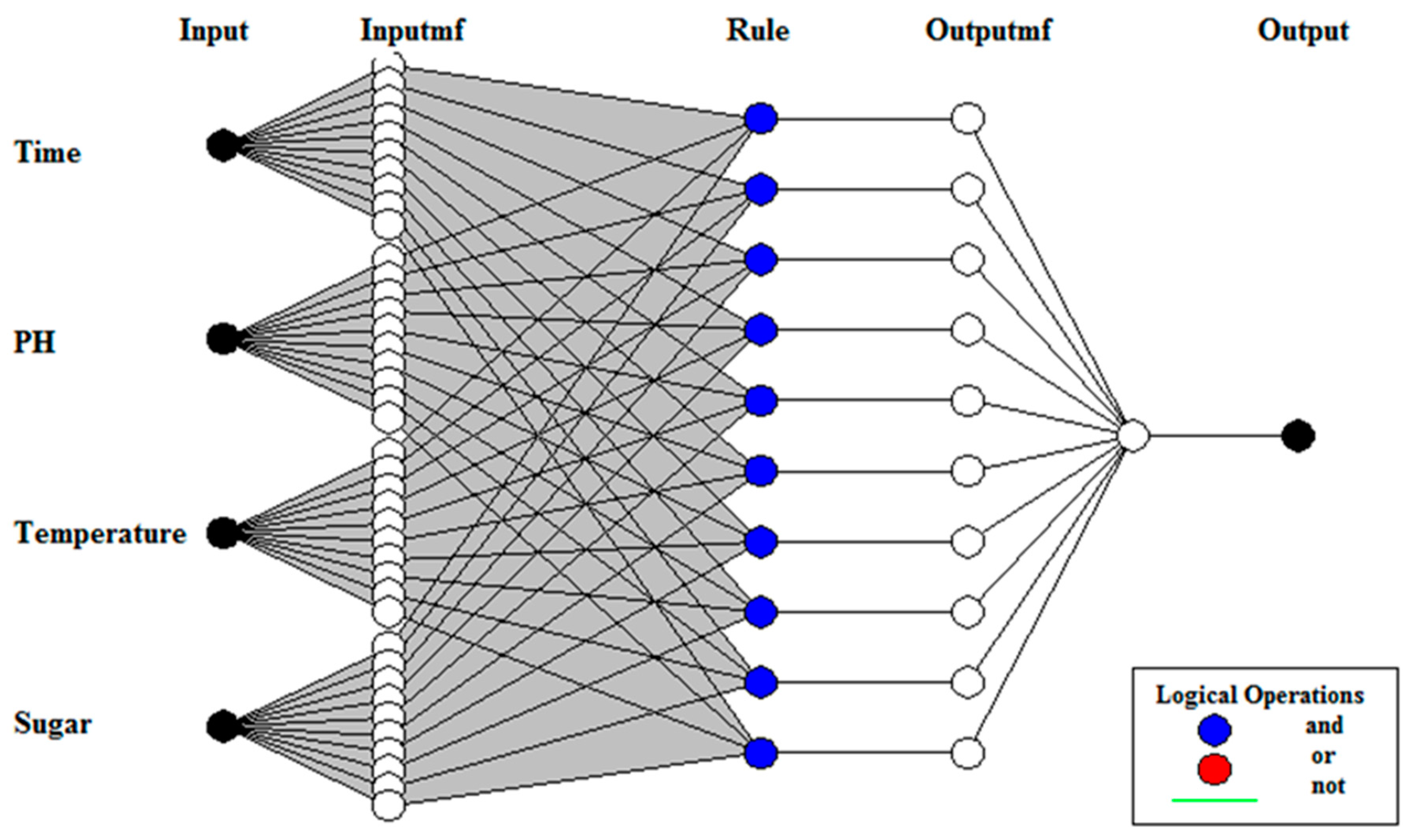
2.3.1. Adaptive Neuro-Fuzzy Inference System
2.3.2. Particle Swarm Optimisation Method
2.3.3. Proposed Modelling of Hybrid ANFIS and PSO
3. Results and Discussion
3.1. Effect of the Input Variables on the Response
3.2. Optimisation of Experimental Conditions
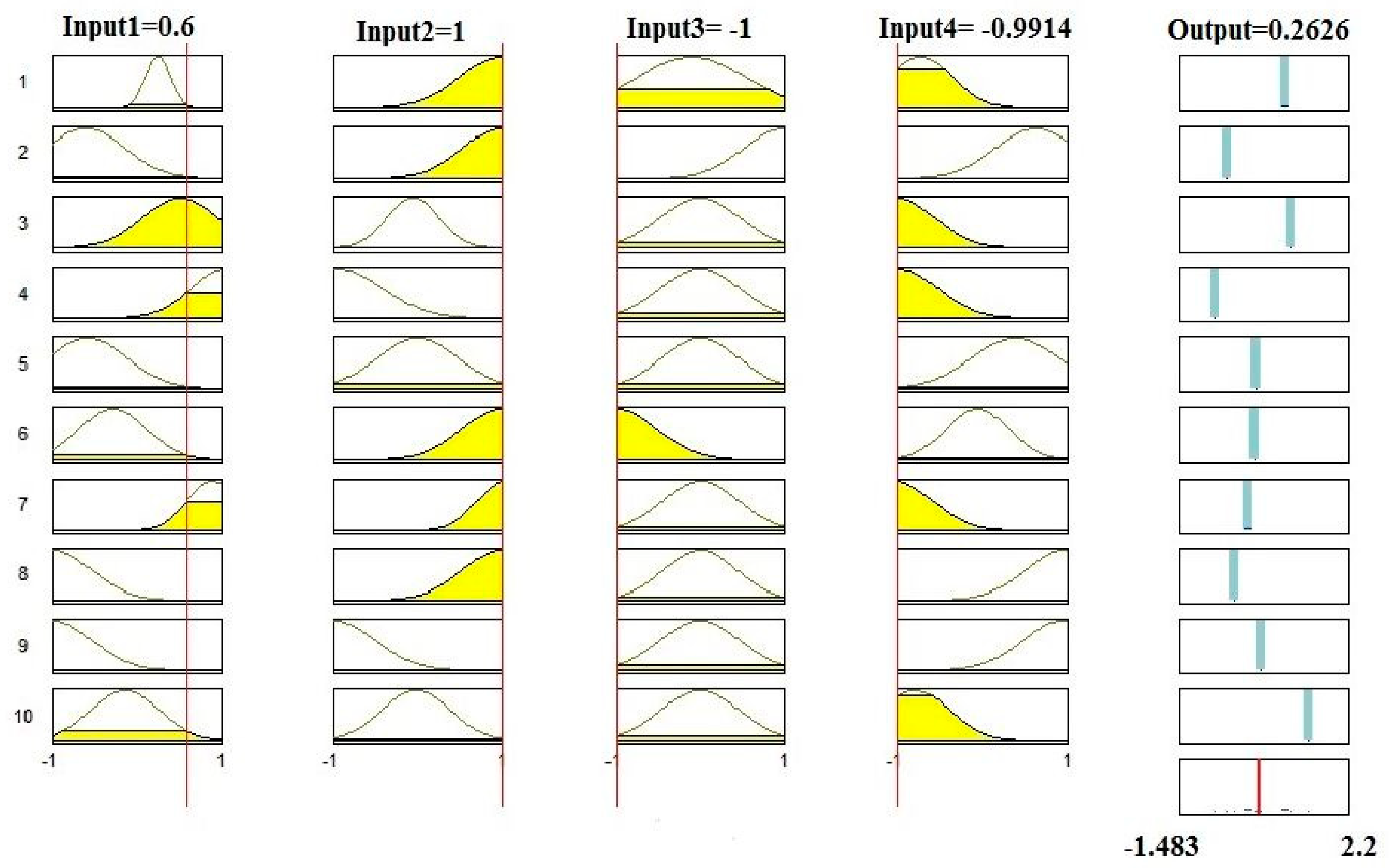
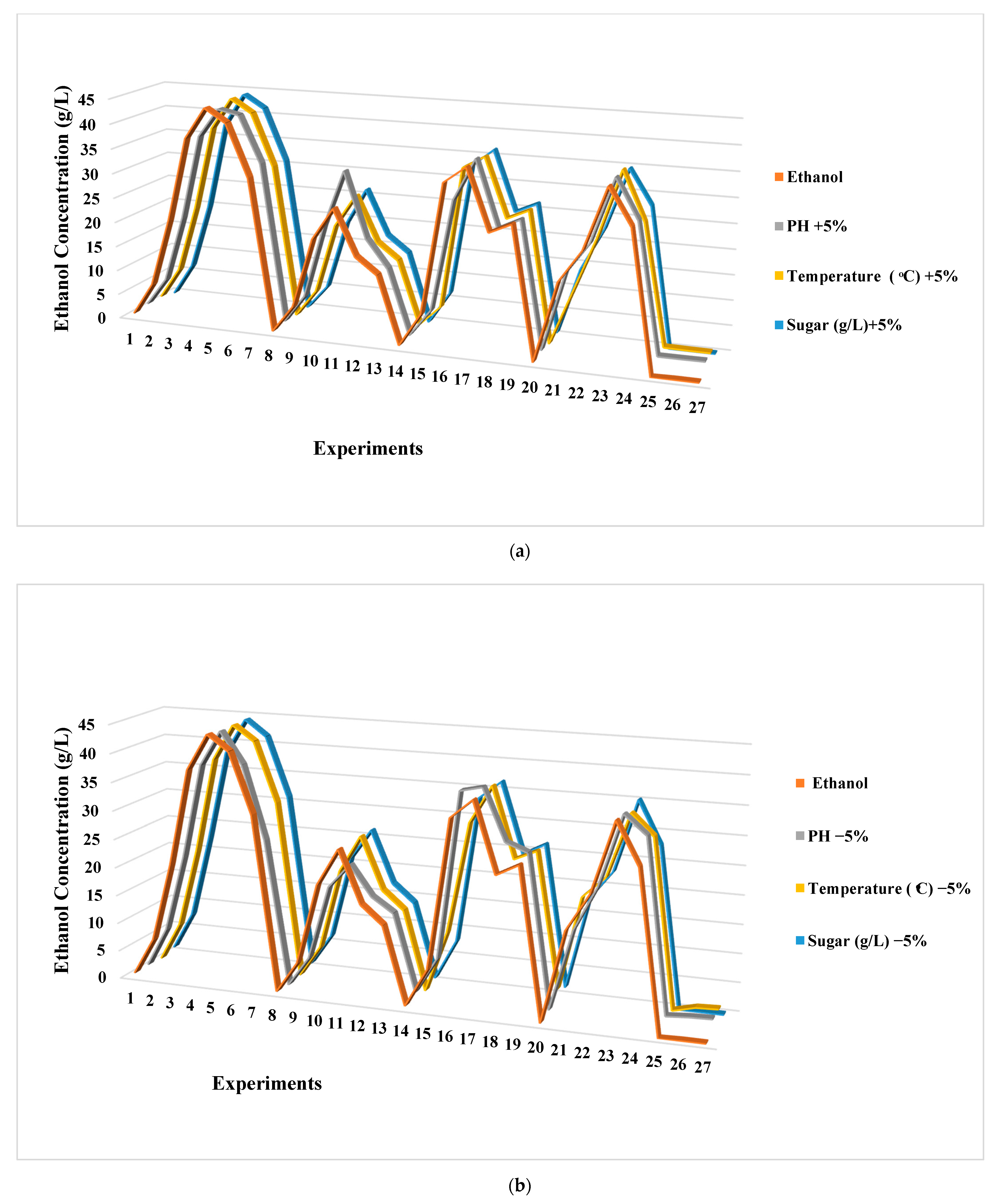
3.3. Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| AAE | Average Absolute Error |
| ARE | Absolute Relative Error |
| AARE% | Average Absolute Relative Error |
| ANFIS | Adaptive-Network-Based Fuzzy Inference System |
| ANN | Artificial Neural Network |
| DOE | Design of Experiment |
| GP | Genetic Programming |
| HPLC | High-Performance Liquid Chromatography |
| MSE | Mean Square Error |
| OPTS | Oil Palm Trunk Sap |
| PSO | Particle Swarm Optimization |
| R | Correlation Coefficient |
| RMSE | Root Mean Square Error |
| RSM | Respond Surface Methodology |
| TSK | Takagi–Sugeno–Kang |
| YPD | Yeast Peptone Dextrose |
References
- Kwiatkowski, J.R.; McAloon, A.J.; Taylor, F.; Johnston, D.B. Modeling the process and costs of fuel ethanol production by the corn dry-grind process. Ind. Crop. Prod. 2006, 23, 288–296. [Google Scholar] [CrossRef]
- Lübken, M.; Gehring, T.; Wichern, M. Microbiological fermentation of lignocellulosic biomass: Current state and prospects of mathematical modeling. Appl. Microbiol. Biotechnol. 2010, 85, 1643–1652. [Google Scholar] [CrossRef]
- Yang, Q.; Gao, H.; Zhang, W.; Chi, Z.; Yi, Z. A new data-driven modeling method for fermentation processes. Chemom. Intell. Lab. Syst. 2016, 152, 88–96. [Google Scholar] [CrossRef]
- bin Mohd Zain, M.Z.; Kanesan, J.; Kendall, G.; Chuah, J.H. Optimization of fed-batch fermentation processes using the Backtracking Search Algorithm. Expert Syst. Appl. 2018, 91, 286–297. [Google Scholar] [CrossRef]
- Lübken, M.; Wichern, M.; Schlattmann, M.; Gronauer, A.; Horn, H. Modelling the energy balance of an anaerobic digester fed with cattle manure and renewable energy crops. Water Res. 2007, 41, 4085–4096. [Google Scholar] [CrossRef] [PubMed]
- Udwadia, F.; Farahani, A. Accelerated Runge-Kutta Methods. Discret. Dyn. Nat. Soc. 2008, 2008, 1–38. [Google Scholar] [CrossRef]
- Nasrah, N.S.M.; Zahari, M.A.K.M.; Masngut, N.; Ariffin, H. Statistical optimization for biobutanol production by clostridium acetobutylicum ATCC 824 from Oil Palm Frond (OPF) juice using response surface methodology. MATEC Web Conf. 2017, 111, 03001. [Google Scholar] [CrossRef] [Green Version]
- Nath, K.; Das, D. Modeling and optimization of fermentative hydrogen production. Bioresour. Technol. 2011, 102, 8569–8581. [Google Scholar] [CrossRef] [PubMed]
- Kyazze, G.; Popov, A.; Dinsdale, R.; Esteves, S.; Hawkes, F.; Premier, G.; Guwy, A. Influence of catholyte pH and temperature on hydrogen production from acetate using a two chamber concentric tubular microbial electrolysis cell. Int. J. Hydrogen Energy 2010, 35, 7716–7722. [Google Scholar] [CrossRef]
- Jana, A.; Maity, C.; Halder, S.K.; Mondal, K.C.; Pati, B.R.; Mohapatra, P.K.D. Tannase production by Penicillium purpurogenum PAF6 in solid state fermentation of tannin-rich plant residues following OVAT and RSM. Appl. Biochem. Biotechnol. 2012, 167, 1254–1269. [Google Scholar] [CrossRef] [PubMed]
- Mandenius, C.F.; Brundin, A. Bioprocess optimization using design-of-experiments methodology. Biotechnol. Prog. 2008, 24, 1191–1203. [Google Scholar] [CrossRef]
- Kana, E.G.; Oloke, J.; Lateef, A.; Adesiyan, M. Modeling and optimization of biogas production on saw dust and other co-substrates using artificial neural network and genetic algorithm. Renew. Energy 2012, 46, 276–281. [Google Scholar] [CrossRef]
- Wang, Y.-X.; Lu, Z.-X. Optimization of processing parameters for the mycelial growth and extracellular polysaccharide production by Boletus spp. ACCC 50328. Process Biochem. 2005, 40, 1043–1051. [Google Scholar] [CrossRef]
- Lotfy, W.A.; Ghanem, K.M.; El-Helow, E.R. Citric acid production by a novel Aspergillus niger isolate: II. Optimization of process parameters through statistical experimental designs. Bioresour. Technol. 2007, 98, 3470–3477. [Google Scholar] [CrossRef]
- Wang, J.; Wan, W. Optimization of fermentative hydrogen production process using genetic algorithm based on neural network and response surface methodology. Int. J. Hydrogen Energy 2009, 34, 255–261. [Google Scholar] [CrossRef]
- Nelofer, R.; Ramanan, R.N.; Abd Rahman, R.N.Z.R.; Basri, M.; Ariff, A.B. Comparison of the estimation capabilities of response surface methodology and artificial neural network for the optimization of recombinant lipase production by E. coli BL21. J. Ind. Microbiol. Biotechnol. 2012, 39, 243–254. [Google Scholar] [CrossRef]
- Yan, Y.; Borhani, T.N.; Clough, P.T. Chapter 14 machine learning applications in chemical engineering. In Machine Learning in Chemistry: The Impact of Artificial Intelligence; The Royal Society of Chemistry: Cambridge, UK, 2020; pp. 340–371. [Google Scholar]
- Ezzatzadegan, L.; Morad, N.A.; Yusof, R. Prediction and optimization of ethanol concentration in biofuel production using fuzzy neural network. J. Teknol. 2016, 78. [Google Scholar] [CrossRef] [Green Version]
- Borhani, T.N.; García-Muñoz, S.; Luciani, C.V.; Galindo, A.; Adjiman, C.S. Hybrid QSPR models for the prediction of the free energy of solvation of organic solute/solvent pairs. Phys. Chem. Chem. Phys. 2019, 21, 13706–13720. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Babamohammadi, S.; Shamiri, A.; Nejad Ghaffar Borhani, T.; Shafeeyan, M.S.; Aroua, M.K.; Yusoff, R. Solubility of CO2 in aqueous solutions of glycerol and monoethanolamine. J. Mol. Liq. 2018, 249, 40–52. [Google Scholar] [CrossRef]
- Morad, N.A.; Ibrahim, W.A.; Muda, N.S.; Shirai, Y.; Aziz, M.K.A.; Lam, H.L. Utilization of felled oil palm trunk: Trunk sections storage on oil palm sap production. In Proceedings of the 2015 10th Asian Control Conference (ASCC), Sabah, Malaysia, 31 May–3 June 2015; pp. 1–5. [Google Scholar]
- Muda, N.S. Utilization of Oil Palm Trunk Sap for Bioethanol Production through Natural and Yeast Fermentation; Universiti Teknologi Malaysia: Johor Bahru, Malaysia, 2015. [Google Scholar]
- Yamada, H.; Tanaka, R.; Sulaiman, O.; Hashim, R.; Hamid, Z.; Yahya, M.; Kosugi, A.; Arai, T.; Murata, Y.; Nirasawa, S. Old oil palm trunk: A promising source of sugars for bioethanol production. Biomass Bioenergy 2010, 34, 1608–1613. [Google Scholar] [CrossRef]
- Lokesh, B.E.; Hamid, Z.A.A.; Arai, T.; Kosugi, A.; Murata, Y.; Hashim, R.; Sulaiman, O.; Mori, Y.; Sudesh, K. Potential of oil palm trunk sap as a novel inexpensive renewable carbon feedstock for polyhydroxyalkanoate biosynthesis and as a bacterial growth medium. Clean–Soil Air Water 2012, 40, 310–317. [Google Scholar] [CrossRef]
- Kosugi, A.; Tanaka, R.; Magara, K.; Murata, Y.; Arai, T.; Sulaiman, O.; Hashim, R.; Hamid, Z.A.A.; Yahya, M.K.A.; Yusof, M.N.M. Ethanol and lactic acid production using sap squeezed from old oil palm trunks felled for replanting. J. Biosci. Bioeng. 2010, 110, 322–325. [Google Scholar] [CrossRef]
- Murai, K.; Kondo, R. Extractable sugar contents of trunks from fruiting and nonfruiting oil palms of different ages. J. Wood Sci. 2011, 57, 140–148. [Google Scholar] [CrossRef]
- Ezzat Zadegan, L. Modelling and Optimization of Fermentation Process to Produce Bio-Ethanol from Oil Palm Trunk Sap and Corn Stover; Universiti Teknologi Malaysia: Johor Bahru, Malaysia, 2018. [Google Scholar]
- Cakmakci, M. Adaptive neuro-fuzzy modelling of anaerobic digestion of primary sedimentation sludge. Bioprocess Biosyst. Eng. 2007, 30, 349–357. [Google Scholar] [CrossRef]
- Xie, Q.; Ni, J.-q.; Su, Z. A prediction model of ammonia emission from a fattening pig room based on the indoor concentration using adaptive neuro fuzzy inference system. J. Hazard. Mater. 2017, 325, 301–309. [Google Scholar] [CrossRef] [PubMed]
- Najafi, B.; Faizollahzadeh Ardabili, S. Application of ANFIS, ANN, and logistic methods in estimating biogas production from spent mushroom compost (SMC). Resour. Conserv. Recycl. 2018, 133, 169–178. [Google Scholar] [CrossRef]
- Sugeno, M.; Kang, G.T. Structure identification of fuzzy model. Fuzzy Sets Syst. 1988, 28, 15–33. [Google Scholar] [CrossRef]
- Jang, J.S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Potter, C.W.; Negnevitsky, M. Very short-term wind forecasting for Tasmanian power generation. IEEE Trans. Power Syst. 2006, 21, 965–972. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Del Valle, Y.; Venayagamoorthy, G.K.; Mohagheghi, S.; Hernandez, J.-C.; Harley, R.G. Particle swarm optimization: Basic concepts, variants and applications in power systems. IEEE Trans. Evol. Comput. 2008, 12, 171–195. [Google Scholar] [CrossRef]
- Karkevandi-Talkhooncheh, A.; Hajirezaie, S.; Hemmati-Sarapardeh, A.; Husein, M.M.; Karan, K.; Sharifi, M. Application of adaptive neuro fuzzy interface system optimized with evolutionary algorithms for modeling CO2-crude oil minimum miscibility pressure. Fuel 2017, 205, 34–45. [Google Scholar] [CrossRef]
- Castillo, O. Type-2 Fuzzy Logic in Intelligent Control Applications; Springer Publishing Company, Incorporated: New York, NY, USA, 2011; p. 200. [Google Scholar]
- Yuan, S.-F.; Chu, F.-L. Fault diagnostics based on particle swarm optimisation and support vector machines. Mech. Syst. Signal Process. 2007, 21, 1787–1798. [Google Scholar] [CrossRef]
- Chen, M.-Y. A hybrid ANFIS model for business failure prediction utilizing particle swarm optimization and subtractive clustering. Inf. Sci. 2013, 220, 180–195. [Google Scholar] [CrossRef]
- Chen, P.-H. Particle Swarm Optimization for Power Dispatch with Pumped Hydro; INTECH Open Access Publisher: London, UK, 2009. [Google Scholar]
- Bakyani, A.E.; Sahebi, H.; Ghiasi, M.M.; Mirjordavi, N.; Esmaeilzadeh, F.; Lee, M.; Bahadori, A. Prediction of CO2–oil molecular diffusion using adaptive neuro-fuzzy inference system and particle swarm optimization technique. Fuel 2016, 181, 178–187. [Google Scholar] [CrossRef]
- Ezzatzadegan, L. Neuro-Fuzzy Kinetic Modeling of Propylene Polymerization; Universiti Teknologi Malaysia: Johor Bahru, Malaysia, 2011. [Google Scholar]
- Dahbi, S.; Ezzine, L.; El Moussami, H. Modeling of surface roughness in turning process by using Artificial Neural Networks. In Proceedings of the 2016 3rd International Conference on Logistics Operations Management (GOL), Fez, Morocco, 23–25 May 2016; pp. 1–6. [Google Scholar]
- Bastianoni, S.; Pulselli, F.M.; Focardi, S.; Tiezzi, E.B.P.; Gramatica, P. Correlations and complementarities in data and methods through Principal Components Analysis (PCA) applied to the results of the SPIn-Eco Project. J. Environ. Manag. 2008, 86, 419–426. [Google Scholar] [CrossRef]
- Dubey, A.K.; Yadava, V. Multi-objective optimization of Nd:YAG laser cutting of nickel-based superalloy sheet using orthogonal array with principal component analysis. Opt. Lasers Eng. 2008, 46, 124–132. [Google Scholar] [CrossRef]
- Ding, M.-Z.; Cheng, J.-S.; Xiao, W.-H.; Qiao, B.; Yuan, Y.-J. Comparative metabolomic analysis on industrial continuous and batch ethanol fermentation processes by GC-TOF-MS. Metabolomics 2009, 5, 229. [Google Scholar] [CrossRef]
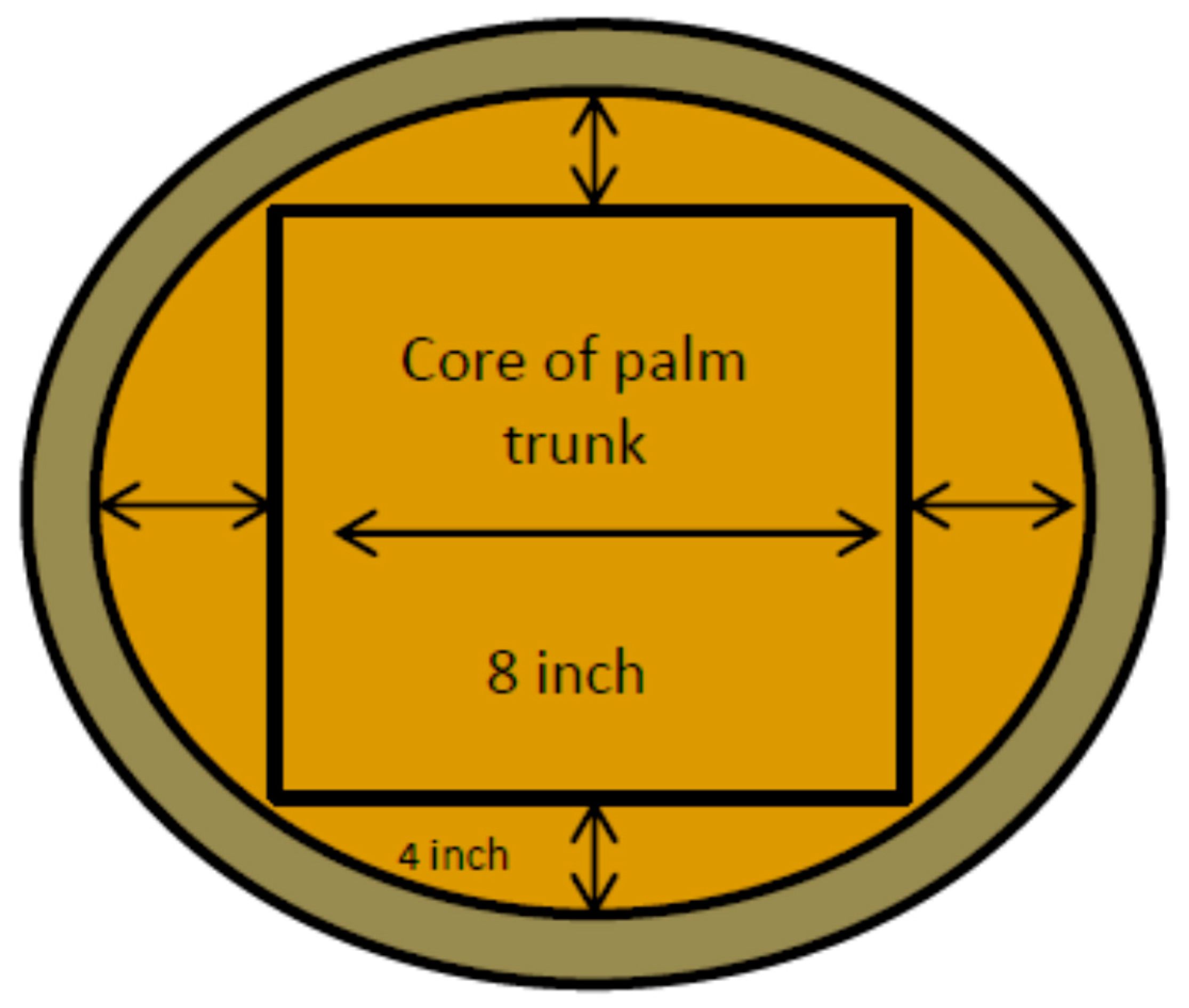









| Storage Time (day) | Section | Initial Trunk (kg) | Cored Trunk (kg) | Wood Waste (kg) | Shredded Trunk (kg) | Oil Palm Trunk Sap (L) | Residue (kg) |
|---|---|---|---|---|---|---|---|
| 1 | U | 200 | 103.96 | 96.04 | 95.90 | 58.66 | 19.46 |
| M1 | 200 | 106.14 | 93.86 | 102.55 | 82.72 | 10.10 | |
| M2 | 200 | 133.25 | 66.75 | 130.22 | 80.56 | 9.80 | |
| B | 300 | 134.22 | 165.78 | 132.16 | 83.04 | 12.10 | |
| Total | 900 | 477.57 | 422.43 | 461.33 | 309.48 | 51.52 | |
| 15 | U | 100.90 | 99.14 | 49.90 | 38.68 | ||
| M1 | 64.66 | 59.72 | 28.18 | 13.16 | |||
| M2 | 110.20 | 102.20 | 64.60 | 19.10 | |||
| B | 117.50 | 115.22 | 45.73 | 29.76 | |||
| Total | 393.26 | 376.28 | 188.41 | 100.7 | |||
| 30 | U | 51.28 | 45.98 | 27.78 | 11.40 | ||
| M1 | 57.42 | 47.84 | 26.93 | 14.28 | |||
| M2 | 73.96 | 69.10 | 51.72 | 10.94 | |||
| B | 87.74 | 82.26 | 57.53 | 13.44 | |||
| Total | 270.40 | 245.18 | 163.96 | 50.06 | |||
| 45 | U | 29.32 | Not shred | 15.32 | 2.55 | ||
| M1 | 53.70 | 47.64 | 20.70 | 13.16 | |||
| M2 | 66.72 | 59.88 | 32.06 | 10.96 | |||
| B | 72.64 | 70.50 | 10.14 | 5.52 | |||
| Total | 222.38 | 178.02 | 78.22 | 32.19 |
| Chemical Properties | Concentration (g/L) | Composition of Total Sugar (%) |
|---|---|---|
| Sucrose | 11.4 | 6.4 |
| Glucose | 150.5 | 84.2 |
| Fructose | 9.3 | 5.2 |
| Xylose | 2.9 | 1.6 |
| Galactose | 2.7 | 1.5 |
| Rhamnose | 1.4 | 0.8 |
| Other | 0.5 | 0.3 |
| Total | 178.7 | 100 |
| Organic Acids | Concentration (µg/g) |
|---|---|
| Succinic Acid | 30.9 |
| Pyruvic Acid | 19.0 |
| Malic Acid | 371.8 |
| Maleic Acid | 119.1 |
| Lactic Acid | 1.3 |
| Fumaric Acid | 8.1 |
| Citric Acid | 380.6 |
| Acetic Acid | 39.8 |
| Total | 970.6 |
| Storage Time (Day) | Total Palm Sap (L) | Average Sugar Concentration (g/L) | Total Sugar (kg) |
|---|---|---|---|
| 1 | 309.48 | 55.15 | 17.07 |
| 15 | 188.41 | 75.53 | 14.23 |
| 30 | 163.96 | 86.93 | 14.25 |
| 45 | 78.22 | 13.07 | 1.02 |
| Parameter | Description |
|---|---|
| Details of Method | Vessel fermenter with 2 L capacity HPLC (Agilent Technologies, USA), was used for sugar content analysis Gas chromatograph, Agilent Technology, USA was used for ethanol analysis |
| Strain | Saccharomyces cerevisiae |
| Time (h) | 30 and 24 |
| Temperature | 30, 25, 35 |
| pH | 4, 5, 6 |
| Sugar content (g/L) | Maximum 118.3650 |
| Ethanol (g/L) | Maximum 44.1485 |
| Details of OPT | The OPT was selected from the local plantation, Selangor, Malaysia The OPT was stored 1, 15, 30, 45 days before mechanically squeezing The OPT was 20 feet tall and was divided into four sections: (1) Upper, (2) Middle1, (3) Middle2, and (4) Bottom The OPT sap sample was stored at −20 °C for further analysis |
| Parameter | Training | Testing | Overall |
|---|---|---|---|
| RMSE | 2.52 × 10−6 | 0.8010 | 0.3447 |
| RMSE of normalised data | 1.14 × 10−6 | 0.0363 | 0.0156 |
| MSE | 6.37 × 10−10 | 0.6417 | 0.1188 |
| MSE of normalised data | 1.31 × 10−12 | 0.0013 | 2.44 × 10−4 |
| R | 1 | 0.9991 | 0.9997 |
| PSO Parameters | |||||||
|---|---|---|---|---|---|---|---|
| Number of Particles | Number of Dimensions | C1 | C2 | Maximum Iteration | Inertia Weight (W) | ||
| 200 | 4 | 2 | 2 | 300 | 0.4 ≤ W ≤ 1.2 | ||
| Optimised Results | |||||||
| Time (h) | pH | Temperature (°C) | Total Sugar (g/L) | Bioethanol (g/L) | |||
| 16.1845 | 4.54 | 27.3407 | 1.3588 | 44.1485 | |||
| Experimental Results | |||||||
| Time (h) | pH | Temperature (°C) | Total Sugar (g/L) | Bioethanol (g/L) | |||
| 18 | 5 | 30 | 8.2639 | 44.1485 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ezzatzadegan, L.; Yusof, R.; Morad, N.A.; Shabanzadeh, P.; Muda, N.S.; Borhani, T.N. Experimental and Artificial Intelligence Modelling Study of Oil Palm Trunk Sap Fermentation. Energies 2021, 14, 2137. https://doi.org/10.3390/en14082137
Ezzatzadegan L, Yusof R, Morad NA, Shabanzadeh P, Muda NS, Borhani TN. Experimental and Artificial Intelligence Modelling Study of Oil Palm Trunk Sap Fermentation. Energies. 2021; 14(8):2137. https://doi.org/10.3390/en14082137
Chicago/Turabian StyleEzzatzadegan, Leila, Rubiyah Yusof, Noor Azian Morad, Parvaneh Shabanzadeh, Nur Syuhana Muda, and Tohid N. Borhani. 2021. "Experimental and Artificial Intelligence Modelling Study of Oil Palm Trunk Sap Fermentation" Energies 14, no. 8: 2137. https://doi.org/10.3390/en14082137
APA StyleEzzatzadegan, L., Yusof, R., Morad, N. A., Shabanzadeh, P., Muda, N. S., & Borhani, T. N. (2021). Experimental and Artificial Intelligence Modelling Study of Oil Palm Trunk Sap Fermentation. Energies, 14(8), 2137. https://doi.org/10.3390/en14082137








