Model-Based Condenser Fan Speed Optimization of Vapor Compression Systems
Abstract
:1. Introduction
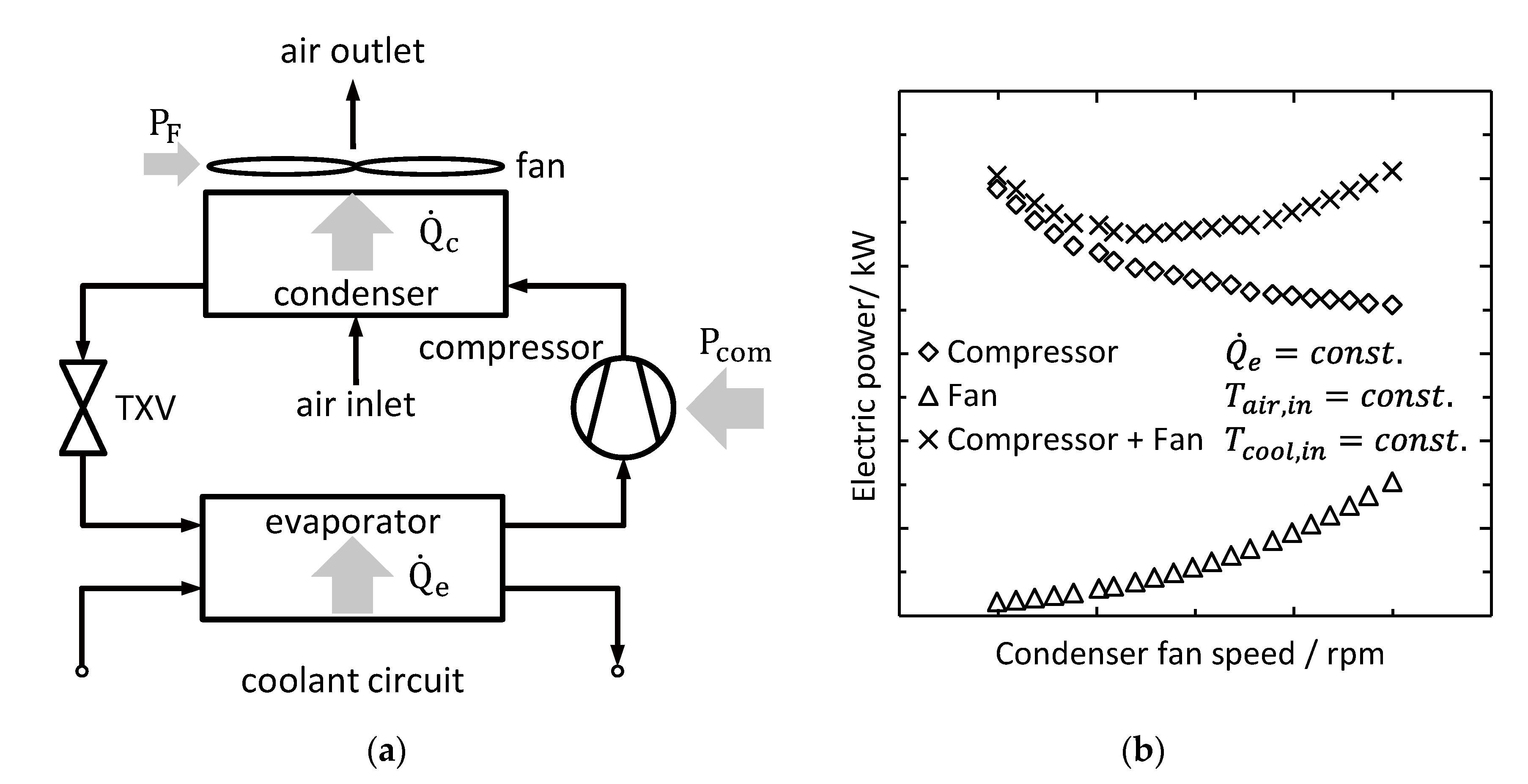
1.1. Ideal Condenser Fan Speed
1.2. Optimization of the Condenser Fan Speed Control
2. Experimental Methodology
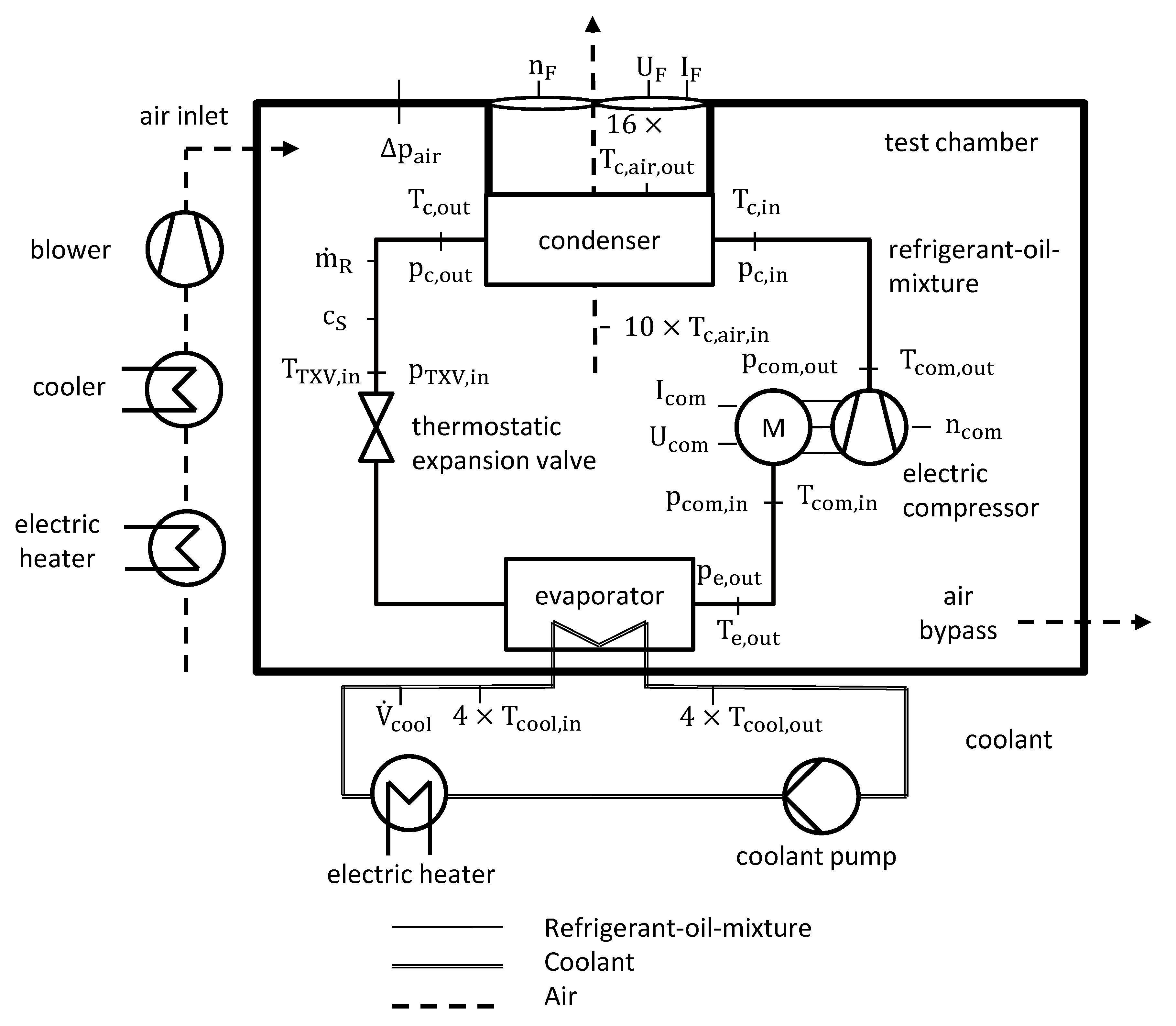
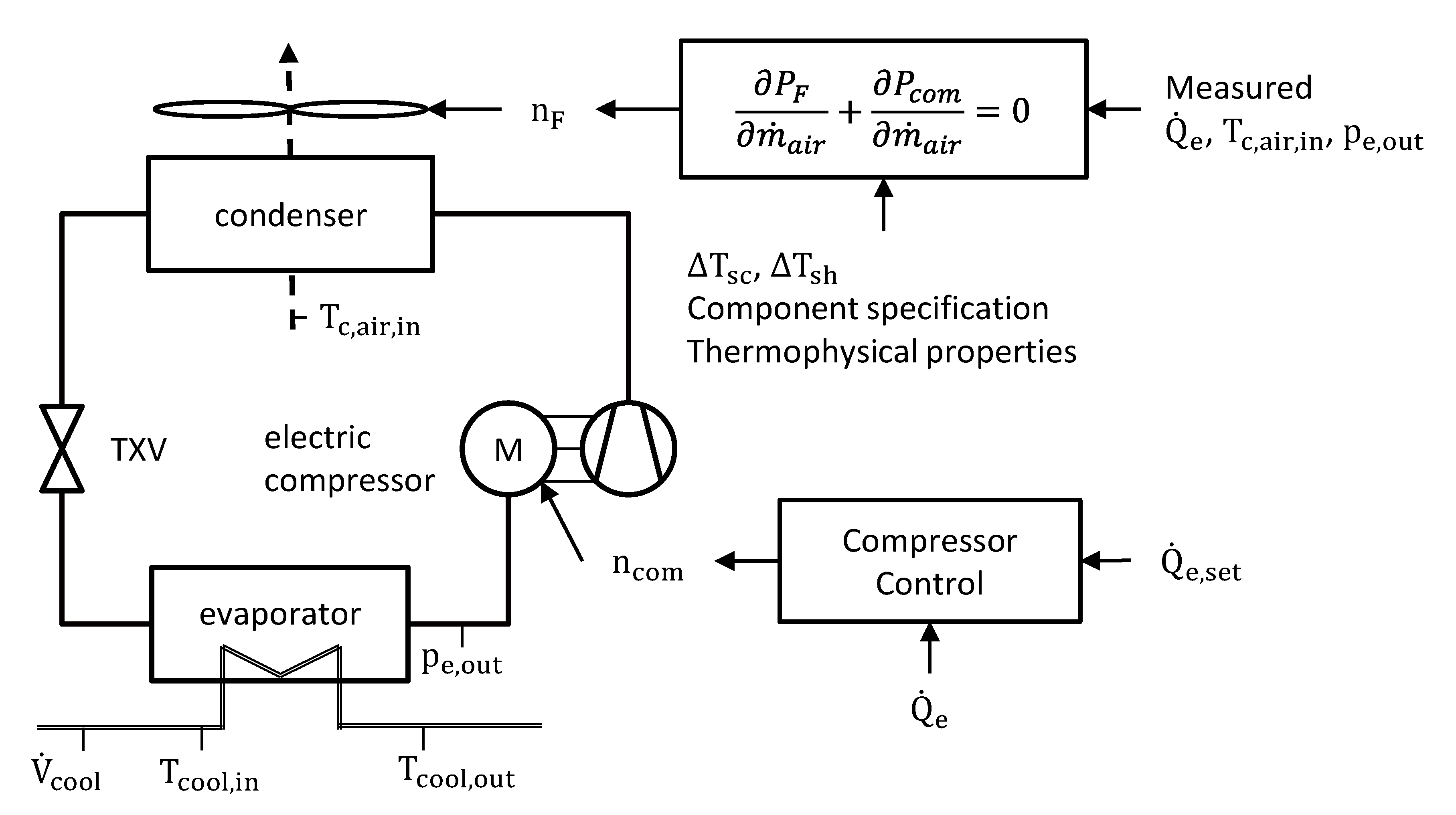
2.1. Test Bench Description
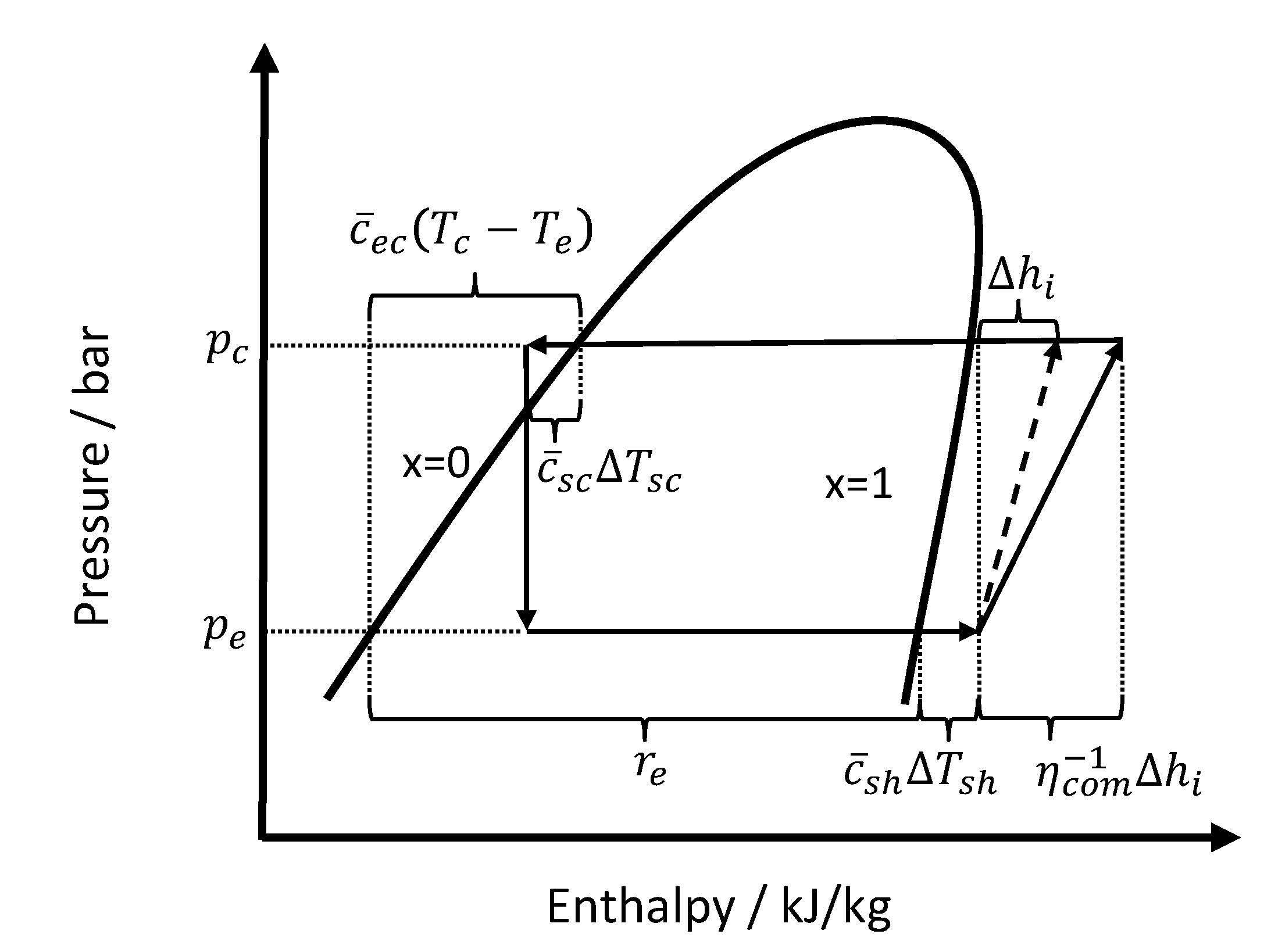
2.2. Calculation Background
2.3. Experimental Procedure and Test Matrix
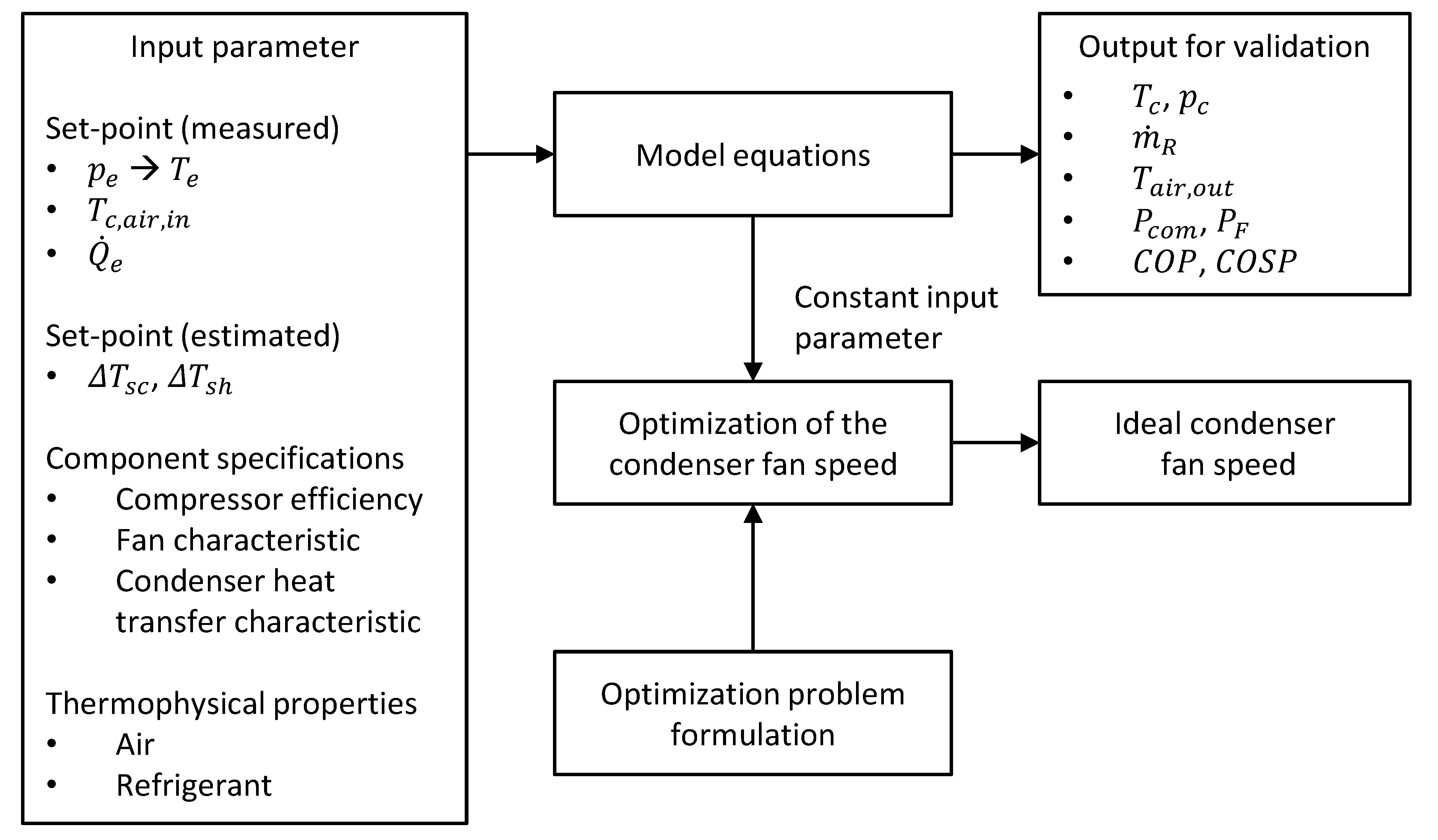
3. Mathematical Model
3.1. Calcualtion Procedure
3.2. Model Description
3.2.1. Condenser Fan
3.2.2. Evaporator and Expansion Valve
3.2.3. Compressor
3.2.4. Condenser
3.2.5. System
3.3. Formulation of the Condenser Fan Speed Optimization Problem
4. Model Validation
- Component model validation (varying model inputs)
- Condenser fan speed optimization validation (constant model inputs)
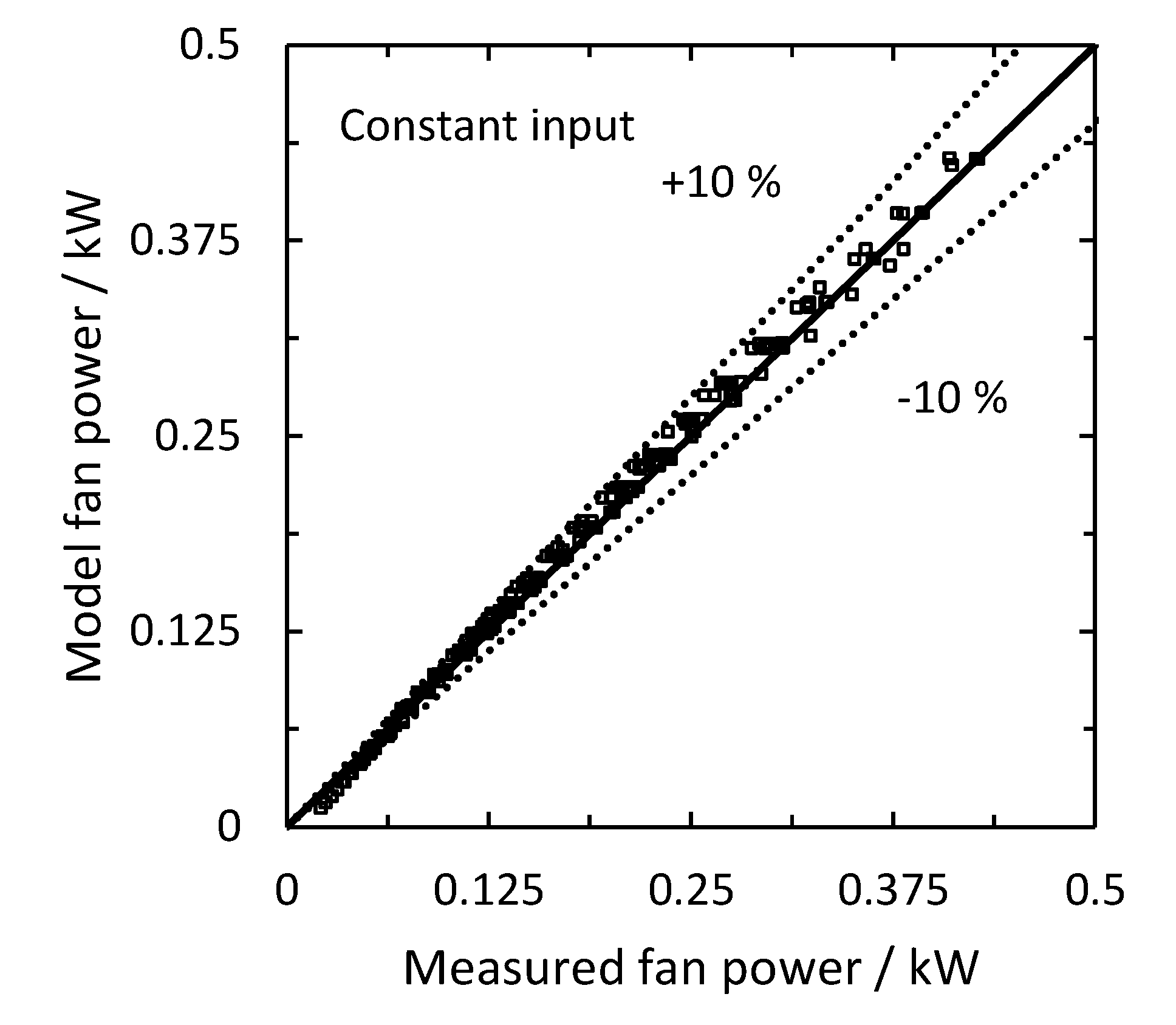
4.1. Condenser Fan
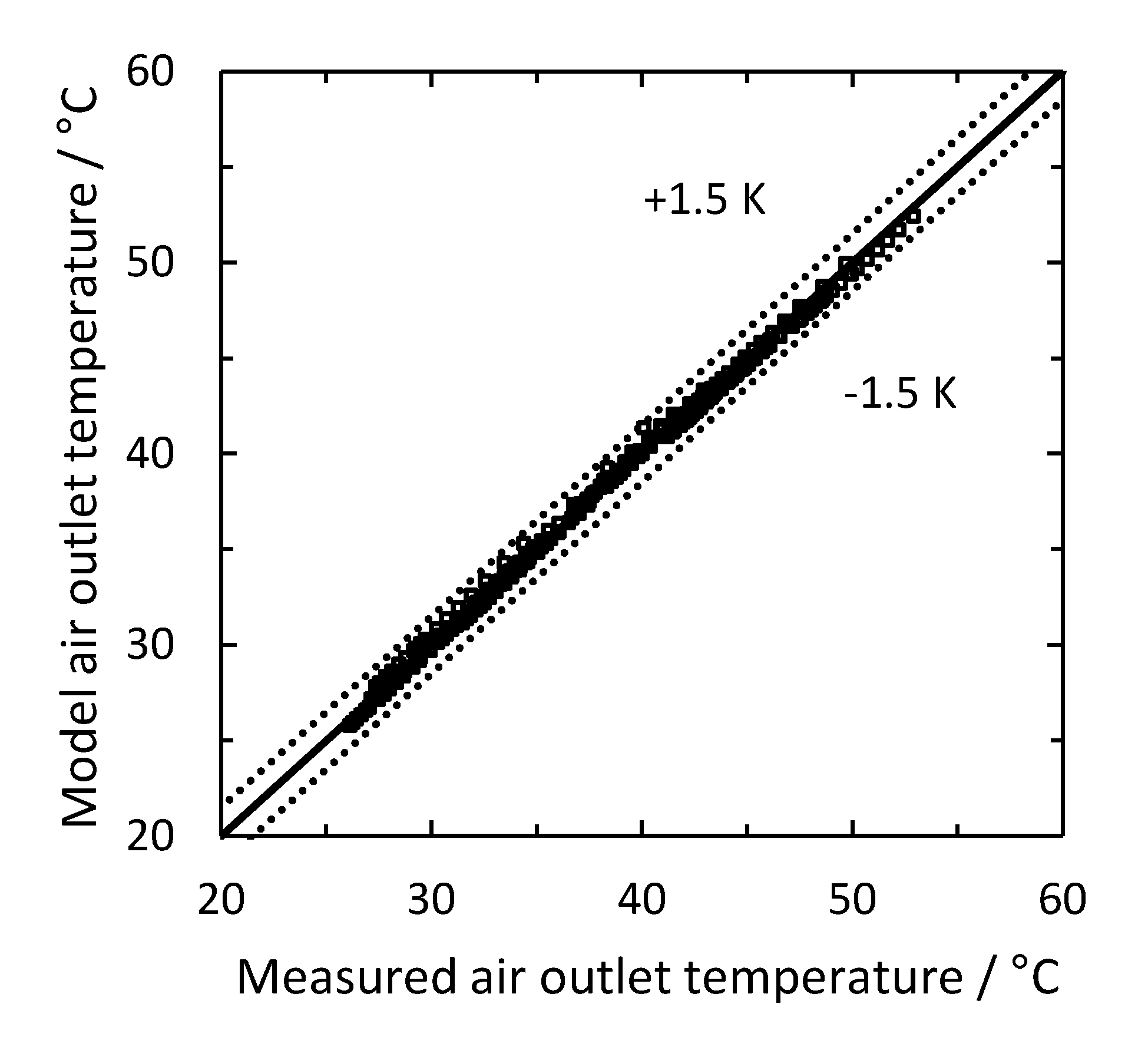
4.2. Evaporator and Expansion Valve
4.3. Compressor
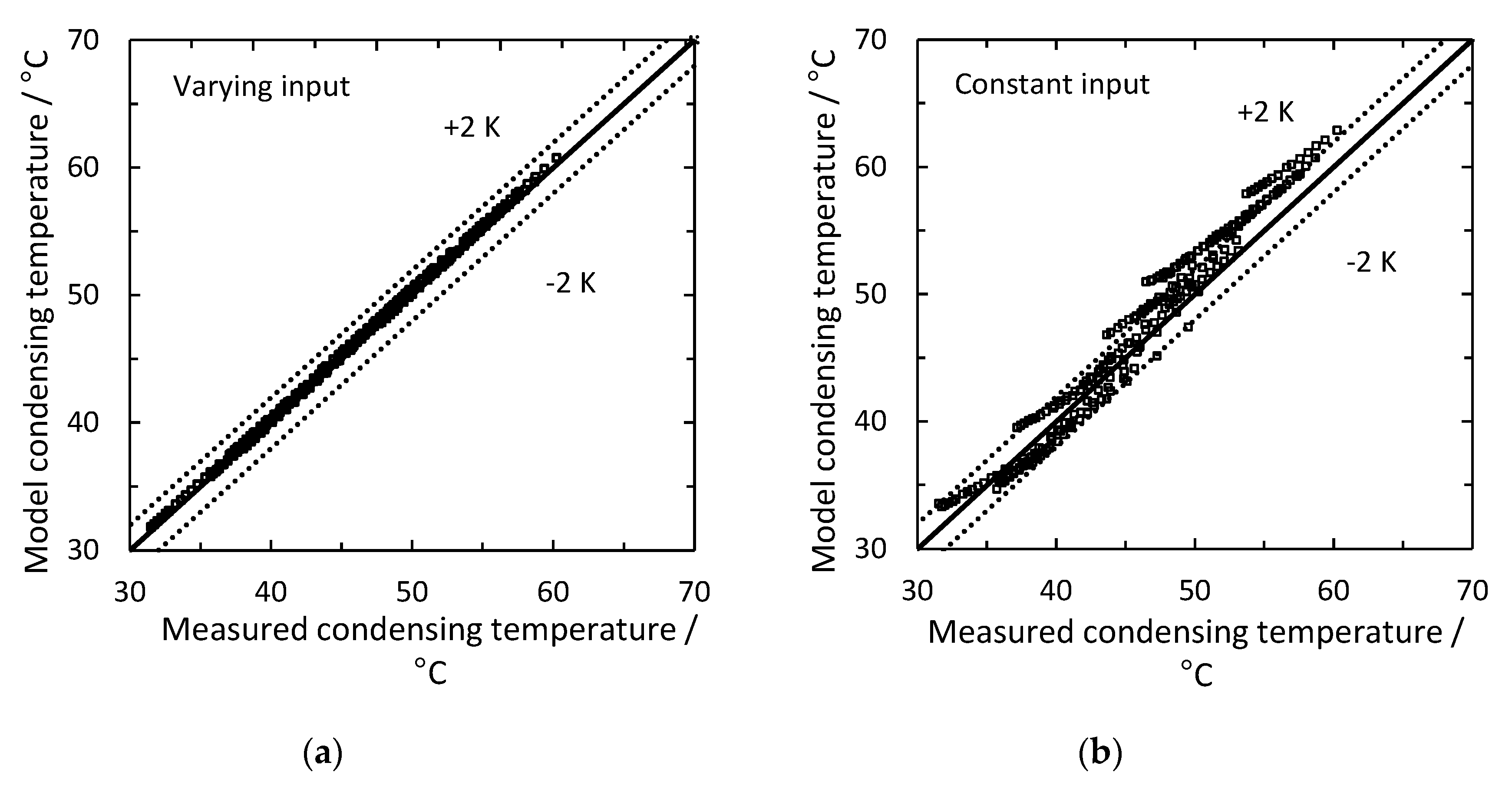
4.4. Condenser
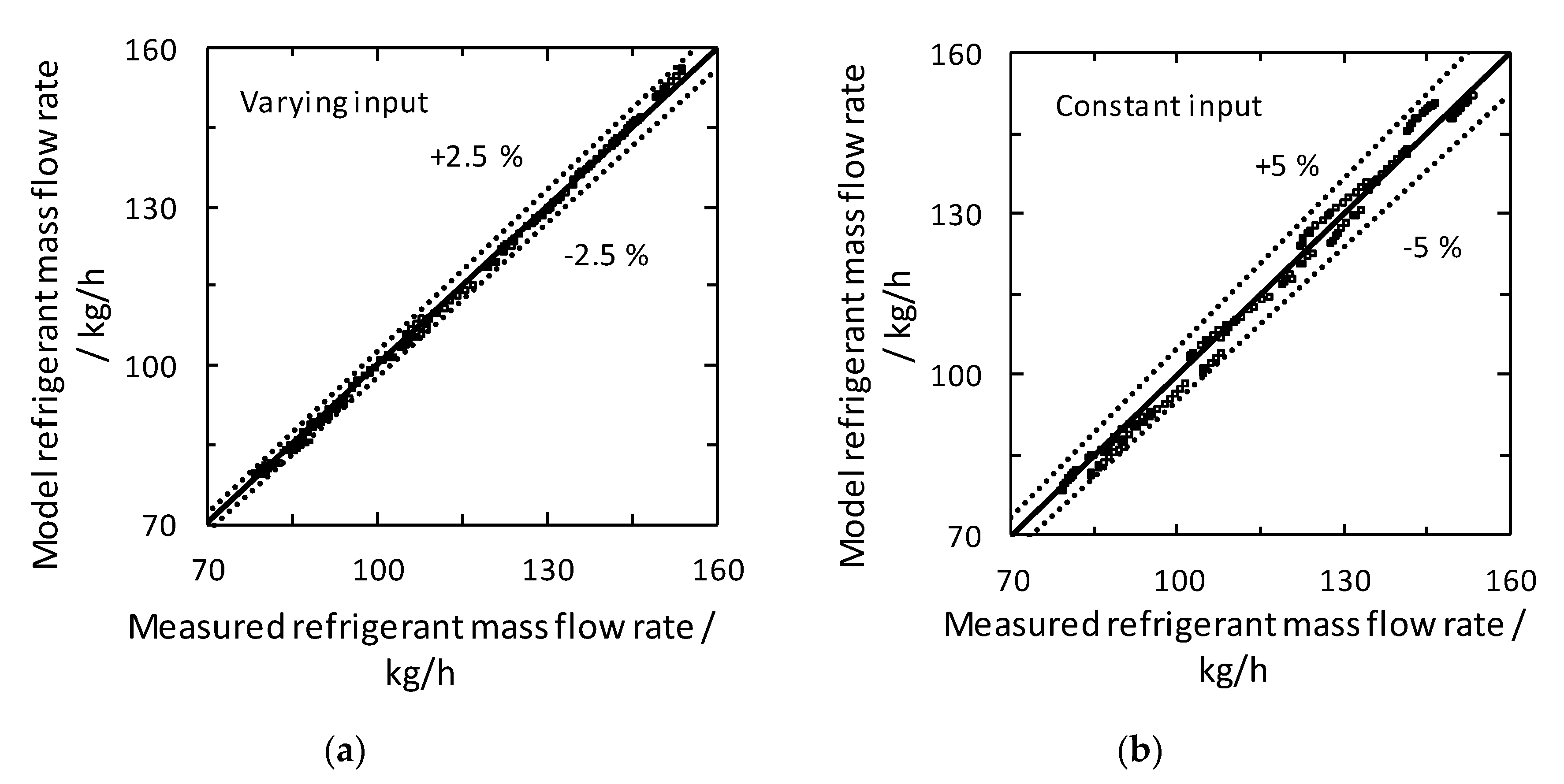
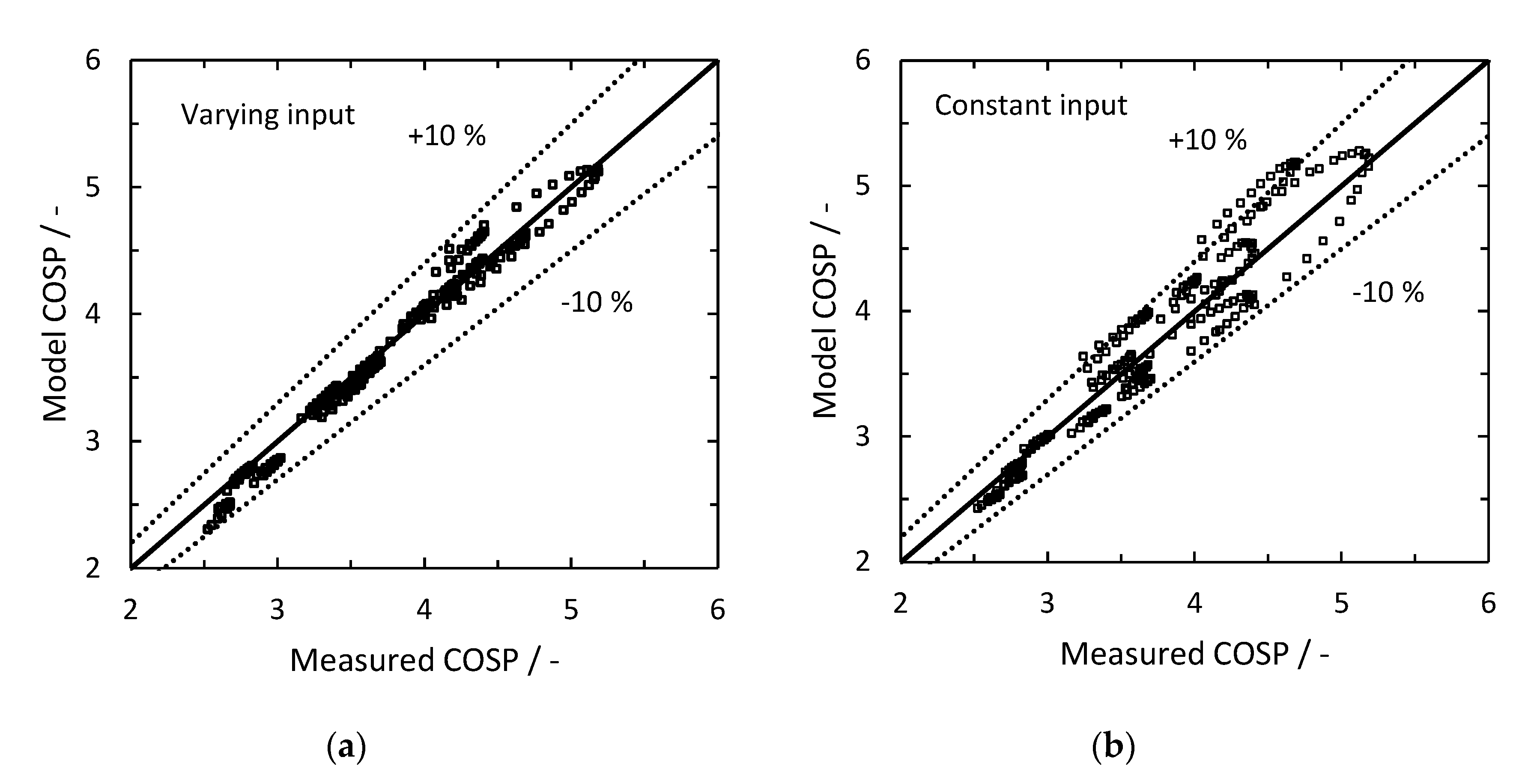
4.5. System
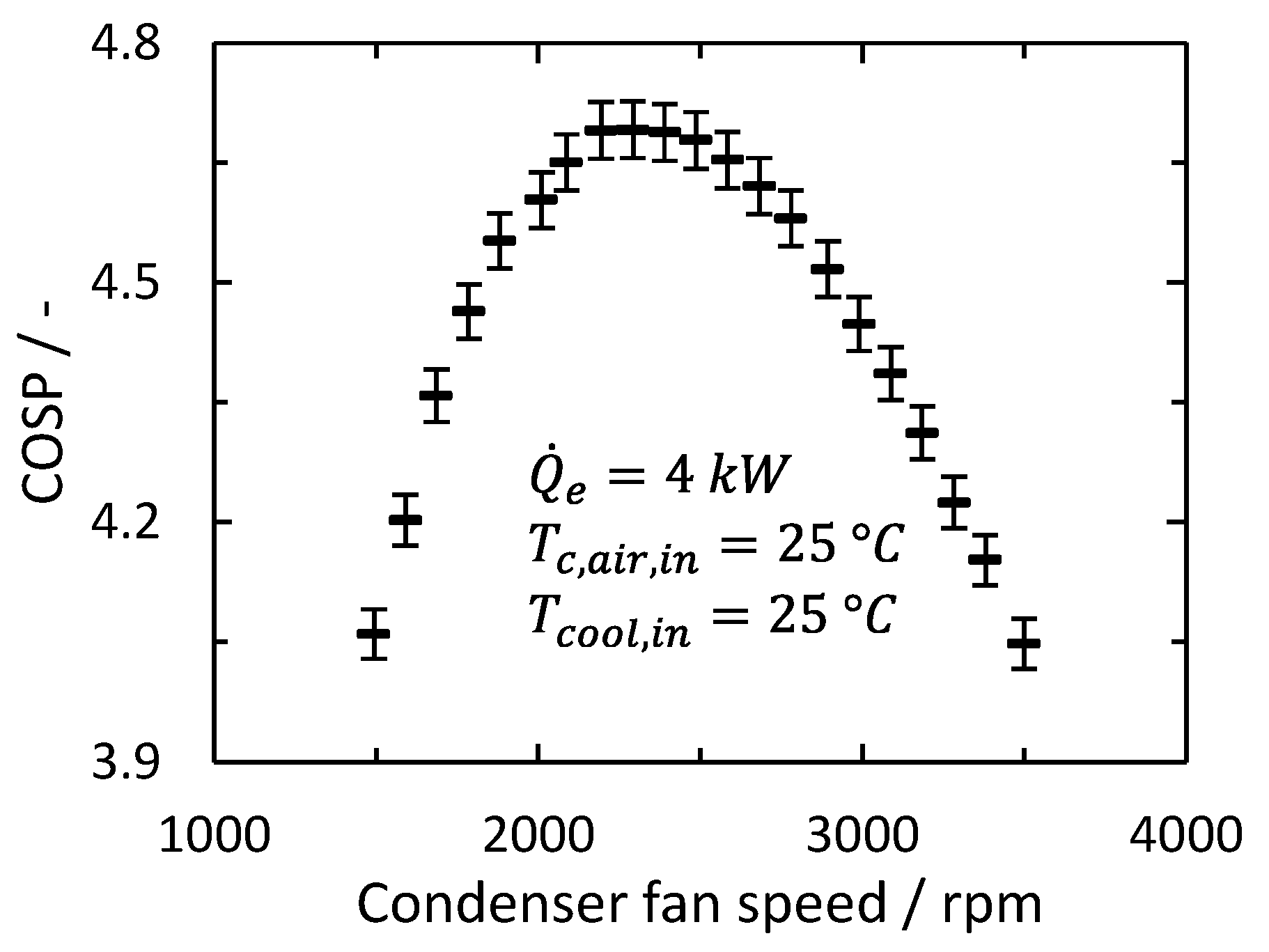
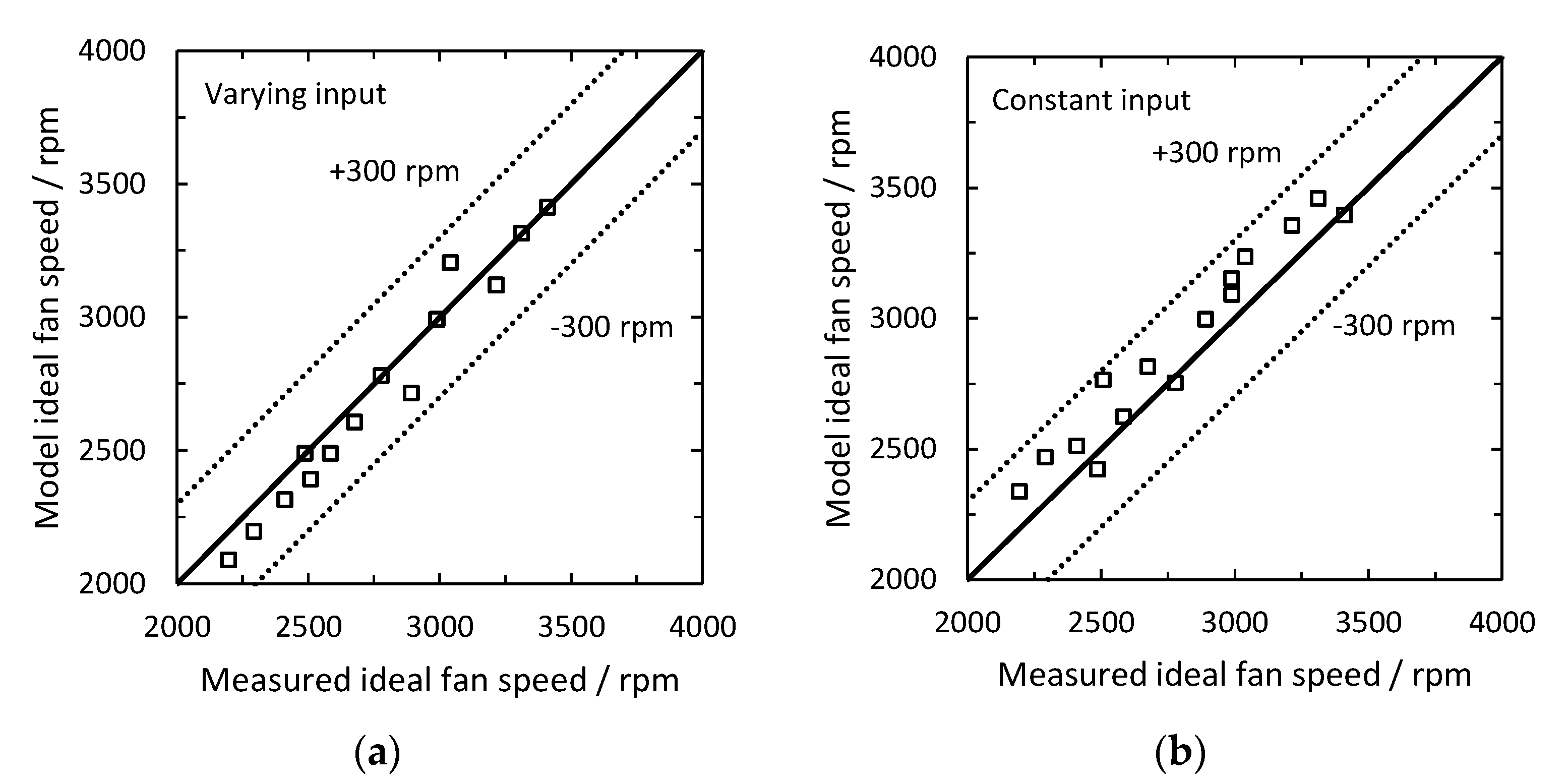
4.6. Prediction of the Ideal Condenser Fan Speed
5. Condenser Fan Speed Optimization
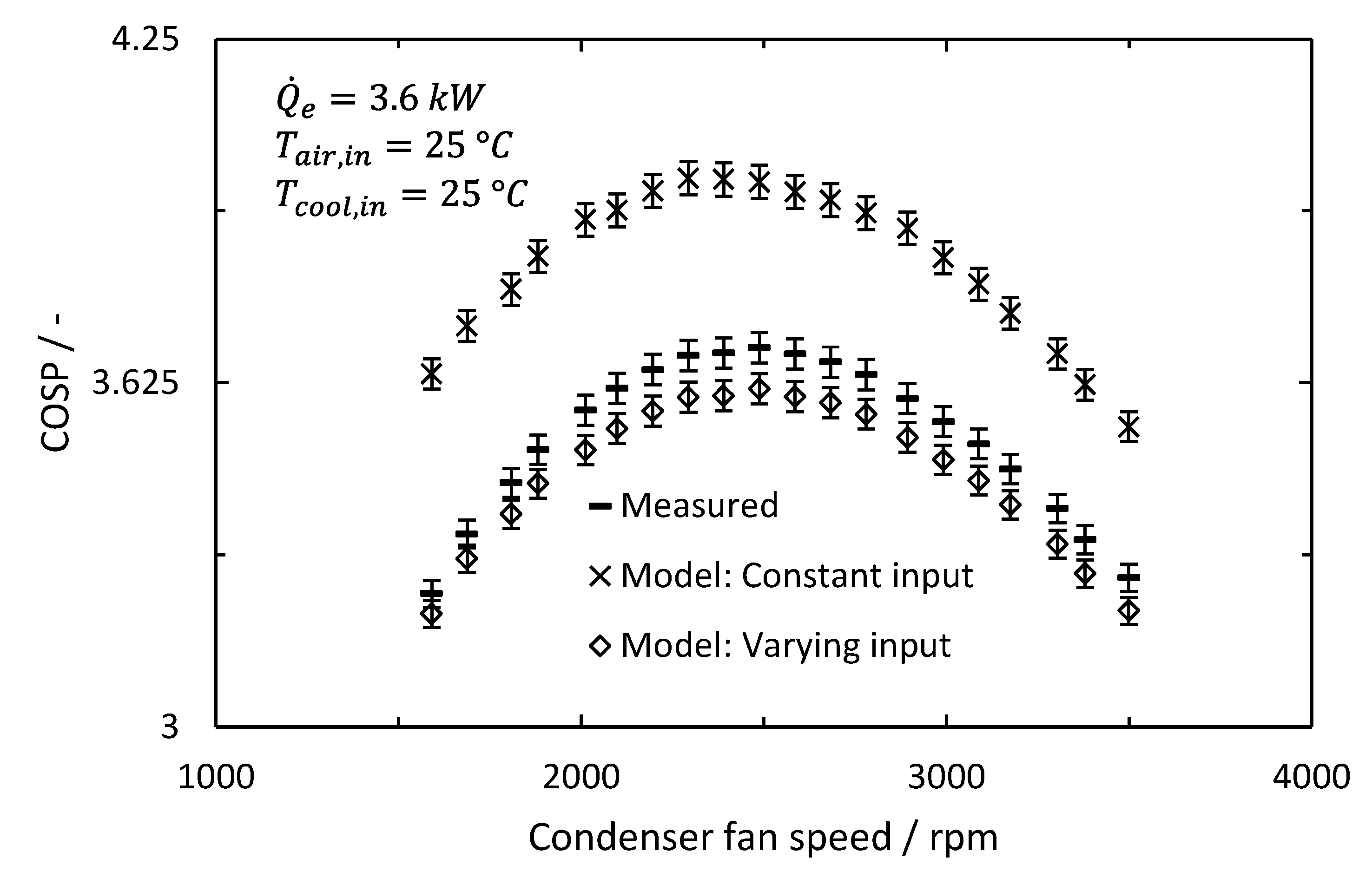
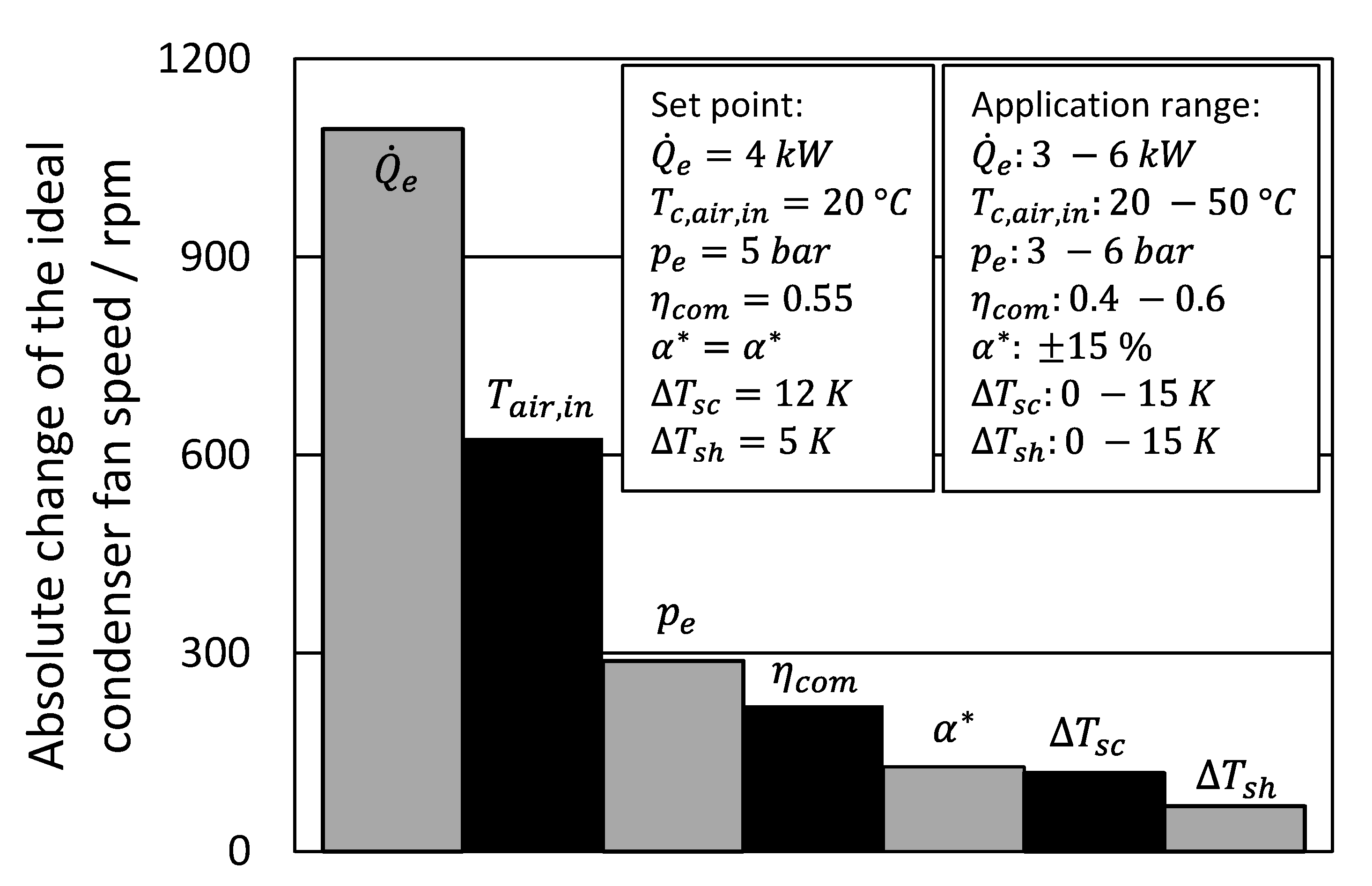
5.1. Influences on the Ideal Condenser Fan Speed
5.2. Control Strategy and Energy Saving Potential
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Area/m2 | |
| Speed of sound/m/s | |
| Mean specific heat capacity/J/(kg∙K) | |
| Specific enthalpy/J/kg | |
| Current/A | |
| Overall heat transfer coefficient/W/(m2∙K) | |
| Refrigerant mass flow rate/kg/s | |
| Rotation speed/rpm | |
| Power/W | |
| Pressure/bar | |
| Heat flux/W | |
| Evaporating enthalpy/J/kg | |
| Specific gas constant/J/(kg∙K) | |
| Coefficient of determination/% | |
| Temperature/°C | |
| Voltage/V | |
| Specific volume m3/kg | |
| Volume flow rate/m3/s | |
| Vapor fraction | |
| Real gas factor/- | |
| Greek Letters | |
| Convective heat transfer coefficient/W/(m2∙K) | |
| Compressor efficiency/- | |
| Substitution | |
| Density/kg/m3 | |
| Heat exchanger characteristic/- | |
| Subscripts | |
| Air | |
| Condenser | |
| Compressor | |
| Coolant | |
| Evaporator | |
| Fan | |
| Isentropic | |
| Ideal | |
| Inlet | |
| Outlet | |
| Refrigerant | |
| Subcooling | |
| Superheating | |
| Abbreviations | |
| Coefficient of Performance/- | |
| Coefficient of System Performance/- | |
| Magnetic inductive flow meter | |
| Number of Transfer Units | |
| Polyalkylene glycol | |
| Root mean square error | |
| 1,1,1,2-Tetrafluorethan | |
| Thermostatic expansion valve | |
| Vapor compression cycle | |
| Vapor compression system | |
Appendix A

| Component | Description | Specification |
|---|---|---|
| Evaporator | Serial component of MAHLE Behr GmbH & Co. KG refrigerant-coolant evaporator (Chiller) | Plate heat exchanger Plate amount: 50 Fluid guidance: Refrigerant “S-Flow”, Coolant “I-Flow” |
| Compressor | Suction gas-cooled electric scroll | Displacement: 24 cm3 Speed: 2400–6000 rpm |
| Condenser | Serial component of MAHLE Behr GmbH & Co. KG air-refrigerant condenser Fin tube type cross-flow system | Four passes with 15, 10, 6 und 4 tubes in1st, 2nd, 3rd and 4th pass respectively Receiver between 3rd and 4th pass |
| Expansion valve | Thermostatic expansion valve of Otto Egelhof GmbH & Co. KG. | Capacity: 2 ton Charge: C6 |
| Fan | Serial component of Spal Automotive | Diameter: 305 mm Speed: 800 to 4000 rpm. |
| Refrigerant-Oil | Serial component of Sanden Inc. Product name: SP-A2 | Polyalkylene glycol (PAG) synthetic oil |
| Sensor | Manufacturer | Product Name |
|---|---|---|
| Data logger | Dewetron GmbH | System: DEWE2-M Cards: 2402-dSTG, 2402dACC, CNT, 2402-V, EPAD2-TH8, EPAD2-RTD8 |
| Thermocouple–refrigerant | Electornic Sensor GmbH | IKT 15/10/2KSTS33/2m/ZEH/MFM.K |
| Thermocouple–coolant | Electornic Sensor GmbH | EST 01 |
| Pt100–coolant | SONTEC Sensorbau GmbH | TP1051-A0B1C3D1, TE6-G1/2-A0B1C4D2 |
| Pt100–air | Electornic Sensor GmbH | PT100A 20/050/NB/4 Cu TT17/2 m/LR12.S30 |
| Current | Deweton GmbH | CLAMP-DC-POWER-4-EXT with PA-IT-65-S-BUNDLE, PA-IT-205-S-BUNDLE |
| Fan speed | Keyence Deutschland GmbH | FS-N40 |
| Compressor speed | Brüel Kjaer GmbH | Type 4524 |
| Sound velocity | Anton Paar Germany GmbH | L-SONIC 6100 with PICO 3000 |
| Pressure | ALTHEN GmbH | PDCR 5060-TB-A2-CC H0-PC-030B0000G |
| Coriolis sensor | Emersson | Micro Motion ELITE Coriolis Messsystem: CMF025M176N4FZGZZZMC with Micro Motion 2700 Messumformer: 2700R12CFZGZZZ |
| MID | Siemens AG | MAG 5100 TW with MAG 6000 IP 67 |
| Element | Measuring Chain | Uncertainty | Distribution |
|---|---|---|---|
| Pt100 | Sensor | 0.05 °C | normal |
| - | Module | 0.08 °C | rectangular |
| Thermocouple | Sensor | 0.5 °C | normal |
| - | Module | 0.2 °C | rectangular |
| Pressure | Sensor | 0.3% | normal |
| - | Module, Input | 0.02%, 0.02% MR | rectangular |
| - | Module, Output | 0.03% | rectangular |
| Coriolis | Sensor | 0.1% | normal |
| - | Module, Input | 0.02%, 0.02% MR | rectangular |
| - | Module, Output | 0.05% | rectangular |
| MID | System | 0.15% | normal |
| Sound Velocity | Sensor | 0.1 m/s | normal |
| - | Transducer | 0.12% | rectangular |
| - | Module, Input | 0.02%, 0.02% MR | rectangular |
| - | Module, Output | 0.05% | rectangular |
| - | Calculation | 0.96% | normal |
| Acceleration (Compressor speed) | System | 1% | normal |
| Fiber optic (Fan speed) | System | 0.1% | normal |
| Current (Compressor) | Sensor | 83 ppm | rectangular |
| - | Module | 0.02%, 0.02% MR | rectangular |
| Voltage (Compressor) | Sensor | 83 ppm | rectangular |
| - | Module | 0.3%, 0.02% MR | rectangular |
| Current (Fan) | Sensor | 270 ppm | rectangular |
| - | Module | 0.02%, 0.02% MR | rectangular |
| Voltage (Fan) | Sensor | 270 ppm | rectangular |
| - | Module | 0.3%, 0.02% MR | rectangular |
Appendix B

Appendix C
Appendix D
References
- EIA. Residential Energy Consumption Survey. U.S. Energy Information Administration 2015. Available online: https://www.eia.gov/consumption/residential/index.php (accessed on 30 September 2020).
- Tiat, S.; Keung, J. Green Building Design Guide. S. Building & Construction Authority, Singapore 2015. Available online: https://www.bca.gov.sg/GreenMark/others/3rd_Green_Building_Masterplan.pdf (accessed on 30 September 2020).
- UN-Enviorment. The Importance of Energy Efficiency in the Refrigeration, Air-conditioning and Heat Pump Sectors 2018. Available online: https://ozone.unep.org/sites/default/files/2019-08/briefingnote-a_importance-of-energy-efficiency-in-the-refrigeration-air-conditioning-and-heat-pump-sectors.pdf (accessed on 30 September 2020).
- Jensen, J.B.; Skogestad, S. Optimal operation of simple refrigeration cycles. Comput. Chem. Eng. 2007, 31, 712–721. [Google Scholar] [CrossRef]
- Jakobsen, A.; Rasmussen, B. Energy-optimal speed control of fans and compressors in a refrigeration system. In Proceedings of the Eurotherm 62, Grenoble, France, 17–18 November 1998; pp. 317–323. [Google Scholar]
- Chan, K.; Yu, F. Optimum Setpoint of Condensing Temperature for Air-Cooled Chillers. HVAC&R Res. 2004, 10, 113–127. [Google Scholar]
- Larsen, L. Model Based Control of Refrigeration Systems. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 2005. Available online: https://www.osti.gov/etdeweb/servlets/purl/20833740 (accessed on 30 September 2020).
- Yu, F.; Chan, K. Tune up of the set point of condensing temperature for more energy efficient air cooled chillers. Energy Convers. Manag. 2006, 47, 2499–2514. [Google Scholar] [CrossRef]
- Wan, H.; Cao, T.; Hwang, Y.; Oh, S. A review of recent advancements of variable refrigerant flow air-conditioning systems. Appl. Therm. Eng. 2020, 169, 114893. [Google Scholar] [CrossRef]
- Zhao, L.; Cai, W.-J.; Ding, X.-D.; Chang, W.-C.; Chang, V.W.-C. Decentralized optimization for vapor compression refrigeration cycle. Appl. Therm. Eng. 2013, 51, 753–763. [Google Scholar] [CrossRef]
- Qiao, H.; Radermacher, R.; Aute, V. A Review for Numerical Simulation of Vapor Compression Systems. In Proceedings of the International Refrigeration and Air Conditioning Conference, Purdue University, West Lafayette, IN, USA, 12–15 July 2010; pp. 1–10. Available online: https://docs.lib.purdue.edu/cgi/viewcontent.cgi?article=2089&context=iracc (accessed on 30 September 2020).
- Zhang, G.; Xiao, H.; Zhang, P.; Wang, B.; Li, X.; Shi, W.; Cao, Y. Review on recent developments of variable refrigerant flow systems since 2015. Energy Build. 2019, 198, 444–466. [Google Scholar] [CrossRef]
- Scarpa, M.; Emmi, G.; De Carli, M. Validation of a numerical model aimed at the estimation of performance of vapor compression based heat pumps. Energy Build. 2012, 47, 411–420. [Google Scholar] [CrossRef]
- Zhao, L.; Cai, W.; Ding, X.; Chang, W. Model-based optimization for vapor compression refrigeration cycle. Energy 2013, 55, 392–402. [Google Scholar] [CrossRef]
- Jakobsen, A.; Rasmussen, B.D.; Skovrupity, M.J.; Fredsted, J. Development of Energy Optimal Capacity Controlin Refrigeration Systems. In Proceedings of the 8th International Refrigeration Conference, Purdue University, West Lafayette, IN, USA, 25–28 July 2000; pp. 329–336. Available online: https://docs.lib.purdue.edu/cgi/viewcontent.cgi?article=1498&context=iracc (accessed on 30 September 2020).
- Braun, M.; Walton, P.; Beck, S. Illustrating the relationship between the coefficient of performance and the coefficient of system performance by means of an R404 supermarket refrigeration system. Int. J. Refrig. 2016, 70, 225–234. [Google Scholar] [CrossRef] [Green Version]
- Ruiz, A.G.; Garrido, J.; Vázquez, F.; Morilla, F. A hybrid modeling approach for steady-state optimal operation of vapor compression refrigeration cycles. Appl. Therm. Eng. 2017, 120, 74–87. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Chan, K.; Dai, T.; Yu, F.; Chen, L. Hybrid Artificial Neural Network−Genetic Algorithm Technique for Condensing Temperature Control of Air-Cooled Chillers. Procedia Eng. 2015, 121, 706–713. [Google Scholar] [CrossRef] [Green Version]
- Yu, F.; Ho, W.; Chan, K.; Sit, R. Logistic regression-based optimal control for air-cooled chiller. Int. J. Refrig. 2018, 85, 200–212. [Google Scholar] [CrossRef]
- Shin, J.-H.; Kim, Y.-I.; Cho, Y.-H. Development of Operating Method of Multi-Geothermal Heat Pump Systems Using Variable Water Flow Rate Control and a COP Prediction Model Based on ANN. Energies 2019, 12, 3894. [Google Scholar] [CrossRef] [Green Version]
- Goyal, A.; Staedter, M.A.; Garimella, S. A review of control methodologies for vapor compression and absorption heat pumps. Int. J. Refrig. 2019, 97, 1–20. [Google Scholar] [CrossRef]
- Behrooz, F.; Mariun, N.; Marhaban, M.; Radzi, M.; Ramli, A. Review of Control Techniques for HVAC Systems—Nonlinearity Approaches Based on Fuzzy Cognitive Maps. Energies 2018, 11, 495. [Google Scholar] [CrossRef] [Green Version]
- Yu, F.; Ho, W. Load allocation improvement for chiller system in an institutional building using logistic regression. Energy Build. 2019, 201, 10–18. [Google Scholar] [CrossRef]
- Larsen, L.F.S.; Thybo, C.; Stoustrup, J.; Rasmussen, H. A method for online steady state energy minimization, with application to refrigeration systems. In Proceedings of the 43rd IEEE Conference on Decision and Control (CDC), Nassau, Bahamas, 14–17 December 2004; Volume 5, pp. 4708–4713. [Google Scholar]
- Ding, X.; Cai, W.; Jia, L.; Wen, C.; Zhang, G. A hybrid condenser model for real-time applications in performance monitoring, control and optimization. Energy Convers. Manag. 2009, 50, 1513–1521. [Google Scholar] [CrossRef]
- Huang, Y.; Khajepour, A.; Ding, H.; Bagheri, F.; Bahrami, M. An energy-saving set-point optimizer with a sliding mode controller for automotive air-conditioning/refrigeration systems. Appl. Energy 2017, 188, 576–585. [Google Scholar] [CrossRef]
- Yeh, T.-J.; Chen, Y.-J.; Hwang, W.-Y.; Lin, J.-L. Incorporating fan control into air-conditioning systems to improve energy efficiency and transient response. Appl. Therm. Eng. 2009, 29, 1955–1964. [Google Scholar] [CrossRef]
- Jain, N.; Alleyne, A.G. Exergy-based optimal control of a vapor compression system. Energy Convers. Manag. 2015, 92, 353–365. [Google Scholar] [CrossRef] [Green Version]
- Burns, D.; Bortoff, S.; Laughman, C.; Guay, M. Comparing Realtime Energy-Optimizing Controllers for Heat Pumps. In Proceedings of the 17th International Refrigeration and Air Conditioning Conference, Purdue University, West Lafayette, IN, USA, 9–12 July 2018; Available online: https://docs.lib.purdue.edu/cgi/viewcontent.cgi?article=3007&context=iracc (accessed on 30 September 2020).
- Wang, W.; Li, Y. Real-time optimization of intermediate temperature for a cascade heat pump via extreme seeking. In Proceedings of the 13th International Modelica Conference, Regensburg, Germany, 4–6 March 2019; pp. 251–258. [Google Scholar]
- Bejarano, G.; Alfaya, J.A.; Ortega, M.G.; Vargas, M. On the difficulty of globally optimally controlling refrigeration systems. Appl. Therm. Eng. 2017, 111, 1143–1157. [Google Scholar] [CrossRef]
- He, X.; Liu, S.; Asada, H. Modeling of vapor compression cycles for advanced controls in HVAC systems. In Proceedings of the 1995 American Control Conference—ACC’95, Seattle, WA, USA, 21–23 June 1995; pp. 3664–3668. [Google Scholar]
- Hipp, C.; Schauer, M.; Zimmermann, R. System for Controlling the Temperature of an Electric Energy Storage Device. Patent Nr. WO 2019/016021 A2, 2019. Available online: https://patentimages.storage.googleapis.com/77/97/f2/7be732563f0615/WO2019016021A2.pdf (accessed on 28 September 2020).
- Youbi-Idrissi, M.; Bonjour, J.; Terrier, M.-F.; Marvillet, C.; Meunier, F. Oil presence in an evaporator: Experimental validation of a refrigerant/oil mixture enthalpy calculation model. Int. J. Refrig. 2004, 27, 215–224. [Google Scholar] [CrossRef]
- Span, R.; Wagner, W. Equations of State for Technical Applications. I. Simultaneously Optimized Functional Forms for Nonpolar and Polar Fluids. Int. J. Thermophys. 2003, 24, 1–39. [Google Scholar] [CrossRef]
- Heide, R. Stoffdatenbestimmung des Gemisches Kältemittel R134a-Öl ND8; Institut für Luft- und Kältetechnik Gemeinnützige Gesellschaft mbH: Dresden, Germany, 1998; Available online: https://www.ilkdresden.de/en/ (accessed on 28 September 2020).
- Jean-Marc, L.; Louis, V.; Evelyne, M.; Lottin, O. Oil Concentration Measurement in Saturated Liquid Refrigerant Flowing Inside a Refrigeration Machine. Int. J. Thermodyn. 2001, 4, 53–60. [Google Scholar]
- Braumoeller, J.; Riedel, R.; Schenk, J. Messung der Schallgeschwindigkeit in R134a-Oel-Gemischen; Institut für Luft- und Kältetechnik gemeinnützige Gesellschaft mbH: Dresden, Germany, 2004; Available online: https://www.ilkdresden.de/en/ (accessed on 28 September 2020).
- JCGM, Evaluation of measurement data—Guide to the expression of uncertainty in measurement. Joint Committee for Guides in Metrology 2008. Available online: https://www.bipm.org/en/publications/guides/gum.html (accessed on 28 September 2020).
- Angermeier, S.; Föhner, L.; Kerler, B.; Karcher, C. Uncertainty in measurement of a vapor compression system. In Proceedings of the 27th Fachtagung für Experimentelle Strömungsmechanik, Erlangen, Germany, 3–5 September 2019; Available online: https://www.gala-ev.org/images/Beitraege/Beitraege2019/pdf/46.pdf (accessed on 28 September 2020).
- Žukauskas, A. Heat transfer from tubes in crossflow. Adv. Heat Transf. 1972, 8, 93–160. [Google Scholar]
- Chi, J.; Didion, D. A simulation model of the transient performance of a heat pump. Int. J. Refrig. 1982, 5, 176–184. [Google Scholar] [CrossRef]


| 3.6 | 35 | 25 |
| 4 | 20/25/30/35/40 | 25 |
| 5 | 20/25/30/35 | 25 |
| 6 | 20/25/30/35 | 25 |
| 6.5 | 20 | 25 |
| Variable | ||||||
|---|---|---|---|---|---|---|
| Max deviation in K; kW; kg/h, - | 0.6/4.5 | 0.12/0.2 | 0/0.02 | 1.3/- | 2.39/4.65 | 0.34/0.57 |
| R-RMSE in % | 0.72/4.36 | 2.65/7.67 | 0/4.15 | 2.73/- | 0.69/2.2 | 2.94/6.12 |
| in % | 99.93/97.07 | 99.69/96.69 | 1/99.67 | 99.78/- | 99.67/99.29 | 98.28/92.59 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Angermeier, S.; Karcher, C. Model-Based Condenser Fan Speed Optimization of Vapor Compression Systems. Energies 2020, 13, 6012. https://doi.org/10.3390/en13226012
Angermeier S, Karcher C. Model-Based Condenser Fan Speed Optimization of Vapor Compression Systems. Energies. 2020; 13(22):6012. https://doi.org/10.3390/en13226012
Chicago/Turabian StyleAngermeier, Sebastian, and Christian Karcher. 2020. "Model-Based Condenser Fan Speed Optimization of Vapor Compression Systems" Energies 13, no. 22: 6012. https://doi.org/10.3390/en13226012
APA StyleAngermeier, S., & Karcher, C. (2020). Model-Based Condenser Fan Speed Optimization of Vapor Compression Systems. Energies, 13(22), 6012. https://doi.org/10.3390/en13226012





