The Mathematical Model for the Secondary Breakup of Dropping Liquid
Abstract
1. Introduction
2. Literature Review
3. Research Methodology
3.1. A Mathematical Model
3.2. A particular Solution of the Model
4. Results
4.1. A Critical Value of the Weber Number
4.2. Characteristics of the Secondary Breakup
4.3. Consideration of the Oscillating Wall
4.4. Consideration of the Resistance Force
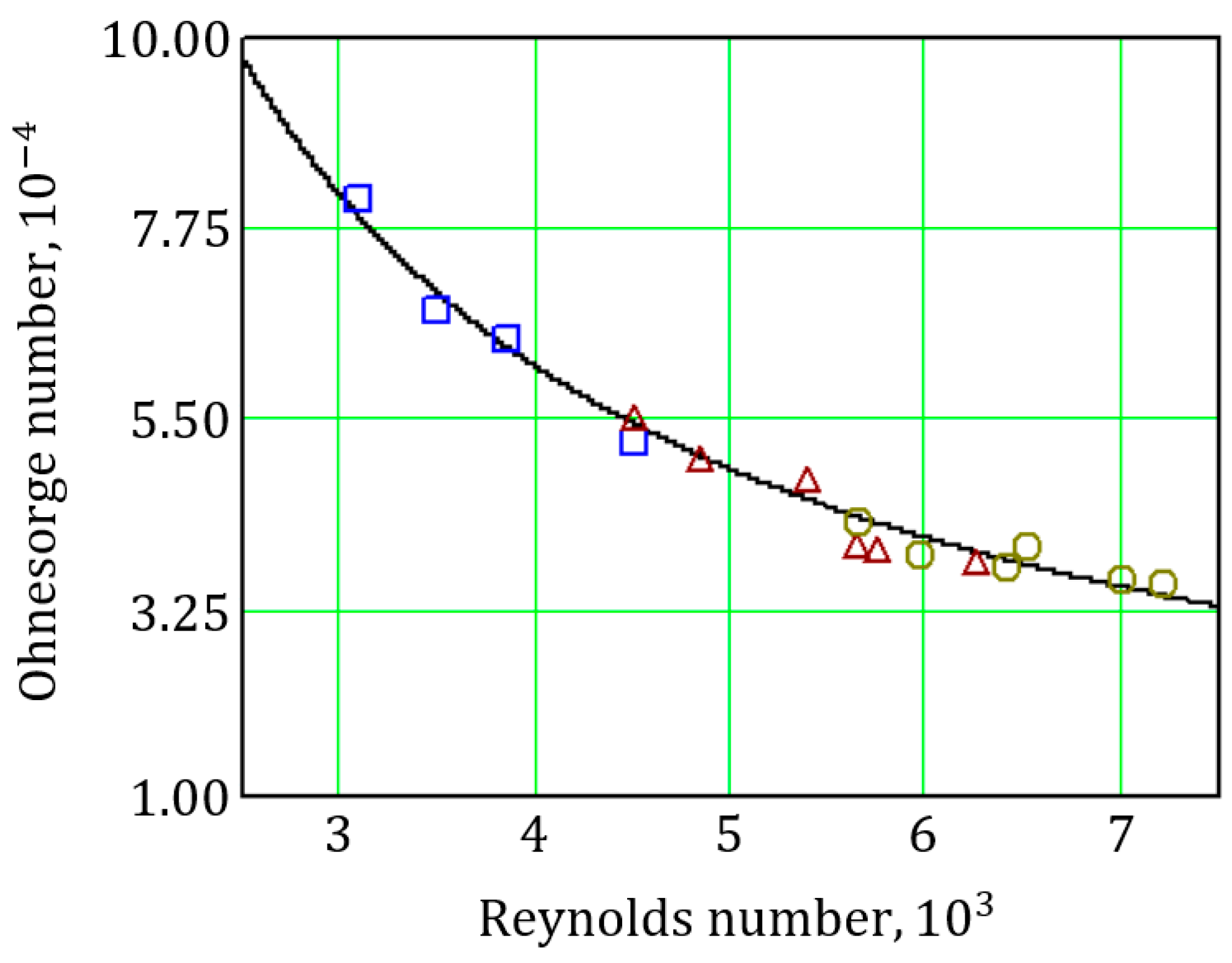
4.5. Validation of the Proposed Model
4.5.1. Experimental Research Data
4.5.2. An Example of Numerical Calculation
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pavlenko, I.; Sklabinskyi, V.; Pitel, J.; Zidek, K.; Kuric, I.; Ivanov, V.; Skydanenko, M.; Liaposhchenko, O. Effect of superimposed vibrations on droplet oscillation modes in prilling process. Processes 2020, 8, 566. [Google Scholar] [CrossRef]
- Wu, Y.; Bao, C.; Zhou, Y. An innovated tower-fluidized bed prilling process. Chin. J. Chem. Eng. 2007, 15, 424–428. [Google Scholar] [CrossRef]
- Daniher, D.; Briens, L.; Tallevi, A. End-point detection in high-shear granulation using sound and vibration signal analysis. Powder Technol. 2008, 181, 130–136. [Google Scholar] [CrossRef]
- Ku, N.; Hare, C.; Ghadiri, M.; Murtagh, M.; Oram, P.; Haber, R.A. Auto-granulation of fine cohesive powder by mechanical vibration. Procedia Eng. 2015, 102, 72–80. [Google Scholar] [CrossRef]
- Pavlenko, I.; Liaposhchenko, O.; Sklabinskyi, V.; Ivanov, V.; Ochowiak, M. Two-phase turbulent flow in the separation channel with an oscillating wall. In Advanced Manufacturing Processes; Tonkonogyi, V., Ed.; InterPartner 2019; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2020; pp. 570–581. [Google Scholar] [CrossRef]
- Morkovnikov, V.E.; Revnov, V.N.; Rodionov, E.P. A new design for continuous separation of granules from liquids by vibration. Chem. Pet. Eng. 2001, 37, 423–427. [Google Scholar] [CrossRef]
- Pai, M.G.; Bermejo-Moreno, I.; Desjardins, O.; Pitsch, H. Role of Weber number in primary breakup of turbulent liquid jets in crossflow. In Center for Turbulence Research Annual Research Briefs; Stanford University: Stanford, CA, USA, 2009; pp. 145–158. [Google Scholar]
- Hillen, N.L.; Taylor, J.S.; Menchini, C.; Morris, G.; Dinc, M.; Gray, D.D.; Kuhlman, J. Droplet impact time histories for a range of Weber numbers and liquid film thicknesses for spray cooling application. In Proceedings of the 43rd AIAA Fluid Dynamics Conference, San Diego, CA, USA, 24–27 June 2013; pp. 1–22. [Google Scholar]
- Gelfand, B.E. Droplet breakup phenomena in flows with velocity lag. Prog. Energy Combust. Sci. 1996, 22, 201–265. [Google Scholar] [CrossRef]
- Solsvik, J.; Maas, S.; Jakobsen, H.A. Definition of the single drop breakup event. Ind. Eng. Chem. Res. 2016, 55, 2872–2882. [Google Scholar] [CrossRef]
- Yadigaroglu, G.; Hewitt, G.F. Introduction to Multiphase Flow: Basic Concepts, Applications and Modelling; Springer Science and Business Media: New York, NY, USA, 2018. [Google Scholar]
- Liang, C.; Feigl, K.A.; Tanner, F.X.; Case, W.R.; Windhab, E.J. Three-dimensional simulations of drop deformation and breakup in air flow and comparisons with experimental observations. At. Sprays 2018, 28, 621–641. [Google Scholar] [CrossRef]
- Pazhi, D.G.; Galustov, V.S. Fundamentals of the Liquid Atomization Technique; Chemistry: Moscow, Russia, 1984. [Google Scholar]
- Ponikarov, S.I. Droplet Breakup in Centrifugal Equipment of Chemical Plants. Ph.D. Thesis, Kazan National Research Technological University, Kazan, Russia, 1984. [Google Scholar]
- Ivlev, L.S.; Dovgalyuk, Y.A. Physics of Atmospheric Aerosol Systems; Saint Petersburgh University Publishing House: Saint Petersburg, Russia, 1984. [Google Scholar]
- Cherdantsev, A.V. The Wave Structure of a Liquid Film and Dispersed Phase Exchange Processes in a Dispersed-Annular Gas-Liquid Flow; Novosibirsk State University Publishing House: Novosibirsk, Russia, 1999. [Google Scholar]
- Ostroha, R.; Yukhymenko, M.; Lytvynenko, A.; Bocko, J.; Pavlenko, I. Granulation process of the organic suspension: Fluidized bed temperature influence on the kinetics of the granule formation. In Advances in Design, Simulation and Manufacturing. DSMIE 2018; Ivanov, V., Ed.; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2019; pp. 463–471. [Google Scholar] [CrossRef]
- Gezerman, A.O.; Corbacioglu, B.D. New approach for obtaining uniform- sized granules by prilling process. Chem. Eng. 2011, 40, 5225–5228. [Google Scholar]
- Pavlenko, I.V.; Liaposhchenko, O.O.; Demianenko, M.M.; Starynskyi, O.Y. Static calculation of the dynamic deflection elements for separation devices. J. Eng. Sci. 2017, 4, B19–B24. [Google Scholar] [CrossRef]
- Liaposhchenko, O.; Pavlenko, I.; Monkova, K.; Demianenko, M.; Starynskyi, O. Numerical simulation of aeroelastic interaction between gas-liquid flow and deformable elements in modular separation devices. In Advances in Design, Simulation and Manufacturing II. DSMIE 2019; Ivanov, V., Ed.; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2020; pp. 765–774. [Google Scholar] [CrossRef]
- Varukha, D.A.; Smirnov, V.A.; Edl, M.; Demianenko, M.M.; Yukhymenko, M.P.; Pavlenko, I.V.; Liaposhchenko, O.O. Modelling of separation and air classification processes of aerodisperse systems in the shelf device. J. Eng. Sci. 2018, 5, F5–F9. [Google Scholar] [CrossRef]
- Pavlenko, I.V.; Yukhymenko, M.P.; Lytvynenko, A.V.; Bocko, J. Solving the nonstationary problem of the disperse phase concentration during the pneumoclassification process of mechanical mixtures. J. Eng. Sci. 2019, 6, F1–F5. [Google Scholar] [CrossRef]
- Shimogouchi, T.; Naganawa, H.; Nagano, T.; Grambow, B.; Nagame, Y. Size distribution of droplets in a two liquid-phase mixture compared between liquid spraying and mechanical stirring. Anal. Sci. 2019, 35, 955–960. [Google Scholar] [CrossRef] [PubMed]
- Ochowiak, M.; Wlodarczak, S.; Pavlenko, I.; Janecki, D.; Krupinska, A.; Markowska, M. Study on interfacial surface in modified spray tower. Processes 2019, 7, 532. [Google Scholar] [CrossRef]
- Chirkov, A.Y.; Khvesyuk, V.I. Kelvin-Helmholtz instability in sheared flows of fluids and plasmas. Eng. J. Sci. Innov. 2013, 5, 1–10. [Google Scholar] [CrossRef]
- Cheng, H.; Zhao, J.; Wang, J. Experimental investigation on the characteristics of melt jet breakup in water: The importance of surface tension and Rayleigh-Plateau instability. Int. J. Heat Mass Transf. 2019, 132, 388–393. [Google Scholar] [CrossRef]
- Yakovenko, S.N. Rayleigh-Taylor instability in two-fluid and stratified media. In Proceedings of the Seminar on Dynamics of Multiphase Media (DMM 2017), Novosibirsk, Russia, 3–5 October 2017; pp. 257–259. [Google Scholar]
- Kelbaliyev, G.I.; Tagiyev, D.B.; Rasulov, S.R. Transport Phenomena in Dispersed Media, 1st ed.; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Pilch, M.; Erdman, C.A. Use of breakup time data and velocity history data to predict the maximum size of stable fragments for acceleration-induced breakup of liquid drop. Int. J. Multiph. Flow 1987, 13, 741–757. [Google Scholar] [CrossRef]
- Ranger, A.A. Shock wave propagation through a two-phase medium. Acta Astronaut. 1972, 17, 675–683. [Google Scholar]
- Clark, M.M. Drop breakup in a turbulent flow-I conceptual and modeling considerations. Chem. Eng. Sci. 1988, 43, 671–679. [Google Scholar] [CrossRef]
- Ye, W.; Zhang, W.; Chen, G. Numerical simulation of laser ablative Rayleigh-Taylor instability. High Power Laser Part. Beams 1998, 10, 403–408. [Google Scholar]
- Chiandussi, G.; Bugeda, G.; Oate, E. Shape variable definition with C0, C1 and C2 continuity functions. Comput. Methods Appl. Mech. Eng. 2000, 188, 727–742. [Google Scholar] [CrossRef]
- Sklabinskij, V.I.; Kholin, B.G. Intesification of internal currents in drop moving in gas flow with cross velocity gradient. Teor. Osn. Khimicheskoi Tekhnologii 1992, 26, 741–745. [Google Scholar]
- Arkhipov, V.A.; Vasenin, I.M.; Trofimov, V.F.; Usanina, A.S. Stability of dispersed-particle shape at small Reynolds numbers. Fluid Dyn. 2013, 48, 143–150. [Google Scholar] [CrossRef]
- Kelbaliev, G.; Ibragimov, Z. Coalescence and fragmentation of drops in an isotropic turbulent flow. Theor. Found. Chem. Eng. 2009, 43, 329–336. [Google Scholar] [CrossRef]
- Arefyev, K.Y.; Voronetsky, A.V. Modelling of the process of fragmentation and vaporization of non-reacting liquid droplets in high-enthalpy gas flows. Thermophys. Aeromech. 2015, 22, 585–596. [Google Scholar] [CrossRef]
- Boiko, V.M.; Poplavski, S.V. Experimental study of two types of stripping breakup of the drop in the flow behind the shock wave. Explos. Shock Waves 2012, 48, 440–445. [Google Scholar] [CrossRef]
- Glaznev, V.N.; Korobeinikov, Y.G. Hartmann effect. Region of existence and oscillation frequencies. J. Appl. Mech. Tech. Phys. 2001, 42, 616–620. [Google Scholar] [CrossRef]
- Wu, Z.; Lv, B.; Cao, Y. Improved Taylor analogy breakup and Clark models for droplet deformation prediction. J. Aerosp. Eng. 2019, 233, 767–775. [Google Scholar] [CrossRef]
- Theofanous, T.G.; Li, G.J. On the physics of aerobreakup. Phys. Fluids 2008, 20, 052103. [Google Scholar] [CrossRef]
- Kucharika, M.; Shashkov, M. Conservative multi-material remap for staggered multimaterial arbitrary Lagrangian–Eulerian methods. J. Comput. Phys. 2014, 258, 268–304. [Google Scholar] [CrossRef]
- Gelfand, B.E.; Vieilli, B.; Gekalp, I.; Chauveau, C. Shock-free breakup of droplets. Temporal characteristics. J. Appl. Mech. Tech. Phys. 2001, 42, 63–66. [Google Scholar] [CrossRef]
- Kim, D.; Moin, P. Subgrid-scale capillary breakup model for liquid jet atomization. Combust. Sci. Technol. 2020, 192, 1334–1357. [Google Scholar] [CrossRef]
- Li, X.; Huang, Y.; Chen, X.; Wu, Z. Breakup dynamics of low-density gas and liquid interface during taylor bubble formation in a microchannel flow-focusing device. Chem. Eng. Sci. 2020, 215, 115473. [Google Scholar] [CrossRef]
- Salari, A.; Xu, J.; Kolios, M.C.; Tsai, S.S.H. Expansion-mediated breakup of bubbles and droplets in microfluidics. Phys. Rev. Fluids 2020, 5, 013602. [Google Scholar] [CrossRef]
- Speirs, N.B.; Langley, K.R.; Taborek, P.; Thoroddsen, S.T. Jet breakup in superfluid and normal liquid. Phys. Rev. Fluids 2020, 5, 044001. [Google Scholar] [CrossRef]
- Tirel, C.; Renoult, M.-C.; Dumouchel, C. Measurement of extensional properties during free jet breakup. Exp. Fluids 2020, 61, 21. [Google Scholar] [CrossRef]
- Dziedzic, A.; Nakrani, M.; Ezra, B.; Syed, M.; Popinet, S.; Afkhami, S. Breakup of finite-size liquid filaments: Transition from no-breakup to breakup including substrate effects. Eur. Phys. J. E 2019, 42, 18. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Wang, Z. In-fiber breakup. In Advanced Fiber Sensing Technologies; Wei, L., Ed.; Progress in Optical Science and Photonics; Springer: Singapore, 2020; Volume 9, pp. 199–216. [Google Scholar] [CrossRef]
- Guo, J.-P.; Wang, Y.-B.; Bai, F.-Q.; Du, Q. Instability breakup model of power-law fuel annular jets in slight multiple airflows. Phys. Fluids 2020, 32, 094109. [Google Scholar] [CrossRef]
- Cheng, Z.; Li, J.; Loh, C.Y.; Luo, L.-S. An exactly force-balanced boundary-conforming arbitrary-lagrangian-eulerian method for interfacial dynamics. J. Comput. Phys. 2020, 408, 109237. [Google Scholar] [CrossRef]
- Blekhman, I.I.; Blekhman, L.I.; Sorokin, V.S.; Vasilkov, V.B.; Yakimova, K.S. Surface and volumetric effects in a fluid subjected to highfrequency vibration. J. Mech. Eng. Sci. 2012, 226, 2028–2043. [Google Scholar] [CrossRef]
- Blekhman, I.I. Vibrational Mechanics. Nonlinear Dynamic Effects, General Approach, Applications; World Scientific Publishing: Singapore, 2000. [Google Scholar]
- Ekiel-Jezewska, M.; Boniecki, R.; Bukowicki, M.; Gruca, M. Stokes velocity generated by a point force in various geometries. Eur. Phys. J. E 2018, 41, 120. [Google Scholar] [CrossRef] [PubMed]
- Pavlenko, I.; Trojanowska, J.; Ivanov, V.; Liaposhchenko, O. Parameter identification of hydro-mechanical processes using artificial intelligence systems. Int. J. Mechatron. Appl. Mech. 2019, 2019, 19–26. [Google Scholar]
- Du, B.-G.; Long, W.-Q.; Feng, L.-Y.; Chen, L.; Liu, Y. Study on multi-piece spray characteristics based on Matlab digital image processing technology. Chin. Intern. Combust. Engine Eng. 2008, 29, 1–5. [Google Scholar]
- Bonello, D.K.; Iano, Y.; Neto, U.B. An algorithm for the detection of circular elements in engineering design. J. Eng. Sci. 2020, 7, E6–E9. [Google Scholar] [CrossRef]
- Veenstra, H.; Van Dam, J.; Posthuma De Boer, A. Formation and stability of co-continuous blends with a poly(ether-ester) block copolymer around its order-disorder temperature. Polymer 1999, 40, 1119–1130. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, P.-F.; Luo, Y.; Guo, Y.; Liu, Y.-Z. Liquid sheet breakup mode and droplet size of free opposed impinging jets by particle image velocimetry. Ind. Eng. Chem. Res. 2020, 59, 11296–11307. [Google Scholar] [CrossRef]
- Basarevsky, A.N.; Kravtsov, A.M.; Shakhrai, D.S. Criterion similarity equation for determining the drops diameter of artificial rain. Mech. Power Eng. 2019, 57, 230–237. [Google Scholar] [CrossRef]





| Liquid Level (m) | Flow Rate (m/s) | Amplitude (V) | Frequency (Hz) | Droplet Diameter (mm) |
|---|---|---|---|---|
| 0.28 | 1.94 | 4.4 | 240 | 1.60–1.80 |
| 500–520 | 1.80 | |||
| 10.6 | 245–260 | 2.25 | ||
| 370–380 | 2.00 | |||
| 500–520 | 1.80 | |||
| 0.38 | 2.44 | 4.4 | 460–560 | 2.20 |
| 10.6 | 235–240 | 2.60 | ||
| 250–260 | 1.85–2.35 | |||
| 380–390 | 2.35 | |||
| 440–480 | 2.30 | |||
| 570–590 | 2.00 | |||
| 0.49 | 3.11 | 4.4 | 400–430 | 2.30 |
| 460–500 | 2.25 | |||
| 520 | 2.10 | |||
| 10.6 | 260 | 1.90–2.05 | ||
| 540–575 | 1.80 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavlenko, I.; Sklabinskyi, V.; Doligalski, M.; Ochowiak, M.; Mrugalski, M.; Liaposhchenko, O.; Skydanenko, M.; Ivanov, V.; Włodarczak, S.; Woziwodzki, S.; et al. The Mathematical Model for the Secondary Breakup of Dropping Liquid. Energies 2020, 13, 6078. https://doi.org/10.3390/en13226078
Pavlenko I, Sklabinskyi V, Doligalski M, Ochowiak M, Mrugalski M, Liaposhchenko O, Skydanenko M, Ivanov V, Włodarczak S, Woziwodzki S, et al. The Mathematical Model for the Secondary Breakup of Dropping Liquid. Energies. 2020; 13(22):6078. https://doi.org/10.3390/en13226078
Chicago/Turabian StylePavlenko, Ivan, Vsevolod Sklabinskyi, Michał Doligalski, Marek Ochowiak, Marcin Mrugalski, Oleksandr Liaposhchenko, Maksym Skydanenko, Vitalii Ivanov, Sylwia Włodarczak, Szymon Woziwodzki, and et al. 2020. "The Mathematical Model for the Secondary Breakup of Dropping Liquid" Energies 13, no. 22: 6078. https://doi.org/10.3390/en13226078
APA StylePavlenko, I., Sklabinskyi, V., Doligalski, M., Ochowiak, M., Mrugalski, M., Liaposhchenko, O., Skydanenko, M., Ivanov, V., Włodarczak, S., Woziwodzki, S., Kruszelnicka, I., Ginter-Kramarczyk, D., Olszewski, R., & Michałek, B. (2020). The Mathematical Model for the Secondary Breakup of Dropping Liquid. Energies, 13(22), 6078. https://doi.org/10.3390/en13226078












