Experimental and Numerical Study on Proppant Transport in a Complex Fracture System
Abstract
:1. Introduction
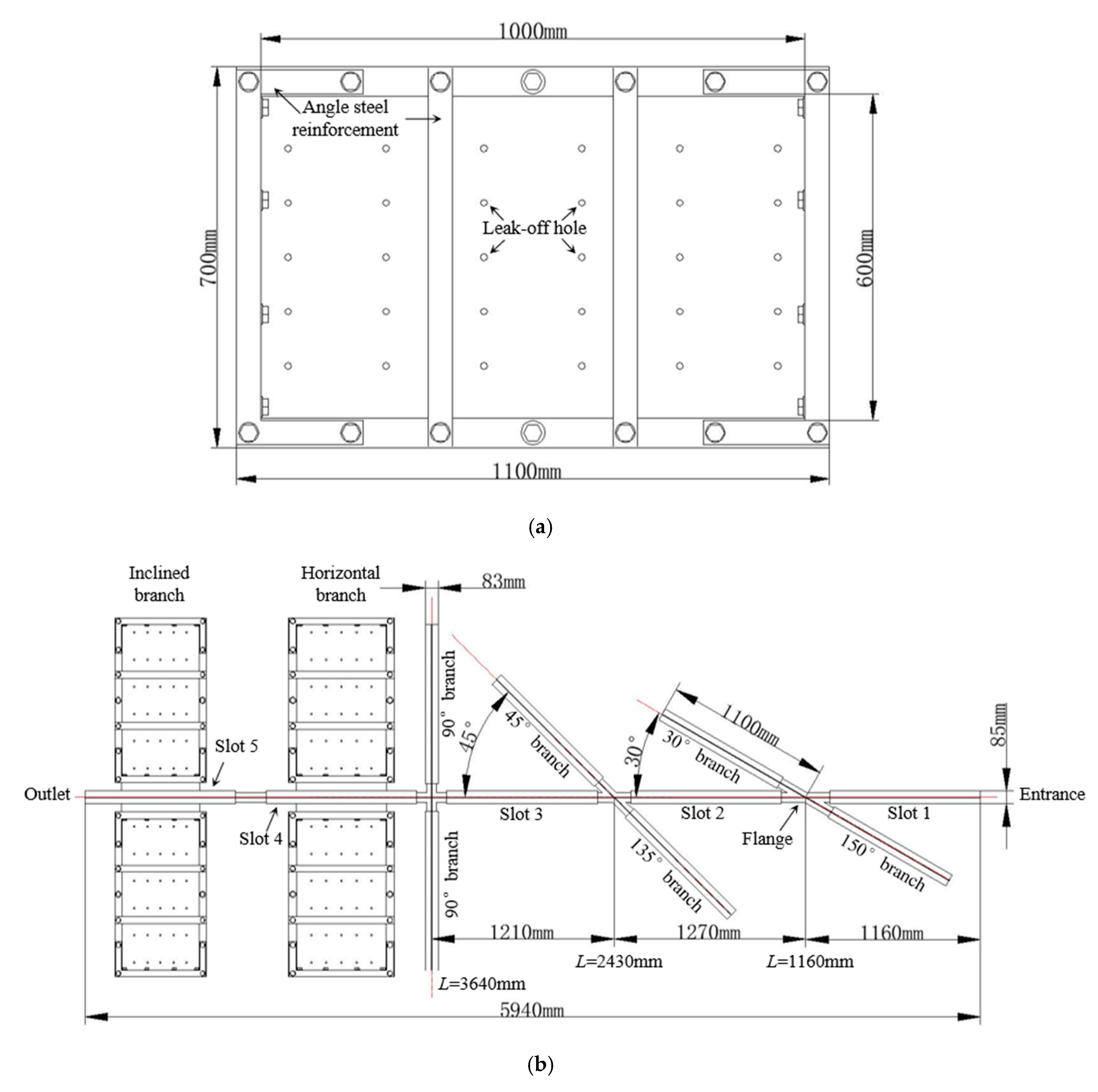
2. Slot Flow Experiment
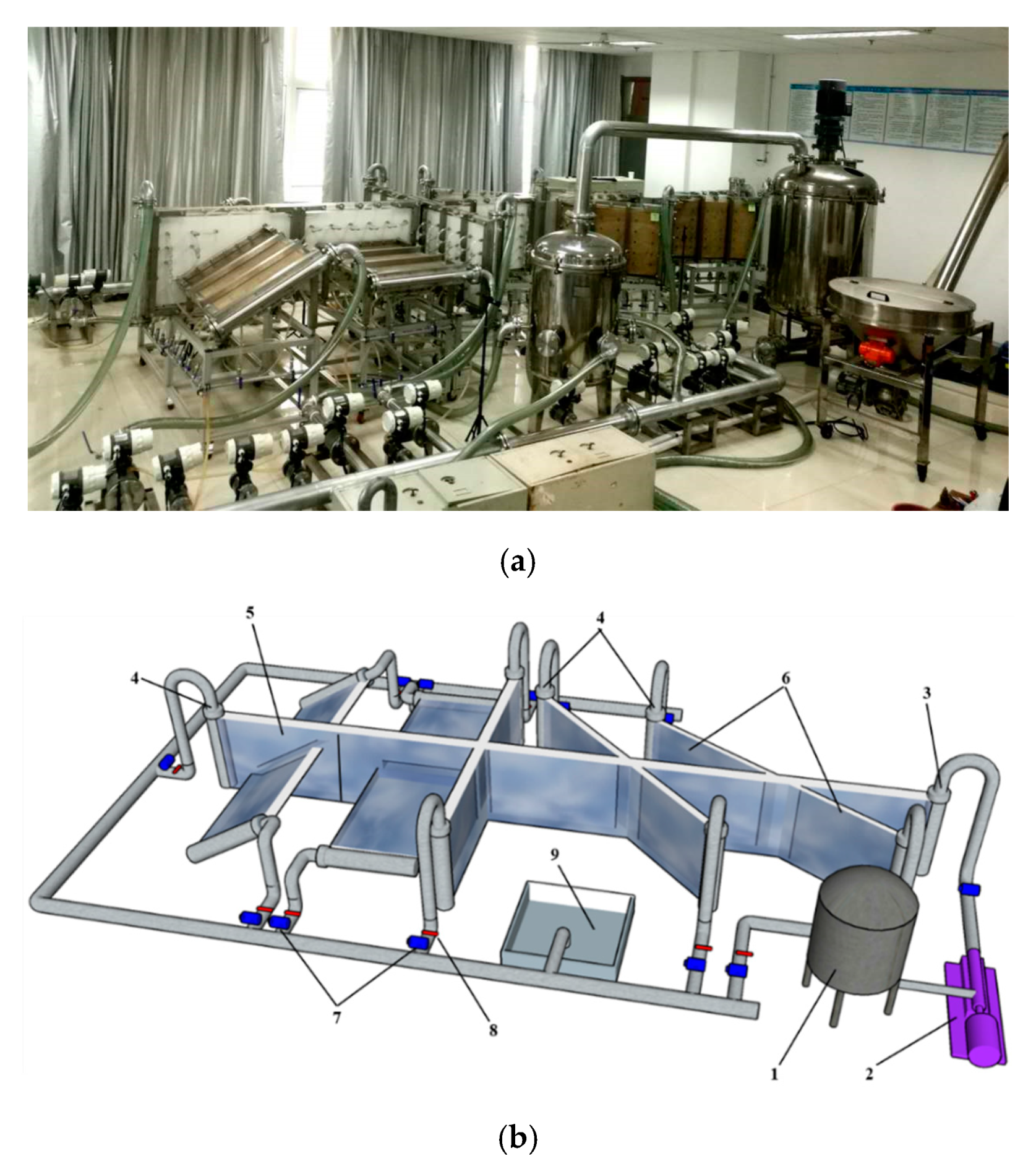
2.1. Experimental Apparatus
2.2. Material Preparation
2.3. Experimental Procedure
2.4. Scaling Design
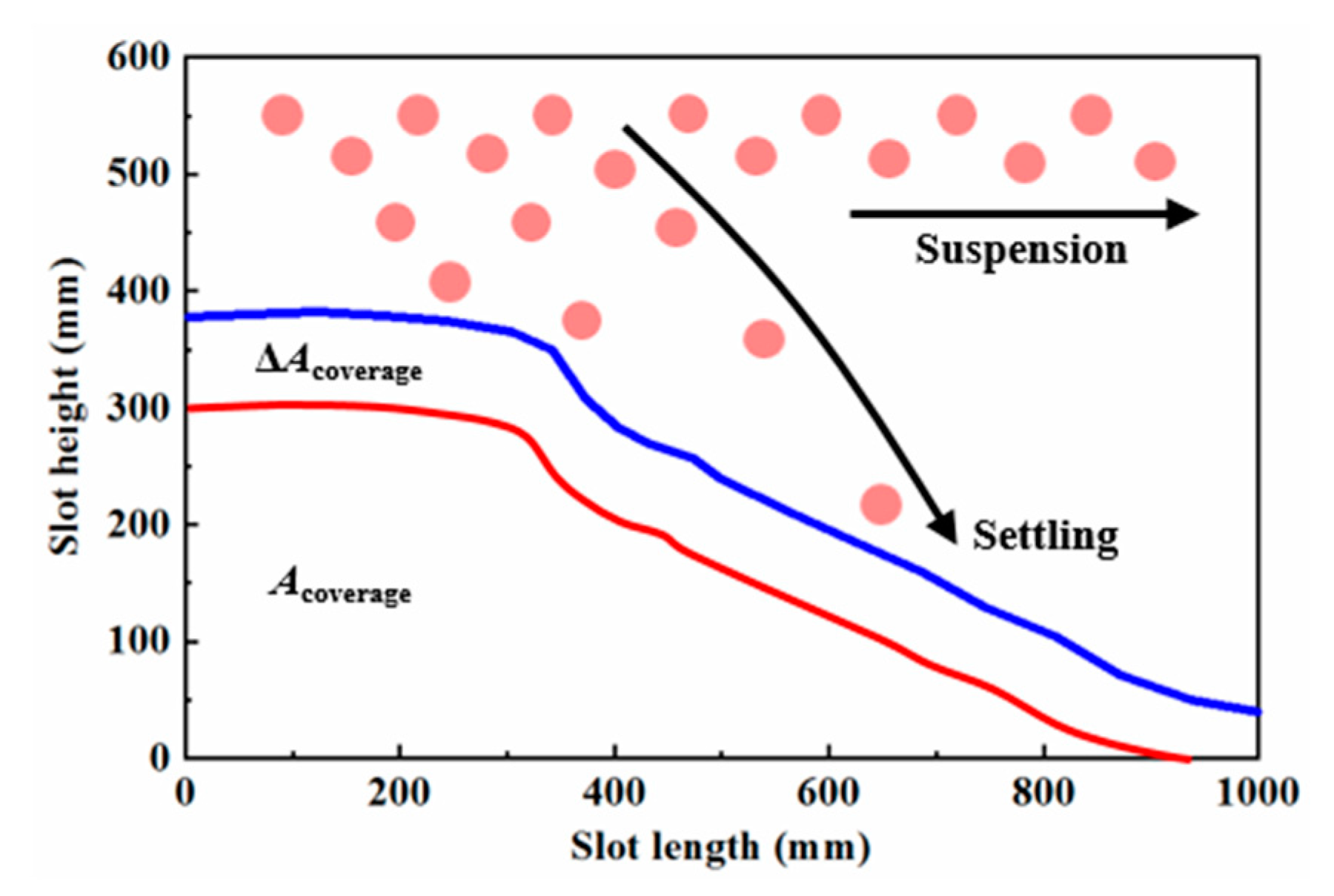
2.5. Characterization of Dune Distribution
3. Proppant Transport in the Complex Fracture System
3.1. Slurry Partition at the Intersection
3.2. Pattern of Dune Development in the Branch
3.3. Evolvement of Dunes in the Complex Fracture System
3.3.1. Effect of the Pumping Rate
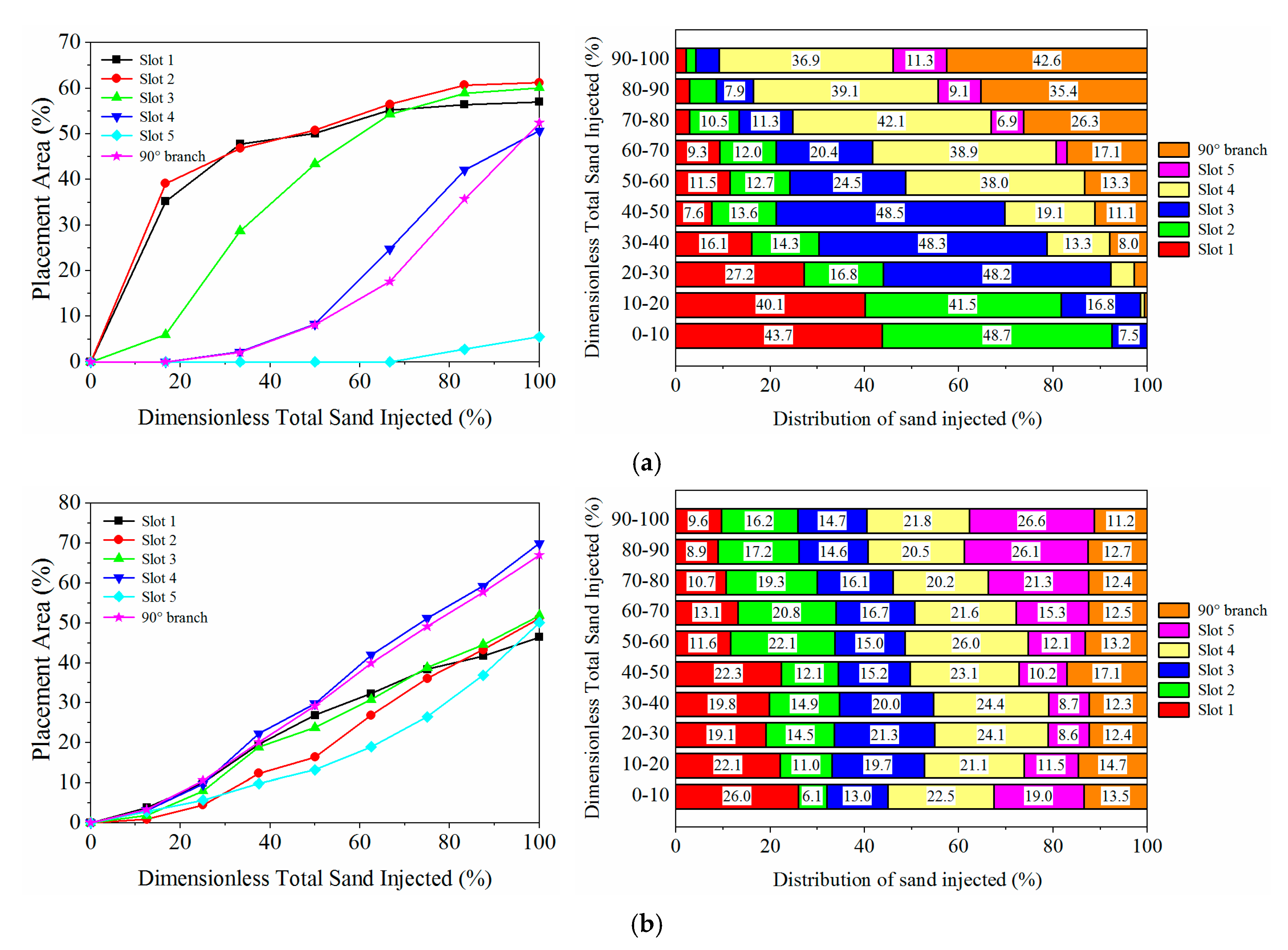
3.3.2. Effect of the Sand Ratio
3.3.3. Effect of the Sand Size
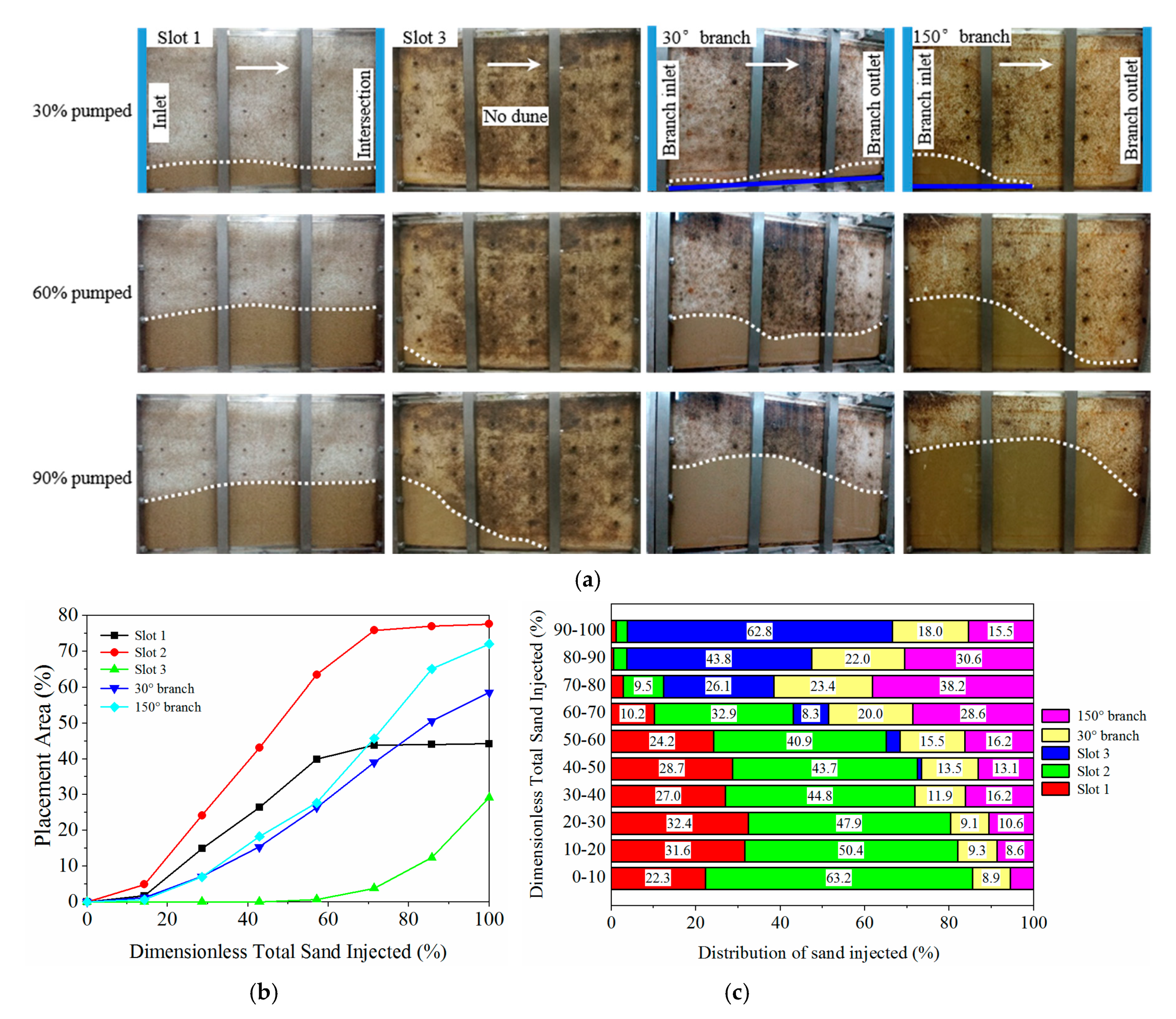
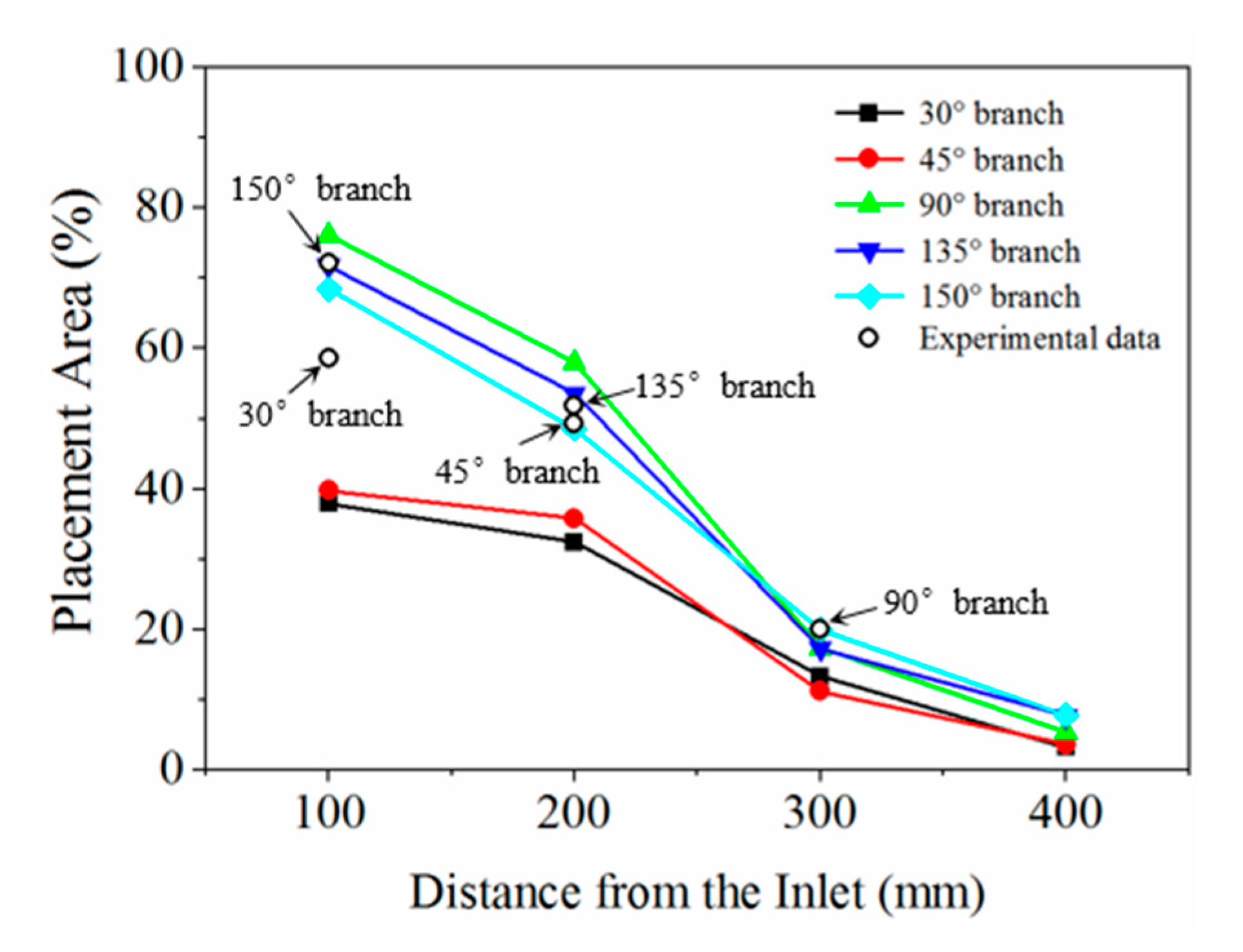
3.3.4. Effect of the Branch Angle
4. Numerical Simulation of Proppant Transport in the Complex Fracture System
4.1. Governing Equations
4.2. Numerical Simulation Model
4.3. Simulation Results and Analysis
4.3.1. Model Validation
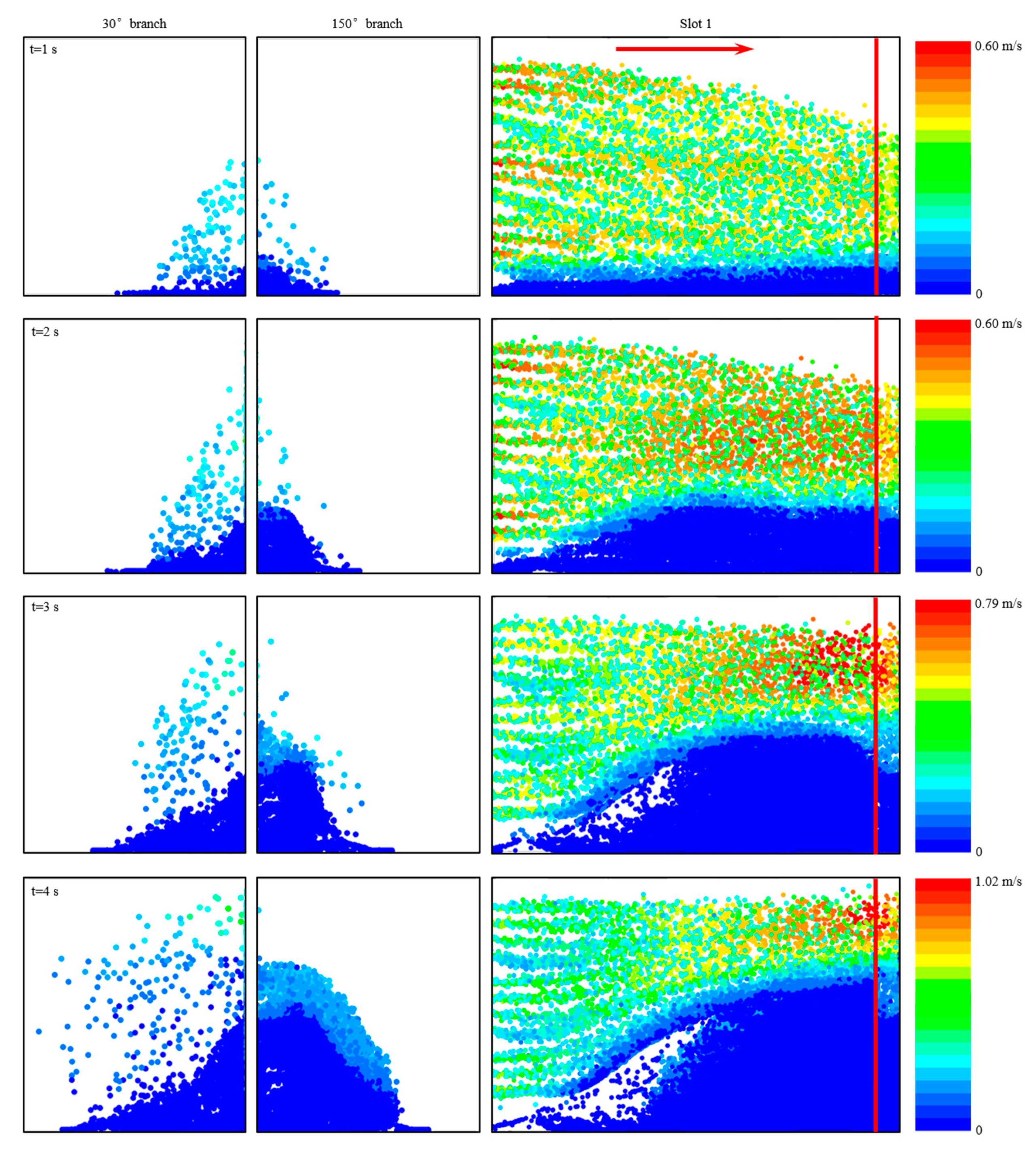
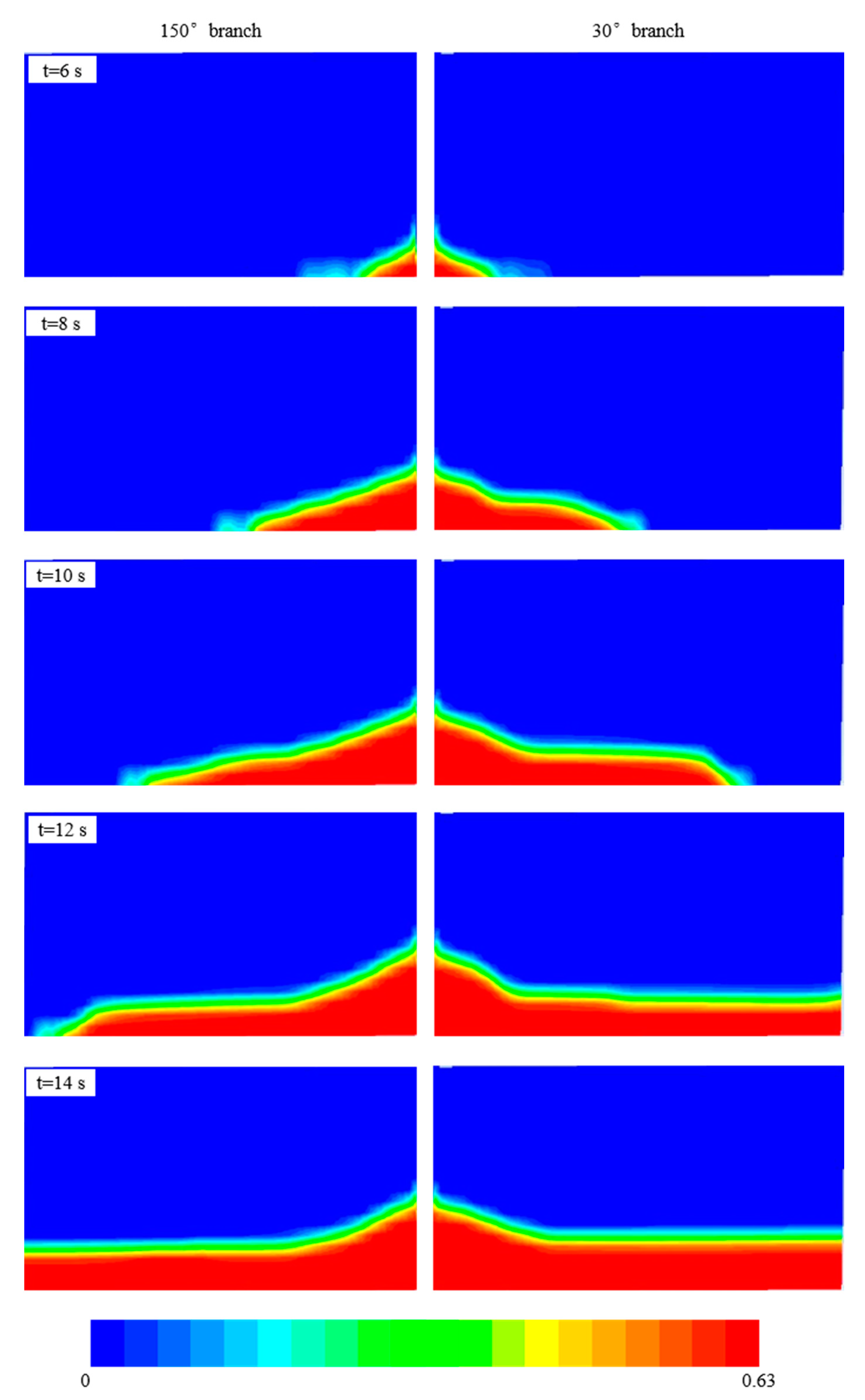
4.3.2. Dune Development in Branches at Different Locations
4.3.3. Dune Development in Branches under a Low Pumping Rate
5. Conclusions
- (1)
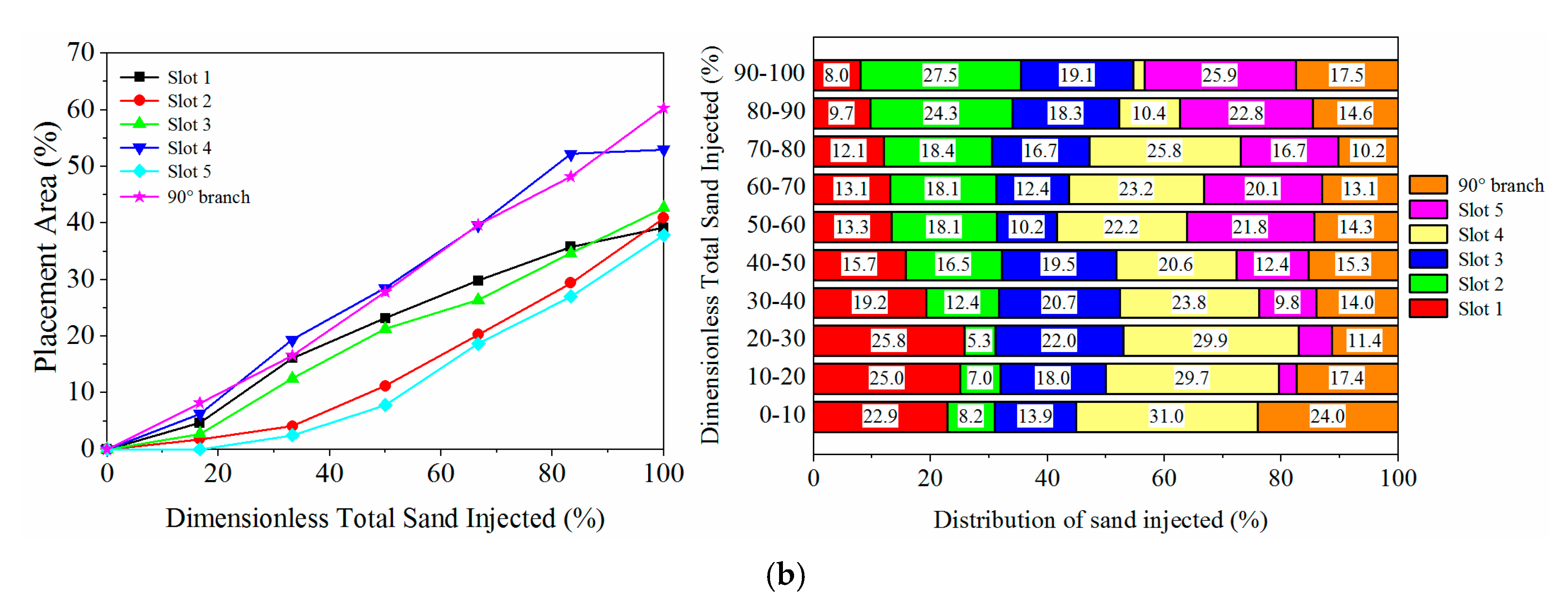
- The flow rate in the primary fracture is partitioned when encountering an intersection. In the case of a 90°-branch, approximately half of the slurry enter the secondary fracture. In the case of two branches, more than 60% of the slurry turn the corner into the branches. As the number of branches that the primary slot encounters increases, the flow rate remaining in the primary slot will decrease correspondingly. It is also found that the flow rate in the branch with a smaller angle is higher than the other with a larger angle.
- (2)
- Two categories of dune development patterns in the complex fracture system are observed in the experiments. One pattern is that the dune development in the subsequent slot is dependent on the development degree of the dune in the precedent fracture; the other pattern is that the dunes in the primary fracture and branch can develop simultaneously.
- (3)
- Under a low pumping rate, the dune in the branch starts to develop only if the dune in the primary fracture has fully developed. Under a high pumping rate, a large of proppants can transport to the branch and the deep of a primary fracture. However, the proportion of sand which transport into the branch is lower than that in the case with a low pumping rate.
- (4)
- Sand ratio has few effects on the proppant distribution in the before-intersection fraction of a primary fracture, but has a significant impact on the proppant distribution in the branch and the after-intersection fraction of a primary fracture. A high sand ratio can result in a low proportion of proppant transporting into the branch, despite a high placement area in the branch due to the large sand amount injected. A low sand ratio leads to poor placement in the branch, but a higher proportion of proppant transporting into the branch can be obtained.
- (5)
- The branch and the deep of the primary fracture can be uniformly covered by fine proppants. However, a higher proportion of proppant transporting into the branch may be obtained in the final stage of the injection using the coarse proppants.
- (6)
- Uneven distribution of proppants can occur in the secondary fracture. Proppants tend to settle along the fracture length in the branch with a small angle, but tend to accumulate along the height in the branch with a large angle. The branch near the fracture inlet can obtain more proppants. Due to the size limit, a long horizontal transport distance cannot be realized in the branch with a small angle, and they will travel out of the system. As a result, a phenomenon that the placement area in the large-angle branch is larger than that in the small-angle branch. Decreasing the experimental pumping rate or extending the branch length is an effective method to prevent the proppants from flowing out of the system.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Maxwell, S.C.; Urbancic, T.I.; Steinsberger, N.; Zinno, R. Microseismic imaging of hydraulic fracture complexity in the Barnett Shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 29 September–2 October 2002. [Google Scholar]
- Cipolla, C.L.; Warpinski, N.R.; Mayerhofer, M.J.; Lolon, E.P.; Vincent, M.C. The relationship between fracture complexity, reservoir properties, and fracture-treatment design. SPE Prod. Oper. 2010, 25, 438–452. [Google Scholar] [CrossRef]
- Zou, Y.S.; Ma, X.F.; Zhou, T.; Li, N.; Chen, M.; Li, S.H.; Zhang, Y.N.; Li, H. Hydraulic fracture growth in a layered formation based on fracturing experiments and discrete element modeling. Rock Mech. Rock Eng. 2017, 50, 2381–2395. [Google Scholar]
- Sahai, R.; Moghanloo, R.G. Proppant transport in complex fracture networks–A review. J. Petrol. Sci. Eng. 2019, 182, Article 106199. [Google Scholar] [CrossRef]
- Mckenna, J.P. Where did the proppant go? In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 25–27 August 2014. [Google Scholar]
- Tan, P.; Jin, Y.; Hou, B.; Zheng, X.; Guo, X.; Gao, J. Experiments and analysis on hydraulic sand fracturing by an improved true tri-axial cell. J. Petrol. Sci. Eng. 2017, 158, 766–774. [Google Scholar] [CrossRef]
- King, G.E. Thirty years of gas shale fracturing: What have we learned? In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010. [Google Scholar]
- Britt, L.K.; Smith, M.B.; Haddad, Z.; Lawrence, P.; Chipperfield, S.; Hellman, T. Water-fracs: We do need proppant after all. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006. [Google Scholar]
- Sahai, R. Laboratory Evaluation of Proppant Transport in Complex Fracture Systems; Colorado School of Mines: Golden, CO, USA, 2012. [Google Scholar]
- Kern, L.R.; Perkins, T.K.; Wyant, R.E. The mechanics of sand movement in fracturing. J. Petrol. Technol. 1959, 11, 55–57. [Google Scholar] [CrossRef]
- Medlin, W.L.; Sexton, J.H.; Zumwalt, G.L. Sand transport experiments in thin fluids. In Proceedings of the SPE Annual Technical Conference and Exhibition, Las Vegas, NV, USA, 22–26 September 1985. [Google Scholar]
- Liu, Y.; Sharma, M.M. Effect of fracture width and fluid rheology on proppant settling and retardation: An experimental study. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 9–12 October 2005. [Google Scholar]
- Brannon, H.D.; Wood, W.D.; Wheeler, R.S. Large scale laboratory investigation of the effects of proppant and fracturing fluid properties on transport. In Proceedings of the SPE International Symposium and Exhibition on Formation Damage Control, Lafayette, LA, USA, 15–17 February 2006. [Google Scholar]
- Fernández, M.E.; Sánchez, M.; Pugnaloni, L.A. Proppant transport in a scaled vertical planar fracture: Vorticity and dune placement. J. Petrol. Sci. Eng. 2019, 173, 1382–1389. [Google Scholar] [CrossRef]
- Raimbay, A.; Babadagli, T.; Kuru, E.; Develi, K. Quantitative and visual analysis of proppant transport in rough fractures. J. Nat. Gas Sci. Eng. 2017, 33, 1291–1307. [Google Scholar] [CrossRef]
- Patankar, N.A.; Joseph, D.D.; Wang, J.; Barree, R.D.; Conway, M.; Asadi, M. Power law correlations for sediment transport in pressure driven channel flows. Int. J. Multiphas. Flow 2002, 28, 1269–1292. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Joseph, D.D.; Patankar, N.A.; Conway, M.; Barree, R.D. Bi-power law correlations for sediment transport in pressure driven channel flows. Int. J. Multiphas. Flow 2003, 29, 475–494. [Google Scholar] [CrossRef]
- Sahai, R.; Miskimins, J.L.; Olson, K.E. Laboratory results of proppant transport in complex fracture systems. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 4–6 February 2014. [Google Scholar]
- Tong, S.; Mohanty, K.K. Proppant transport study in fractures with intersections. Fuel 2016, 181, 463–477. [Google Scholar] [CrossRef]
- Alotaibi, M.A.; Miskimins, J.L. Slickwater proppant transport in hydraulic fractures - new experimental findings and scalable correlation. SPE Prod. Oper. 2018, 33, 164–178. [Google Scholar] [CrossRef]
- Li, N.; Li, J.; Zhao, L.; Luo, Z.; Liu, P.; Guo, Y. Laboratory testing on proppant transport in complex-fracture systems. SPE Prod. Oper. 2017, 32, 382–391. [Google Scholar] [CrossRef]
- Pan, L.; Zhang, Y.; Cheng, L.; Lu, Z.; Kang, Y.; He, P.; Dong, B. Migration and distribution of complex fracture proppant in shale reservoir volume fracturing (In Chinese). Natur. Gas Ind. 2018, 38, 61–70. [Google Scholar]
- Ma, W.; Perng, J.; Tomac, I. Experimental investigation of proppant flow and transport dynamics through fracture intersections. arXiv 2020, arXiv:2009.09986. [Google Scholar]
- Zhang, G.; Li, M.; Gutierrez, M. Simulation of the transport and placement of multi-sized proppant in hydraulic fractures using a coupled CFD-DEM approach. Adv. Powder Technol. 2017, 28, 1704–1718. [Google Scholar] [CrossRef]
- Zhang, G.; Gutierrez, M.; Li, M. A coupled CFD-DEM approach to model particle-fluid mixture transport between two parallel plates to improve understanding of proppant micromechanics in hydraulic fractures. Powder Technol. 2017, 308, 235–248. [Google Scholar] [CrossRef]
- Baldini, M.; Carlevaro, C.M.; Pugnaloni, L.A.; Sánchez, M. Numerical simulation of proppant transport in a planar fracture: A study of perforation placement and injection strategy. Int. J. Multiphas. Flow 2018, 109, 207–218. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J. A comparison of two-fluid model, dense discrete particle model and CFD-DEM method for modeling impinging gas–solid flows. Powder Technol. 2014, 254, 94–102. [Google Scholar] [CrossRef]
- Zeng, J.; Li, H.; Zhang, D. Numerical simulation of proppant transport in hydraulic fracture with the upscaling CFD-DEM method. J. Nat. Gas Sci. Eng. 2016, 33, 264–277. [Google Scholar] [CrossRef]
- Hu, X.; Wu, K.; Li, G.; Tang, J.; Shen, Z. Effect of proppant addition schedule on the proppant distribution in a straight fracture for slickwater treatment. J. Petrol. Sci. Eng. 2018, 167, 110–119. [Google Scholar] [CrossRef]
- Mao, S.; Shang, Z.; Chun, S.; Li, J.; Wu, K. An efficient three-dimensional multiphase particle-in-cell model for proppant transport in the field scale. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 22–24 July 2019. [Google Scholar]
- Siddhamshetty, P.; Mao, S.; Wu, K.; Kwon, J.S. Multi-size proppant pumping schedule of hydraulic fracturing: Application to a MP-PIC model of unconventional reservoir for enhanced gas production. Processes 2020, 8, 570. [Google Scholar] [CrossRef]
- Zeng, J.; Li, H.; Zhang, D. Numerical simulation of proppant transport in propagating fractures with the multi-phase particle-in-cell method. Fuel 2019, 245, 316–335. [Google Scholar] [CrossRef]
- McClure, M. Bed load proppant transport during slickwater hydraulic fracturing: Insights from comparisons between published laboratory data and correlations for sediment and pipeline slurry transport. J. Petrol. Sci. Eng. 2018, 161, 599–610. [Google Scholar] [CrossRef] [Green Version]
- Zou, Y.S.; Zhang, S.C.; Ma, X.F.; Zhou, T.; Zeng, B. Numerical investigation of hydraulic fracture network propagation in naturally fractured shale formations. J. Struct. Geol. 2016, 84, 1–13. [Google Scholar] [CrossRef]
- Miller, M.C.; McCave, I.N.; Komar, P.D. Threshold of sediment motion under unidirectional currents. Sedimentology 1997, 24, 507–527. [Google Scholar] [CrossRef]
- Ogawa, S.; Umemura, A.; Oshima, N. On the equation of fully fluidized granular materials. J. Appl. Math. Phys. 1980, 31, 483–484. [Google Scholar] [CrossRef]
- Lun, C.K.; Savage, S.B.; Jeffrey, D.J.; Chepurniy, N. Kinetic theories for granular flow: Inelastic particles in Couette flow and slightly inelastic particles in a general flowfield. J. Fluid Mech. 1984, 140, 223–256. [Google Scholar] [CrossRef]
- Ding, J.; Gidaspow, D. A bubbling fluidization model using kinetic theory of granular flow. AIChE J. 1990, 36, 523–538. [Google Scholar] [CrossRef]
- Johnson, P.C.; Jackson, R. Frictional–collisional constitutive relations for granular materials, with application to plane shearing. J. Fluid Mech. 1987, 176, 67–93. [Google Scholar] [CrossRef]
- Cloete, S.; Johansen, S.T.; Amini, S. Performance evaluation of a complete Lagrangian KTGF approach for dilute granular flow modeling. Powder Technol. 2012, 226, 43–52. [Google Scholar] [CrossRef] [Green Version]
- Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Ma, D.; Ahmadi, G. A thermodynamical formulation for dispersed multiphase turbulent flows. Int. J. Multiph. Flow 1990, 16, 323–351. [Google Scholar] [CrossRef]
- Shih, T.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ε eddy viscosity model for high Reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]








| Parameter | Slot System | Unit | Field | Unit |
|---|---|---|---|---|
| Fracture height H | 0.6 | m | 20 | m |
| Half-length of the primary fracture L | 5.0 | m | 167 | m |
| Width of the primary fracture w | 0.005 | m | 0.005 | m |
| Fluid density ρf | 1000 | kg/m3 | 1000 | kg/m3 |
| Proppant density ρs | 3350 | kg/m3 | 3350 | kg/m3 |
| Fluid viscosity μf | 0.001 | Pa·s | 0.001 | Pa·s |
| Proppant diameter ds | 0.0001–0.001 | m | 0.0001–0.001 | m |
| Darcy friction factor fD | 0.04 [33] | - | 0.04 [33] | - |
| Fluid Reynolds number Ref | 5000–11,667 | - | 5000–11,667 | - |
| Particle Reynolds number Rep | 100–980 | - | 100–980 | - |
| Shields number S | 0.065–1.825 | - | 0.065–1.825 | - |
| Mean velocity in the fracture vi | 0.5–1.2 | m/s | 0.5–1.2 | m/s |
| Pumping rate Q | 5.4–12.6 | m3/h | 360–840 | m3/h |
| Case | Branch Angle (°) | Pumping Rate Q (m3/h) | Sand Ratio (%) | Proppant Size | Proppant Amount (kg) |
|---|---|---|---|---|---|
| 1 | 90 (a single branch) | 5.4 | 6.0 | 20/40 | 42.0 |
| 2 | 90 (a single branch) | 7.8 | 6.0 | 20/40 | 42.0 |
| 3 | 90 (a single branch) | 10.2 | 6.0 | 20/40 | 42.0 |
| 4 | 90 (a single branch) | 12.6 | 6.0 | 20/40 | 42.0 |
| 5 | 90 (a single branch) | 10.2 | 4.0 | 20/40 | 28.0 |
| 6 | 90 (a single branch) | 10.2 | 8.0 | 20/40 | 56.0 |
| 7 | 90 (a single branch) | 10.2 | 6.0 | 16/20 | 42.0 |
| 8 | 90 (a single branch) | 10.2 | 6.0 | 30/50 | 42.0 |
| 9 | 90 (a single branch) | 10.2 | 6.0 | 40/70 | 42.0 |
| 10 | 90 (a single branch) | 10.2 | 6.0 | 70/140 | 42.0 |
| 11 | 30/150 (two branches) | 12.6 | 6.0 | 20/40 | 42.0 |
| 12 | 45/135 (two branches) | 12.6 | 6.0 | 20/40 | 42.0 |
| Case | Inflow Rate Qi (m3/h) | Outflow Rate in the Branch Qb (m3/h) | Outflow Rate in the Primary Slot Qp (m3/h) | Qb/Qi |
|---|---|---|---|---|
| 1 | 5.40 | 2.74 (90°-branch) | 2.66 | 0.507 |
| 2 | 7.80 | 3.91 (90°-branch) | 3.83 | 0.501 |
| 3 | 10.20 | 5.17 (90°-branch) | 5.01 | 0.507 |
| 4 | 12.60 | 6.64 (90°-branch) | 5.91 | 0.527 |
| 5 | 10.20 | 4.68 (90°-branch) | 5.57 | 0.459 |
| 6 | 10.20 | 4.98 (90°-branch) | 5.16 | 0.488 |
| 7 | 10.20 | 4.72 (90°-branch) | 5.41 | 0.463 |
| 8 | 10.20 | 5.29 (90°-branch) | 4.91 | 0.519 |
| 9 | 10.20 | 5.70 (90°-branch) | 4.44 | 0.559 |
| 10 | 10.20 | 5.86 (90°-branch) | 4.34 | 0.575 |
| 11 | 12.60 | 4.48 (30°-branch) 4.05 (150°-branch) | 4.09 | 0.677 |
| 12 | 12.60 | 4.23 (45°-branch) 3.70 (135°-branch) | 4.57 | 0.629 |
| Parameter | Unit | Value |
|---|---|---|
| Inlet fluid velocity | m/s | 0.6 |
| Inlet proppant velocity | m/s | 0.6 |
| Total proppant mass rate | kg/s | 0.018 |
| Proppant diameter | m | 0.00064 (20/40 ceramic) |
| Fluid density | kg/m3 | 998.2 |
| Proppant density | kg/m3 | 3350 |
| Angle of internal friction | ° | 30 |
| Friction pressure | Pa | Based KTGF |
| Friction modulus | Pa | derived |
| Friction packing limit | - | 0.61 |
| Elasticity Modulus | Pa | derived |
| Packing limit | - | 0.63 |
| Transition factor | - | 0.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhang, S.; Ma, X.; Guo, T.; Zhang, W.; Zou, Y. Experimental and Numerical Study on Proppant Transport in a Complex Fracture System. Energies 2020, 13, 6290. https://doi.org/10.3390/en13236290
Zhang Z, Zhang S, Ma X, Guo T, Zhang W, Zou Y. Experimental and Numerical Study on Proppant Transport in a Complex Fracture System. Energies. 2020; 13(23):6290. https://doi.org/10.3390/en13236290
Chicago/Turabian StyleZhang, Zhaopeng, Shicheng Zhang, Xinfang Ma, Tiankui Guo, Wenzhe Zhang, and Yushi Zou. 2020. "Experimental and Numerical Study on Proppant Transport in a Complex Fracture System" Energies 13, no. 23: 6290. https://doi.org/10.3390/en13236290
APA StyleZhang, Z., Zhang, S., Ma, X., Guo, T., Zhang, W., & Zou, Y. (2020). Experimental and Numerical Study on Proppant Transport in a Complex Fracture System. Energies, 13(23), 6290. https://doi.org/10.3390/en13236290





