Power Performance Analysis According to the Configuration and Load Control Algorithm of Power Take-Off System for Oscillating Water Column Type Wave Energy Converters
Abstract
1. Introduction
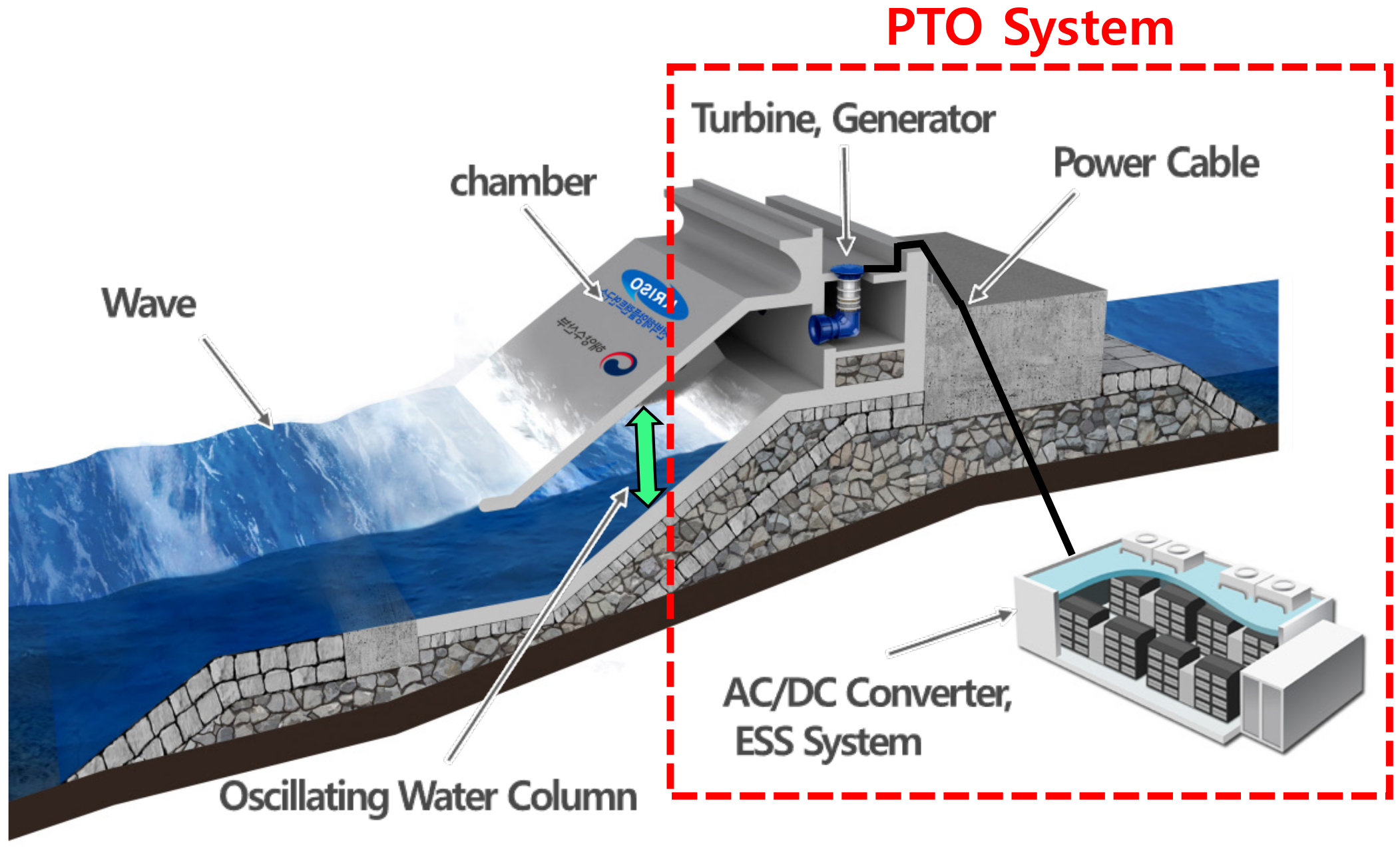
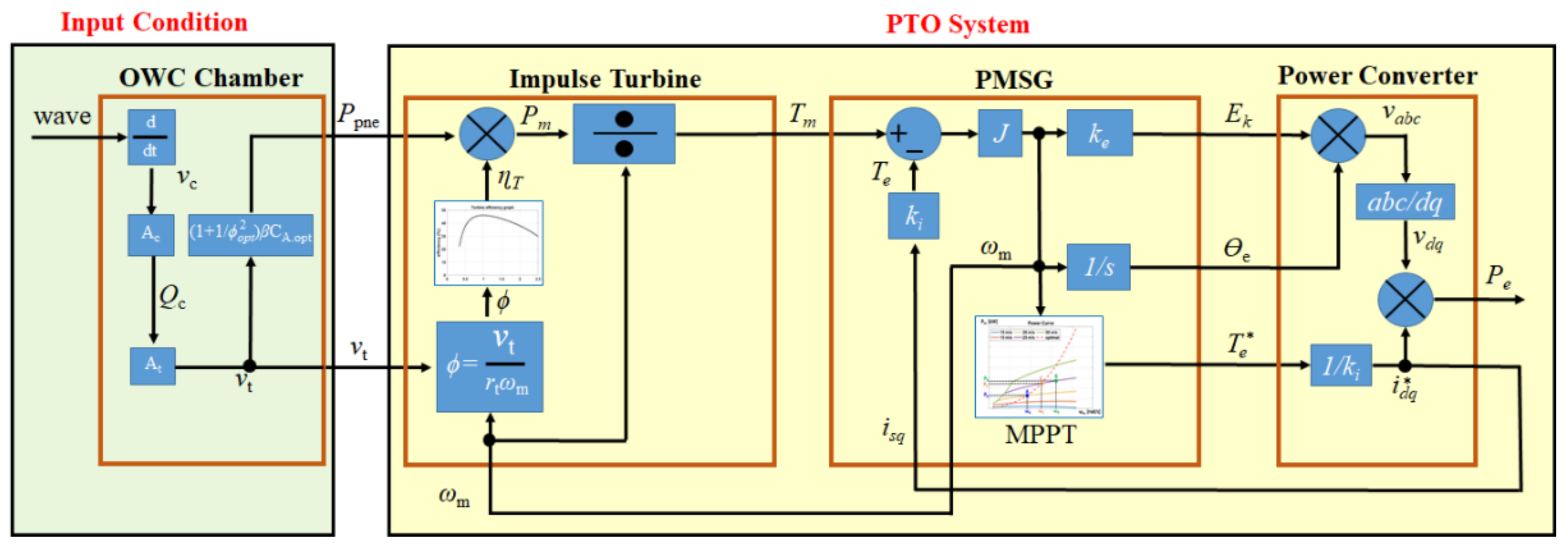
2. PTO System Configuration and Modeling
2.1. PTO System Composition of the OWC-Type Wave Energy Converter
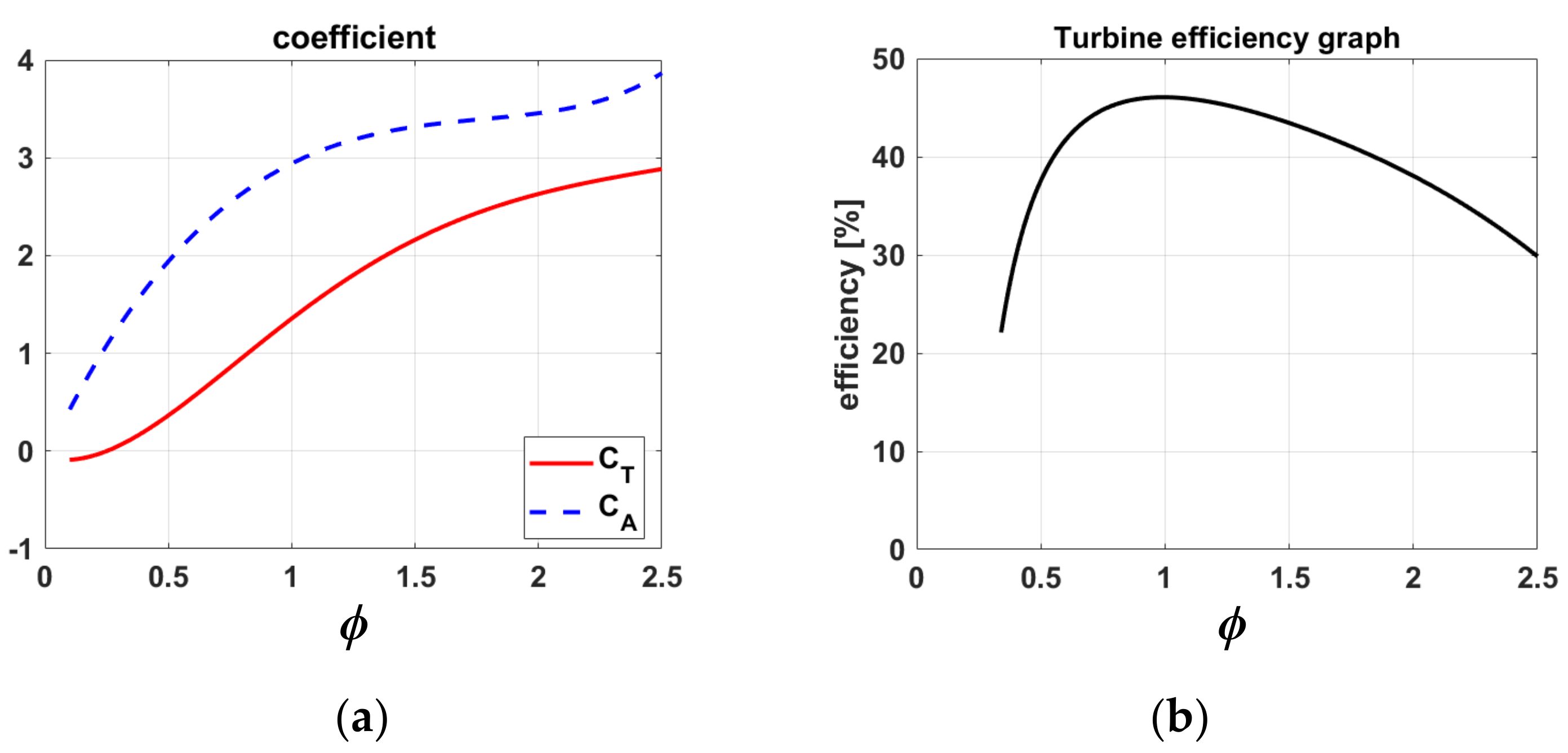
2.2. Impulse Turbine Modeling
2.3. Generator Modeling
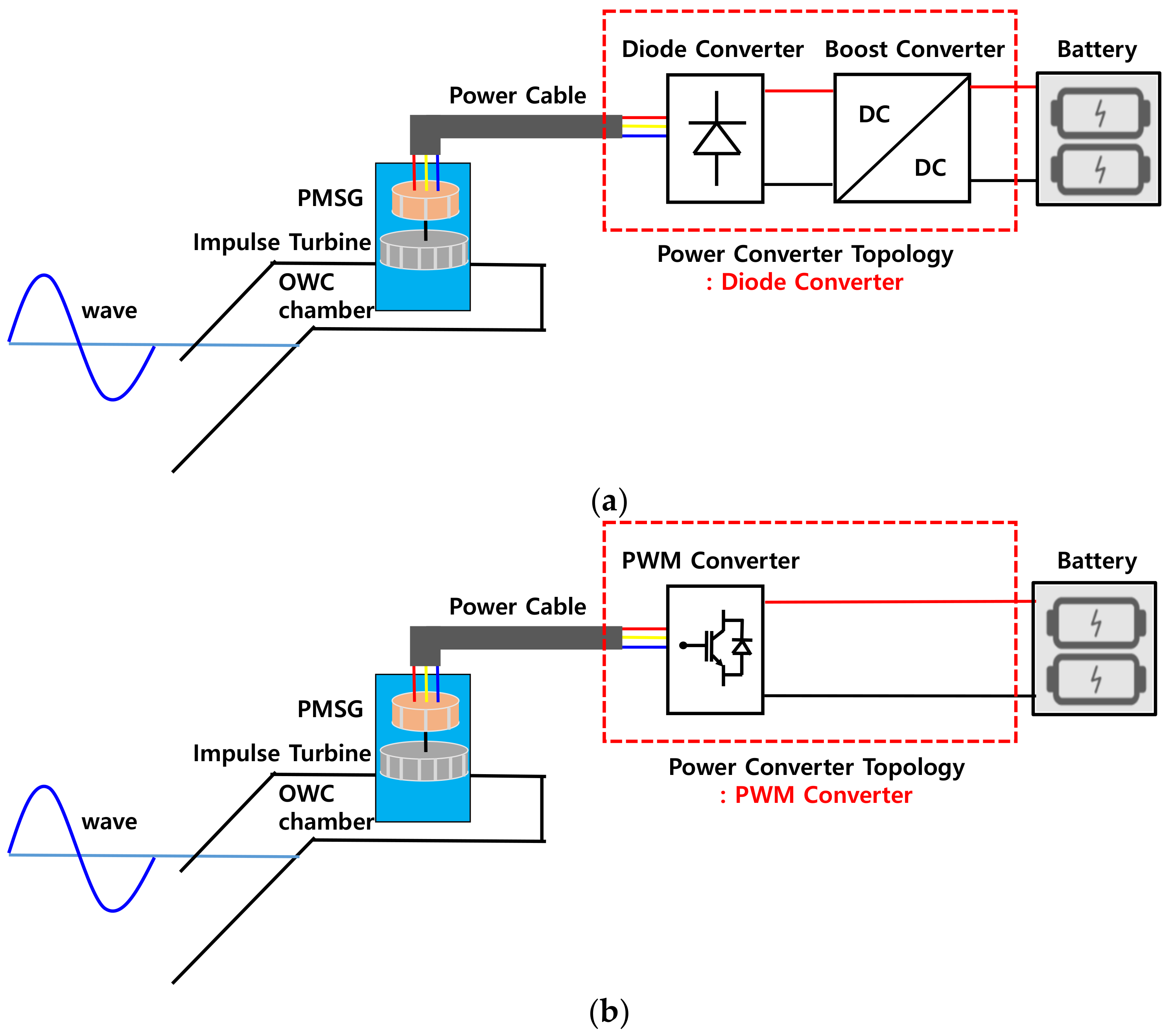
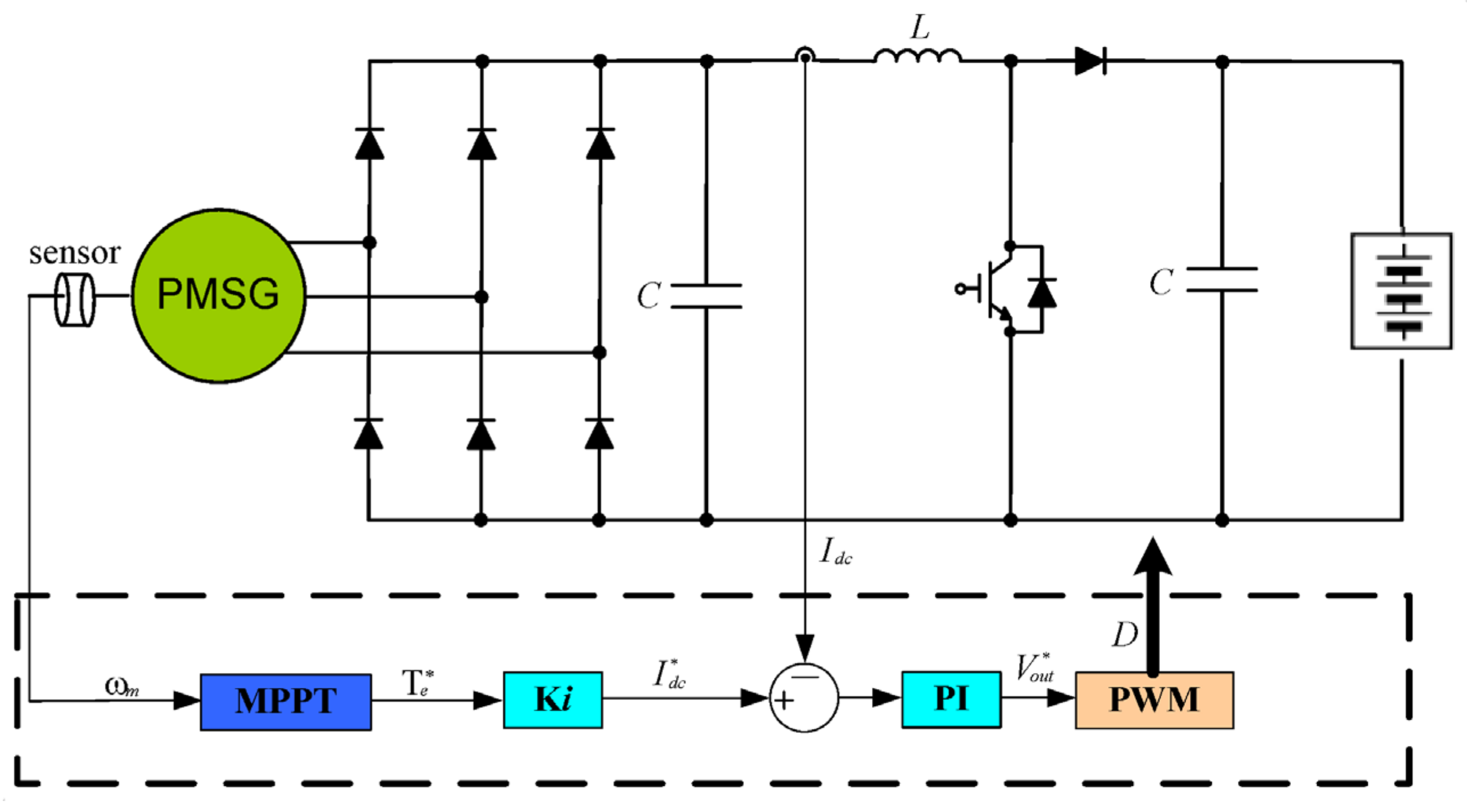
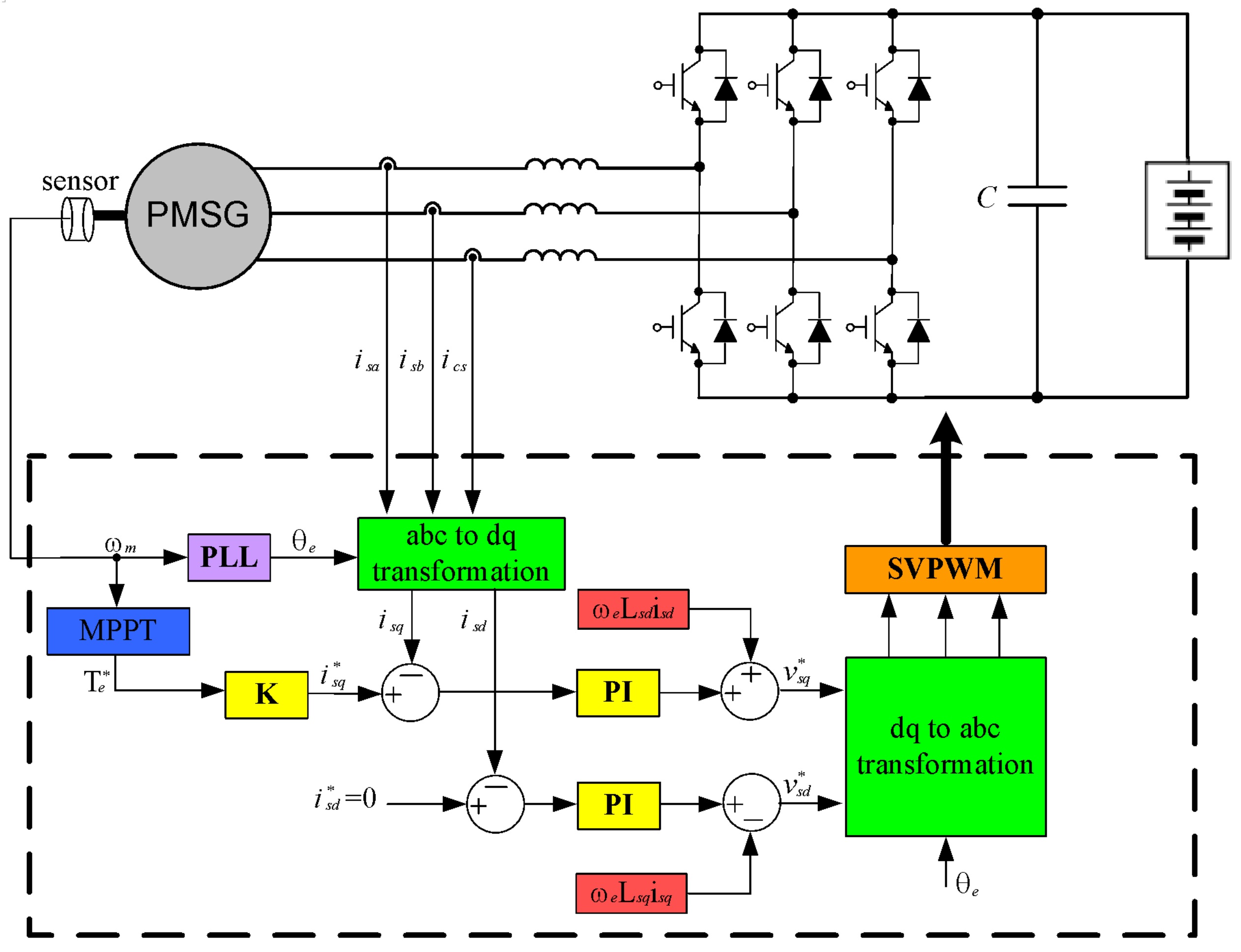
3. Power Converter Topology and Modeling
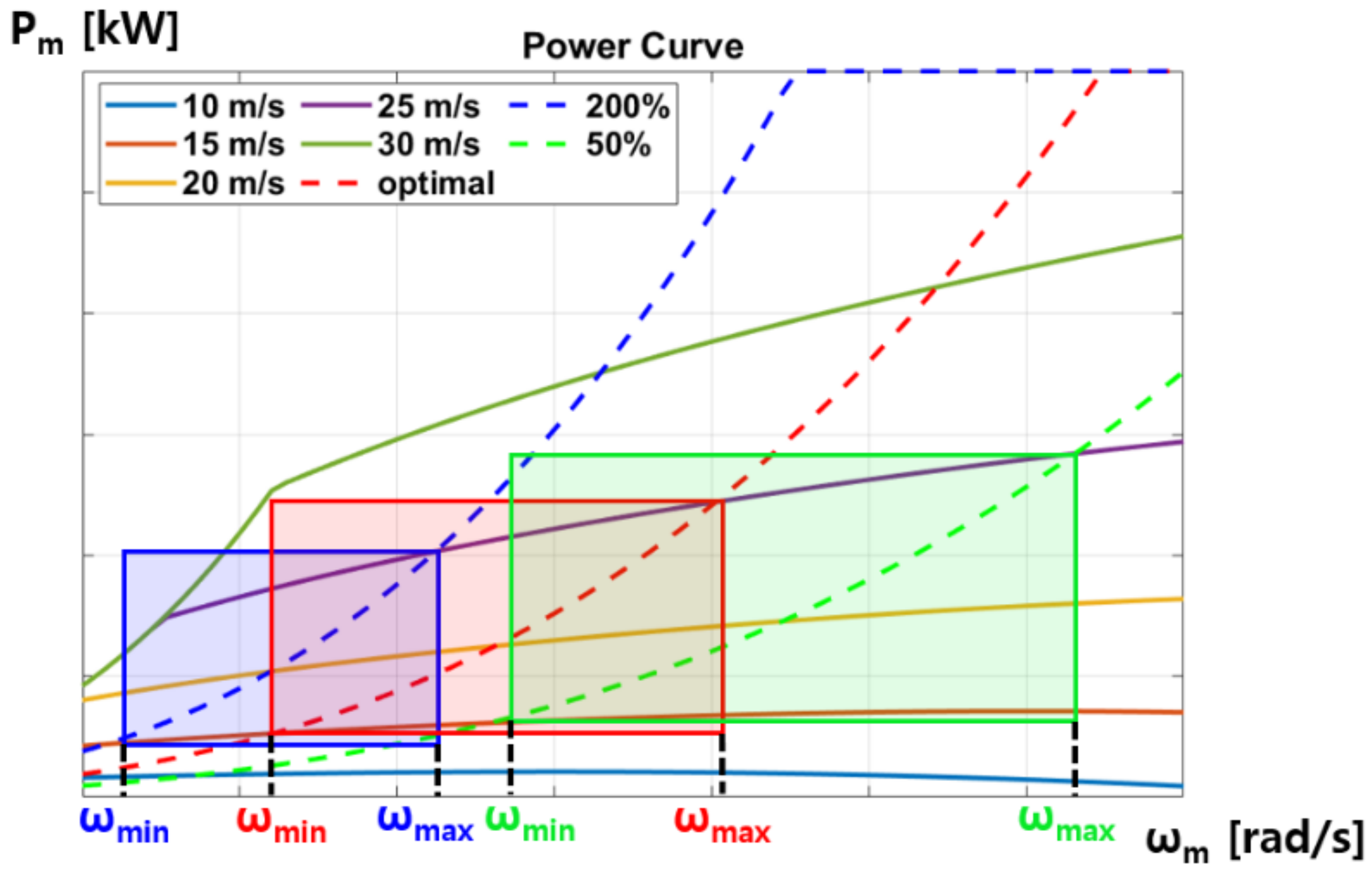
4. Maximum Power-Point Tracking Algorithm for OWC-WEC
5. Results
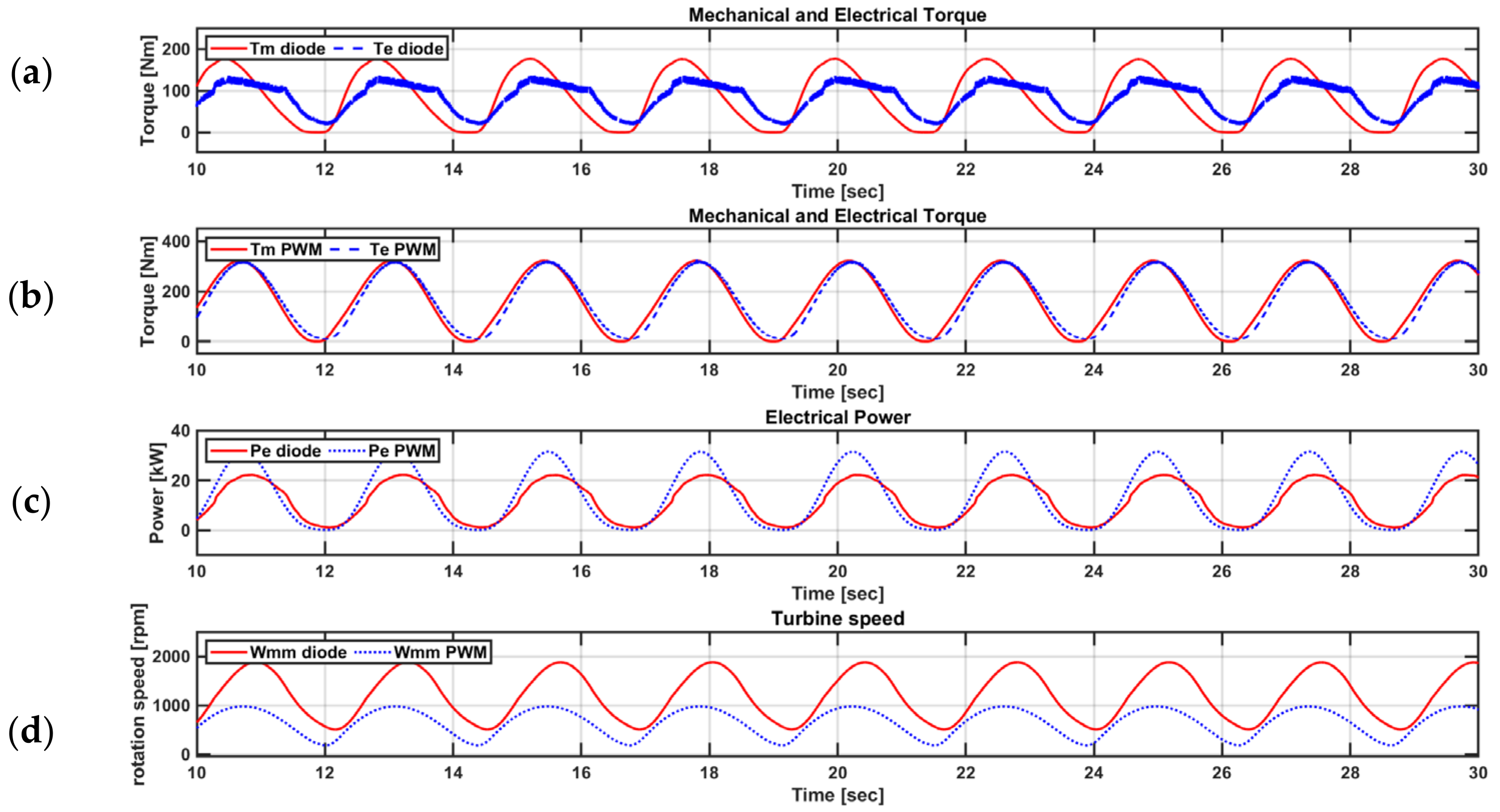
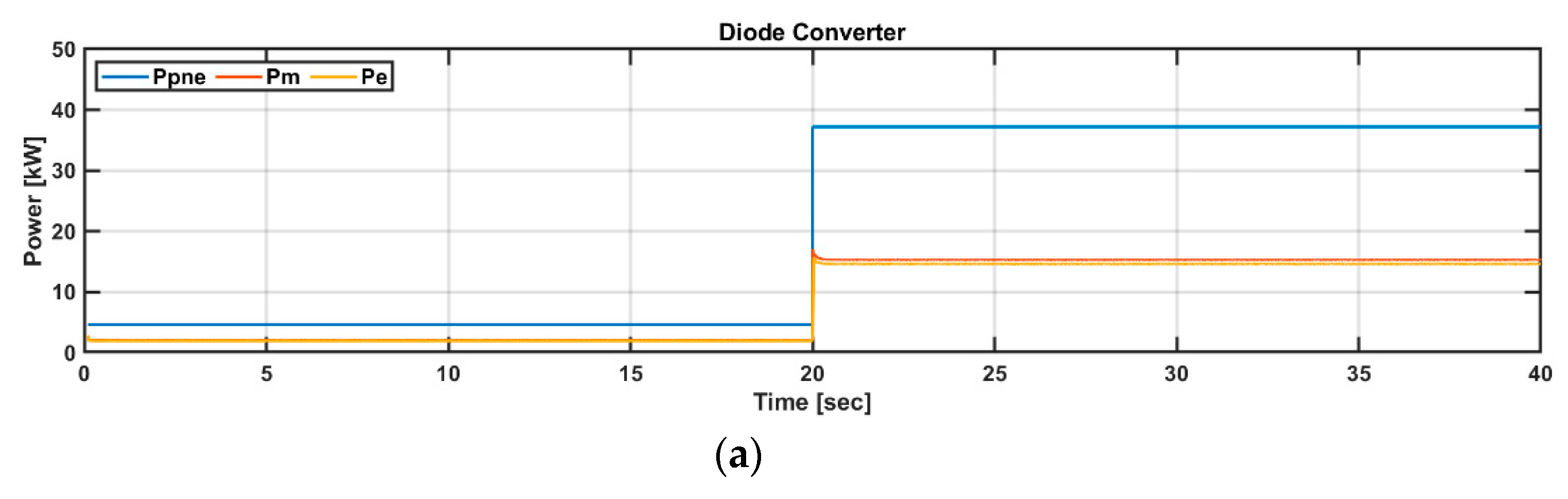
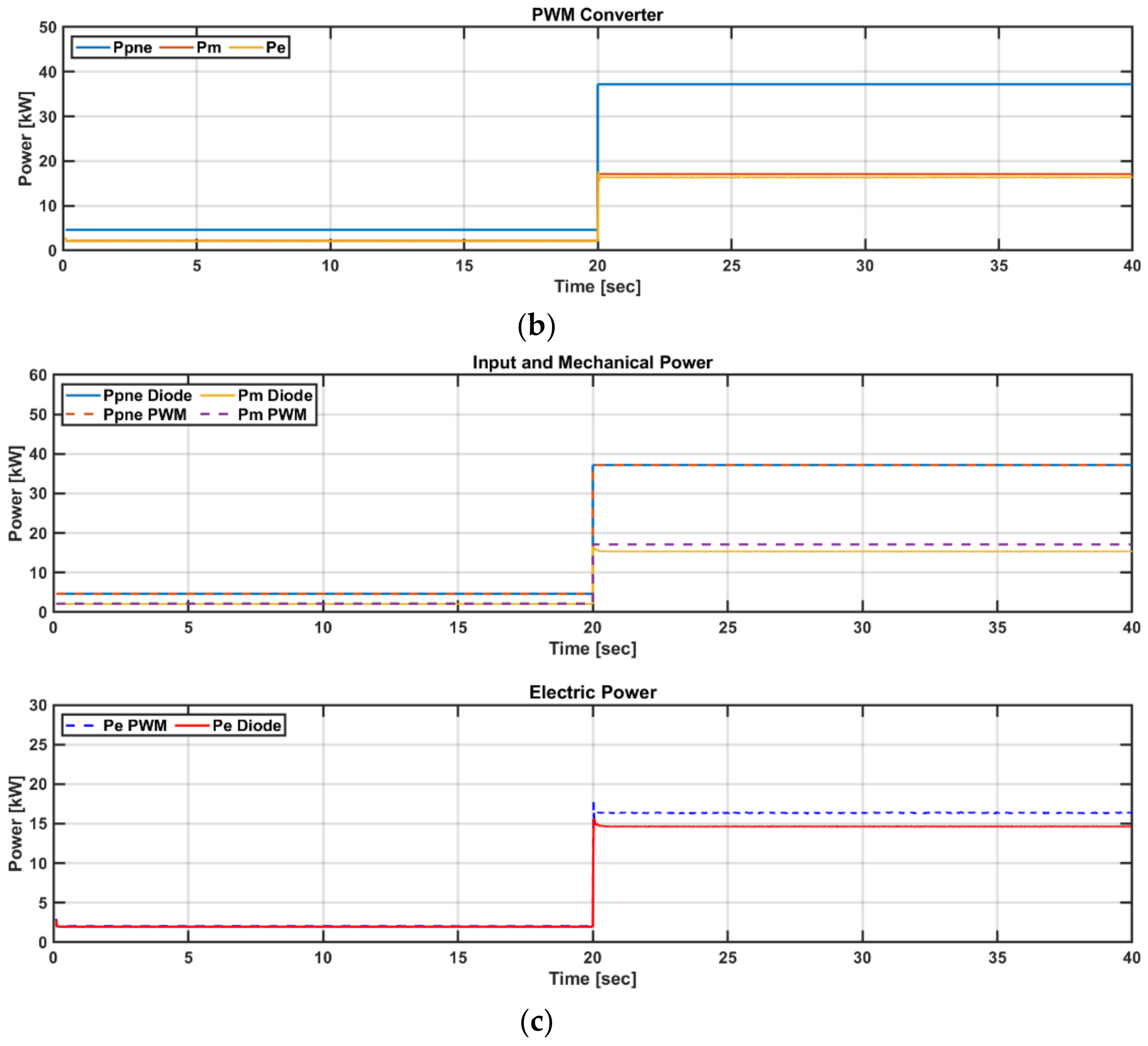
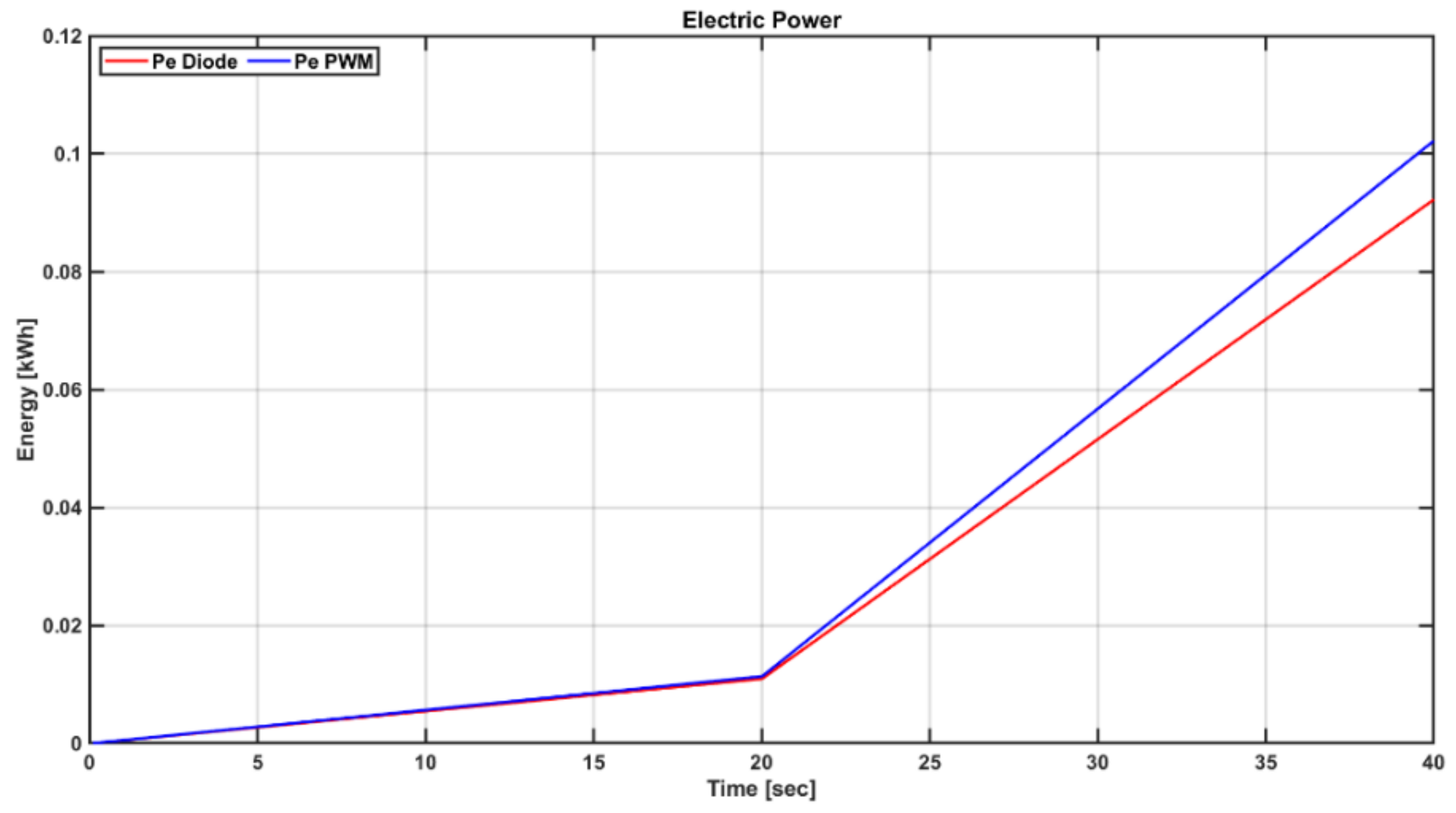
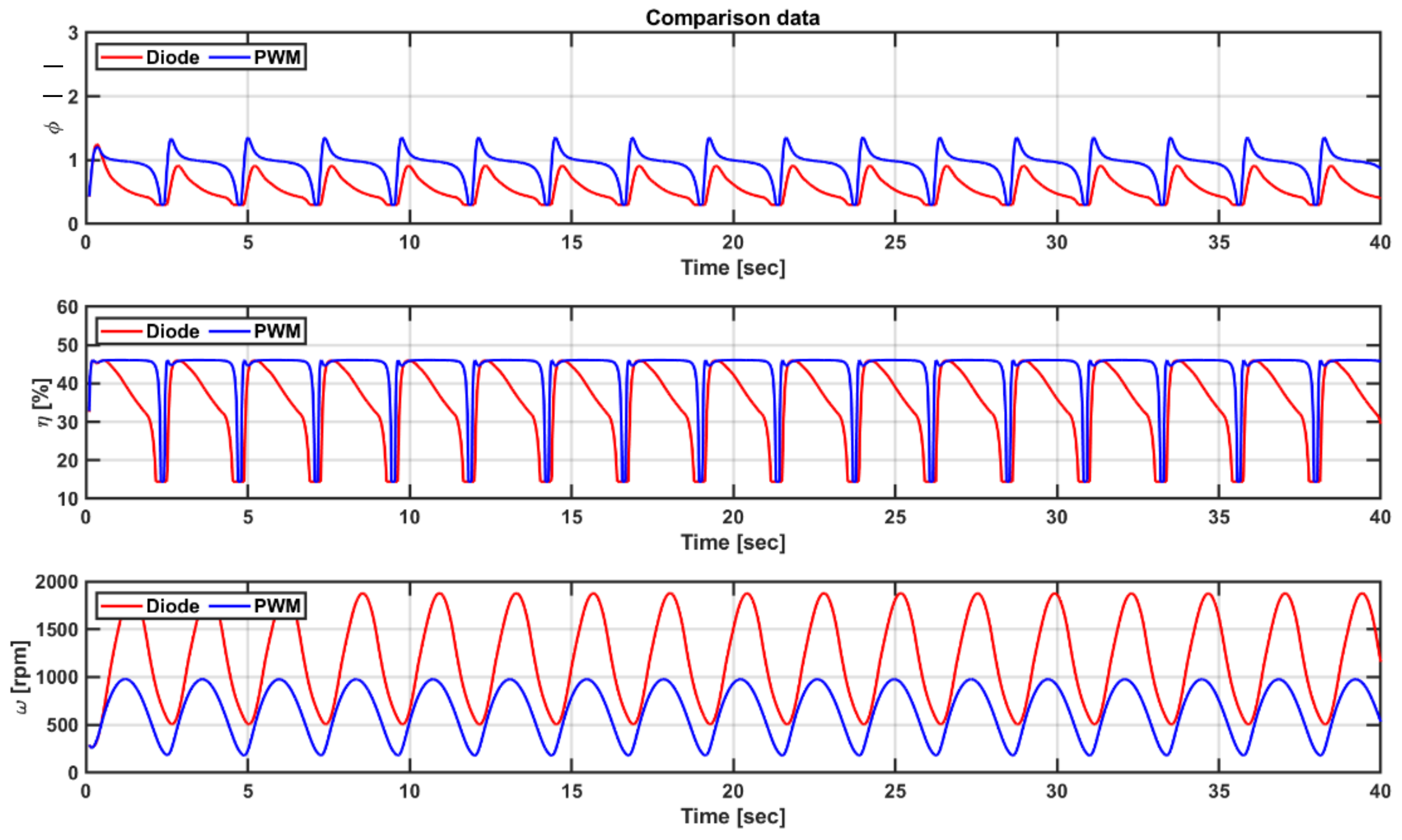
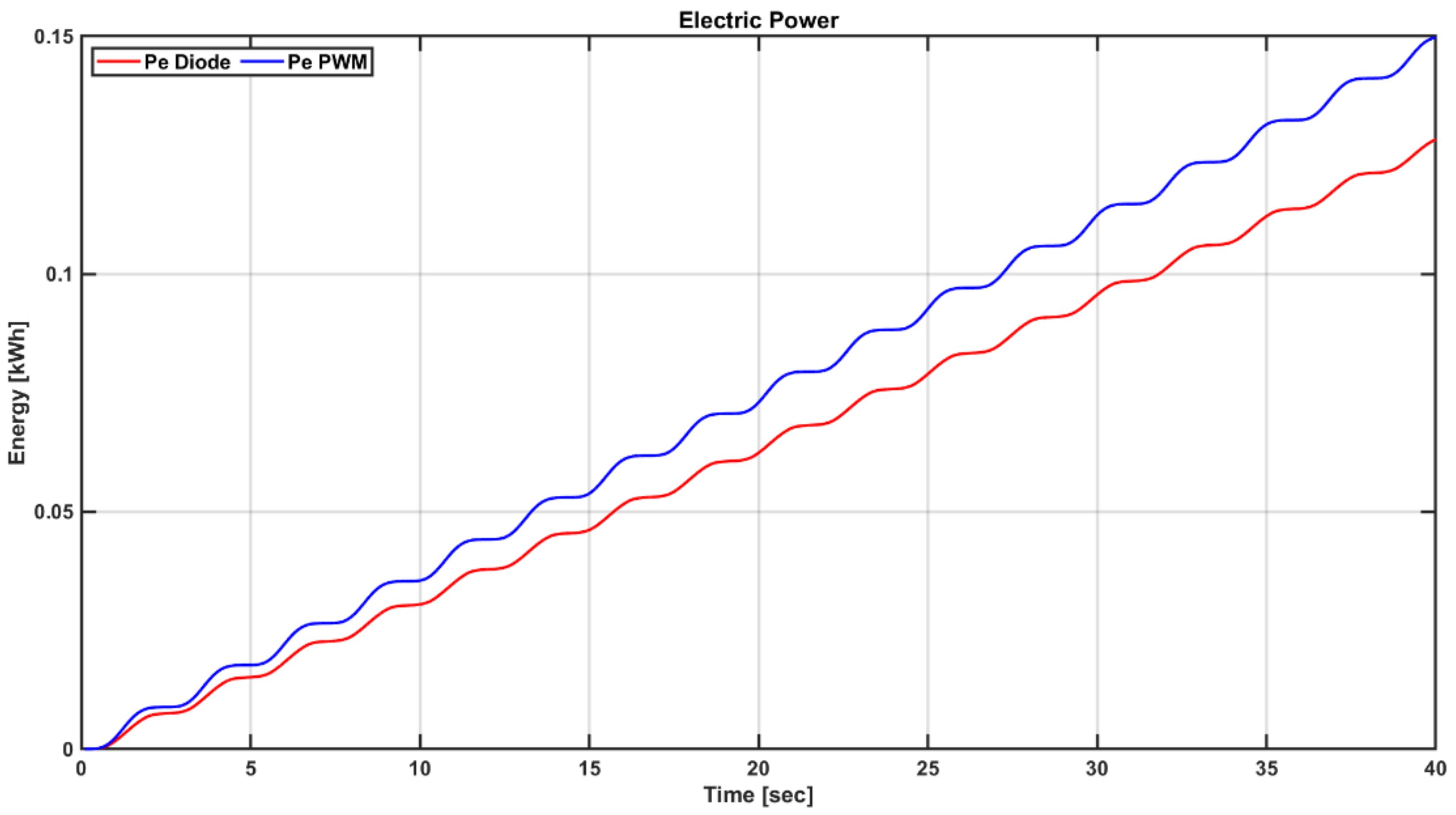
5.1. Dynamic Simulation in Steady and Transient States
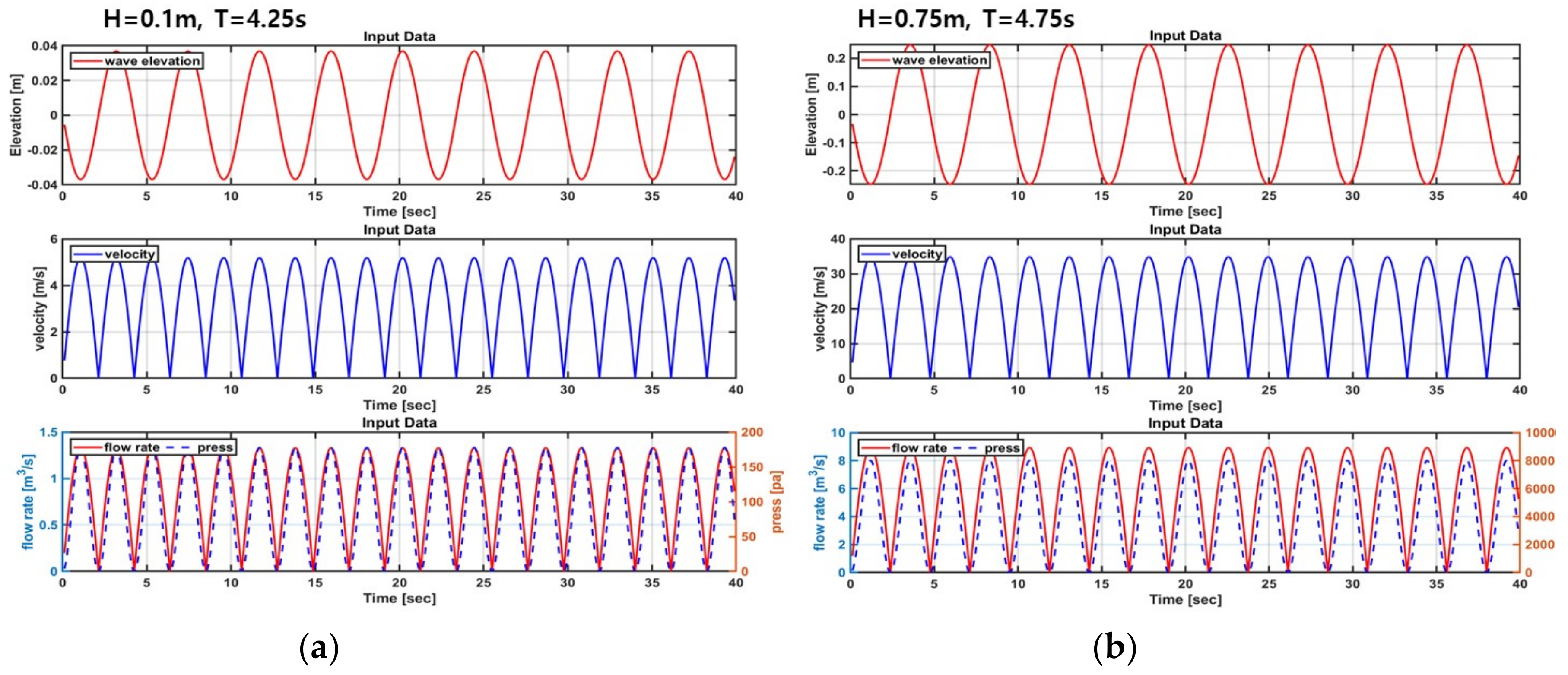
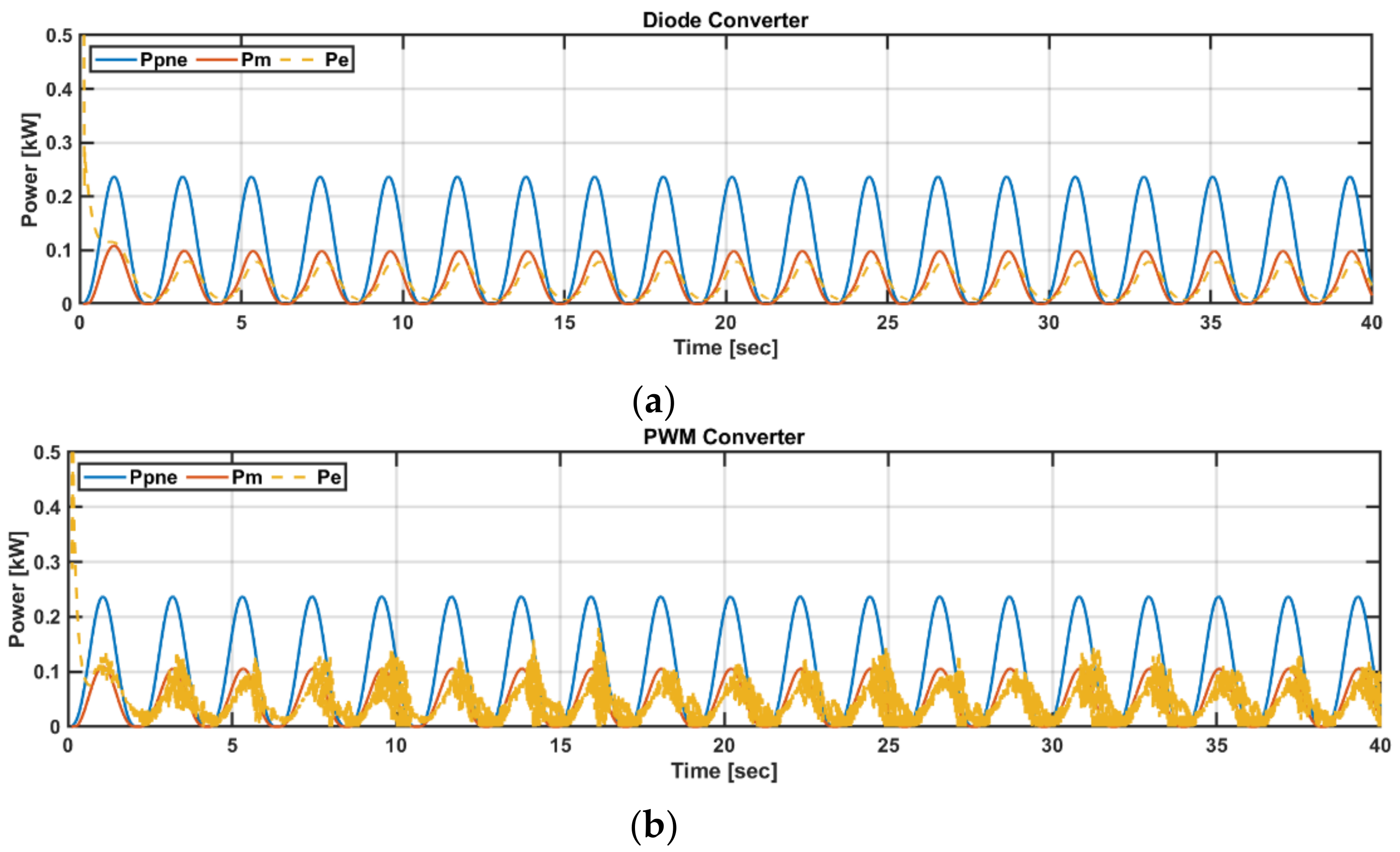
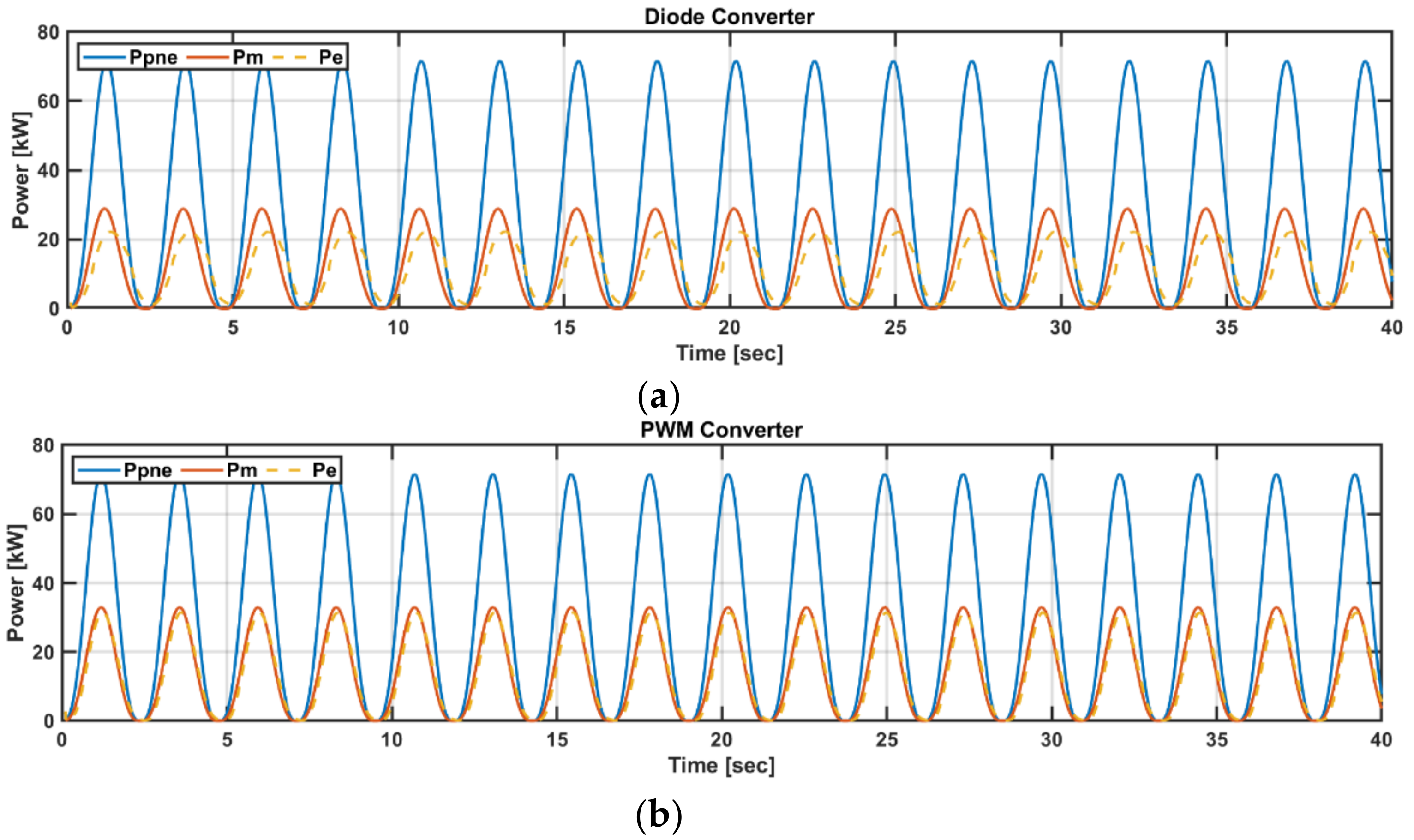
5.2. Dynamic Simulation in Regular Wave States
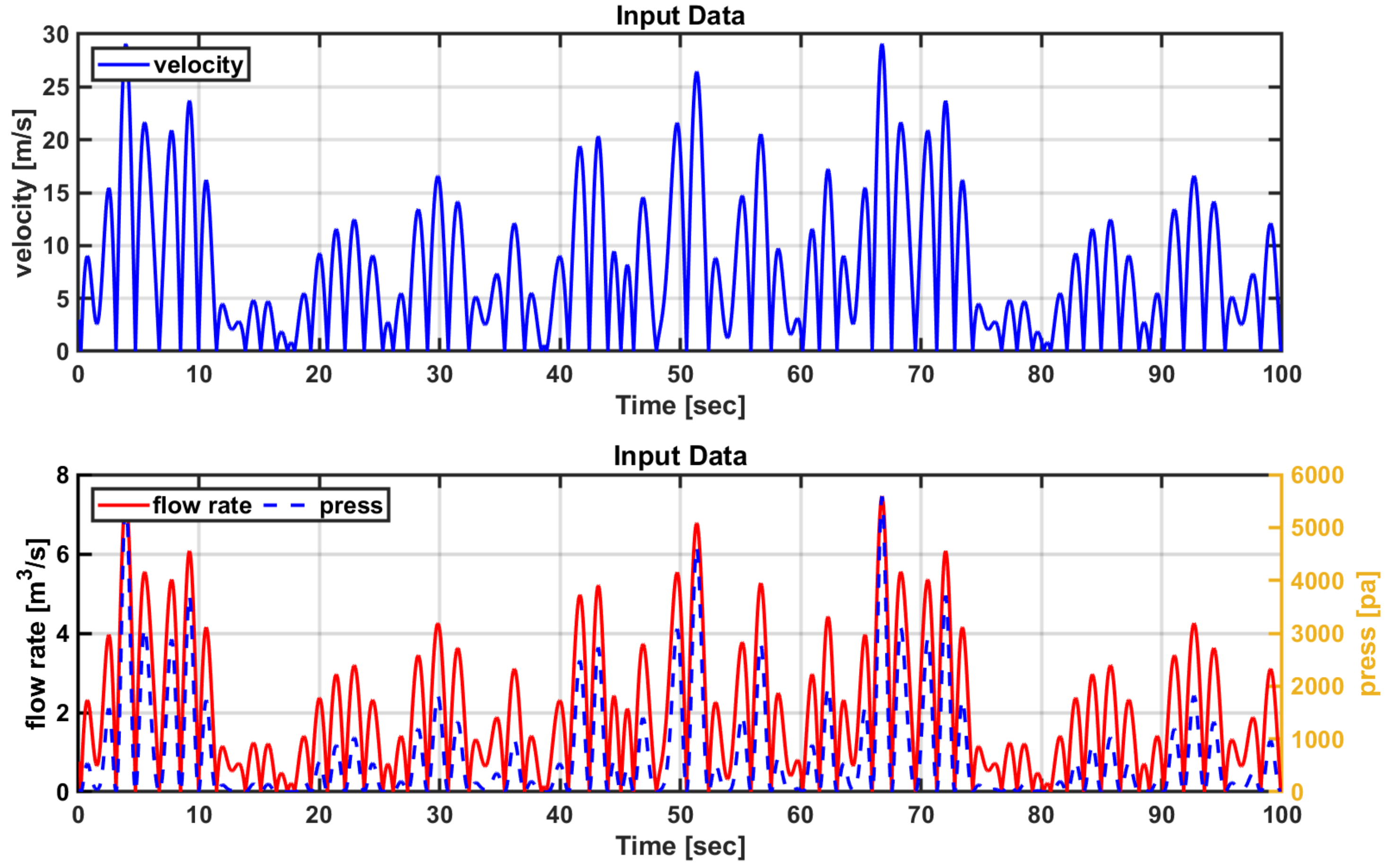
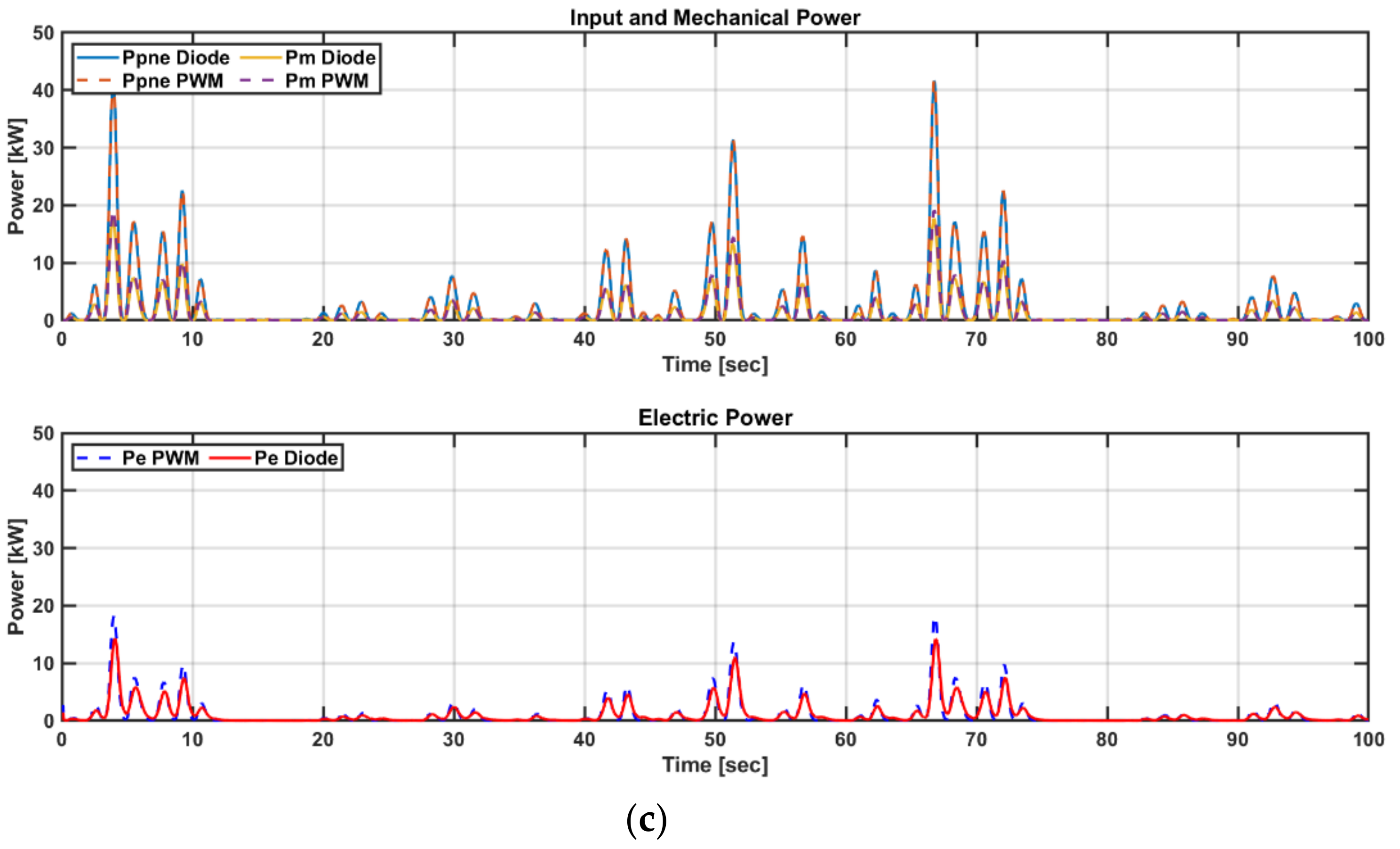
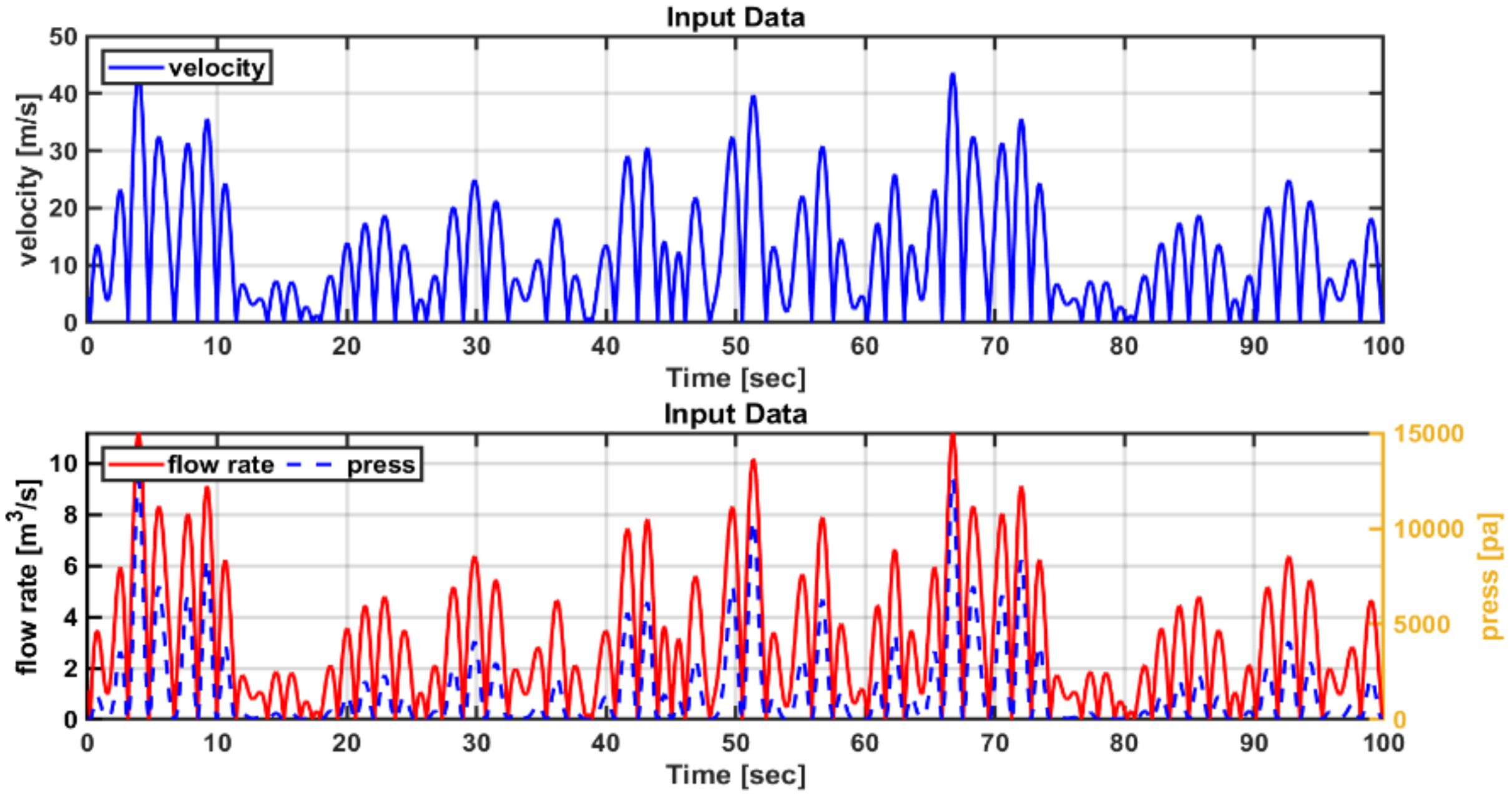
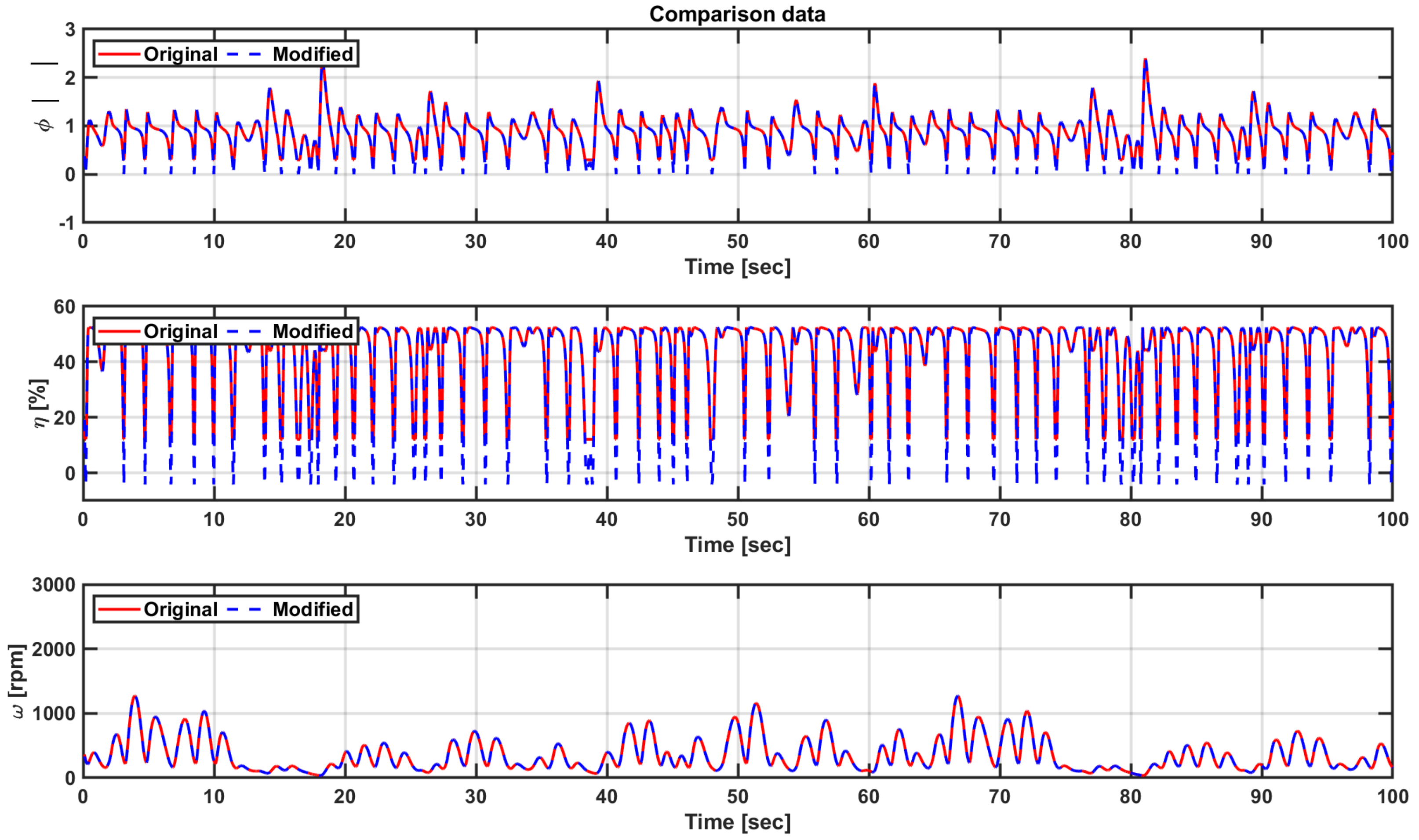
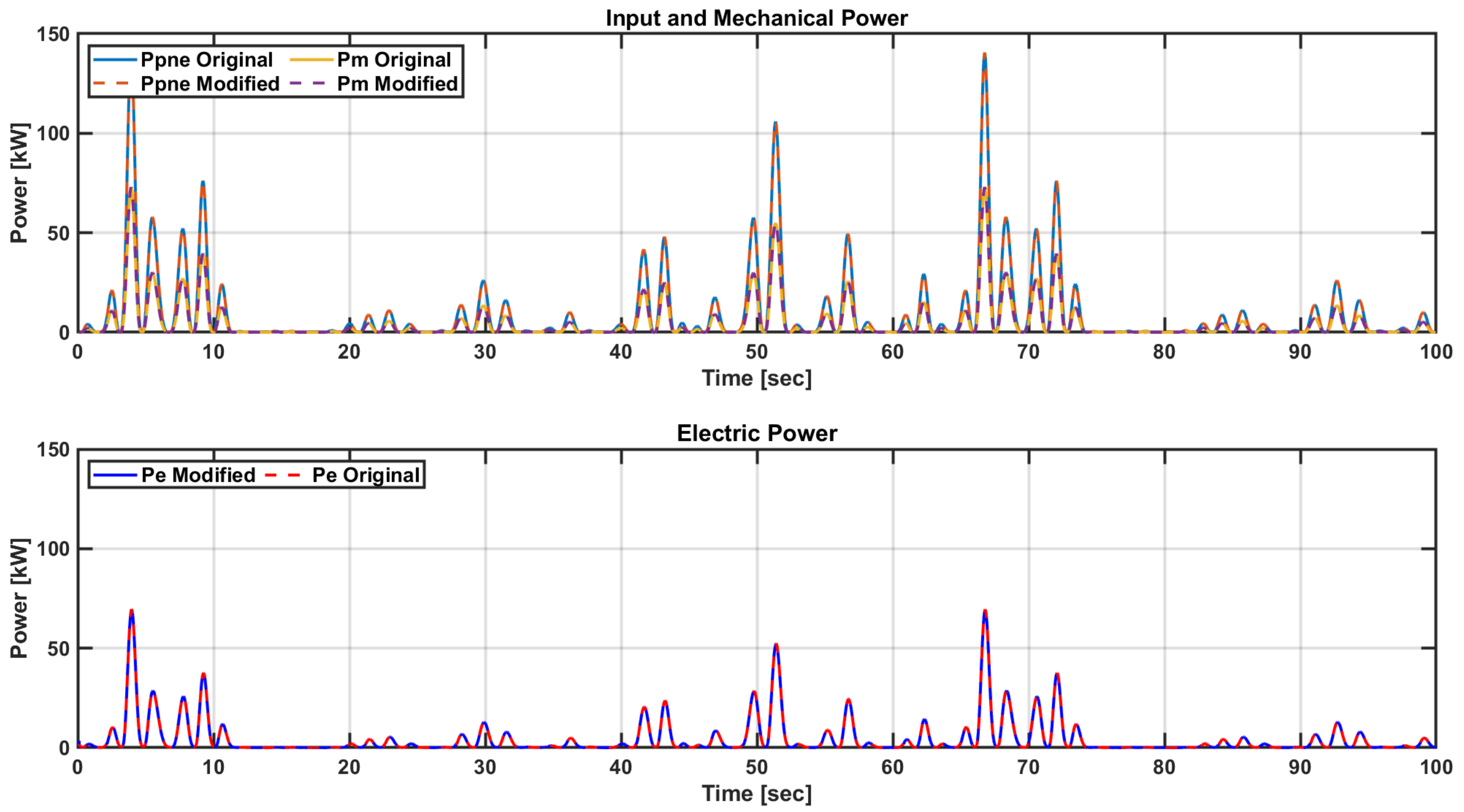
5.3. Dynamic Simulation in Irregular Wave States
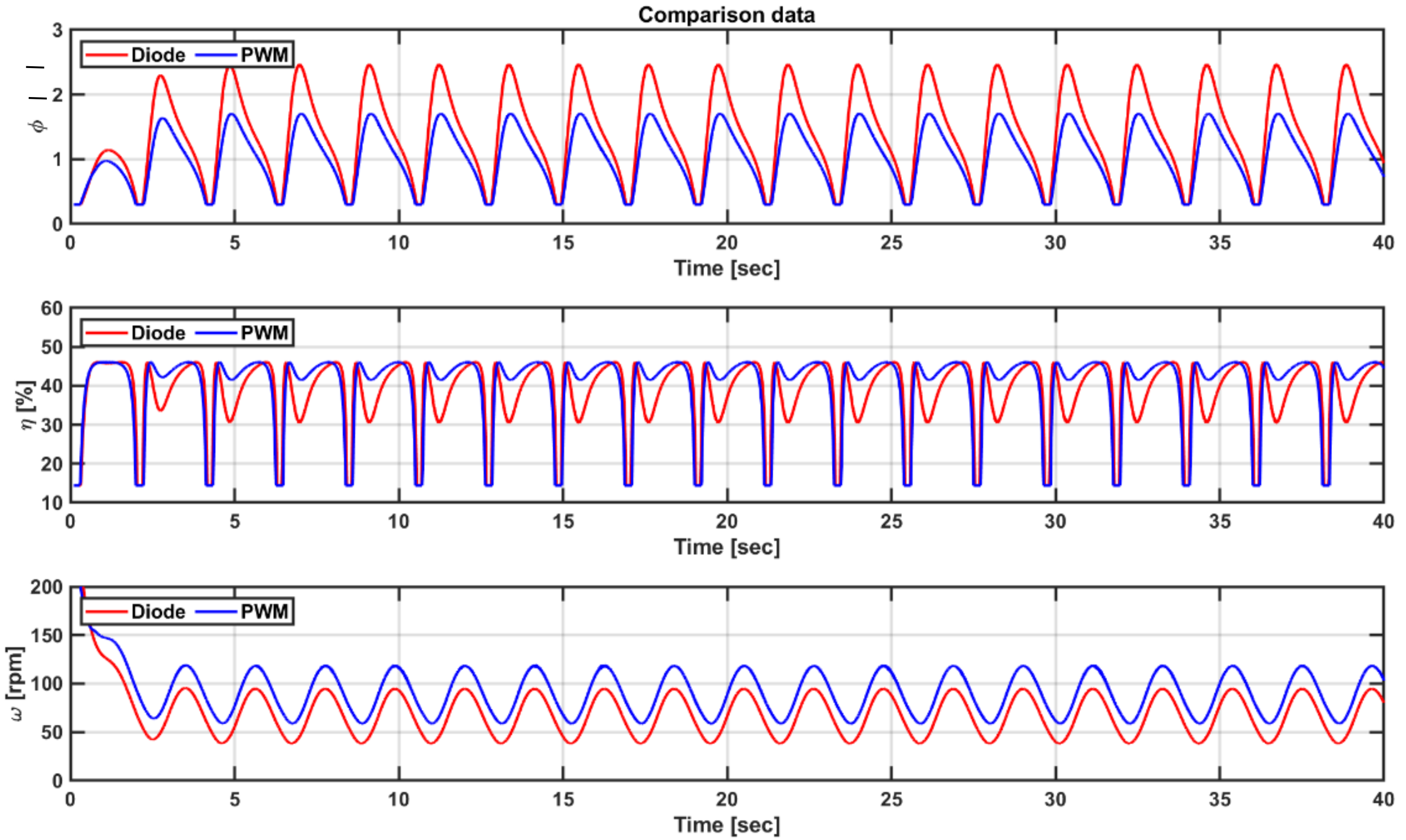
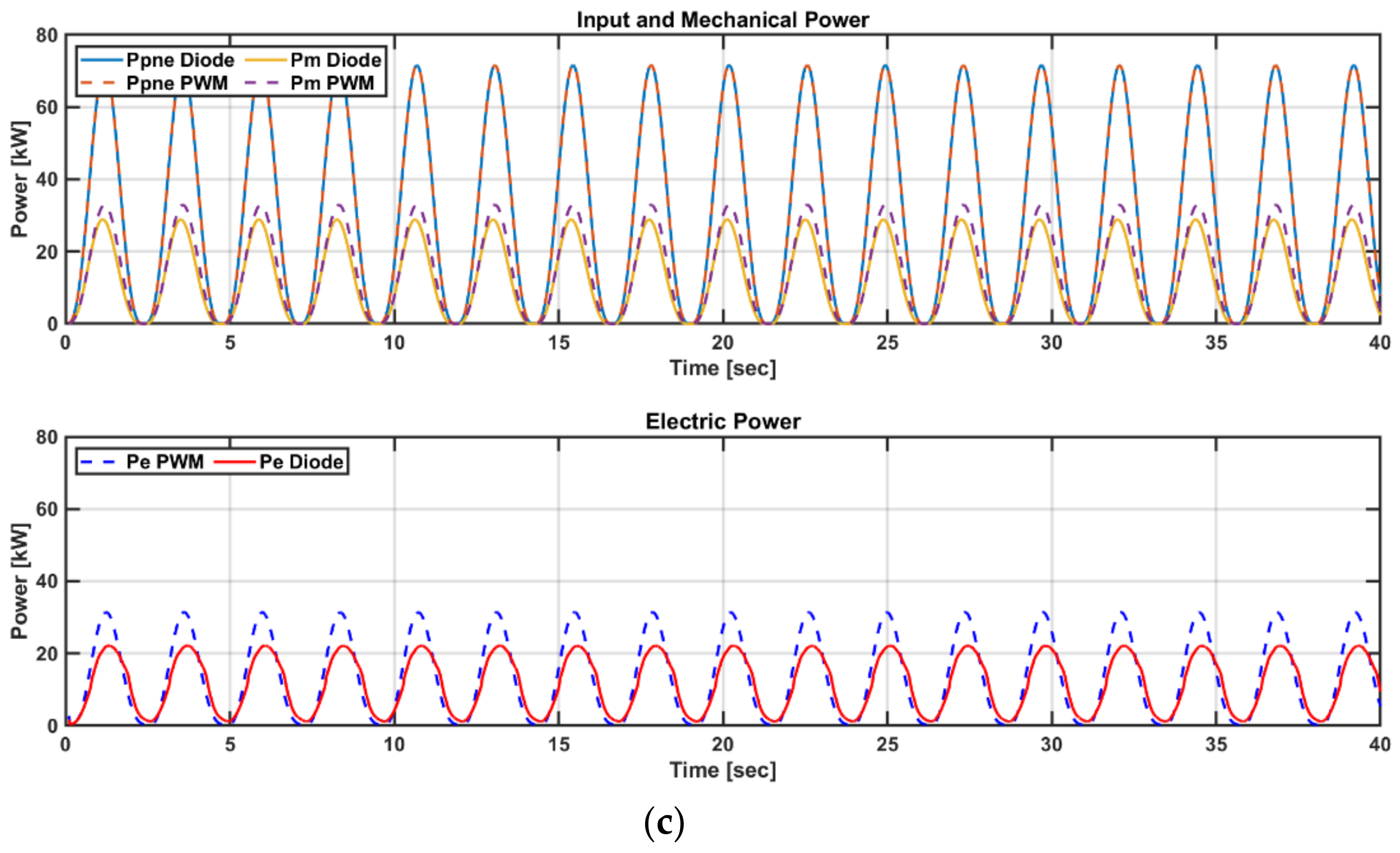
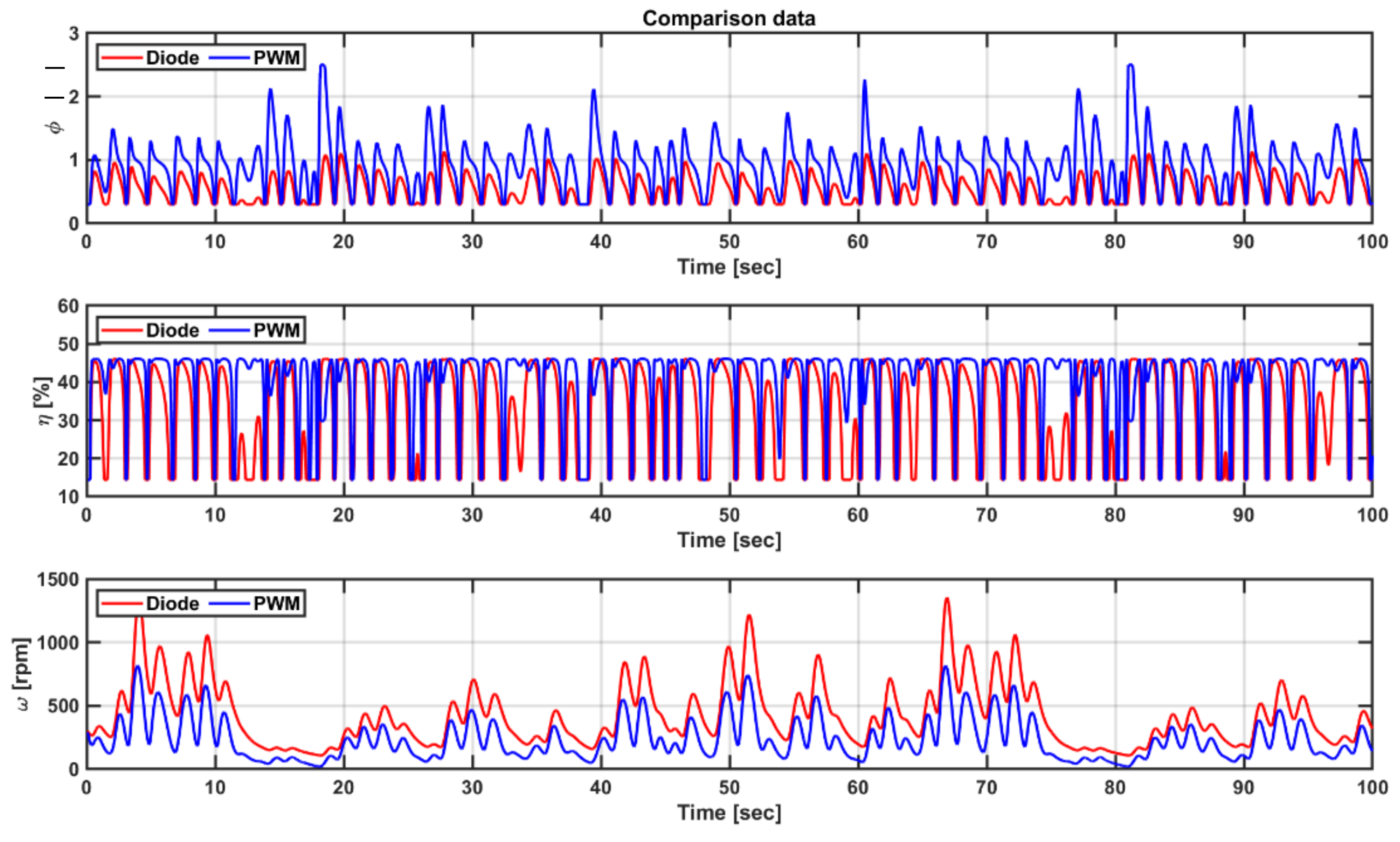
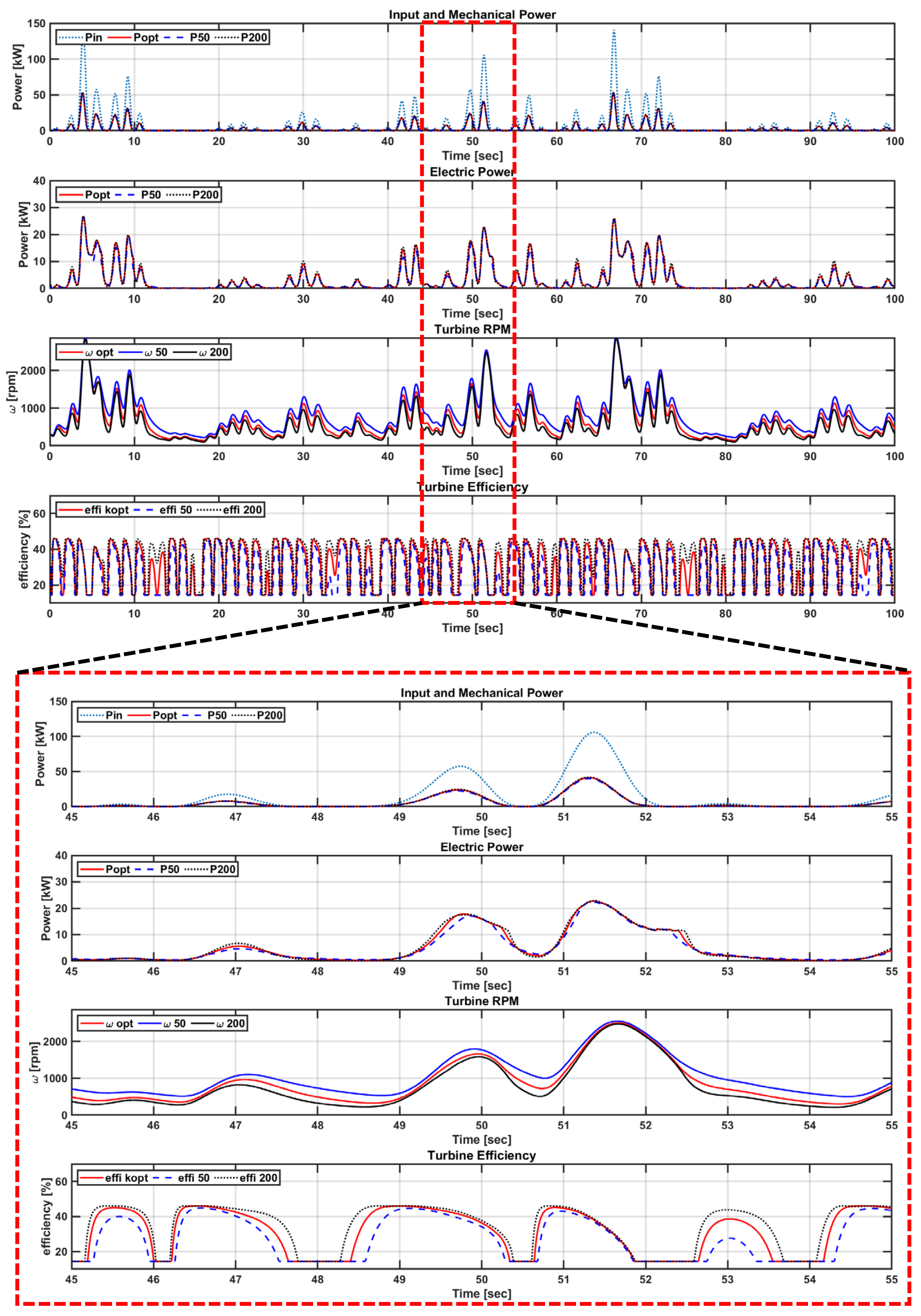
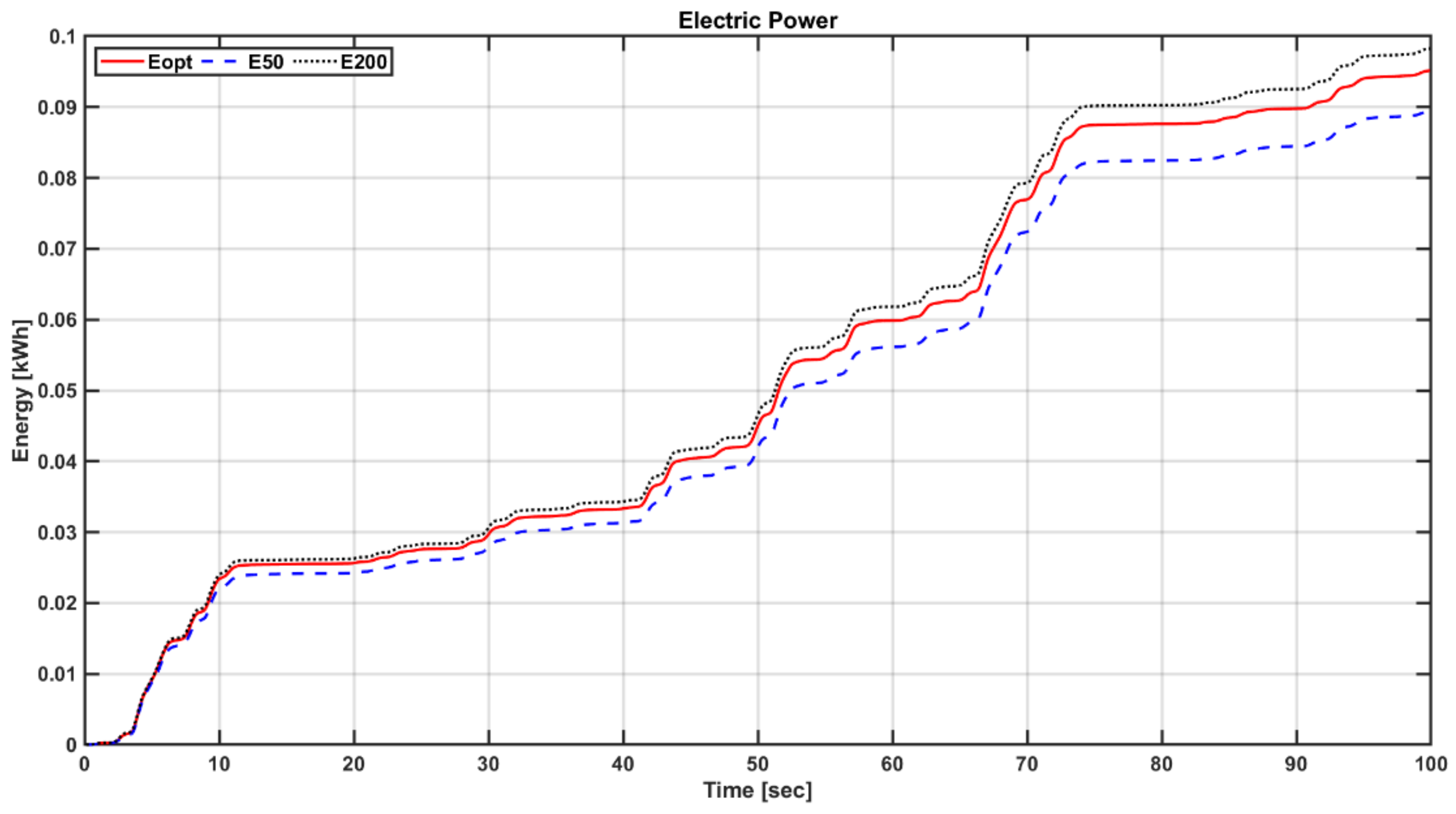
5.4. Comparison of Power Performance according to the Torque Factor of Load Control
5.5. Comparison of Power Performance according to the Flow Coefficient Range
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Input and torque coefficients | |
| Ac, At | Cross-sectional area of the chamber and turbine duct |
| , | Flow coefficient and optimal value at the maximum turbine efficiency |
| Air density | |
| Blade span | |
| Chord length of the turbine rotor blade | |
| Number of turbine rotor blades | |
| Mechanical power | |
| Pneumatic incident power | |
| Pressure drop across the turbine | |
| Flow rate | |
| Turbine rotor mean radius | |
| Airflow speed at the turbine duct | |
| Mechanical angular frequency | |
| Mechanical torque | |
| Electrical torque | |
| Turbine angular velocity | |
| J | Inertia of the turbine and generator rotors |
| d-q voltage of generator | |
| d-q inductance of generator | |
| d-q current of generator | |
| Generator flux linkage | |
| Electrical angular frequency | |
| Phase resister of generator | |
| Electric power | |
| Number of generator pole pair | |
| Input voltage of DC/DC converter | |
| Output voltage of DC/DC converter | |
| Duty ration for power converter | |
| Control sampling time for power converter | |
| Output power according to the optimal torque factor | |
| Output power according to 50% of the optimal torque factor | |
| Output power according to 200% of the optimal torque factor | |
| Tsimulation | Simulation sampling time |
References
- Kester, G.; Clym, S.W. Quantifying the global wave power resource. Renew. Energy 2012, 44, 296–304. [Google Scholar]
- Arena, F.; LaFace, V.; Malara, G.; Romolo, A.; Viviano, A.; Fiamma, V.; Sannino, G.; Carillo, A. Wave climate analysis for the design of wave energy harvesters in the Mediterranean Sea. Renew. Energy 2015, 77, 125–141. [Google Scholar] [CrossRef]
- Falcão, A.F.D.O.; Henriques, J.C. Oscillating-water-column wave energy converters and air turbines: A review. Renew. Energy 2016, 85, 1391–1424. [Google Scholar] [CrossRef]
- Lindroth, S.; Leijon, M. Offshore wave power measurements—A review. Renew. Sustain. Energy Rev. 2011, 15, 4274–4285. [Google Scholar] [CrossRef]
- Evans, D.V. Power from Water Waves. Annu. Rev. Fluid Mech. 1981, 13, 157–187. [Google Scholar] [CrossRef]
- Falnes, J. Optimum control of oscillation of wave-energy converters. Int. J. Offshore Polar Eng. 2002, 12, 1–12. [Google Scholar]
- Falnes, J. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Falcão, A.F.D.O.; Sarmento, A.J.; Gato, L.; Crowley, S. The Pico OWC wave power plant: Its lifetime from conception to closure 1986–2018. Appl. Ocean Res. 2020, 98, 102104. [Google Scholar] [CrossRef]
- Heath, T.; Whittaker, T.J.T.; Boake, C.B. The design, construction and operation of the LIMPET wave energy converter (Islay, Scotland). In Proceedings of the 4th European Wave Energy Conference, Aalborg, Denmark, 4–6 December 2000; pp. 49–55. [Google Scholar]
- Zhang, D.; Li, W.; Lin, Y. Wave energy in China: Current status and perspectives. Renew. Energy 2009, 34, 2089–2092. [Google Scholar] [CrossRef]
- Gomes, R.; Henriques, J.; Gato, L.; Falcão, A. Hydrodynamic optimization of an axisymmetric floating oscillating water column for wave energy conversion. Renew. Energy 2012, 44, 328–339. [Google Scholar] [CrossRef]
- Falcão, A.F.D.O.; Henriques, J.C.; Cândido, J.J. Dynamics and optimization of the OWC spar buoy wave energy converter. Renew. Energy 2012, 48, 369–381. [Google Scholar] [CrossRef]
- McCormick, M.E. A Theoretical Analysis of a Self-Propelled Backward-Bent Duct Wave Energy Conversion System. J. Energy Resour. Technol. 1991, 113, 94–100. [Google Scholar] [CrossRef]
- Hong, D.; Hong, S. Numerical study on the reverse drift force of floating BBDB wave energy absorbers. Ocean Eng. 2004, 31, 1257–1294. [Google Scholar] [CrossRef]
- Washio, Y.; Osawa, H.; Nagata, Y.; Fujii, F.; Furuyama, H.; Fujita, T. The offshore floating type wave power device “Mighty Whale”: Open sea tests. In Proceedings of the Tenth International Offshore and Polar Engineering Conference, Seattle, WA, USA, 28 May–2 July 2000; pp. 373–380. [Google Scholar]
- Jefferys, R.; Whittaker, T.; Falcão, A.F.D.O. Latching control of an oscillating water column device with air compressibility. In Hydrodynamics of Ocean Wave-Energy Utilization; Springer: Berlin, Germany, 1986; pp. 281–291. [Google Scholar]
- Hoskin, R.E.; Count, B.M.; Nichols, N.K.; Nicol, D.A.C.; Falcão, A.F.D.O. Phase Control for the Oscillating Water Column. In Hydrodynamics of Ocean Wave-Energy Utilization; Springer: Berlin, Germany, 1986; pp. 257–268. [Google Scholar]
- Falcão, A.F.D.O.; Henriques, J.; Gato, L.; Gomes, R.P.F. Air turbine choice and optimization for floating oscillating-water-column wave energy converter. Ocean Eng. 2014, 75, 148–156. [Google Scholar] [CrossRef]
- Falcão, A.F.D.O.; Rodrigues, R. Stochastic modelling of OWC wave power plant performance. Appl. Ocean Res. 2002, 24, 59–71. [Google Scholar] [CrossRef]
- Falcão, A.F.D.O. Control of an oscillating-water-column wave power plant for maximum energy production. Appl. Ocean Res. 2002, 24, 73–82. [Google Scholar] [CrossRef]
- Song, S.K.; Park, J.B. Control Strategy of an Impulse Turbine for an Oscillating Water Column-Wave Energy Converter in Time-Domain Using Lyapunov Stability Method. Appl. Sci. 2016, 6, 281. [Google Scholar] [CrossRef]
- Yu, Z.; Jiang, N.; You, Y. Load control method and its realization on an OWC wave power converter. In OMAE; ASME: New York, NY, USA, 1994; Volume 1. [Google Scholar]
- Justino, P.A.P.; Falcão, A.F.D.O. Rotational Speed Control of an OWC Wave Power Plant. J. Offshore Mech. Arct. Eng. 1999, 121, 65–70. [Google Scholar] [CrossRef]
- Falcão, A.F.D.O.; Henriques, J.; Gato, L. Rotational speed control and electrical rated power of an oscillating-water-column wave energy converter. Energy 2017, 120, 253–261. [Google Scholar] [CrossRef]
- Amundarain, M.; Alberdi, M.; Garrido, A.; Garrido, I. Neural rotational speed control for wave energy converters. Int. J. Control. 2011, 84, 293–309. [Google Scholar] [CrossRef]
- Mishra, S.K.; Purwar, S.; Kishor, N. An optimal and non-linear speed control of oscillating water column wave energy plant with wells turbine and DFIG. Int. J. Renew. Energy Res. 2016, 6, 995–1006. [Google Scholar]
- Mishra, S.K.; Purwar, S.; Kishor, N. Event-triggered nonlinear control of OWC ocean wave energy plant. IEEE Trans. Sustain. Energy 2018, 9, 1750–1760. [Google Scholar] [CrossRef]
- Henriques, J.; Lemos, J.M.; Eça, L.; Gato, L.M.; Falcão, A.F.D.O. A high-order Discontinuous Galerkin Method with mesh refinement for optimal control. Automatica 2017, 85, 70–82. [Google Scholar] [CrossRef]
- Vicinanza, D.; Di Lauro, E.; Contestabile, P.; Gisonni, C.; Lara, J.L.; Losada, I.J. Review of Innovative Harbor Breakwaters for Wave-Energy Conversion. J. Waterw. Port Coast. Ocean Eng. 2019, 145, 03119001. [Google Scholar] [CrossRef]
- Carrelhas, A.; Gato, L.; Henriques, J.; Falcão, A.; Varandas, J. Test results of a 30 kW self-rectifying biradial air turbine-generator prototype. Renew. Sustain. Energy Rev. 2019, 109, 187–198. [Google Scholar] [CrossRef]
- Kim, S.H.; Ryu, W.J.; Shin, S.H.; Hong, K.Y.; Kim, Y.D.; Kim, G.W. Application of the Orifice as A Turbine Substitute of OWC Wave Energy Converter. Available online: http://www.dbpia.co.kr/Article/NODE02040148 (accessed on 28 September 2016).
- Ma, M.; Liu, X.; Lee, K.Y. Maximum Power Point Tracking and Voltage Regulation of Two-Stage Grid-Tied PV System Based on Model Predictive Control. Energies 2020, 13, 1304. [Google Scholar] [CrossRef]
- Markel, P.; John, V.R. A review of wave-to-wire models for wave energy converters. Energies 2016, 9, 506. [Google Scholar]
- Huang, H.; Mao, C.; Lu, J.; Wang, D. Small-signal modelling and analysis of wind turbine with direct drive permanent magnet synchronous generator connected to power grid. IET Renew. Power Gener. 2012, 6, 48–58. [Google Scholar] [CrossRef]











| Parameter | Value | Unit |
|---|---|---|
| Ac | 36 | m2 |
| ηc | 50 | % |
| At | 0.25635 | m2 |
| bt | 0.12 | m |
| lt | 0.16 | m |
| nt | 30 | |
| rt | 0.34 | m |
| J | 32.12 | kg m2 |
| ρa | 1.226 | kg/m3 |
| opt | 1 | |
| Np | 28 | pole |
| ωrate | 800 | rpm |
| Vp.rate | 306.8 | V |
| Prate | 30 | kW |
| Tsimulation | 5 | µsec |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chan, R.; Kim, K.-W.; Park, J.-Y.; Park, S.-W.; Kim, K.-H.; Kwak, S.-S. Power Performance Analysis According to the Configuration and Load Control Algorithm of Power Take-Off System for Oscillating Water Column Type Wave Energy Converters. Energies 2020, 13, 6415. https://doi.org/10.3390/en13236415
Chan R, Kim K-W, Park J-Y, Park S-W, Kim K-H, Kwak S-S. Power Performance Analysis According to the Configuration and Load Control Algorithm of Power Take-Off System for Oscillating Water Column Type Wave Energy Converters. Energies. 2020; 13(23):6415. https://doi.org/10.3390/en13236415
Chicago/Turabian StyleChan, Roh, Kil-Won Kim, Ji-Yong Park, Se-Wan Park, Kyong-Hwan Kim, and Sang-Shin Kwak. 2020. "Power Performance Analysis According to the Configuration and Load Control Algorithm of Power Take-Off System for Oscillating Water Column Type Wave Energy Converters" Energies 13, no. 23: 6415. https://doi.org/10.3390/en13236415
APA StyleChan, R., Kim, K.-W., Park, J.-Y., Park, S.-W., Kim, K.-H., & Kwak, S.-S. (2020). Power Performance Analysis According to the Configuration and Load Control Algorithm of Power Take-Off System for Oscillating Water Column Type Wave Energy Converters. Energies, 13(23), 6415. https://doi.org/10.3390/en13236415







