The Potential of Depleted Oil Reservoirs for High-Temperature Storage Systems
Abstract
:1. Introduction
2. Description of Depleted Oil Reservoirs
2.1. Regional and Petroleum Geology
2.2. Thermal and Petrophysical Data of Reservoir Rocks
3. Numerical Modeling
3.1. Modeling Approach
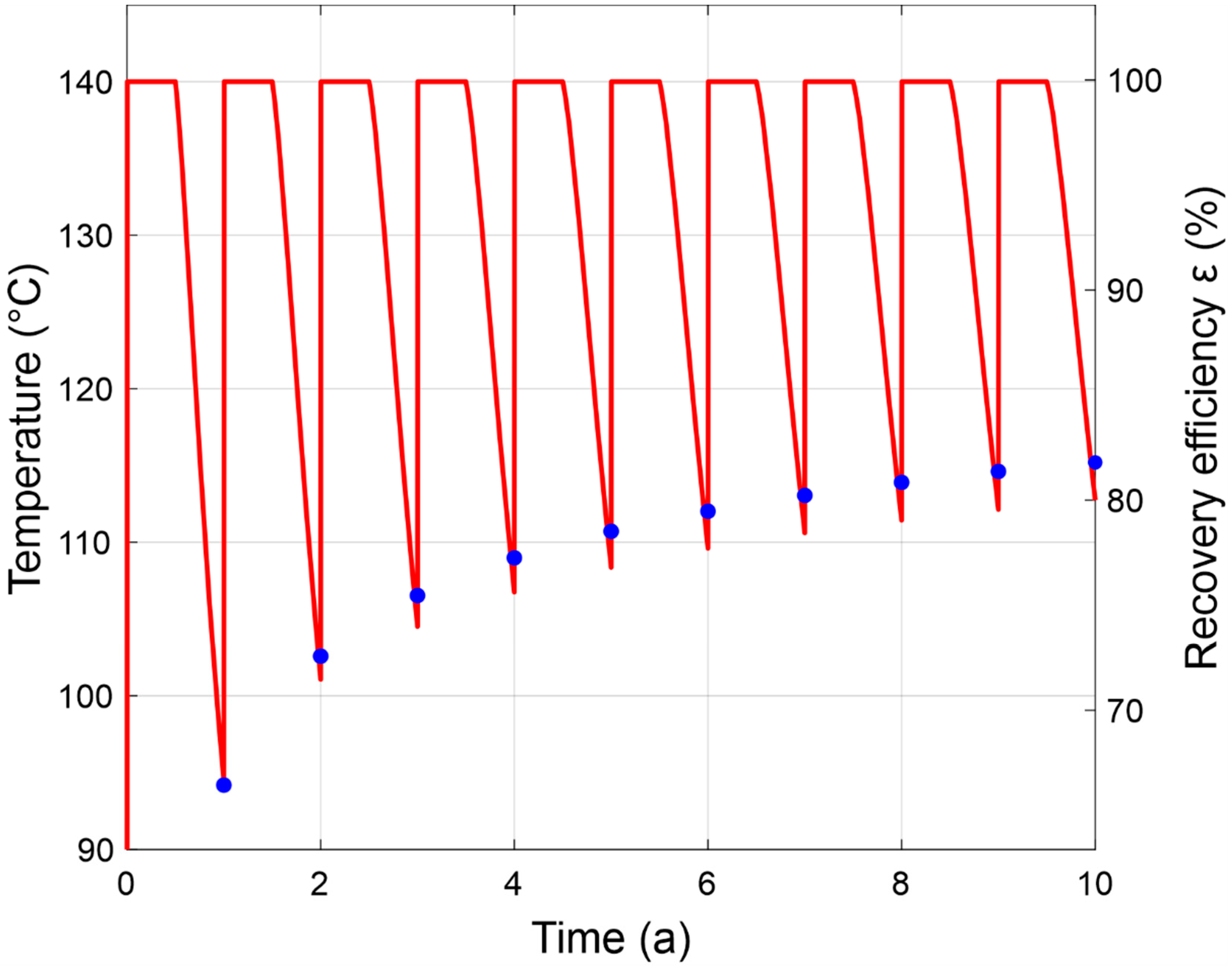
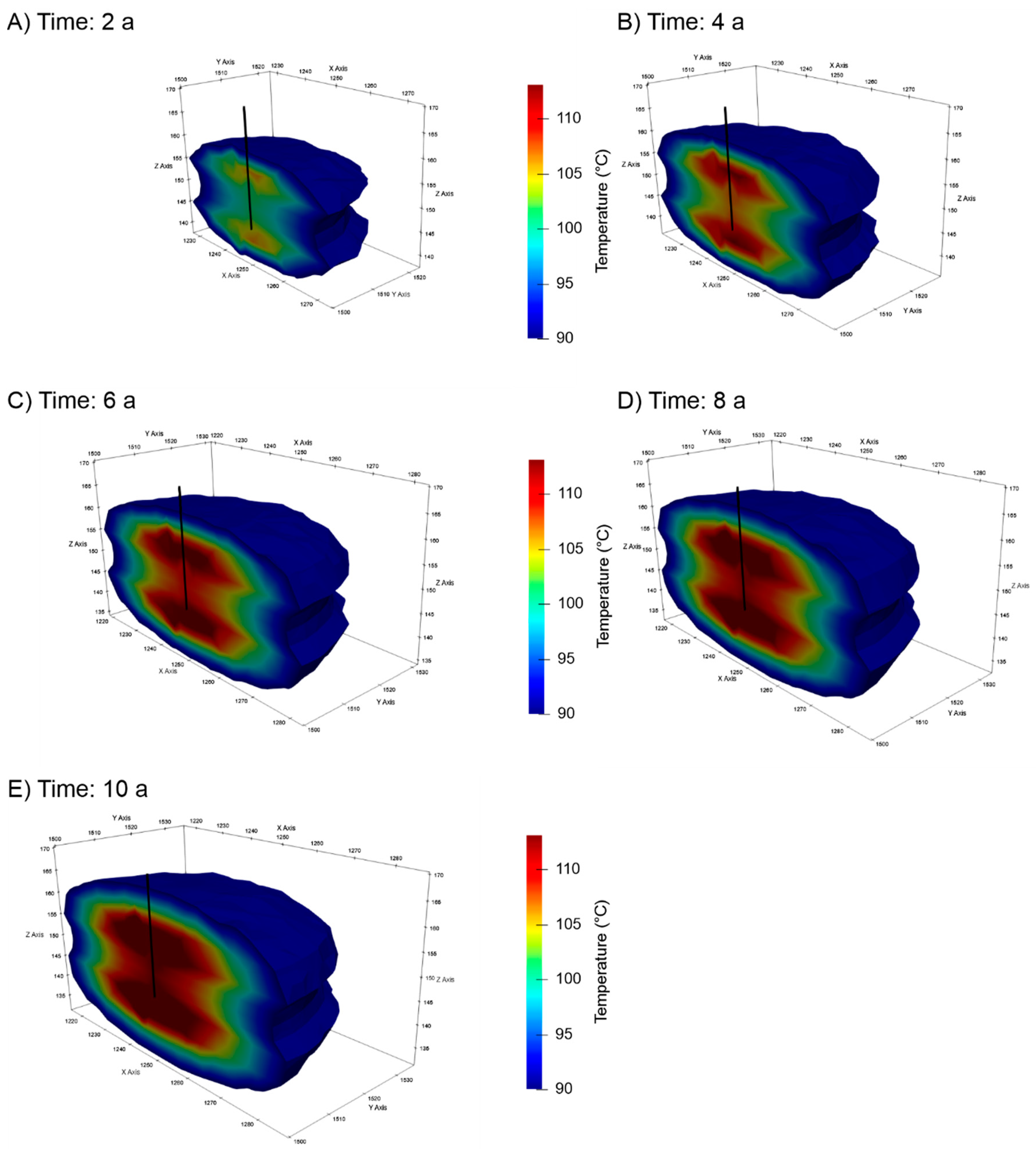
3.2. Reference Case
4. Parameter Sensitivity on Recovery Efficiency
4.1. Parameter Variation for the Vertical Well Setup
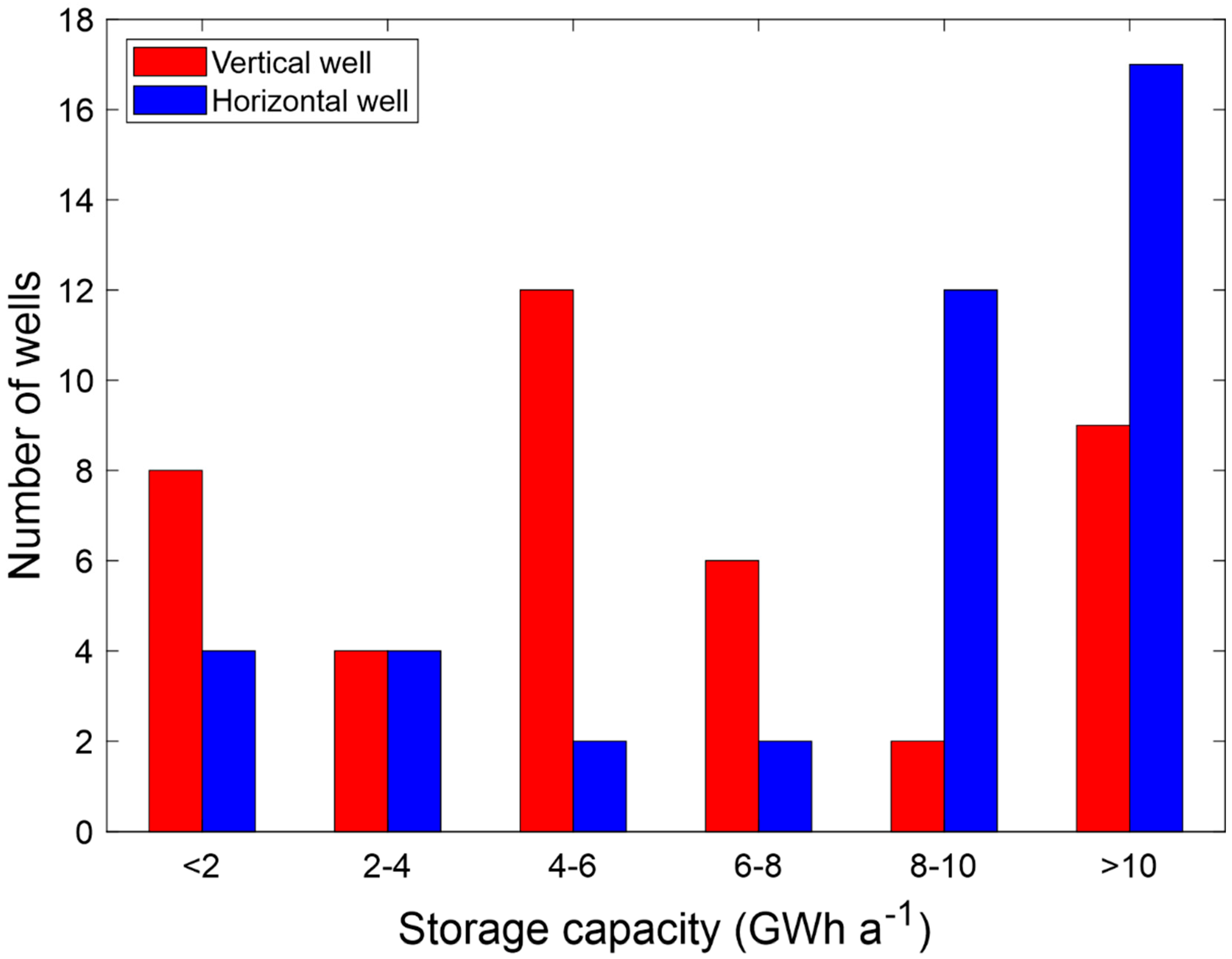
4.2. Comparison of Vertical and Horizontal Well Setups
5. Discussion and Possible Energy Extraction in the URG
6. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Parameter | Variation | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Reservoir permeability [m²] | Vertical well | 6.6 × 10−15 | 1 × 10−14 | 3.3 × 10−14 | 6.6 × 10−14 | 1 × 10−13 | 3.3 × 10−13 | ||
| Horizontal well | 1 × 10−15 | 3.3 × 10−15 | 6.6 × 10−15 | 1 × 10−14 | 3.3 × 10−14 | 6.6 × 10−14 | 1 × 10−13 | 3.3 × 10−13 | |
| Reservoir thickness [m] | 5 | 10 | 20 | ||||||
| Thermal conductivity [Wm−1K−1] | Reservoir (λres) | 2 | 2.5 | 3 | |||||
| Cap rock (λcap) | 1 | 1.4 | 2 | ||||||
| Injection/production flow rate [Ls−1] | 1 | 2 | 5 | 7.5 | 10 | ||||
| Field | Well | Reservoir Formation | ReservoirDepth [m] | ReservoirThickness [m] | Permeability Min [m²] | Permeability Avg [m²] | Permeability Max [m²] | Source |
|---|---|---|---|---|---|---|---|---|
| Eich-Königsgarten | Eich 27 | PBF | 1760–1855 | 20–30 | 1 × 10−14 | 2 × 10−13 | 4 × 10−12 | [88] |
| Landau | 104 | EBS | 25 | 5 × 10−15 | 7.1 × 10−15 | 10−14 | [19,61,89] | |
| Leopolds-hafen | N 1 | NF | 1196 | 5,6 | 2.4 × 10−15 | 1.4 × 10−14 | 7.7 × 10−14 | [24] |
| N 1a | Me | 1233.3–1237.4 | 18 | 1.3 × 10−15 | 2.2 × 10−15 | 3.8 × 10−15 | [24] | |
| Neureut | 2H | NF | 1107–1111.2 | 9 | 1.1 × 10−13 | 1.1 × 10−13 | 1.1 × 10−13 | [24] |
| Offenbach | CyM, Me | 11 | 4 × 10−13 | 6.6 × 10−13 | 1.1 × 10−12 | [58,89] | ||
| Stockstadt | PBF | 1400–1700 | 10 | 1 × 10−15 | 3.2 × 10−15 | 1 × 10−14 | [89] | |
| Weingarten | Wiag-Deutag 204 | Me | 408.2 | 7 | 1.4 × 10−13 | 1.4 × 10−13 | 1.4 × 10−13 | [19,24] |
| Wiag-Deutag 205 | 243.3 | 16 | 1.3 × 10−13 | 1.3 × 10−13 | 1.3 × 10−13 | [24] | ||
| Eschau | 1 | NF, CyM, Me | 280–450 | 34 | 1 × 10−14 | 3.2 × 10−14 | 1 × 10−13 | [23] |
| 2 | SG | 375–552 | 17,5 | 1 × 10−14 | 3.2 × 10−14 | 1 × 10−13 | [23] | |
| 3 | SG | 390.2–608.3 | 15 | 1 × 10−14 | 3.2 × 10−14 | 1 × 10−13 | [23] | |
| 5 | SG | 599.7–633.3 | 11 | 1 × 10−14 | 3.2 × 10−14 | 1 × 10−13 | [23] | |
| 6 | NF | 294–352 | 10 | 1 × 10−14 | 3.2 × 10−14 | 1 × 10−13 | [23] | |
| 6 | SG | 475–575 | 7 | 1 × 10−14 | 3.2 × 10−14 | 1 × 10−13 | [23] | |
| 7 | NF | 30 | 1 × 10−14 | 3.2 × 10−14 | 1 × 10−13 | [23] | ||
| 7 | SG | 433–465 | 22 | 1 × 10−14 | 3.2 × 10−14 | 1 × 10−13 | [23] | |
| 9 | NF | 318–324 | 6 | 1 × 10−14 | 3.2 × 10−14 | 1 × 10−13 | [23] | |
| 9 | SG | 450–555 | 19 | 1 × 10−14 | 3.2 × 10−14 | 1 × 10−13 | [23] | |
| 10 | SG | 432–520 | 48 | 1 × 10−14 | 3.2 × 10−14 | 1 × 10−13 | [23] | |
| 11 | NF | 287–392 | 28 | 1 × 10−14 | 3.2 × 10−14 | 1 × 10−13 | [23] | |
| 11 | SG | 400–620 | 25 | 1 × 10−14 | 3.2 × 10−14 | 1 × 10−13 | [23] | |
| 101 | NF | 290–440 | 37 | 1 × 10−14 | 3.2 × 10−14 | 1 × 10−13 | [23] | |
| 102 | NF | 305–490 | 41 | 1 × 10−14 | 3.2 × 10−14 | 1 × 10−13 | [23] | |
| 103 | NF | 290–440 | 23 | 1 × 10−14 | 3.2 × 10−14 | 1 × 10−13 | [23] | |
| 104 | NF | 543–550 | 3 | 1 × 10−14 | 3.2 × 10−14 | 1 × 10−13 | [23] | |
| Souffenheim | 8 | SG | 188–193 | 5 | 1 × 10−13 | 1 × 10−13 | 1 × 10−13 | [23] |
| 10 | 166–183 | 11 | 1 × 10−13 | 1 × 10−13 | 1 × 10−13 | [23] | ||
| 11 | 150–167 | 15 | 1 × 10−13 | 1 × 10−13 | 1 × 10−13 | [23] | ||
| 12 | 160–180 | 18 | 1 × 10−13 | 1 × 10−13 | 1 × 10−13 | [23] | ||
| 13 | 162–180 | 13 | 1 × 10−13 | 1 × 10−13 | 1 × 10−13 | [23] | ||
| 14 | 151–167 | 10 | 1 × 10−13 | 1 × 10−13 | 1 × 10−13 | [23] | ||
| 17 | 151–223 | 36 | 1 × 10−13 | 1 × 10−13 | 1 × 10−13 | [23] | ||
| 18 | 158–187 | 10 | 1 × 10−13 | 1 × 10−13 | 1 × 10−13 | [23] | ||
| 20 | 169–183 | 8 | 1 × 10−13 | 1 × 10−13 | 1 × 10−13 | [23] | ||
| 21 | 161–176 | 13 | 1 × 10−13 | 1 × 10−13 | 1 × 10−13 | [23] | ||
| 24 | 167–187 | 16 | 1 × 10−13 | 1 × 10−13 | 1 × 10−13 | [23] | ||
| 25 | 149–223 | 36 | 1 × 10−13 | 1 × 10−13 | 1 × 10−13 | [23] | ||
| Schaffhouse | BS | 950 | 7.5–20 | 1 × 10−12 | 1 × 10−12 | 1 × 10−12 | [23] | |
| 2 | 950 | 10 | 1 × 10−12 | 1 × 10−12 | 1 × 10−12 | [23] | ||
| 3 | 945 | 15 | 1 × 10−12 | 1 × 10−12 | 1 × 10−12 | [23] |
References
- IEA. Energy Technology Perspectives 2017. Catalyzing Energy Technology Transformations; IEA Publications, International Energy Agency: Paris, France, 2017. [Google Scholar]
- REN21. Renewables 2019 Global Status Report. 2019. Available online: https://www.ren21.net/wp-content/uploads/2019/05/gsr_2019_full_report_en.pdf (accessed on 18 November 2020).
- Dinçer, İ.; Rosen, M.A. Thermal Energy Storage. Systems and Applications, 2nd ed.; Wiley: Hoboken, NJ, USA, 2011; ISBN 978-0-470-97073-7. [Google Scholar]
- Lee, K.S. Underground Thermal Energy Storage; Springer: London, UK, 2013; ISBN 978-1-4471-4273-7. [Google Scholar]
- Li, G. Sensible heat thermal storage energy and exergy performance evaluations. Renew. Sustain. Energy Rev. 2016, 53, 897–923. [Google Scholar] [CrossRef]
- Bär, K.; Rühaak, W.; Welsch, B.; Schulte, D.; Homuth, S.; Sass, I. Seasonal High Temperature Heat Storage with Medium Deep Borehole Heat Exchangers. Energy Procedia 2015, 76, 351–360. [Google Scholar] [CrossRef] [Green Version]
- Rad, F.M.; Fung, A.S. Solar community heating and cooling system with borehole thermal energy storage—Review of systems. Renew. Sustain. Energy Rev. 2016, 60, 1550–1561. [Google Scholar] [CrossRef]
- Dickinson, J.S.; Buik, N.; Matthews, M.C.; Snijders, A. Aquifer thermal energy storage: Theoretical and operational analysis. Géotechnique 2009, 59, 249–260. [Google Scholar] [CrossRef]
- van Heekeren, V.; Bakema, G. Country Update the Netherlands; World Geothermal Congress: Melbourne, Australia, 2015. [Google Scholar]
- Fleuchaus, P.; Godschalk, B.; Stober, I.; Blum, P. Worldwide application of aquifer thermal energy storage—A review. Renew. Sustain. Energy Rev. 2018, 94, 861–876. [Google Scholar] [CrossRef]
- Fraunhofer ISI. Baseline Scenario of the Heating and Cooling Demand in Buildings and Industry in the 14 MSs until 2050. 2017. Available online: https://heatroadmap.eu/wp-content/uploads/2018/11/HRE4_D3.3andD3.4.pdf (accessed on 18 November 2020).
- Sayegh, M.A.; Jadwiszczak, P.; Axcell, B.P.; Niemierka, E.; Bryś, K.; Jouhara, H. Heat pump placement, connection and operational modes in European district heating. Energy Build. 2018, 166, 122–144. [Google Scholar] [CrossRef]
- Wesselink, M.; Liu, W.; Koornneef, J.; van den Broek, M. Conceptual market potential framework of high temperature aquifer thermal energy storage—A case study in the Netherlands. Energy 2018, 147, 477–489. [Google Scholar] [CrossRef]
- Sanner, B.; Knoblich, K. Thermische Untergrundspeicherung auf Höherem Temperaturniveau: Begleitforschung mit Messprogramm Aquiferspeicher Reichstag. Schlussbericht zum FuE-Vorhaben 0329809 B; Justus-Liebig-Universität Giessen: Giessen, Germany, 2004. [Google Scholar]
- Kabus, F.; Richlak, U.; Wolfgramm, M.; Gehrke, D.; Beuster, H.; Seibt, A. Aquiferspeicherung in Neubrandenburg—Betriebsmonitoring über drei Speicherzyklen. Conf. Proc. Der Geotherm. 2008, 2008, 383–392. [Google Scholar]
- Holstenkamp, L.; Meisel, M.; Neidig, P.; Opel, O.; Steffahn, J.; Strodel, N.; Lauer, J.J.; Vogel, M.; Degenhart, H.; Michalzik, D.; et al. Interdisciplinary Review of Medium-deep Aquifer Thermal Energy Storage in North Germany. Energy Procedia 2017, 135, 327–336. [Google Scholar] [CrossRef]
- Baillieux, P.; Schill, E.; Edel, J.-B.; Mauri, G. Localization of temperature anomalies in the Upper Rhine Graben: Insights from geophysics and neotectonic activity. Int. Geol. Rev. 2013, 55, 1744–1762. [Google Scholar] [CrossRef]
- LBEG. Erdöl und Erdgas in der Bundesrepublik Deutschland 2009; Landesamt für Bergbau, Energie und Geologie Niedersachsen: Hannover, Germany, 2010. [Google Scholar]
- Böcker, J. Petroleum System and Thermal History of the Upper Rhine Graben: Implications from Organic Geochemical Analyses, Oil-Source Rock Correlations and Numerical Modelling. Ph.D Thesis, RWTH Aachen, Aachen, Germany, 2015. [Google Scholar]
- Moscariello, A. Exploring for geo-energy resources in the Geneva Basin (Western Switzerland): Opportunities and challenges. Swiss Bull. Angew. Geol. 2019, 24, 105–124. [Google Scholar]
- Böcker, J.; Littke, R.; Forster, A. An overview on source rocks and the petroleum system of the central Upper Rhine Graben. Int. J. Earth Sci. 2017, 106, 707–742. [Google Scholar] [CrossRef]
- Grimmer, J.C.; Ritter, J.R.R.; Eisbacher, G.H.; Fielitz, W. The Late Variscan control on the location and asymmetry of the Upper Rhine Graben. Int. J. Earth Sci. 2017, 106, 827–853. [Google Scholar] [CrossRef]
- Grandarovski, G. Possibilites d’injection en Couches Profondes d’effluents Industriels. Etude de Quelques Réservoirs Sableux et Gréseux Dans les Formations Tertiaires du Nord. de l’Alsace; Bureau de Rechereches Géologiques et Minières (BRGM): Strasbourg, France, 1971. [Google Scholar]
- Bruss, D. Zur Herkunft der Erdöle im Mittleren Oberrheingraben und ihre Bedeutung für die Rekonstruktion der Migrationsgeschichte und der Speichergesteinsdiagenese. Ph.D. Thesis, Forschungszentrum Jülich/Universität Erlangen-Nürnberg: Jülich, Germany, 2000. [Google Scholar]
- O’Sullivan, M.J.; Pruess, K.; Lippmann, M.J. State of the art of geothermal reservoir simulation. Geothermics 2001, 30, 395–429. [Google Scholar] [CrossRef]
- Kohl, T.; Andenmatten, N.; Rybach, L. Geothermal resource mapping—Example from northern Switzerland. Geothermics 2003, 32, 721–732. [Google Scholar] [CrossRef]
- Gao, L.; Zhao, J.; An, Q.; Wang, J.; Liu, X. A review on system performance studies of aquifer thermal energy storage. Energy Procedia 2017, 142, 3537–3545. [Google Scholar] [CrossRef]
- Bakr, M.; van Oostrom, N.; Sommer, W. Efficiency of and interference among multiple Aquifer Thermal Energy Storage systems; A Dutch case study. Renew. Energy 2013, 60, 53–62. [Google Scholar] [CrossRef]
- Bridger, D.W.; Allen, D.M. Influence of geologic layering on heat transport and storage in an aquifer thermal energy storage system. Hydrogeol. J. 2014, 22, 233–250. [Google Scholar] [CrossRef]
- Major, M.; Poulsen, S.E.; Balling, N. A numerical investigation of combined heat storage and extraction in deep geothermal reservoirs. Geotherm. Energy 2018, 6, 540. [Google Scholar] [CrossRef] [Green Version]
- Kastner, O.; Norden, B.; Klapperer, S.; Park, S.; Urpi, L.; Cacace, M.; Blöcher, G. Thermal solar energy storage in Jurassic aquifers in Northeastern Germany: A simulation study. Renew. Energy 2017, 104, 290–306. [Google Scholar] [CrossRef]
- Drijver, B.; van Aarssen, M.; de Zwart, B. High-temperature aquifer thermal energy storage (HT-ATES): Sustainable and multi-usable. In Proceedings of the Innostock 2012—The 12th International Conference on Energy Storage, Lleida, Spain, 16–18 May 2012; Cabeza, L.F., Ed.; Universitat de Lleida: Lleida, Spain, 2012. ISBN 9788493879334. [Google Scholar]
- Sommer, W.T.; Doornenbal, P.J.; Drijver, B.C.; van Gaans, P.F.M.; Leusbrock, I.; Grotenhuis, J.T.C.; Rijnaarts, H.H.M. Thermal performance and heat transport in aquifer thermal energy storage. Hydrogeol. J. 2014, 22, 263–279. [Google Scholar] [CrossRef]
- Ganguly, S.; Mohan Kumar, M.S.; Date, A.; Akbarzadeh, A. Numerical investigation of temperature distribution and thermal performance while charging-discharging thermal energy in aquifer. Appl. Therm. Eng. 2017, 115, 756–773. [Google Scholar] [CrossRef]
- Kim, J.; Lee, Y.; Yoon, W.S.; Jeon, J.S.; Koo, M.-H.; Keehm, Y. Numerical modeling of aquifer thermal energy storage system. Energy 2010, 35, 4955–4965. [Google Scholar] [CrossRef]
- Xiao, X.; Jiang, Z.; Owen, D.; Schrank, C. Numerical simulation of a high-temperature aquifer thermal energy storage system coupled with heating and cooling of a thermal plant in a cold region, China. Energy 2016, 112, 443–456. [Google Scholar] [CrossRef]
- Winterleitner, G.; Schütz, F.; Wenzlaff, C.; Huenges, E. The Impact of Reservoir Heterogeneities on High-Temperature Aquifer Thermal Energy Storage Systems. A Case Study from Northern Oman. Geothermics 2018, 74, 150–162. [Google Scholar] [CrossRef]
- Kohl, T.; Bächler, D.; Rybach, L. Steps towards a comprehensive thermo-hydraulic analysis of the HDR test site Soultz-sous-Forêts. In Proceedings of the World Geothermal Congress Kyushu, Tohoku, Japan, 28 May–10 June 2000; pp. 3459–3464. [Google Scholar]
- Bächler, D.; Kohl, T.; Rybach, L. Impact of graben-parallel faults on hydrothermal convection—Rhine Graben case study. Phys. Chem. Earth Parts A B C 2003, 28, 431–441. [Google Scholar] [CrossRef]
- Egert, R.; Korzani, M.G.; Held, S.; Kohl, T. Implications on large-scale flow of the fractured EGS reservoir Soultz inferred from hydraulic data and tracer experiments. Geothermics 2020, 84, 101749. [Google Scholar] [CrossRef]
- Geyer, O.F.; Gwinner, M.P.; Simon, T. Geologie von Baden-Württemberg, 5, Völlig neu Bearbeitete Auflage; Schweizerbart: Stuttgart, Germany, 2011; ISBN 978-3-510-65267-9. [Google Scholar]
- Rotstein, Y.; Behrmann, J.H.; Lutz, M.; Wirsing, G.; Luz, A. Tectonic implications of transpression and transtension: Upper Rhine Graben. Tectonics 2005, 24. [Google Scholar] [CrossRef]
- Schnaebelé, R. Monographie géologique du champ pétrolifière de Pechelbronn. Mém. Serv. Cart. Geol D Alsace Et Lorraine 1948, 7, 1–254. [Google Scholar]
- Rinck, G. Bilan de L‘Exploration et de L‘Exploitation du Petrole en Alsace Durant la Derniere Decennie; Service Géologique Régional Alsace: Strasbourg, France, 1987. [Google Scholar]
- Reinhold, C.; Schwarz, M.; Bruss, D.; Heesbeen, B.; Perner, M.; Suana, M. The Northern Upper Rhine Graben: Re-dawn of a mature petroleum province? Swiss Bull. Angew. Geol. 2016, 21, 35–56. [Google Scholar] [CrossRef]
- Derer, C.E. Tectono-Sedimentary Evolution of the Northern Upper Rhine Graben (Germany), with Special Regards to the Early Syn-Rift Stage. Ph.D Thesis, Universität Bonn, Bonn, Germany, 2003. [Google Scholar]
- Berger, J.-P.; Reichenbacher, B.; Becker, D.; Grimm, M.; Grimm, K.; Picot, L.; Storni, A.; Pirkenseer, C.; Schaefer, A. Eocene-Pliocene time scale and stratigraphy of the Upper Rhine Graben (URG) and the Swiss Molasse Basin (SMB). Int. J. Earth Sci. 2005, 94, 711–731. [Google Scholar] [CrossRef]
- Pirkenseer, C.; Spezzaferri, S.; Berger, J.-P. Reworked microfossils as a paleogeographic tool. Geology 2011, 39, 843–846. [Google Scholar] [CrossRef] [Green Version]
- Pirkenseer, C.; Berger†, J.-P.; Reichenbacher, B. The position of the Rupelian/Chattian boundary in the southern Upper Rhine Graben based on new records of microfossils. Swiss J. Geosci. 2013, 106, 291–301. [Google Scholar] [CrossRef] [Green Version]
- Agemar, T.; Schellschmidt, R.; Schulz, R. Subsurface temperature distribution in Germany. Geothermics 2012, 44, 65–77. [Google Scholar] [CrossRef]
- NASA; METI; AIST; Japan Spacesystems. ASTER Global Digital Elevation Model V003; NASA EOSDIS Land Processes DAAC, 2019. Available online: https://asterweb.jpl.nasa.gov/index.asp (accessed on 18 November 2020).
- NLfB. Bericht über den Erdölbohr- und Förderverlauf im Jahre 1962 in Westdeutschland; Niedersächsisches Landesamt für Bodenforschung: Hannover, Germany, 1963. [Google Scholar]
- Wolf, A.; Hinners, G. Antrennung gelöster Kohlenwasserstoffe aus Lagerstättenwasser. In DGMK/ÖGEW-Frühjahrstagung des Fachbereiches Aufsuchung und Gewinnung am 18. und 19. April 2013 in Celle, Autorenmanuskripte; DGMK: Hamburg, Germany, 2013; ISBN 978-3-941721-31-9. [Google Scholar]
- Sauer, K.; Nägele, R.; Tietze, R. Geothermische Synthese des Oberrheingrabens zwischen Karlsruhe und Mannheim (Anteil Baden-Württemberg); Geologisches Landesamt Baden-Württemberg: Freiburg im Breisgau, Germany, 1981. [Google Scholar]
- Wirth, E. Die Erdöllagerstätten Badens. Abh. Geol. 1962, 4, 81–101. [Google Scholar]
- Caron, E. Réalisation D‘Une Base de Données Porosité-Perméabilité Dans le Fossé Rhénan. Bachelor’s Thesis, Université Lille Nord de France, Lille, France, 2012. [Google Scholar]
- GeORG-Projektteam. Geopotenziale des Tieferen Untergrundes im Oberrheingraben, Fachlich-Technischer Abschlussbericht des Interreg-Projekts GeORG, Teil 3: Daten, Methodik, Darstellungsweise. Landesamt für Geologie, Rohstoffe und Bergbau (RP Freiburg, Baden-Württemberg): Freiburg i. Br., Germany, 2013. [Google Scholar]
- Durst, H. Aspects of exploration history and structural style in the Rhine Graben area. In Generation, Accumulation, and Production of Europe’s Hydrocarbons; Spencer, A., Ed.; Oxford University Press: Oxford, UK, 1991; pp. 247–261. [Google Scholar]
- Blumenroeder, J. Le pétrole en Alsace. Abh. Geol. Landesamt Baden Württemberg 1962, 4, 41–62. [Google Scholar]
- Straub, E.W. Die Erdöl- und Erdgaslagerstätten in Hessen und Rheinhessen. Abh. Geol. Landesamt Baden Württemberg 1962, 4, 123–136. [Google Scholar]
- Schad, A. Das Erdölfeld Landau. Abh. Geol. Landesamt Baden Württemberg 1962, 4, 81–101. [Google Scholar]
- LBEG. Erdöl und Erdgas in der Bundesrepublik Deutschland (2018); Landesamt für Bergbau, Energie und Geologie Niedersachsen: Hannover, Germany, 2019. [Google Scholar]
- Baillieux, P.; Schill, E.; Abdelfettah, Y.; Dezayes, C. Possible natural fluid pathways from gravity pseudo-tomography in the geothermal fields of Northern Alsace (Upper Rhine Graben). Geotherm. Energy 2014, 2, 226. [Google Scholar] [CrossRef] [Green Version]
- Pribnow, D.; Schellschmidt, R. Thermal tracking of upper crustal fluid flow in the Rhine graben. Geophys. Res. Lett. 2000, 27, 1957–1960. [Google Scholar] [CrossRef]
- Bär, K.; Reinsch, T.; Bott, J. P3—PetroPhysical Property Database—A global compilation of lab measured rock properties. Earth Syst. Sci. Data Open Access Discuss. 2020. [Google Scholar] [CrossRef]
- Sattel, G. In-situ-Bestimmung Thermischer Gesteinsparameter aus Ihrem Zusammenhang mit Kompressionswellengeschwindigkeit und Dichte. Ph.D Thesis, Universität Karlsruhe, Karlsruhe, Germany, 1982. [Google Scholar]
- Hintze, M.; Plasse, B.; Bär, K.; Sass, I. Preliminary studies for an integrated assessment of the hydrothermal potential of the Pechelbronn Group in the northern Upper Rhine Graben. Adv. Geosci. 2018, 45, 251–258. [Google Scholar] [CrossRef] [Green Version]
- Scheck, M. Dreidimensionale Strukturmodellierung des Nordostdeutschen Beckens unter Einbeziehung von Krustenmodellen. Ph.D Thesis, Geoforschungszentrum Potsdam, Potsdam, Germany, 1997. [Google Scholar]
- Magri, F.; Bayer, U.; Tesmer, M.; Möller, P.; Pekdeger, A. Salinization problems in the NEGB: Results from thermohaline simulations. Int. J. Earth Sci. 2008, 97, 1075–1085. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier: New York, NY, USA, 1972; ISBN 9780444001146. [Google Scholar]
- Clauser, C.; Villinger, H. Analysis of conductive and convective heat transfer in a sedimentary basin, demonstrated for the Rheingraben. Geophys. J. Int. 1990, 100, 393–414. [Google Scholar] [CrossRef]
- Smith, L.; Chapman, D.S. On the thermal effects of groundwater flow: 1. Regional scale systems. J. Geophys. Res. 1983, 88, 593. [Google Scholar] [CrossRef]
- Gholami Korzani, M.; Held, S.; Kohl, T. Numerical based filtering concept for feasibility evaluation and reservoir performance enhancement of hydrothermal doublet systems. J. Pet. Sci. Eng. 2020, 106803. [Google Scholar] [CrossRef]
- Gaston, D.; Newman, C.; Hansen, G.; Lebrun-Grandié, D. MOOSE: A parallel computational framework for coupled systems of nonlinear equations. Nucl. Eng. Des. 2009, 239, 1768–1778. [Google Scholar] [CrossRef] [Green Version]
- Permann, C.J.; Gaston, D.R.; Andrš, D.; Carlsen, R.W.; Kong, F.; Lindsay, A.D.; Miller, J.M.; Peterson, J.W.; Slaughter, A.E.; Stogner, R.H.; et al. MOOSE: Enabling massively parallel multiphysics simulation. SoftwareX 2020, 11, 100430. [Google Scholar] [CrossRef]
- Sommer, W.; Valstar, J.; Leusbrock, I.; Grotenhuis, T.; Rijnaarts, H. Optimization and spatial pattern of large-scale aquifer thermal energy storage. Appl. Energy 2015, 137, 322–337. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.-F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Meth. Engng 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Evans, K.F.; Zappone, A.; Kraft, T.; Deichmann, N.; Moia, F. A survey of the induced seismic responses to fluid injection in geothermal and CO2 reservoirs in Europe. Geothermics 2012, 41, 30–54. [Google Scholar] [CrossRef]
- Zang, A.; Oye, V.; Jousset, P.; Deichmann, N.; Gritto, R.; McGarr, A.; Majer, E.; Bruhn, D. Analysis of induced seismicity in geothermal reservoirs—An overview. Geothermics 2014, 52, 6–21. [Google Scholar] [CrossRef] [Green Version]
- Millero, F.J.; Chen, C.-T.; Bradshaw, A.; Schleicher, K. A new high pressure equation of state for seawater. Deep Sea Res. Part. A Oceanogr. Res. Pap. 1980, 27, 255–264. [Google Scholar] [CrossRef]
- Coker, A.K.; Ludwig, E.E. Ludwig’s Applied Process. Design for Chemical and Petrochemical Plants, 4th ed.; Elsevier Gulf Professional: Amsterdam, The Netherlands; Boston, MA, USA, 2007; Volume 1, ISBN 978-0-7506-7766-0. [Google Scholar]
- Sommer, W.; Valstar, J.; van Gaans, P.; Grotenhuis, T.; Rijnaarts, H. The impact of aquifer heterogeneity on the performance of aquifer thermal energy storage. Water Resour. Res. 2013, 49, 8128–8138. [Google Scholar] [CrossRef]
- Burgess, T.; van de Slijke, P. Horizontal Drilling Comes of Age. Oil Field Rev. 1991, 2, 22–23. [Google Scholar]
- Allouche, E.N.; Ariaratnam, S.T.; Lueke, J.S. Horizontal Directional Drilling: Profile of an Emerging Industry. J. Constr. Eng. Manag. 2000, 126, 68–76. [Google Scholar] [CrossRef]
- Kabus, F.; Seibt, P. Aquifer thermal energy storage for the Berlin Reichstag building—New seat of the German parliament. In Proceedings of the World Geothermal Congress, Tohoku, Japan, 28 May–10 June 2000. [Google Scholar]
- BDEW. Energy Market. Germany 2019. 2019. Available online: https://www.bdew.de/media/documents/Pub_20190603_Energy-Market-Germany-2019.pdf (accessed on 18 November 2020).
- EURES. Regionalprofil Oberrhein—2008. Statistische Daten, Analyse der wirtschaftlichen Lage und des Arbeitsmarktes; 2008. Available online: https://www.eures-t-oberrhein.eu/fileadmin/user_upload/Downloads/de/Regionalprofil_2008_dt.pdf (accessed on 18 November 2020).
- Jantschik, R.; Strauß, C.; Weber, R. Sequence-Stratigraphy as a Tool to Improve Reservoir Management of the Eich/Königsgarten Oil Field (Upper Rhine Graben, Germany). In Proceedings of the SPE European Petroleum Conference, Milan, Italy, 22–24 October 1996. [Google Scholar]
- Boigk, H. Erdöl und Erdölgas in der Bundesrepublik Deutschland. Erdölprovinzen, Felder, Förderung, Vorräte, Lagerstättentechnik; Enke: Stuttgart, Germany, 1981; ISBN 3432912714. [Google Scholar]

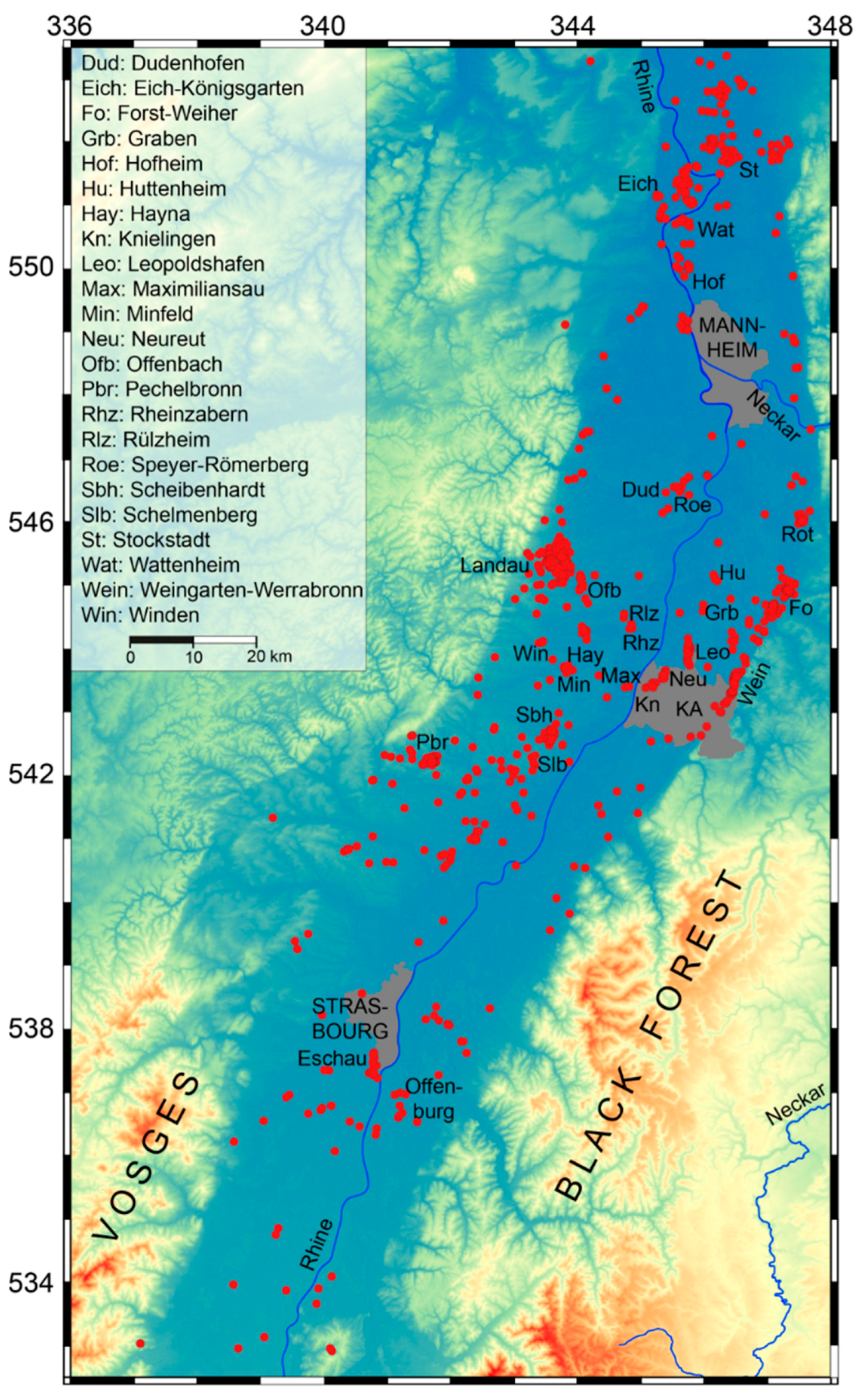
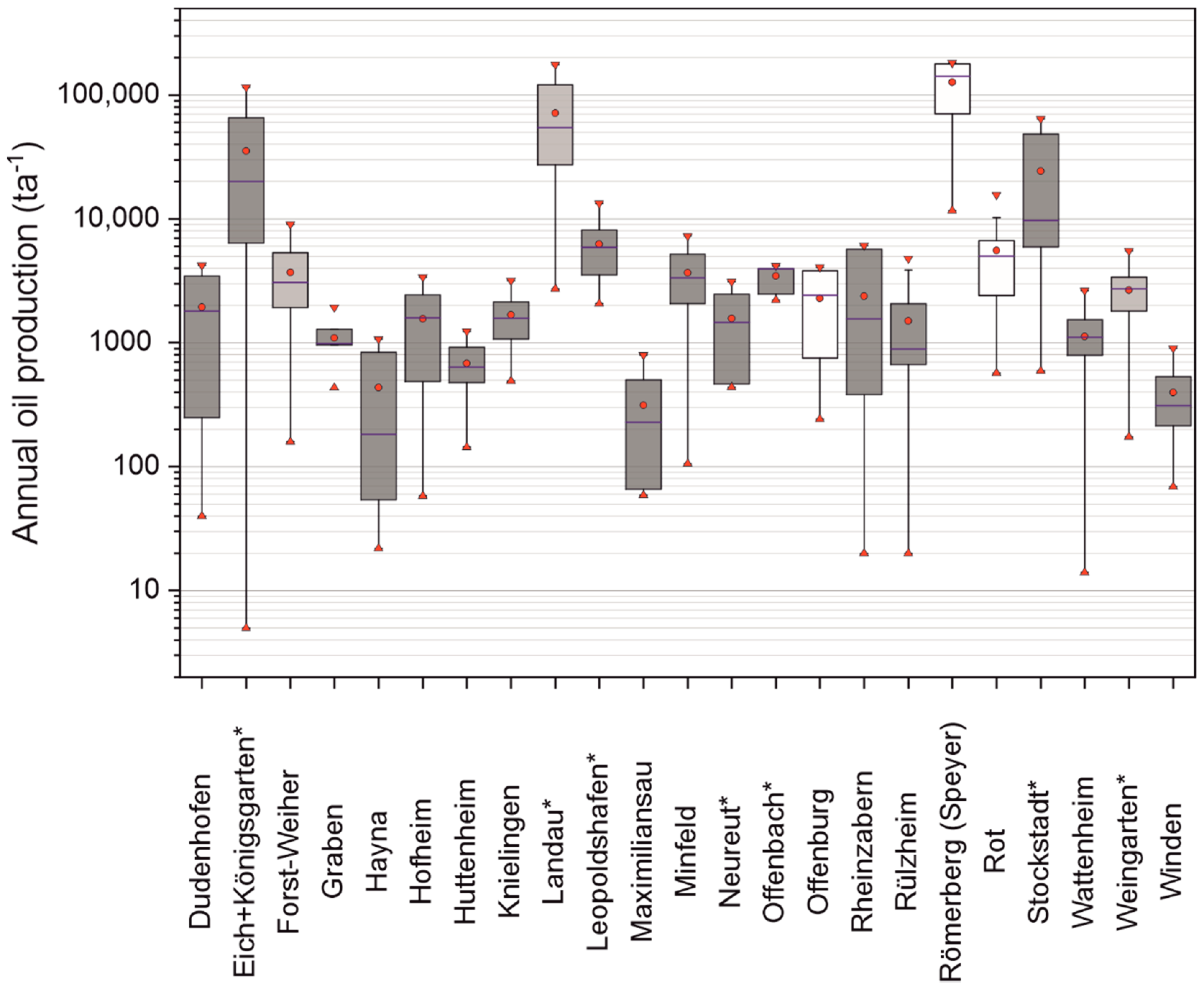
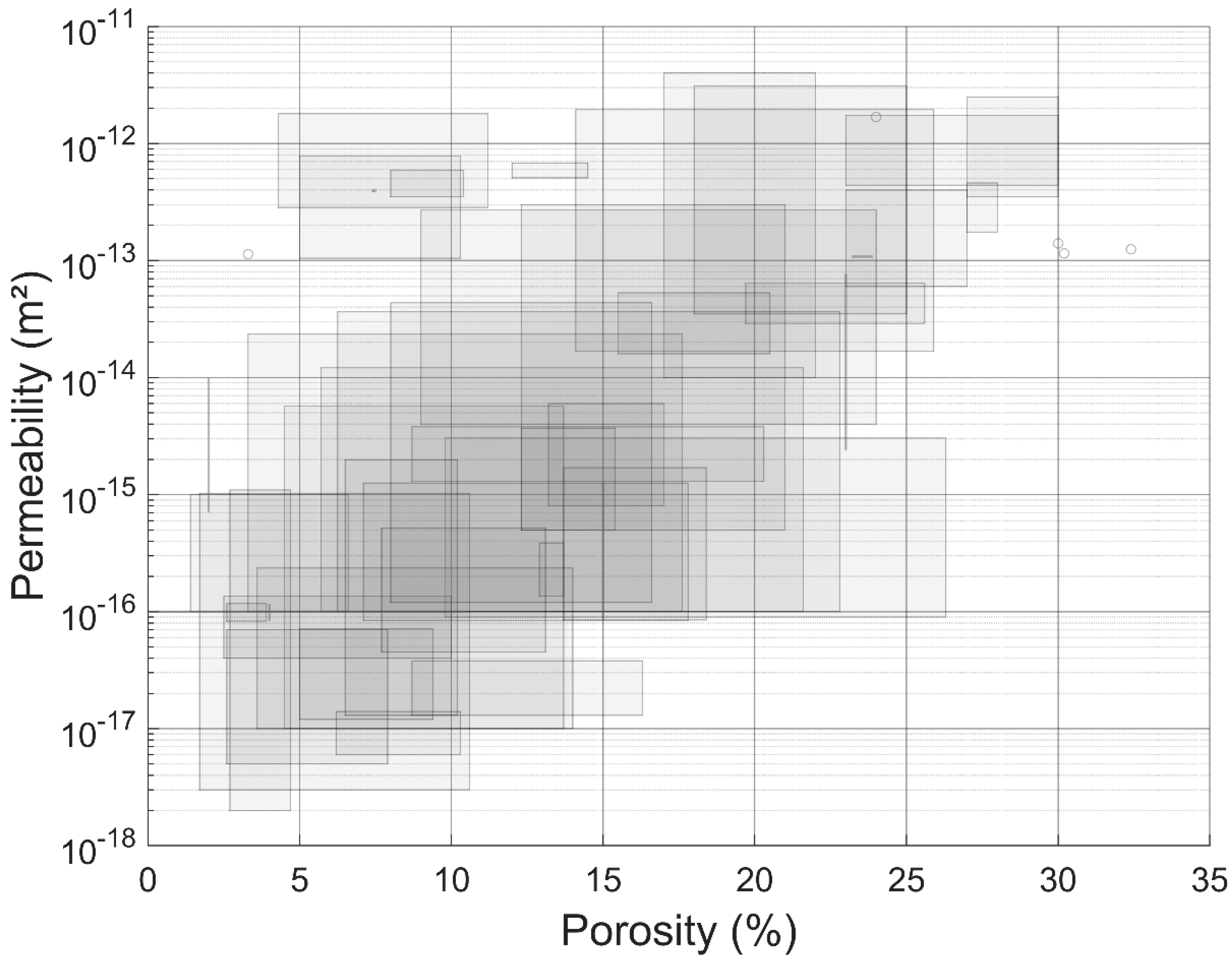
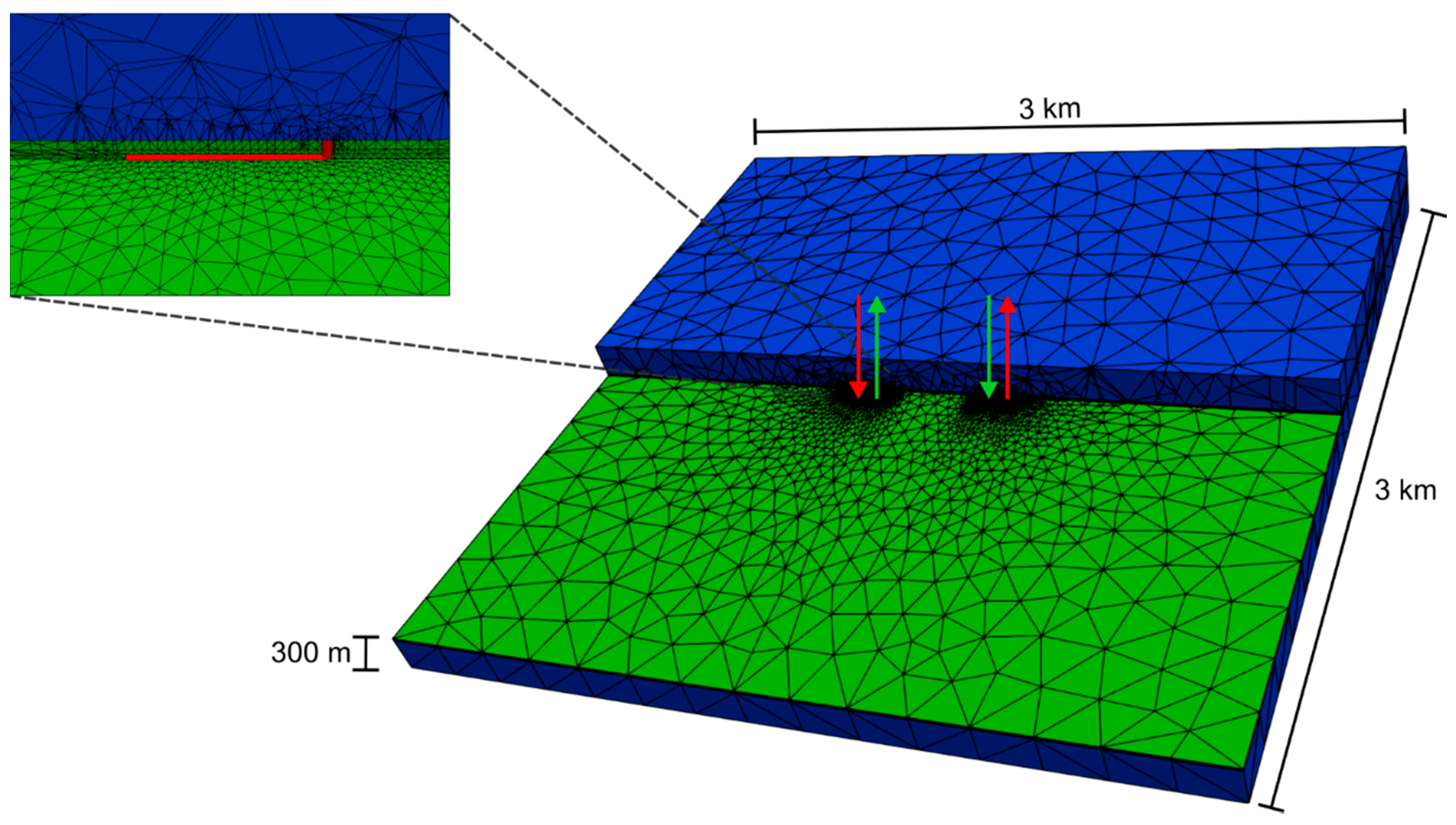





| Parameter | Value |
|---|---|
| Reservoir thickness (m) | 10 a |
| Reservoir permeability (m²) | 6.6 × 10−14 a |
| Thermal conductivity of the reservoir (Wm−1K−1 ) | 2.5 a |
| Thermal conductivity of the caprock (Wm−1K−1 ) | 1.4 a |
| Injection/production flow rate (Ls−1) | 2 a |
| Injection temperature of the cold well (°C) | 70 a |
| Injection temperature of the hot well (°C) | 140 a |
| Porosity (reservoir and cap rock) (-) | 0.15 a |
| Permeability of the caprock (m²) | 10−18 a |
| Volumetric heat capacity of the reservoir (MJ.m−3K−1) | 3.15 e |
| Volumetric heat capacity of the caprock (MJ.m−3K−1) | 3.3 e |
| Fluid thermal conductivity (W.m−1K−1 ) | 0.65 d |
| Fluid specific heat capacity (J.kg−1K−1 ) | 4194 |
| Fluid density (kg.m−3 ) | 1060 b |
| Fluid dynamic viscosity (Pa.s) | f(T,p) c |
| Well diameter (m) | 0.2159 a |
| Parameter | Range | ||
|---|---|---|---|
| Min | Max | ||
| Reservoir permeability (m²) | Vertical well | 6.6 × 10−15 | 3.3 × 10−13 |
| Horizontal well | 1 × 10−15 | 3.3 × 10−13 | |
| Reservoir thickness (m) | 5 | 20 | |
| Thermal conductivity (Wm−1K−1) | Reservoir (λres) | 2 | 3 |
| Cap rock (λcap) | 1 | 2 | |
| Injection/production flow rate (Ls−1) | 1 | 10 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stricker, K.; Grimmer, J.C.; Egert, R.; Bremer, J.; Korzani, M.G.; Schill, E.; Kohl, T. The Potential of Depleted Oil Reservoirs for High-Temperature Storage Systems. Energies 2020, 13, 6510. https://doi.org/10.3390/en13246510
Stricker K, Grimmer JC, Egert R, Bremer J, Korzani MG, Schill E, Kohl T. The Potential of Depleted Oil Reservoirs for High-Temperature Storage Systems. Energies. 2020; 13(24):6510. https://doi.org/10.3390/en13246510
Chicago/Turabian StyleStricker, Kai, Jens C. Grimmer, Robert Egert, Judith Bremer, Maziar Gholami Korzani, Eva Schill, and Thomas Kohl. 2020. "The Potential of Depleted Oil Reservoirs for High-Temperature Storage Systems" Energies 13, no. 24: 6510. https://doi.org/10.3390/en13246510
APA StyleStricker, K., Grimmer, J. C., Egert, R., Bremer, J., Korzani, M. G., Schill, E., & Kohl, T. (2020). The Potential of Depleted Oil Reservoirs for High-Temperature Storage Systems. Energies, 13(24), 6510. https://doi.org/10.3390/en13246510







