PV Power Prediction, Using CNN-LSTM Hybrid Neural Network Model. Case of Study: Temixco-Morelos, México
Abstract
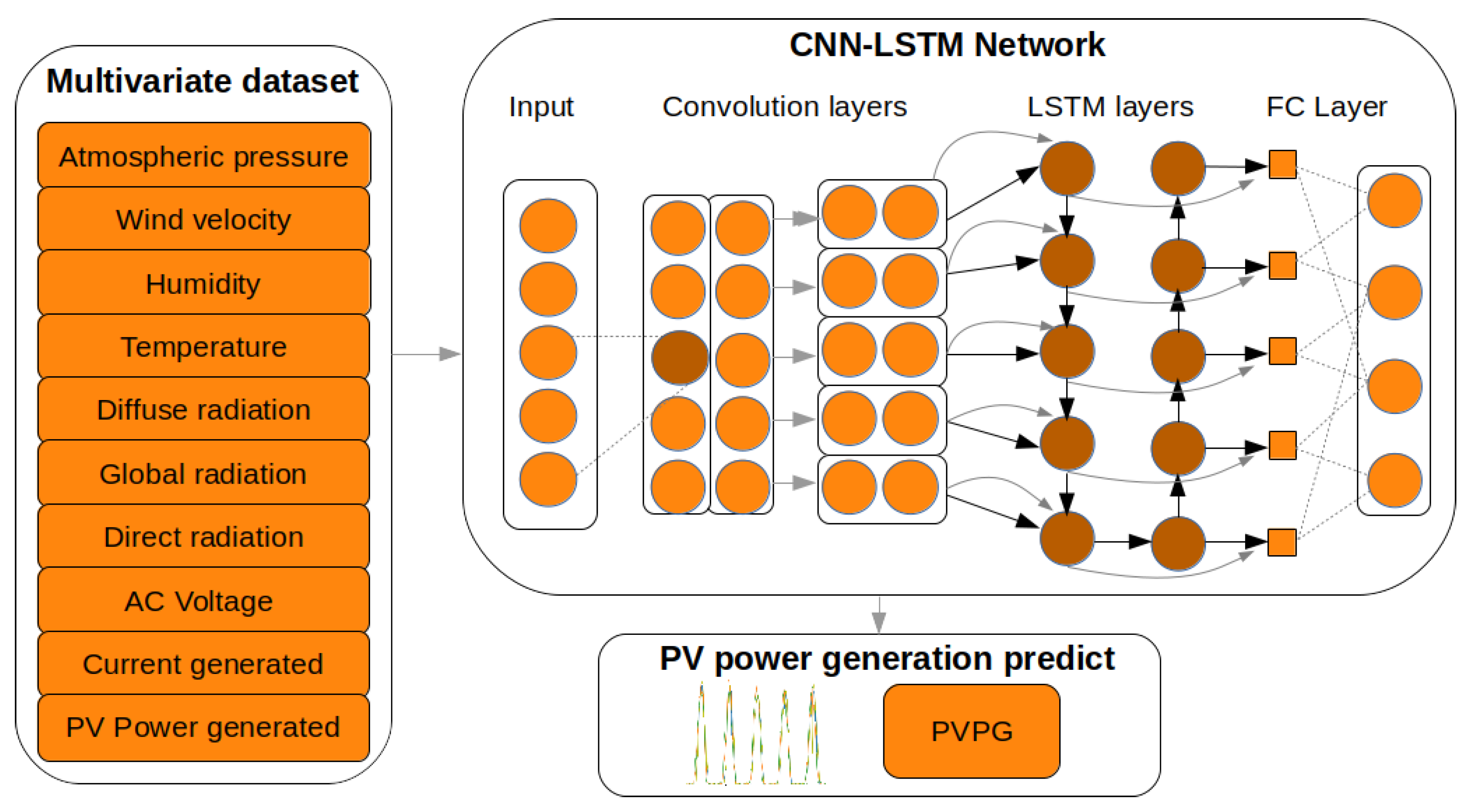
:1. Introduction
- They proposed a hybrid photo voltaic power prediction deep learning model which considers the temporal and local features.
- The temporal features of the data were first extracted (using a LSTM model) and then the local features using a CNN model.
- They reduced the complexity of the model by selecting the 1D-CNN model to extract the local features, and then the data conversion link was eliminated. Therefore PV power prediction is greatly facilitated.
- They compared with other models (CNN, LSTM, CNN-LSTM), to prove the validity of the model.
2. The Dataset
3. Proposed Hybrid Model
3.1. Local Feature Learning with CNN
3.2. Temporal Feature Learning with LSTM

3.3. CNN-LSTM Hybrid Model
4. Performance Evaluation Metrics
5. Results
5.1. Performance Comparison with Other Deep Learning Models
5.2. Performance Comparison with Competitive Benchmarks
6. Conclusions
7. Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| RE | Renewable energy |
| CNN | Convolutional neural network |
| 1D-CNN | One dimension convolutional neural network |
| 5D-CNN | Five dimension convolutional neural network |
| LSTM | Long short term memory |
| ReLU | Rectified Liniar Unit |
| PV | Photo voltaic |
| PVPG | Photo voltaic power generated |
| PVSS | Photo voltaic solar system |
| SHS | Solar home system |
| JRC | Joint Research Centre |
| ANN | Artificial neural network |
| RNN | Recurrent neural network |
| DRN | Deep belief network |
| EMS | Energy management system |
| SVR | Support Vector Regression |
| ECG | Electrocardiogram |
| UNAM | Universidad Nacional Autónoma de México |
| IER | Instituto de Energías Renovables |
| TPU | Tensor Processing Unit |
References
- Data, G. Solar Photovoltaic (PV) Market, Update 2019—Global Market Size, Market Share, Average Price, Regulations, and Key Country Analysis to 2030; GlobalData: London, UK, 2019. [Google Scholar]
- Jaeger-Waldau, A. PV Status Report 2019, EUR 29938 EN; Publications Office of the European Union: Luxembourg, 2019. [Google Scholar]
- Sobri, S.; Koohi-kamali, S.; Rahim, N.A. Solar photovoltaic generation forecasting methods: A review Number of Day. Energy Convers. Manag. 2020, 156, 459–497. [Google Scholar] [CrossRef]
- Soltowski, B.; Campos-gaona, D.; Strachan, S.; Anaya-lara, O. Bottom-Up Electrification Introducing New Smart Grids Architecture—Concept Based on Feasibility Studies Conducted in Rwanda. Energies 2019, 12, 2439. [Google Scholar] [CrossRef] [Green Version]
- Inegi; Sener, C. Encuesta Nacional Sobre Consumo de Energéticos en Viviendas Particulares. ENCEVI, 2018 Consulted on June 2020. Available online: https://www.inegi.org.mx/contenidos/programas/encevi/2018/doc/encevi2018_presentacion_resultados.pdf (accessed on 10 June 2020).
- Bahaj, A.; Blunden, L.; Kanani, C.; James, P.; Kiva, I.; Matthews, Z.; Price, H.; Essendi, H.; Falkingham, J.; George, G. The Impact of an Electrical Mini-grid on the Development of a Rural Community in Kenya. Energies 2019, 12, 778. [Google Scholar] [CrossRef] [Green Version]
- Khorasany, M.; Donald Azuatalam, R.G.A.L.; Razzaghi, R. Transactive Energy Market for Energy Management in Microgrids: The Monash Microgrid Case Study. Energies 2020, 13, 2010. [Google Scholar] [CrossRef]
- Mengelkamp, E.; Kessler, S.; Gärttner, J.; Rock, K.; Orsini, L.; Weinhardt, C. Designing microgrid energy markets. Appl. Energy 2017, 210, 870–880. [Google Scholar] [CrossRef]
- El-baz, W.; Tzscheutschler, P.; Wagner, U. Integration of energy markets in microgrids: A double-sided auction with device-oriented bidding strategies. Appl. Energy 2019, 241, 625–639. [Google Scholar] [CrossRef]
- Bahrami, S.; Amini, M.H. A Decentralized Framework for Real-Time Energy Trading in Distribution Networks with Load and Generation Uncertainty. arXiv 2017, arXiv:1705.02575v1. [Google Scholar]
- Blaga, R.; Sabadus, A.; Stefu, N.; Dughir, C.; Paulescu, M. A current perspective on the accuracy of incoming solar energy forecasting. Prog. Energy Combust. Sci. 2019, 70, 119–144. [Google Scholar] [CrossRef]
- Haji, R.; Zargar, M.; Yaghmaee, M.H.; Member, S. Development of a Markov-Chain-Based Solar Generation Model for Smart Microgrid Energy Management System. IEEE Trans. Sustain. Energy 2020, 11, 736–745. [Google Scholar]
- Gao, M.; Wang, K.; Chain, A.C.T.M. Probabilistic Model Checking for Green Energy Router System in Energy Internet. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017. [Google Scholar]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Chandler, S.A.; Hughes, J.G. Smart Grid Distribution Prediction and Control Using Computational Intelligence. In Proceedings of the 2013 1st IEEE Conference on Technologies for Sustainability (SusTech), Portland, OR, USA, 1–2 August 2013; pp. 86–89. [Google Scholar]
- Gómez-Gil, P.; Ramírez-Cortes, J.M.; Pomares Hernández, S.E.; Alarcón-Aquino, V. A neural network scheme for long-term forecasting of chaotic time series. Neural Process. Lett. 2011, 33, 215–233. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Mahmoud, K. Accurate photovoltaic power forecasting models using deep LSTM-RNN. Neural Comput. Appl. 2019, 31, 2727–2740. [Google Scholar] [CrossRef]
- Ba, Ü.; Filik, T. Wind Speed Prediction Using Artificial Neural Networks Based on Multiple Local Measurements in Eskisehir. Energy Procedia 2017, 107, 264–269. [Google Scholar]
- Le, T.; Vo, M.T.; Vo, B.; Hwang, E.; Rho, S. Improving Electric Energy Consumption Prediction. Appl. Sci. 2019, 9, 4237. [Google Scholar] [CrossRef] [Green Version]
- Muralitharan, K.; Sakthivel, R.; Vishnuvarthan, R. Neural Network based Optimization Approach for Energy Demand Prediction in Smart Grid AC PT US CR. Neurocomputing 2017. [Google Scholar] [CrossRef]
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Diffusion convolutional recurrent neural network: Data-driven traffic forecasting. In Proceedings of the 6th International Conference on Learning Representations, ICLR 2018—Conference Track Proceedings, Vancouver, BC, Canada, 30 April–3 May 2018; pp. 1–16. [Google Scholar]
- Al-Dahidi, S.; Ayadi, O.; Adeeb, J.; Alrbai, M.; Qawasmeh, B.R. Extreme Learning Machines for Solar Photovoltaic Power Predictions. Energies 2018, 11, 2725. [Google Scholar] [CrossRef] [Green Version]
- Tang, Q.; Yang, M. ST-LSTM: A Deep Learning Approach Combined Spatio-Temporal Features for Short-Term Forecast in Rail Transit. J. Adv. Transp. 2019, 2019, 8392592. [Google Scholar] [CrossRef] [Green Version]
- Madondo, M.; Gibbons, T. Learning and Modeling Chaos Using LSTM Recurrent Neural Networks. In Proceedings of the Midwest Instruction and Computing Symposium, Duluth, Minnesota, 6–7 April 2018. [Google Scholar]
- Kim, T.Y.; Cho, S.B. Predicting residential energy consumption using CNN-LSTM neural networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Wang, K.; Qi, X.; Liu, H. Photovoltaic power forecasting based LSTM-Convolutional Network. Energy 2019, 189, 116225. [Google Scholar] [CrossRef]
- Alex, G.; Schmidhuber, J. Offline Handwriting Recognition with Multidimensional Recurrent Neural Networks. In Proceedings of the NIPS Proceedings 2008, Vancouver, BC, Canada, 8–11 December 2008. [Google Scholar]
- Sainath, T.N.; Vinyals, O.; Senior, A.; Sak, H. Convolutional, long short-term memory, fully connected deep neural networks. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015. [Google Scholar]
- Solarimetric and Weather Station (Esolmet). National Autonomous University of Mexico Institute of Renewable Energies. 2020. Available online: http://esolmet.ier.unam.mx/ESOLMET-IER.pdf (accessed on 10 June 2020).
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Pedro, H.T.C.; Larson, D.P.; Coimbra, C.F. A comprehensive dataset for the accelerated development and benchmarking of solar forecasting methods. J. Renew. Sustain. Energy 2019, 11, 036102. [Google Scholar] [CrossRef] [Green Version]
- Donahue, J.; Hendricks, L.A.; Guadarrama, S.; Rohrbach, M.; Venugopalan, S.; Saenko, K.; Darrell, T.; Austin, U.T.; Lowell, U.; Berkeley, U.C. Long-term Recurrent Convolutional Networks for Visual Recognition and Description. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 677–691. [Google Scholar] [CrossRef] [PubMed]
- Santos Navarrete, M. Analysis and Prediction of Electricity Consumption in the Balearic Islands. Bachelor’s Thesis, Polytechnic University of Madrid, Madrid, Spain, 2016. [Google Scholar]
- UNAM, M.A.T.R. ESOLMET2019. Github. 2020. Available online: https://github.com/mariotovarrosas/ESOLMET2019 (accessed on 10 June 2020).
- Yang, D. A guideline to solar forecasting research practice: Reproducible, operational, probabilistic or physically-based, ensemble, and skill (ROPES). J. Renew. Sustain. Energy 2019, 11, 022701. [Google Scholar] [CrossRef]
- Al-Messabi, N.; Yun, L.; El-Amin, I.; Goh, C. Forecasting of photovoltaic power yield using dynamic neural networks. In Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, Australia, 10–15 June 2012. [Google Scholar]
- Li, G.; Xie, S.; Wang, B.; Xin, J.; Li, Y.; Du, S. Photovoltaic Power Forecasting With a Hybrid Deep Learning Approach. IEEE Access 2020, 8, 175871–175880. [Google Scholar] [CrossRef]
- Mordjaoui, M.; Haddad, S.; Medoued, A.; Laouafi, A. Electric load forecasting by using dynamic neural network. Int. J. Hydrog. Energy 2017, 42, 17655–17663. [Google Scholar] [CrossRef]
- Widergren, S. A Society of Devices. IEEE 2016, 14, 34–45. [Google Scholar]
- Google. Coral USB Accelerator Consulted on August 2020. Available online: https://coral.ai/products/accelerator/ (accessed on 20 August 2020).
- Haghifam, S.; Zare, K.; Abapour, M.; Muñoz-delgado, G. A Stackelberg Game-Based Approach for Transactive Energy Management in Smart Distribution Networks. Energies 2020, 13, 3621. [Google Scholar] [CrossRef]
- Hammerstrom, D.J.; Ngo, H. A Transactive Network Template for Decentralized Coordination of Electricity. In Proceedings of the 2019 IEEE PES Transactive Energy Systems Conference (TESC), Minneapolis, MN, USA, 8–11 July 2019; pp. 1–5. [Google Scholar]
- Ozmen, O.; Nutaro, J.; Starke, M.; Roberts, L.; Kou, X.; Im, P.; Dong, J.; Li, F.; Kuruganti, T.; Zandi, H. Power Grid Simulation Testbed for Transactive Energy Management Systems. Sustainability 2020, 12, 4402. [Google Scholar] [CrossRef]












| Layer | Configuration | Activation Function | |
|---|---|---|---|
| Convolution 1 | filters = 64; kernel size = 3 | ReLU | loss function = mse |
| Max-pooling 1 | kernel size = 2; stride = 2 | ||
| Convolution 2 | filters = 128; kernel size = 3 | ReLU | optimizer = adam |
| Max-pooling 2 | kernel size = 2; stride = 2 | ||
| Convolution 3 | filters = 256; kernel size = 3 | ReLU | batch size = 64 |
| Max-pooling 3 | kernel size = 2; stride = 2 | ||
| Convolution 4 | filters = 128; kernel size = 3 | ReLU | |
| Max-pooling 4 | kernel size = 2; stride = 2 | ||
| Convolution 5 | filters = 64; kernel size = 3 | ReLU | |
| Max-pooling 5 | kernel size = 2; stride = 2 | ||
| LSTM 1 | Units = 64 | Tanh, Sigmoid | |
| LSTM 2 | Units = 128 | Tanh, Sigmoid | |
| LSTM 3 | Units = 256 | Tanh, Sigmoid | |
| LSTM 4 | Units = 128 | Tanh, Sigmoid | |
| LSTM 5 | Units = 64 | Tanh, Sigmoid | |
| Dropout | dropout = 0.1 | ||
| Fully connected | Neurons = 2048 | ||
| Fully connected | Neurons = 1024 |
| Model | MSE | RMSE | MAE |
|---|---|---|---|
| 5D-LSTM | 0.0854788623 | 0.2923676835 | 0.1666727318 |
| 2D CNN-LSTM | 0.059041463 | 0.242984493 | 0.1410550836 |
| 5D CNN-LSTM | 0.006897012 | 0.083048253 | 0.0519295306 |
| Model | Time [s] |
|---|---|
| 5D-LSTM | 9.1394 |
| 2D CNN-LSTM | 8.0362 |
| 5D CNN-LSTM | 69.1148 |
| Model | MSE | RMSE | MAE |
|---|---|---|---|
| Ridge | 0.689931245 | 0.830620999 | 5.270156623 |
| Lasso | 0.626782312 | 0.791695845 | 4.928345520 |
| 5D CNN-LSTM | 0.006897012 | 0.083048251 | 0.0519295306 |
| Prediction horizon = 10 min. | |||
| Ridge | 1.397775392 | 1.182275514 | 10.24442325 |
| Lasso | 1.288235656 | 1.135004694 | 9.10778134 |
| 5D CNN-LSTM | 0.050930126 | 0.225677041 | 0.589563061 |
| Prediction horizon = 30 min. | |||
| Ridge | 3.155511992 | 1.776376084 | 23.83114626 |
| Lasso | 2.984087426 | 1.727451135 | 21.17831734 |
| 5D CNN-LSTM | 0.21093012 | 0.459271299 | 1.7129381706 |
| Prediction horizon = 60 min. | |||
| Ridge | 4.597775392 | 2.144242381 | 39.22693581 |
| Lasso | 4.388235656 | 2.094811603 | 34.78419132 |
| 5D CNN-LSTM | 0.531245673 | 0.728866018 | 4.691195306 |
| Prediction horizon = 90 min. | |||
| Ridge | 6.209805443 | 2.491948122 | 41.22371890 |
| Lasso | 6.008834922 | 2.451292500 | 40.10123278 |
| 5D CNN-LSTM | 1.121145975 | 1.058841808 | 10.014495238 |
| Prediction horizon = 120 min. | |||
| Ridge | 8.158007231 | 2.856222545 | 50.532978262 |
| Lasso | 7.989883492 | 2.826638196 | 50.1027657134 |
| 5D CNN-LSTM | 2.084572014 | 1.443804702 | 20.012299575 |
| Prediction horizon = 150 min. | |||
| Ridge | 11.01253333 | 3.318513723 | 61.82278104 |
| Lasso | 10.87665156 | 3.297976888 | 60.16298833 |
| 5D CNN-LSTM | 4.231144792 | 2.056974669 | 29.059911306 |
| Prediction horizon = 180 min. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tovar, M.; Robles, M.; Rashid, F. PV Power Prediction, Using CNN-LSTM Hybrid Neural Network Model. Case of Study: Temixco-Morelos, México. Energies 2020, 13, 6512. https://doi.org/10.3390/en13246512
Tovar M, Robles M, Rashid F. PV Power Prediction, Using CNN-LSTM Hybrid Neural Network Model. Case of Study: Temixco-Morelos, México. Energies. 2020; 13(24):6512. https://doi.org/10.3390/en13246512
Chicago/Turabian StyleTovar, Mario, Miguel Robles, and Felipe Rashid. 2020. "PV Power Prediction, Using CNN-LSTM Hybrid Neural Network Model. Case of Study: Temixco-Morelos, México" Energies 13, no. 24: 6512. https://doi.org/10.3390/en13246512






