Cell-Set Modelling for a Microtab Implementation on a DU91W(2)250 Airfoil
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Setup
2.2. MT Configurations
2.3. Cell-Set Model
3. Results
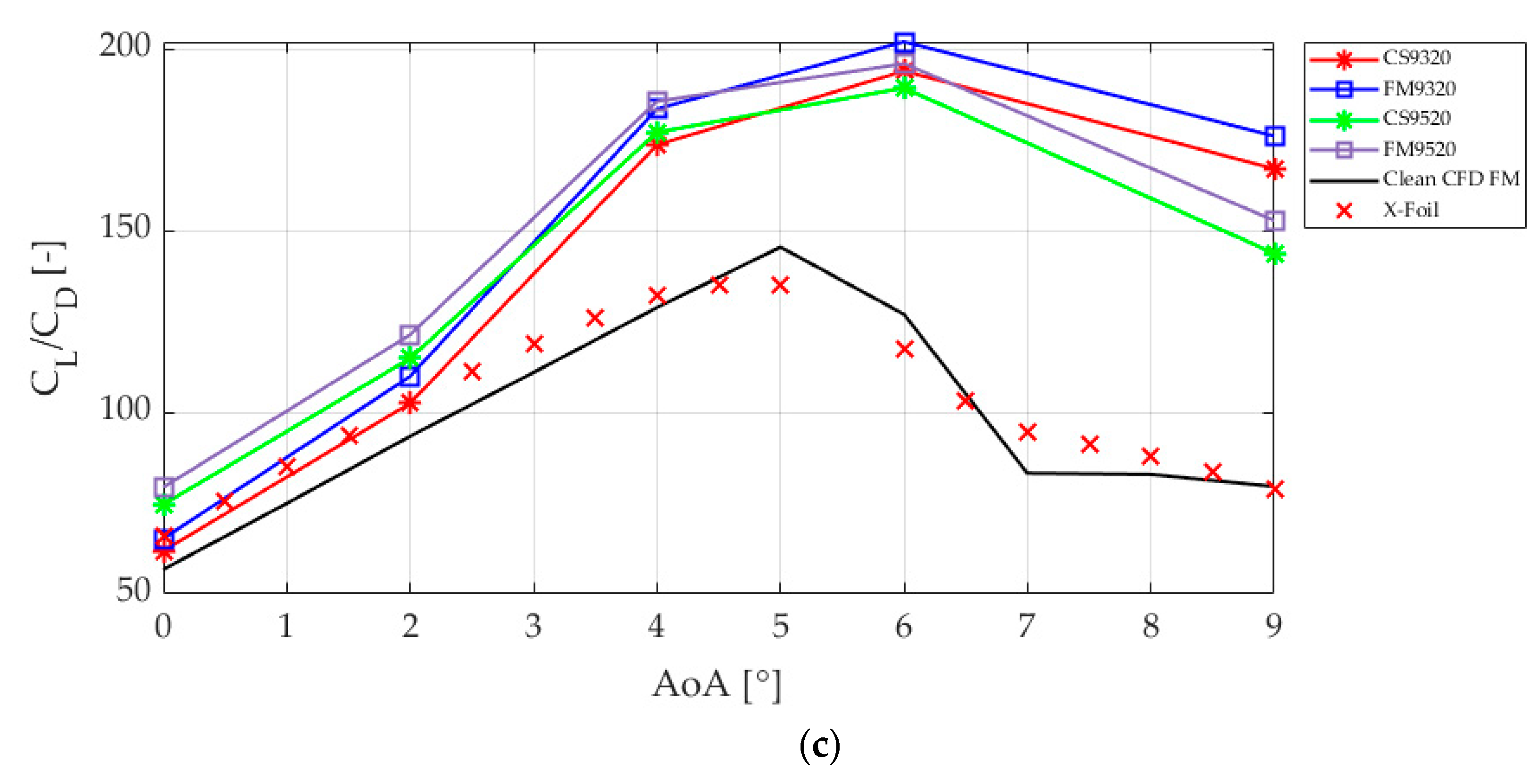
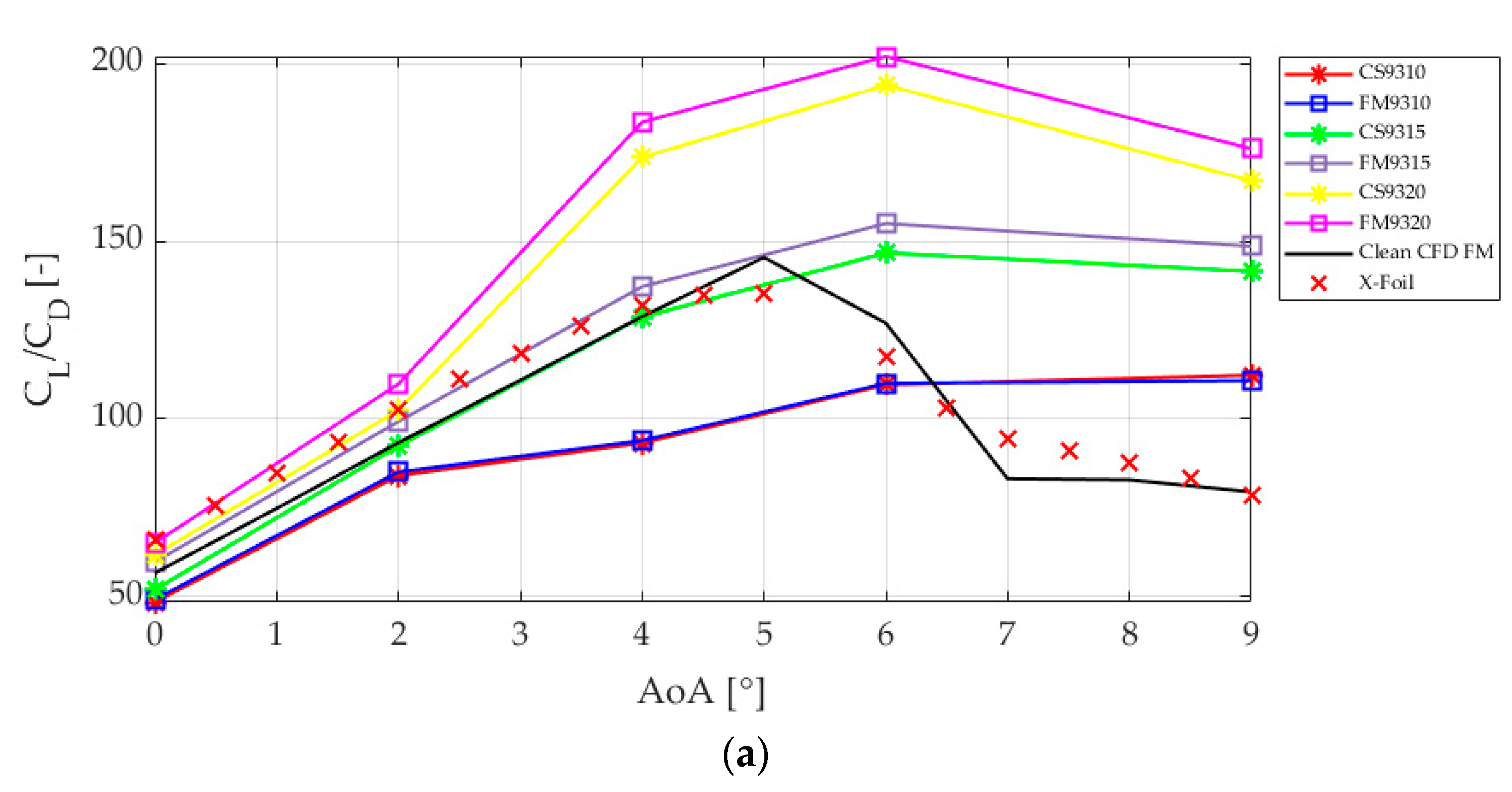
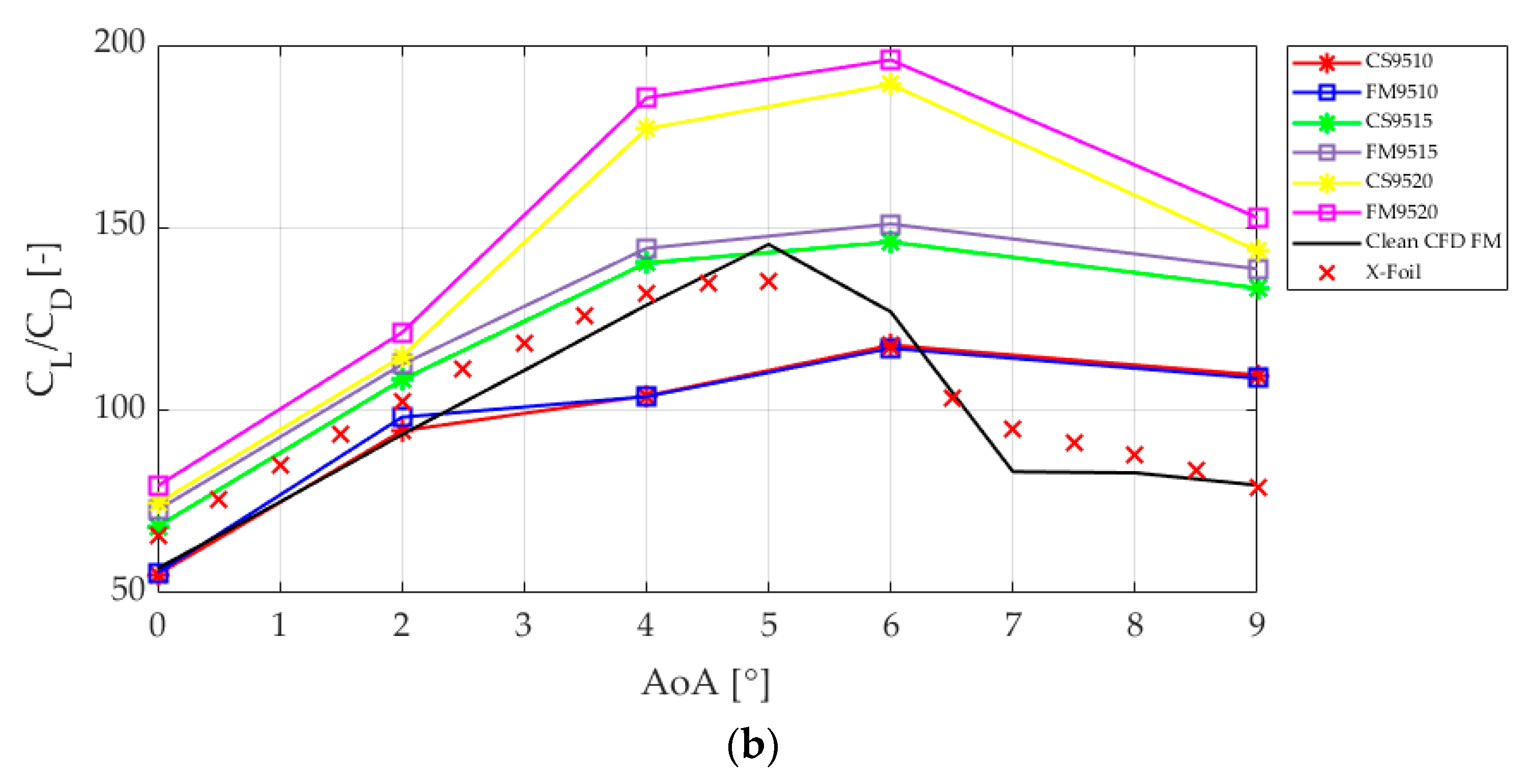
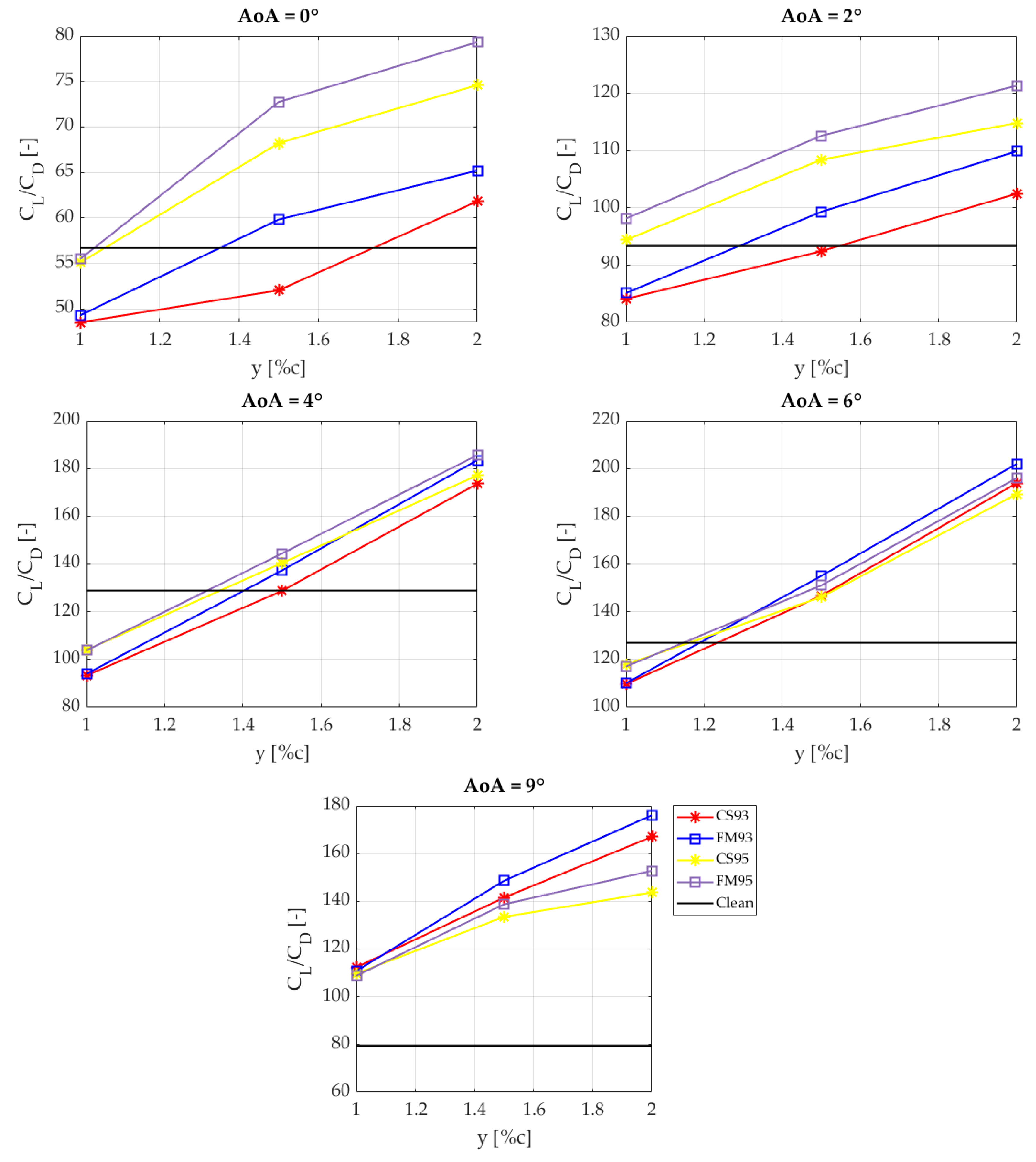
3.1. Cell-Set Model Performance for a Microtab Implementation
3.2. Error Calculations
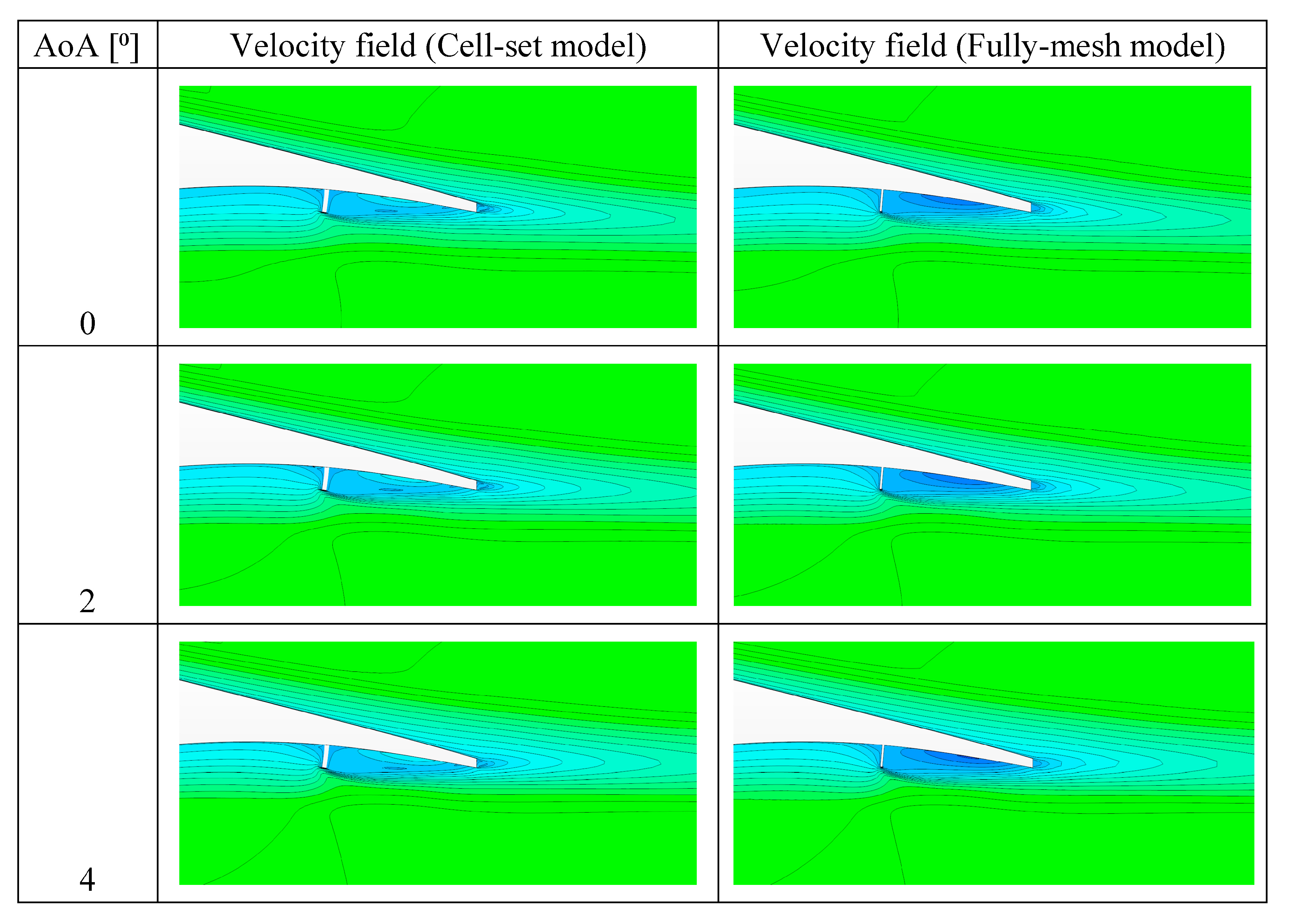
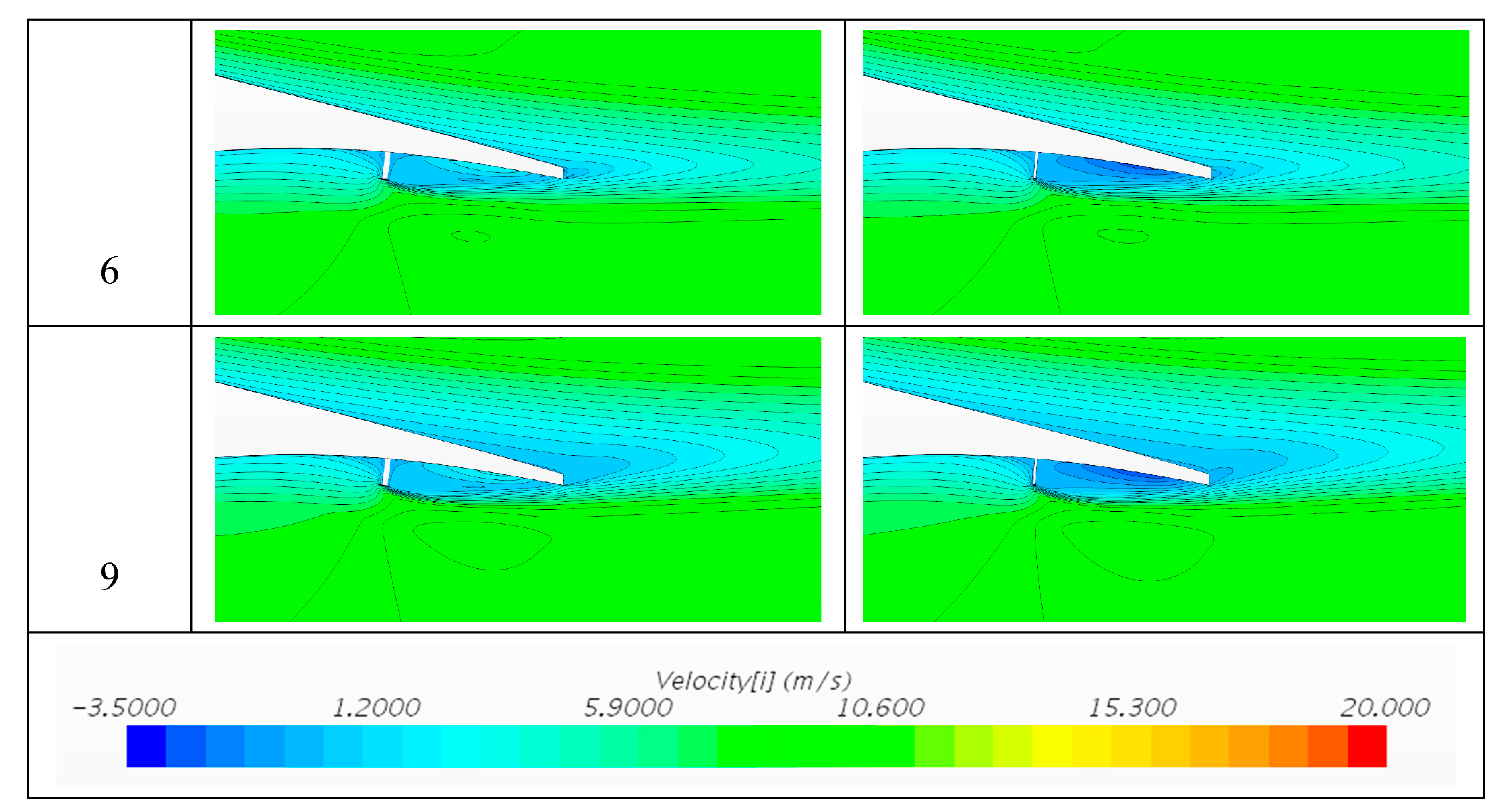
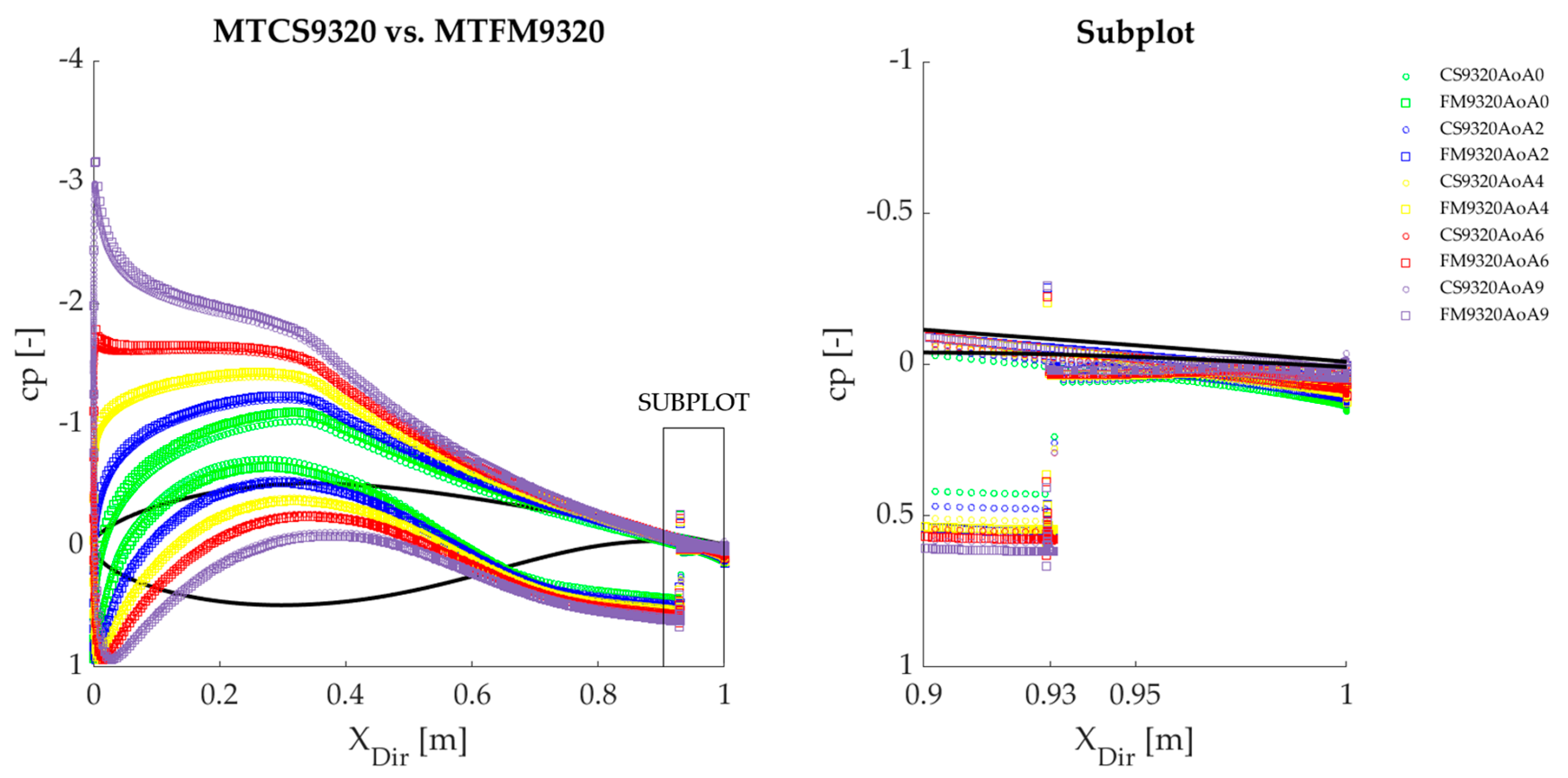
3.3. Qualitative Comparison between Cell-Set and Fully Mesh Models
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Definition | Unit | |
| CFD | Computational fluid dynamics | - |
| MT | Microtab | - |
| GF | Gurney Flap | - |
| VG | Vortex generator | - |
| Local density | kg/m3 | |
| Dynamic viscosity | Pa∙s | |
| AoA | Angle of attack | deg |
| c | Airfoil chord length | m |
| RANS | Reynolds-Averaged Navier–Stokes | - |
| SST | Shear stress transport | - |
| ANN | Artificial neural network | - |
| NREL | National Renewable Energy Laboratory | - |
| POD | Proper orthogonal decomposition | - |
| Relative error | % | |
| Average relative error | % | |
| Maximum relative error | % | |
| Global relative error | % | |
| CL | Lift coefficient | - |
| CD | Drag coefficient | - |
| cP | Pressure coefficient | - |
| Re | Reynolds number | - |
| Relative wind velocity | m/s |
References
- Howell, R.; Qin, N.; Edwards, J.; Durrani, N. Wind tunnel and numerical study of a small vertical axis wind turbine. Renew. Energy 2010, 35, 412–422. [Google Scholar] [CrossRef] [Green Version]
- Vermeer, L.J.; Sørensen, J.N.; Crespo, A. Wind turbine wake aerodynamics. Prog. Aerosp. Sci. 2003, 39, 467–510. [Google Scholar] [CrossRef]
- Aramendia Iradi, I.; Fernandez Gamiz, U.; Sancho Saiz, J.; Zulueta Guerrero, E. State of the art of active and passive flow control devices for wind turbines. DYNA Ing. E Ind. 2016, 91, 512–516. [Google Scholar] [CrossRef] [Green Version]
- Aramendia, I.; Fernandez-Gamiz, U.; Ramos-Hernanz, J.A.; Sancho, J.; Lopez-Guede, J.M.; Zulueta, E. Flow control devices for wind turbines. In Energy Harvesting and Energy Efficiency; Bizon, N., Mahdavi Tabatabaei, N., Blaabjerg, F., Kurt, E., Eds.; Lecture Notes in Energy; Springer International Publishing: Cham, Switzerland, 2017; Volume 37, pp. 629–655. ISBN 978-3-319-49874-4. [Google Scholar]
- Velte, C.M.; Hansen, M.O.L. Investigation of flow behind vortex generators by stereo particle image velocimetry on a thick airfoil near stall. Wind Energy 2013, 16, 775–785. [Google Scholar] [CrossRef]
- Godard, G.; Stanislas, M. Control of a decelerating boundary layer. Part 1: Optimization of passive vortex generators. Aerosp. Sci. Technol. 2006, 10, 181–191. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, H.; Liu, Y.; Han, S. Effects of vortex generators on a blunt trailing-edge airfoil for wind turbines. Renew. Energy 2015, 76, 303–311. [Google Scholar] [CrossRef]
- Timmer, W.A.; van Rooij, R. Summary of the Delft University wind turbine dedicated airfoils. J. Sol. Energy Eng. 2003, 125, 488–496. [Google Scholar] [CrossRef]
- Timmer, W.A.; Schaffarczyk, A.P. The effect of roughness at high Reynolds numbers on the performance of aerofoil DU 97-W-300Mod. Wind Energy 2004, 7, 295–307. [Google Scholar] [CrossRef]
- Martínez-Filgueira, P.; Fernandez-Gamiz, U.; Zulueta, E.; Errasti, I.; Fernandez-Gauna, B. Parametric study of low-profile vortex generators. Int. J. Hydrog. Energy 2017, 42, 17700–17712. [Google Scholar] [CrossRef]
- Lin, J.C. Review of research on low-profile vortex generators to control boundary-layer separation. Prog. Aerosp. Sci. 2002, 38, 389–420. [Google Scholar] [CrossRef]
- Kumar, P.M.; Samad, A. Introducing Gurney flap to Wells turbine blade and performance analysis with OpenFOAM. Ocean Eng. 2019, 187, 106212. [Google Scholar] [CrossRef]
- Alber, J.; Pechlivanoglou, G.; Paschereit, C.O.; Twele, J.; Weinzierl, G. Parametric investigation of gurney flaps for the use on wind turbine blades. In Proceedings of the Volume 9: Oil and Gas Applications; Supercritical CO2 Power Cycles; Wind Energy; American Society of Mechanical Engineers, Charlotte, NC, USA, 26–30 June 2017; p. V009T49A015. [Google Scholar]
- Aramendia, I.; Fernandez-Gamiz, U.; Zulueta, E.; Saenz-Aguirre, A.; Teso-Fz-Betoño, D. Parametric study of a gurney flap implementation in a DU91W(2)250 airfoil. Energies 2019, 12, 294. [Google Scholar] [CrossRef] [Green Version]
- Zhu, B.; Huang, Y.; Zhang, Y. Energy harvesting properties of a flapping wing with an adaptive Gurney flap. Energy 2018, 152, 119–128. [Google Scholar] [CrossRef]
- Saenz-Aguirre, A.; Fernandez-Gamiz, U.; Zulueta, E.; Ulazia, A.; Martinez-Rico, J. Optimal wind turbine operation by artificial neural network-based active gurney flap flow control. Sustainability 2019, 11, 2809. [Google Scholar] [CrossRef] [Green Version]
- Gruschwitz, E.; Schrenk, O. A Simple Method for Increasing the Lift of Airplane Wings by Means of Flaps; NASA: Washington, DC, USA, 1933. [Google Scholar]
- Van Dam, C.P.; Nakafuji, D.Y.; Bauer, C.; Standish, K.; Chao, D. Computational design and analysis of a microtab-based aerodynamic load control system for lifting surfaces. In Proceedings of the MEMS Components and Applications for Industry, Automobiles, Aerospace, and Communication II, San Jose, CA, USA, 25–31 January 2003; Volume 4981. [Google Scholar]
- Baker, J.P.; Standish, K.J.; van Dam, C.P. Two-dimensional wind tunnel and computational investigation of a microtab modified airfoil. J. Aircr. 2007, 44, 563–572. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Movahhedi, M. Wind turbine power improvement utilizing passive flow control with microtab. Energy 2018, 150, 575–582. [Google Scholar] [CrossRef]
- Cooperman, A.M.; Chow, R.; van Dam, C.P. Active load control of a wind turbine airfoil using microtabs. J. Aircr. 2013, 50, 1150–1158. [Google Scholar] [CrossRef]
- Johnson, S.J.; Baker, J.P.; van Dam, C.P.; Berg, D. An overview of active load control techniques for wind turbines with an emphasis on microtabs. Wind Energy 2010, 13, 239–253. [Google Scholar] [CrossRef]
- Sanderse, B.; Pijl, S.P.; Koren, B. Review of computational fluid dynamics for wind turbine wake aerodynamics: Review of CFD for wind turbine wake aerodynamics. Wind Energy 2011, 14, 799–819. [Google Scholar] [CrossRef] [Green Version]
- Ballesteros-Coll, A.; Fernandez-Gamiz, U.; Aramendia, I.; Zulueta, E.; Lopez-Guede, J.M. Computational methods for modelling and optimization of flow control devices. Energies 2020, 13, 3710. [Google Scholar] [CrossRef]
- Jirasek, A. Vortex-generator model and its application to flow control. J. Aircr. 2005, 42, 1486–1491. [Google Scholar] [CrossRef]
- Errasti, I.; Fernández-Gamiz, U.; Martínez-Filgueira, P.; Blanco, J. Source term modelling of vane-type vortex generators under adverse pressure gradient in OpenFOAM. Energies 2019, 12, 605. [Google Scholar] [CrossRef] [Green Version]
- Chillon, S.; Uriarte-Uriarte, A.; Aramendia, I.; Martínez-Filgueira, P.; Fernandez-Gamiz, U.; Ibarra-Udaeta, I. jBAY modeling of vane-type vortex generators and study on airfoil aerodynamic performance. Energies 2020, 13, 2423. [Google Scholar] [CrossRef]
- Fernandez, U.; Réthoré, P.-E.; Sørensen, N.N.; Velte, C.M.; Zahle, F.; Egusquiza, E. Comparison of four different models of vortex generators. In Proceedings of the EWEA 2012—European Wind Energy Conference & Exhibition; European Wind Energy Association (EWEA), Copenhagen, Denmark, 16–19 April 2012. [Google Scholar]
- Fernandez-Gamiz, U.; Gomez-Mármol, M.; Chacón-Rebollo, T. Computational modeling of gurney flaps and microtabs by POD method. Energies 2018, 11, 2091. [Google Scholar] [CrossRef] [Green Version]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical Report No. NREL/TP-500-38060; National Renewable Energy Lab.: Golden, CO, USA, 2009; p. 7. [Google Scholar]
- Siemens Star CCM+ Version 14.02.012. Available online: https://www.plm.automation.siemens.com/global/en/ (accessed on 3 February 2020).
- Sørensen, N.N.; Mendez, B.; Munoz, A.; Sieros, G.; Jost, E.; Lutz, T.; Papadakis, G.; Voutsinas, S.; Barakos, G.N.; Colonia, S.; et al. CFD code comparison for 2D airfoil flows. J. Phys. Conf. Ser. 2016, 753, 082019. [Google Scholar] [CrossRef] [Green Version]
- Fernandez-Gamiz, U.; Zulueta, E.; Boyano, A.; Ramos-Hernanz, J.; Lopez-Guede, J. Microtab design and implementation on a 5 MW wind turbine. Appl. Sci. 2017, 7, 536. [Google Scholar] [CrossRef]
- Thompson, J.F.; Warsi, Z.U.A.; Mastin, C.W. Numerical Grid Generation: Foundations and Applications; Elsevier Science (North-Holland Publishing Co.): New York, NY, USA, 1985; ISBN 978-0-444-00985-2. [Google Scholar]
- Vinokur, M. On one-dimensional stretching functions for finite-difference calculations. J. Comput. Phys. 1983, 50, 215–234. [Google Scholar] [CrossRef] [Green Version]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Kral, L.D. Recent experience with different turbulence models applied to the calculation of flow over aircraft components. Prog. Aerosp. Sci. 1998, 34, 481–541. [Google Scholar] [CrossRef]
- Reck, M. Computational Fluid Dynamics, with Detached Eddy Simulation and the Immersed Boundary Technique, Applied to Oscillating Airfoils and Vortex Generators. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 28 September 2005. [Google Scholar]
- Kooijman, H.J.T.; Lindenburg, C.; Winkelaar, D.; Hooft, E.L.V.D. Aero-Elastic Modelling of the DOWEC 6 MWpre-Design in PHATAS; DOWEC-F1W2-HJK-01-046/9; Tech. Rep. ECN-CX-01-135, DOWEC 10046_009; Energy Research Center of the Netherlands: Petten, The Netherlands, 2003. [Google Scholar]
- Lindenburg, C. Aeroelastic Modelling of the LMH64-5 Blade; DOWEC-02-KL-083/0, DOWEC 10083_001; Energy Research Center of the Netherlands: Petten, The Netherlands, 2002. [Google Scholar]


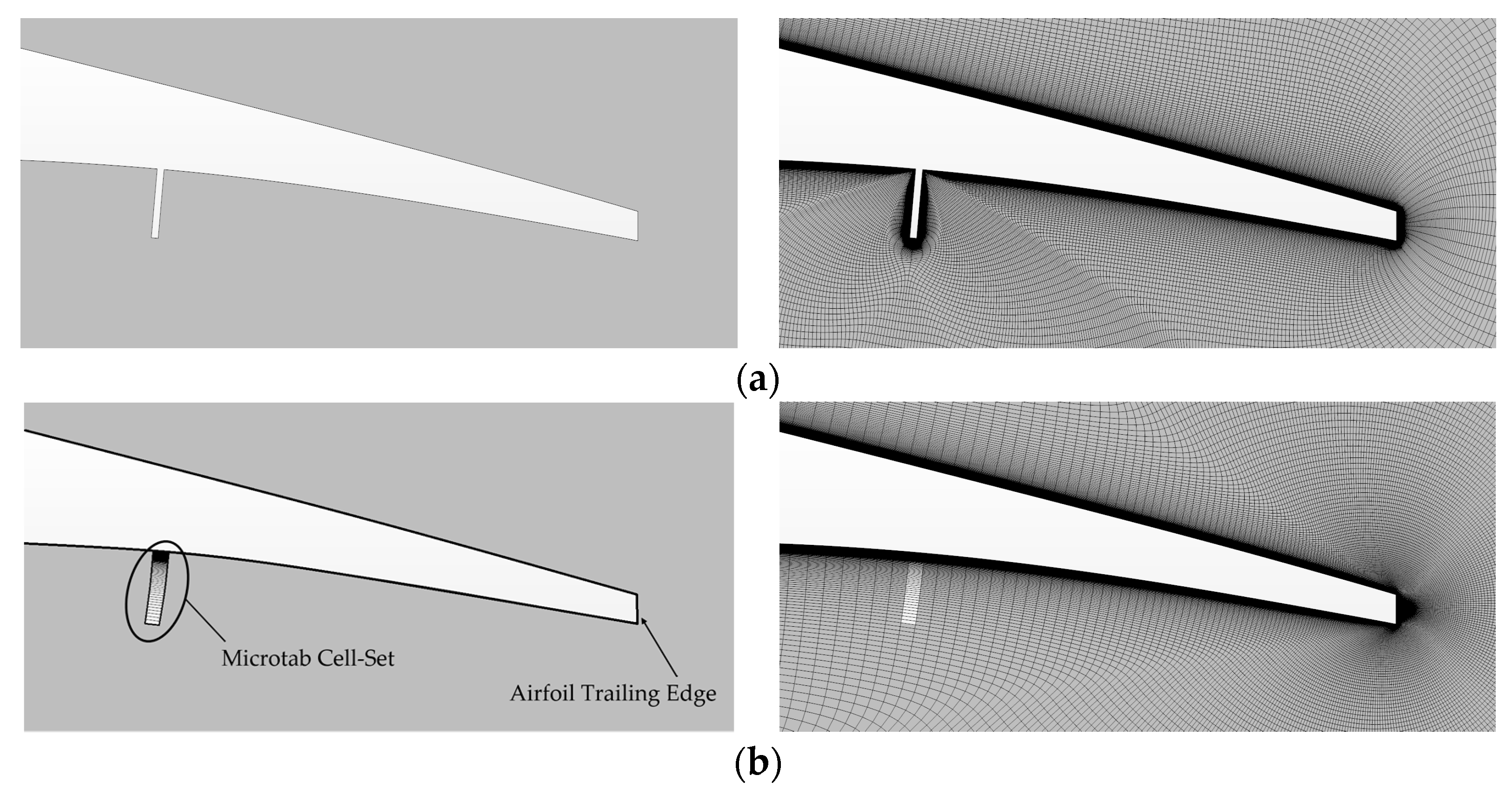

| Case | Short Ref. | x [%c] | y [%c] | Model |
|---|---|---|---|---|
| DU91W(2)250 | clean | no MT | no MT | Fully mesh |
| DU91W(2)250_MTCS9310 | CS9310 | 93 | 1.0 | Cell-set |
| DU91W(2)250_MTCS9315 | CS9315 | 93 | 1.5 | Cell-set |
| DU91W(2)250_MTCS9320 | CS9320 | 93 | 2.0 | Cell-set |
| DU91W(2)250_MTCS9510 | CS9510 | 95 | 1.0 | Cell-set |
| DU91W(2)250_MTCS9515 | CS9515 | 95 | 1.5 | Cell-set |
| DU91W(2)250_MTCS9520 | CS9520 | 95 | 2.0 | Cell-set |
| DU91W(2)250_MTFM9310 | FM9310 | 93 | 1.0 | Fully mesh |
| DU91W(2)250_MTFM9315 | FM9315 | 93 | 1.5 | Fully mesh |
| DU91W(2)250_MTFM9320 | FM9320 | 93 | 2.0 | Fully mesh |
| DU91W(2)250_MTFM9510 | FM9510 | 95 | 1.0 | Fully mesh |
| DU91W(2)250_MTFM9515 | FM9515 | 95 | 1.5 | Fully mesh |
| DU91W(2)250_MTFM9520 | FM9520 | 95 | 2.0 | Fully mesh |
| MT Case | ||||||
|---|---|---|---|---|---|---|
| AoA (°) | 9310 | 9315 | 9320 | 9510 | 9515 | 9520 |
| 0 | 1.562 | 7.332 | 5.173 | 0.728 | 6.213 | 5.953 |
| 2 | 1.188 | 6.939 | 6.741 | 3.813 | 3.699 | 5.371 |
| 4 | 0.748 | 6.231 | 5.412 | 0.211 | 2.762 | 4.568 |
| 6 | 0.351 | 5.343 | 3.996 | 0.724 | 3.250 | 3.422 |
| 9 | 1.378 | 4.741 | 5.115 | 0.822 | 3.782 | 5.946 |
| 1.045 | 7.247 | 5.288 | 1.260 | 3.941 | 5.052 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ballesteros-Coll, A.; Fernandez-Gamiz, U.; Aramendia, I.; Zulueta, E.; Ramos-Hernanz, J.A. Cell-Set Modelling for a Microtab Implementation on a DU91W(2)250 Airfoil. Energies 2020, 13, 6723. https://doi.org/10.3390/en13246723
Ballesteros-Coll A, Fernandez-Gamiz U, Aramendia I, Zulueta E, Ramos-Hernanz JA. Cell-Set Modelling for a Microtab Implementation on a DU91W(2)250 Airfoil. Energies. 2020; 13(24):6723. https://doi.org/10.3390/en13246723
Chicago/Turabian StyleBallesteros-Coll, Alejandro, Unai Fernandez-Gamiz, Iñigo Aramendia, Ekaitz Zulueta, and José Antonio Ramos-Hernanz. 2020. "Cell-Set Modelling for a Microtab Implementation on a DU91W(2)250 Airfoil" Energies 13, no. 24: 6723. https://doi.org/10.3390/en13246723
APA StyleBallesteros-Coll, A., Fernandez-Gamiz, U., Aramendia, I., Zulueta, E., & Ramos-Hernanz, J. A. (2020). Cell-Set Modelling for a Microtab Implementation on a DU91W(2)250 Airfoil. Energies, 13(24), 6723. https://doi.org/10.3390/en13246723






