Characterizing Meteorological Forecast Impact on Microgrid Optimization Performance and Design
Abstract
:1. Introduction
1.1. Meteorological Forecasting
1.2. PV Power Forecasting
1.3. Load Forecasting
1.4. Energy Management Systems
2. Microgrid Component Models
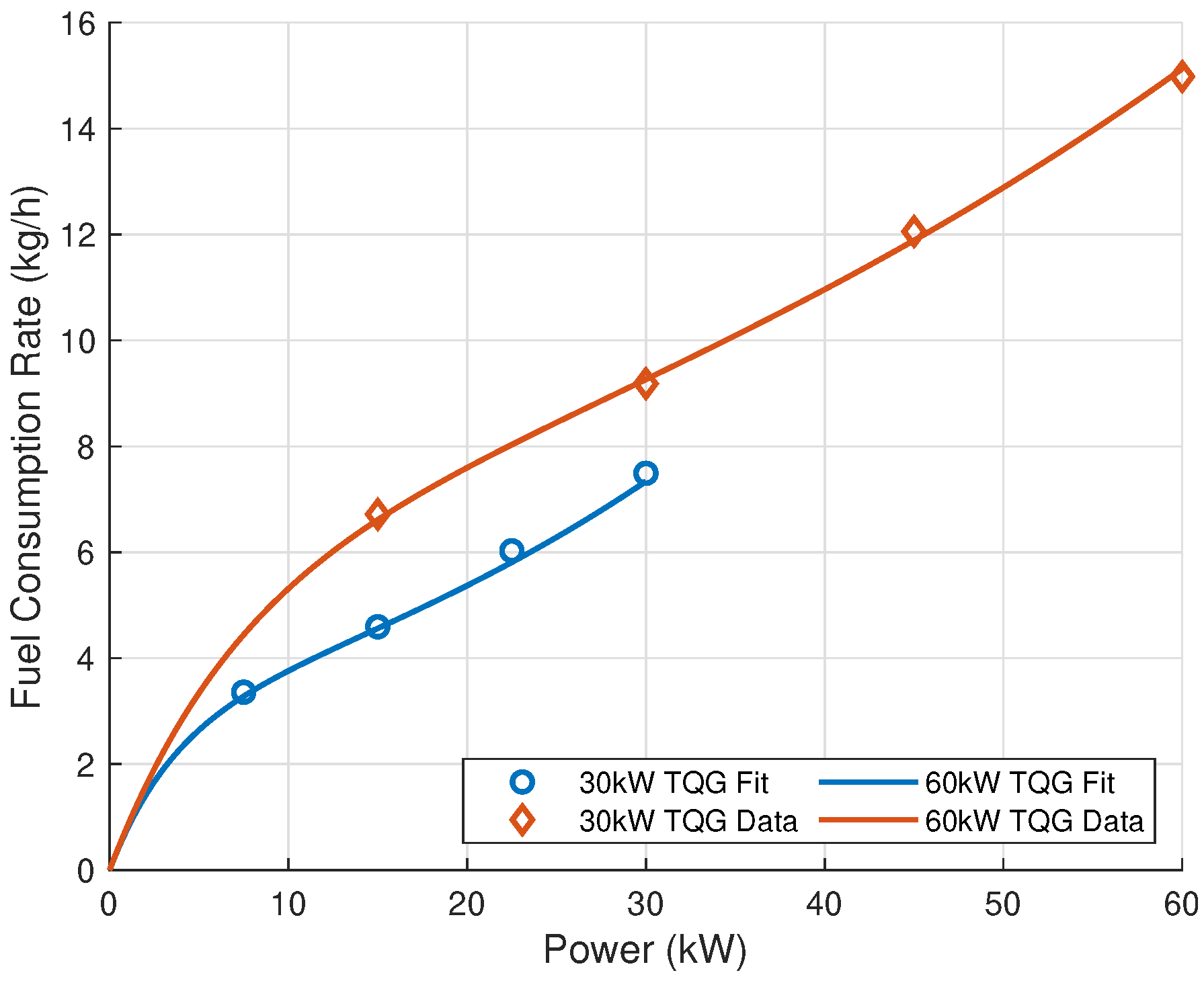
2.1. Generator Model
2.2. Energy Storage Model
2.3. Photovoltaic Array with Collocated Storage Model
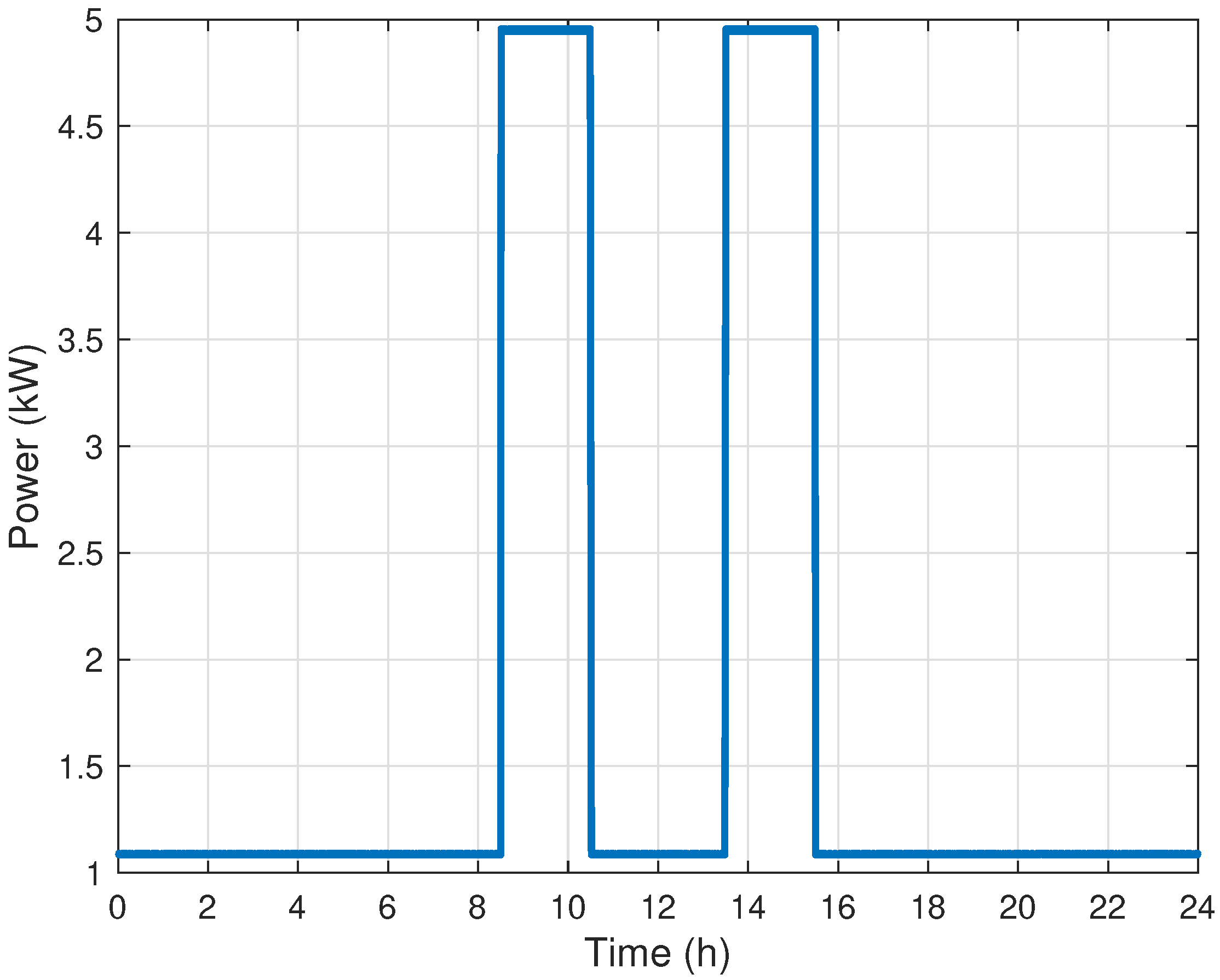
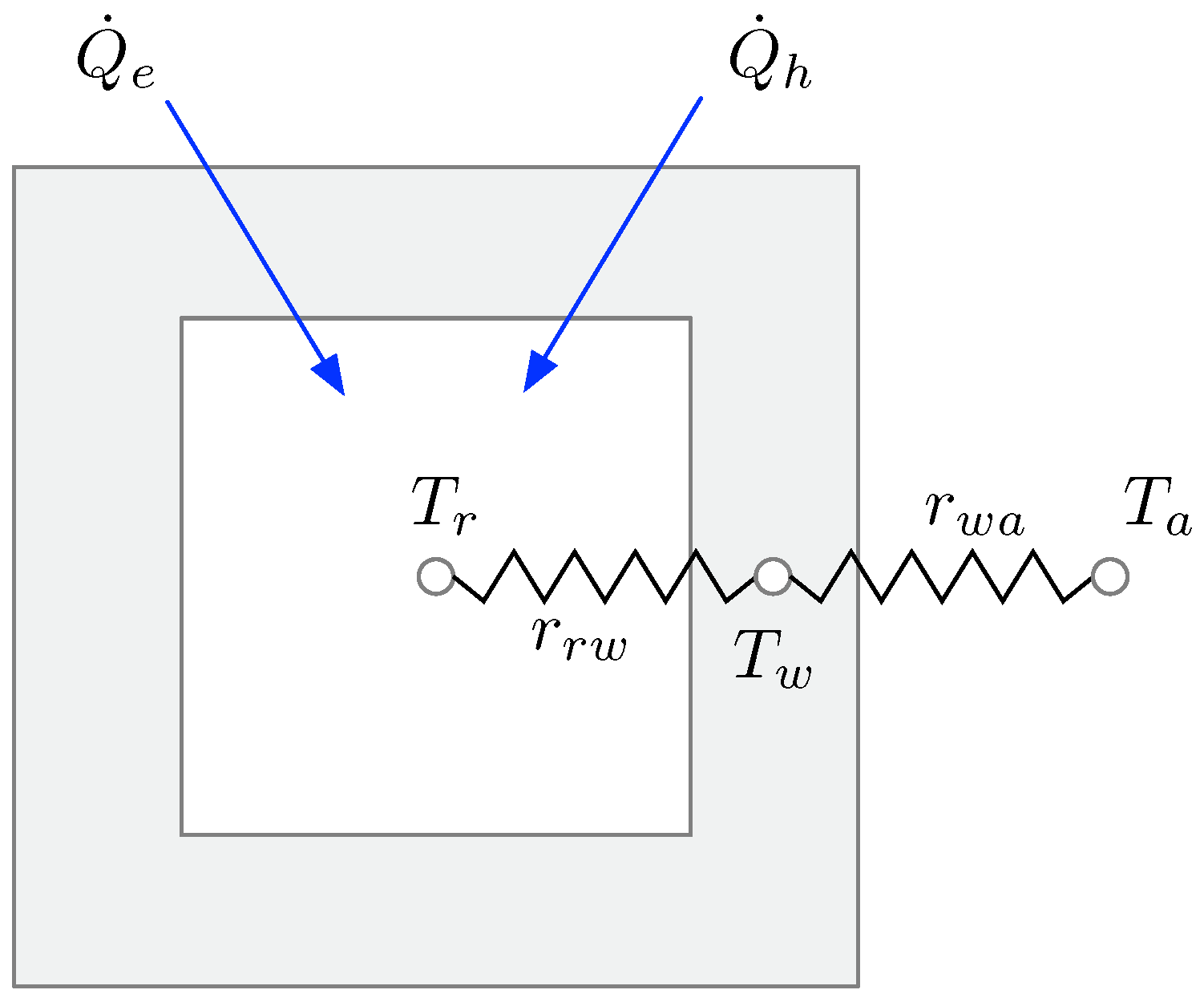
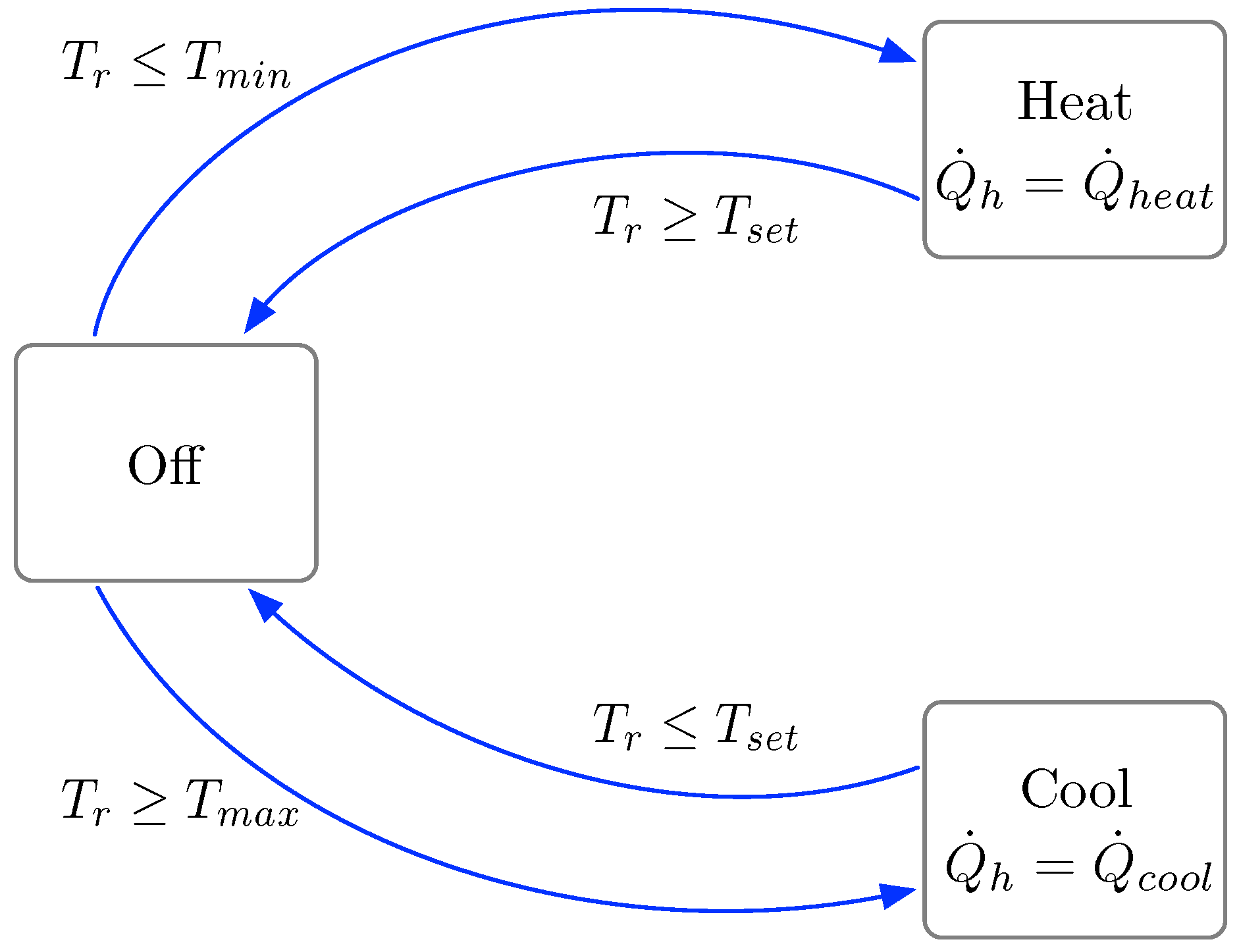
2.4. Electrical Load Model
3. Energy Management System
4. Meteorological Forecast Study
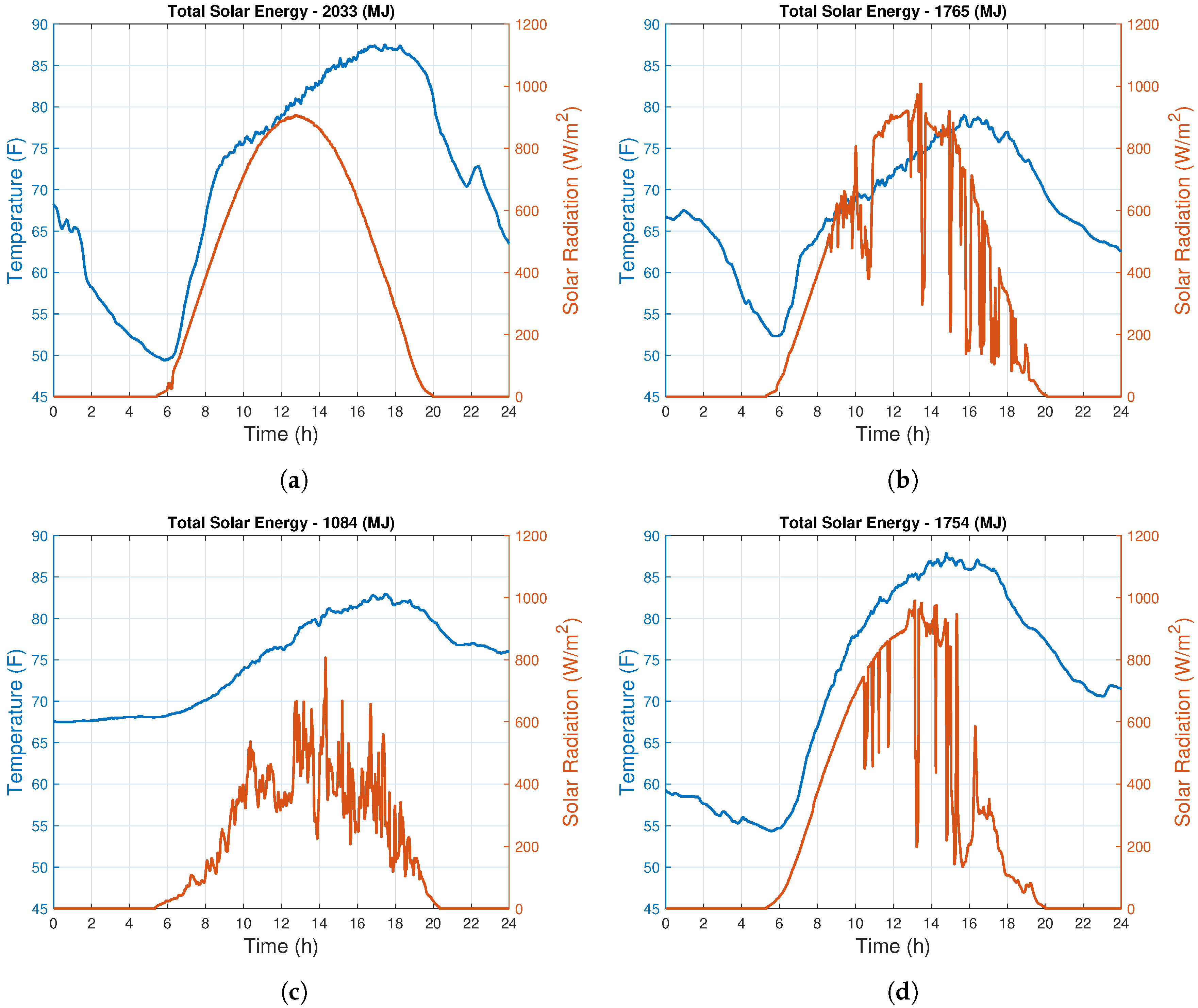
4.1. Meteorological Conditions
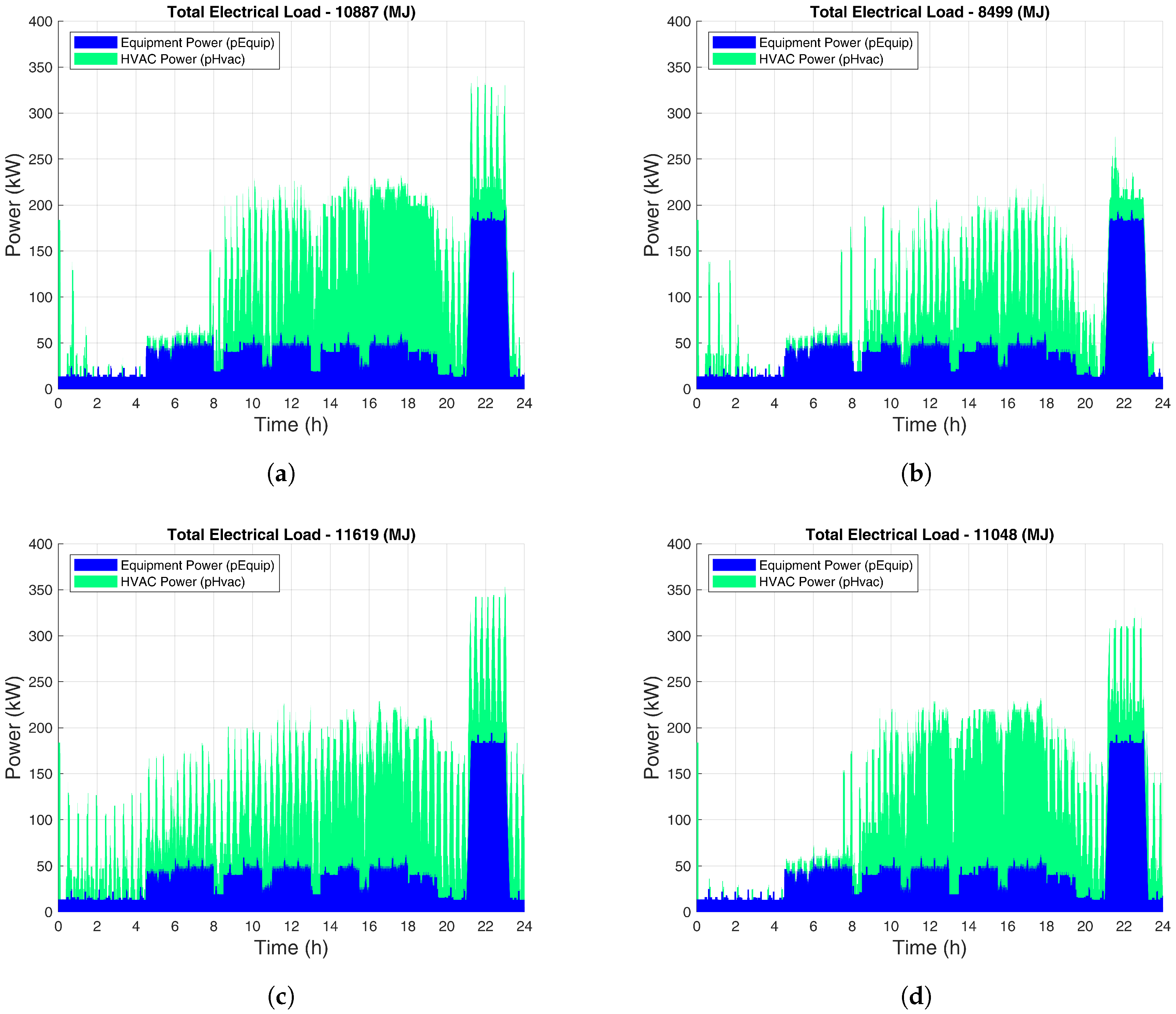
4.2. Microgrid and Electrical Load
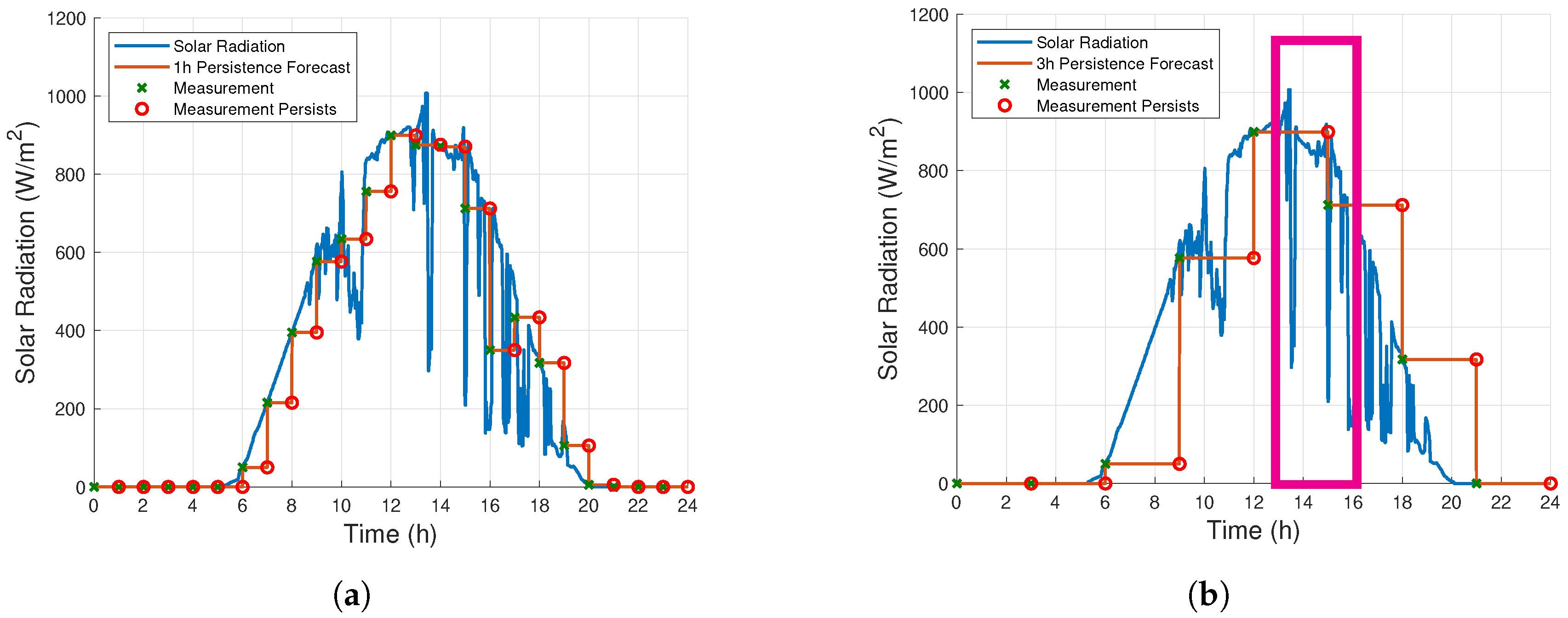
4.3. Persistence Weather Forecast (PWF)
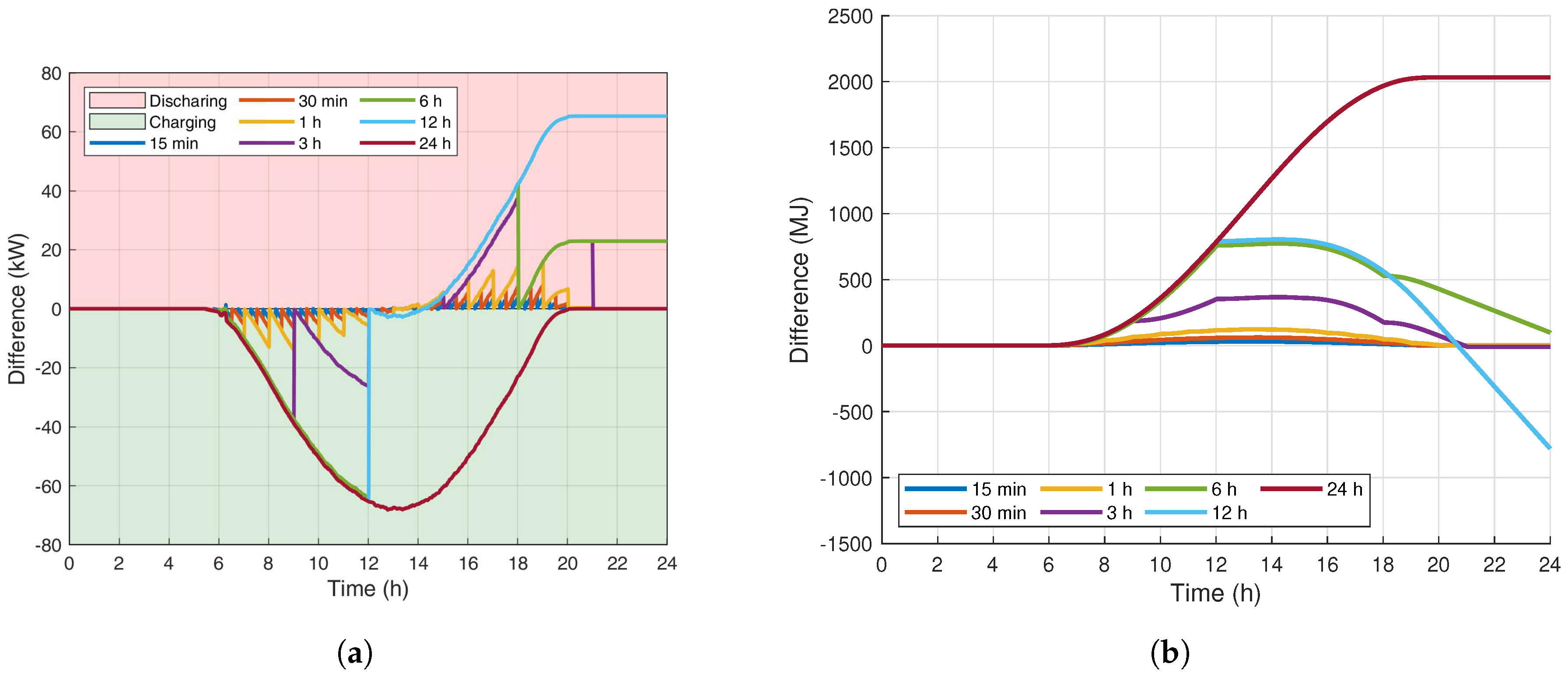
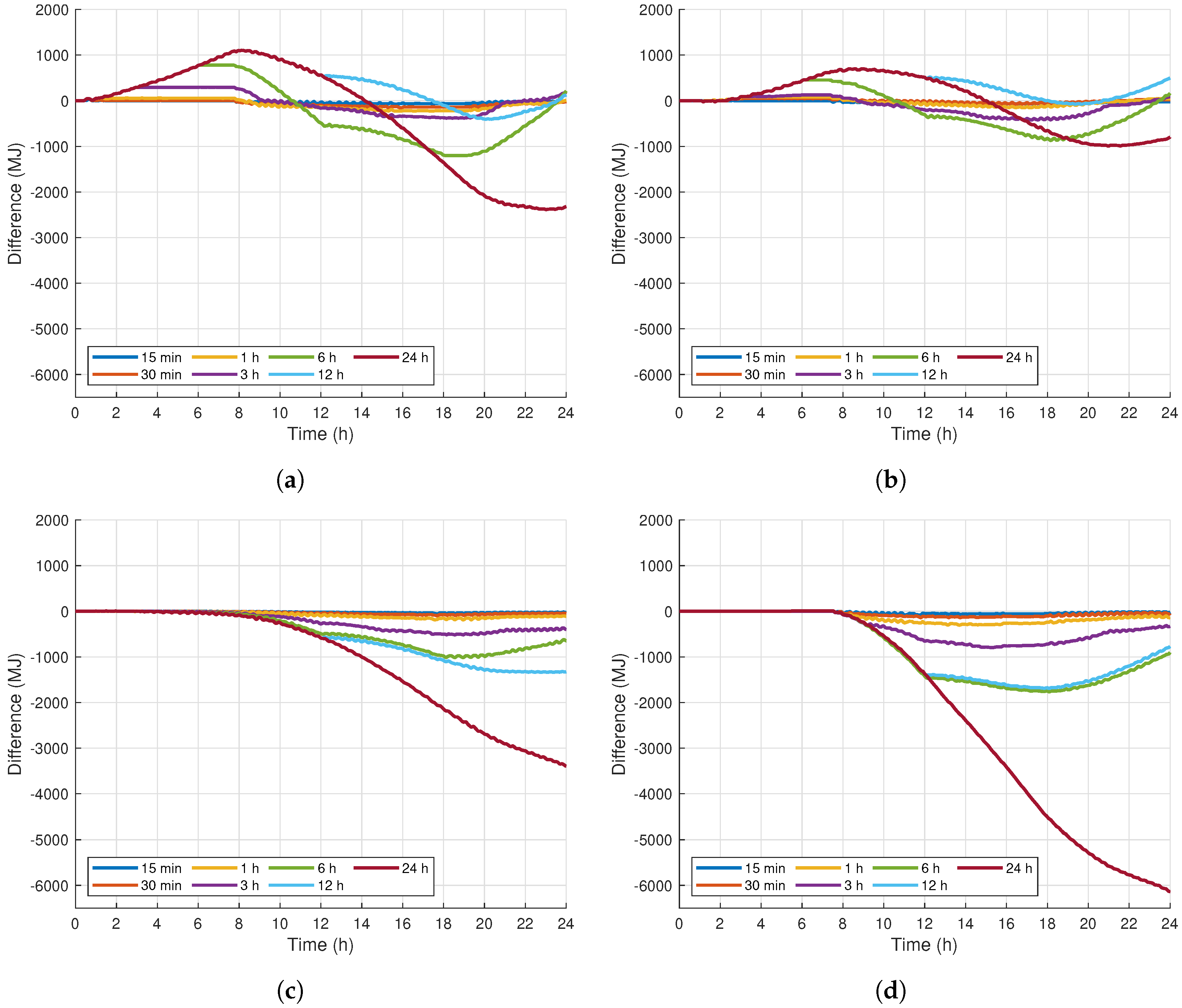
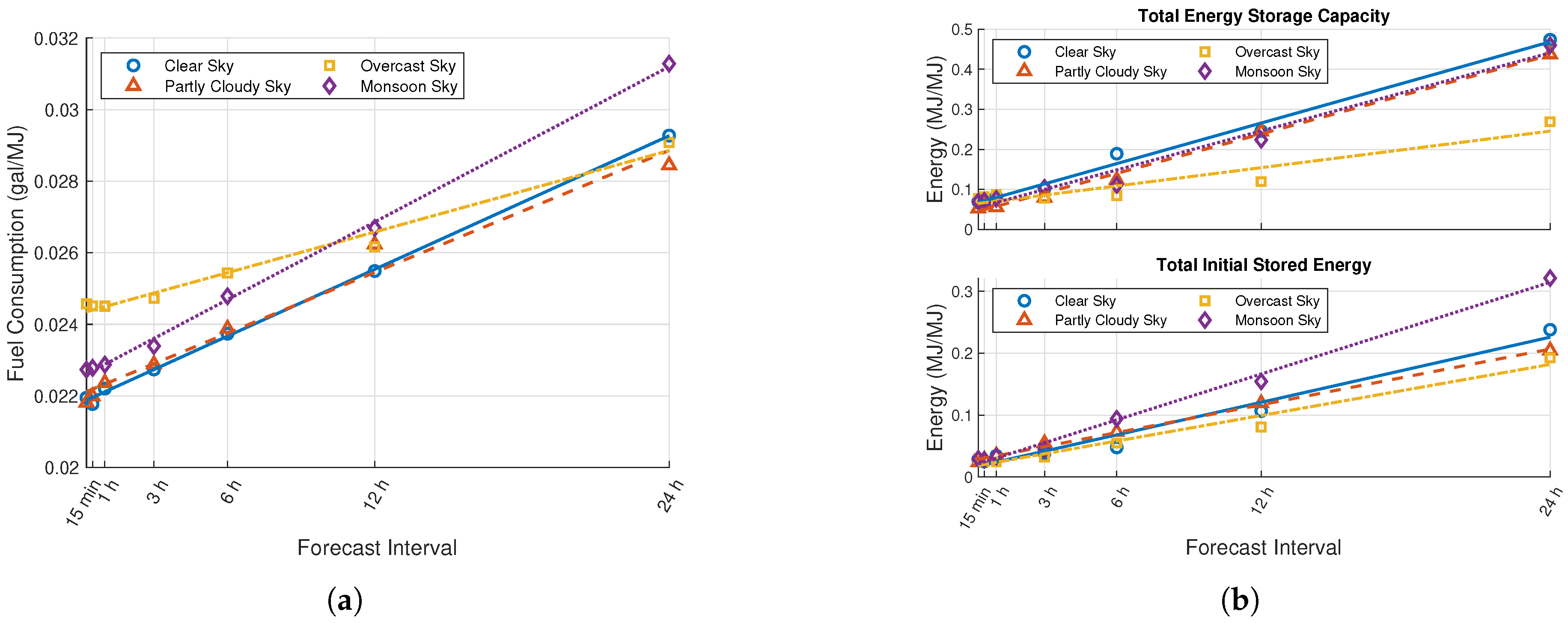
4.4. Results and Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Disclaimer
Appendix A
Appendix A.1. Partly Cloudy Sky Results
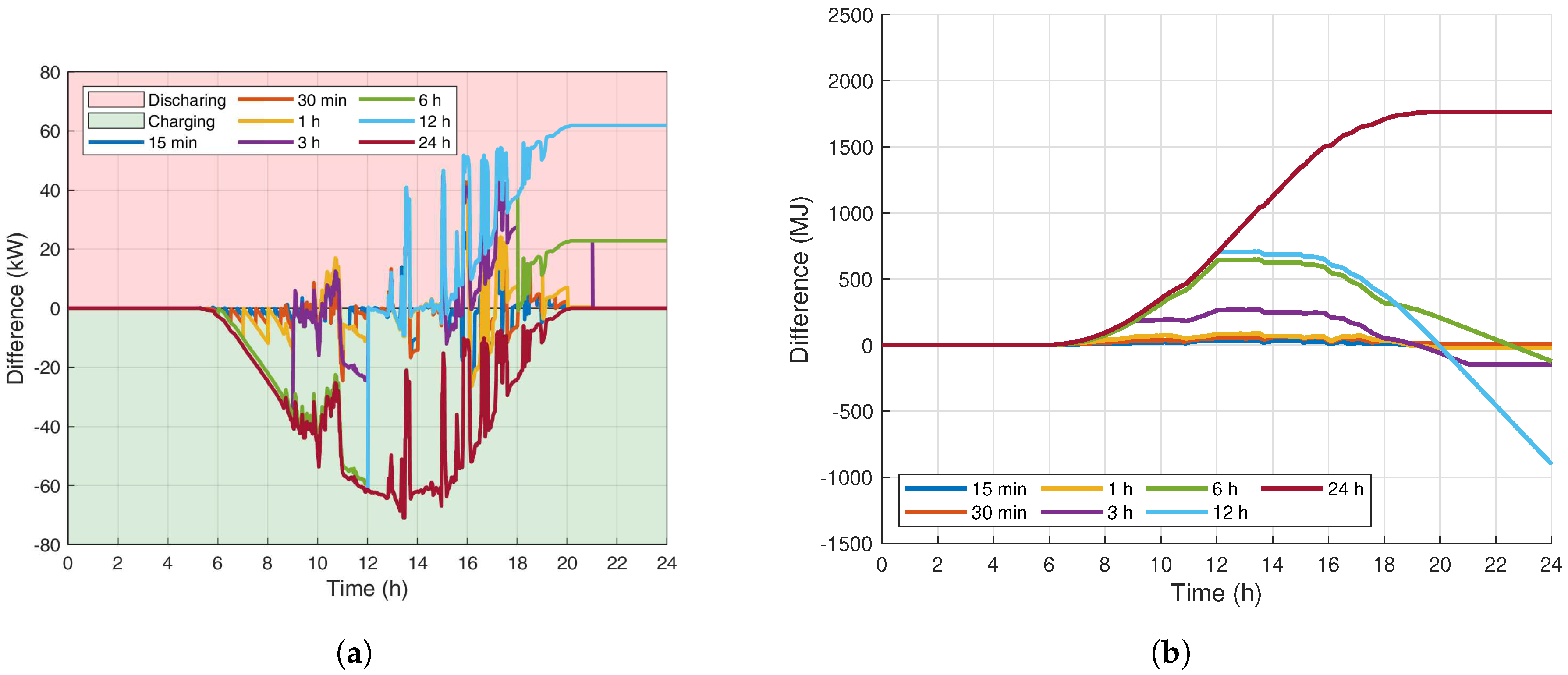
Appendix A.2. Overcast Sky Results
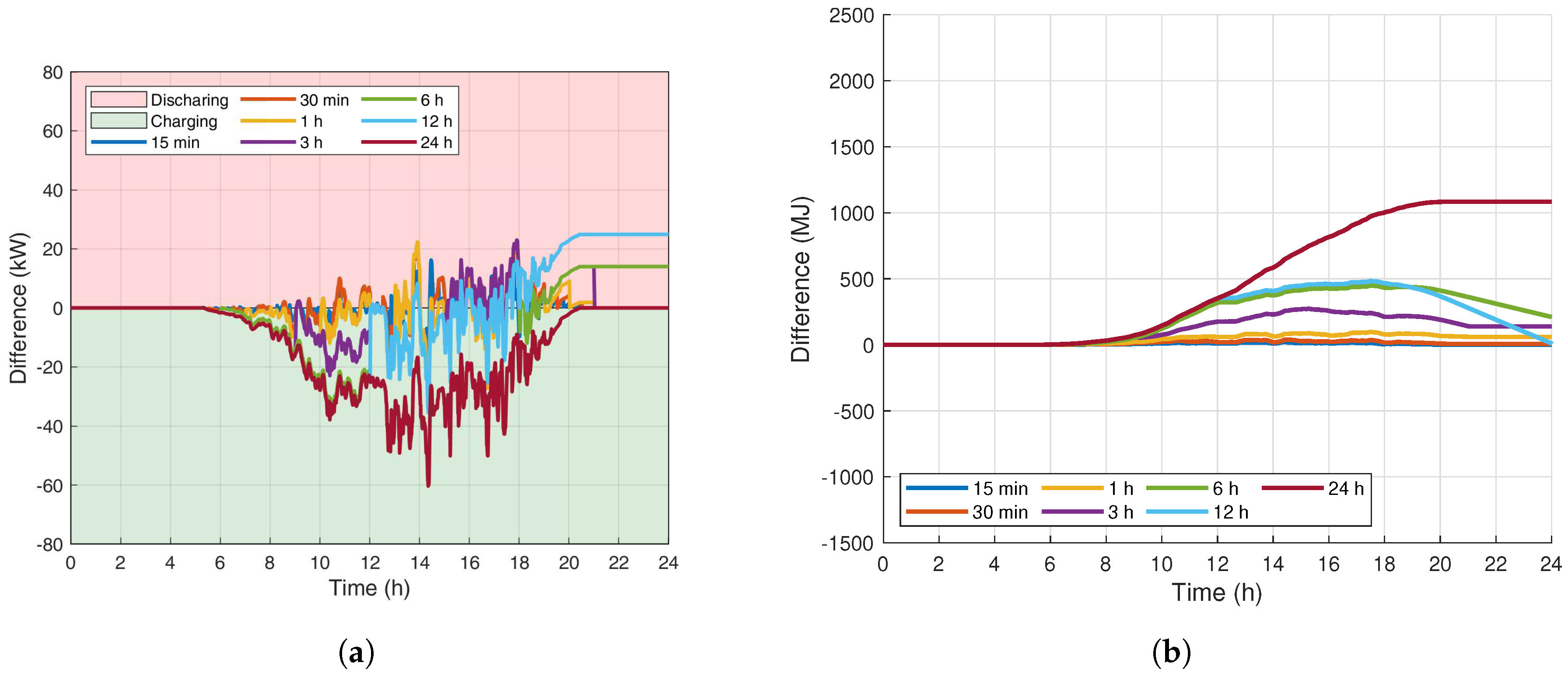
Appendix A.3. Monsoon Sky Results
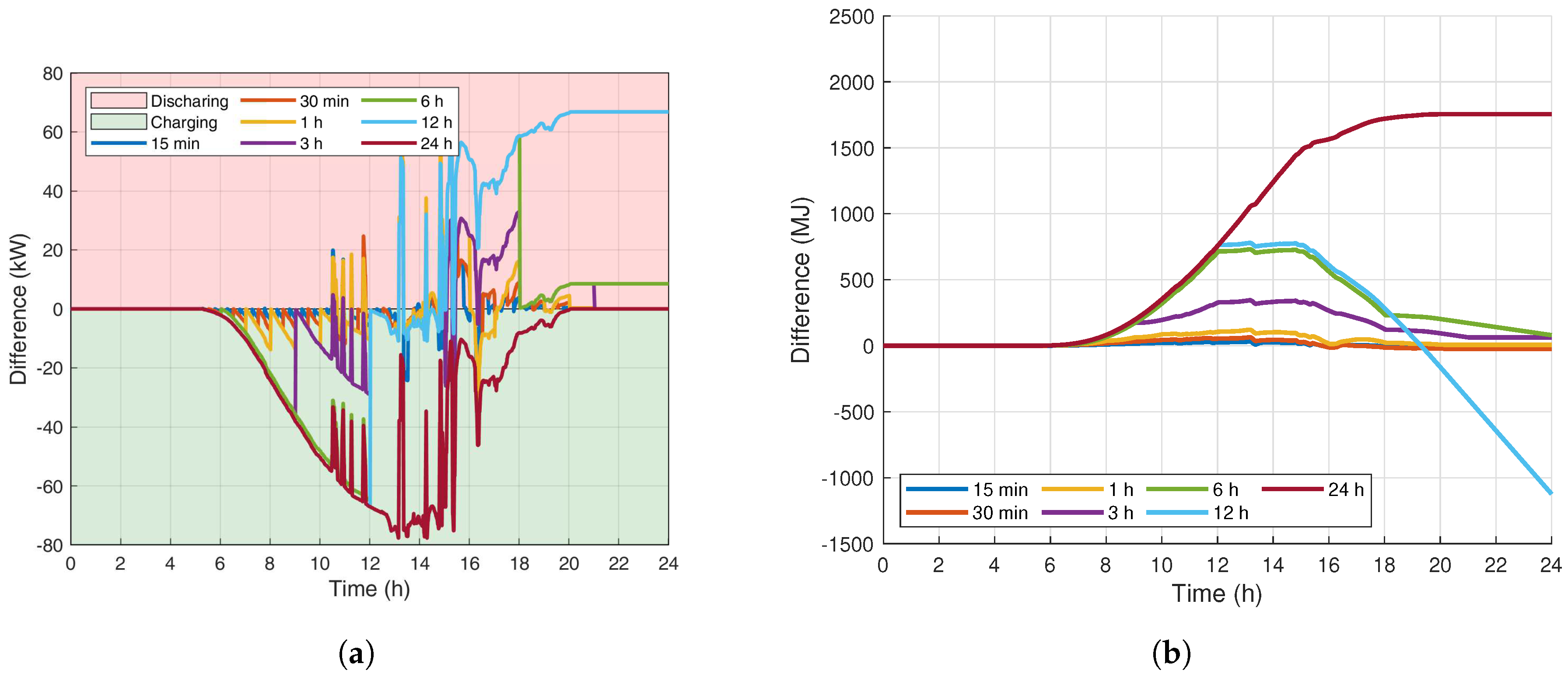
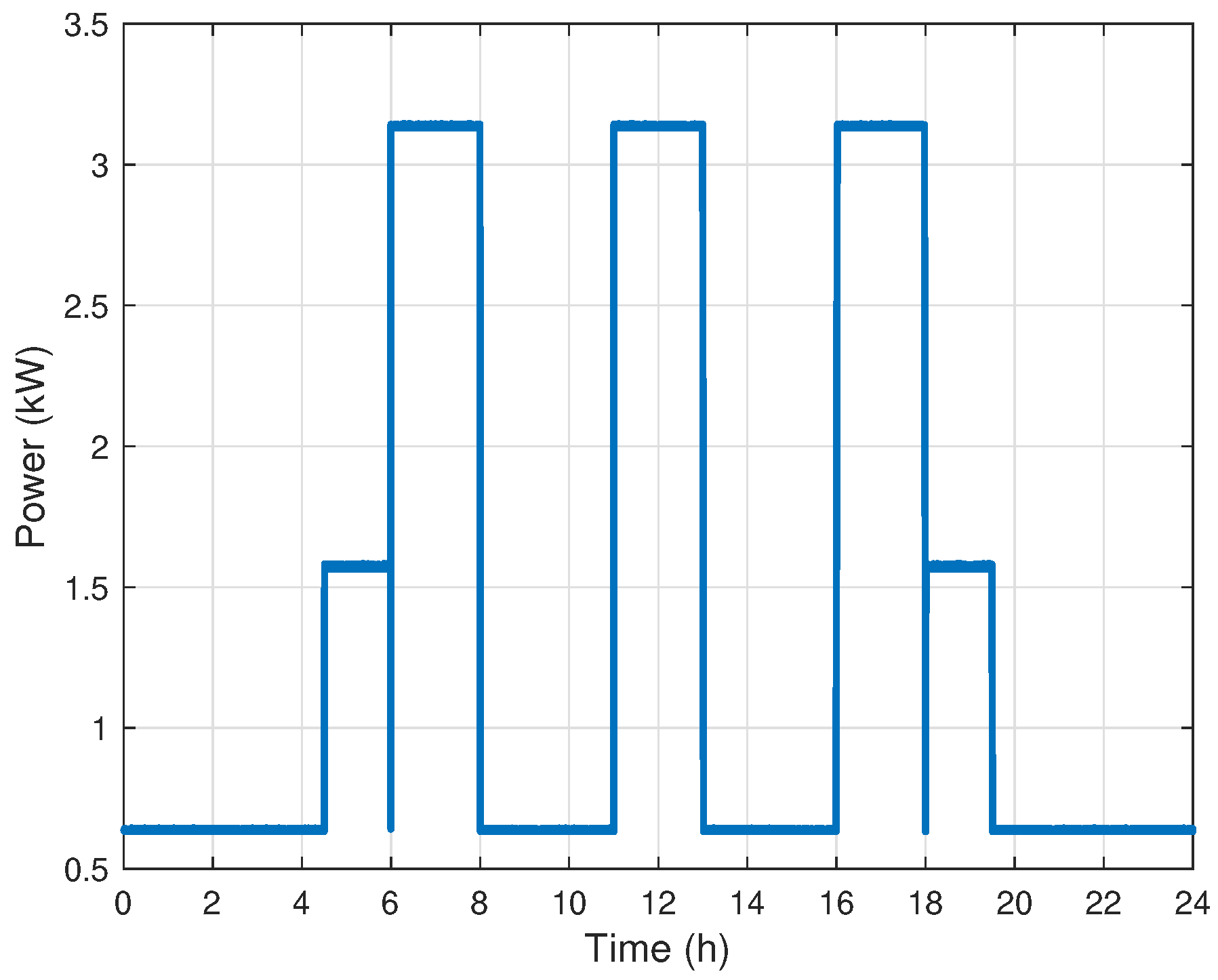
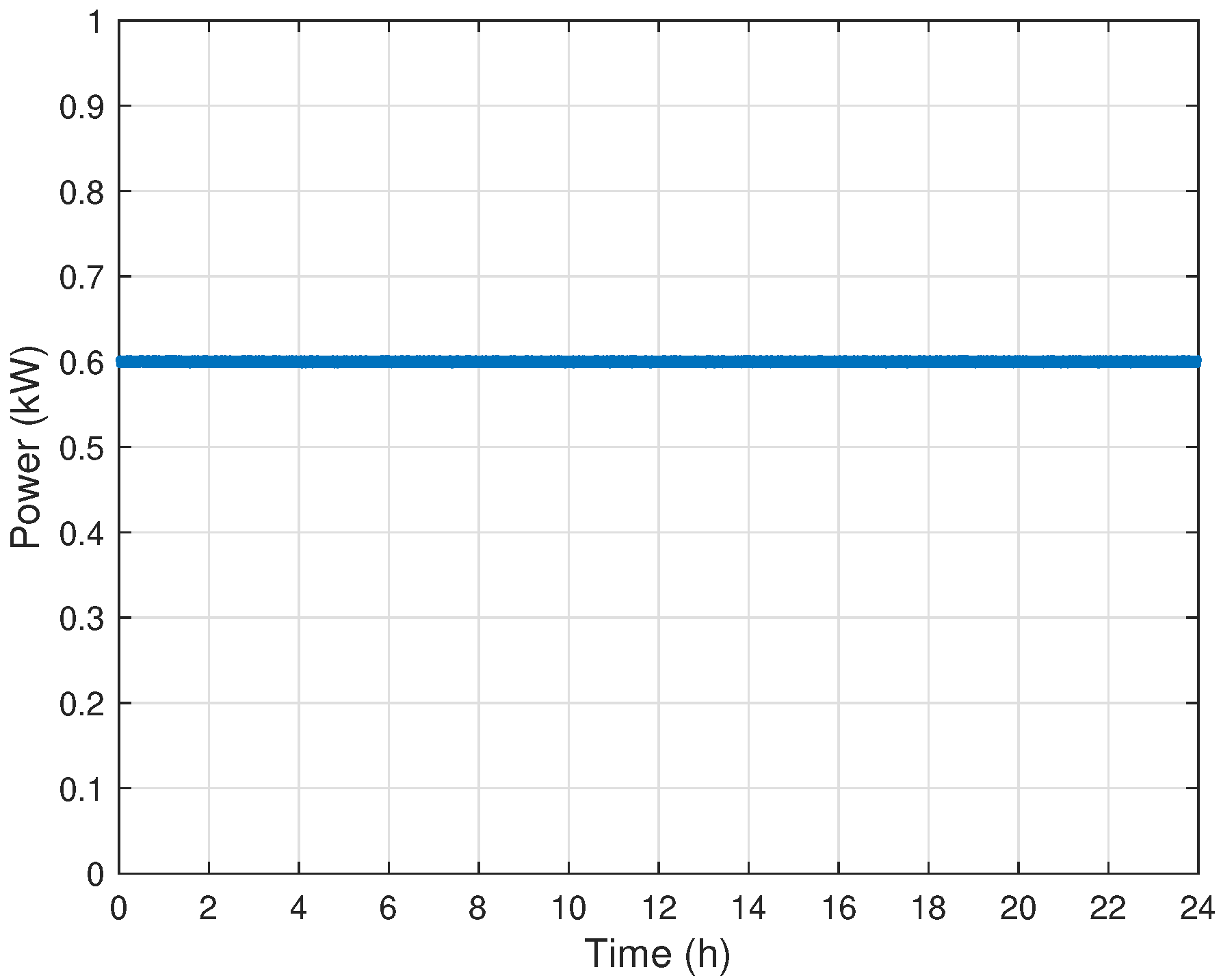
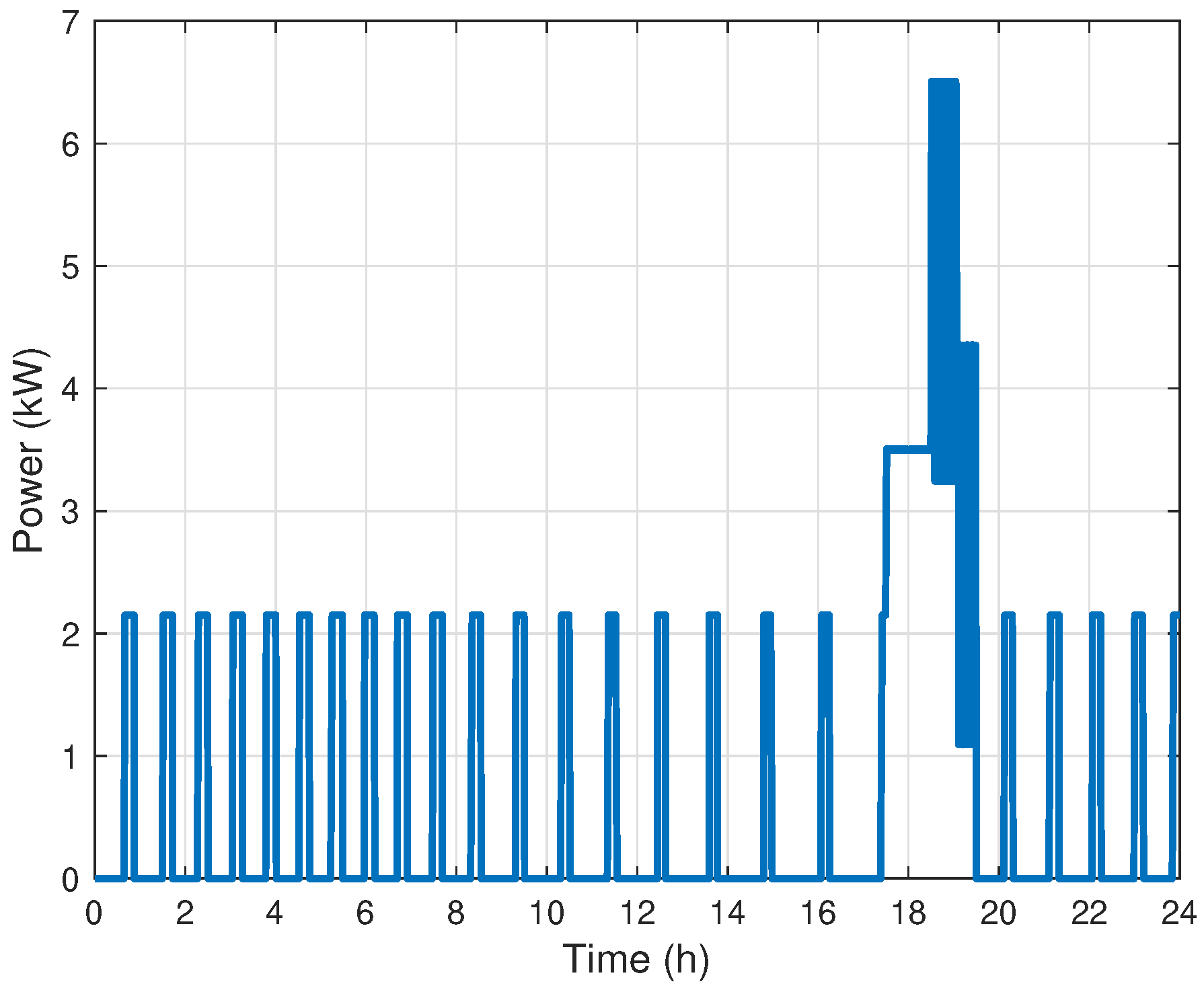
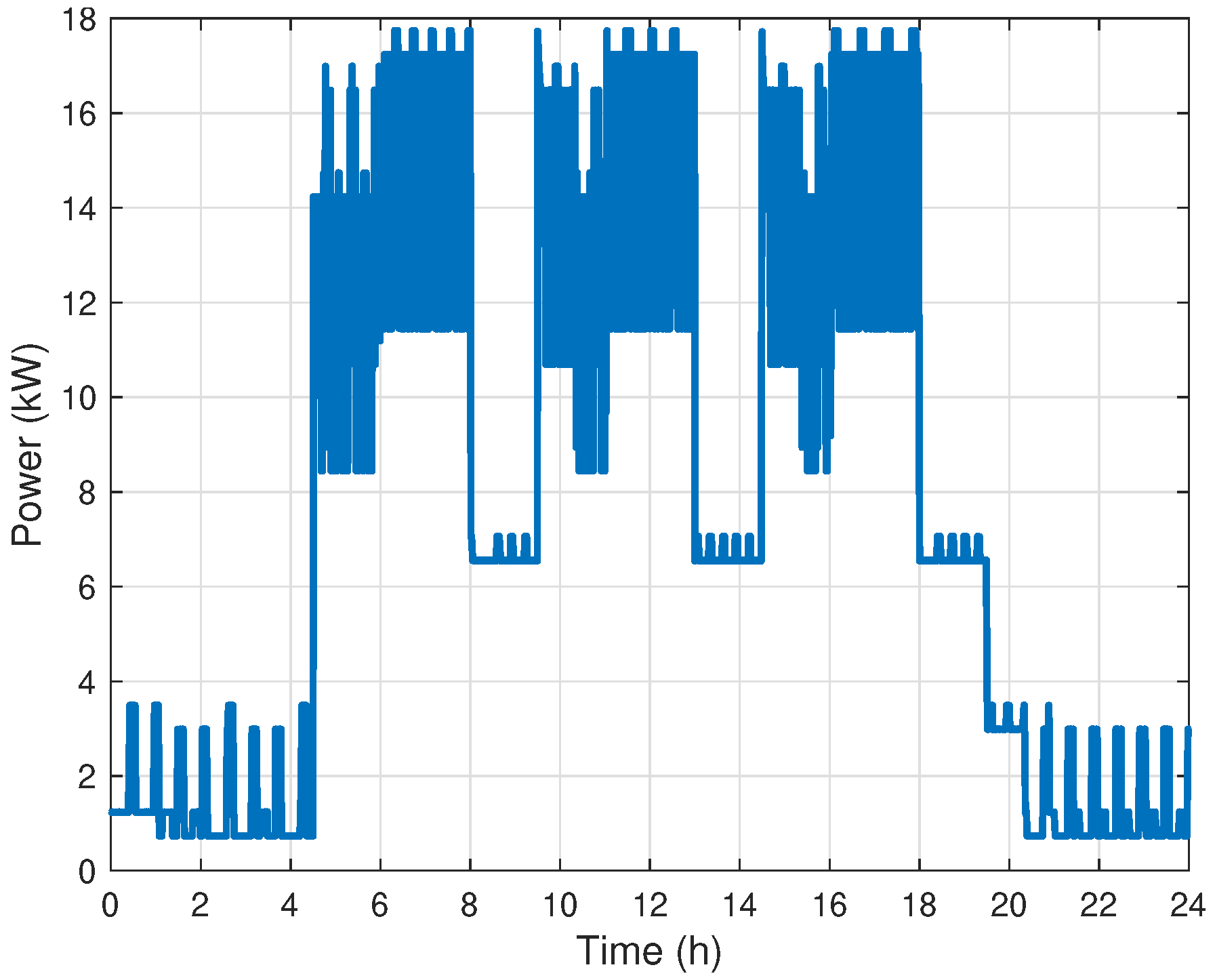
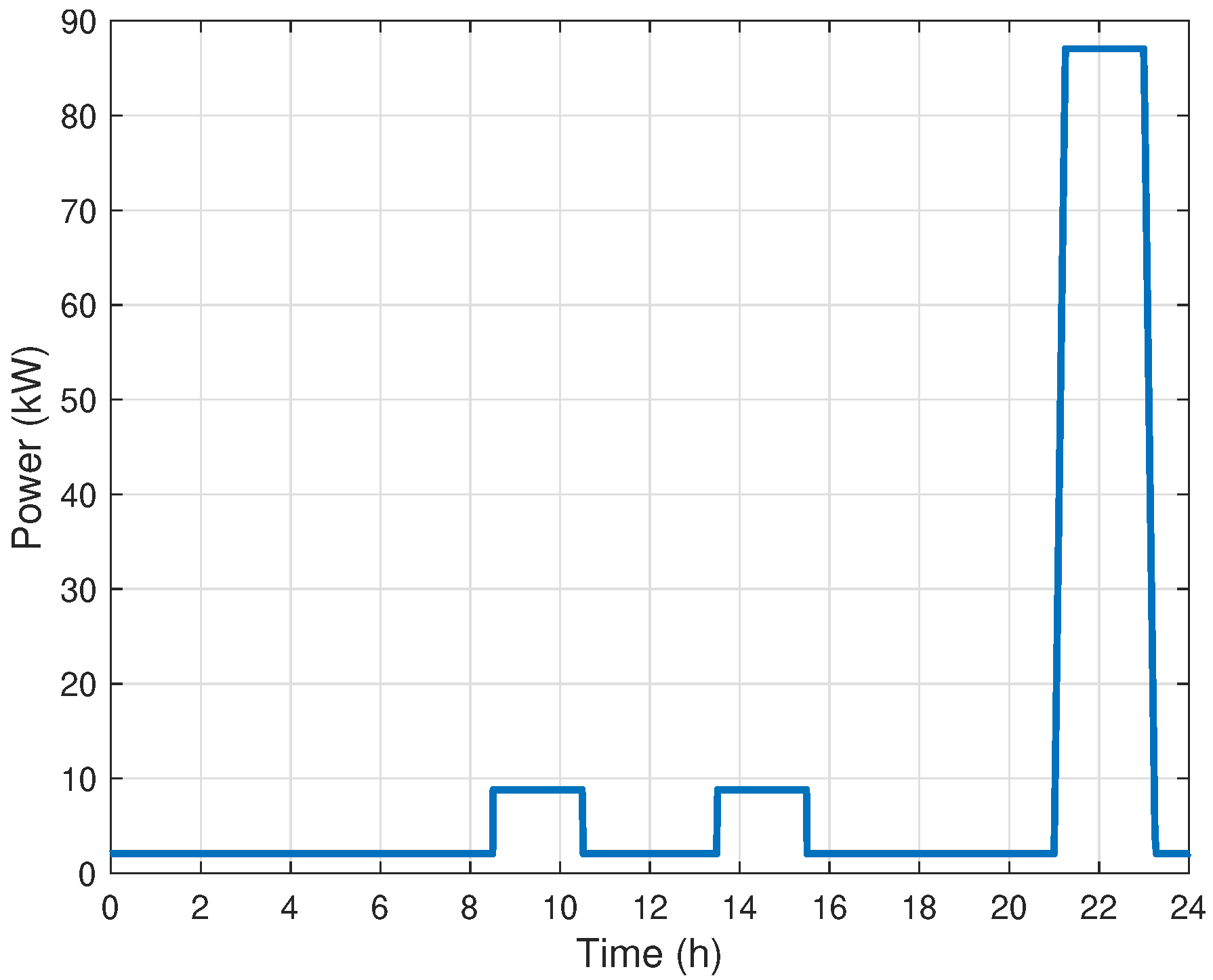
Appendix A.4. Electrical Load

| Symbol | Description | Unit | Value |
|---|---|---|---|
| Average specific heat of air | 1.005 | ||
| Density of air | 1.19 | ||
| Room volume | 650.0 |
| Shelter | Shelter | Wall | Wall Time | Room Time |
|---|---|---|---|---|
| Number | Type | Capacitance, | Constant, | Constant, |
| kJ kg | s | s | ||
| 1 | Billeting | 23 | 23 | 23 |
| 2 | Billeting | 30 | 30 | 30 |
| 3 | Billeting | 29 | 29 | 29 |
| 4 | Billeting | 25 | 25 | 25 |
| 5 | Latrine | 26 | 26 | 26 |
| 6 | Billeting | 30 | 30 | 30 |
| 7 | Billeting | 23 | 23 | 23 |
| 8 | Billeting | 30 | 30 | 30 |
| 9 | Billeting | 28 | 28 | 28 |
| 10 | Latrine | 21 | 21 | 21 |
| 11 | Shower | 24 | 24 | 24 |
| 12 | Shower | 30 | 30 | 30 |
| 13 | Laundry | 29 | 29 | 29 |
| 14 | Kitchen | 12 | 147 | 147 |
| 15 | COC | 21 | 21 | 21 |
| 16 | COM | 26 | 26 | 26 |
| 17 | Office | 20 | 20 | 20 |
| 18 | Office | 27 | 27 | 27 |
References
- Li, F.; Li, R.; Zhou, F. Microgrid Technology and Engineering Application; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Brewster, K.; Degelia, S.; Mueller, D. Potential Availability and Stability of Solar Power in Oklahoma White Paper. 2014. Available online: https://studylib.net/doc/8691353/solar-white-paper (accessed on 5 August 2019).
- Blumsack, S.; Richardson, K. Cost and emissions implications of coupling wind and solar power. Smart Grid Renew. Energy 2012, 3, 308. [Google Scholar] [CrossRef] [Green Version]
- Inman, R.H.; Pedro, H.T.; Coimbra, C.F. Solar forecasting methods for renewable energy integration. Prog. Energy Combust. Sci. 2013, 39, 535–576. [Google Scholar] [CrossRef]
- Reikard, G. Predicting solar radiation at high resolutions: A comparison of time series forecasts. Solar Energy 2009, 83, 342–349. [Google Scholar] [CrossRef]
- Husein, M.; Chung, I.Y. Day-Ahead Solar Irradiance Forecasting for Microgrids Using a Long Short-Term Memory Recurrent Neural Network: A Deep Learning Approach. Energies 2019, 12, 1856. [Google Scholar] [CrossRef] [Green Version]
- Chow, C.W.; Urquhart, B.; Lave, M.; Dominguez, A.; Kleissl, J.; Shields, J.; Washom, B. Intra-hour forecasting with a total sky imager at the UC San Diego solar energy testbed. Solar Energy 2011, 85, 2881–2893. [Google Scholar] [CrossRef] [Green Version]
- Chow, C.W.; Belongie, S.; Kleissl, J. Cloud motion and stability estimation for intra-hour solar forecasting. Solar Energy 2015, 115, 645–655. [Google Scholar] [CrossRef]
- Abdel-Aal, R.E. Hourly temperature forecasting using abductive networks. Eng. Appl. Artif. Intell. 2004, 17, 543–556. [Google Scholar] [CrossRef]
- Dombaycı, Ö.A.; Gölcü, M. Daily means ambient temperature prediction using artificial neural network method: A case study of Turkey. Renew. Energy 2009, 34, 1158–1161. [Google Scholar] [CrossRef]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-de-Pison, F.J.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Solar Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Shi, J.; Lee, W.J.; Liu, Y.; Yang, Y.; Wang, P. Forecasting power output of photovoltaic systems based on weather classification and support vector machines. IEEE Trans. Ind. Appl. 2012, 48, 1064–1069. [Google Scholar] [CrossRef]
- Tao, C.; Duan, S.; Chen, C. Forecasting power output for grid-connected photovoltaic power system without using solar radiation measurement. In Proceedings of the 2nd International Symposium on Power Electronics for Distributed Generation Systems, Hefei, China, 16–18 June 2010. [Google Scholar]
- Islahi, A.; Saani, S.; Mostafa, H. Hottel’s Clear Day Model for a typical arid city-Jeddah. Int. J. Eng. Sci. Invent. 2015, 4, 32–37. [Google Scholar]
- Yang, H.T.; Huang, C.M.; Huang, Y.C.; Pai, Y.S. A weather-based hybrid method for 1-day ahead hourly forecasting of PV power output. IEEE Trans. Sustain. Energy 2014, 5, 917–926. [Google Scholar] [CrossRef]
- Bouzerdoum, M.; Mellit, A.; Pava, N.A.M. A hybrid model (SARIMA–SVM) for short-term power forecasting of a small-scale grid-connected photovoltaic plant. Solar Energy 2013, 98, 226–235. [Google Scholar] [CrossRef]
- Sáez, D.; Ávila, F.; Olivares, D.; Cañizares, C.; Marín, L. Fuzzy prediction interval models for forecasting renewable resources and loads in microgrids. IEEE Trans. Smart Grid 2014, 6, 548–556. [Google Scholar] [CrossRef] [Green Version]
- Nespoli, A.; Mussetta, M.; Ogliari, E.; Leva, S.; Fernández-Ramírez, L.; García-Triviño, P. Robust 24 Hours ahead Forecast in a Microgrid: A Real Case Study. Electronics 2019, 8, 1434. [Google Scholar] [CrossRef] [Green Version]
- Sala, S.; Amendola, A.; Leva, S.; Mussetta, M.; Niccolai, A.; Ogliari, E. Comparison of Data-Driven Techniques for Nowcasting Applied to an Industrial-Scale Photovoltaic Plant. Energies 2019, 12, 4520. [Google Scholar] [CrossRef] [Green Version]
- Hong, T.; Wilson, J.; Xie, J. Long term probabilistic load forecasting and normalization with hourly information. IEEE Trans. Smart Grid 2013, 5, 456–462. [Google Scholar] [CrossRef]
- Hernandez, L.; Baladron, C.; Aguiar, J.M.; Carro, B.; Sanchez-Esguevillas, A.J.; Lloret, J.; Massana, J. A survey on electric power demand forecasting: Future trends in smart grids, microgrids and smart buildings. IEEE Commun. Surv. Tutor. 2014, 16, 1460–1495. [Google Scholar] [CrossRef]
- Yu, C.N.; Mirowski, P.; Ho, T.K. A sparse coding approach to household electricity demand forecasting in smart grids. IEEE Trans. Smart Grid 2016, 8, 738–748. [Google Scholar] [CrossRef]
- Zhou, H.; Bhattacharya, T.; Tran, D.; Siew, T.S.; Khambadkone, A.M. Composite energy storage system involving battery and ultracapacitor with dynamic energy management in microgrid applications. IEEE Trans. Power Electron. 2010, 26, 923–930. [Google Scholar] [CrossRef]
- Lu, D.; Francois, B. Strategic framework of an energy management of a microgrid with a photovoltaic-based active generator. In Proceedings of the 2009 8th International Symposium on Advanced Electromechanical Motion Systems & Electric Drives Joint Symposium, Lille, France, 1–3 July 2009. [Google Scholar]
- Moretti, L.; Polimeni, S.; Meraldi, L.; Raboni, P.; Leva, S.; Manzolini, G. Assessing the impact of a two-layer predictive dispatch algorithm on design and operation of off-grid hybrid microgrids. Renew. Energy 2019, 143, 1439–1453. [Google Scholar] [CrossRef]
- Shi, W.; Xie, X.; Chu, C.C.; Gadh, R. Distributed optimal energy management in microgrids. IEEE Trans. Smart Grid 2014, 6, 1137–1146. [Google Scholar] [CrossRef]
- Su, W.; Wang, J.; Roh, J. Stochastic energy scheduling in microgrids with intermittent renewable energy resources. IEEE Trans. Smart Grid 2013, 5, 1876–1883. [Google Scholar] [CrossRef]
- Hayes, B.P.; Prodanovic, M. State forecasting and operational planning for distribution network energy management systems. IEEE Trans. Smart Grid 2015, 7, 1002–1011. [Google Scholar] [CrossRef]
- GlobalSecurity.org. Tactical Quiet Generators. Available online: https://www.globalsecurity.org/military/systems/ground/mep-tqg.htm (accessed on 22 July 2019).
- Rizzo, D.M. US Army CCDC Ground Vehicle Systems Center, Warren, MI, USA. Fuel Consumption of Generators. Private Communication, 2016. [Google Scholar]
- Vergura, S. A complete and simplified datasheet-based model of pv cells in variable environmental conditions for circuit simulation. Energies 2016, 9, 326. [Google Scholar] [CrossRef]
- Jane, R.S. Networked Microgrid Optimization and Energy Management. Ph.D. Thesis, Michigan Technological University, Houghton, MI, USA, 2019. [Google Scholar]

| Symbol | Unit | 30 kW TQG | 60 kW TQG |
|---|---|---|---|
| 2.896 | 5.793 | ||
| 0.031 | 0.016 | ||
| −2.896 | −5.791 | ||
| −0.273 | −0.136 |
| Symbol | Description | Unit | Value |
|---|---|---|---|
| Cell Rated Power | 180.0 | ||
| Open circuit voltage at STC | 45.0 | ||
| Short circuit current at STC | 5.3 | ||
| Voltage at maximum power at STC | 36.8 | ||
| Current at maximum power at STC | 4.9 | ||
| Nominal operating cell temp. | C | 48.0 | |
| Short circuit current temp. coeff. | %/C | 0.1 | |
| Open circuit voltage temp. coeff. | %/C | 0.1 | |
| Number of series cells | # | 9 | |
| Number of parallel cells | # | 7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jane, R.; Parker, G.; Vaucher, G.; Berman, M. Characterizing Meteorological Forecast Impact on Microgrid Optimization Performance and Design. Energies 2020, 13, 577. https://doi.org/10.3390/en13030577
Jane R, Parker G, Vaucher G, Berman M. Characterizing Meteorological Forecast Impact on Microgrid Optimization Performance and Design. Energies. 2020; 13(3):577. https://doi.org/10.3390/en13030577
Chicago/Turabian StyleJane, Robert, Gordon Parker, Gail Vaucher, and Morris Berman. 2020. "Characterizing Meteorological Forecast Impact on Microgrid Optimization Performance and Design" Energies 13, no. 3: 577. https://doi.org/10.3390/en13030577






