Experimental Investigation on the Post-Peak Short-Term and Creep Behavior of Fractured Sandstone
Abstract
:1. Introduction
2. Experimental Materials and Methods
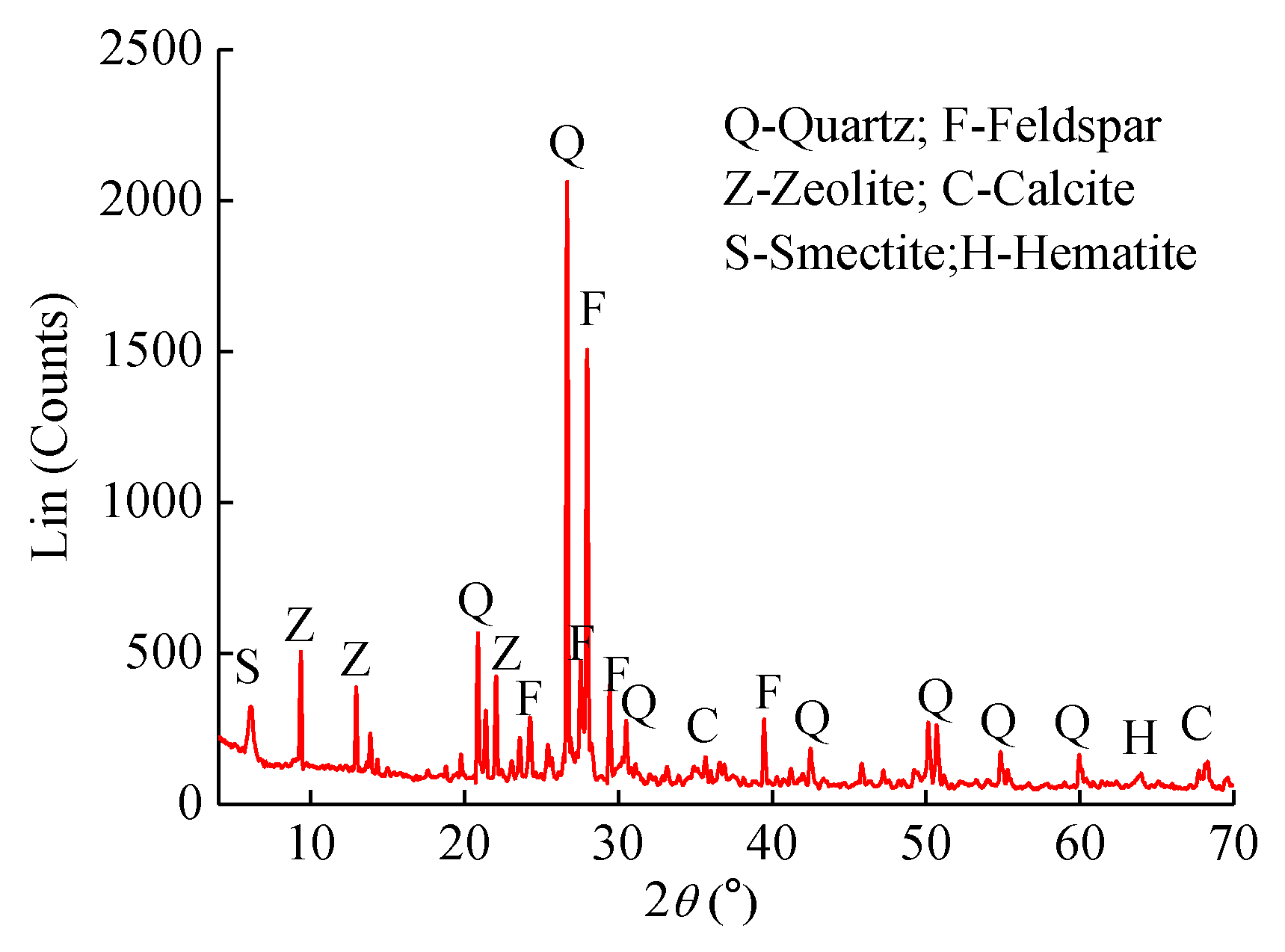
2.1. Red Sandstone
2.2. Experimental Equipment
2.3. Fractured Specimen Preparation
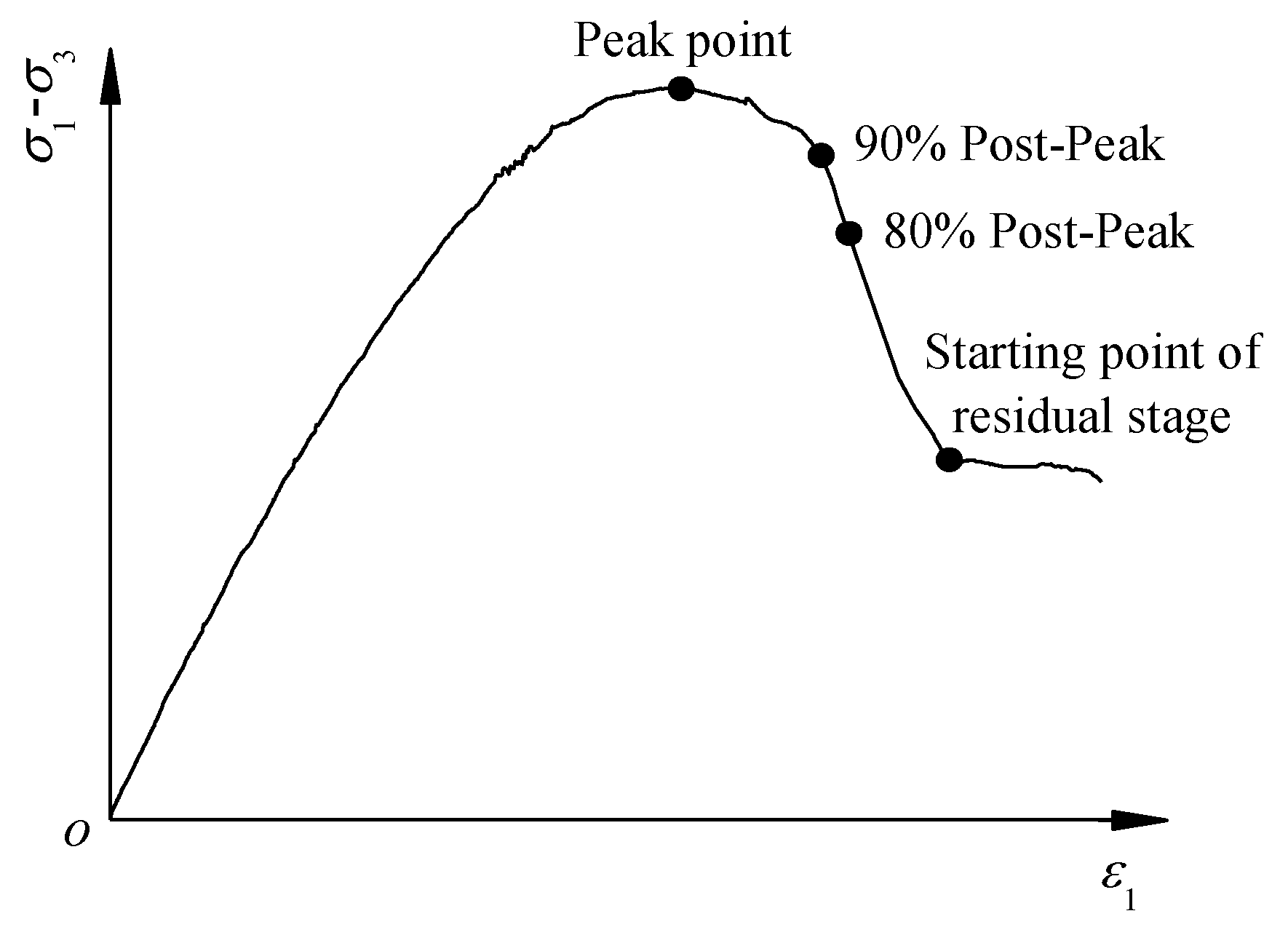
2.4. Experimental Procedures
3. Short-Term Strength and Deformation Failure Behavior
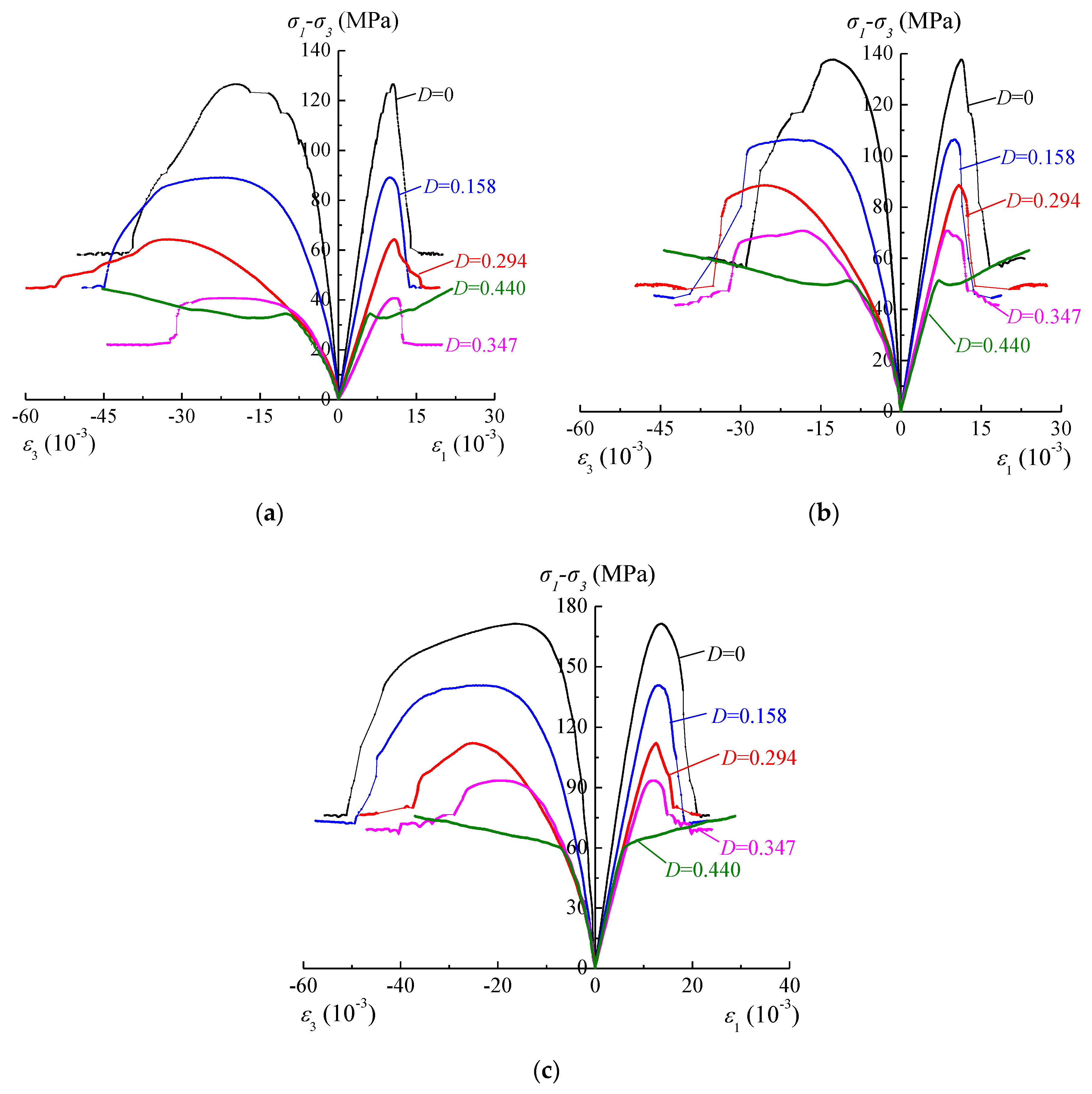
3.1. Short-Term Strength and Failure Behavior
3.2. Short-Term Deformation Behavior
4. Creep Mechanical Behavior of Intact and Fractured Sandstone
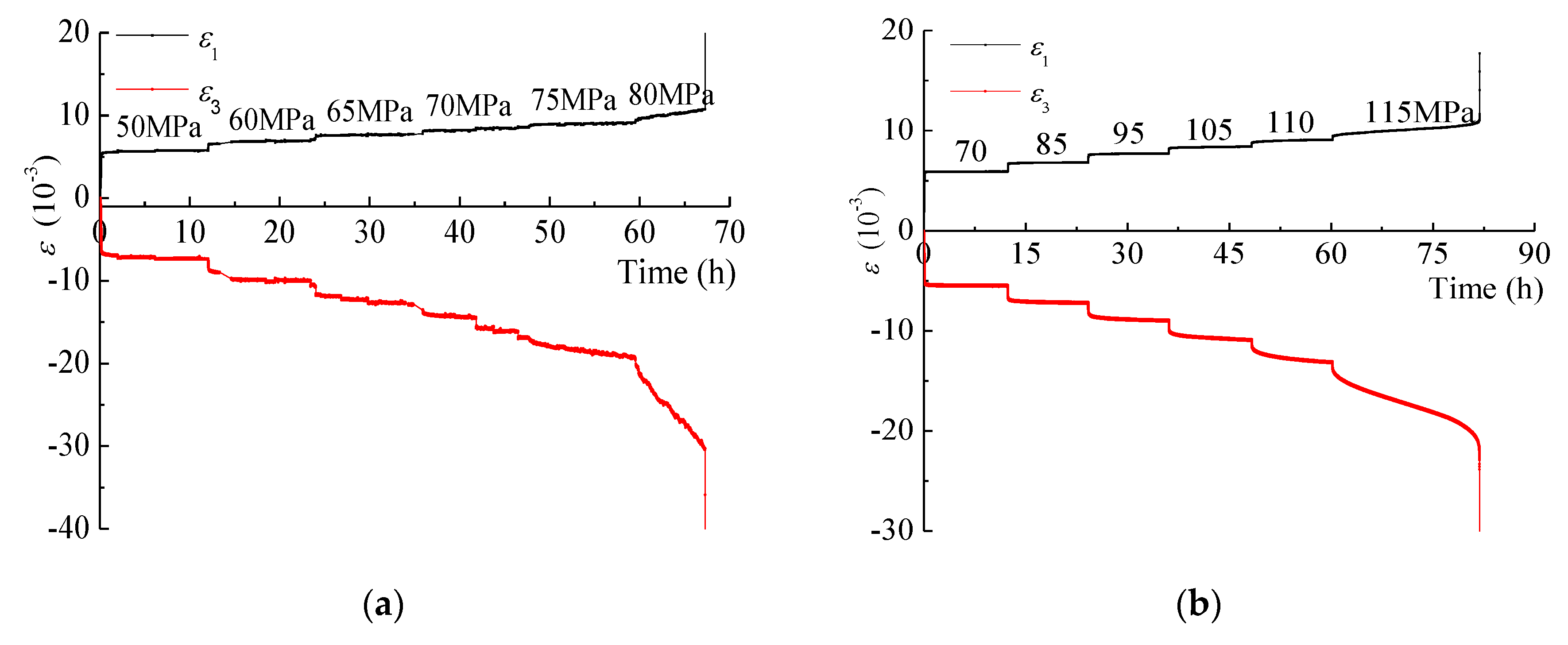
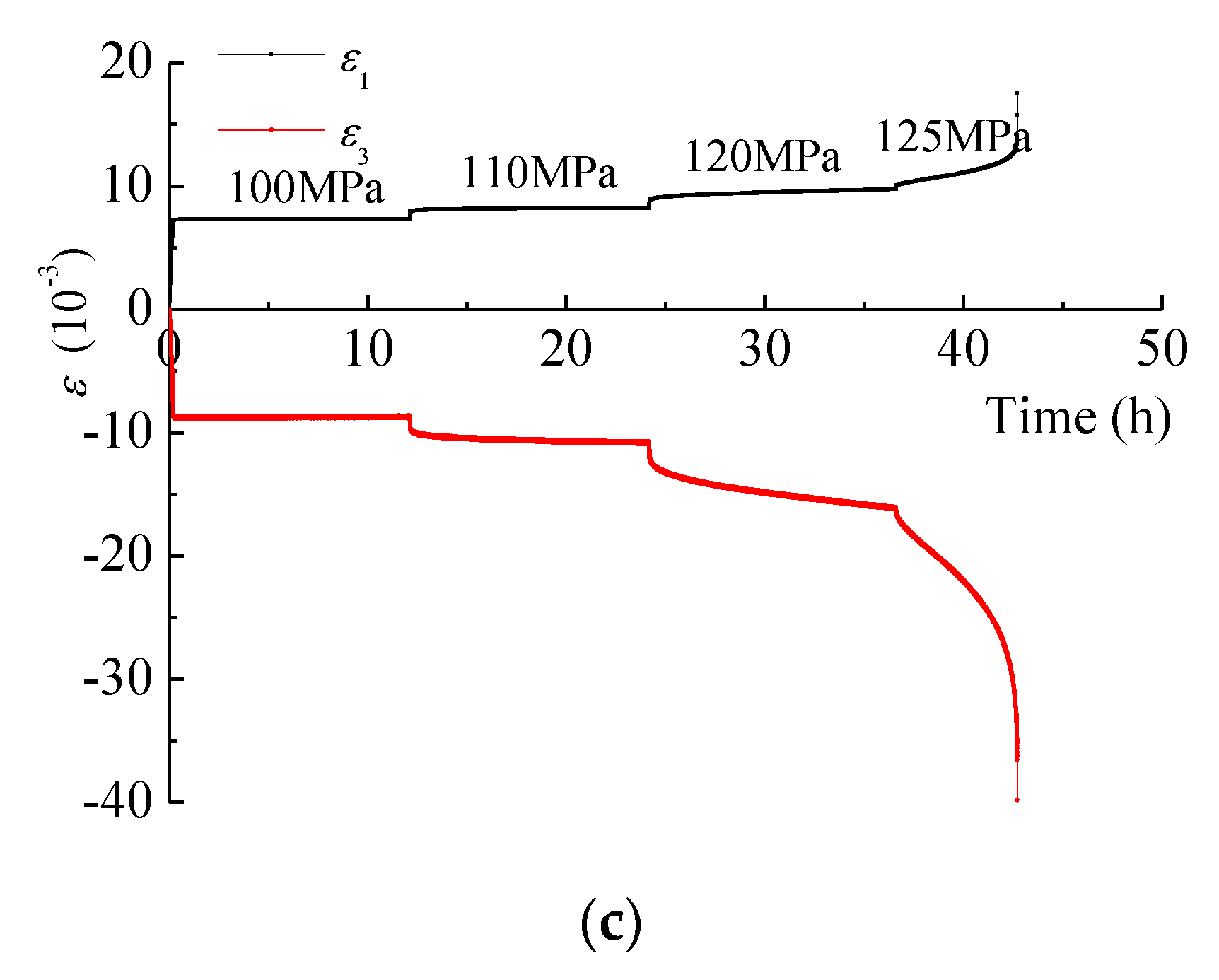
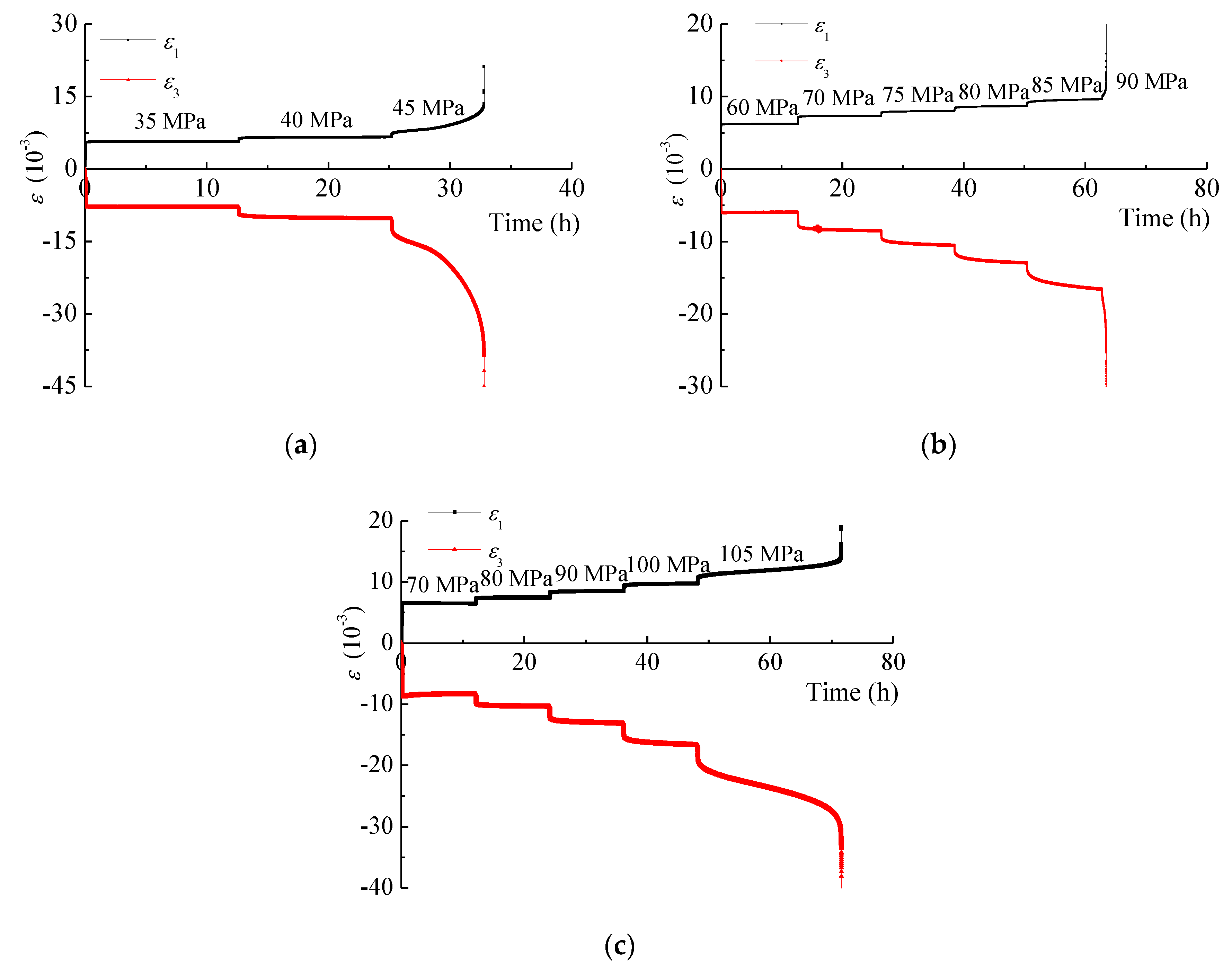
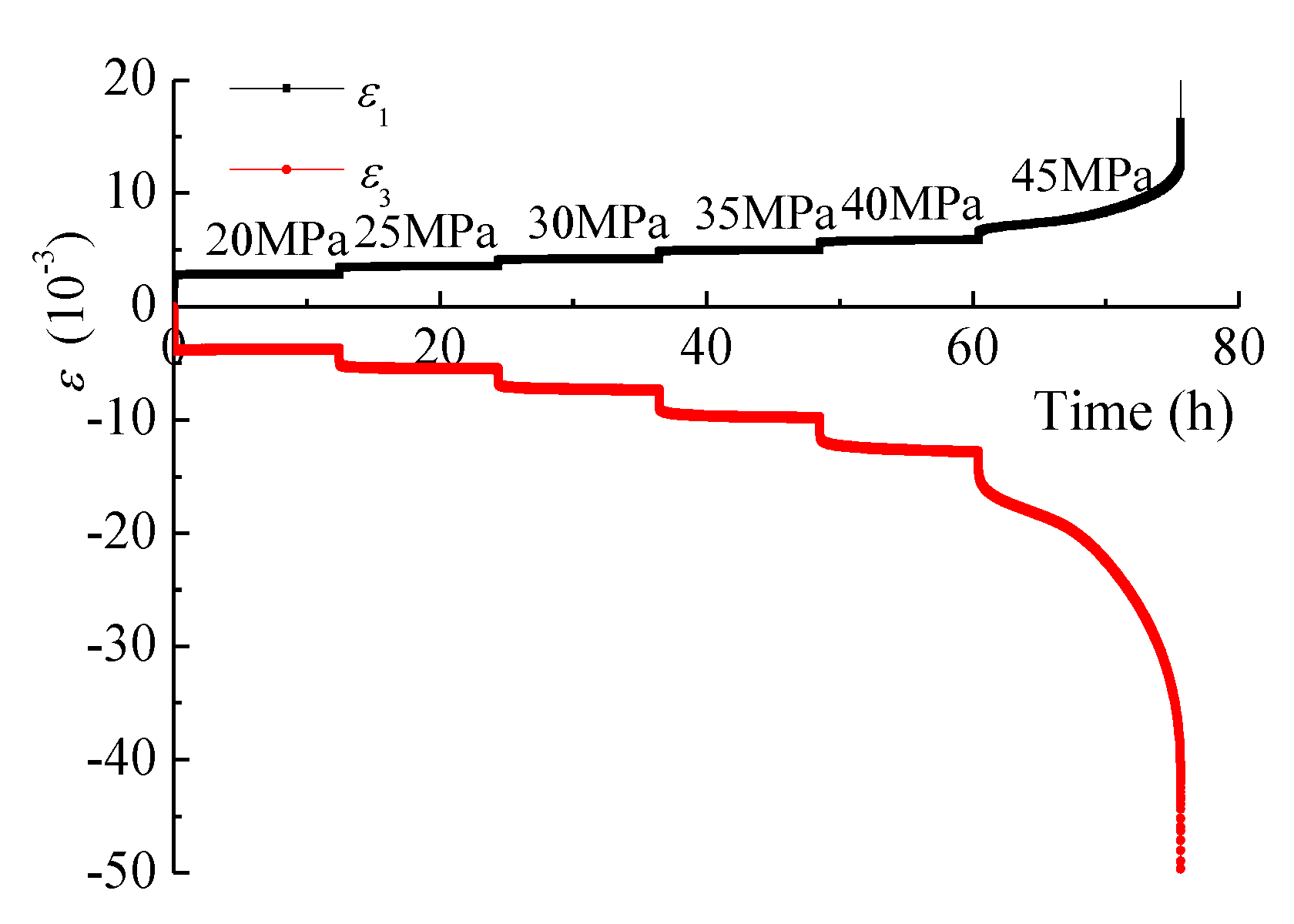
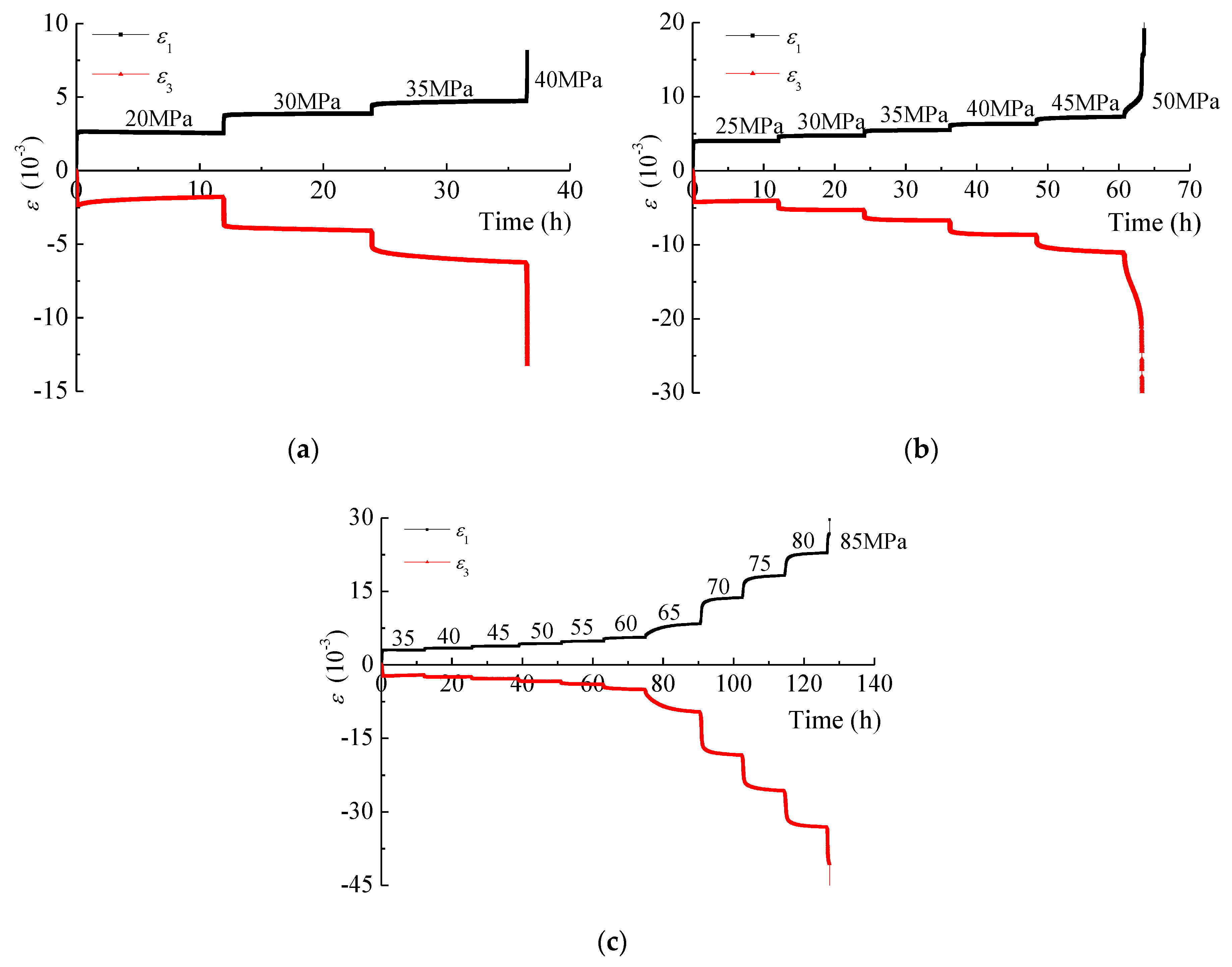
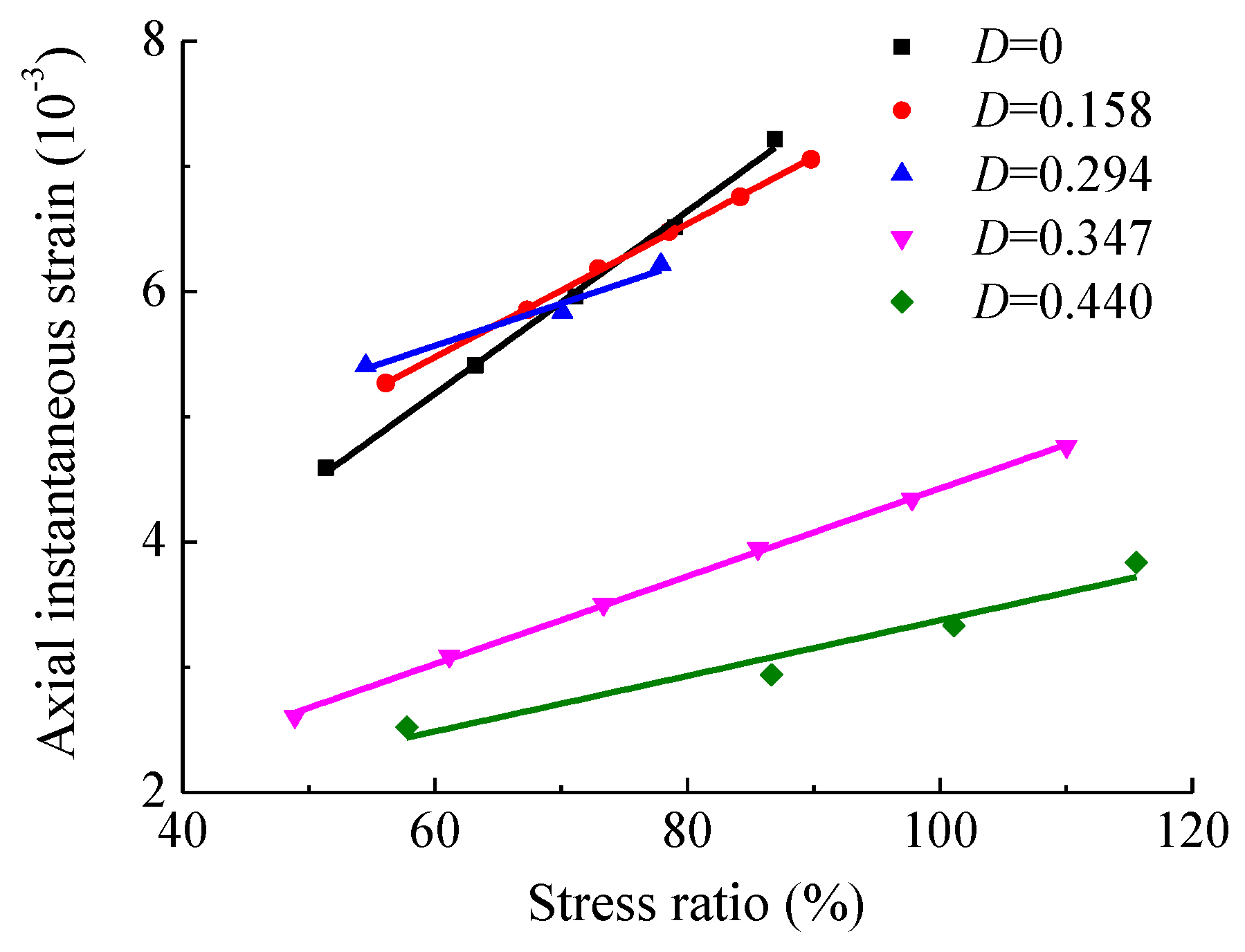
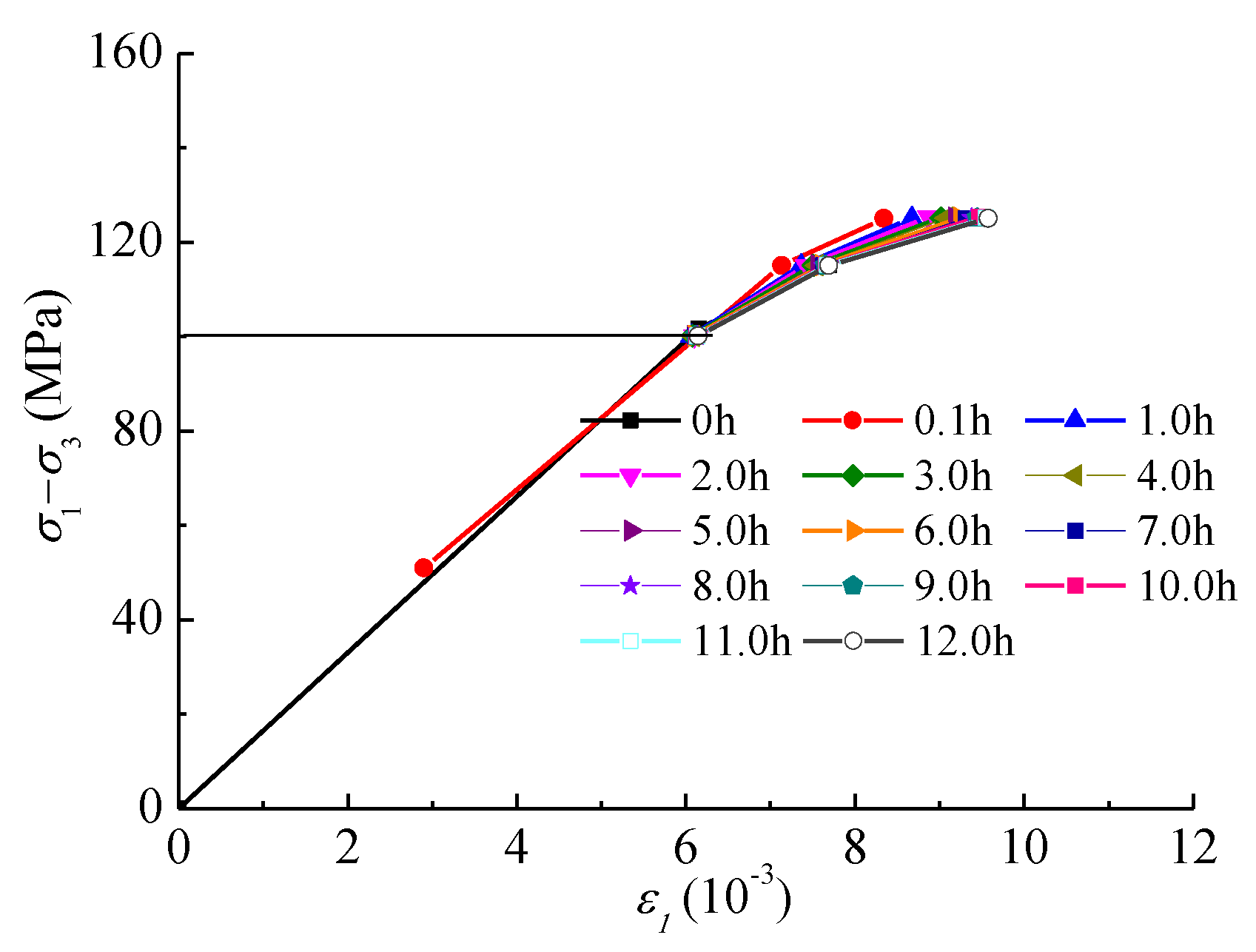
4.1. Creep Strain Behavior
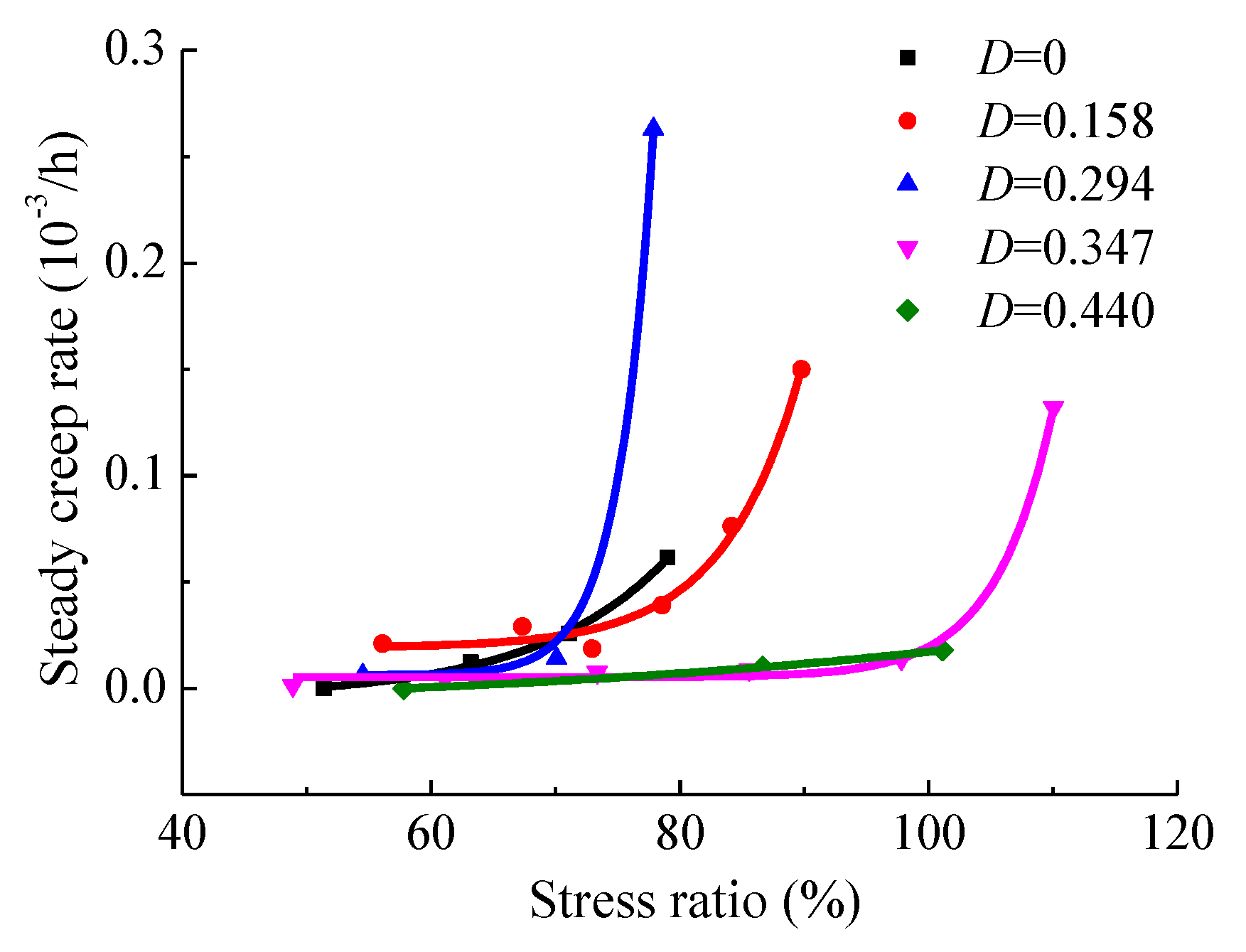
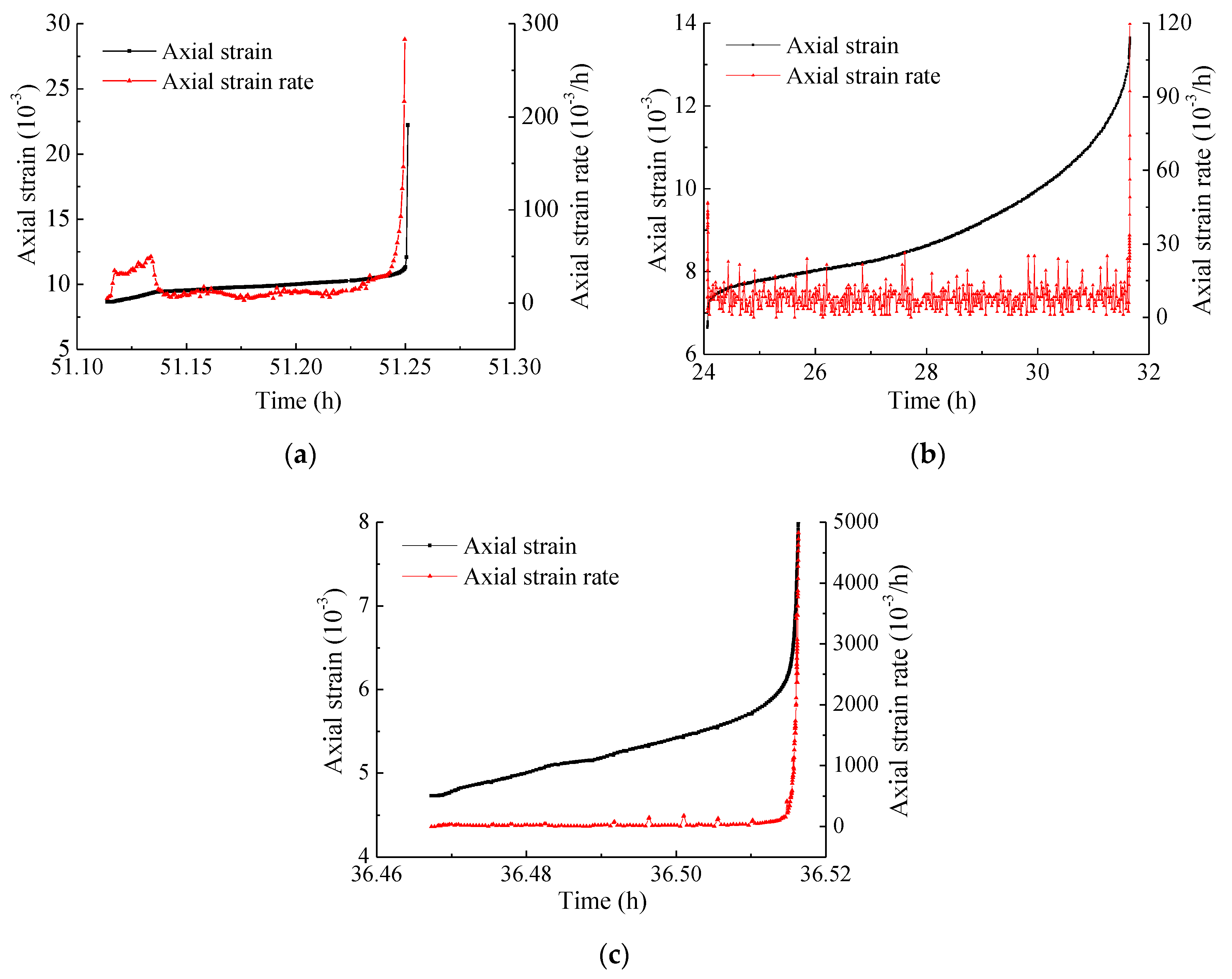
4.2. Creep Strain Rate
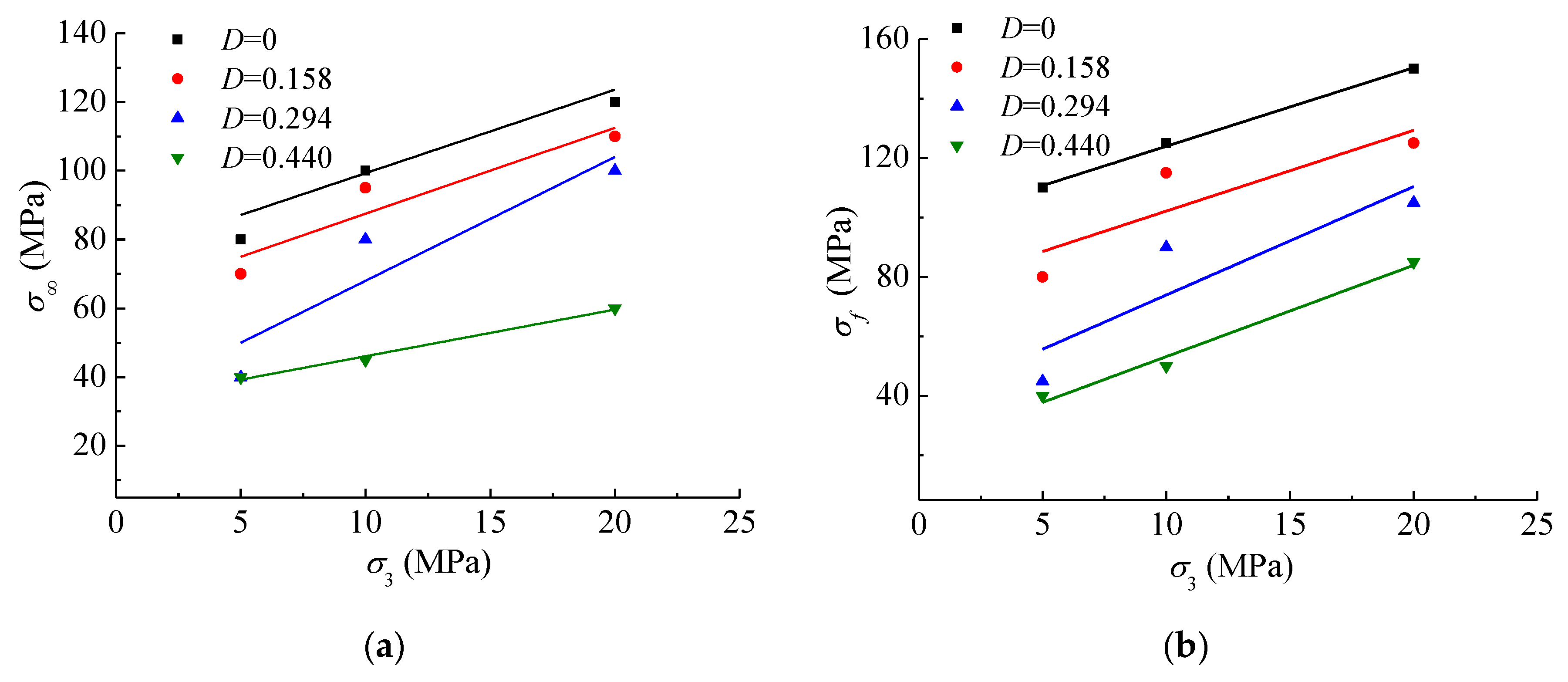
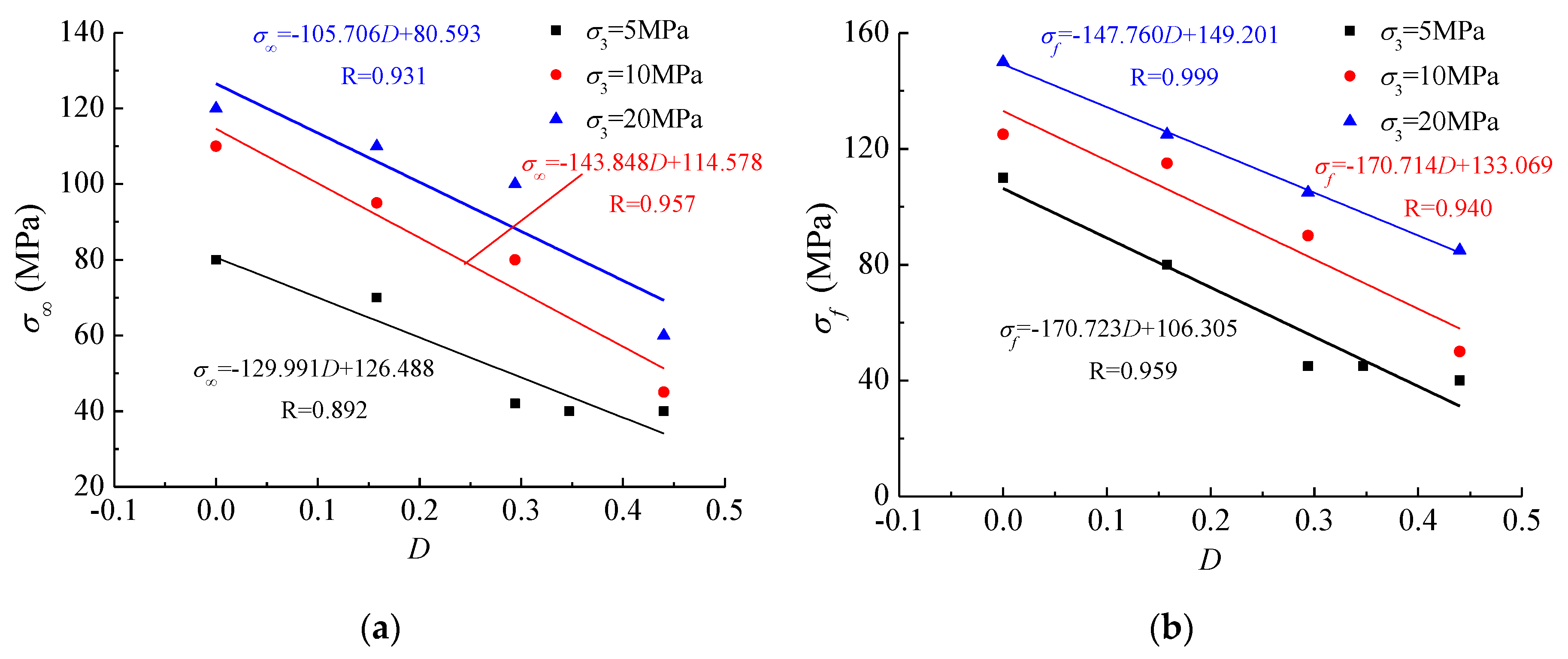
4.3. Long-Term Strength and Failure Behavior
5. Conclusions
- (1)
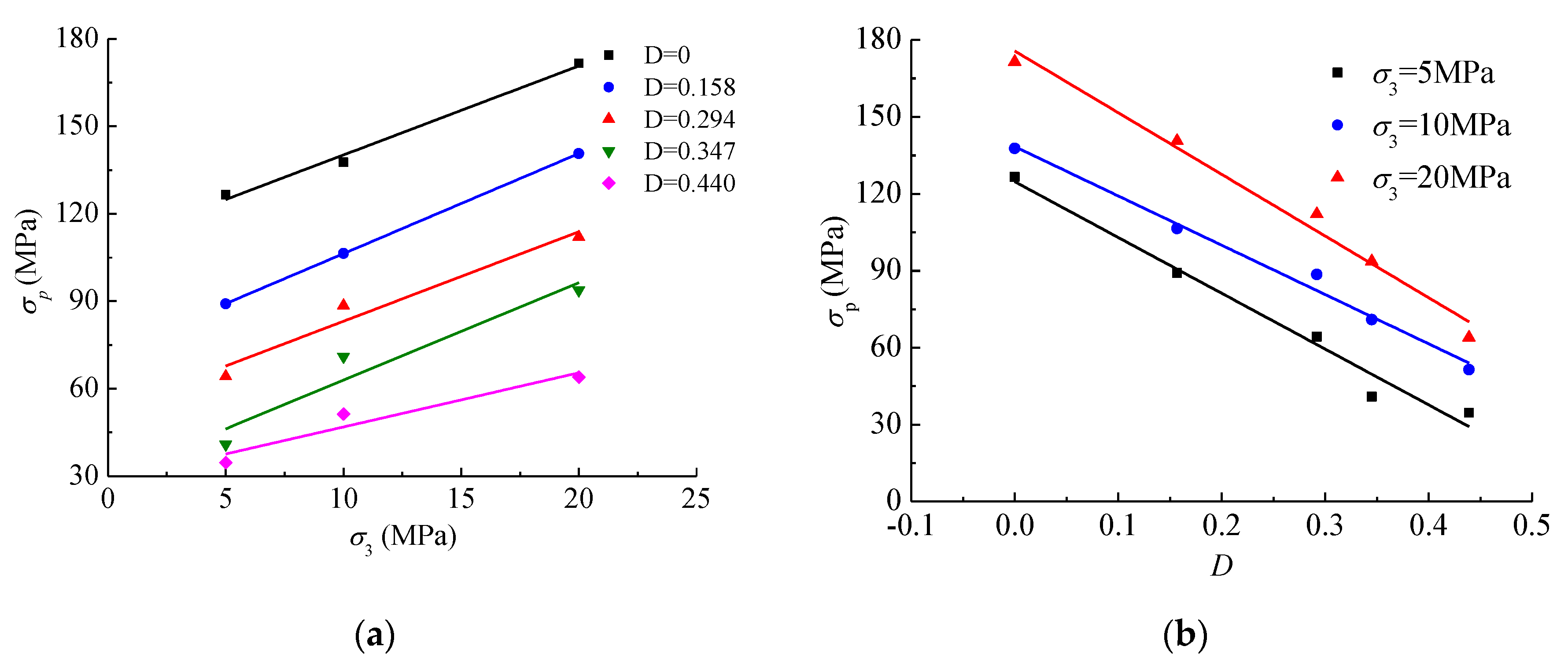
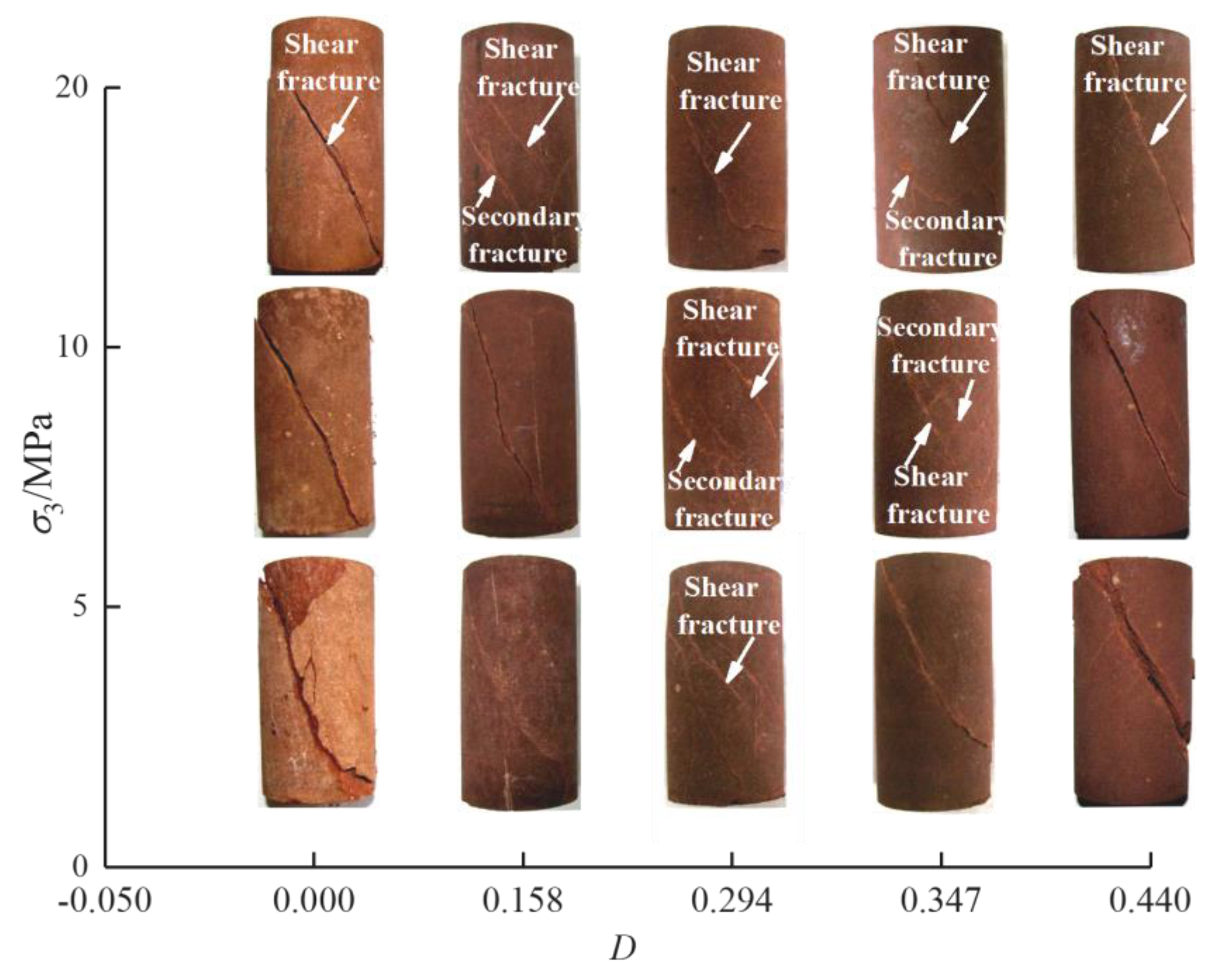
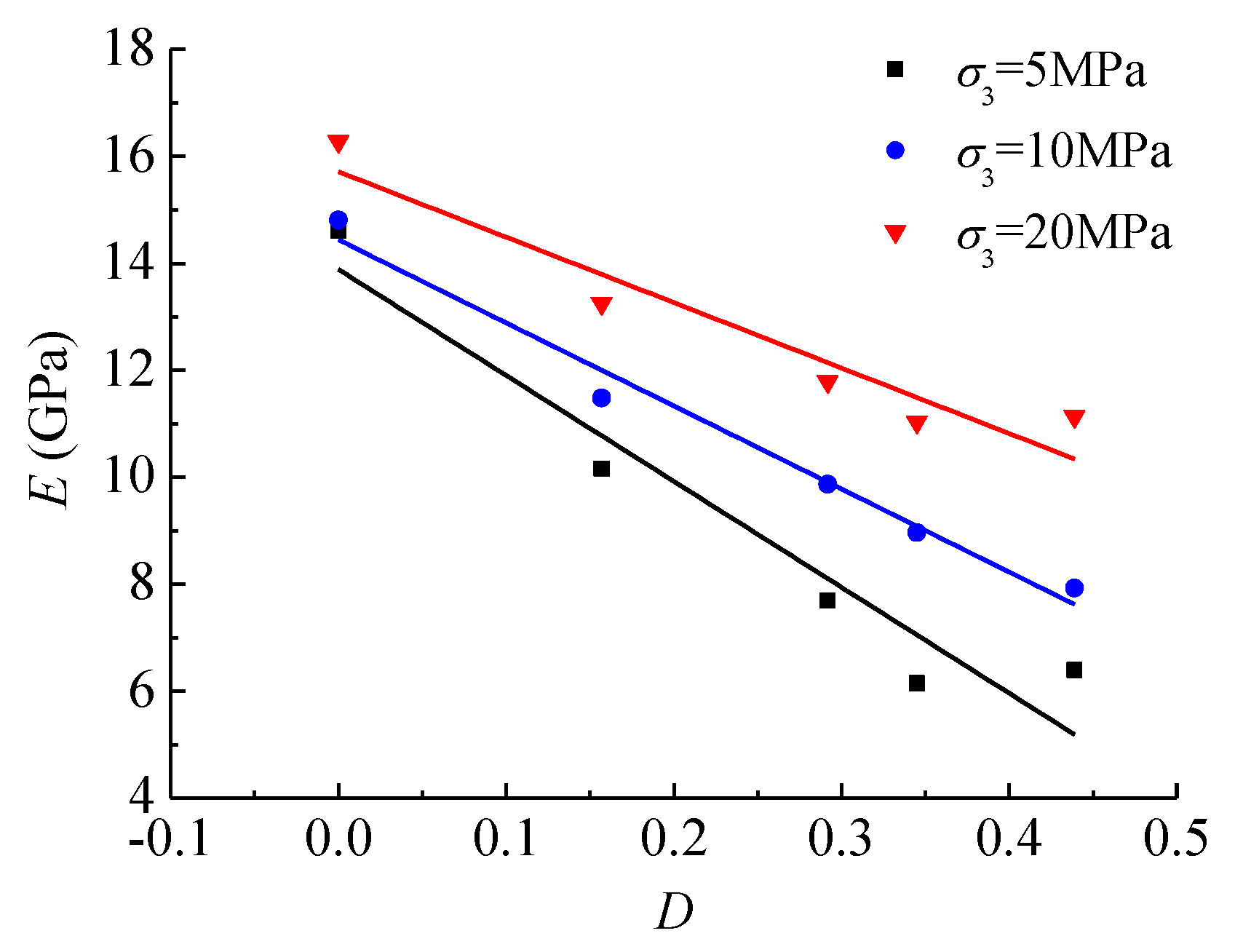
- The peak strength and residual strength of intact and fractured specimens increase linearly with increasing confining pressure, which is in good agreement with the linear Mohr-Coulomb criterion. However, the peak strength and the equivalent cohesion of fractured specimens decrease linearly and non-linearly with increasing damage, respectively. The elastic and secant modulus of fractured specimens increase linearly with increasing confining pressure but decrease with the damage. The short-term failure modes depend on the damage and change from typical shear failure modes to multiple shear failure modes with increasing damage.
- (2)
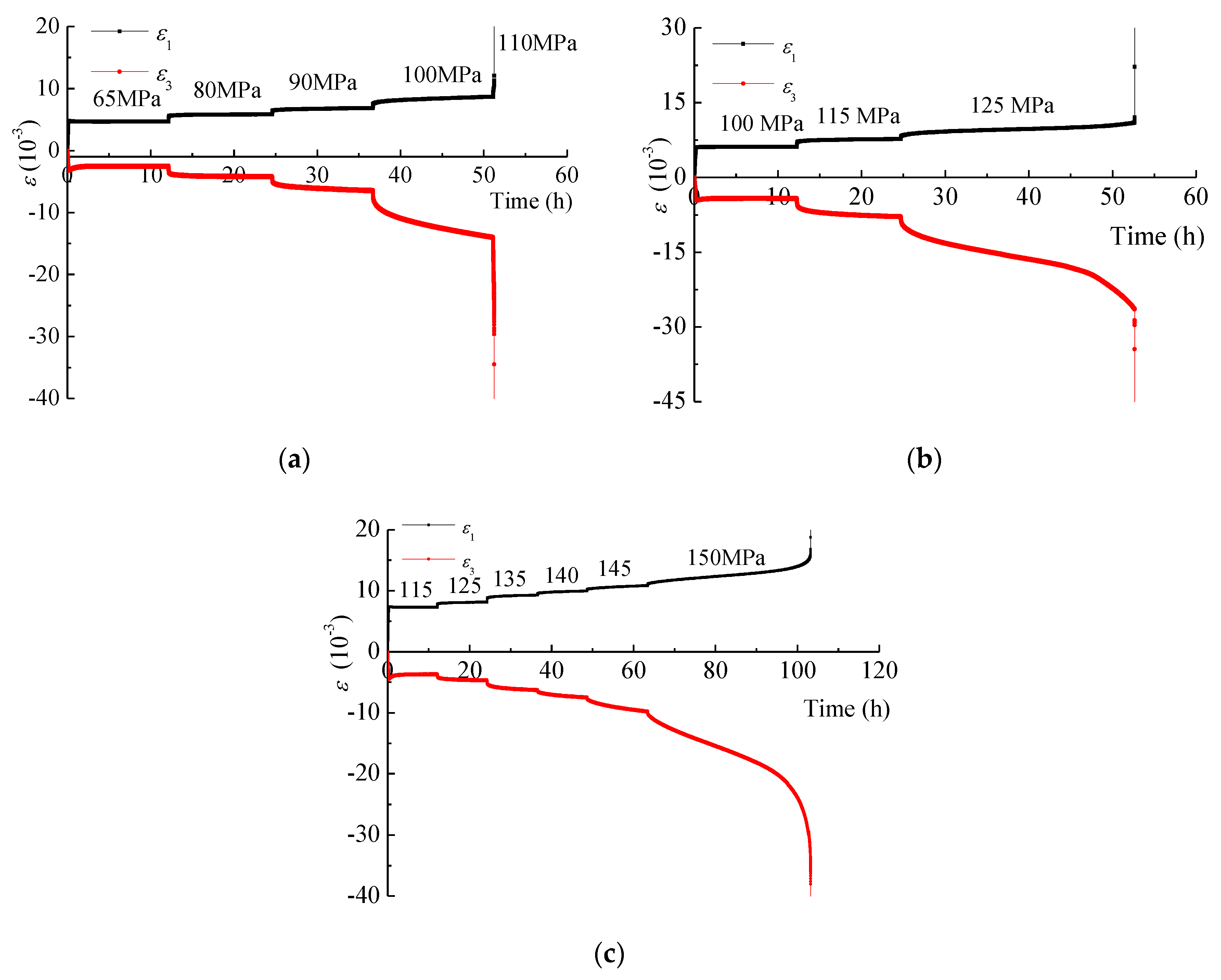
- The differential stress, confining pressure, and damage significantly affect the instantaneous and creep strain behavior of intact and fractured specimens. The instantaneous axial strain and creep strain increase linearly with increasing differential stress, exhibiting significant time-dependent behavior at high differential stress. However, for a given differential stress, the creep contribution to the deformation of specimens decreases with increasing confining pressure and damage.
- (3)
- The creep deformation of fractured specimens with different degrees of damage experienced primary, steady-rate and attenuated creep stage. Steady creep rate increases with increasing differential stress, but decreases with increasing confining pressure and damage. At the final stress level, the creep deformation of specimens is mainly accelerated creep or steady creep followed by accelerated creep, resulting in the creep failure.
- (4)
- The long-term and creep failure strength of fractured specimens increases linearly with increasing confining pressure, but decrease linearly with the damage. The creep failure modes of intact and fractured specimens depend on the damage and are mainly shear failure modes, which change from typical shear failure modes to multiple shear failure modes with increasing damage.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| D | Damage variable (0 ≤ D ≤ 1) |
| K | Correction factor |
| E | Elastic modulus |
| E50 | Secant modulus |
| c | Equivalent cohesion |
| R2 | Adj. R-Square |
| S | Differential stress |
| σ1 | Axial stress |
| σ3 | Confining pressure |
| σr | Residual strength |
| σp | Peak strength |
| σ∞ | Long-term strength |
| σf | Creep failure strength |
| ε1 | Axial strain |
| ε3 | Radial strain |
| ε | Strain |
| εv | Volumetric strain |
| εvd | Maximum compressive volumetric strain |
| εvr | Volumetric strain of the starting points of the residual stage |
| ε1d | Axial strain of the corresponding point for the maximum compressive volumetric strain |
| ε1p | Axial strain at the peak point |
| ε3p | Radial strain at the peak point |
| εvp | Volumetric strain at the peak point |
| εo | Instantaneous strain |
| εc | Creep strain |
| φ | Internal friction angle |
References
- Li, X.B.; Gong, F.Q.; Tao, M.; Dong, L.J.; Du, K.; Ma, C.D.; Zhou, Z.L.; Yin, T.B. Failure mechanism and coupled static-dynamic loading theory in deep hard rock mining: A review. J. Rock Mech. Geotech. Eng. 2017, 9, 767–782. [Google Scholar] [CrossRef]
- Xie, H.P.; Gao, M.Z.; Zhang, R.; Peng, G.Y.; Wang, W.Y.; Li, A.Q. Study on the mechanical properties and mechanical response of coal mining at 1000 m or deeper. Rock Mech. Rock. Eng. 2018, 52, 1475–1490. [Google Scholar] [CrossRef]
- Frantziskonis, G.; Desai, C.S. Constitutive model with strain softening. Int. J. Solids Struct. 1987, 23, 733–750. [Google Scholar] [CrossRef]
- Jing, L. A review of techniques, advances and outstanding issues in numerical modelling for rock mechanics and rock engineering. Int. J. Rock Mech. Min. Sci. 2003, 40, 283–353. [Google Scholar] [CrossRef]
- Malan, D.F. Simulation of the time-dependent behavior of excavations in hard rock. Rock Mech. Rock. Eng. 2002, 35, 225–254. [Google Scholar] [CrossRef]
- Bieniawski, Z.T. Mechanism of brittle fracture of rock: Parts I, II and III. Int. J. Rock Mech. Min. Sci. 1967, 4, 395–430. [Google Scholar] [CrossRef]
- Zhang, L.M.; Wang, Z.Q.; Li, H.F.; Sun, H. Theoretical and experimental study on siltstone brittle stress drop in post-failure region. J. Exp. Mech. 2008, 23, 234–240. [Google Scholar]
- Yang, S.Q.; Jing, H.W.; Cheng, L. Influences of pore pressure on short-term and creep mechanical behavior of red sandstone. Eng. Geol. 2014, 179, 10–23. [Google Scholar] [CrossRef]
- Han, L.J.; Yang, M.J. Re-fracture process and mechanical characteristics of cracked rock samples. Int. J. Rock Mech. Min. Sci. 2009, 46, 738–747. [Google Scholar] [CrossRef]
- Zhang, H.J.; Li, C.C. Effects of confining stress on the post-peak behaviour and fracture angle of fauske marble and iddeford granite. Rock Mech. Rock Eng. 2018, 52, 1377–1385. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, R.P.; Rao, K.S. Post failure behaviour of a rock mass under the influence of triaxial and true triaxial confinement. Eng. Geol. 2006, 84, 112–129. [Google Scholar] [CrossRef]
- Yang, S.Q.; Jiang, Y.Z.; Xu, W.Y.; Chen, X.Q. Experimental investigation on strength and failure behavior of pre-cracked marble under conventional triaxial compression. Int. J. Solids Struct. 2008, 45, 4796–4819. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.Q.; Huang, Y.H.; Ranjith, P.G. Failure mechanical and acoustic behavior of brine saturated sandstone containing two pre-existing flaws under different confining pressures. Eng. Fract. Mech. 2018, 193, 108–121. [Google Scholar] [CrossRef]
- Niu, S.J.; Jing, H.W.; Yang, X.X.; Yang, S.Q. Experimental study of strength degradation law of surrounding rock in fractured zone of deep roadway. Chin. J. Rock Mech. Eng. 2012, 31, 1587–1596. [Google Scholar]
- Fabre, G.; Pellet, F. Creep and time-dependent damage in argillaceous rocks. Int. J. Rock Mech. Min. Sci. 2016, 43, 950–960. [Google Scholar] [CrossRef]
- Ma, Z.G.; Gu, R.X.; Huang, Z.M.; Peng, G.; Zhang, L.; Ma, D. Experimental study on creep behavior of saturated disaggregated sandstone. Int. J. Rock Mech. Min. Sci. 2014, 66, 76–83. [Google Scholar] [CrossRef]
- Wang, Z.; Shen, M.R.; Gu, L.L.; Zhang, F. Creep behavior and long-term strength characteristics of greenschist under different confining pressures. Geotech. Test. J. 2018, 41, 55–71. [Google Scholar] [CrossRef]
- Zhao, J.; Feng, X.T.; Zhang, X.W.; Yang, C.X.; Zhou, Y.Y. Time-dependent behaviour and modeling of Jinping marble under true triaxial compression. Int. J. Rock Mech. Min. Sci. 2018, 110, 218–230. [Google Scholar] [CrossRef]
- Bieniawski, Z.T. Time-dependent behaviour of fractured rock. Rock Mech. 1970, 2, 123–137. [Google Scholar] [CrossRef]
- Guo, C.Y.; Xian, X.F.; Jiang, Y.D.; Tang, H.M.; Yao, W.J. Experimental research on creep of fractured sandstone. Chin. J. Rock Mech. Eng. 2009, 29, 990–995. [Google Scholar]
- Hamza, O.; Stace, R. Creep properties of intact and fractured muddy siltstone. Int. J. Rock Mech. Min. Sci. 2018, 106, 109–116. [Google Scholar] [CrossRef] [Green Version]
- Niu, S.J.; Dang, Y.H.; Feng, W.L.; Yang, D.F. Uniaxial experimental study of creep properties of sandstone in damage and fracture states. Rock Soil Mech. 2016, 37, 1249–1258. [Google Scholar]
- Yang, S.Q.; Jing, H.W.; Wang, S.Y. Experimental investigation on the strength, deformability, failure behavior and acoustic emission locations of red sandstone under triaxial compression. Rock Mech. Rock Eng. 2018, 45, 583–606. [Google Scholar] [CrossRef]
- Yang, S.Q.; Liu, X.R.; Jing, H.W. Experimental investigation on fracture coalescence behavior of red sandstone containing two unparallel fissures under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2013, 63, 82–92. [Google Scholar] [CrossRef]
- Duda, M.; Renner, J. The weakening effect of water on the brittle failure strength of sandstone. Geophys. J. Int. 2013, 192, 1091–1108. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.F.; Zhang, D.Y.; Niu, S.J.; Dang, Y.H.; Feng, W.L.; Ge, S.S. Experiment and study on mechanical property of sandstone post-peak under the cyclic loading and unloading. Geotech. Geol. Eng. 2018, 36, 1609–1620. [Google Scholar] [CrossRef]
- Liu, J.F.; Wang, L.; Pei, J.L.; Zheng, L.; Bian, Y. Experimental study on creep deformation and long-term strength of unloading-fractured marble. Eur. J. Environ. Civ. Eng. 2015, 19, s97–s107. [Google Scholar]
- Zong, Y.J.; Han, L.J.; Wei, J.J.; Wen, S.Y. Mechanical and damage evolution properties of sandstone under triaxial compression. Int. J. Min. Sci. Technol. 2016, 26, 601–607. [Google Scholar] [CrossRef]
- Zong, Y.J.; Han, L.J.; Meng, Q.B.; Wang, Y.C. Strength properties and evolution laws of cracked sandstone samples in re-loading tests. Int. J. Min. Sci. Technol. 2019. [Google Scholar] [CrossRef]
- Fairhurst, C.E.; Hudson, J.A. Draft ISRM suggested method for the complete stress-strain curve for the intact rock in uniaxial compression. Int. J. Rock Mech. Min. Sci. 1999, 36, 279–289. [Google Scholar]
- Zhang, Y.; Shao, J.F.; Xu, W.Y.; Jia, Y. Time-dependent behavior of cataclastic rocks in a multi-loading triaxial creep test. Rock Mech. Rock Eng. 2016, 49, 3793–3803. [Google Scholar] [CrossRef]
- Yang, S.Q.; Jiang, J.Z. Triaxial mechanical creep behavior of sandstone. Min. Sci. Technol. 2010, 20, 339–349. [Google Scholar] [CrossRef]
- Vaneghi, R.G.; Ferdosi, B.; Okoth, A.D.; Kuek, B. Strength degradation of sandstone and granodiorite under uniaxial cyclic loading. J. Rock Mech. Geotech. Eng. 2018, 10, 117–126. [Google Scholar] [CrossRef]
- Niu, S.J.; Ge, S.S.; Yang, D.F.; Dang, Y.H.; Yu, J.; Zhang, S. Mechanical properties and energy mechanism of saturated sandstones. J. Cent. South Univ. Technol. 2018, 25, 1447–1463. [Google Scholar] [CrossRef]
- Alonso, E.; Alejano, L.R.; Varas, F.; Fdez-Manin, G.; Carranza-Torres, C. Ground response curves for rock masses exhibiting strain-softening behavior. Int. J. Numer. Anal. Methods Geomech. 2003, 27, 1153–1185. [Google Scholar] [CrossRef]
- Pourhosseini, O.; Shabanimashcool, M. Development of an elasto-plastic constitutive model for intact rocks. Int. J. Rock Mech. Min. Sci. 2014, 66, 1–12. [Google Scholar] [CrossRef]
- Xu, P.; Yang, S.Q. Permeability evolution of sandstone under short-term and long-term triaxial compression. Int. J. Rock Mech. Min. Sci. 2016, 85, 152–164. [Google Scholar] [CrossRef]
- Shen, M.R.; Chen, H.J. Testing study of long-term strength characteristics of red sandstone. Rock Soil Mech. 2011, 32, 3301–3305. [Google Scholar]
- Zhang, Q.Y.; Yang, W.D.; Chen, F.; Li, W.G.; Wang, J.H. Long-term strength and microscopic failure mechanism of hard brittle rocks. Chin. J. Geotech. Eng. 2011, 33, 1910–1918. [Google Scholar]

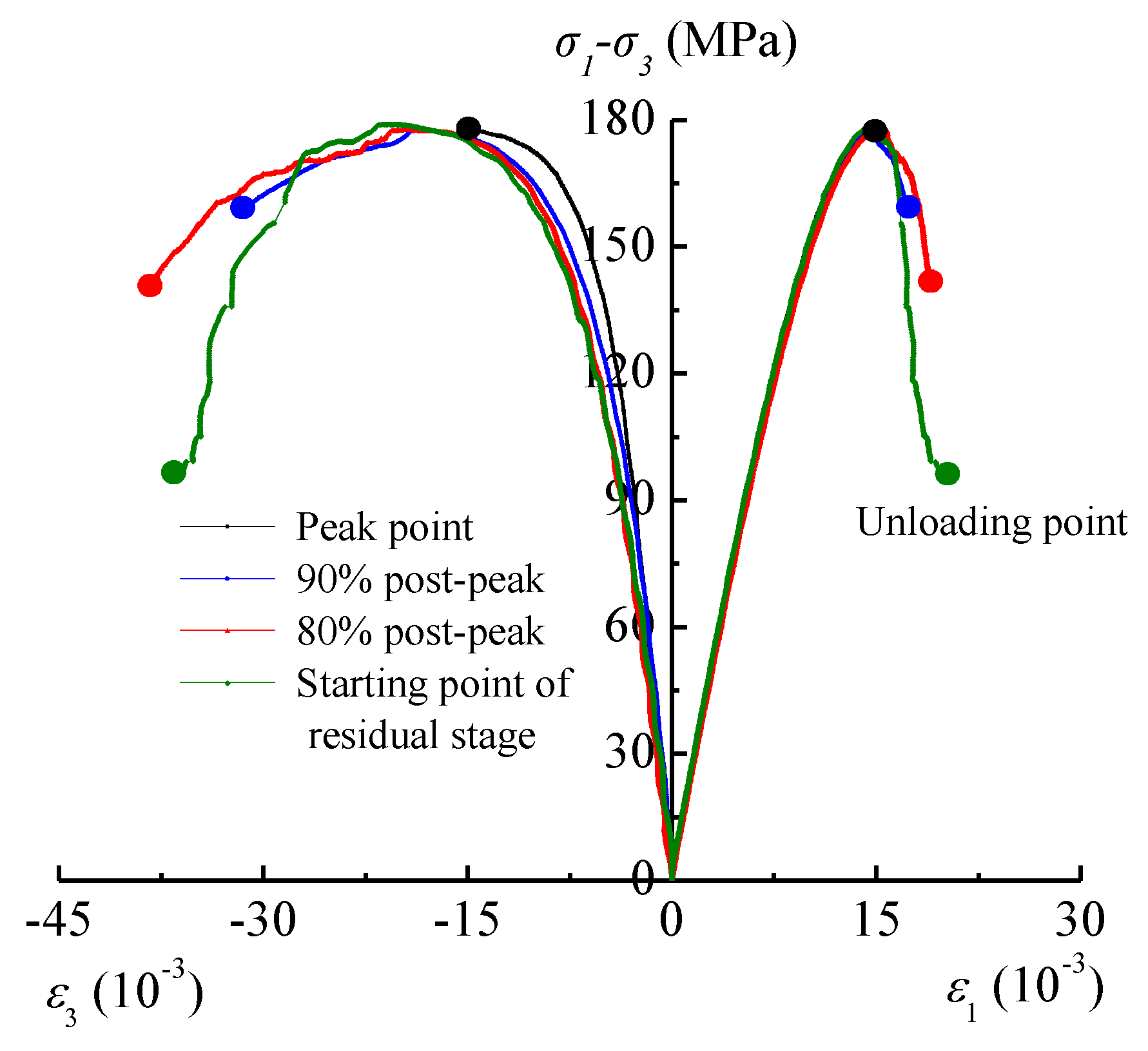


| Specimen | Design Unloading Points | Actual Unloading Points | Strain at Unloading Points (10−3) | Damage at Unloading Points | |||||
|---|---|---|---|---|---|---|---|---|---|
| Stress (MPa) | Location on Curve | Stress (MPa) | Percentage of Strength (%) | Axial | Radial | Volumetric | Actual Damage | Average Damage | |
| T-4 | 177.24 | Peak point | 177.51 | 100.15 | 15.25 | −20.53 | −25.81 | 0.158 | 0.158 |
| T-5 | 177.19 | 99.97 | 14.54 | −20.12 | −25.70 | 0.157 | |||
| T-6 | 177.27 | 100.02 | 14.36 | −20.08 | −25.80 | 0.158 | |||
| R-4 | 176.95 | 99.84 | 14.25 | −19.88 | −25.50 | 0.156 | |||
| R-5 | 177.84 | 100.34 | 14.99 | −20.53 | −26.08 | 0.160 | |||
| R-6 | 178.11 | 100.49 | 14.59 | −20.17 | −25.75 | 0.158 | |||
| T-7 | 159.52 | 90% post-peak | 159.43 | 89.89 | 17.71 | −33.12 | −48.53 | 0.297 | 0.294 |
| T-8 | 162.80 | 89.93 | 18.22 | −32.23 | −46.24 | 0.283 | |||
| T-9 | 159.25 | 89.31 | 18.19 | −33.67 | −49.15 | 0.301 | |||
| R-7 | 158.78 | 89.64 | 17.32 | −32.41 | −47.50 | 0.291 | |||
| R-8 | 160.80 | 90.36 | 17.49 | −32.67 | −47.85 | 0.293 | |||
| R-9 | 159.70 | 90.22 | 18.44 | −33.43 | −48.42 | 0.296 | |||
| T-10 | 141.79 | 80% post-peak | 142.21 | 80.17 | 19.62 | −37.13 | −54.64 | 0.334 | 0.347 |
| T-11 | 142.05 | 80.03 | 19.5 | −38.90 | −58.30 | 0.357 | |||
| T-12 | 141.84 | 80.02 | 18.96 | −38.17 | −57.38 | 0.351 | |||
| R-10 | 141.63 | 79.94 | 18.71 | −37.62 | −56.53 | 0.346 | |||
| R-11 | 142.00 | 80.22 | 19.09 | −38.02 | −56.94 | 0.348 | |||
| T-13 | 100.20 | Starting point of residual stage | 101.46 | 56.04 | 21.16 | −46.54 | −71.92 | 0.440 | 0.440 |
| T-14 | 101.33 | 57.24 | 22.80 | −46.86 | −70.92 | 0.434 | |||
| T-15 | 100.92 | 56.54 | 21.69 | −46.41 | −71.13 | 0.435 | |||
| R-13 | 102.19 | 57.40 | 21.01 | −46.76 | −72.51 | 0.443 | |||
| R-14 | 102.40 | 57.90 | 24.06 | −48.58 | −73.10 | 0.447 | |||
| R-15 | 100.62 | 56.77 | 23.76 | −48.01 | −72.26 | 0.442 | |||
| Specimen | D | σ3 (MPa) | σp (MPa) | σr (MPa) | E (GPa) | E50 (GPa) | ε1p (10−3) | ε3p (10−3) | εvp (10−3) |
|---|---|---|---|---|---|---|---|---|---|
| T-1 | 0 | 5 | 126.54 | 58.14 | 14.73 | 14.76 | 10.56 | −19.86 | −29.17 |
| T-2 | 10 | 137.69 | 59.73 | 14.81 | 14.97 | 11.31 | −12.63 | −13.91 | |
| T-3 | 20 | 171.53 | 76.15 | 16.28 | 17.15 | 13.63 | −15.41 | −17.19 | |
| T-4 | 0.158 | 5 | 89.10 | 44.82 | 10.16 | 10.31 | 9.92 | −27.15 | −44.39 |
| T-5 | 10 | 106.43 | 45.44 | 11.48 | 11.32 | 10.00 | −20.18 | −30.37 | |
| T-6 | 20 | 140.63 | 73.45 | 13.25 | 13.13 | 13.20 | −24.53 | −35.86 | |
| T-7 | 0.294 | 5 | 64.20 | 44.95 | 7.69 | 7.77 | 10.77 | −33.01 | −55.24 |
| T-8 | 10 | 88.51 | 51.43 | 9.87 | 9.77 | 10.89 | −25.64 | −40.39 | |
| T-9 | 20 | 112.06 | 76.37 | 11.79 | 11.38 | 12.54 | −25.29 | −38.04 | |
| T-10 | 0.347 | 5 | 40.90 | 22.01 | 6.15 | 6.16 | 10.84 | −21.33 | −31.82 |
| T-11 | 10 | 70.94 | 41.78 | 8.97 | 8.83 | 8.61 | −18.15 | −27.68 | |
| T-12 | 20 | 93.71 | 68.86 | 11.03 | 10.88 | 12.11 | −20.00 | −38.79 | |
| T-13 | 0.440 | 5 | 34.62 | 36.43 | 6.39 | 6.46 | 5.63 | −7.51 | −9.39 |
| T-14 | 10 | 51.37 | 63.13 | 7.92 | 7.87 | 7.14 | −10.16 | −13.19 | |
| T-15 | 20 | 63.97 | 75.89 | 11.13 | 10.79 | 5.69 | −6.76 | −12.94 |
| D | c (MPa) | φ (°) |
|---|---|---|
| 0 | 31.31 | 30.52 |
| 0.157 | 19.17 | 33.93 |
| 0.294 | 14.84 | 30.97 |
| 0.347 | 7.99 | 33.12 |
| 0.440 | 10.47 | 17.06 |
| Specimen | D | σ3 (MPa) | σp (MPa) | S1 (MPa) | S2 (MPa) | S3 (MPa) | S4 (MPa) | S5 (MPa) | S6 (MPa) |
|---|---|---|---|---|---|---|---|---|---|
| R-1 | 0 | 5 | 126.54 | 65 | 80 | 90 | 100 | 110 | / |
| R-2 | 10 | 137.69 | 100 | 115 | 125 | / | / | / | |
| R-3 | 20 | 171.53 | 115 | 125 | 135 | 140 | 145 | 150 | |
| R-4 | 0.158 | 5 | 89.10 | 50 | 60 | 65 | 70 | 75 | 80 |
| R-5 | 10 | 106.43 | 70 | 85 | 95 | 105 | 110 | 115 | |
| R-6 | 20 | 140.63 | 100 | 110 | 120 | 125 | / | / | |
| R-7 | 0.294 | 5 | 64.20 | 35 | 45 | 50 | / | / | / |
| R-8 | 10 | 88.51 | 60 | 70 | 75 | 80 | 85 | 90 | |
| R-9 | 20 | 112.06 | 70 | 80 | 90 | 100 | 105 | / | |
| R-10 | 0.347 | 5 | 40.90 | 20 | 25 | 30 | 35 | 40 | 45 |
| R-13 | 0.440 | 5 | 34.62 | 20 | 30 | 35 | 40 | / | / |
| R-14 | 10 | 51.37 | 25 | 30 | 35 | 40 | 45 | 50 | |
| R-15 | 20 | 63.97 | 35 | 40 | 45 | 50 | 55 | 60 |
| Specimen | D | σ3 (MPa) | S1 | S2 | S3 | S4 | S5 | S6 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| εo | εc | εo | εc | εo | εc | εo | εc | εo | εc | εo | εc | |||
| R-1 | 0 | 5 | 4.591 | 0.052 | 0.820 | 0.356 | 0.550 | 0.493 | 0.551 | 1.238 | 0.706 | 48.740 | / | / |
| R-2 | 10 | 5.862 | 0.274 | 0.815 | 0.738 | 0.533 | 49.880 | / | / | / | / | / | / | |
| R-3 | 20 | 7.181 | 0.131 | 0.458 | 0.351 | 0.545 | 0.620 | 0.178 | 0.505 | 0.180 | 0.680 | 0.213 | 22.228 | |
| R-4 | 0.158 | 5 | 5.269 | 0.502 | 0.583 | 0.323 | 0.331 | 0.590 | 0.298 | 0.665 | 0.275 | 0.896 | 0.300 | 32.346 |
| R-5 | 10 | 5.796 | 0.132 | 0.657 | 0.408 | 0.445 | 0.243 | 0.481 | 0.236 | 0.283 | 0.382 | 0.300 | 8.357 | |
| R-6 | 20 | 7.141 | 0.170 | 0.553 | 0.384 | 0.514 | 1.003 | 0.202 | 7.620 | / | / | / | / | |
| R-7 | 0.294 | 5 | 5.409 | 0.327 | 0.428 | 0.476 | 0.381 | 6.757 | / | / | / | / | / | / |
| R-8 | 10 | 5.939 | 0.265 | 0.811 | 0.344 | 0.291 | 0.346 | 0.313 | 0.382 | 0.307 | 0.645 | 0.296 | 12.148 | |
| R-9 | 20 | 6.387 | 0.087 | 0.655 | 0.322 | 0.656 | 0.391 | 0.640 | 0.632 | 0.581 | 8.687 | / | / | |
| R-10 | 0.347 | 5 | 2.606 | 0.245 | 0.483 | 0.216 | 0.416 | 0.284 | 0.442 | 0.341 | 0.395 | 0.456 | 0.422 | 14.879 |
| R-13 | 0.440 | 5 | 2.524 | 0.027 | 0.417 | 0.904 | 0.395 | 0.464 | 0.502 | 2.824 | / | / | / | / |
| R-14 | 10 | 3.718 | 0.296 | 0.389 | 0.332 | 0.392 | 0.341 | 0.409 | 0.471 | 0.318 | 0.651 | 0.418 | 13.983 | |
| R-15 | 20 | 2.842 | 0.129 | 0.242 | 0.187 | 0.260 | 0.184 | 0.270 | 0.224 | 0.262 | 0.225 | 0.287 | 0.475 | |
| S7 | S8 | S9 | S10 | S11 | / | |||||||||
| 0.232 | 2.538 | 0.288 | 5.095 | 0.258 | 4.263 | 0.262 | 4.327 | 0.275 | 6.575 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zong, Y.; Han, L.; Jin, Y.; Zhao, W.; Meng, L. Experimental Investigation on the Post-Peak Short-Term and Creep Behavior of Fractured Sandstone. Energies 2020, 13, 598. https://doi.org/10.3390/en13030598
Zong Y, Han L, Jin Y, Zhao W, Meng L. Experimental Investigation on the Post-Peak Short-Term and Creep Behavior of Fractured Sandstone. Energies. 2020; 13(3):598. https://doi.org/10.3390/en13030598
Chicago/Turabian StyleZong, Yijiang, Lijun Han, Yuhao Jin, Weisheng Zhao, and Lingdong Meng. 2020. "Experimental Investigation on the Post-Peak Short-Term and Creep Behavior of Fractured Sandstone" Energies 13, no. 3: 598. https://doi.org/10.3390/en13030598
APA StyleZong, Y., Han, L., Jin, Y., Zhao, W., & Meng, L. (2020). Experimental Investigation on the Post-Peak Short-Term and Creep Behavior of Fractured Sandstone. Energies, 13(3), 598. https://doi.org/10.3390/en13030598






