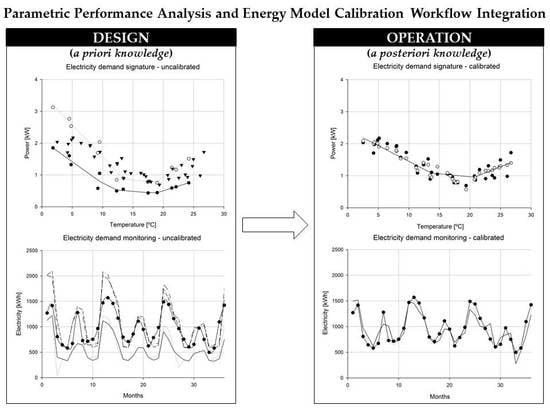
Parametric Performance Analysis and Energy Model Calibration Workflow Integration—A Scalable Approach for Buildings

Abstract

High efficiency paradigms and rigorous normative standards for new and existing buildings are fundamental components of sustainability and energy transitions strategies today. However, optimistic assumptions and simplifications are often considered in the design phase and, even when detailed simulation tools are used, the validation of simulation results remains an issue. Further, empirical evidences indicate that the gap between predicted and measured performance can be quite large owing to different types of errors made in the building life cycle phases. Consequently, the discrepancy between a priori performance assessment and a posteriori measured performance can hinder the development and diffusion of energy efficiency practices, especially considering the investment risk. The approach proposed in the research is rooted on the integration of parametric simulation techniques, adopted in the design phase, and inverse modelling techniques applied in Measurement and Verification (M&V) practice, i.e., model calibration, in the operation phase. The research focuses on the analysis of these technical aspects for a Passive House case study, showing an efficient and transparent way to link design and operation performance analysis, reducing effort in modelling and monitoring. The approach can be used to detect and highlight the impact of critical assumptions in the design phase as well as to guarantee the robustness of energy performance management in the operational phase, providing parametric performance boundaries to ease monitoring process and identification of insights in a simple, robust and scalable way.

1. Introduction

The increasing effort towards resource efficiency and sustainability in the building sector [1] is progressively changing the way buildings are designed and managed. The decarbonisation of the built environment is a key objective for energy and environmental policies in the EU [2,3] and worldwide [4]. New efficiency paradigms (i.e., NZEBs) regarding existing and new buildings [5] have been introduced in recent years in the EU and other countries, at the global level. Passive design strategies making use of solar energy and internal gains are well established [6]. However, optimistic assumptions are often made in the design phase and semi-stationary calculation methodologies are still commonly employed [7]. Further, the gap between simulated and measured performance is a general issue [8] and the benefits of “green” design practices should be critically evaluated [9,10], by assessing transparently the impact of human and technical factors [11]. With respect to human factors in particular, the effects of occupants’ behaviour [12] and of their comfort preferences [13] on building performance are generally overlooked in the design phase. This paper aims to present a way to integrate modelling methodologies used across building life cycle phases, from design to operation, in a simple and scalable way. A residential building has been chosen as a case study. The building is a detached single family certified Passive House built in Italy, in the Province of Forlì-Cesena, in the Emilia Romagna region. It has been monitored for three years, learning incrementally insights by comparing the original design phase simulation data with actual measured data.

2. Background and Motivation

The research work answers to the necessity of linking parametric performance analysis and model calibration from a conceptual and practical point of view. Building performance parametric and probabilistic analysis is an essential tool today to ensure robustness of performance and the importance of the Design of Experiments (DOE) is becoming clear [14,15,16,17], both for new and retrofitted buildings [18,19]. For example, accounting for the robustness of performance estimates with respect to economic indicators (e.g., in cost-optimal analysis [20,21,22]) is important because uncertainty can affect the credibility and, consequently, hinder the success of policies oriented to investments on efficiency in the built environment. In this research, baseline design simulation, i.e., original design simulation for the building project, was used as baseline and multiple Design of Experiments (DOE) simulations were run to compute the impact of the variability of multiple inputs (envelope components performance, operational settings, occupant’s behaviour and comfort preferences, etc.), as specified in detail in Section 3.1. The parametric approach aims at detecting critical assumptions in the preliminary design stage, to guarantee a more robust evaluation of performance [15,23]. In simpler terms, the objective of the parametric simulation is to include from the very beginning more realistic, and possibly less optimistic, assumptions, and use the simulation outcomes as boundaries for comparative performance analysis during the operation phase. In order to reduce the computational effort, meta-modelling techniques can be used [24] (i.e., surrogate, reduced-order). The choice of meta-modelling techniques depends on several factors [25]: they are very flexible and they can be employed for different uses such as the optimization of design [26], model calibration [24] and control [27]. Additionally, different meta-models can give similar performance on the same problem [24,28]. In this research regression models were tested for performance prediction, using energy signatures [29,30] regressed against weather data [24,31,32,33]. Therefore, multiple piecewise linear multivariate regression models are trained first on simulation data, as described in Section 3.2. These models are, then, updated and calibrated on measured data during three years of operation. Visualization and numerical techniques are combined to allow an intuitive results interpretation as well as to facilitate human interaction in the calibration process, encompassing model training and testing phases. While being less sophisticated than other machine learning techniques available today, multivariate regression models have been chosen because of a set of important features. First of all, standardization [29,30], temporal [34,35] and spatial scalability [36,37], weather normalization using Variable Base Degree-Days (VBDD) [38,39]. After that, the applicability to multiple types of building end-uses [33] and the flexibility with respect to diverse operational strategies and conditions [12,40,41], e.g., accounting for different levels of thermal inertia [42]. Further, the possibility to easily extend their applicability using techniques such as Monte Carlo simulation [41], Bayesian analysis [43,44], eventually exploiting the approximated physical interpretation of coefficients [33,45]. Finally, this technique is suitable for performance tracking with periodic recalibration in changing climate conditions [46,47] and can complement the analysis of performance of technologies such as heat pumps and cooling machines [48,49], considering also exergy balance [50,51]. In the next Section the research methodology is explained, starting from parametric simulation and, then, moving to regression analysis on energy signatures.

3. Research Methodology

In the original design of the building, Passive House Planning package (PHPP) [52] was used for simulation. Instead, in this study we used a validated grey-box dynamic model [53,54] to perform multiple simulation runs in a reduced time frame. Indeed, grey-box models are very flexible and can be used in the inverse mode to estimate lumped properties of the actual building, eventually extending their applicability with Bayesian analysis [55,56] or Dempster-Shafer theory of the evidence [57]. In this case, the original building design configuration was considered as a baseline. Then parametric simulations were run using the Design of Experiments (DOE) methodology [58], similarly to other research studies on the variability in building performance simulation [15,16,59]. Variations and multiple runs are meant to reproduce the actual variability of the performance of envelope components, air-change rates and of occupants’ behaviour and comfort preferences. As described before, these variations in the operation phase (generally) entail a significant gap between simulation and actual measured performance.

3.1. Parametric Performance Analysis of the Case Study

The case study chosen is a single family detached Passive House built in Italy, in the Province of Forlì-Cesena, in the Emilia Romagna region. The case study was chosen because it represents an example of a high efficiency building design and we wanted to analyse its actual performance in operation (as well as its evolution in time) together with the applicability of the approach proposed, based on an extension of well-established M&V techniques. The approach proposed substantially anticipates the use of inverse modelling at the design stage and the goal of parametric simulation is that of creating an envelopment of data to be considered as possible scenarios of actual building performance in operation. The building has a high level of insulation of envelope components and it is equipped with mechanical ventilation with heat recovery (air/air heat exchanger), a solar thermal to integrate DHW production, a ground-source heat pump system (GSHP) and a PV plant for local electricity production. Simulation input data are summarized in

Table 1. Simulation data from baseline and two-level Design of Experiments (DOE).

Group	Type	Unit	Baseline	Design of Experiment
				Levels
				−1	+1
Climate	UNI 10349:2016	-
Geometry	Gross volume	m3	1557
	Net volume	m3	1231
	Heat loss surface area	m2	847
	Net floor area	m2	444
	Surface/volume ratio	1/m	0,54
Envelope	U value external walls	W/(m2K)	0.18	0.23	0.27
	U value roof	W/(m2K)	0.17	0.21	0.26
	U value transparent components	W/(m2K)	0.83	1.04	1.25
Activities	Internal gains (lighting, appliances and occupancy, daily average)	W/m2	1	1	1.5
	Occupants	-	5	5	5
Control and operation	Heating set-point temperature	°C	20	20	22
	Cooling set-point temperature	°C	26	26	28
	Air-change rate (infiltration and mechanical ventilation with heat recovery in heating mode)	vol/h	0.2	0.2	0.4
	Shading factor (solar control summer mode)	-	0.5	0.5	0.7
	Domestic hot water demand	l/person/day	50	50	70
	Schedules—DOE constant operation	-	0.00–23.00	0.00–23.00	0.00–23.00
	Schedules—DOE behaviour 1	-	7.00–22.00	7.00–22.00	7.00–22.00
	Schedules—DOE behaviour 2	-	7.00–9.00, 17.00–22.00	7.00–9.00, 17.00–22.00	7.00–9.00, 17.00–22.00

, reporting baseline configuration with respect to the two level Design of Experiments (DOE) configurations. The U values in Table 1 were averaged with respect to the external surface of components (summarized then in the heat loss surface area) and considered the impact of thermal bridges. Technical systems data are synthesized hereafter in

Table 2. Technical systems data.

Technical System	Technology	Type	Unit	Value
Heating/Cooling system	Ground Source Heat Pump	Brine/Water Heat Pump	kW	8.4
	Ground heat exchanger	Borehole Heat Exchanger (2 double U boreholes)	m	100
On-site energy generation	Building Integrated Photo-Voltaic (BIPV)	Polycrystalline Silicon	kWp	9.2
	Solar Thermal	Glazed flat plate collector	m2	4.32
		Domestic Hot Water storage	m3	0.74

.

In order to simulate realistically multiple operating conditions, different schedules for internal gains (lighting, appliances and people), heating, cooling and air-exchange rates (ventilation/infiltration) have been created. Three DOE simulation runs were performed, one for each operational schedule, (simulating diverse occupants’ behaviour) namely continuous operation (constant operation profile), operation mainly from 7.00 to 22.00 (behaviour 1), operation mainly from 7.00 to 9.00 and from 17.00 to 22.00 (behaviour 2).

The typical Key Performance Indicators (KPIs) considered in building energy analysis are final energy use (e.g., thermal demand for heating, cooling and domestic hot water), energy demand (e.g., energy carriers such as electricity, natural gas, etc.), cost of energy services, primary energy use and CO₂ emissions. In this study, we concentrate on aggregated electricity demand for heating, cooling, domestic hot water (DHW), lighting and appliances, because all these services are supplied by electricity.

3.2. Parametric Performance Analysis and Model Calibration Integrated Workflow

The choice in this research is to adopt a piecewise linear multivariate regression approach, using energy signature technique [29] to analyse both data generated by means of parametric simulation in the design phase and monitored data during the calibration phase. As a matter of fact, for the calibration purpose, many types of meta-models are available. A regression approach is proposed in this study following the arguments presented in Section 2.

Table 3. Regression models for heating, cooling and baseline demand analysis.

Demand	Model Type 1	Model Type 2
Heating	$q_{h,1}=a_0+a_1{\theta }_e+\epsilon$	$q_{h,2}=b_0+b_1{\theta }_e+b_2{I}_{sol}+\epsilon$
Cooling	$q_{c,1}=c_0+c_1{\theta }_e+\epsilon$	$q_{c,2}=d_0+d_1{\theta }_e+d_2{I}_{sol}+\epsilon$
Base load	$q_{b,1}=e_0+e_1{\theta }_e+\epsilon$	$q_{b,2}=f_0+f_1{\theta }_e+f_2{I}_{sol}+\epsilon$

shows the piecewise linear multivariate regression models [30] implemented. Three linear sub-models compose the overall predictive model, each one defined between specific boundaries for heating and cooling and baseline demand, respectively. Dummy variables are added to enable a piecewise linear model formulation. Dummy variables are binary (0,1) and are multiplied by the original independent variable to obtain interaction variables, in such a way that the total model is the sum of heating, cooling and base load components (piecewise linear components). Regression models consider only external temperature dependence, in the case of model type 1 while, external temperature together with solar radiation dependence, in the case of model type 2.

To assess and compare the simulation data in the design phase and measured data in the operation phase, basic statistical indicators are used together with statistical indicators specific for state-of-the-art model calibration procedures [30,60,61]. The basic statistical indicators chosen were R² and Mean Absolute Percentage Error (MAPE). The determination coefficient R² expresses the goodness of a regression model fit, varying from 0 to 1 (or 0% to 100%), where the maximum values indicate that the model fits perfectly the data. The R² was calculated as 1 minus the ratio between the sum of the squares of residuals and total sum of the squares using Equation (1). Mean Absolute Percentage Error (MAPE) represents the average absolute value of the difference between measured and predicted data, normalized to measured data. Equation (2) reports the MAPE calculation (we can substitute M_i with S_i when simulated data are used instead of measured ones).

$$R^2=1-\frac{S{S}_{res}}{S{S}_{tot}}=1-\frac{{\displaystyle \sum _i}{\left(y_i-{\hat{y}}_i\right)}^2}{{\displaystyle \sum _i}{\left(y_i-{\overline{y}}_i\right)}^2}$$

(1)

$$MAPE=\frac{1}{n}{\displaystyle \sum _i\left|\frac{M_i-P_i}{M_i}\right|}·100$$

(2)

Going to the specific indicators for calibration, Normalized Mean Bias Error (NMBE) and Cv(RMSE) Coefficient of Variation of Root Mean Squared Error (RMSE) were used. NMBE is the total sum of the differences between measured (or simulated in the case of design phase, replacing M_i with S_i) and predicted energy consumption at the calculated time intervals, in this case monthly, divided by the sum of the measured (or simulated) energy consumption. NMBE is reported in Equation (3). An overestimation of energy consumption determines a positive value of NMBE while an underestimation determines a negative one.

$$NMBE=-\frac{{\displaystyle \sum _i(M_i-P_i)}}{{\displaystyle \sum _i{M}_i}}·100$$

(3)

Cv(RMSE) is the normalized measure of the differences between measured M_i (or simulated S_i in the case of design phase) and predicted data P_i. It is based on RMSE, a measure of the sample deviation of the differences among values measured and predicted by the model divided by A, which represents measured (or simulated in the case of design phase, replacing M_i with S_i) average energy consumption. The lower the Cv(RMSE) value the better calibrated the model is. Cv(RMSE) calculation is illustrated in Equations (4), (5) and (6).

$$Cv\left(RMSE\right)=\frac{RMSE}{A}·100$$

(4)

$$RMSE=\sqrt{\frac{{\displaystyle \sum _i{\left(M_i-P_i\right)}^2}}{n}}$$

(5)

$$A=\frac{{\displaystyle \sum _i{M}_i}}{n}$$

(6)

The threshold metrics considered in different protocols for M&V and calibration at the state-of-the-art [23,44,45], are discussed in the literature [62] and reported in

Table 4. Threshold limits of metrics for model calibration with monthly data.

Metric	ASHRAE Guidelines 14	IPMVP	FEMP
NMBE (%)	±5	±20	±5
Cv(RMSE) (%)	15	-	15

for calibration with monthly data.

Finally, the analysis of deviations (differences) between measurements and predictions can be useful to discover hidden patterns in data. Equation (7) was used for this purpose. The energy consumption is underestimated when a positive deviation occurs at a certain point (i.e., measured consumption M_i is higher than predicted P_i) while an overestimation takes place when a negative deviation derives from calculation (i.e., measured consumption M_i is lower than predicted P_i).

$$D_i=M_i-P_i$$

(7)

4. Results and Discussion

This study aimed to illustrate an integrated workflow from the parametric performance analysis to model calibration through its essential steps, using a Passive House case study as example. First, the results obtained from the baseline and DOE simulations, performed according to the input data reported in Section 3.1 in Table 1, were used to calculate Key Performance Indicators (KPIs) on a yearly base. These indicators serve as a basis for the comparison of parametric simulation output data. In Figure 1 we report a summary of the weather data used for simulation (design weather data file) and during model calibration (the monitoring period). More specifically, weather data reported are monthly average external air temperatures and daily average global solar radiation on the horizontal surface. These data are representative of typical average days for every month.

While the integrated workflow presented could be applied in a more general way, following the arguments reported in Section 2, the focus of this study was put on analysing the aggregated electricity demand data. Electricity demand was divided by the square meters of the net floor area and reported hereafter in

Table 5. Comparison of the baseline and two-level DOE simulation data—lower bound and upper bound of Key Performance Indicator (KPI) yearly values with respect to the baseline.

KPI	Unit	Baseline	Design of Experiment
			LB	UB
Electricity consumption	kWh/m2	20.8	16.9	31.7

for the baseline, lower bound (LB) and upper bound (UB), which corresponded to the envelopment of outputs from the DOE simulation.

In Figure 2 the detailed composition of electricity demand for baseline simulation configuration (input configuration is provided in Table 1) is shown. The electricity demand for domestic hot water service was negligible in the summer months as it was supplied by the solar thermal system (Table 2).

Simulation data were then used to train regression models type 1 and type 2, as explained in Section 3.2. In this phase models were still uncalibrated, i.e., they were not calibrated on measured data but simply trained on simulation data, in order to verify their applicability and goodness of fit (i.e., the ability to approximate the results of dynamic simulations). The statistical indicators obtained, introduced in Section 3.2, are reported in

Table 6. Model training on the design phase data (uncalibrated models, a priori data)

Model Type	Calibration Process Stage	Training Dataset	Testing Dataset	Statistical Indicators
				R2	MAPE	NMBE	Cv(RMSE)
				%	%	%	%
Type 1	Uncalibrated	DOE - Overall LB	-	93.65	9.34	0.06	13.58
Type 1	Uncalibrated	DOE - Overall UB	-	96.64	7.33	0.02	9.01
Type 2	Uncalibrated	DOE - Overall LB	-	99.90	1.42	−0.02	1.65
Type 2	Uncalibrated	DOE - Overall UB	-	99.78	1.93	−0.01	2.36

, showing that both model types can fit simulation data reasonably well, even though the performance of model type 2 was comparatively higher.

Subsequently, the first step of the parametric analysis corresponds to the comparison of monthly electric energy demand data for the baseline and DOE lower bound and upper bound configurations, as in Table 1 (parametric simulation input). The comparison is reported in Figure 3, showing on the left side the monthly energy values obtained by simulation and on the right side the corresponding parametric energy signatures (expressed as average power). Energy signatures enable the comparison between simulated and measured data during the subsequent monitoring process and represent the a priori knowledge we have about the building performance, which we could use to identify anomalies visually and numerically. Indeed, the regression models developed were independent of the specific weather data used, as weather data were the independent variables (air temperature and solar radiation in this case), while the average power was the dependent variable. As shown in Figure 1, 4 years of weather data were considered in this study, 1 design weather data file and 3 years of monitoring data.

After that, the results of the incremental model calibration process during the three year monitoring period are reported for both model types in

Table 7. Model training and testing on the operation phase data (calibrated models, a posteriori knowledge).

Model Type	Calibration Process Stage	Training Dataset	Testing Dataset	Statistical Indicators
				R2	MAPE	NMBE	Cv(RMSE)
				%	%	%	%
Type 1	Partial Calibrated	Measured data—Year 1 and 2		82.64	11.44	0.04	13.44
			Measured data—Year 3	69.74	18.40	−6.95	19.75
Type 2	Calibrated	Measured data—Year 1 and 2	-	86.07	9.97	0.05	12.02
		-	Measured data—Year 3	87.54	11.97	−2.21	12.50

. The measured data were more scattered compared to the simulated ones, leading to higher R², MAPE and Cv(RMSE). In this phase, the type 1 model did not reach the calibration threshold with 2 years of monthly data because Cv(RMSE) was 19.75%, higher than 15% threshold reported in Table 4. So, it could be defined as partially calibrated. Instead, model type 2 was calibrated, as confirmed by statistical indicators in training and testing phases.

In any case, a reasonable amount of data and a corresponding time span are needed. In this case study, two years of monthly data to reach calibration or partial calibration of regression models were necessary. As described before, uncalibrated design models, reported in Table 6 and depicted in Figure 3, could provide a useful support in the monitoring process, as they represent estimated bounds of performance (lower and upper bounds of a data envelopment) determined by means of parametric simulation. The assumptions that characterize parametric building performance simulation themselves can be updated based on experience gained in model calibration processes in real buildings, e.g., by reducing or increasing the level of variability of a certain input quantity (Table 1) when more detailed information is available. For this purpose, a priori knowledge represented by simulated data, i.e., uncalibrated models can be compared with a posteriori knowledge, represented by measured data, as shown on the left side of Figure 4. In the same figure, on the right side, a posteriori knowledge, i.e., calibrated models with measured data (at the end of the monitoring period) are reported for comparison.

The analysis of the changes of models’ regression coefficients during the calibration process and, in particular, changes of slopes and break points for piecewise linear energy signature models, constitute starting points for a more in depth analysis, based on approximate physical interpretation as explained in Section 2 and Section 3. Hereafter, we illustrate how the monitoring process evolved in time. By plotting the data with respect to time, i.e., months of monitoring, we obtained Figure 5 and Figure 6 for uncalibrated (a priori knowledge) and calibrated (a posteriori knowledge) models, respectively.

As reported in Table 7, the calibrated models were trained on the first two years of data and then tested on the third year of data (36 months of the total monitoring period). In Figure 5 we could observe the evolution of building performance in time with respect to our (pre)established performance boundaries, while in Figure 6 we could verify how measured data and calibrated (or partially calibrated in the case of type 1) models data reasonably overlaps on a monthly base. On the right side of both Figure 5 and Figure 6, the deviations between measured and predicted data are plotted. Deviations in Figure 5 indicate that, at many points in time, the building had an energy consumption near to the upper bound of simulated electricity consumption while, in just a few points in time, it has an energy consumption near to the lower bound of simulation.

Finally, in Figure 6 the deviations between measured and predicted data exhibited a pattern in time (similar for both types of models). Variations can depend on multiple factors and, among them, on behavioural change of occupants that may have determined different values of internal gains and/or differences in operation schedules and settings of technical systems. Understanding this requires a more in depth analysis that will be part of future research, together with the application of the same methodology for a multi-level (regression-based) model calibration with physical interpretation of regression coefficients, as reported before.

5. Conclusions

Rigorous normative standards for new and existing buildings are an essential part of energy and sustainability policies today. The effort put in modelling in the design phase is not, by itself, a guarantee of optimal measured performance. Optimistic assumptions and simplifications are often considered in the design phase and the validation of simulation results represents an issue, as well as model calibration on measured data and long-term monitoring. In this research a simple and scalable way to validate and monitor building performance using monthly data was proposed. It uses an envelopment of data generated in the design phase by means of the Design Of Experiment (DOE) technique together with multivariate regression models, periodically retrained during building operation. In this way, a continuous improvement in design and operation practices becomes possible by linking parametric performance analysis to model calibration, i.e., using inverse modelling already in the design phase, considering multiple configurations. In fact, the assumptions that characterize building performance analysis can be updated based on the experience gained in model calibration, e.g., by reducing or increasing the level of variability of a certain input quantity when more detailed information is available. Further research should be devoted, on the one hand, to the creation of a transparent connection between this approach and ongoing technical standardization, using verification and validation standards for forward models. On the other hand, the use of inverse modelling techniques, i.e., surrogate models, meta-models, in Measurement and Verification (M&V) during the operation phase should become increasingly common, making use of the current state-of-the art of technical standardization. All these elements are scientifically and empirically consolidated but their integration and synthesis are still open issues. Therefore, we believe that future research efforts should be oriented in this direction, in particular with respect to the robustness of performance estimates, i.e., identification of realistic boundaries for performance at multiple levels such as building zones, technical systems and meters under realistic operating conditions. It must be also considered the possibility to scale models from single buildings to building clusters and stock for large scale performance benchmarking. In fact, scalability of analysis techniques can greatly contribute to the definition of effective policies in energy and sustainability transition in the future, supported by large scale data analytics.