A Comprehensive Coal Reservoir Classification Method Base on Permeability Dynamic Change and Its Application
Abstract
:1. Introduction
2. Methods
2.1. Reservoir Properties in the Single-Phase Water Flow Stage
2.2. Reservoir Properties in the CBM Desorption Stage
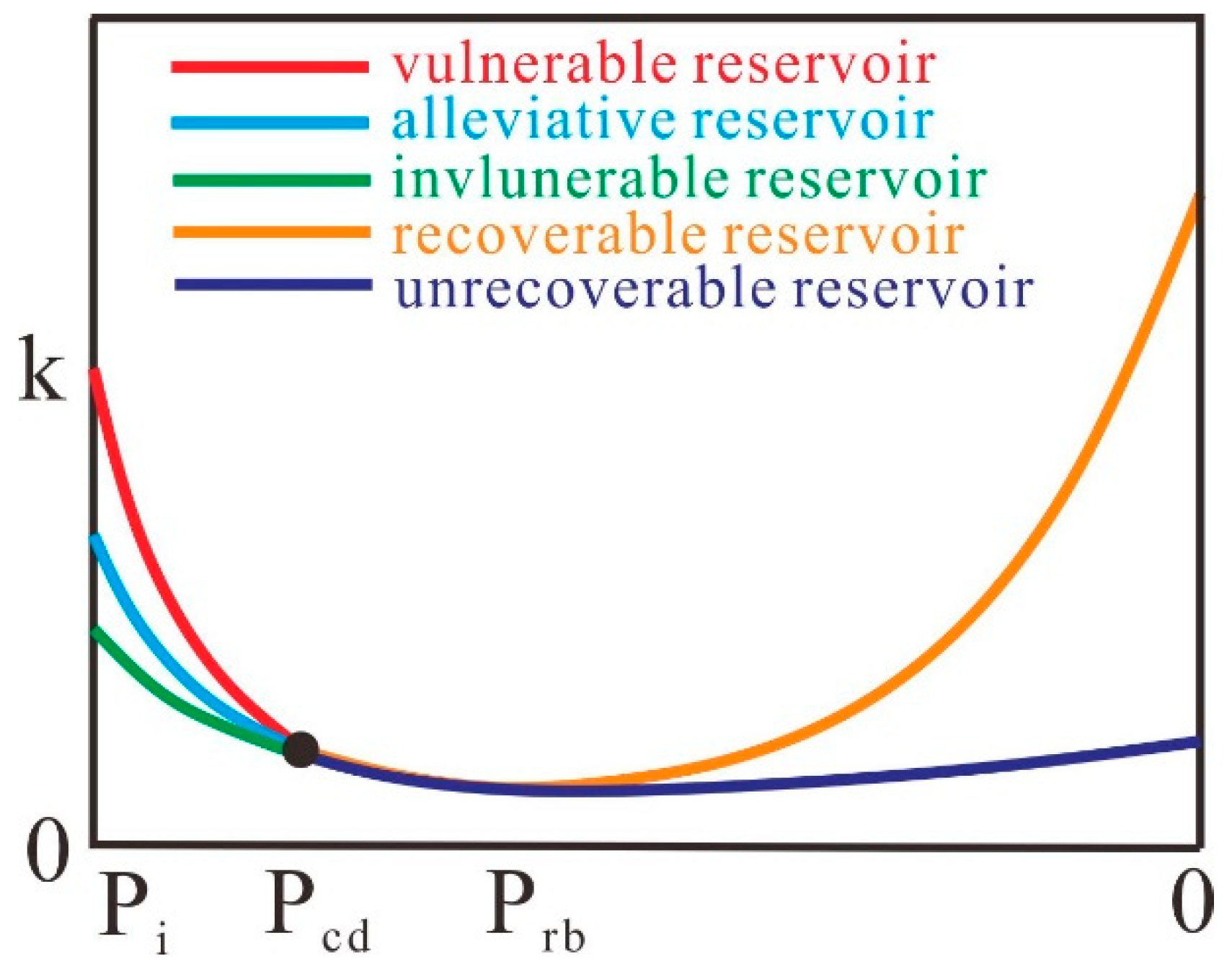
2.3. Reservoir Properties in the Whole Production Stage
3. Discussion
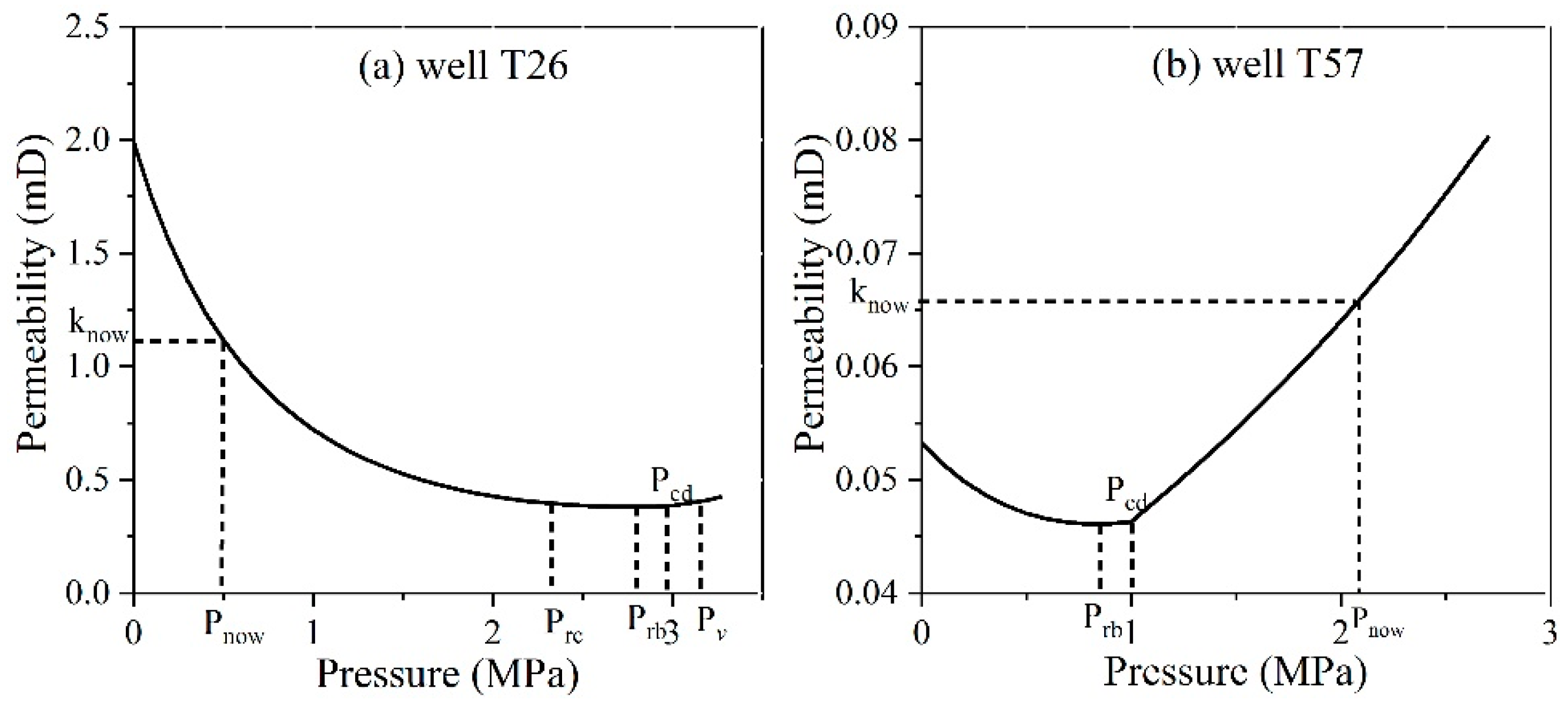
3.1. Advanced Characterization of the Four Demarcating Pressures in the Single-Phase Water Stage
3.2. Advanced Characterization of and
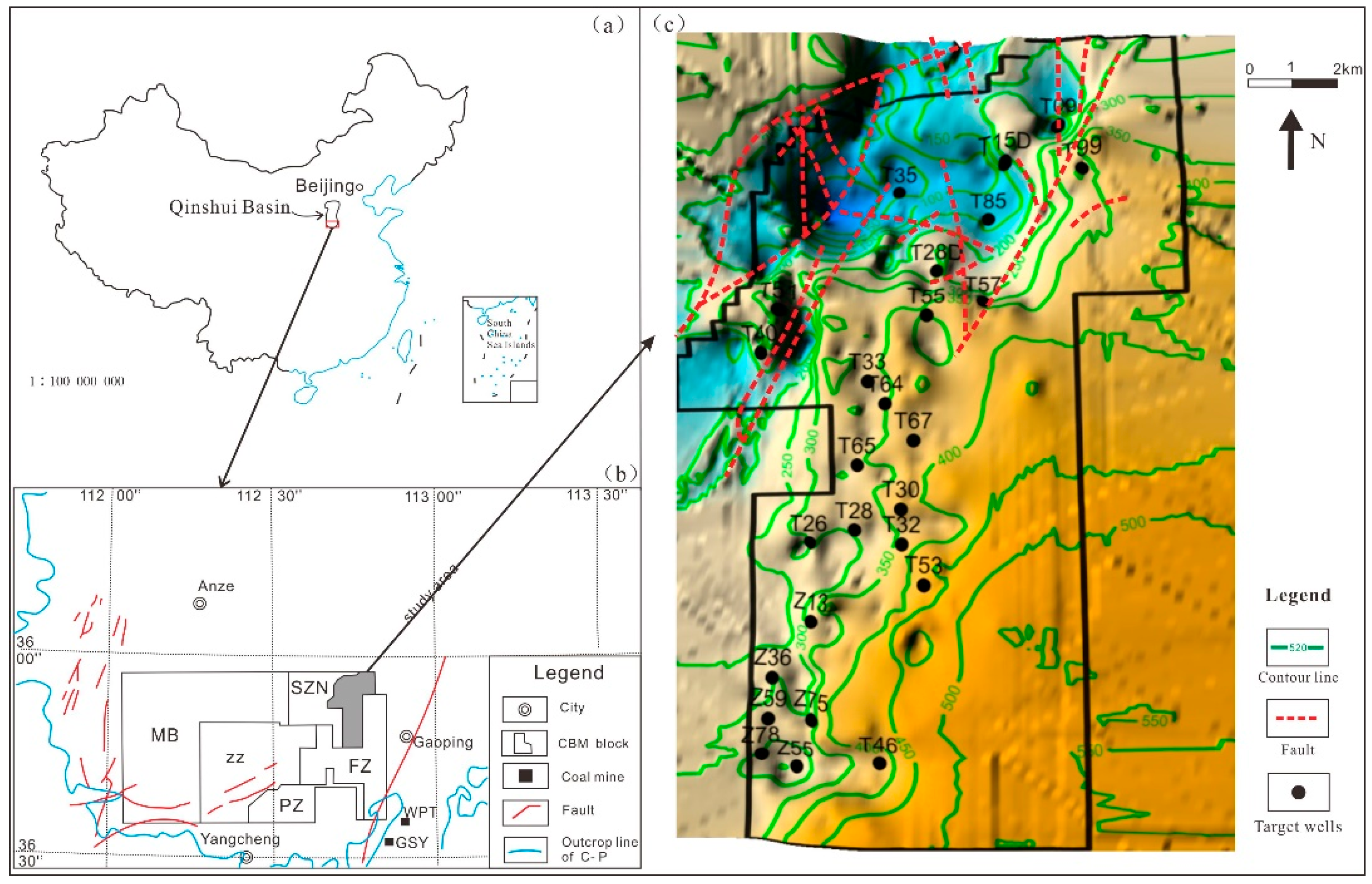
3.3. Example Analysis in the Shizhuangnan Block
3.3.1. Regional Geology
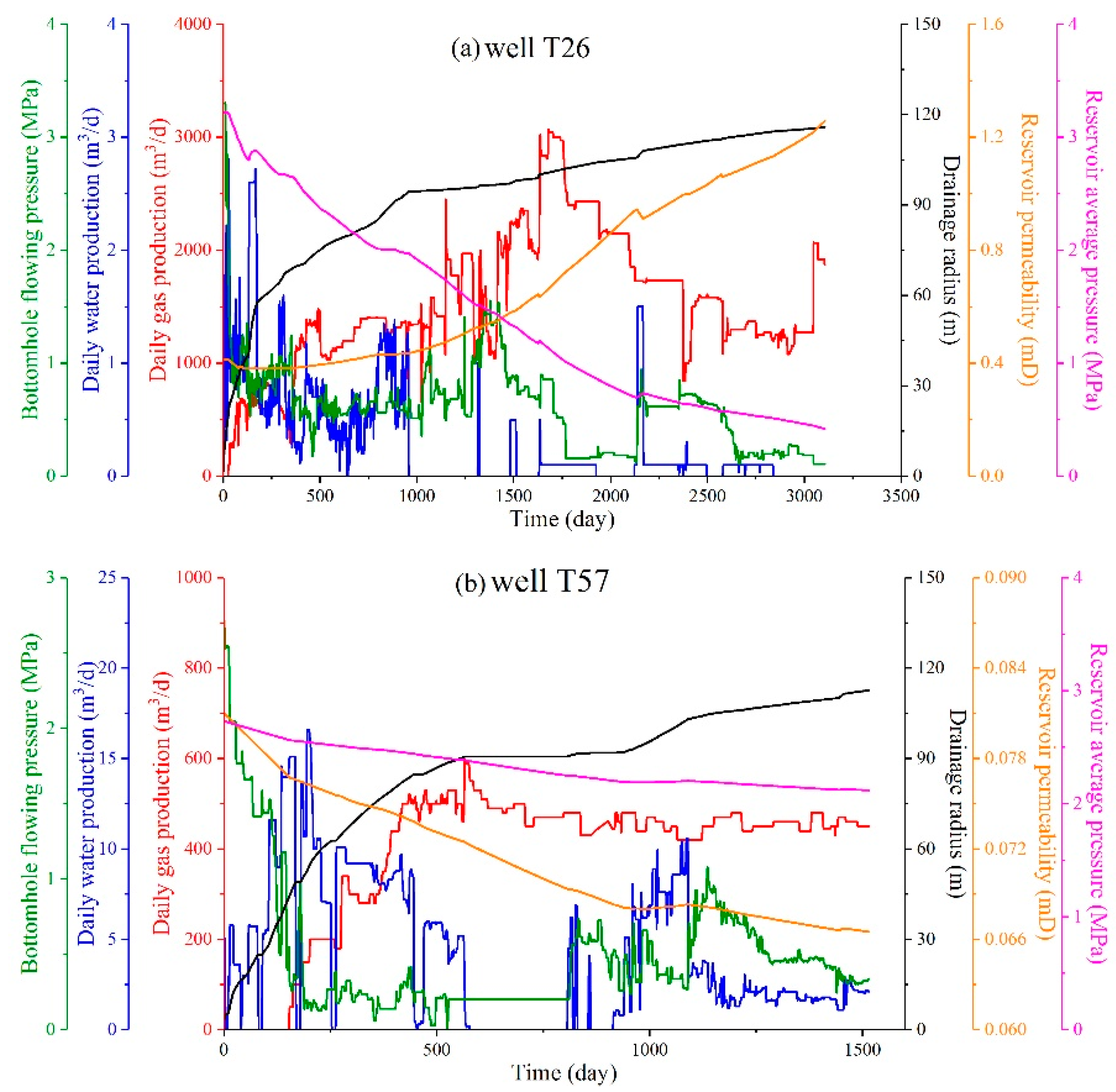
3.3.2. Characteristic Analysis of the Target Wells
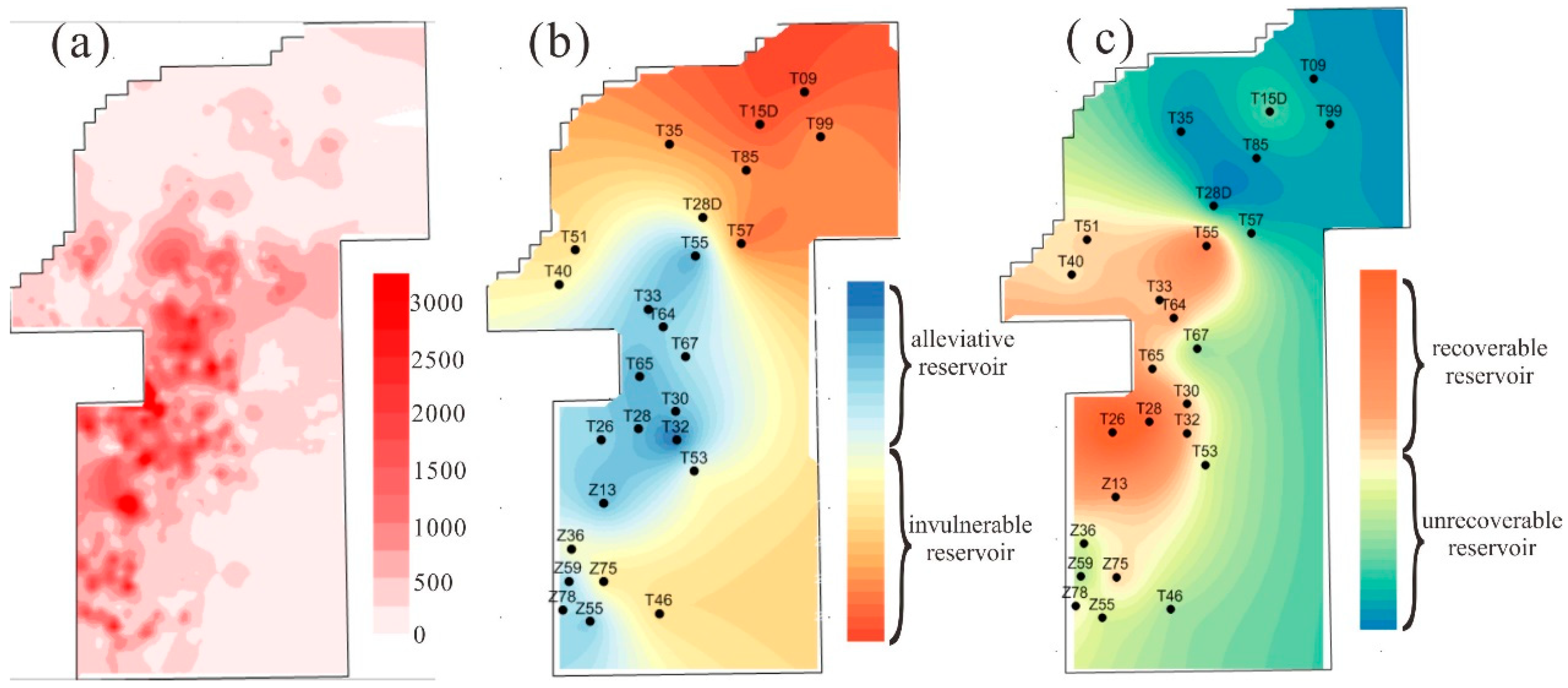
3.3.3. Coal Reservoir Classification
4. Conclusions
- (1)
- The damage of effective stress on reservoir permeability in the single-water flow stage is analyzed. The coal permeability damage rate can be divided into the vulnerable stage, vulnerable transition stage, alleviative transition stage, alleviative stage, and invulnerable stage based on the law of decreasing permeability. Vulnerable pressure, turning pressure, alleviate pressure, and invulnerable pressure are defined as the demarcating pressures. The permeability damage rate of these demarcating pressures is constant, and their permeability is only related to the reservoir physical properties, but not to initial reservoir permeability.
- (2)
- The influence of geologic factors on the rebound pressure and recovery pressure is quantitatively analyzed. The critical desorption pressure has the greatest influence on rebound pressure, followed by cleat-volume compressibility, porosity, and Langmuir volume. The influence order of recovery pressure with the geological parameters is as follows: the critical desorption pressure, density, formation compressibility, and Langmuir volume. Cleat-volume compressibility, porosity, and Langmuir pressure are inversely proportional to rebound pressure and recovery pressure. At large critical desorption pressure, Langmuir volume and coal density are conducive to permeability rebound and recovery. The higher the critical desorption pressure, the smaller the ratio of rebound pressure to critical desorption pressure, indicating that gas lock should be prevented in coal reservoirs with high gas content.
- (3)
- Coal reservoirs are classified according to the coal reservoir dynamic characteristics. When the initial reservoir pressure is greater than the critical desorption pressure, coal reservoirs can be classified as vulnerable, alleviative, or invulnerable based on the effect of effective stress. When the reservoir pressure is less than the critical desorption pressure, coal reservoirs can be classified as recoverable and unrecoverable reservoirs on the permeability recovery properties. In addition, this study on the types of coal reservoirs in the Shizhuangnan Block found that there is a significant correspondence between the types of coal reservoirs and CBM well gas production.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Durucan, S.; Edwards, J.S. The effects of stress and fracturing on permeability of coal. Min. Sci. Technol. 1986, 3, 205–216. [Google Scholar] [CrossRef]
- Tao, S.; Tang, D.Z.; Xu, H.; Gao, L.J.; Fang, Y. Factors controlling high-yield coalbed methane vertical wells in the Fanzhuang Block, Southern Qinshui Basin. Int. J. Coal. Geol. 2014, 134–135, 38–45. [Google Scholar] [CrossRef]
- Harpalani, S.; Chen, G.L. Influence of gas production induced volumetric strain on permeability of coal. Geotech. Geolog. Eng. 1997, 15, 303–325. [Google Scholar] [CrossRef]
- Wang, X. Effect of variation in coal permeability with pressure drop on coalbed methane production. In 2004 International Coalbed Methane Symposium Proceedings; Univ. Alabama: Tuscaloosa, AL, USA, 2004; No. 0401. [Google Scholar]
- Cui, X.J.; Bustin, R.M. Volumetric strain associated with methane desorption and its impact on coalbed gas production from deep coal seams. AAPG Bull. 2005, 89, 1181–1202. [Google Scholar] [CrossRef]
- Li, J.Q.; Liu, D.M.; Yao, Y.B.; Cai, Y.D.; Chen, Y. Evaluation and modeling of gas permeability changes in anthracite coals. Fuel 2013, 111, 606–612. [Google Scholar] [CrossRef]
- Somerton, W.H.; Söylemezoḡlu, I.M.; Dudley, R.C. Effect of stress on permeability of coal. Int. J. Rock Mech. Min. 1975, 12, 129–145. [Google Scholar] [CrossRef]
- Zheng, G.Q.; Pan, Z.J.; Chen, Z.W.; Tang, S.H.; Connell, L.D.; Zhang, S.H.; Wang, B. Laboratory study of gas permeability and cleat compressibility for CBM/ECBM in Chinese coals. Energy Explor. Exploit. 2012, 30, 451–476. [Google Scholar] [CrossRef] [Green Version]
- Fan, L.; Liu, S.M. Numerical prediction of in situ horizontal stress evolution in coalbed methane reservoirs by considering both poroelastic and sorption induced strain effects. Int. J. Rock Mech. Min. 2018, 104, 156–164. [Google Scholar] [CrossRef]
- Robertson, E.; Christiansen, R. Measurement of Sorption-Induced Strain. Soc. Pet. Eng. 2005, 17–19. [Google Scholar] [CrossRef] [Green Version]
- Karacan, C. Swelling-induced volumetric strains internal to a stressed coal associated with CO2 sorption. Int. J. Coal Geol. 2007, 72, 209–220. [Google Scholar] [CrossRef]
- Chen, Y.X.; Liu, D.M.; Yao, Y.B.; Cai, Y.D.; Chen, L.W. Dynamic permeability change during coalbed methane production and its controlling factors. J. Nat. Gas. Sci. Eng. 2015, 25, 335–346. [Google Scholar] [CrossRef]
- Meng, Y.; Wang, J.Y.; Li, Z.P.; Zhang, J.X. An improved productivity model in coal reservoir and its application during coalbed methane production. J. Nat. Gas. Sci. Eng. 2018, 49, 342–351. [Google Scholar] [CrossRef]
- Seidle, J.; Huitt, L. Experimental Measurement of Coal Matrix Shrinkage Due to Gas Desorption and Implications for Cleat Permeability Increases. In Proceedings of the International Meeting on Petroleum Engineering, Beijing, China, 14–17 November 1995; pp. 575–582. [Google Scholar]
- Zhao, J.L.; Tang, D.Z.; Lin, W.J.; Xu, H.; Li, Y.; Tao, S.; Lv, Y.M. Permeability dynamic variation under the action of stress in the medium and high rank coal reservoir. J. Nat. Gas. Sci. Eng. 2015, 26, 1030–1041. [Google Scholar] [CrossRef]
- Schwerer., F.; Pavone, A. Effect of pressure-dependent permeability on well-test analyses and long-term production of methane from coal seams. In Proceedings of the SPE Unconventional Gas Recovery Symposium, Pittsburgh, PA, USA, 13–15 May 1984. [Google Scholar]
- Pan, Z.J.; Connell, L.D. A theoretical model for gas adsorption-induced coal swelling. Int. J. Coal. Geol. 2007, 69, 243–252. [Google Scholar] [CrossRef]
- Gray, I. Reservoir Engineering in Coal Seams Part 1-The Physical Process of Gas Storage and Movement in Coal Seams. SPE Reserv. Eval. Eng. 1987, 2, 28–34. [Google Scholar] [CrossRef]
- Shi, J.Q.; Pan, Z.J.; Durucan, S. Analytical models for coal permeability changes during coalbed methane recovery: Model comparison and performance evaluation. Int. J. Coal. Geol. 2014, 136, 17–24. [Google Scholar] [CrossRef]
- Palmer, I.; Mansoori, J. How permeability depends on stress and pore pressure in coalbeds, a new model. SPE Reserv. Eval. Eng. 1998, 1, 539–544. [Google Scholar] [CrossRef]
- Shi, J.Q.; Durucan, S. Drawdown Induced Changes in Permeability of Coalbeds: A New Interpretation of the Reservoir Response to Primary Recovery. Transport. Porous. Med. 2004, 56, 1–16. [Google Scholar] [CrossRef]
- Shi, J.Q.; Durucan, S. A model for changes in coalbed permeability during primary and enhanced methane recovery. SPE Reserv. Eval. Eng. 2005, 8, 291–299. [Google Scholar] [CrossRef]
- Pan, Z.J.; Connell, L.D. Modelling of anisotropic coal swelling and its impact on permeability behaviour for primary and enhanced coalbed methane recovery. Int. J. Coal. Geol. 2011, 85, 257–267. [Google Scholar] [CrossRef]
- Pan, Z.J.; Connell, L.D. Modelling permeability for coal reservoirs: A review of analytical models and testing data. Int. J. Coal. Geol. 2012, 92, 1–44. [Google Scholar] [CrossRef]
- Connell, L.D. Coupled flow and geomechanical processes during gas production from coal seams. Int. J. Coal. Geol. 2009, 79, 18–28. [Google Scholar] [CrossRef]
- Connell, L.D.; Detournay, C. Coupled flow and geomechanical processes during enhanced coal seam methane recovery through CO2 sequestration. Int. J. Coal. Geol. 2009, 77, 222–233. [Google Scholar] [CrossRef]
- Gu, F.G.; Chalaturnyk, R. Permeability and porosity models considering anisotropy and discontinuity of coalbeds and application in coupled simulation. J. Petrol. Sci. Eng. 2010, 74, 113–131. [Google Scholar] [CrossRef]
- Wei, Z.J.; Zhang, D.X. Coupled fluid-flow and geomechanics for triple-porosity/dual-permeability modeling of coalbed methane recovery. Int. J. Rock Mech. Min. 2010, 47, 1242–1253. [Google Scholar] [CrossRef]
- Clarkson, C.; Bustin, R. Variation in permeability with lithotype and maceral composition of Cretaceous coals of the Canadian Cordillera. Int. J. Coal. Geol. 1997, 33, 135–151. [Google Scholar] [CrossRef]
- Harpalani, S. Compressibility of coal and its impact on gas production from coalbed reservoirs. Rock Mech. Industry 1999, 1–2, 301–308. [Google Scholar]
- Peng, Y.; Liu, J.S.; Pan, Z.J.; Connell, L.D.; Chen, Z.W.; Qu, H.Y. Impact of coal matrix strains on the evolution of permeability. Fuel 2017, 189, 270–283. [Google Scholar] [CrossRef]
- Yao, Y.B.; Liu, D.M.; Tang, D.Z.; Huang, W.H.; Tang, S.H.; Che, Y. A Comprehensive Model for Evaluating Coalbed Methane, Reservoirs in China. ACTA Geol. Sin. Eng. 2008, 82, 1253–1270. [Google Scholar]
- Cai, Y.D.; Liu, D.M.; Yao, Y.B.; Li, J.Q.; Qiu, Y.K. Geological controls on prediction of coalbed methane of No. 3 coal seam in Southern Qinshui Basin, North China. Int. J. Coal. Geol. 2011, 88, 101–112. [Google Scholar] [CrossRef]
- Meng, Y.J.; Tang, D.Z.; Xu, H.; Li, C.; Li, L.; Meng, S.Z. Geological controls and coalbed methane production potential evaluation: A case study in Liulin area, eastern Ordos Basin, China. J. Nat. Gas. Sci. Eng. 2014, 21, 95–111. [Google Scholar] [CrossRef]
- Yang, G.Q.; Tang, S.H.; Zhang, S.H.; Hu, W.H.; Xi, Z.D.; Li, L.; Li, Y.P.; Li, J.; Wang, M.X.; Gong, M.H. Impacts of vertical variation of different coal texture types on coalbed methane production in Zaoyuan area of the Shizhuangnan Block, Southern Qinshui Basin, North China. Energ. Source Part A 2017, 39, 1617–1624. [Google Scholar] [CrossRef]
- Zhang, S.H.; Tang, S.H.; Li, Z.C.; Guo, Q.L.; Pan, Z.J. Stable isotope characteristics of CBM co-produced water and implications for CBM development: The example of the Shizhuangnan block in the southern Qinshui Basin, China. J. Nat. Gas. Sci. Eng. 2015, 27, 1400–1411. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Liu, D.M.; Cai, Y.D.; Pan, Z.J.; Yao, Y.B.; Wang, Y.J. Geological and hydrological controls on the accumulation of coalbed methane within the No. 3 coal seam of the southern Qinshui Basin. Int. J. Coal. Geol. 2017, 182, 94–111. [Google Scholar] [CrossRef]
- Yan, X.L.; Zhang, S.H.; Tang, S.H.; Li, Z.C.; Wang, K.F.; Hu, Q.P. The Prediction Model of Coal Reservoir Pressure and its Implication for the Law of Coal Reservoir Depressurization. ACTA Geol. Sin Eng. 2019, 93, 692–703. [Google Scholar] [CrossRef]
- Seidle, J.; Jeansonne, M.; Erickson, D. Application of Matchstick Geometry to Stress Dependent Permeability in Coals. In Proceedings of the SPE Rocky Mountain Regional Meeting, Casper, Wyoming, 18–21 May 1992; pp. 433–444. [Google Scholar]
- Su, X.B.; Fang, W.D. Permeability of coal-bed methane reservoir and its grade and classification. J. Jiaozuo Inst. Technol. 1998, 17, 94–99, (In Chinese with English abstract). [Google Scholar]
- Meng, Y.J.; Tang, D.Z.; Xu, H.; Qiu, Y.J.; Li, Y.; Zhang, W.Z. Division of coalbed methane desorption stages and its significance. Petrol. Explor. Dev. 2014, 41, 671–677. [Google Scholar] [CrossRef]
- Lai, F.P.; Li, Z.P.; Fu, Y.K.; Yang, Z.H. A drainage data-based calculation method for coalbed permeability. J. Geophys. Eng. 2013, 10, 1–8. [Google Scholar] [CrossRef]
- Lai, F.P.; Li, Z.P.; Wang, Y.J.; Yao, J.J. Theoretical method for calculating porosity and permeability under self-regulating effect. Int. J. Min. Sci. Technol. 2013, 5, 18–22. [Google Scholar]
- Ross, P.J. Taguchi Techniques for Quality Engineering: Loss Function, Orthogonal Experiments, Parameter and Tolerance Design; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Li, S. Applied Statistics; Tsinghua University Press: Beijing, China, 2005. (In Chinese) [Google Scholar]
- Li, J.Q.; Liu, D.M.; Yao, Y.B.; Cai, Y.D.; Xu, L.L.; Huang, S.P. Control of CO2 permeability change in different rank coals during pressure depletion: An experimental study. Energ. Fuel 2014, 28, 987–996. [Google Scholar] [CrossRef]
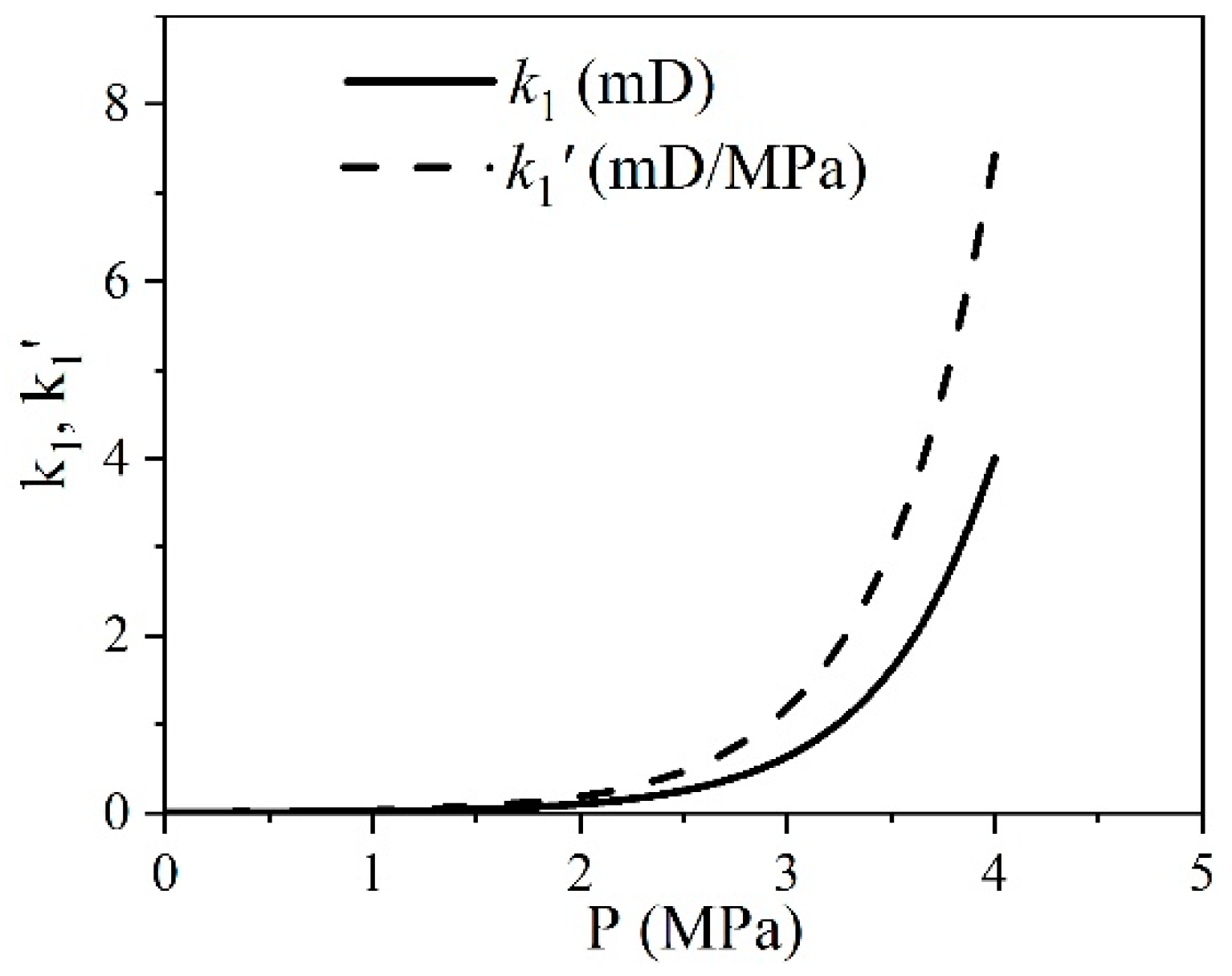
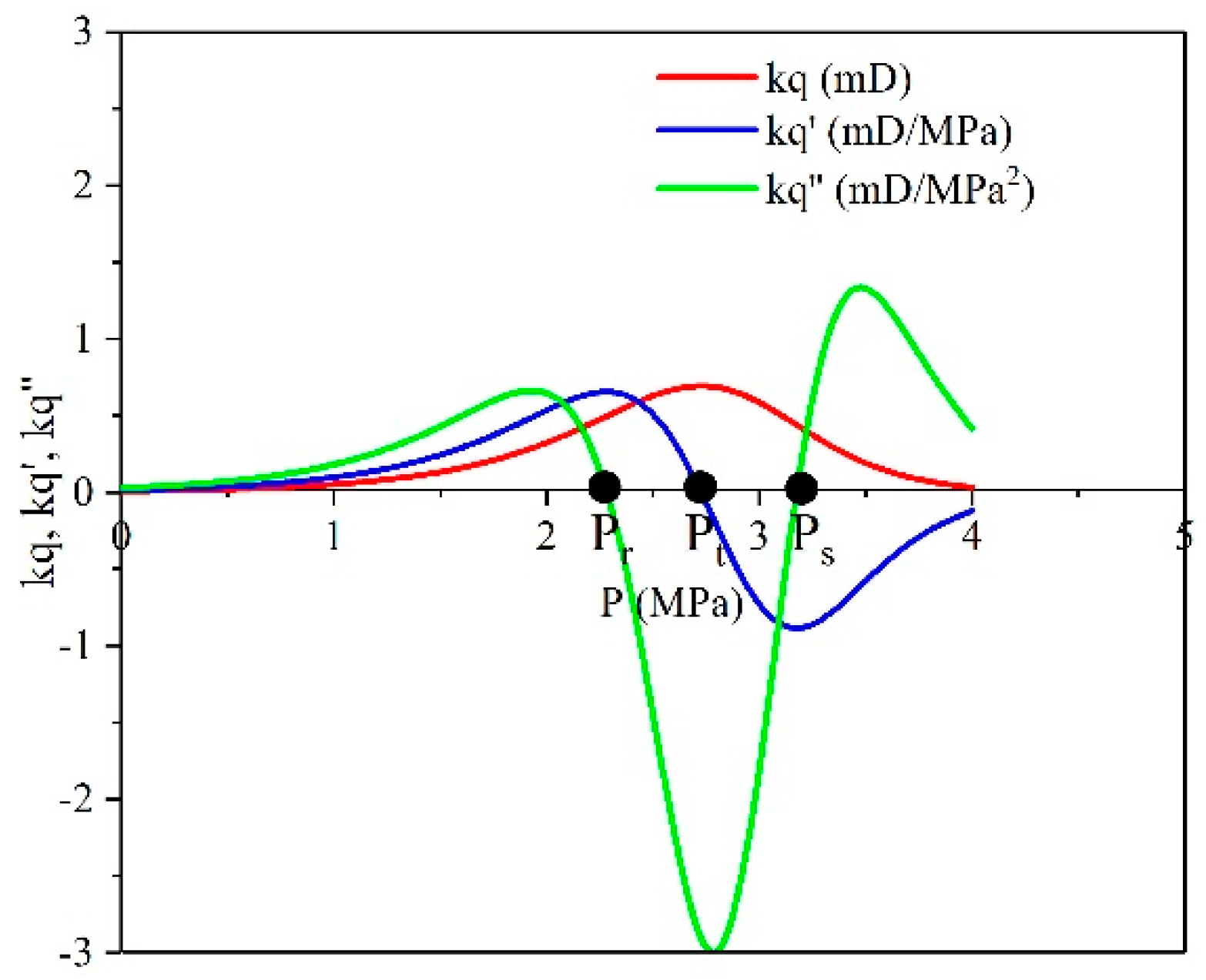
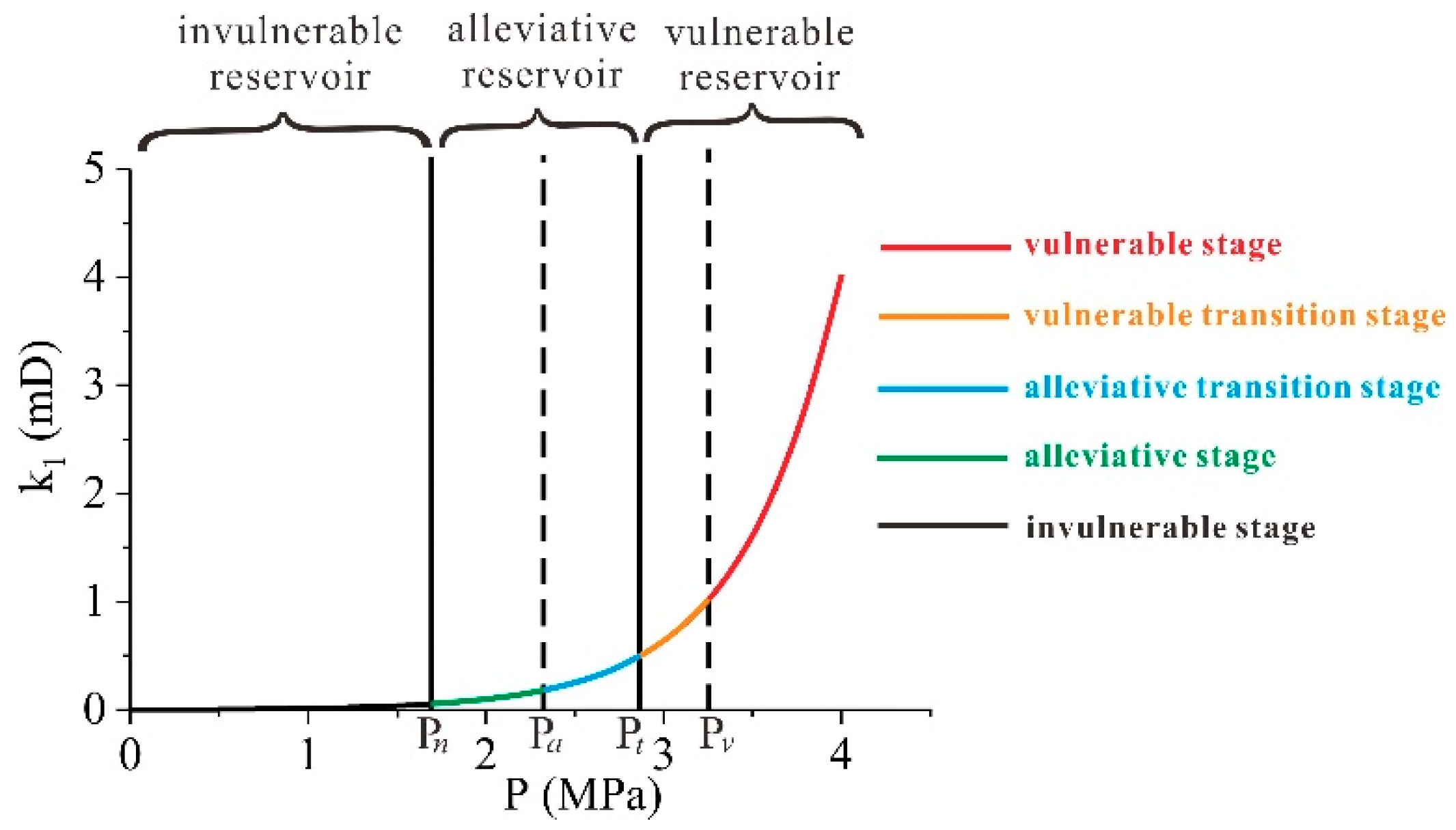

| Demarcating Pressure and Stages | Conditions | (mD) | (mD/MPa) |
|---|---|---|---|
| Vulnerable stage | |||
| Vulnerable pressure | |||
| Vulnerable transition stage | |||
| Turing pressure | |||
| Alleviative transition stage | |||
| Alleviate pressure | |||
| Alleviative stage | |||
| Invulnerable pressure | 0.1 | ||
| Invulnerable stage ) |
| Cf(MPa−1) | (g/cm3) | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 0.1 | 0.2 | 2 | 0.02 | 20 | 2 | 1.2 |
| 2 | 0.2 | 0.3 | 3 | 0.03 | 30 | 3 | 1.4 |
| 3 | 0.3 | 0.4 | 4 | 0.04 | 40 | 4 | 1.6 |
| Parameters | Results | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
(MPa−1) | (MPa) | (m3/t) | (MPa) | (g/cm3) | (MPa) | (MPa) | ||||
| 1 | 0.1 | 0.2 | 2 | 0.02 | 20 | 2 | 1.2 | 2.61 | 1.31 | 0.4 |
| 2 | 0.1 | 0.3 | 3 | 0.03 | 30 | 3 | 1.4 | 3.00 | 1.00 | 1.4 |
| 3 | 0.1 | 0.4 | 4 | 0.04 | 40 | 4 | 1.6 | 3.39 | 0.85 | 3.6 |
| 4 | 0.2 | 0.2 | 2 | 0.03 | 30 | 4 | 1.6 | 1.94 | 0.97 | 0.2 |
| 5 | 0.2 | 0.3 | 3 | 0.04 | 40 | 2 | 1.2 | 2.06 | 0.69 | 0 |
| 6 | 0.2 | 0.4 | 4 | 0.02 | 20 | 3 | 1.4 | 2.62 | 0.66 | 1.3 |
| 7 | 0.3 | 0.2 | 3 | 0.02 | 40 | 3 | 1.6 | 2.95 | 0.98 | 1.9 |
| 8 | 0.3 | 0.3 | 4 | 0.03 | 20 | 4 | 1.2 | 1.88 | 0.47 | −0.9 |
| 9 | 0.3 | 0.4 | 2 | 0.04 | 30 | 2 | 1.4 | 1.16 | 0.58 | −0.9 |
| 10 | 0.1 | 0.2 | 4 | 0.04 | 30 | 3 | 1.2 | 2.98 | 0.74 | 1.1 |
| 11 | 0.1 | 0.3 | 2 | 0.02 | 40 | 4 | 1.4 | 3.25 | 1.63 | 1.1 |
| 12 | 0.1 | 0.4 | 3 | 0.03 | 20 | 2 | 1.6 | 2.29 | 0.76 | 1.1 |
| 13 | 0.2 | 0.2 | 3 | 0.04 | 20 | 4 | 1.4 | 1.31 | 0.44 | −0.9 |
| 14 | 0.2 | 0.3 | 4 | 0.02 | 30 | 2 | 1.6 | 3.36 | 0.84 | 3.4 |
| 15 | 0.2 | 0.4 | 2 | 0.03 | 40 | 3 | 1.2 | 1.62 | 0.81 | −0.8 |
| 16 | 0.3 | 0.2 | 4 | 0.03 | 40 | 2 | 1.4 | 2.94 | 0.74 | 2 |
| 17 | 0.3 | 0.3 | 2 | 0.04 | 20 | 3 | 1.6 | 0.87 | 0.43 | −1.2 |
| 18 | 0.3 | 0.4 | 3 | 0.02 | 30 | 4 | 1.2 | 2.07 | 0.69 | −0.6 |
| Results | (MPa−1) | v | (MPa) | (m3/t) | (MPa) | (g/cm3) | ||
|---|---|---|---|---|---|---|---|---|
| K1 | 17.52 | 14.73 | 11.44 | 16.87 | 11.56 | 14.42 | 13.21 | |
| K2 | 12.90 | 14.41 | 13.68 | 13.67 | 14.51 | 14.04 | 14.28 | |
| K3 | 11.87 | 13.15 | 17.16 | 11.75 | 16.21 | 13.83 | 14.80 | |
| k1 | 2.92 | 2.45 | 1.91 | 2.81 | 1.93 | 2.40 | 2.20 | |
| k2 | 2.15 | 2.40 | 2.28 | 2.28 | 2.42 | 2.34 | 2.38 | |
| k3 | 1.98 | 2.19 | 2.86 | 1.96 | 2.70 | 2.31 | 2.47 | |
| R | 0.94 | 0.26 | 0.95 | 0.85 | 0.77 | 0.10 | 0.27 | |
| Influence order | ② | ⑥ | ① | ③ | ④ | ⑦ | ⑤ | |
| Correlation | negative | negative | positive | negative | positive | negative | positive | |
| / | K1 | 6.29 | 5.17 | 5.72 | 6.10 | 4.06 | 4.91 | 4.70 |
| K2 | 4.40 | 5.05 | 4.56 | 4.75 | 4.82 | 4.63 | 5.03 | |
| K3 | 3.89 | 4.35 | 4.29 | 3.72 | 5.69 | 5.04 | 4.84 | |
| k1 | 1.05 | 0.86 | 0.95 | 1.02 | 0.68 | 0.82 | 0.78 | |
| k2 | 0.73 | 0.84 | 0.76 | 0.79 | 0.80 | 0.77 | 0.84 | |
| k3 | 0.65 | 0.72 | 0.72 | 0.62 | 0.95 | 0.84 | 0.81 | |
| R | 0.40 | 0.14 | 0.24 | 0.40 | 0.27 | 0.07 | 0.05 | |
| Influence order | ① | ⑤ | ④ | ① | ③ | ⑥ | ⑦ | |
| Correlation | negative | negative | negative | negative | positive | - | - | |
| K1 | 8.70 | 4.70 | −1.20 | 7.50 | −0.20 | 6.00 | −0.80 | |
| K2 | 3.20 | 3.80 | 2.90 | 3.00 | 4.60 | 3.70 | 4.00 | |
| K3 | 0.30 | 3.70 | 10.50 | 1.70 | 7.80 | 2.50 | 9.00 | |
| k1 | 1.45 | 0.78 | −0.20 | 1.25 | −0.03 | 1.00 | −0.13 | |
| k2 | 0.53 | 0.63 | 0.48 | 0.50 | 0.77 | 0.62 | 0.67 | |
| k3 | 0.05 | 0.62 | 1.75 | 0.28 | 1.30 | 0.42 | 1.50 | |
| R | 1.40 | 0.17 | 1.95 | 0.97 | 1.33 | 0.58 | 1.63 | |
| Influence order | ③ | ⑦ | ① | ⑤ | ④ | ⑥ | ② | |
| Correlation | negative | negative | positive | negative | positive | negative | positive | |
| Parameters | T26 | T57 | Date Sources | Results | T26 | T57 |
|---|---|---|---|---|---|---|
| (MPa−1) | 0.164 | 0.173 | calculation by the method from [46] | (MPa) | 11.2 | 15.4 |
| (MPa) | 3.3 | 2.7 | actual field date | (MPa) | 8.7 | 12.9 |
| (MPa) | 2.97 | 1.02 | actual field date | (MPa) | 6.2 | 10.5 |
| (m3/t) | 36.68 | 34.39 | experimental data | (MPa) | 2.4 | 6.9 |
| (MPa) | 1.5 | 2.4 | experimental data | (MPa) | 2.7 | 0.8 |
| (mD) | 0.42 | 0.081 | simulation historical matching | (MPa) | 2.3 | <0 |
| 0.02 | 0.06 | simulation historical matching | Rc | 51.0% | 13.3% |
| Wells | φ | (MPa) | Pcd (MPa) | VL (m3/d) | PL (MPa) | ki (mD) | (MPa−1) | Pv (MPa) | Pt (MPa) | (MPa) | (MPa) | Prb (MPa) | (MPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T99 | 0.08 | 3.3 | 3.1 | 26.8 | 3.3 | 0.07 | 0.168 | 16.7 | 14.2 | 11.6 | 7.9 | 0.9 | <0 |
| T09 | 0.08 | 6.0 | 2.6 | 33.3 | 3.0 | 0.01 | 0.166 | 25.6 | 23.1 | 20.5 | 16.7 | 1.1 | <0 |
| T15D | 0.08 | 4.4 | 2 | 35.8 | 1.7 | 0.03 | 0.162 | 21.4 | 18.9 | 16.3 | 12.4 | 1.8 | <0 |
| T85 | 0.08 | 5.4 | 3.8 | 26.8 | 3.1 | 0.03 | 0.163 | 22.1 | 19.5 | 16.9 | 13.1 | 1.3 | <0 |
| T35 | 0.08 | 4.9 | 1.1 | 28.8 | 2.5 | 0.05 | 0.162 | 20.4 | 17.8 | 15.2 | 11.3 | 0.8 | <0 |
| T51 | 0.02 | 3.4 | 2.2 | 33.5 | 2.8 | 0.13 | 0.167 | 15.1 | 12.6 | 10.1 | 6.3 | 2.1 | 0.7 |
| T40 | 0.02 | 3.8 | 1.8 | 33.3 | 3.0 | 0.17 | 0.164 | 15.1 | 12.6 | 10.0 | 6.2 | 1.8 | 0.5 |
| T55 | 0.015 | 3.5 | 2.6 | 34.4 | 2.4 | 0.58 | 0.166 | 10.4 | 7.8 | 5.3 | 1.5 | 2.6 | 1.8 |
| T28D | 0.06 | 4.6 | 1.2 | 33.9 | 2.6 | 0.12 | 0.162 | 17.0 | 14.4 | 11.8 | 7.9 | 0.9 | <0 |
| T33 | 0.015 | 3.0 | 1.3 | 34.5 | 2.1 | 0.44 | 0.170 | 10.6 | 8.1 | 5.6 | 1.9 | 1.3 | 0.7 |
| T64 | 0.015 | 2.9 | 1.5 | 36.6 | 1.5 | 0.38 | 0.171 | 10.9 | 8.4 | 6.0 | 2.3 | 1.5 | 1 |
| T65 | 0.015 | 3.6 | 1.5 | 27.9 | 1.8 | 0.56 | 0.165 | 10.8 | 8.2 | 5.7 | 1.9 | 1.5 | 0.7 |
| T67 | 0.05 | 3.0 | 1.8 | 33.6 | 2.7 | 0.32 | 0.170 | 11.5 | 9.0 | 6.6 | 2.9 | 1.3 | <0 |
| T30 | 0.02 | 3.4 | 1.8 | 35.5 | 1.8 | 0.47 | 0.167 | 10.9 | 8.4 | 5.9 | 2.1 | 1.8 | 0.8 |
| T28 | 0.015 | 3.4 | 2.7 | 36.3 | 2.1 | 0.57 | 0.167 | 10.3 | 7.8 | 5.3 | 1.5 | 2.7 | 2.3 |
| T26 | 0.02 | 3.2 | 3.0 | 36.6 | 1.5 | 0.42 | 0.168 | 11.1 | 8.6 | 6.1 | 3.2 | 3 | 2.3 |
| T32 | 0.02 | 3.4 | 1.9 | 35.5 | 2.3 | 0.88 | 0.166 | 9.1 | 6.5 | 4.0 | 0.2 | 1.9 | 0.8 |
| T53 | 0.02 | 3.0 | 0.8 | 34 | 1.5 | 0.20 | 0.170 | 13.0 | 10.5 | 8.1 | 4.4 | 0.8 | 0.2 |
| Z13 | 0.02 | 3.1 | 1.7 | 34 | 1.7 | 0.47 | 0.170 | 10.4 | 7.9 | 5.5 | 1.7 | 1.7 | 0.9 |
| Z36 | 0.03 | 4.3 | 2.1 | 27.7 | 1.5 | 0.16 | 0.162 | 15.8 | 13.2 | 10.7 | 6.8 | 1.9 | 0.1 |
| Z59 | 0.04 | 4.4 | 1.9 | 35.1 | 2.0 | 0.41 | 0.162 | 12.7 | 10.2 | 7.6 | 3.7 | 1.7 | <0 |
| Z75 | 0.03 | 3.2 | 2.3 | 33.2 | 3.1 | 0.14 | 0.168 | 14.4 | 12.0 | 9.5 | 5.7 | 2.1 | 0.7 |
| Z78 | 0.03 | 3.6 | 2.3 | 34 | 2.8 | 0.34 | 0.165 | 12.4 | 9.9 | 7.3 | 3.5 | 2.1 | 0.5 |
| Z55 | 0.04 | 4.0 | 2.3 | 34.6 | 2.1 | 0.46 | 0.163 | 12.0 | 9.4 | 6.8 | 2.9 | 1.9 | 0.1 |
| T46 | 0.03 | 3.3 | 1.3 | 33.4 | 3.0 | 0.13 | 0.167 | 15.2 | 12.634 | 10.1 | 6.3 | 1.3 | <0 |
| T57 | 0.06 | 2.7 | 1.0 | 34.4 | 2.3 | 0.08 | 0.173 | 15.4 | 12.9 | 10.5 | 6.9 | 0.8 | <0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Zhang, S.; Tang, S.; Li, Z.; Yi, Y.; Zhang, Q.; Hu, Q.; Liu, Y. A Comprehensive Coal Reservoir Classification Method Base on Permeability Dynamic Change and Its Application. Energies 2020, 13, 644. https://doi.org/10.3390/en13030644
Yan X, Zhang S, Tang S, Li Z, Yi Y, Zhang Q, Hu Q, Liu Y. A Comprehensive Coal Reservoir Classification Method Base on Permeability Dynamic Change and Its Application. Energies. 2020; 13(3):644. https://doi.org/10.3390/en13030644
Chicago/Turabian StyleYan, Xinlu, Songhang Zhang, Shuheng Tang, Zhongcheng Li, Yongxiang Yi, Qian Zhang, Qiuping Hu, and Yuxin Liu. 2020. "A Comprehensive Coal Reservoir Classification Method Base on Permeability Dynamic Change and Its Application" Energies 13, no. 3: 644. https://doi.org/10.3390/en13030644
APA StyleYan, X., Zhang, S., Tang, S., Li, Z., Yi, Y., Zhang, Q., Hu, Q., & Liu, Y. (2020). A Comprehensive Coal Reservoir Classification Method Base on Permeability Dynamic Change and Its Application. Energies, 13(3), 644. https://doi.org/10.3390/en13030644




