Efficiency Optimization and Control Strategy of Regenerative Braking System with Dual Motor
Abstract
:1. Introduction
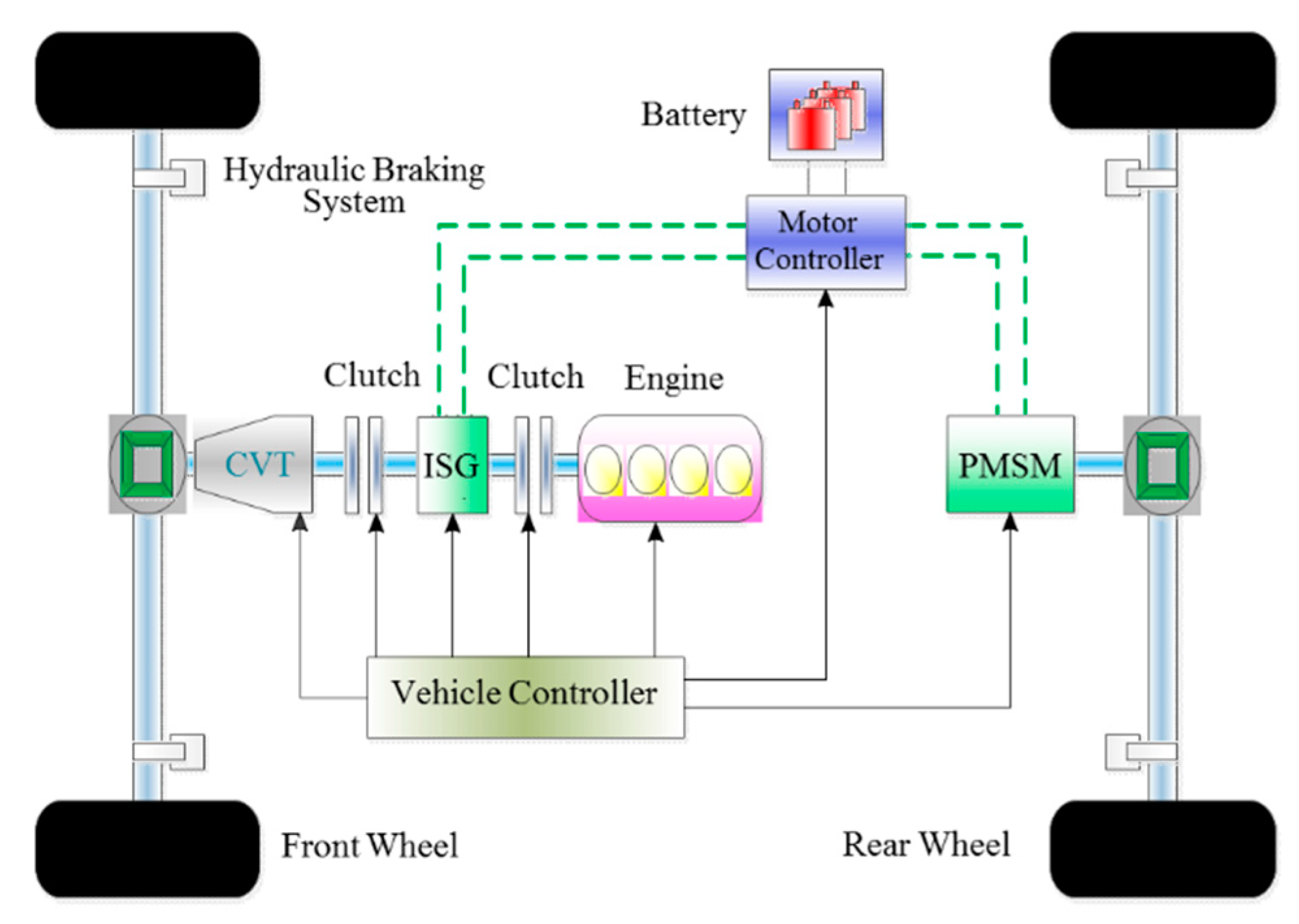
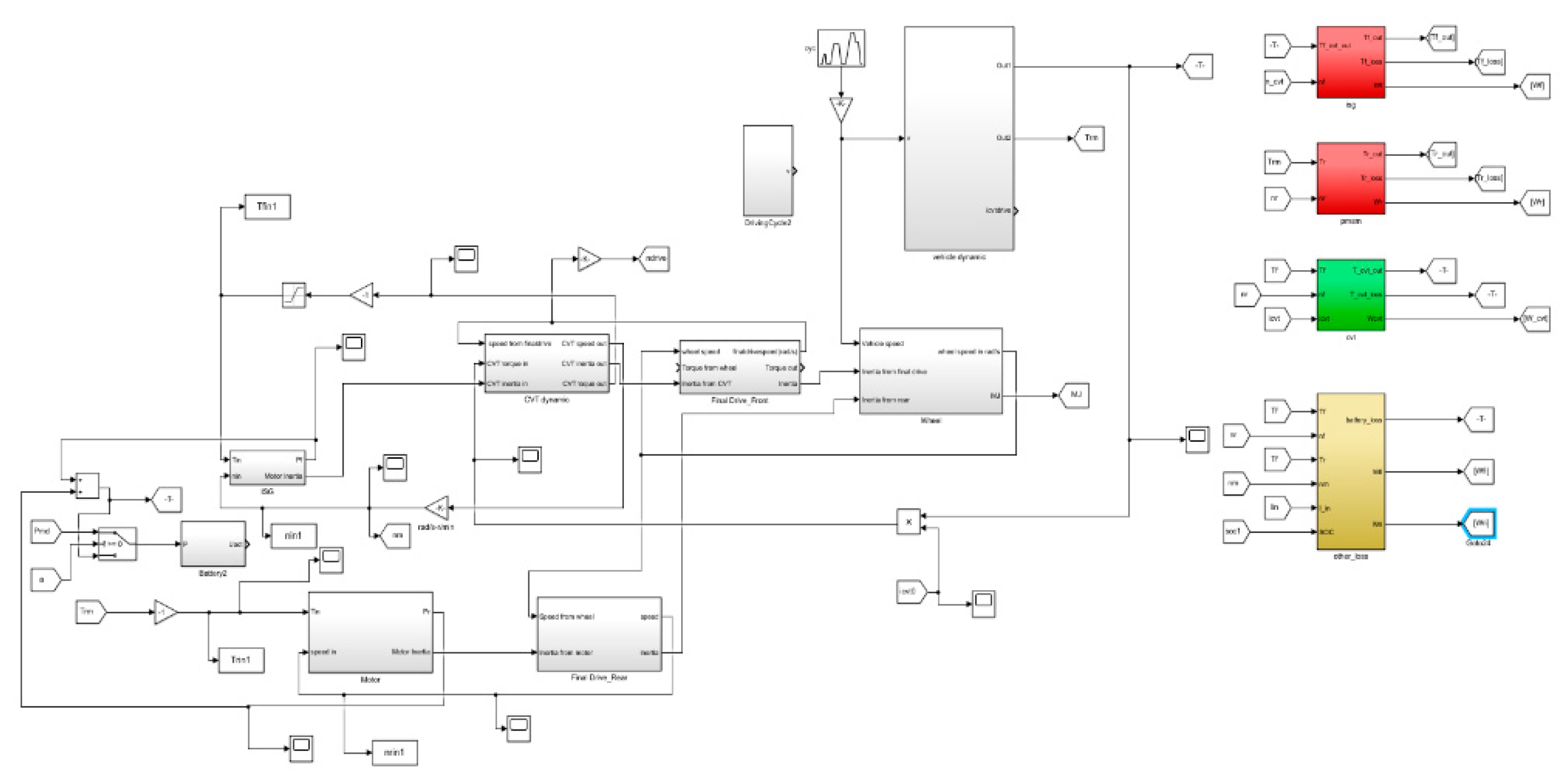
2. Hybrid Electric Vehicle System Structure and Parameters
3. Motor Loss Model and Control Strategy
3.1. Motor Loss Model
3.2. Motor Control Strategy
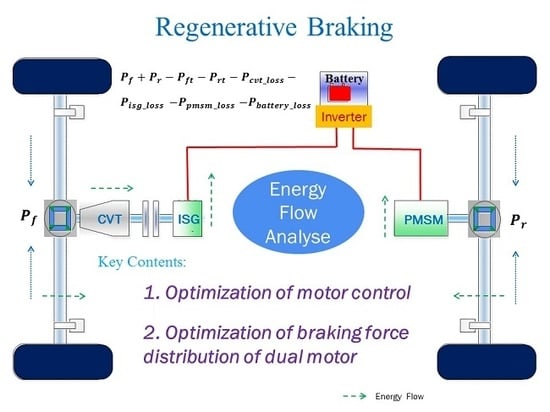
4. Optimization of the Electric Braking Power Flow Efficiency and the Braking Force Distribution
4.1. Optimization of the Electric Braking Power Flow Efficiency
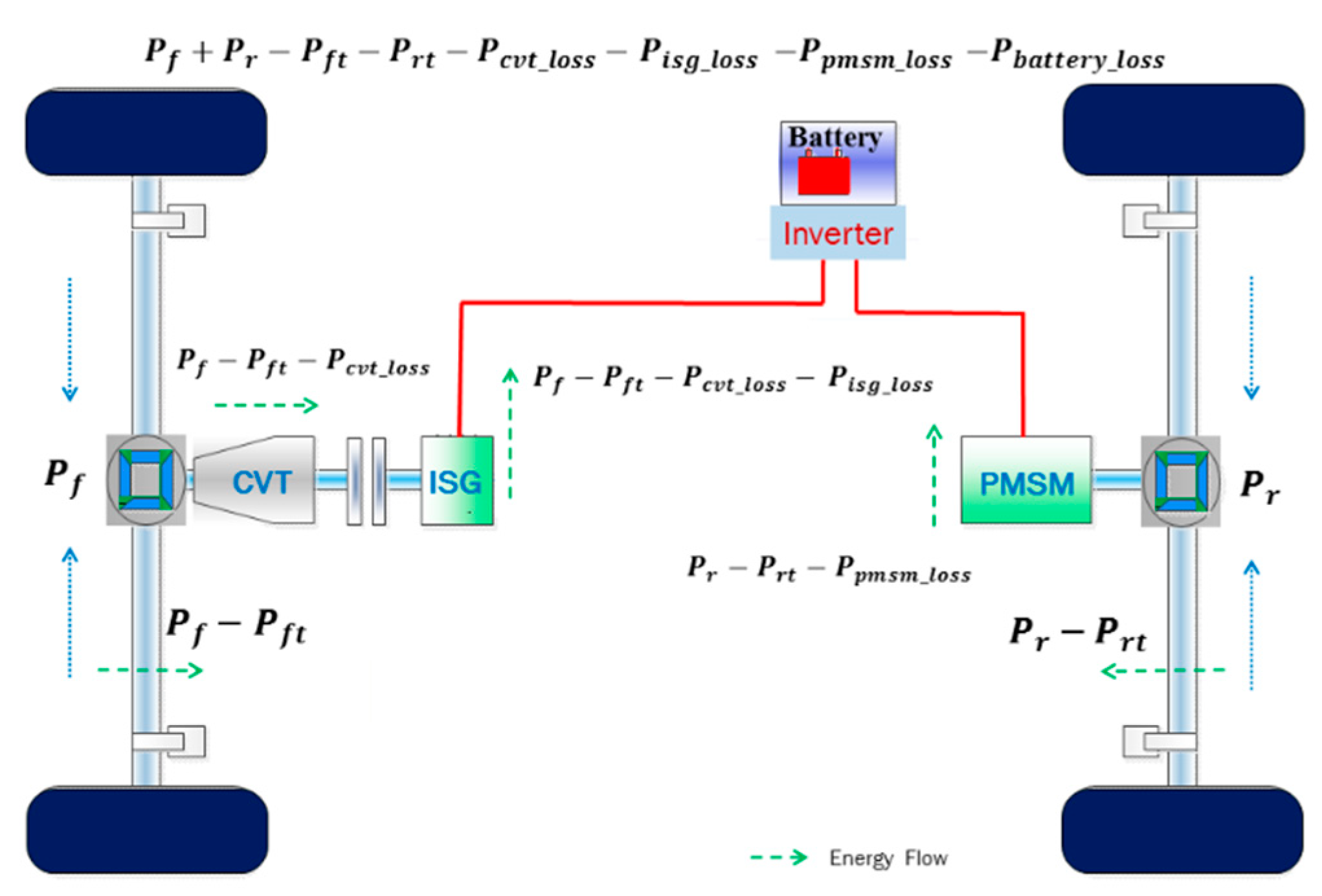
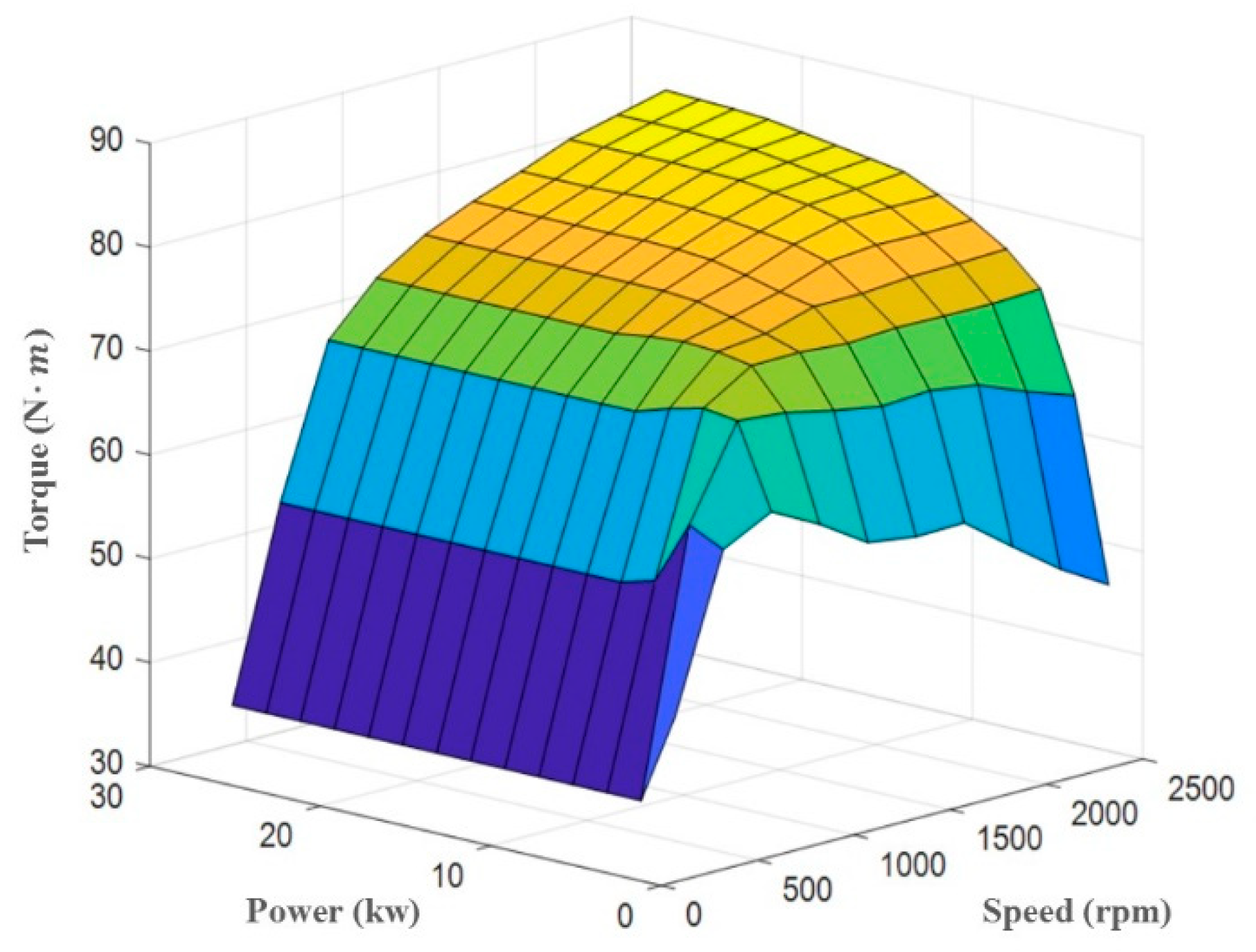
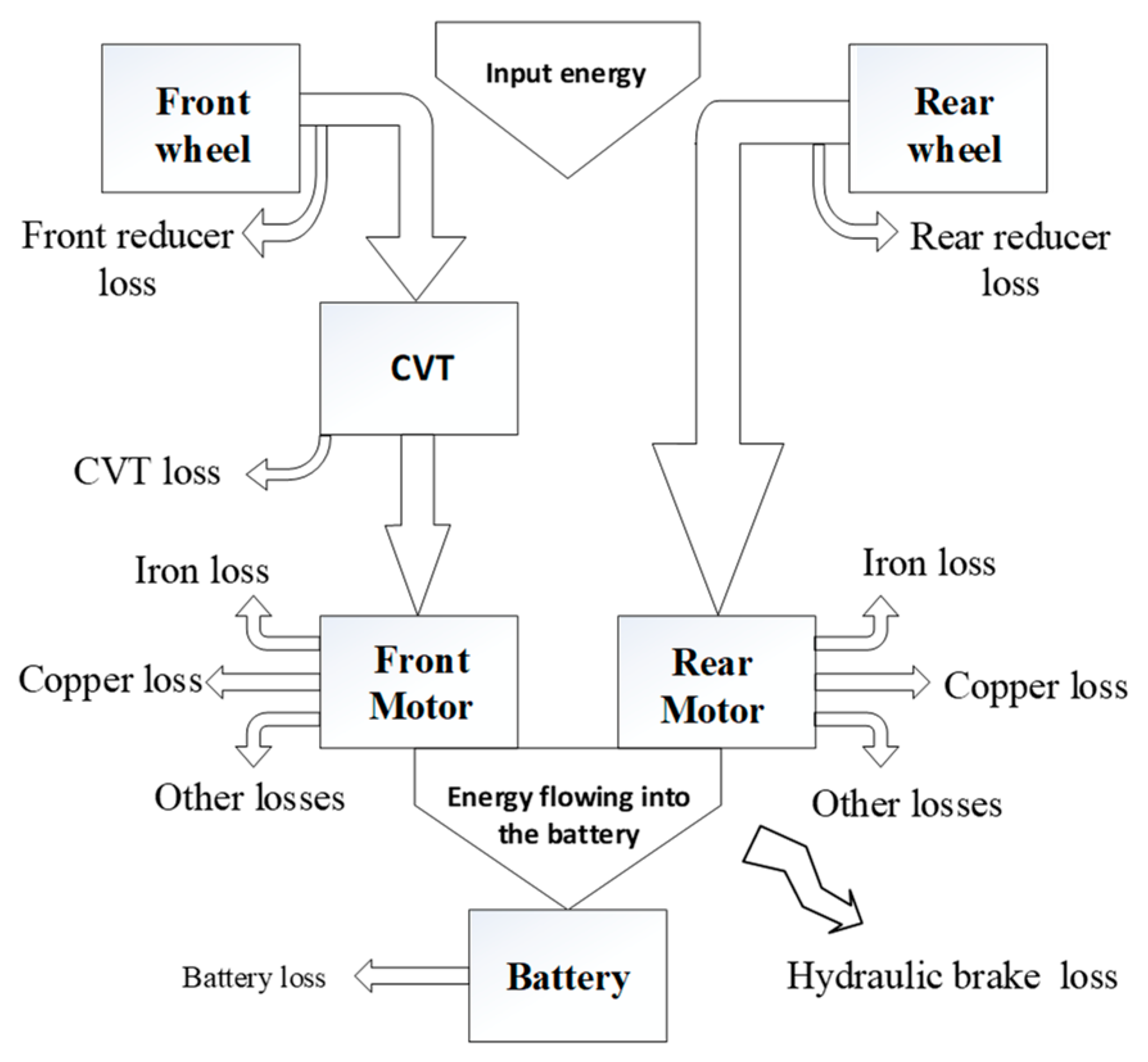
4.1.1. Power Flow Analysis of Electric Braking
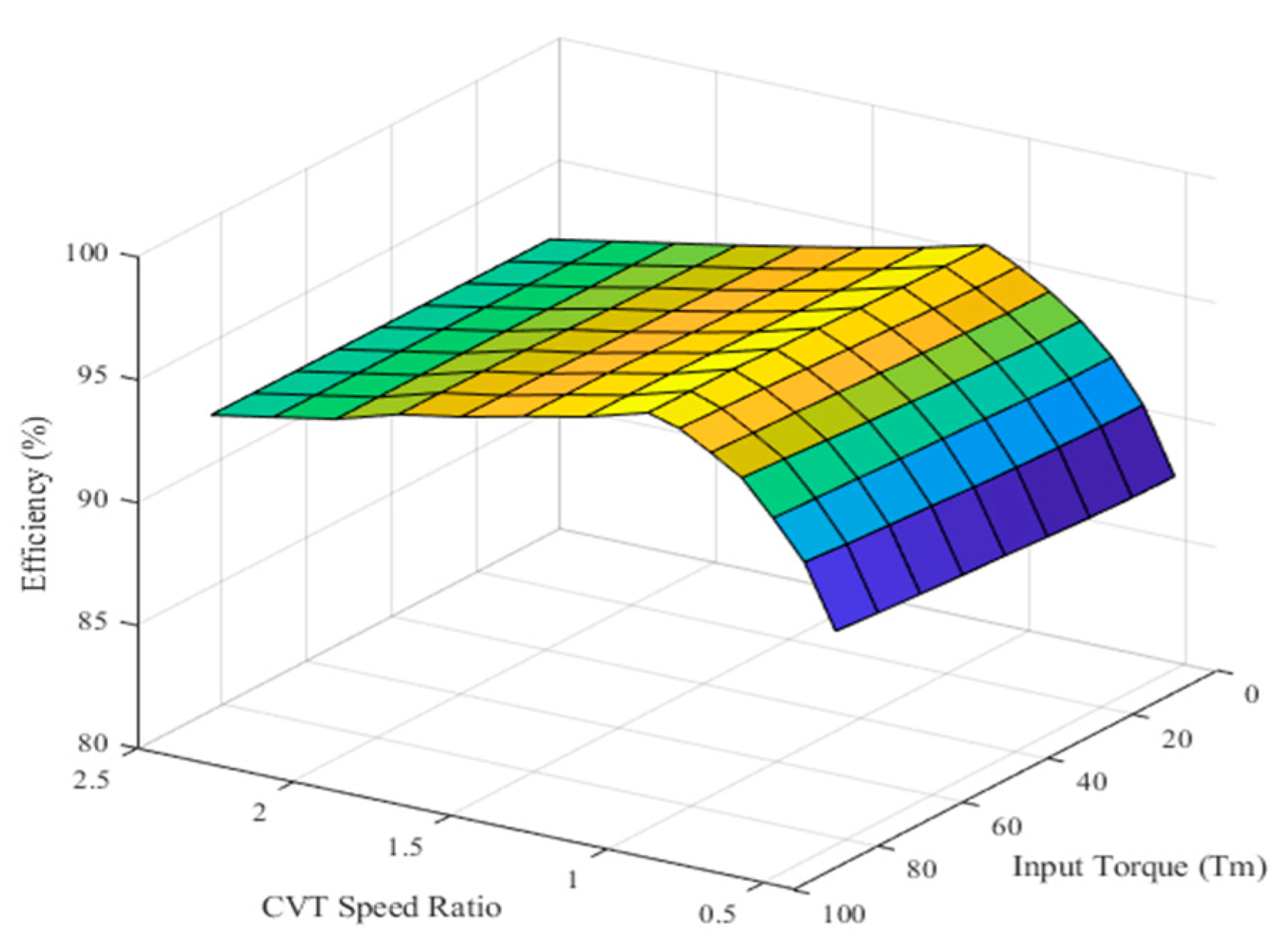
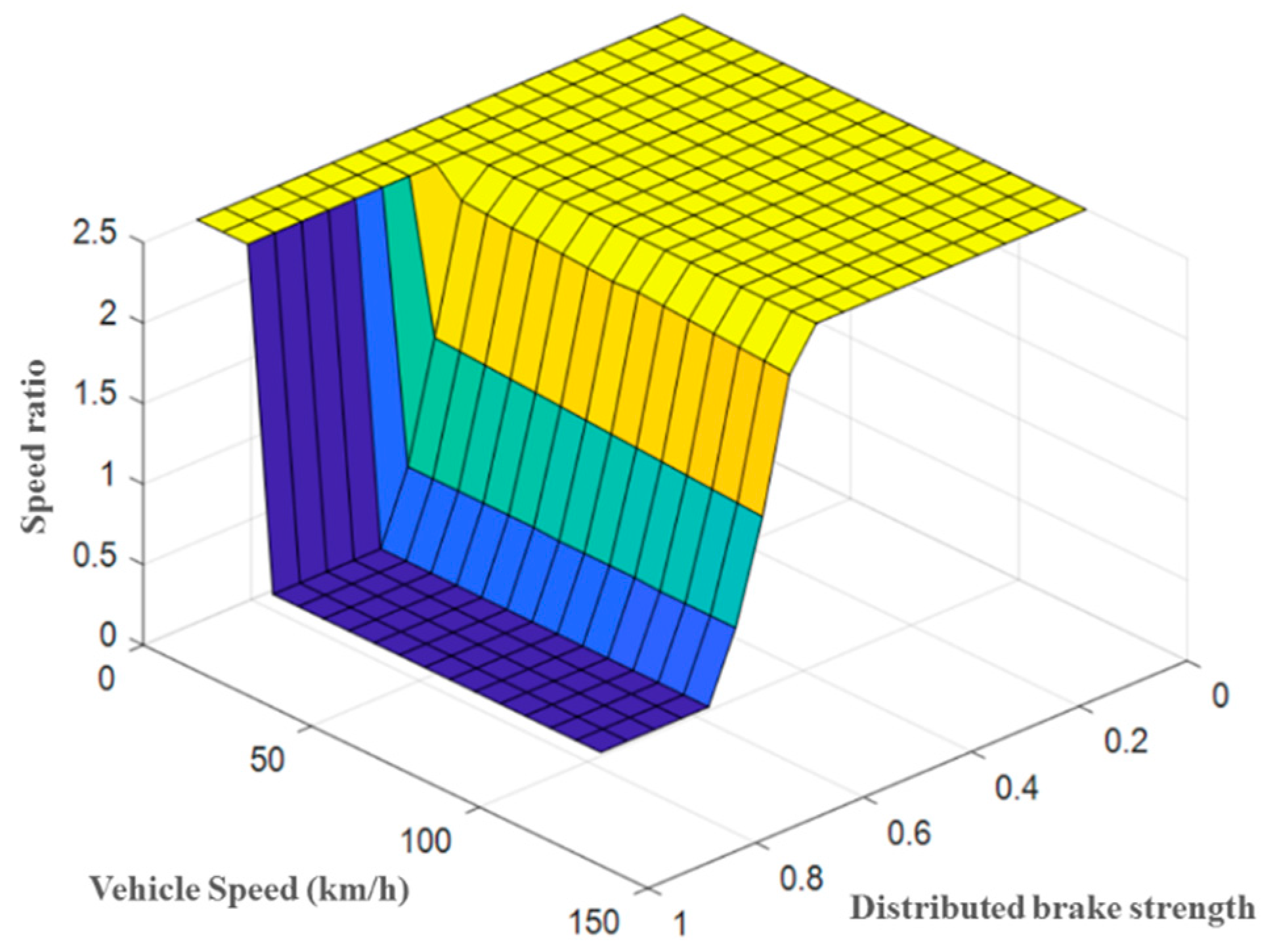
4.1.2. Establishment of the Joint Efficiency Model and Optimization of the CVT Speed Ratio
4.1.3. Input and Output Characteristics of the Front and Rear Axis Joint Models
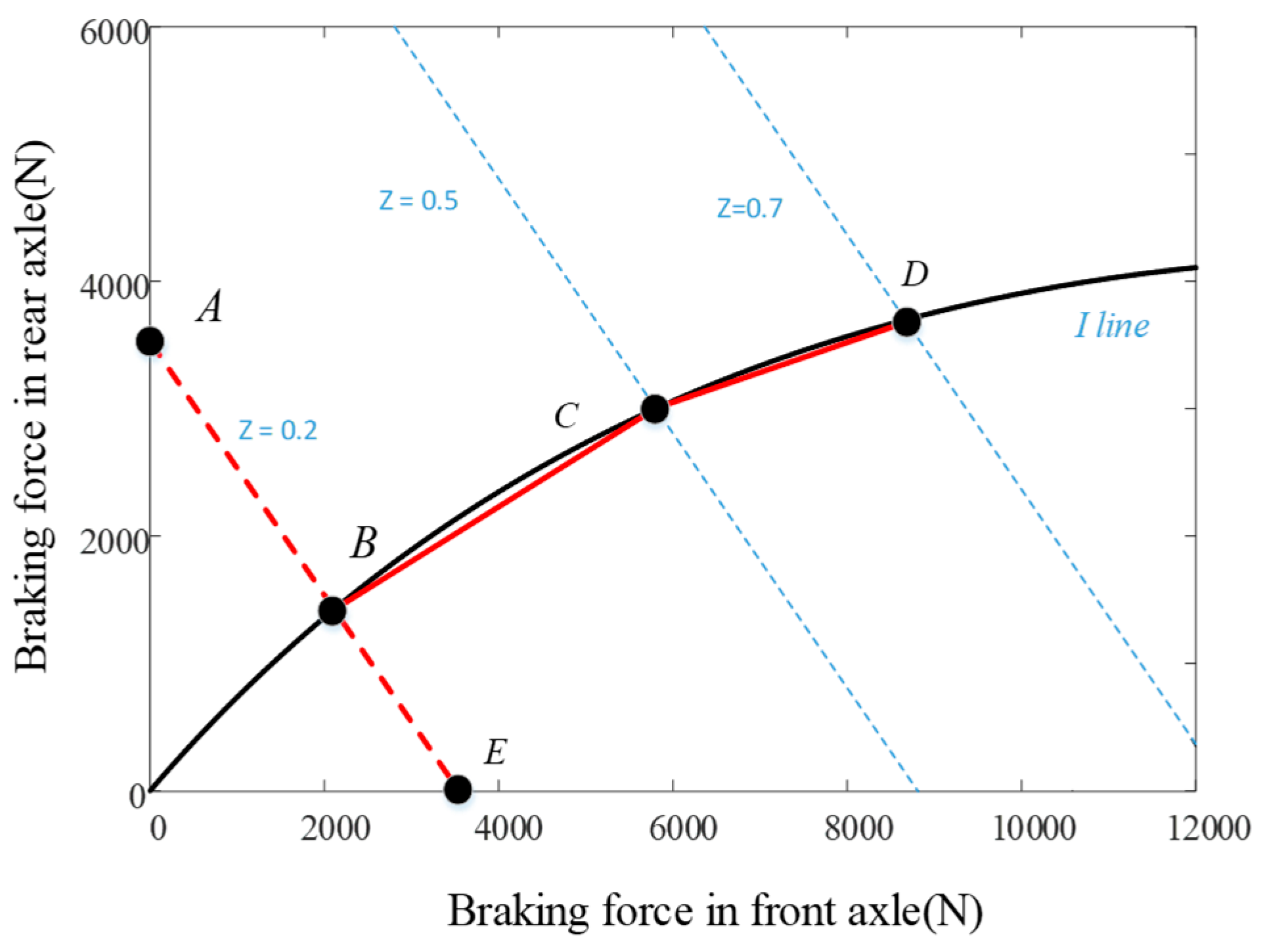
4.2. The Braking Force Distribution Strategy with the Maximum Joint Efficiency
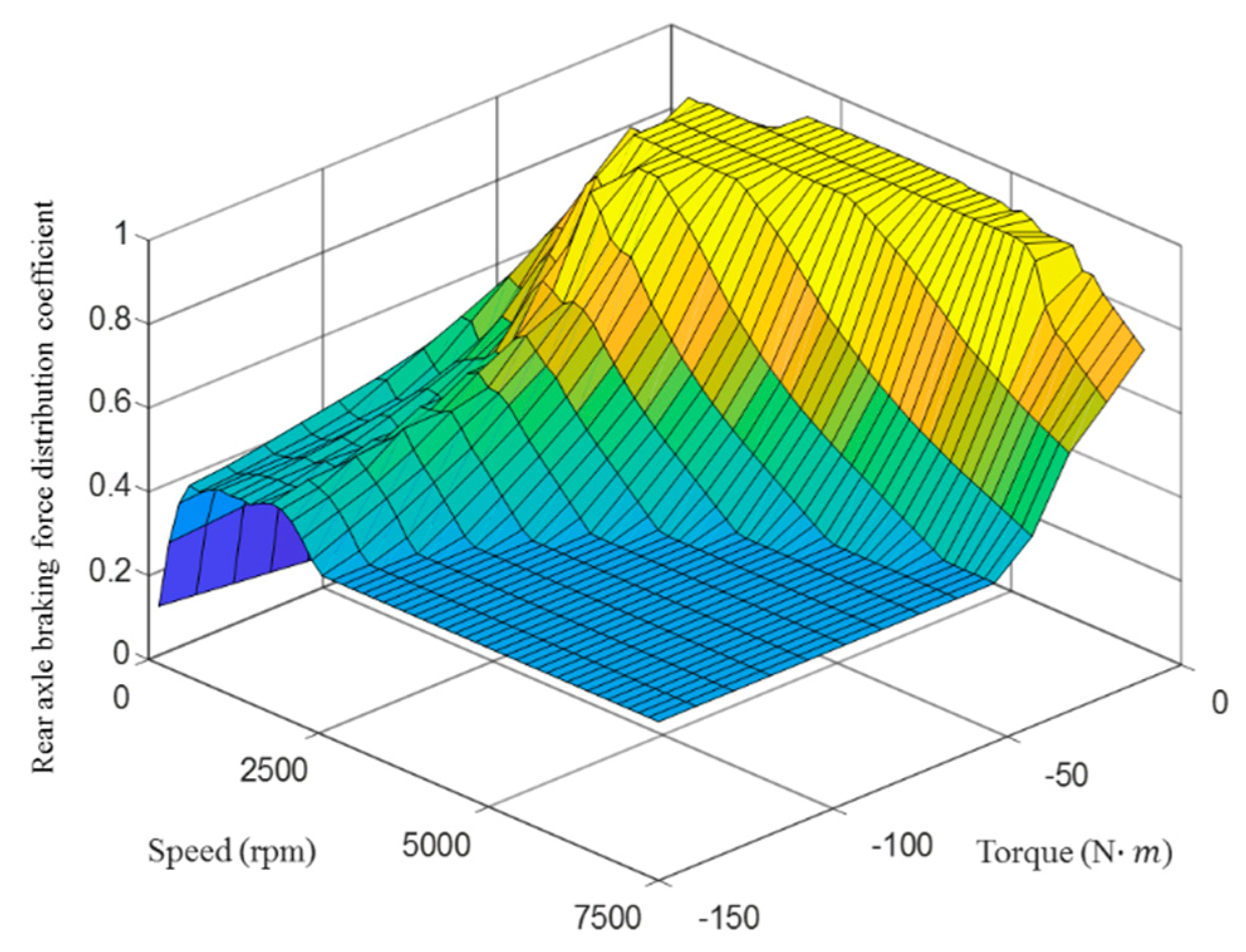
4.2.1. Front and Rear Motors Braking Force Distribution
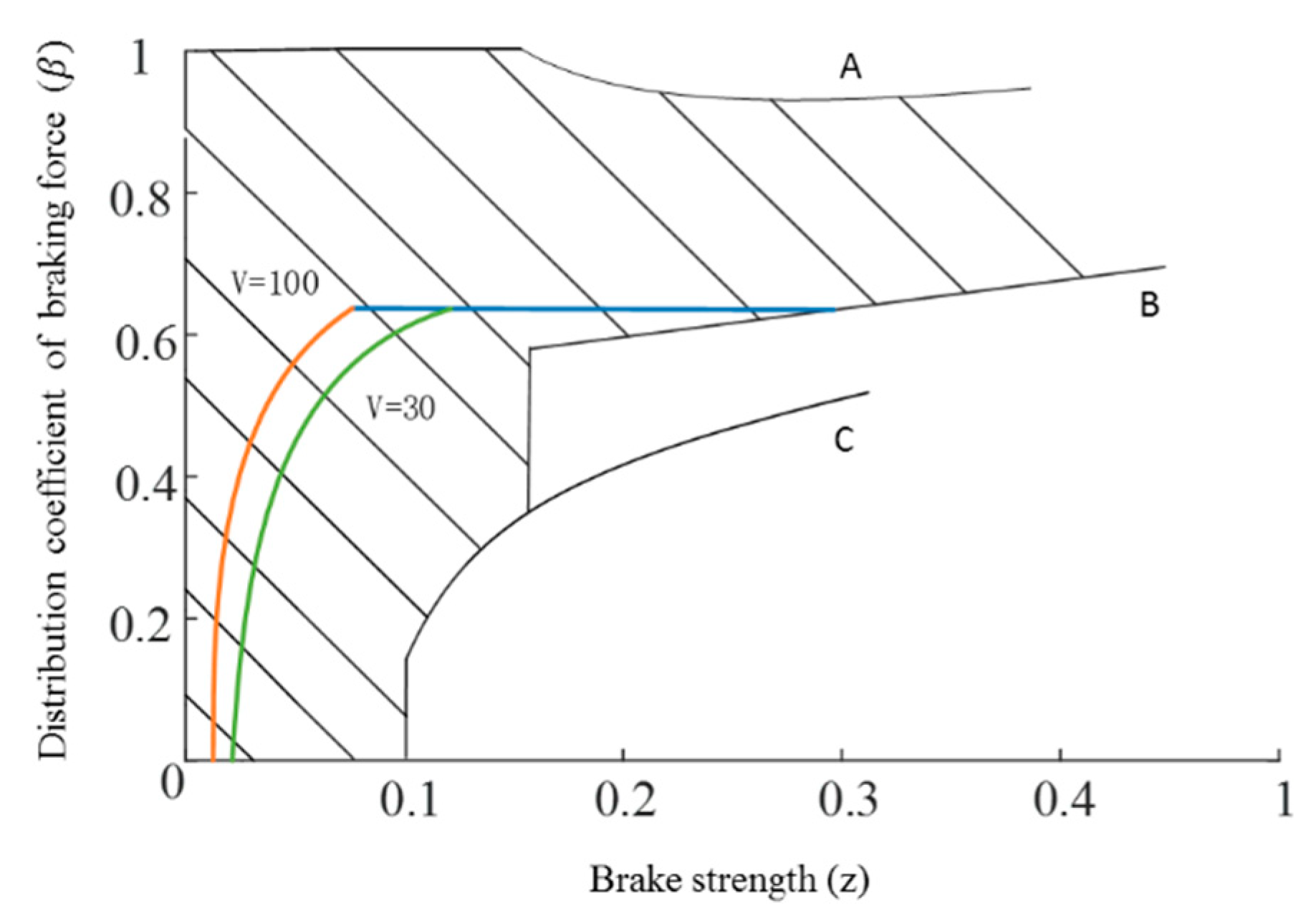
4.2.2. Vehicle Braking Force Distribution Strategy
5. Vehicle Performance Simulation and Analysis
5.1. Simulation of Typical Braking Conditions
5.1.1. Braking Strength z = 0.2
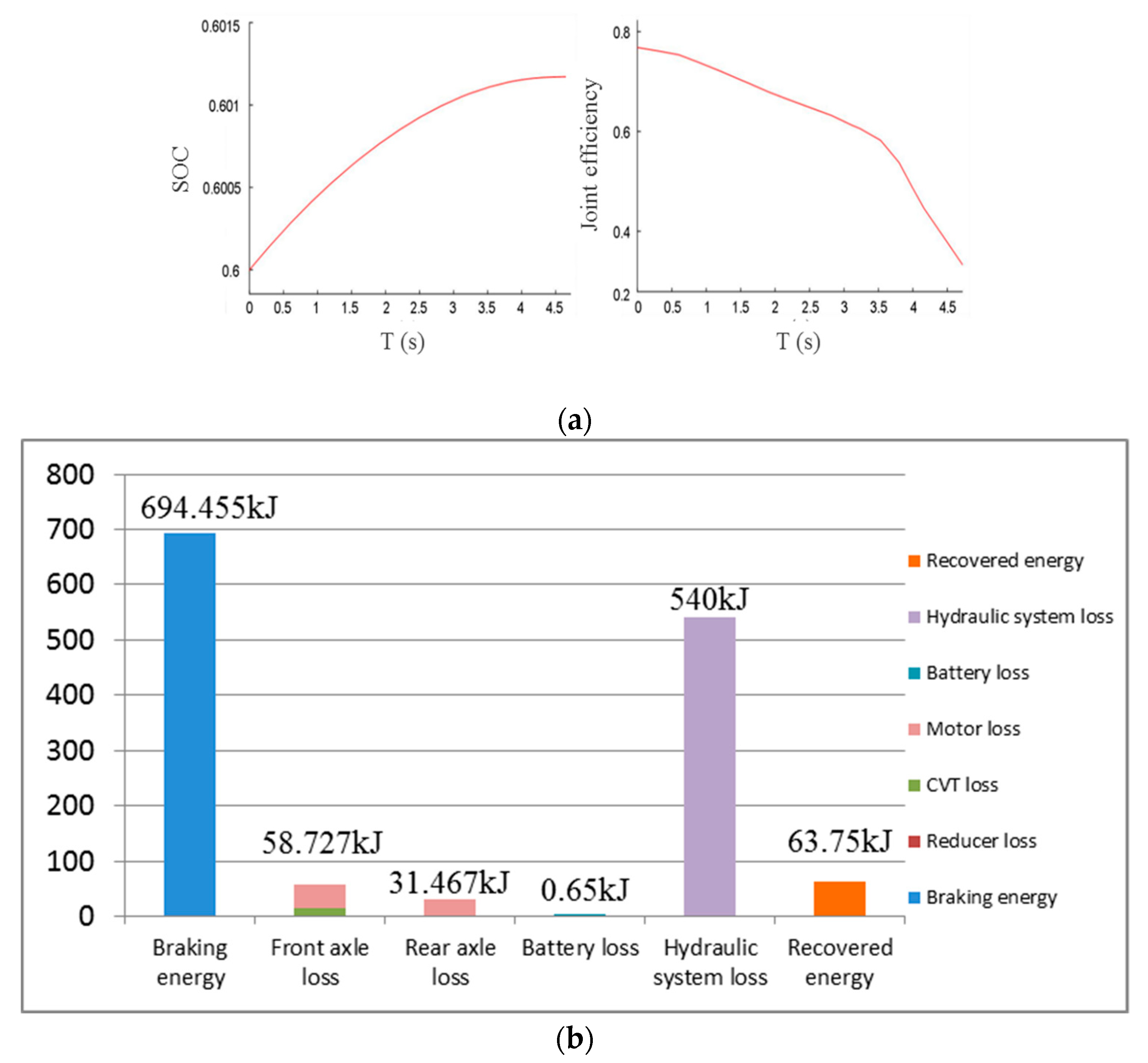
5.1.2. Braking Strength z = 0.4
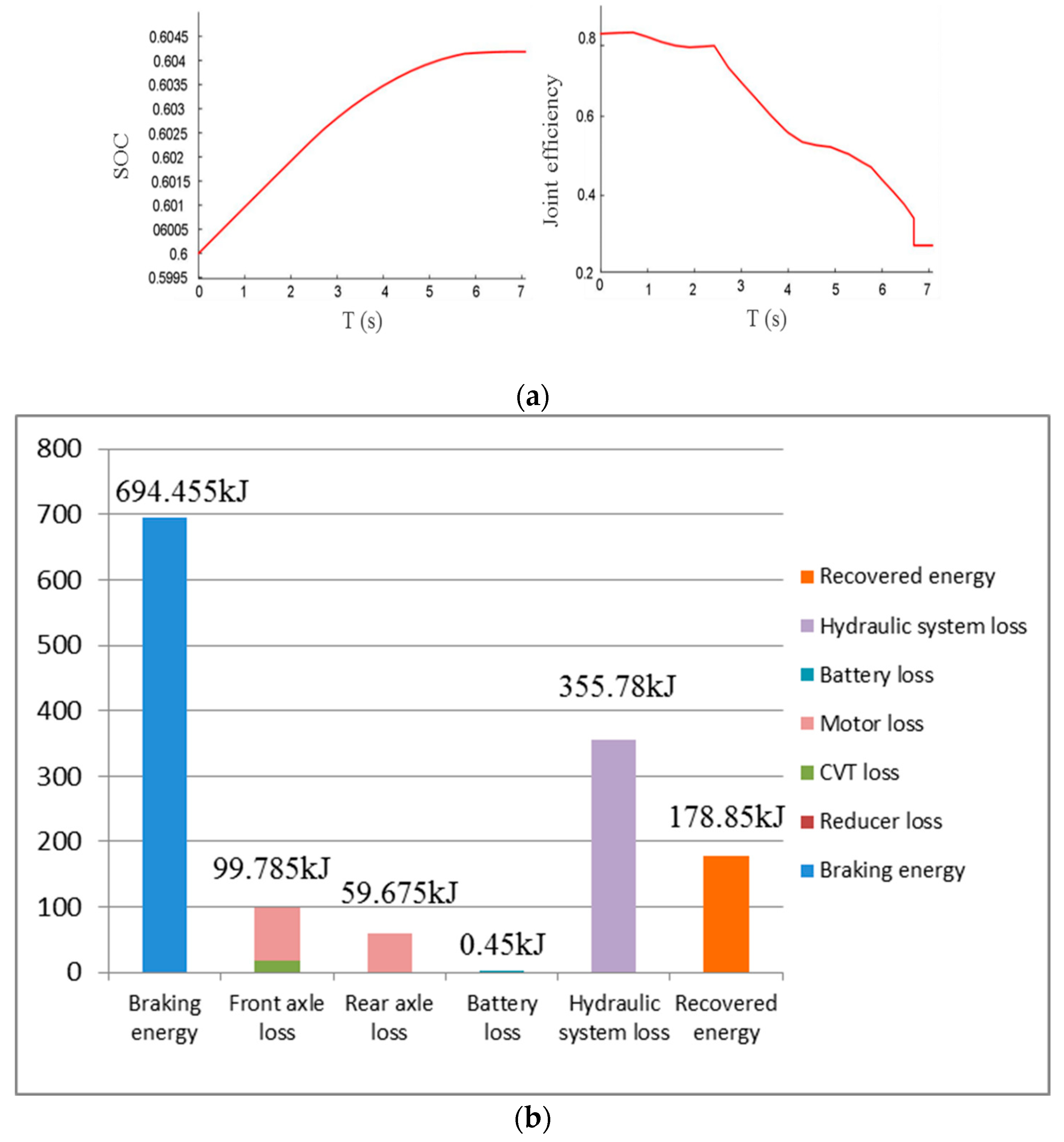
5.1.3. Braking Strength z = 0.6
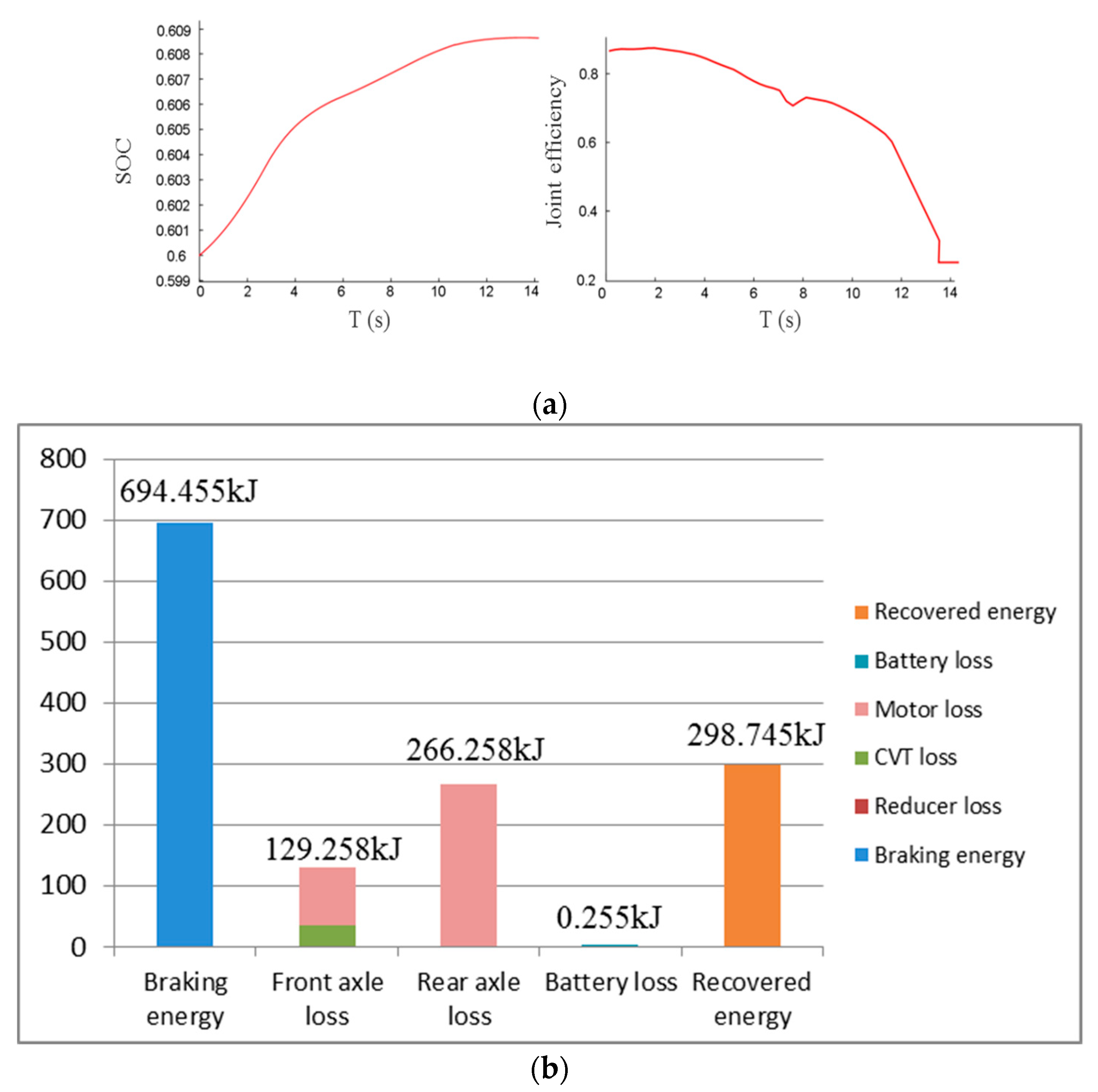
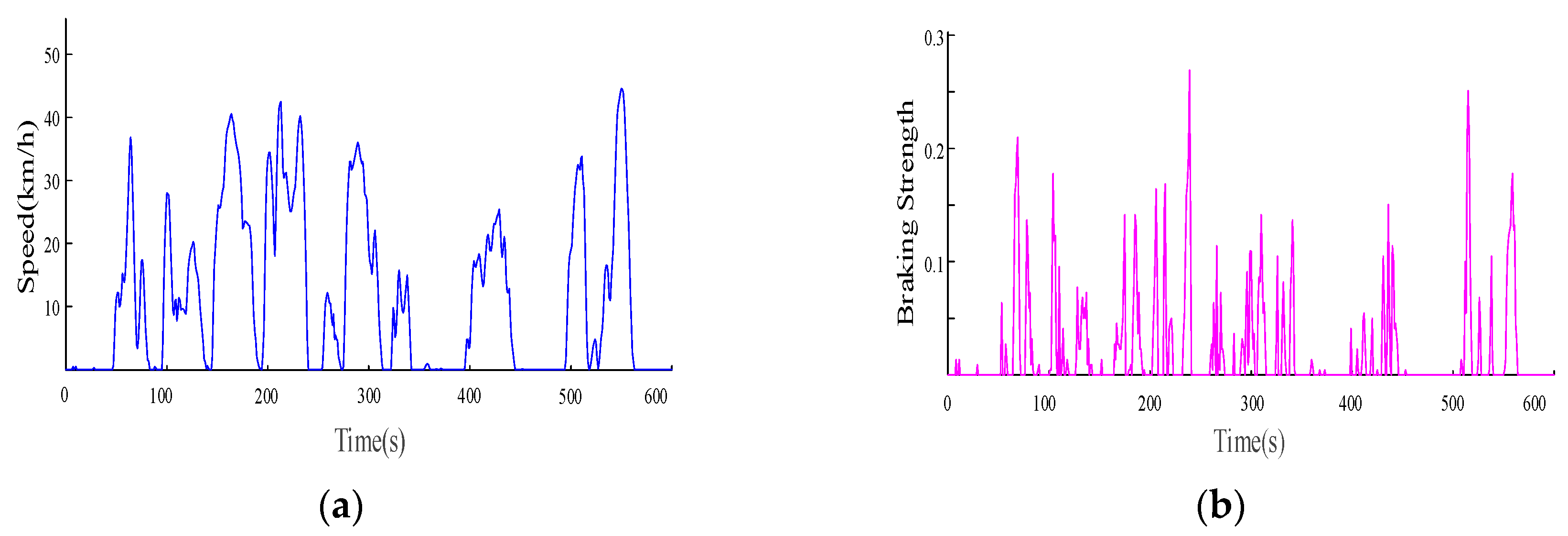
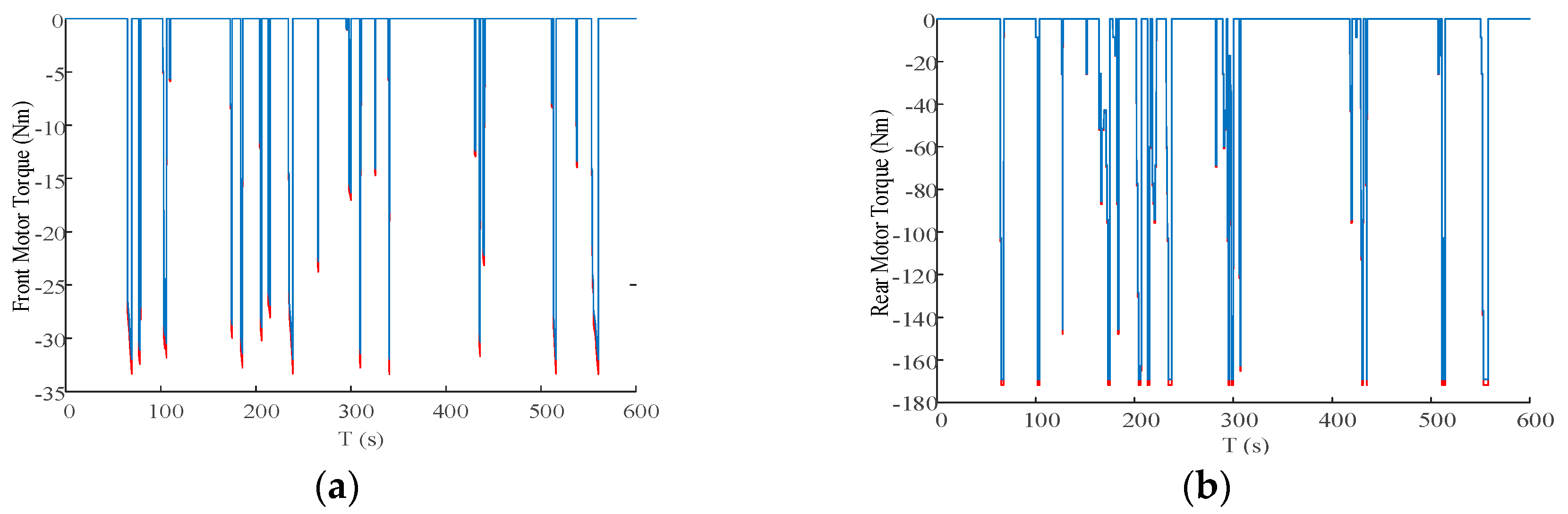
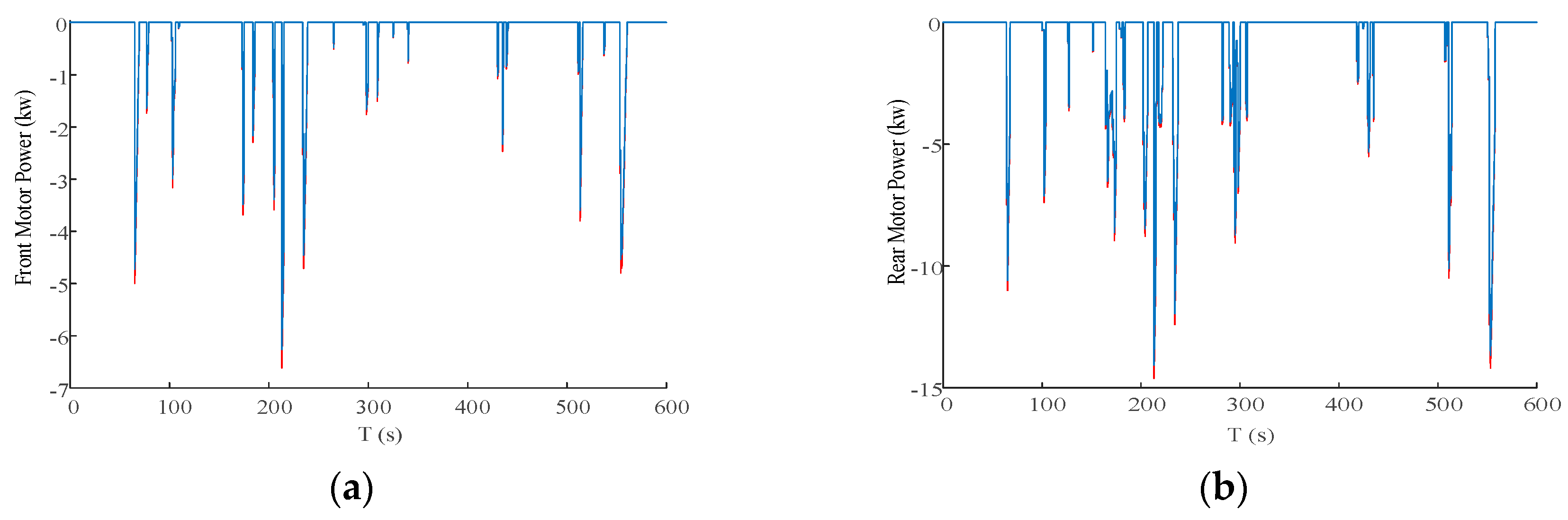
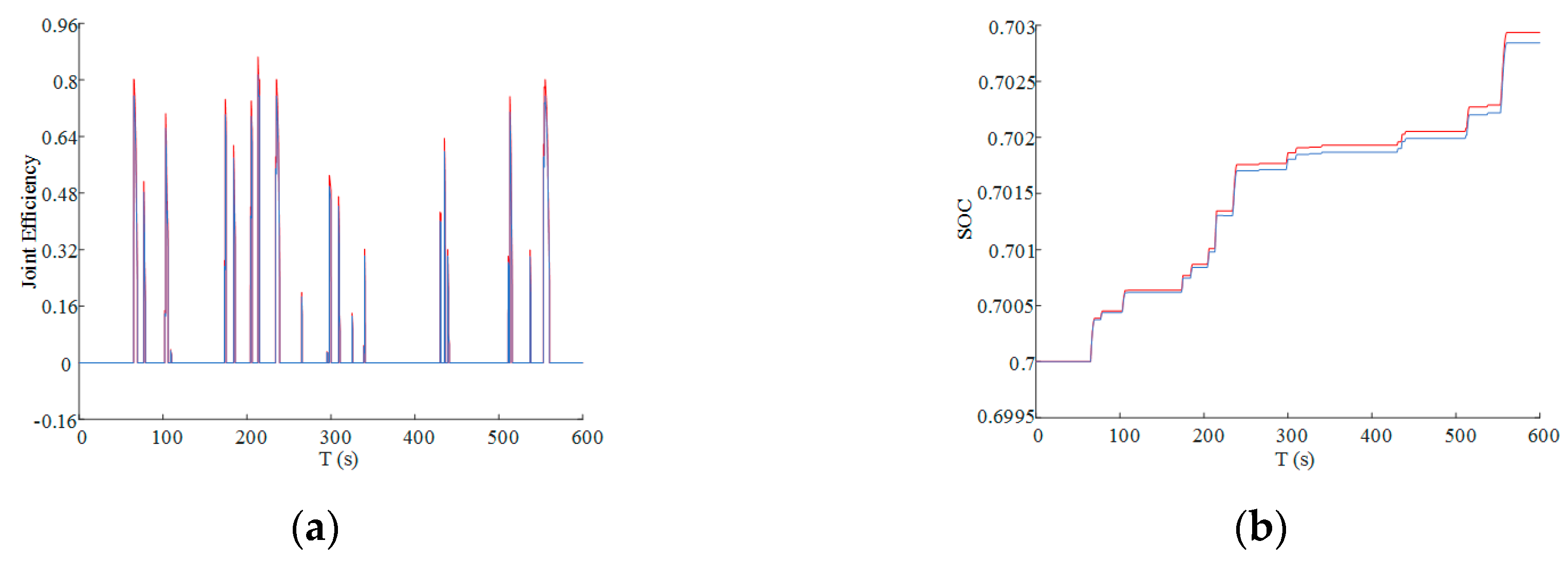
5.2. Cycle Simulation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hannan, M.A.; Azidin, F.A.; Mohamed, A. Hybrid Electric Vehicles and Their Challenges: A Review. Renew. Sustain. Energy Rev. 2014, 29, 135–150. [Google Scholar] [CrossRef]
- Khodaparastan, M.; Mohamed, A.A.; Brandauer, W. Recuperation of Regenerative Braking Energy in Electric Rail Transit Systems. IEEE Trans. Intell. Transp. 2019, 20, 2831–2847. [Google Scholar] [CrossRef] [Green Version]
- Tang, X.L.; Zhang, D.J.; Liu, T.; Khajepour, A.; Yu, H.S.; Wang, H. Research on the Energy Control of a Dual-Motor Hybrid Vehicle during Engine Start-Stop Process. Energy 2019, 166, 1181–1193. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Lv, C.; Yuan, Y. New Regenerative Braking Control Strategy for Rear-Driven Electrified Minivans. Energy Convers. Manag. 2014, 82, 135–145. [Google Scholar]
- Qiu, C.; Wang, G.; Meng, M.; Shen, Y.J.E. A Novel Control Strategy of Regenerative Braking System for Electric Vehicles under Safety Critical Driving Situations. Energy 2018, 149, 329–340. [Google Scholar] [CrossRef]
- Itani, K.; De Bernardinis, A.; Khatir, Z.; Jammal, A. Comparative Analysis of Two Hybrid Energy Storage Systems Used in a Two Front Wheel Driven Electric Vehicle during Extreme Start-Up and Regenerative Braking Operations. Energy Convers. Manag. 2017, 144, 69–87. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, J.Z.; Li, Y.T.; Li, C. A Novel Regenerative Electrohydraulic Brake System: Development and Hardware-in-Loop Tests. IEEE Trans. Veh. Technol. 2018, 67, 11440–11452. [Google Scholar] [CrossRef]
- Chen, J.; Yu, J.Z.; Zhang, K.X.; Ma, Y. Control of Regenerative Braking Systems for Four-Wheel-Independently-Actuated Electric Vehicles. Mechatronics 2018, 50, 394–401. [Google Scholar] [CrossRef]
- Deng, T.; Lin, C.S.; Chen, B.; Ma, C.F. Regenerative Braking Control Strategy Based on Joint High-Efficiency Optimization. Adv. Mech. Eng. 2016, 8. [Google Scholar] [CrossRef] [Green Version]
- Shu, H. Regenerative Braking Energy Management Strategy for Mild Hybrid Electric Vehicles. J. Mech. Eng. 2009, 45, 167–173. [Google Scholar] [CrossRef]
- Bera, T.K.; Bhattacharya, K.; Samantaray, A.K. Bond Graph Model-Based Evaluation of a Sliding Mode Controller for a Combined Regenerative and Antilock Braking System. Proc. Inst. Mech. Eng. I-J. Sys. 2011, 225, 918–934. [Google Scholar] [CrossRef]
- Tripathi, S.M.; Dutta, C. Enhanced Efficiency in Vector Control of a Surface-Mounted PMSM Drive. J. Franklin Inst. 2018, 355, 2392–2423. [Google Scholar] [CrossRef]
- Uddin, M.N.; Zou, H.B. Comparison of DTFC and Vector Control Techniques for PMSM Drive with Loss Minimization Approach. In Proceedings of the 2014 IEEE 27th Canadian Conference on Electrical and Computer Engineering (CCECE), Toronto, ON, Canada, 4–7 May 2014. [Google Scholar]
- Inoue, Y.; Morimoto, S.; Sanada, M. Comparative Study of PMSM Drive Systems Based on Current Control and Direct Torque Control in Flux-Weakening Control Region. IEEE Trans. Ind. Appl. 2012, 48, 2382–2389. [Google Scholar] [CrossRef]
- Wang, Y.; Geng, L.; Hao, W.J.; Xiao, W.Y. Control Method for Optimal Dynamic Performance of DTC-Based PMSM Drives. IEEE Trans. Energy Convers. 2018, 33, 1285–1296. [Google Scholar] [CrossRef]
- Vido, L.; Le Ballois, S. A Simple Method for Optimal Control of PMSM with Loss Minimization Including Copper Loss and Iron Loss. In Proceedings of the 2017 Twelfth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 11–13 April 2017. [Google Scholar]
- Lee, J.; Nam, K.; Choi, S.; Kwon, S. Loss-Minimizing Control of PMSM With the Use of Polynomial Approximations. IEEE Trans. Power Electron. 2009, 24, 1071–1082. [Google Scholar]
- Estima, J.O.; Cardoso, A.J.M. Performance Analysis of a PMSM Drive for Hybrid Electric Vehicles. In Proceedings of the International Conference on Electrical Machines, Rome, Italy, 6–8 September 2010. [Google Scholar]
- Estima, J.O.; Cardoso, A.J.M. Performance Evaluation of DTC-SVM Permanent Magnet Synchronous Motor Drives under Inverter Fault Conditions. In Proceedings of the 2009 35th Annual Conference of IEEE Industrial Electronics, Porto, Portugal, 3–5 November 2009. [Google Scholar]
- Urasaki, N.; Senjyu, T.; Uezato, K. An Accurate Modeling for Permanent Magnet Synchronous Motor Drives. In Proceedings of the APEC 2000 Fifteenth Annual IEEE Applied Power Electronics Conference and Exposition (Cat. No. 00CH37058), New Orleans, LA, USA, 6–10 Feburary 2000. [Google Scholar]
- Deng, W.W.; Zhao, Y.; Wu, J. Energy Efficiency Improvement via Bus Voltage Control of Inverter for Electric Vehicles. IEEE Trans. Veh. Technol. 2017, 66, 1063–1073. [Google Scholar] [CrossRef]
- Xiong, H.Y.; Zhu, X.L.; Zhang, R.H. Energy Recovery Strategy Numerical Simulation for Dual Axle Drive Pure Electric Vehicle Based on Motor Loss Model and Big Data Calculation. Complexity 2018, 2018. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; He, X.L.; Zhang, Y.; Qin, D.T. Regenerative Braking Compensatory Control Strategy Considering CVT Power Loss for Hybrid Electric Vehicles. Energies 2018, 11, 497. [Google Scholar] [CrossRef] [Green Version]
- Geller, B.M.; Bradley, T.H. Analyzing Drive Cycles for Hybrid Electric Vehicle Simulation and Optimization. J. Mech. Des. 2015, 6328, 137. [Google Scholar] [CrossRef]






| Name | Description | Value |
|---|---|---|
| Vehicle | Curb weight Windward area Wheel radius Wheelbase | 1800 kg 2.5 m2 0.335 m 2.7 m |
| The ISG motor | Peak power Rated power Maximum torque Number of pole pairs Armature resistance d/q axis inductance Magnet flux linkage iron losses resistance | 28 kW 14 kW 89.13 N∙m 6 0.017 ohm 0.00021 H 0.037 Wb 0.008 w + 1.8 ohm |
| Rear axle motor | Peak power Rated power Maximum torque Pole of pairs Armature resistance d/q axis inductance Magnet flux linkage Iron losses resistance | 27 kW 13.5 kW 171.9 N∙m 8 0.012 ohm 0.00012 H 0.042 Wb 0.011 w + 1.9 ohm |
| Lithium-ion battery pack | Rated capacity | 38.43 Ah |
| CVT | Speed ratio range | [0.4, 2.5] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; He, Q.; Chen, Y.; Fu, C. Efficiency Optimization and Control Strategy of Regenerative Braking System with Dual Motor. Energies 2020, 13, 711. https://doi.org/10.3390/en13030711
Yang Y, He Q, Chen Y, Fu C. Efficiency Optimization and Control Strategy of Regenerative Braking System with Dual Motor. Energies. 2020; 13(3):711. https://doi.org/10.3390/en13030711
Chicago/Turabian StyleYang, Yang, Qiang He, Yongzheng Chen, and Chunyun Fu. 2020. "Efficiency Optimization and Control Strategy of Regenerative Braking System with Dual Motor" Energies 13, no. 3: 711. https://doi.org/10.3390/en13030711
APA StyleYang, Y., He, Q., Chen, Y., & Fu, C. (2020). Efficiency Optimization and Control Strategy of Regenerative Braking System with Dual Motor. Energies, 13(3), 711. https://doi.org/10.3390/en13030711