Exergetic Analysis and Exergy Loss Reduction in the Milk Pasteurization for Italian Cheese Production
Abstract
:1. Introduction
2. Methods
2.1. Pasteurization System with Heat Recovery Exchanger
2.2. Exergetic Analysis of Thermal Exchangers
2.2.1. Recovery Exchanger
2.2.2. Heating Exchanger
2.2.3. Cooling Exchanger
2.3. Cost-Benefit Analysis
2.3.1. Unit Cost of Thermal and Electric Energy vs. Recovery Efficiency
2.3.2. Unit Cost of Heat Exchanger Area vs. Recovery Efficiency
2.3.3. Optimization of Recovery Efficiency
3. Results and Discussion
3.1. Survey of Energy Recovery Efficiency of the Italian Milk Pasteurization
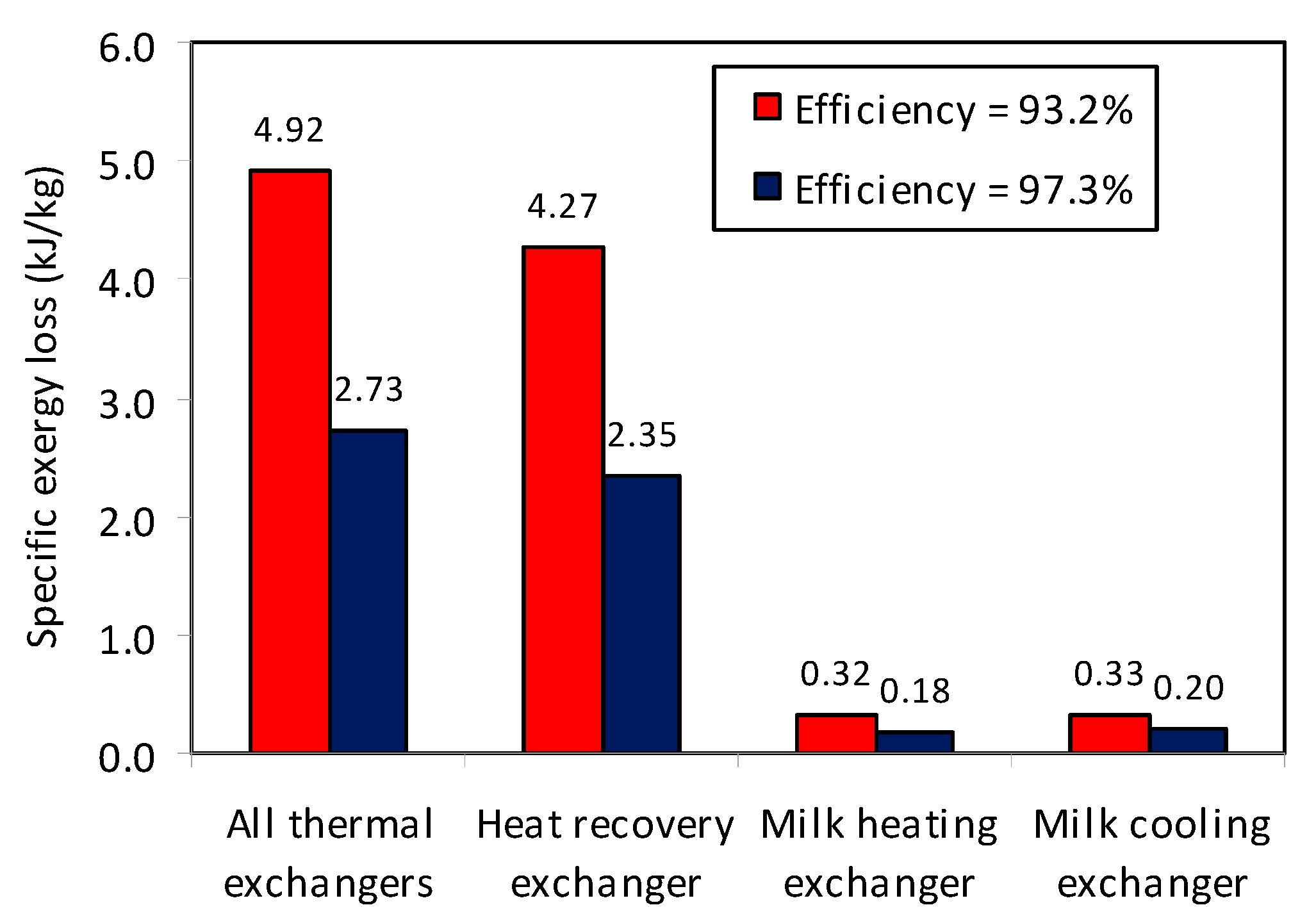
3.2. Exergetic Analysis of Heat Exchangers of Actual Pasteurization Equipment
3.3. Cost-Benefit Analysis and Assessment of Optimized Efficiency
3.4. Exergetic Analysis of Heat Exchangers for Optimized Pasteurization Equipment
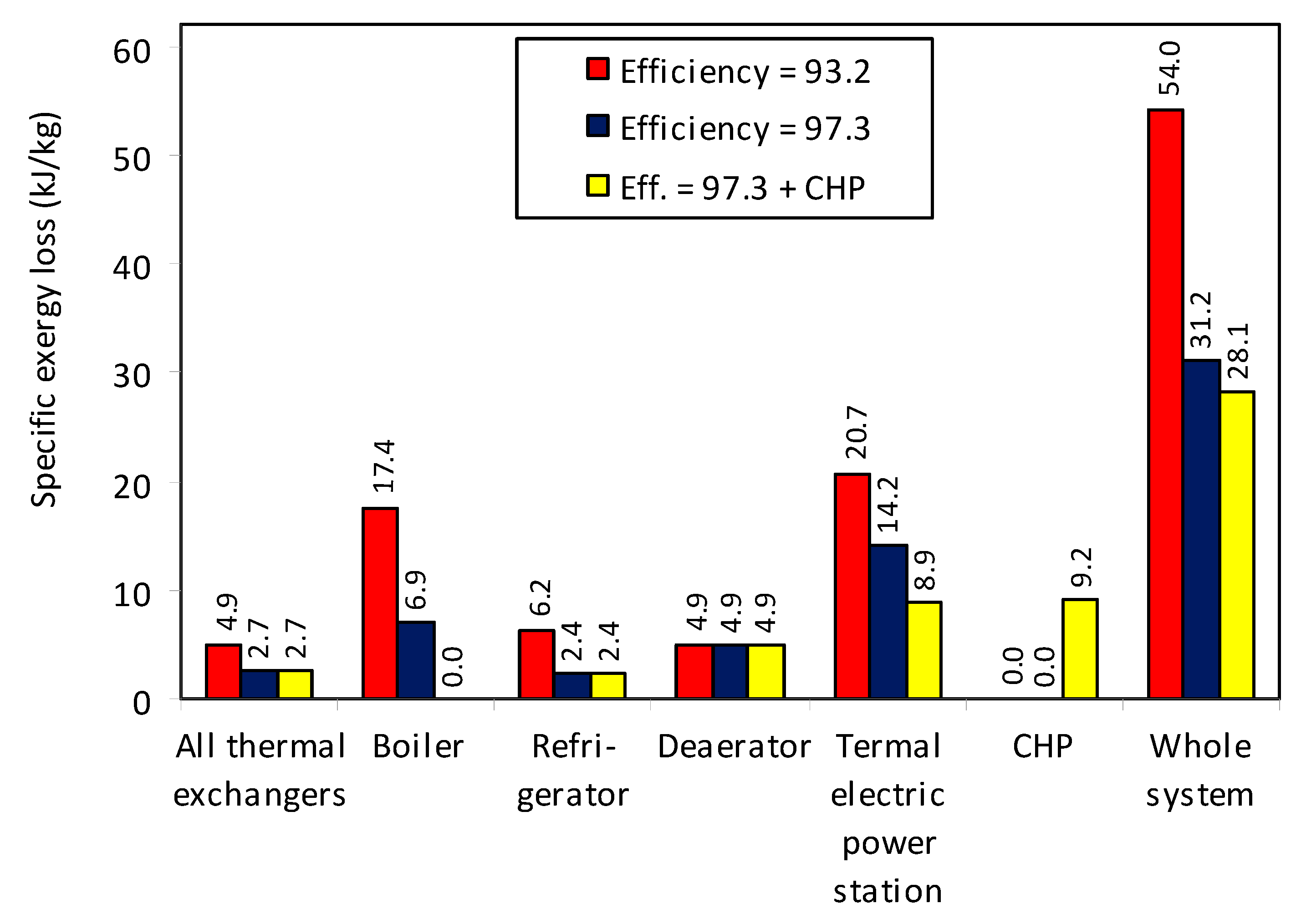
3.5. Exergetic Analysis of the Whole System and with CHP
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CHP | cogeneration heat and power |
| COP | coefficient of performance of refrigerator |
| HTST | high temperature/short time |
| PHE | plate heat exchanger |
Nomenclature
| A | m2 | exchange area |
| B | y | useful life of the equipment |
| C | Euro kg−1milk Euro m−2 Euro Sm−3 Euro kWh−1 | unit cost |
| c | kJ kg−1 K−1 | specific heat capacity |
| E | kWh kg−1milk | electric consumption |
| G | Kg s−1 | flow rate |
| h | kJ kg−1 | specific enthalpy |
| HV | kJ Sm−3 | heat value of natural gas |
| L | kW Kg−1milk | exergy flux loss |
| KJ kg−1milk | specific exergy loss | |
| N | h y−1 | running pasteurization time |
| P | kW | mechanical power |
| p | kPa | pressure |
| q | W | heat transfer rate |
| S | kJ kg−1K−1 | specific entropy |
| T | K or °C | temperature |
| K or °C | average temperature | |
| U | kW m−2 K−1 | overall heat transfer coefficient |
| Δp | kPa | pressure drop |
| ΔT | K or °C | temperature difference |
| ε | % | energy recovery efficiency |
| ƞ | % | efficiency |
Subscript
| A | area unit (cost) |
| a | ambient |
| C, c | cooling exchanger |
| cond | condensation in refrigerator |
| D | deaerator |
| DP | deaerator + pumps |
| dr | heat dispersion |
| E | Equipment (cost) |
| en | energetic |
| ev | evaporation in refrigerator |
| ex | exergetic |
| F | fuel unit (cost) |
| H | heat unit (cost) |
| H, h | heating exchanger |
| hb | heating boiler |
| irr | irreversibility |
| m | milk |
| M | unit (cost) for refrigeration |
| mC | milk in cooling exchanger |
| mci | cooling exchanger milk input |
| mco | cooling exchanger milk output |
| mH | milk in heating exchanger |
| mi | raw milk input |
| mP | pasteurized milk in recovery exchanger |
| mpo | pasteurized hot milk output |
| mR | raw milk in recovery exchanger |
| mro | recovery exchanger milk output |
| opt | optimized |
| P | pump |
| PA | actual pump |
| Pcw | cold water pump |
| Phw | hot water pump |
| Ppm | pasteurized milk pump |
| Prm | raw milk pump |
| R, r | recovery exchanger |
| tot | total |
| w | water |
| W | electric energy |
| wC | water in cooling exchanger |
| wci | cooling exchanger water input |
| wco | cooling exchanger water output |
| wH | water in heating exchanger |
| whi | heating exchanger water input |
| who | heating exchanger water output |
References
- ISTAT (Italian National Institute of Statistics). Available online: http://dati.istat.it/Index.aspx?lang=en&SubSessionId=978a3f3ce0ac-4efd-b344-e8a8bdde7994 (accessed on 16 October 2019).
- France Agroalimentaire. Available online: https://www.franceagroalimentaire.com (accessed on 16 October 2019).
- FAO. Available online: http://www.fao.org/dairy-production-products/en/ (accessed on 16 October 2019).
- CLAL (Italian Dairy Economic Consulting). Available online: https://www.clal.it/en (accessed on 16 October 2019).
- EDA (European Dairy Association). Available online: http://eda.euromilk.org (accessed on 16 October 2019).
- Munir, M.T.; Yu, W.; Young, B.R. Can exergy be a useful tool for the dairy Industry? Comput. Aided Chem. Eng. 2014, 33, 1129–1134. [Google Scholar]
- Barchyn, D.; Cenkowski, S. Process analysis of superheated steam pretreatment of wheat straw and its relative effect on ethanol selling price. Biofuel Res. J. 2014, 1, 123–128. [Google Scholar] [CrossRef]
- De, S.; Luque, R. Upgrading of waste oils into transportation fuels using hydrotreating technologies. Biofuel Res. J. 2014, 1, 107–109. [Google Scholar] [CrossRef]
- Aladetuyi, A.; Olatunji, G.A.; Ogunniyi, D.S.; Odetoye, T.E.; Oguntoye, S.O. Production and characterization of biodiesel using palm kernel oil; fresh and recovered from spent bleaching earth. Biofuel Res. J. 2014, 1, 134–138. [Google Scholar] [CrossRef]
- Jaber, R.; Shirazi, M.M.A.; Toufaily, J.; Hamieh, A.T.; Noureddin, A.; Ghanavati, H.; Ghaffari, A.; Zenouzi, A.; Karout, A.; Ismail, A.F.; et al. Biodiesel wash-water reuse using microfiltration: Toward zero-discharge strategy for cleaner and economized biodiesel production. Biofuel Res. J. 2015, 2, 148–151. [Google Scholar] [CrossRef]
- Kumar, G.; Bakonyi, P.; Sivagurunathan, P.; Nemestothy, N.; Belafi-Bako, K.; Lin, C.Y. Improved microbial conversion of de-oiled Jatropha waste into biohydrogen via inoculum pretreatment: Process optimization by experimental design approach. Biofuel Res. J. 2015, 2, 209–214. [Google Scholar] [CrossRef]
- Rant, Z. Exergie, Ein neues Wort für technische Arbeitsfähigkeit. (exergy, a new word for technical availability). Forsch. Geb. Ing. 1956, 22, 36–37. [Google Scholar]
- Bosnjakovic, F. Technische Thermodinamik; Theodor Steinkopf: Dresden, Germany, 1965. [Google Scholar]
- Borel, L.; Favrat, D. Thermodynamique et énergétique; Presses Polytechniques et Universitaires Romandes: Lausanne, Switzerland, 2005. [Google Scholar]
- Pandey, A.K.; Tyagi, V.V.; Tyagi, S.K. Exergetic analysis and parametric study of multi-crystalline solar photovoltaic system at a typical climatic zone. Clean. Technol. Environ. 2013, 15, 333–343. [Google Scholar] [CrossRef]
- Park, S.R.; Pandey, A.K.; Tyagi, V.V.; Tyagi, S.K. Energy and exergy analysis of typical renewable energy systems. Renew. Sust. Energy Rev. 2014, 30, 105–123. [Google Scholar] [CrossRef]
- Dadak, A.; Aghbashlo, M.; Tabatabaei, M.; Najafpour, G.; Younesi, H. Exergy analysis as a tool for decision making on substrate concentration and light intensity in photobiological hydrogen production. Energy Technol. 2015, 4, 429–440. [Google Scholar] [CrossRef]
- Hosseini, S.S.; Aghbashlo, M.; Tabatabaei, M.; Najafpour, G.; Younesi, H. Thermodynamic evaluation of a photobioreactor for hydrogen production from syngas via a locally isolated Rhodopseudomonas palustris PT. Int. J. Hydrogen Energy 2015, 40, 14246–14256. [Google Scholar] [CrossRef]
- Hu, P.; Zhang, G.W.; Chen, L.X.; Liu, M.H. Theoretical Analysis for Heat Transfer Optimization in Subcritical Electrothermal Energy Storage Systems. Energies 2017, 10, 198. [Google Scholar] [CrossRef] [Green Version]
- Dorosz, P.; Wojcieszak, P.; Malecha, Z. Exergetic Analysis, Optimization and Comparison of LNG Cold Exergy Recovery Systems for Transportation. Entropy 2018, 20, 59. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Q.; Gan, Y.; Su, W.; Liu, Y.; Sun, W.; Xu, Y. Research on Exergy Flow Composition and Exergy Loss Mechanisms for Waxy Crude Oil Pipeline Transport Processes. Energies 2017, 10, 1956. [Google Scholar] [CrossRef] [Green Version]
- Hasan, M.F.; Mahadi, M.S.U.R.; Miyazaki, T.; Koyama, S.; Thu, K. Exergy Analysis of Serpentine Thermosyphon Solar Water Heater. Appl. Sci. 2018, 8, 391. [Google Scholar] [CrossRef] [Green Version]
- Soufiyan, M.M.; Aghbashlo, M.; Mobli, H. Exergetic performance assessment of a long-life milk processing plant: A comprehensive survey. J. Clean. Prod. 2017, 140, 590–607. [Google Scholar] [CrossRef]
- Jafaryani Jokandan, M.; Aghbashlo, M.; Mohtasebi, S.S. Comprehensive exergy analysis of an industrial-scale yogurt production plant. Energy 2015, 93, 1832–1851. [Google Scholar] [CrossRef]
- Mahar, A.; Shaikh, M.S.; Bhatti, I. Performance analysis of plate type heat exchanger for milk pasteurization. In AIP Conference Proceedings, Proceedings of 5th International Conference on Energy, Environment & Sustainable Development, Jamshoro, Sindh, Pakistan, 14–16 November 2018; AIP Publishing: Melville, NY, USA, 2019. [Google Scholar]
- Bühler, F.; Nguyen, T.V.; Jensen, J.K.; Holm, F.M.; Elmegaard, B. Energy, exergy and advanced exergy analysis of a milk processing factory. Energy 2018, 162, 576–592. [Google Scholar] [CrossRef] [Green Version]
- Fang, Z.; Larson, D.L.; Fleishmen, G. Exergy analysis of a milk processing system. Trans. ASAE 1995, 38, 1825–1832. [Google Scholar] [CrossRef]
- Miller, E. Energy management in milk processing. In Energy in Food Processing; Singh, R.P., Ed.; Elsevier: Amsterdam, The Netherlands, 1986; Volume 1, pp. 137–154. [Google Scholar]
- Ramirez, C.A.; Patel, M.; Blok, K. From fluid milk to milk powder: Energy use and energy efficiency in the European dairy industry. Energy 2006, 31, 1984–2004. [Google Scholar] [CrossRef] [Green Version]
- Srinivasan, B.; Pal, J.; Srinivasan, R. Enhancement of energy efficiency at an Indian milk processing plant using exergy analysis. In Sustainable Energy Technology and Policies; De, S., Bandyopadhyay, S., Assadi, M., Mukherjee, D., Eds.; Springer: Singapore, 2018; pp. 425–450. [Google Scholar]
- Xu, T.; Flapper, J. Energy use and implications for efficiency strategies in global fluid-milk processing industry. Energ. Policy 2009, 37, 5334–5341. [Google Scholar] [CrossRef]
- Yildirim, N.; Genc, S. Energy and exergy analysis of a milk powder production system. Energ. Convers. Manage. 2017, 149, 698–705. [Google Scholar] [CrossRef]
- Friso, D. Energy Saving with Total Energy System for Cold Storage in Italy: Mathematical Modeling and Simulation, Exergetic and Economic Analysis. Appl. Math. Scie. 2014, 8, 6529–6546. [Google Scholar] [CrossRef]
- Friso, D.; Grigolato, S.; Cavalli, R. Energetic and exergetic analysis of steam production for the extraction of coniferous essential oils. Biomass Bioenerg. 2011, 35, 4045–4056. [Google Scholar] [CrossRef]
- Woldemariam, D.; Martin, A.; Santarelli, M. Exergy Analysis of Air-Gap Membrane Distillation Systems for Water Purification Applications. Appl. Sci. 2017, 7, 301. [Google Scholar] [CrossRef] [Green Version]
- Mohsenin, N.N. Thermal Properties of Foods and Agricultural Materials; Gordon and Breach Science Publishers: New York, NY, USA, 1980. [Google Scholar]


| Symbol | Name | Unit | Value |
|---|---|---|---|
| cm | Milk specific heat capacity [36] | kJ kg−1 K−1 | 3933 |
| cw | Water specific capacity | kJ kg−1 K−1 | 4187 |
| Ta | Ambient temperature | °C | 20 |
| Tmi | Raw milk input temperature | °C | 4 |
| Tmci | Cooling exchanger milk input temperature | °C | 9 |
| Tmco | Cooling exchanger milk output temperature | °C | 4 |
| Tmpo | Pasteurized hot milk output temperature | °C | 77 |
| Tmro | Recovery exchanger milk output temperature | °C | 72 |
| Twci | Cooling exchanger water input temperature | °C | 1 |
| Twco | Cooling exchanger water output temperature | °C | 6 |
| Twhi | Heating exchanger water input temperature | °C | 82 |
| Twho | Heating exchanger water output temperature | °C | 77 |
| Δpr | Recovery exchanger pressure drop | kPa | 125 |
| Δpc | Cooling exchanger pressure drop | kPa | 50 |
| Δph | Heating exchanger pressure drop | kPa | 50 |
| Symbol | Name | Unit | Value |
|---|---|---|---|
| B | Useful life of the equipment | y | 10 |
| CA | Area unit cost of pasteurization equipment | Euro m−2 | 600 |
| CF | Fuel unit cost | Euro Sm−3 | 0.86 |
| CW | Electric energy unit cost | Euro kWh−1 | 0.18 |
| COP | Coefficient of performance of refrigerator | - | 2.68 |
| ED | Electric consumption of deaerator | kWh kg−1milk | 1.36·10−3 |
| EPA | Actual unit electric consumption of pumps | kWh kg−1milk | 3.06·10−4 |
| HV | Heat value of natural gas | kJ Sm−3 | 34,333 |
| N | Running pasteurization time | h y−1 | 8000 |
| Tcond | Condensation temperature of refrigerator | °C | 45 |
| Tev | Evaporation temperature of refrigerator | °C | −5 |
| U | Overall heat transfer coefficient | kW m−2 K−1 | 1.5 |
| ΔTC | Temperature difference in cooling exchanger | °C | 3 |
| ΔTH | Temperature difference in heating exchanger | °C | 5 |
| ηhb | Thermal efficiency of the heating boiler | - | 0.95 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Friso, D.; Bortolini, L.; Tono, F. Exergetic Analysis and Exergy Loss Reduction in the Milk Pasteurization for Italian Cheese Production. Energies 2020, 13, 750. https://doi.org/10.3390/en13030750
Friso D, Bortolini L, Tono F. Exergetic Analysis and Exergy Loss Reduction in the Milk Pasteurization for Italian Cheese Production. Energies. 2020; 13(3):750. https://doi.org/10.3390/en13030750
Chicago/Turabian StyleFriso, Dario, Lucia Bortolini, and Federica Tono. 2020. "Exergetic Analysis and Exergy Loss Reduction in the Milk Pasteurization for Italian Cheese Production" Energies 13, no. 3: 750. https://doi.org/10.3390/en13030750
APA StyleFriso, D., Bortolini, L., & Tono, F. (2020). Exergetic Analysis and Exergy Loss Reduction in the Milk Pasteurization for Italian Cheese Production. Energies, 13(3), 750. https://doi.org/10.3390/en13030750







