An Optimal Design of an Electromagnetic Actuation System towards a Large Homogeneous Magnetic Field and Accessible Workspace for Magnetic Manipulation
Abstract
1. Introduction
2. Design of the Magnetic Manipulation System
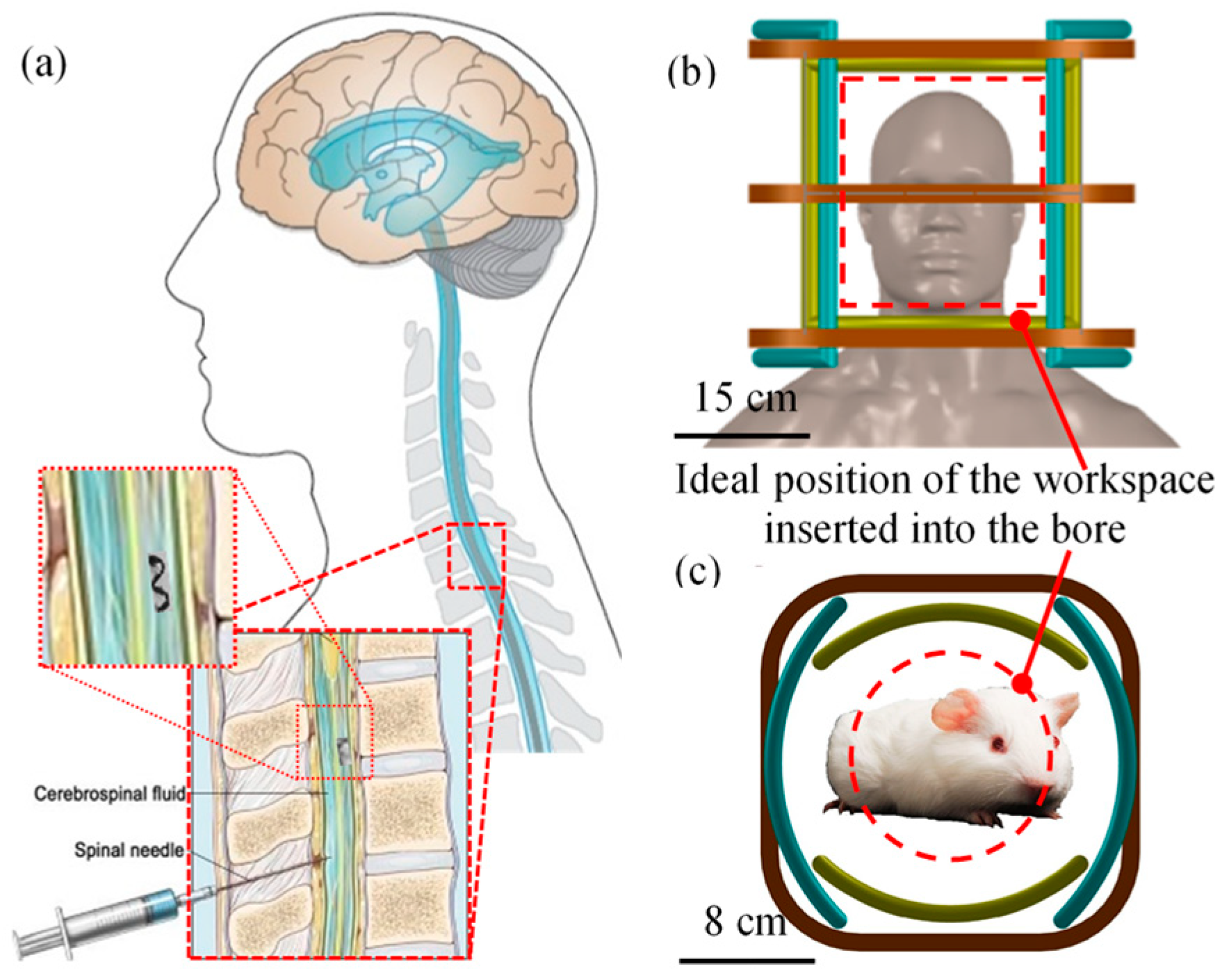
2.1. Motivations
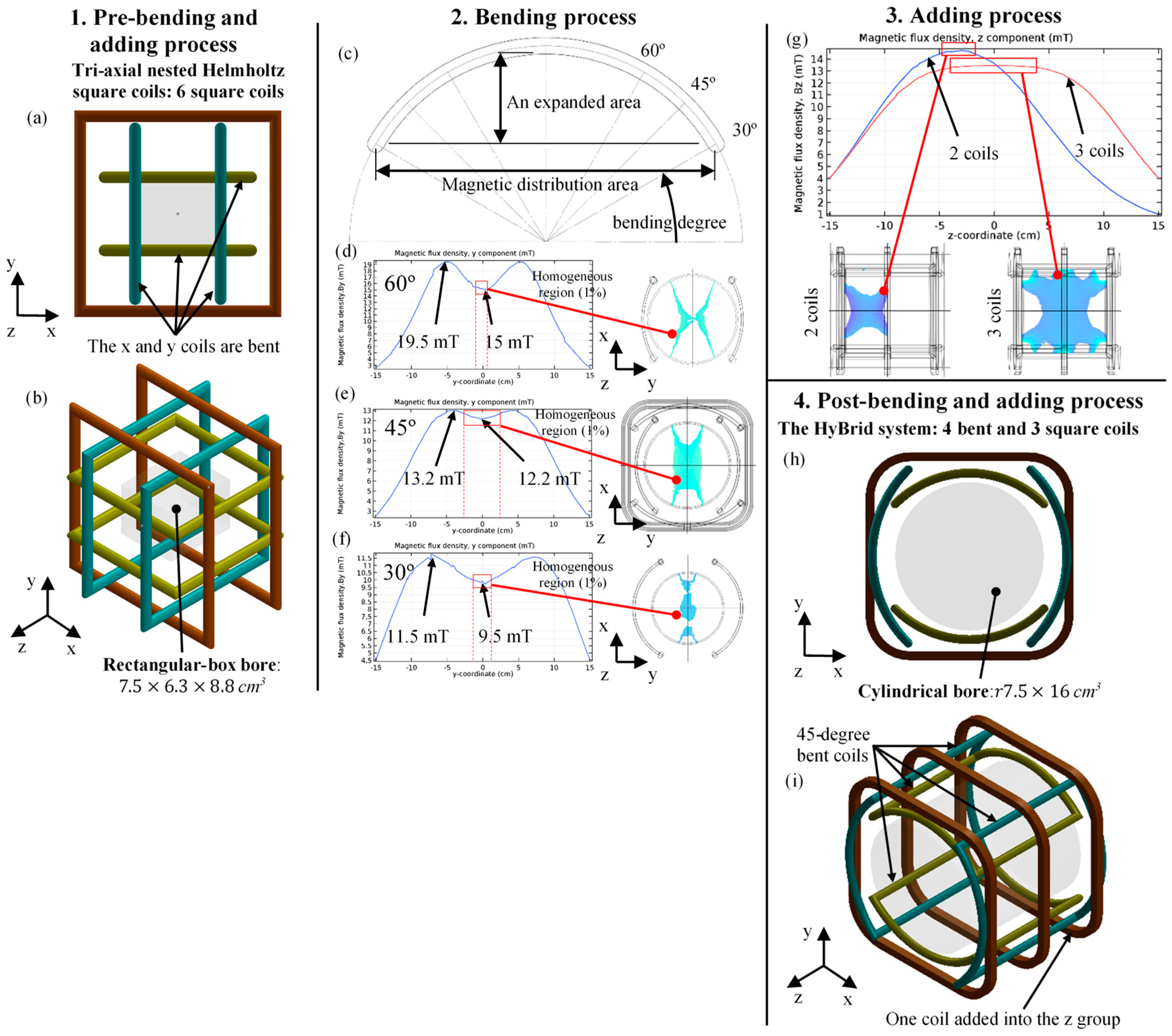
2.2. Design and Optimization
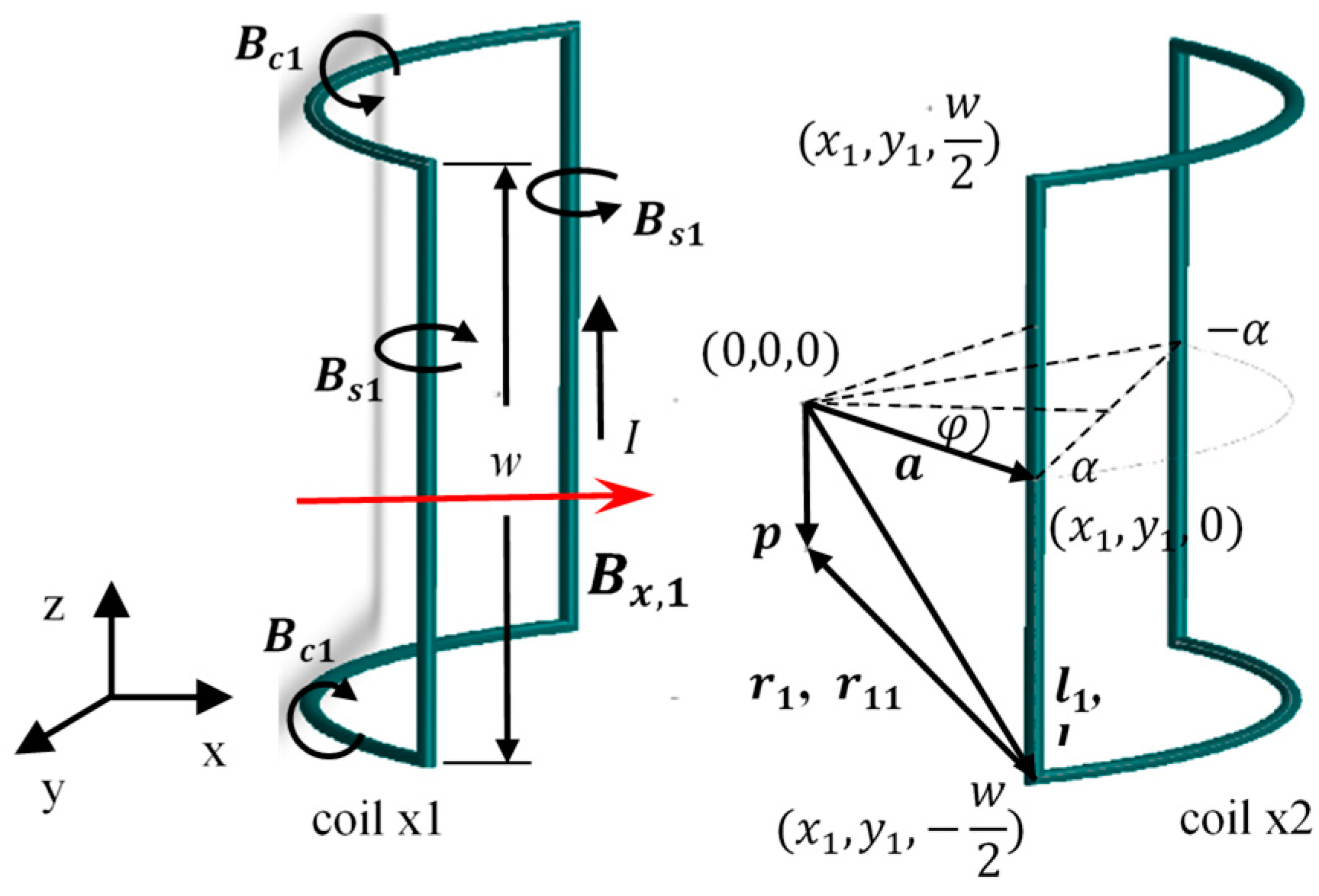
2.3. Mathematic Models of Magnetic Field Generation
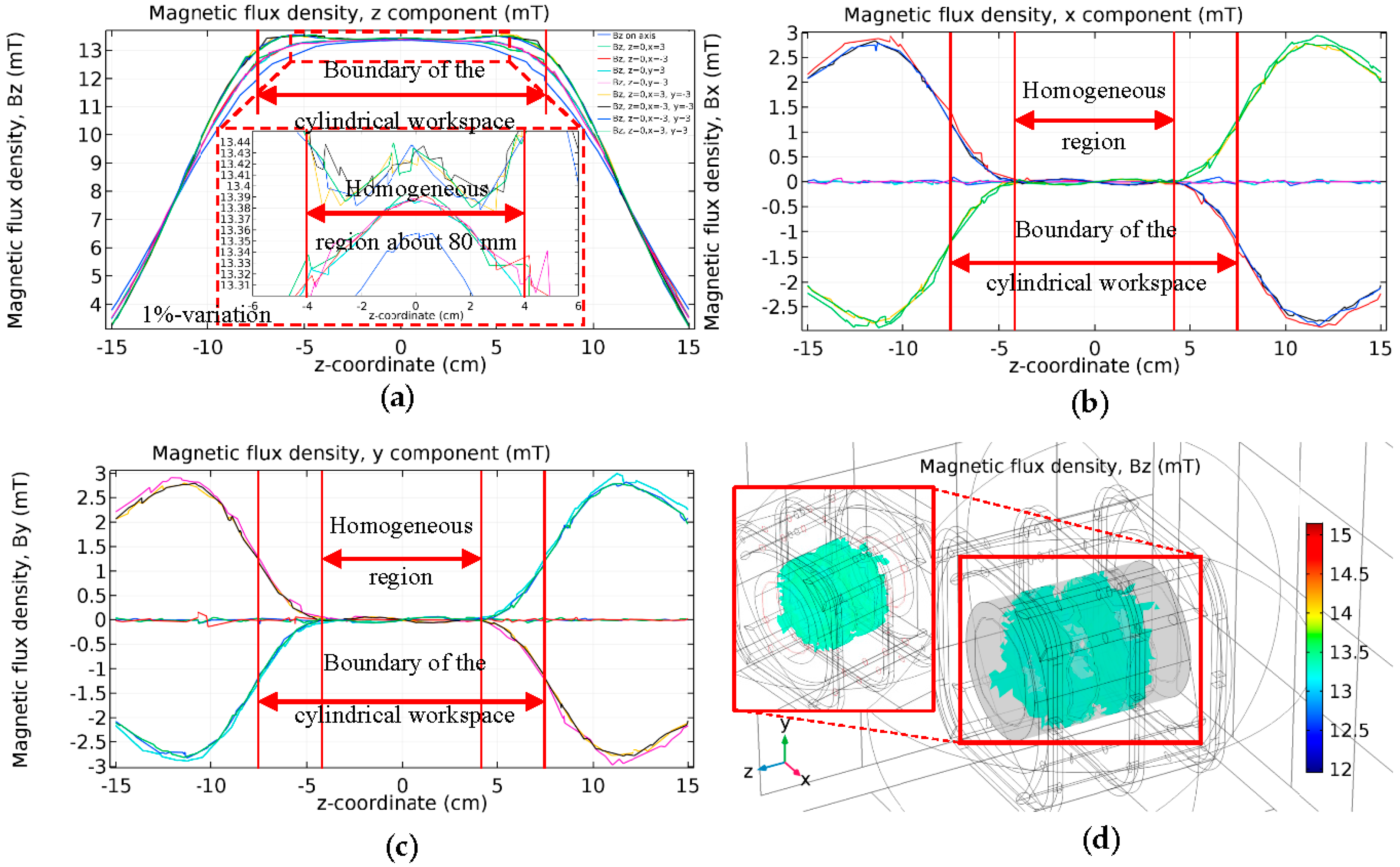
2.3.1. Uniform Field Generation
2.3.2. Non-Uniform Field Generation
2.4. Conclusion of Magnetic Field Generation Investigated by Numerical Simulation Results
2.5. Conclusion of Homogeneous Region of Uniform Field
3. System Building and Implementation
3.1. Coils and Control Hardware Setup
3.2. Microrobots
4. System Demonstrations
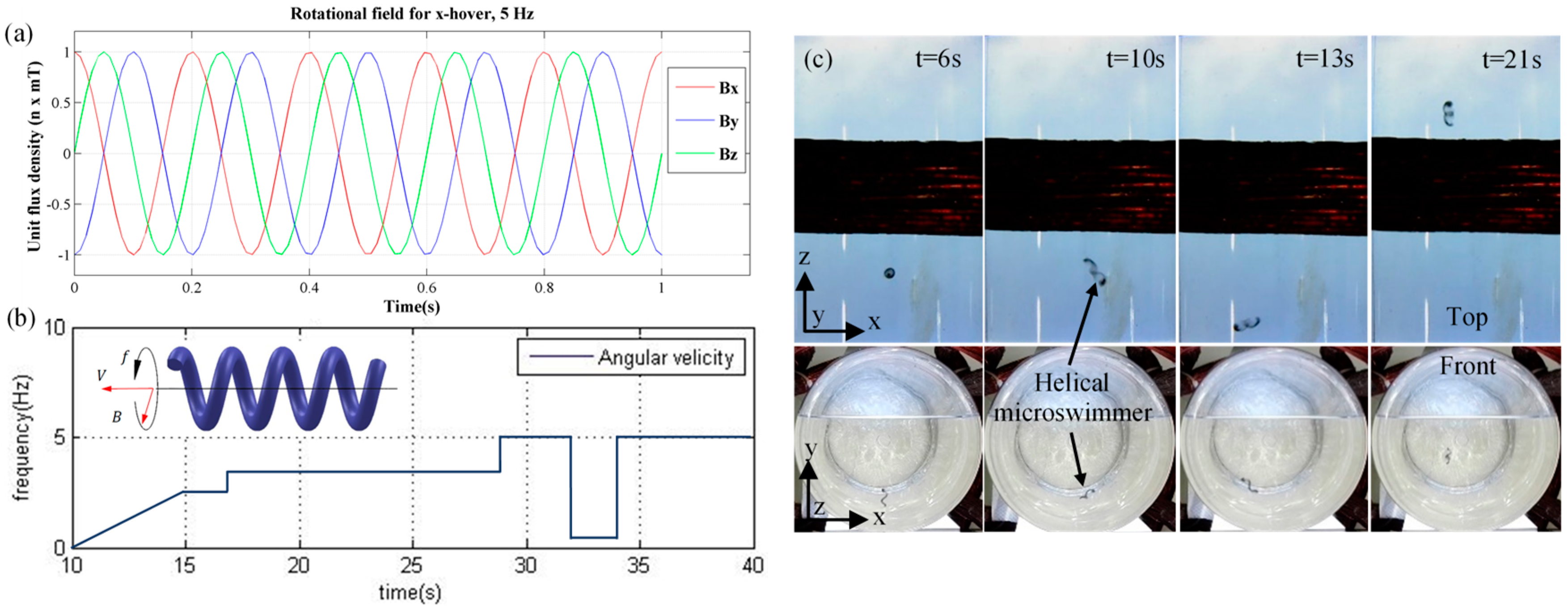
4.1. Three-D-Helical Propulsion in the Large Workspace by Rotating Magnetic Field
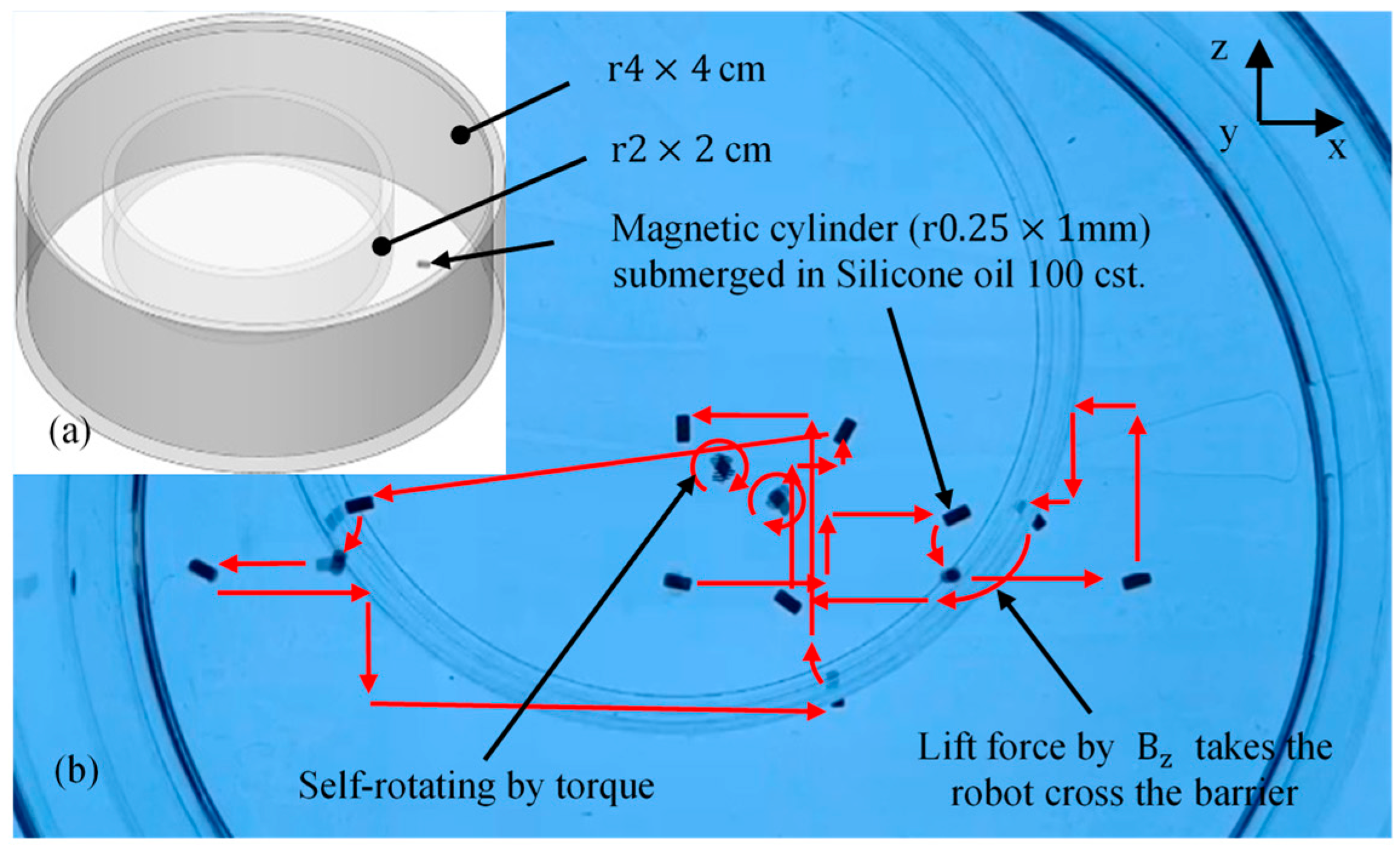
4.2. Translation by Pulling Force of Gradient-Based Field
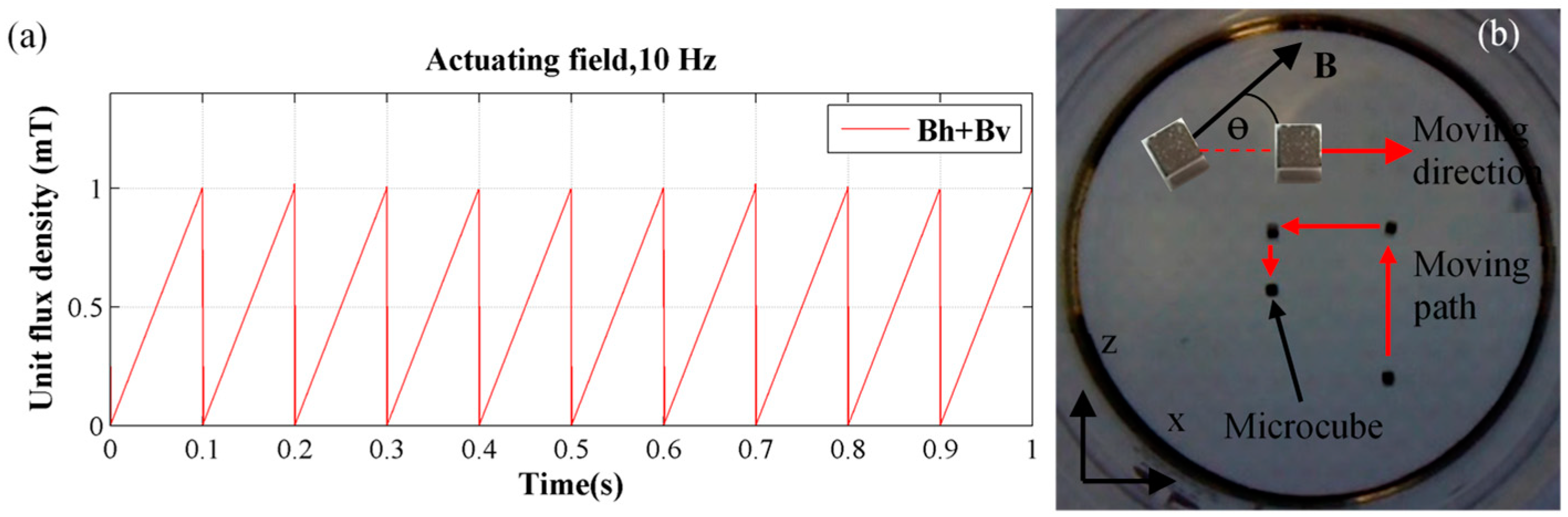
4.3. Sweeping-Slip Locomotion by Oscillating Field
4.4. Rocking-Slip Locomotion by Gradient-Based Field
4.5. Helical Propulsion Following the Complex Network Path
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Analyses of the Coil Separation Distance

| [I] Field Difference | Coordinate Range Defined by Homogeneity, (cm) | The Biggest Available Workspace | |||
|---|---|---|---|---|---|
| 19% | −1.6 to 1.6 | −3.3 to 3.3 | −4.1 to 4.1 | ||
| 14% | −1.0 to 1.0 | −4.0 to 4.0 | −4.8 to 4.8 | ||
| 5% | −0.3 to 0.3 | −2.6 to 2.6 | −5.1 to 5.1 | ||
| 23% | −0.1 to 0.1 | −0.7 to 0.7 | −2.0 to 2.0 | ||
Appendix A.2. Analyses of the Coil Separation Distance
Appendix A.3. Investigation into the Influence of Other Field Components to Homogeneous Region
References
- Purcell, E.M. Life at low Reynolds number. Am. J. Phys. 1977, 45, 3–11. [Google Scholar] [CrossRef]
- Abbott, J.J.; Peyer, K.E.; Lagomarsino, M.C.; Zhang, L.; Dong, L.X. How should microrobots swim? Int. J. Robot. Res. 2009, 28, 1434–1447. [Google Scholar] [CrossRef]
- Zhang, L.; Abbott, J.J.; Dong, L.X.; Kratochvil, B.E.; Bell, D.J.; Nelson, B.J. Artificial bacterial flagella: Fabrication and magnetic control. Appl. Phys. Lett. 2009, 94, 064107. [Google Scholar] [CrossRef]
- Abbott, J.J.; Ergeneman, O.; Kummer, M.P.; Hirt, A.M.; Nelson, B.J. Modeling magnetic torque and force for controlled manipulation of soft-magnetic bodies. IEEE Trans. Robot. 2007, 23, 1247–1252. [Google Scholar] [CrossRef]
- Yesin, K.B.; Vollmers, K.; Nelson, B.J. Modeling and control of untethered biomicrorobots in a fluidic environment using electromagnetic fields. Int. J. Robot. Res. 2006, 25, 527–536. [Google Scholar] [CrossRef]
- Pawashe, C.; Floyd, S.; Sitti, M. Modeling and experimental characterization of an untethered magnetic micro-robot. Int. J. Robot. Res. 2009, 28, 1077–1094. [Google Scholar] [CrossRef]
- Qiu, T.; Lee, T.C.; Mark, A.G.; Morozov, K.I.; Munster, R.; Mierka, O.; Turek, S.; Leshansky, A.M.; Fischer, P. Swimming by reciprocal motion at low Reynolds Number. Nat. Commun. 2014, 25, 514–519. [Google Scholar] [CrossRef]
- Nelson, B.J.; Kaliakatsos, I.K.; Abbott, J.J. Microrobots for Minimally Invasive Medicine. Ann. Rev. Biomed. Eng. 2010, 12, 55–85. [Google Scholar] [CrossRef]
- Zhu, W.; Li, J.; Leong, Y.J.; Rozen, I.; Qu, X.; Dong, R.; Wu, Z.; Gao, W.; Chung, P.H.; Wang, J.; et al. 3D-Printed Artificial Microfish. Adv. Mater. 2015, 27, 4411–4417. [Google Scholar] [CrossRef]
- Gultepe, E.; Randhawa, J.S.; Kadam, S.; Yamanaka, S.; Selaru, F.M.; Shin, E.J.; Kalloo, A.N.; Gracias, D.H. Biopsy with Thermally-Responsive Untethered Microtools. Appl. Phys. Lett. 2013, 25, 514–519. [Google Scholar] [CrossRef]
- Felfoul, O.; Mohammadi, M. Magneto-aerotactic bacteria deliver drug-containing nanoliposomes in tumour hypoxic regions. Nat. Nanotechnol. 2016, 11, 941–947. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Sakar, M.S.; Petruska, A.J.; Pane, S.; Nelson, B.J. Soft micromachines with programmable motility and morphology. Nat. Commun. 2016, 7, 12263. [Google Scholar] [CrossRef] [PubMed]
- Lum, G.Z.; Zhou, Y.; Dong, X.; Marvi, H.; Erin, O.; Hua, W.; Sitti, M. Shape-programmable magnetic soft matter. Proc. Natl. Acad. Sci. USA 2016, 113, E6007–E6015. [Google Scholar] [CrossRef] [PubMed]
- Diller, E.; Giltinan, J.; Lum, G.Z.; Ye, Z.; Sitti, M. Six-degree-of-freedom magnetic actuation for wireless microrobotics. Int. J. Robot. Res. 2015, 35, 114–128. [Google Scholar] [CrossRef]
- Fountain, T.W.R.; Kailat, P.V.; Abbott, J.J. Wireless control of magnetic helical microrobots using a rotating-permanent-magnet manipulator. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 576–581. [Google Scholar]
- Mahoney, A.W.; Abbott, J.J. Generating Rotating Magnetic Fields with a Single Permanent Magnet for Propulsion of Untethered Magnetic Devices in a Lumen. IEEE Trans. Robot. 2014, 30, 411–420. [Google Scholar] [CrossRef]
- Abbott, J.J. Parametric design of tri-axial nested Helmholtz coils. Rev. Sci. Instrum. 2015, 86, 054701. [Google Scholar] [CrossRef]
- Xu, T.; Guan, Y.; Liu, J.; Wu, X. Image-Based Visual Servoing of Helical Microswimmers for Planar Path Following. IEEE Trans. Auto. Sci. Eng. 2019. [Google Scholar] [CrossRef]
- Yu, C.; Kim, J.; Choi, H.; Choi, J.; Jeong, S.; Cha, K.; Park, J.O.; Park, S. Novel electromagnetic actuation system for three-dimensional locomotion and drilling of intravascular microrobot. Sens. Actuators Phys. 2010, 161, 297–304. [Google Scholar] [CrossRef]
- Kummer, M.P.; Abbott, J.J.; Kratochvil, B.E.; Borer, R.; Sengul, A.; Nelson, B.J. OctoMag: An electromagnetic system for 5-DOF wireless micromanipulation. IEEE Trans. Robot. 2010, 26, 1006–1017. [Google Scholar] [CrossRef]
- Rahmer, J.; Stehning, C.; Gleich, B. Spatially selective remote magnetic actuation of identical helical micromachines. Sci. Robot. 2017, 2, eaal2845. [Google Scholar] [CrossRef]
- Martel, S.; Felfoul, O.; Mathieu, J.B.; Chanu, A.; Samaz, S.; Mohammadi, M.; Mankiewicz, M.; Tabatabaei, N. MRI based medical nanorobotic platform for the control of magnetic nanoparticles and flagellated bacteria for target interventions in human capillaries. Int. J. Robot. Res. 2009, 28, 1169–1182. [Google Scholar] [CrossRef] [PubMed]
- Folio, D.; Dahmen, C.; Wortmann, T.; Zeeshan, M.A.; Shou, K.; Pane, S.; Nelson, B.J.; Ferreira, A.; Fatikow, S. MRI magnetic signature imaging, tracking and navigation for targeted micro/nano-capsule therapeutics. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011. [Google Scholar]
- Becker, A.; Felfoul, O.; Dupont, P.E. Simultaneously Powering and Controlling Many Actuators with a Clinical MRI Scanner. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2017–2023. [Google Scholar]
- Martel, S. Beyond imaging: Macro- and microscale medical robots actuated by clinical MRI scanners. Sci. Robot. 2017, 2, eaam8119. [Google Scholar] [CrossRef]
- Berg, H.C.; Turner, L. Movement of microorganisms in viscous environments. Nature 1979, 278, 349–351. [Google Scholar] [CrossRef] [PubMed]
- Grady, M.; Howard, M.; Molloy, J.; Ritter, R.; Quate, E.; Gillies, G. Preliminary experimental investigation of in vivo magnetic manipulation: Results and potential application in hyperthermia. Med. Phys. 1989, 16, 263–272. [Google Scholar] [CrossRef]
- Manamanchaiyaporn, L.; Xu, T.; Wu, X. The HyBrid System with a Large Workspace towards Magnetic Micromanipulation within the Human Head. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 402–407. [Google Scholar]
- Ulaby, F.T.; Ravaioli, U. Fundamentals of Electromagnetics; Pearson Education Inc.: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Merritt, R.; Purcell, C.; Stroink, G. Uniform magnetic field produced by three, four, and five square coils. Rev. Sci. Instrum. 1983, 54, 879. [Google Scholar] [CrossRef]
- Mahoney, A.W.; Sarrazin, J.C.; Bamberg, E.; Abbott, J.J. Velocity Control with Gravity Compensation for Magnetic Helical Microswimmers. Adv. Robot. 2011, 25, 1007–1028. [Google Scholar] [CrossRef]
- Diller, E.; Floyd, S.; Pawashe, C.; Sitti, M. Control of multiple heterogeneous magnetic microrobots in two dimensions on nonspecialized surfaces. IEEE Trans. Robot. 2012, 28, 172–182. [Google Scholar] [CrossRef]
- Xu, T.; Yu, J.; Vong, C.I.; Wang, B.; Wu, X.; Zhang, L. Dynamic Morphology and Swimming Properties of Rotating Miniature Swimmers with Soft Tails. IEEE/ASME Trans. Mech. 2019, 24, 924–934. [Google Scholar] [CrossRef]
- Lu, H.; Zhang, M.; Yang, Y.; Qiang, H.; Fukuda, T.; Wang, Z.; Shen, Y. A bioinspired multilegged soft millirobot that functions in both dry and wet conditions. Nat. Commun. 2018, 9, 3944. [Google Scholar] [CrossRef]
- Li, T.; Zhang, A.; Shao, G.; Wei, M.; Guo, B.; Zhang, G.; Li, L.; Wang, W. Janus microdimer surface walkers propelled by oscillating magnetic fields. Adv. Funct. Mater. 2018, 28, 1706066. [Google Scholar] [CrossRef]
- Li, T.; Chang, X.; Wu, Z.; Li, J.; Shao, G.; Deng, X.; Qiu, J.; Guo, B.; Zhang, G.; He, Q.; et al. Autonomous collision-free navigation of microvehicles in complex and dynamically changing environments. ACS Nano 2017, 11, 9268–9275. [Google Scholar] [CrossRef] [PubMed]
- Sapuppo, F.; Intaglietta, M.; Bucolo, M. Bio-microfluidics real-time monitoring using CNN technology. IEEE Trans. Biomed. Circuits. Syst. 2008, 2, 78–87. [Google Scholar] [CrossRef] [PubMed]
- Bucolo, M.; Buscarino, A.; Famoso, C.; Fortuna, L.; Frasca, M. Control of imperfect dynamical systems. Nonlinear Dyn. 2018, 98, 2989–2999. [Google Scholar] [CrossRef]
- Wu, X.; Liu, L.; Huang, C.; Su, M.; Xu, T. 3D Path Following of Helical Micro-swimmers with An Adaptive Orientation Compensation Model. IEEE Trans. Autom. Sci. Eng. 2019. [Google Scholar] [CrossRef]






| The Coil Group | Homogeneity, H (%) | Coordinate Range on the Axis | Covered Area (% of the Workspace) |
|---|---|---|---|
| x | −0.3 to 0.3 | 4% | |
| .5 | −1.0 to 1.0 | 13% | |
| −2.5 to 2.5 | 34% | ||
| −3.8 to 3.8 | 51% | ||
| −5.0 to 5.0 | 67% | ||
| y | −0.3 to 0.3 | 4% | |
| .5 | −1.1 to 1.1 | 15% | |
| −2.6 to 2.6 | 35% | ||
| −4.0 to 4.0 | 53% | ||
| −5.1 to 5.1 | 68% | ||
| z | −1.0 to 1.0 | 14% | |
| .5 | −2.0 to 2.0 | 28% | |
| −3.0 to 3.0 | 43% | ||
| −4.0 to 4.0 | 57% | ||
| −6.5 to 6.5 | 73% |
| The Coil Group | Coil Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A [I] | B | C | D | E [II] | F | G [III] | H [IV] | I | J | |
| x | 200 | 13.05 | 3.6 | 3.63 | 17.5 | 12.72/12.2 | 76 | Cylinder: 8 | 5 | |
| y | 170 | 7.82 | 2.7 | 2.9 | 15 | 12.65/12.5 | 72 | |||
| z | 200 | 15.83 | 3.9 | 4.06 | 20 | 12.91/13.5 | 78 | |||
| Microrobots | Materials | Dimension | Actuation Methods, Field Magnitude and Frequency | Environment Setup | Locomotion Types and Details | |
|---|---|---|---|---|---|---|
Helical microswimmers | PVA/ PEG double-network hydrogel embedded by Fe3O4 | 45 pitch angle, 0.6-mm helical radius | (a) 300-µm ribbon stripe, 3.5 turns, 9-mm long | 3D-Rotating uniform field for torque, 2.5-7.5Hz, 12 mT of the x, y and z field | A cm3 cylinder filled by 350-cst. silicone oil | Helical propulsion -Rotating body caused by alignment with the direction of rotating field -Transforming the rotating body to forward or backward propulsion -Able to propel in various viscosity of fluid -The actuation needs the velocity control to balance between the body weight and swimming direction of the swimmer [31] -Velocity depends on rotating frequency |
| (b) 500-µm ribbon stripe, 2.5 turns, 6-mm long | 3D-Rotating uniform field for torque, 3-5Hz, 12 mT of the x, y and z field | The complex network path ( mm diameter) filled by 350-cst. silicone oil | ||||
Micro-cylindrical robot | CoNi | (c) mm | 3D-Gradient-based field: force by 12 mT of the x and y field and 16 mT of the z field. Rotating uniform field for torque by 12 mT | a double-layer cylinder containing 100-cst. silicone oil | Translation and rotation locomotion -3D-translation caused by the pulling magnetic force, but torque is applied to rotate the robot -Velocity depends on field magnitude to vary the pulling force | |
Micro-cubic robot | NdFeB | (d) 500-µm cube | Oscillating uniform field, 12 mT of the x and z field (the planar field), 2.5Hz and 10Hz | A 500-mL cylinder containing 100-cst. silicone oil | Sweeping-slip locomotion -Side-to-side sweeping to slip forward, caused by alignment with the direction of oscillating field -Velocity depends on oscillating frequency | |
| NdFeB | (d) 500-µm cube | Periodical gradient-based field, 10 mT of the superposition of the vertical and horizontal field, 10Hz | A 500-mL cylinder containing 100-cst. silicone oil | Rocking-slip locomotion-The robot is wrenched by magnetic force to slip forward. -The actuation method is the switching between on- and off-field rapidly -Velocity depends on the actuating frequency | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manamanchaiyaporn, L.; Xu, T.; Wu, X. An Optimal Design of an Electromagnetic Actuation System towards a Large Homogeneous Magnetic Field and Accessible Workspace for Magnetic Manipulation. Energies 2020, 13, 911. https://doi.org/10.3390/en13040911
Manamanchaiyaporn L, Xu T, Wu X. An Optimal Design of an Electromagnetic Actuation System towards a Large Homogeneous Magnetic Field and Accessible Workspace for Magnetic Manipulation. Energies. 2020; 13(4):911. https://doi.org/10.3390/en13040911
Chicago/Turabian StyleManamanchaiyaporn, Laliphat, Tiantian Xu, and Xinyu Wu. 2020. "An Optimal Design of an Electromagnetic Actuation System towards a Large Homogeneous Magnetic Field and Accessible Workspace for Magnetic Manipulation" Energies 13, no. 4: 911. https://doi.org/10.3390/en13040911
APA StyleManamanchaiyaporn, L., Xu, T., & Wu, X. (2020). An Optimal Design of an Electromagnetic Actuation System towards a Large Homogeneous Magnetic Field and Accessible Workspace for Magnetic Manipulation. Energies, 13(4), 911. https://doi.org/10.3390/en13040911






