Experimental Investigation on Heat Transfer of Supercritical Water Flowing in the Subchannel with Grid Spacer in Supercritical Water-Cooled Reactor

Abstract

Experimental investigations on the heat transfer performance of supercritical water flowing in the subchannel of supercritical water-cooled reactor (SCWR) simulated by a triangular channel were conducted at pressures of 23–28 MPa, mass flow rates of 700–1300 kg·m⁻²·s⁻¹, and inner wall surface heat fluxes of 200–600 kW·m⁻². An 8 mm diameter fuel rod with a 1.4 pitch to diameter ratio was used. The effects of pressure, mass flow rate, and heat flux on the heat transfer performance under the resistance of a standard grid spacer were analyzed. Experimental results showed the significant positive influence of the grid spacer on the supercritical water in the subchannel. Moreover, in the presence of the grid spacer, the parameters influenced the heat transfer with different degrees of strengthening reaction. In view of the phenomenon in the tests, the rule of the supercritical heat transfer was further revealed by the comparison between empirical formulas and experimental data. This paper mainly studied the positioning grid function and the fluid flow characteristics downstream of the subchannel under the influence of the standard grid spacer and the impact mechanism of each parameter on the whole heat transfer process coefficient.

1. Introduction

The supercritical water-cooling reactor is the only fourth generation nuclear technology that uses light water as a coolant. It brings several advantages, such as a simpler structure, better system security, and better thermal efficiency. There is no liquid-vapor phase transition beyond the critical point. The supercritical water experiences continuous variation from a liquid-like fluid to a vapor-like fluid with the increasing temperature. Its unique properties and heat transfer characteristics in the outstanding specific heat capacity area are the focus of many international scholars [1,2,3,4,5,6,7]. Cheng [8] studied the heat transfer differences between three different subchannels using computational fluid dynamics (CFD) numerical simulation. The application of the grid structure and the turbulence model was proposed. The stronger non-uniform heat transfer was also observed. In the heat transfer process, several factors affect the heat transfer performance. Hassan H. et al. [9] used direct numerical simulations to study the effect of thermal boundary conditions on developing turbulent pipe flows with fluids at supercritical pressure. Wang et al. [10] studied the influence of the system parameters of pressure, mass flow, and heat flux density on the heat transfer due to the strong change of supercritical hydrothermal physical properties. Based on the triangle subchannel as the focus of experimental research, this paper studies the influence of various parameters on the heat transfer coefficient in different enthalpy regions with an existing standard grid spacer.

Due to the sharp change of physical properties and heat transfer characteristics near the supercritical point, the heat transfer will deteriorate to some extent. Yoo, J.Y. [11] studied heat transfer characteristics and deterioration under the existence of buoyancy. Gu et al. [12] studied the heat transfer characteristics of a supercritical fluid in a smaller diameter rod. The heat transfer characteristics, even the deterioration of supercritical fluid in a vertical pipeline, were investigated through numerical simulation by Jaromin, M. [13]. Liu et al. [14] suggested that with the low Reynolds number model, the pipe diameter increase led to the heat transfer deterioration which was more evident in the region with a low mass flow rate. According to Liu and Zhu [15], under a smaller pipe diameter, the inlet and outlet Reynolds numbers significantly influenced the heat transfer characteristics. The higher Reynolds number significantly strengthened the heat transfer, whereas the lower inlet Reynolds number diminished the heat transfer coefficient. However, there is always a way to enhance the heat transfer.

The grid spacer is an indispensable part in the fuel rod assembly. It is used for accurate positioning of fuel bundle, determination of relative position between the fuel bundle, and optimization of fluid motion through the vibration of fuel components. The fluid flow plays a blocking role. The fluid disturbance in the subchannel is strengthened. Due to the addition of the grid spacer, the heat transfer downstream the fluid is greatly enhanced. Simultaneously, the value of the downstream fluid dynamics is decreased as more evident in lower Reynolds number. Therefore, the grid spacer influence on the working fluid heat transfer in the channel center should be emphasized in the entire analysis. The special heat transfer and pressure drop characteristics caused by the four existing grid spacer designs were thoroughly discussed by analyzing the effects of the grid strap length, flow enhancing features, and Reynolds numbers. The heat transfer within the grid strap is greatly enhanced due to the increased flow velocity caused by the flow blockage. Zhu et al. [16] and Yao [17] studied heat transfer augmentation using straight grid spacers in rod bundles or single-phase flow for post-critical heat flux dispersed flow. The presence of grid spacers generally augmented the heat transfer at its surroundings. Duo Ting et al. [18] studied the deterioration of heat transfer with the existence of the grid spacer. The heat transfer development downstream the spacer is complex rather than in simple exponential decaying law. It is stabilized with oscillating regression. The results of Holloway M.V. [19] indicated the greatest heat transfer enhancement downstream the support grid designs with disk blockages. The correlations demonstrated the tradeoff between the initial heat transfer enhancement downstream the support grid and the pressure drop created by the support grid.

Wen et al. [20,21,22] numerically investigated the heat transfer deterioration phenomenon in supercritical water through heated vertical tubes. In the case of high-power heat release, the threshold decrease of heat conduction in supercritical regions was discussed in detail. Influences of parameters were studied and the simulation results were assessed with some experimental data. Thus, it achieved good agreement. Wang et al. [23,24,25] experimentally studied the heat transfer and flow resistance of supercritical pressure water in a supercritical water-cooled reactor (SCWR) sub-channel, vertical annular channels, and 2 × 2 rod bundle. Experimental results showed that the system parameters of heat flux, pressure, and mass flux have great effects on heat transfer, a new empirical heat transfer correlation was developed to improve the predicted accuracy. It was found that the heat transfer performance of the present flow channel is worse than that of the real central sub-channel. The flow resistance of supercritical water is reflected in the form of pressure drop, which was discussed with the bulk-flow enthalpy and mass flux.

Several works have investigated the heat transfer characteristic under supercritical pressure condition. However, only a little experimental research has been devoted to the subchannel heat transfer at supercritical pressures especially lacking the experimental data with the effect of the grid spacer. Under the background of developing a SCWR, it is essential to study the effect of a grid spacer on it. Therefore, experiments on heat transfer of supercritical water in a single subchannel with grid spacer were meaningfully carried out. More reference characteristics about the influence mechanism of the grid spacer can be observed through this experiment.

2. Experimental System and Method

2.1. Test Loop

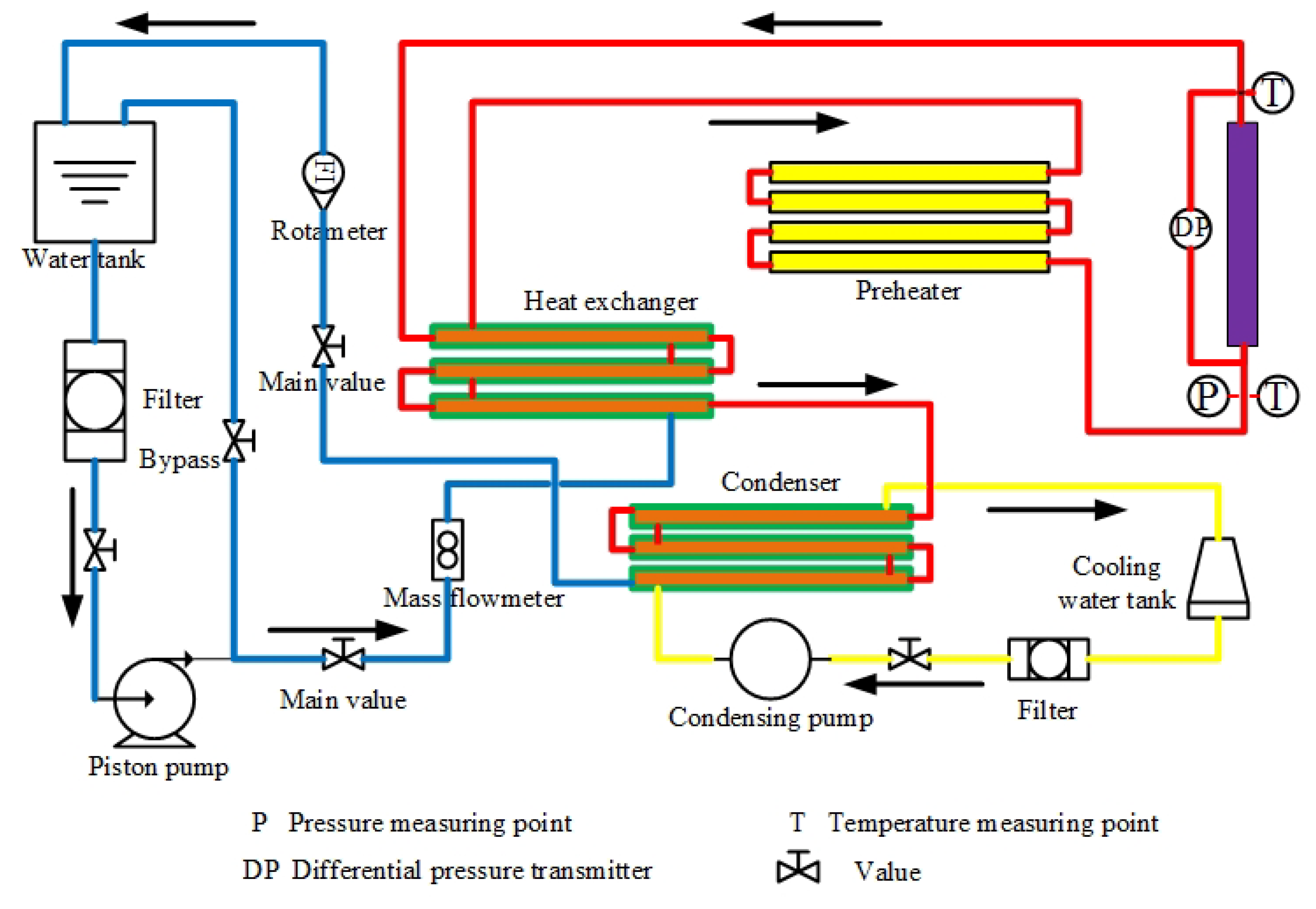
The experiment was carried out on the supercritical water thermal test device of the State Key Laboratory of Multiphase Flow in Power Engineering at Xi’an Jiao Tong University. It uses lower voltage and higher electronic current to directly heat the preheating section and the testing section, respectively. The test circuit is shown in Figure 1. Experimental system consists of two loops: the main loop system for testing and the bypass system for pressure and flow conditioning. To ensure a stable and reliable test process, deionized water was used to prevent the test circuit from scaling. Deionized water flowed into the main test circuit through the high-pressure pump and control valve. Simultaneously, part of the water flowed back to the water tank through the bypass. After the flow meter measurement, the flow poured into the preheating section for heating by heat absorption. Working medium flowed into the testing part until the temperature achieved the experimental requirements. To form a closed cycle, condensed liquid entered the water tank after the condenser. The pressure and mass flux in the test section were controlled by adjustment of the main and bypass valves shown in Figure 1.

2.2. Test Parameters

The section structure of the test part is clearly shown in Figure 2. The wire cutting process is made of 1Cr18Ni9Ti stainless steel. To ensure the accuracy of the whole test, the joints in the test section were welded with the same material as the actual test section. The test section is a triangular-shaped subchannel with a standard grid spacer of an 8 mm core rod diameter, 1.4 pitch ratio, 990 mm total length, and 2.5 mm thickness. The grid spacer was located 550 mm from the inlet. The detailed structure is shown in Figure 2. The test section effective heating length is 990 mm. A standard egg crate grid spacer was placed in the test section center to study the grid spacer influence on the flow and heat transfer. The experimental grid spacer has a wall thickness of 0.5 mm and a height of 50 mm. The grid spacer preheating pipe was welded together. The upstream location of the preheating segment has a mass flow meter with a precision of 0.1% used to measure the flow of the test work. Along the direction of flow, seven temperature measurement sections were arranged to measure the temperature of the outlet wall surface. The measurement points arrangement is also shown clearly in Figure 3. The fluid temperatures of inlet and outlet were measured by the armored thermocouples arranged at the inlet and outlet, respectively. A Rosemount-3051 pressure transmitter was used to measure the inlet pressure, and the pressure drop over the test section was measured with a Rosemount-3051 differential pressure transmitter with a precision of 0.075%. All test data were collected by IMP3595 collection system and inputted to an industrial computer for storage. The test mainly adopted a fixed heat load method.

The influence of pressure, flow rate, and heat flux on the standard grid spacer within the framework of subchannel flow heat transfer characteristics of supercritical water were studied. With the inevitable errors, the experimental errors include systematic error, accidental error, and gross error. With the accuracy of the experimental equipment and measuring tools, the systematic and gross errors in this experiment were negligible. With the severe experimental conditions and relatively unstable working conditions under supercritical conditions, the accidental error was relatively inevitable and can only be minimized. However, its deviation from the experiment was within the allowable range as compared with previous experimental data. Therefore, the experimental data is desirable and can be used in heat transfer characteristics discussion and analysis.

The system parameters were used in the following ranges: pressure, p = 23, 24, and 25 MPa; heat flux, q = 200, 400, 600, and 800 kW·m⁻²; and mass flow rate, G = 700, 1000, and 1300 kg·m⁻²·s⁻¹.

2.3. Test Procedures

The test section was wrapped with thick aluminosilicate fibers to minimize heat loss and guarantee the accuracy of the wall temperature measurements. Prior to beginning the heat transfer experiments, a heat balance test was conducted to estimate the thermal efficiency of the test section. The thermal efficiency is equal to the enthalpy increase through the test tube divided by the total power [27].

In this study, the average thermal efficiency was approximately 95%.

The tests were carried out with the procedure as follows [28]:

The average heat flux of the test section was regulated to a desired value and then the heating power of the preheater was adjusted to heat the water to an expected temperature. At each working condition, experimental data was collected continuously for 90 s after all the parameters had achieved a steady state.

3. Results and Discussion

3.1. The Circumferential Inhomogeneity of Heat Transfer Characteristic

In the cross-section perpendicular to the main flow direction in the subchannel, the local heat transfer coefficient between the fluid and pipe wall first increased and then decreased with the circumferential angle increase. Moreover, the heat transfer coefficient was largest in the subchannel central and smallest in the narrow gap. The inner wall temperature variation with the circumferential angle was contrasting. Hence, it can be concluded that severe circumferential heat transfer inhomogeneity in the subchannel and degree of uneven heat transfer were different in various mainstream sections. The circumferential heat transfer inequality in the large specific heat zone was most significant.

In this paper, the circumferential distribution was averaged in the process of calculating data, which was equivalent to the round tube to some extent. The significance of examining the noncircular tube is the stronger turbulence produced by the working medium produces in the subchannel with triangle, which makes it easier to remove the bubble like a small density fluid produced by the wall. It shows that the supercritical fluid is more likely to pass through the pseudocritical region in the subchannel with triangle than in the annular channel. Therefore, the pseudocritical region imparts less influence on the subchannel with a triangle channel than that of the annular channel.

3.2. Analysis of Heat Transfer Characteristic

The structure of the standard grid spacer is shown in Figure 2. The flow passage region abruptly changed when the fluid passed through the grid spacer. The variation in the section velocity and fluid medium impact on the grid spacer will evidently change the core channel transfer process of heat and mass. The flow field disturbance resulted in a local pressure drop and local heat transfer performance. Hence, the grid spacer influence on the flowing heat transfer of core is significant.

Figure 4 shows the distribution curve of the heat transfer coefficient changed with the enthalpy in several working conditions. Case 5 was the condition without the grid spacer, whereas the rest of the cases were with the grid spacer. After the comparison of the five curves, it was evident that the positioning grid was greatly influenced on the same enthalpy value. The heat transfer coefficient of the positioning lattice frame was greater with a standard grid spacer than without.

With the comparison of the five curves, the grid spacer greatly influenced the heat transfer characteristic of the entire flow, especially in the downstream. In the downstream flow direction, the fluid disturbance was reduced due to the decreasing blockage area. The circulation area abruptly widened than that of the grid spacer. In comparison to the prior conditions, a more moderate flow velocity, and lower thermal efficiency between the fluid and inner wall was observed. The heat transfer coefficient exhibited an exponential decay as the enthalpy decreased. After the fluid disturbance by the grid spacer, it traversed a longer distance to achieve streamline reorganization and restore the flow heat transfer as a same situation of the position prior the grid spacer, because the fluid density and dynamic viscosity decrease by crossing the grid spacer. Therefore, the experiment can also be conducted in the supercritical pressure condition with the downstream more affected by the grid spacer than the upstream manifested in a deeper degree and further distance. The following details concerned with the heat transfer characteristics of the supercritical fluid in the case of the grid spacer.

Figure 5 shows the axial distribution curve of the wall temperature and heat transfer coefficient in the grid spacer triangular subchannel with an inlet temperature of 230.86 °C. The T_f stands for the fluid temperature. The L is for the axial location. From left to right on the x coordinate, there are eight points representing the inner wall temperature of the eight sections from No. 1 to No. 8, respectively. The area between the dotted lines is the positioning grid location. In the grid spacer upstream, the wall temperature was observed to rise slowly along the flow direction, whereas there was no significant change in the heat transfer coefficient. When the workflow passed through the grid spacer, the internal wall temperature dramatically decreased in the grid spacer position with the minimum value obtained exactly at the grid spacer. The heat transfer coefficient suddenly increased with the maximum value reached at the grid spacer. The presence of the grid spacer which blocks the fluid flow and resulted in a sudden passage area contraction around the grid spacer. The flow rate significantly increased when the fluid was placed at the grid spacer. The sudden fluid shrinkage and the fluid impact on the grid spacer produced a harsher fluid flow disturbance at the said position. The heat transfer performance between the fluid and rod was clearly enhanced and the temperature difference between the inner wall temperature and fluid was minimized. Hence, an exceptional heat transfer effect was achieved. The internal wall temperature then rapidly increased and the heat transfer coefficient sharply dropped. After outflow of the grid spacer, the inner wall temperature slightly improved relative to the positioning grid. As the distance between the position grid and fluid increased, the heat transfer performance effect in the subchannel gradually decreased until it disappeared. The inner wall temperature showed a linear trend of the change and a fairly constant heat transfer coefficient.

Figure 6 shows the distribution of the wall temperature and heat transfer coefficient along the cross-section of the grid spacer. Mp3–mp5 in Figure 6 stand for the wall temperatures and heat transfer coefficients of the cross-section 3–5 in Figure 2. The data in Figure 6 was taken from the cross-section of No. 3, No. 4, and No. 5 as shown in Figure 2. The large capacity region was placed between the two dashed lines. The grid spacer was located between the three cross-sections to efficiently the impact. In the grid spacer inner wall temperature curve, an obvious increase was observed with the enthalpy change in the lower enthalpy region and the heat transfer coefficient considerately increased. After arriving at the pseudocritical area, the inner wall temperature was flatter and an evident increase in the heat transfer coefficient was observed. This is due to the drastic change of the supercritical water property in the pseudocritical region. The water heat capacity increase led to more heat absorption in the flow process resulting in effective cooling of the heated wall to strengthen the heat transfer performance. It then enters the higher enthalpy region with an increasing inner wall temperature trend and increasing heat transfer coefficient distribution trend similar to that in the low enthalpy region. From Figure 6, the distribution trend of the temperature and heat transfer coefficient before the grid spacer and after the grid spacer were fairly similar to that of the right side of the grid spacer. It was indicated that the grid spacer will not change the distribution of heat transfer coefficient with the enthalpy, instead, it will enhance the heat transfer effect on the same level.

3.3. The Heat Transfer Performance in the Pseudocritical Enthalpy Region

From the above Figure 4, the inner wall temperature and heat transfer coefficient were observed to vary with the bulk enthalpy. A different heat transfer was noted in different enthalpy region.

The critical enthalpies at the pressures of 23, 25, and 28 MPa were 2126, 2137, and 2150 kJ·kg⁻¹. Hence, the pseudocritical enthalpy area can be defined from 1750 to 2300 kJ·kg⁻¹. The experiment focused on the pseudocritical conditions due to the severe variation of the supercritical water properties in the area.

3.3.1. Effects of Pressure

As shown in Figure 7, the trial was carried out at three different pressure. The influence of pressure on the heat transfer characteristics of the supercritical fluid in the subchannel was investigated by changing the supercritical pressure value. The points in Figure 7 were taken from cross-section No. 5. The strengthening effect of the grid spacer on the heat transfer performance in comparison to section No. 6, with a larger distance between the fluid and grid spacer with a weak reinforcement, was clearly shown. This would help in better data processing and comparison. As seen from the bulk distribution curve, the influence of heat transfer was mainly reflected in the pseudocritical region.

The inner wall temperature gradually increased with the increasing of enthalpy value. In the pseudocritical region, the inner wall temperature continuously increased with the increasing of enthalpy. However, this increasing trend was relatively smoother compared with that of the remaining region where the temperature difference between the wall and fluid temperature decreased and consequently, the evident effect of stress on it. In the same enthalpy value, the internal wall temperature significantly increased with the pressure increase, and similarly, the temperature difference between the fluids followed the similar trend.

The distribution trend of the heat transfer coefficient first increased and then decreased with an increase of enthalpy upon entering the pseudocritical area. The heat exchange coefficient rapidly increased with the enthalpy increase and then rapidly decreased after reaching the peak. Pressure clearly has a significant effect on the heat transfer coefficient. Since the big heat capacity in the area, the increased fluid temperature has a larger heat capacity than the common fluid at a similar heat and smaller temperature difference. Thus, the heat transfer coefficient increased and the heat transfer coefficient decreased with the pressure increase. The maximum heat transfer coefficient appeared in the same region under different pressures, with a slightly different specific peak position. The peak position seemingly increased with the pressure rise.

3.3.2. The Effect of Mass Flow Rate

As shown in Figure 8 [p = 23 MPa, and q = 600 kW·m⁻²], the mass flow rate influence on the wall temperature and heat transfer characteristics of the subchannel flow was investigated in three different working conditions: G = 700 kg·m⁻²·s⁻¹, G = 1000 kg·m⁻²·s⁻¹, and G = 1300 kg·m⁻²·s⁻¹.

It can be indicated that a higher bulk enthalpy leads to a higher inner wall temperature. The slope of the wall temperature curves in the pseudocritical region are higher than that in the low enthalpy region. Both in the low enthalpy region and the pseudocritical region, the mass flow rate plays an important role in wall temperature curves.

The heat transfer coefficient increases sharply with an increasing bulk enthalpy of 1400–1900 kJ·kg⁻¹ and then decreased rapidly when the bulk enthalpy over 1400–1900 kJ·kg⁻¹.The mass flow rate has a more evident influence on the flow and heat transfer characteristics in the channel. The peak value of the heat transfer coefficient increased with the increasing mass flow rate. The improvement of the mass flow rate resulted to a significant increase on the heat transfer in the subchannel.

3.3.3. Effect of Heat Flux

As shown in Figure 9 (p = 25 MPa and G = 1000 kg·m⁻²·s⁻¹), the flow and heat transfer characteristics of the supercritical water in standard grid spacer core were compared and analyzed under different heat fluxes (q = 200, 400, and 600 kW·m⁻²).

In Figure 9, the inner wall temperature gradually increased with an increase of enthalpy, showing three regions the low enthalpy region and high enthalpy, and the large specific heat capacity region. In the pseudocritical section, the tendency of the inner wall temperature to increase with the enthalpy rise appeared to be moderate. After entering the higher enthalpy zone, the heat flux effect on the inner wall temperature was enhanced thereby evidently increasing the wall temperature.

The heat transfer coefficient exhibited a trend of first increasing and then decreasing with the enthalpy increase. With the increase of enthalpy, the overall trend was relatively smooth. The coefficient of heat transfer in the pseudocritical region peaked with the enthalpy increase. The heat flux effect on heat transfer enhanced. The peak value of the heat transfer coefficient decreased with the heat flux increase. Simultaneously, the heat flux increase and the heat transfer coefficient peak value shifted to the corresponding low enthalpy region. The increasing heat flux weakened the heat transfer enhancement.

3.4. The Heat Transfer Performance in the Lower Enthalpy and Higher Enthalpy Region

3.4.1. Effect of Pressure

As shown in Figure 10 (G = 1000 kg·m⁻²·s⁻¹, and q = 400 kW·m⁻²), the trial was carried out at p = 23 MPa, 25 MPa, and 28 MPa. The stress influence on the heat transfer characteristics of the supercritical fluid in the subchannel was investigated by changing the supercritical pressure. As seen from the bulk distribution curve, the pressure influence on heat transfer performance can be negligible in the low enthalpy and high enthalpy region compared with the pseudocritical region.

From Figure 10, the inner wall temperature gradually increased with the increasing enthalpy. In the low enthalpy area, with the simultaneous enthalpy increasing, the inner surface temperature rising rate was relatively evident, and the inner wall temperature distribution curve basically coincided under different pressure values. The influence of changing the value on the impact was unnoticeable. In the high enthalpy region, the pressure effect diminished, and the temperature distribution trend of the inner wall was roughly similar to that in the low enthalpy region, both with a tendency to slowly rise.

The distribution trend of heat transfer coefficient first increased and then decreased with the enthalpy increase in the low enthalpy region. The heat transfer coefficient slowly increased slowly with the growing enthalpy, and the heat transfer coefficient distribution curve under different pressure was nearly coincident. The heat transfer coefficient slowly increased with the increasing enthalpy, and the heat transfer coefficient distribution curve nearly coincided under different pressures. The pressure has nearly no evident effect.

3.4.2. The Effect of Mass Flow Rate

As shown in Figure 11 (p = 23 MPa, and q = 600 kW·m⁻²), the influence of the mass flow rate and heat transfer characteristics of the subchannel flow was investigated with three different working conditions: G = 700 kg·m⁻²·s⁻¹, 1000 kg·m⁻²·s⁻¹, and 1300 kg·m⁻²·s⁻¹. In the low enthalpy region, the inner wall temperature significantly increased with the increase of the enthalpy. Different mass flow rates have different effects on the temperature distribution curve. A higher mass velocity resulted in a lower inner wall temperature and lower temperature difference. The distribution trend of the high enthalpy region was fairly similar to that of the low enthalpy region where the inner wall temperature significantly increased with the enthalpy increase.

The distribution curve of the heat transfer coefficient with the changing enthalpy is shown in Figure 11. In the low enthalpy region, the heat transfer coefficient slowly increased with the increase of the enthalpy. The change of the mass flow rate significantly affected the distribution curve. The heat transfer coefficient increased with the increase of the mass flow rate. This is due to the increase of the fluid mass flow rate, resulting in a rise of the corresponding Reynolds number, enhanced effect of the inertia force, and the heat transfer enhancement effect. Secondly, as the mass flow rate increased, the fluid turbulence and perturbation intensity in the subchannels increased thereby enhancing the heat transfer between the wall surface and fluid. The mass flow rate has a more evident influence on the flow and heat transfer characteristics in the channel. The peak value of the heat transfer coefficient increased with the increasing mass flow rate. The mass flow rate enhancement has a significantly strengthened the heat transfer in the subchannel.

3.4.3. The Effect of Heat Flux

As shown in Figure 12 (p = 25 MPa and G = 1000 kg·m⁻²·s⁻¹), the flow and heat transfer characteristics of the supercritical water in the standard grid spacer core were compared and analyzed under different heat fluxes (q = 200, 400, and 600 kW·m⁻²).

As shown in Figure 12, the inner wall temperature gradually increased with the increase of enthalpy, showing the three respective regions; low enthalpy region and high enthalpy, away from the large specific heat capacity region, and the large specific heat capacity region. In the lower enthalpy region, the inner wall temperature increased with the increasing enthalpy, and a weak heat flux effect on the inner wall temperature was observed. After entering the higher enthalpy zone, the heat flux effect on the inner wall temperature was enhanced thereby clearly increasing the wall temperature.

The heat transfer coefficient exhibits a trend of increasing first and then decreasing with the increase of enthalpy. In the low enthalpy region, the change of heat flux has minimal effect on the heat transfer coefficient. With the enthalpy increase, the overall trend was relatively smooth. The heat transfer coefficient in the pseudocritical region peaked with the increase of the enthalpy. The heat flux effect on heat transfer was enhanced. The peak value of the heat transfer coefficient decreased with the heat flux increase. Moreover, with the heat flux increase, the heat transfer coefficient peak value shifted to the low enthalpy region. The increasing heat flux led to weakened heat transfer enhancement. In the high enthalpy range, the heat transfer coefficient continuously decreased. The heat flux increase resulted in a significant decrease in the heat transfer coefficient. This is due to heat flux reaching a certain value where a layer of small density fluid-like air bubbles covering the walls near the pseudocritical point, thereby hindering the heat exchange between the pipe wall and the fluid resulting to heat transfer deterioration.

4. Assessment of Supercritical Heat Transfer Correlations

As the fluid surface becomes zero under supercritical conditions during the heating process, phase change was not visible where a single phase was exhibited. Generally, the prediction formula for the heat transfer relationship of the supercritical fluid was based on a single-phase heat transfer prediction relationship. In this paper, the heat transfer relationship under the existing supercritical conditions was studied and analyzed and correlations for the local heat transfer downstream the standard grid spacer design was developed.

In a standard grid spacer, the local heat transfer coefficients within and downstream the grid were increasing due to increased flow velocity and turbulence caused by the flow blockage. The standard support grid design was used as a baseline design and flow enhancing features attached to a base strap design. In addition, several investigations of the single-phase heat transfer coefficients in rod bundles with standard grid spacer have been conducted. The present literature review will focus on investigations reporting the average local heat transfer coefficients around the rod diameter.

Correlations predicting the axial development of the local heat transfer downstream the standard grid spacer have also been proposed. Experimental results indicated that the heat transfer downstream the standard grid spacer design is a function of z/Dh. This functional relationship can either take the form of an exponential decay or a power law. Yao et al. [17] used an exponential decay function to correlate the heat transfer downstream of a standard grid spacer:

$$\frac{Nu}{N{u}_x}=\left(1+5.55{\epsilon }_s{}^2{e}^{-0.13z/D_h}\right)$$

(1)

where εs is the blockage ratio.

Moreover, Yao et al. [17] established two more correlation for the local Nusselt number downstream of a standard grid spacer are as follows:

$$\frac{Nu}{N{u}_x}=1+6.5{\epsilon }_{\mathrm{s}}{}^2{e}^{-0.8z/D_h}$$

(2)

$$\frac{Nu}{N{u}_x}=1+3.0{\epsilon }_{\mathrm{s}}{}^2{\left(\frac{\mathrm{z}}{D_{\mathrm{h}}}\right)}^{-1.3}$$

(3)

This equation is valid in a range of z/Dh = 1.4 to z/Dh = 33.6. The correlation for the standard support grid designs was presented by Yao et al. [17]. Both the power fit correlation, Equation (2), and the exponential decay fit correlation, Equation (3), accurately captured the heat transfer behavior on the downstream of the standard support grid designs. These three correlations are valid for axial locations between z/Dh = 1.4 to z/Dh = 33.6.

As shown in Figure 13, the comparison of the heat transfer coefficient of the spacer grid under similar enthalpy and parameters is shown. Figure 13 shows the analysis of the heat transfer characteristics in two different structural subchannels under the same condition of p = 25 MPa, G = 700 kg·m⁻²·s⁻¹, and q = 200 kg·m⁻². In the upstream of the grid spacer, the heat transfer coefficient gradually increased. The presence or absence of the grid spacer has minimal effect on the heat transfer performance. As a result of the drastic change of the fluid specific heat capacity, the heat transfer coefficient first sharply increased to the peak and then abruptly dropped. The subchannel with the spacer grid peaked due to the strengthening effect of the standard grid spacer. As it increased, the degree of change in the heat transfer coefficient became more severe. After entering the high enthalpy region, the heat transfer coefficient gradually decreased, and the influence of the grid spacer on the heat transfer coefficient was minimal. There was no significant difference between the heat transfer characteristics of the subchannel with and without the grid spacer. From Figure 13, when the supercritical fluid flowed out of the positioning grid, the heat transfer coefficient exponentially decreased under the influence of the standard grid spacer compared with that of the non-positioning grid. When the fluid gradually flowed to a certain distance from the positioning grid, the effect slowly disappeared. Consequently, the influence of the positioning grid was no longer relevant. The difference in the heat transfer coefficient between these two conditions was reducing consistently with the distribution of the formula in Figure 14. In conclusion, after exiting the positioning grid, a certain but fairly significant influence it was observed. With a certain distance from the grid spacer, the influence decreased. The strength effect of the standard grid spacer on the downstream was relatively small compared to those of the staggered blades which caused the downstream heat transfer coefficient of the grid to exponentially decrease with enhanced features.

This is due to the standard grid spacer, which has weak heat transfer enhancement characteristics, unlike that of staggered blades which will cause the downstream heat transfer coefficient of the grid to exponentially decrease with enhanced features.

5. Conclusions

In this paper, we observed that the standard grid spacer significantly strengthened the fluid heat exchange effect in the subchannel. The grid spacer did not change the distribution trend of the fluid heat transfer coefficient in the cross-section, but it did greatly enhance the heat transfer effect in the axial direction.

In the supercritical pressure region, the inner wall temperature increased with increasing enthalpy. In the low enthalpy region far from the pseudocritical point, the heat transfer coefficient increased with the enthalpy increase. In the high enthalpy region far from the pseudocritical point, the heat transfer coefficient decreased with the enthalpy increase. Under the same pressure, heat flux, and mass flow rate, the heat transfer performance of the supercritical fluid was better than that of supercritical steam.

With the presence of the positioning grid, the pressure has a certain degree of enhancement to the heat transfer coefficient. The influence of pressure on heat transfer characteristics was mainly shown in the larger specific heat capacity zone. In the said zone, the heat transfer coefficient peak value decreased with the pressure increase. The increase of pressure decreased the degree of thermal property change of the supercritical fluid and weakened the heat transfer enhancement between the inner wall and fluid.

The positioning grid also played a role in the influence of mass flow rate and heat flux on the heat transfer coefficient. The decrease of heat flux and the increase of mass flow rate resulted to a decrease in the wall temperature and increase in the heat transfer coefficient. In the pseudocritical section, the change of heat flux and mass flow rate significantly impacted the heat transfer performance. A higher heat load resulted in a lower mass flow rate, more severe wall temperature increase and a more evident decrease in the heat transfer coefficient.

Compared with the experimental data, the standard grid can strengthen the reduction of the downstream heat transfer coefficient, which resulted in a sharp decrease of the heat transfer coefficient downstream the positioning grid. In the downstream of the subchannel, the heat transfer coefficient exponentially decreased due to the standard grid obstruction. When the fluid flowed out of a certain distance, the influence of the positioning grid was gradually reduced, and the heat transfer coefficient distribution trend was consistent with that of the subchannel without the positioning grid.