Separated Flow Control of Small Horizontal-Axis Wind Turbine Blades Using Dielectric Barrier Discharge Plasma Actuators
Abstract
1. Introduction
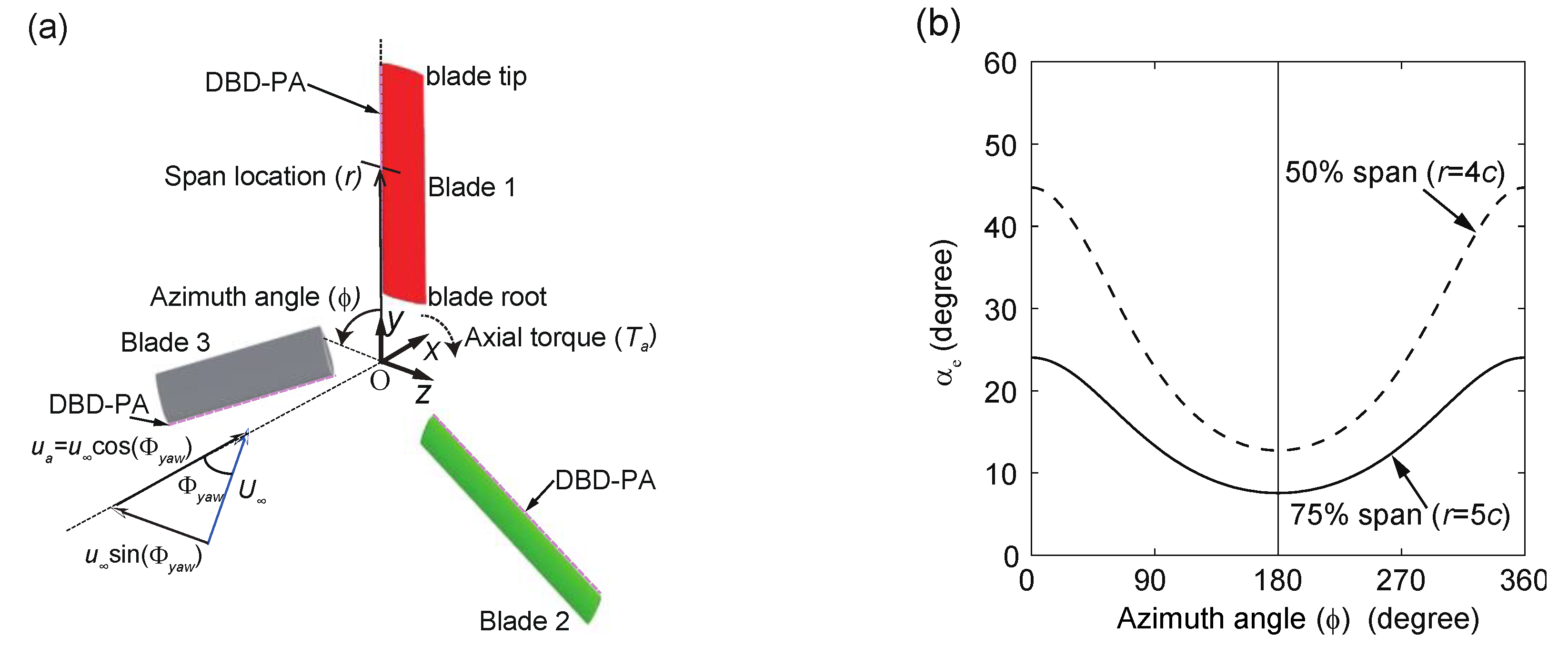
2. Case Description
Flow Conditions and Wind Turbine Blade Model
3. Materials and Methodologies
3.1. Governing Equations
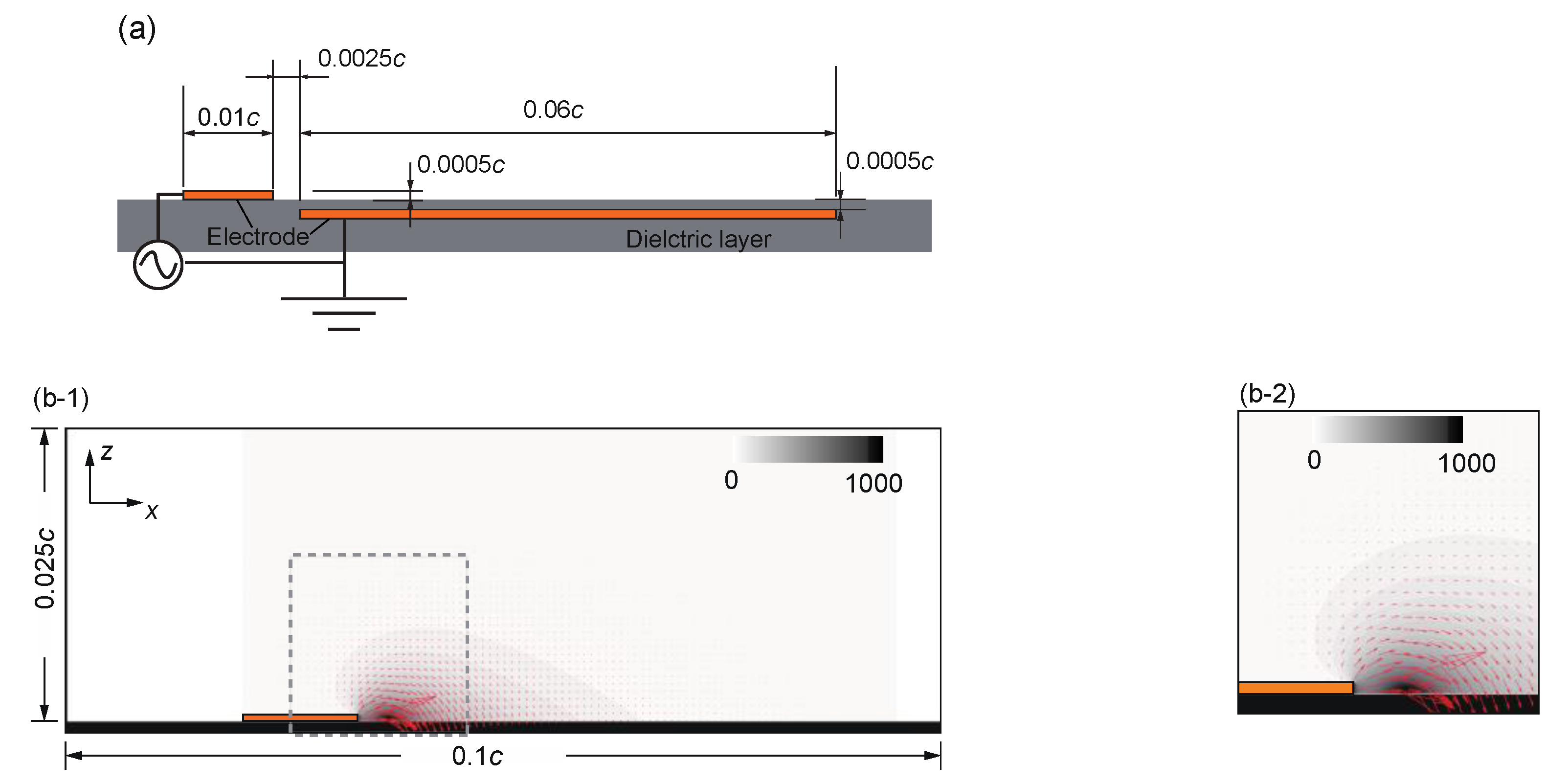
3.2. DBD-PA Body Force Model
3.3. Note of Reliability of Approach and Adopted DBD-PA Body Force Model
3.4. Numerical Methods
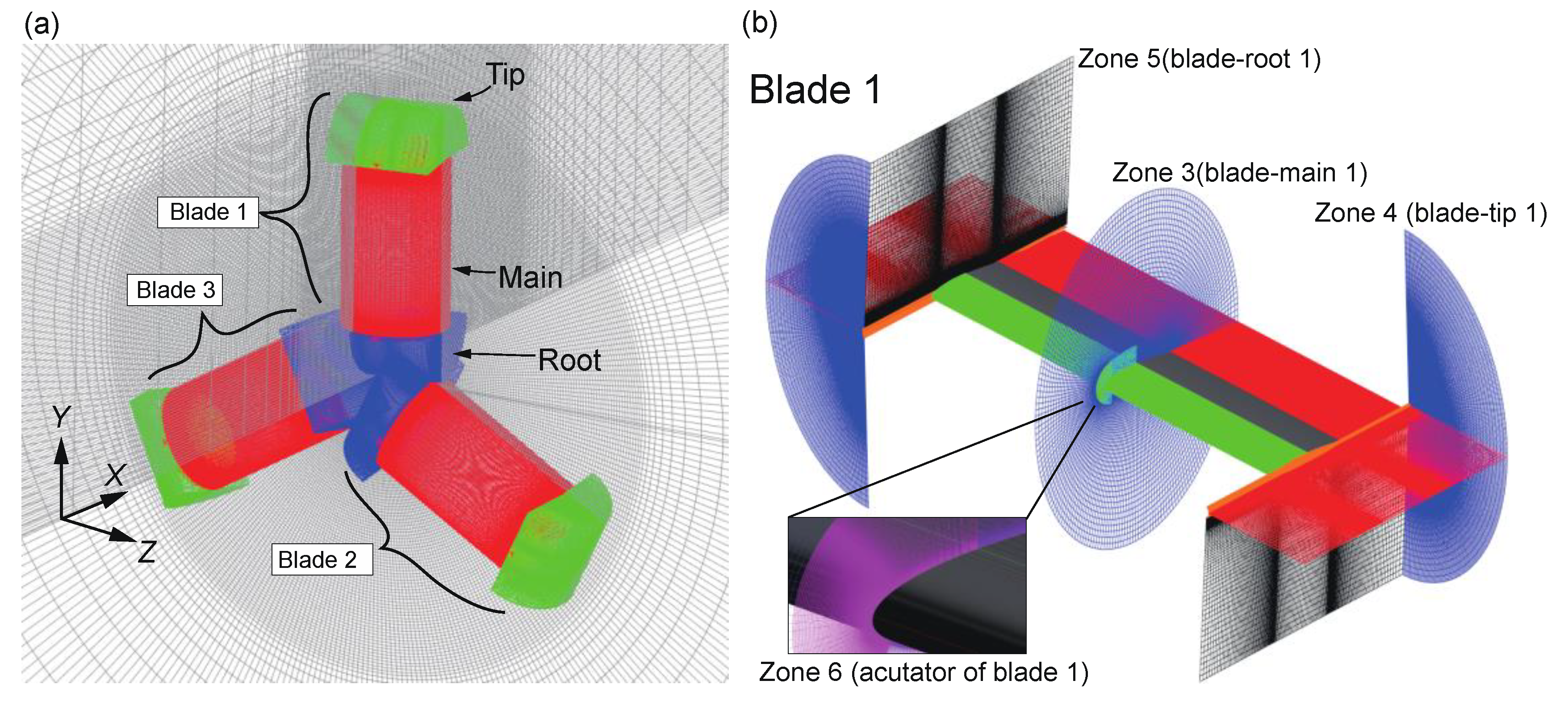
3.5. Computational Grids and Boundary Conditions
3.6. Computational Cases
4. Data Processing
5. Results and Discussion
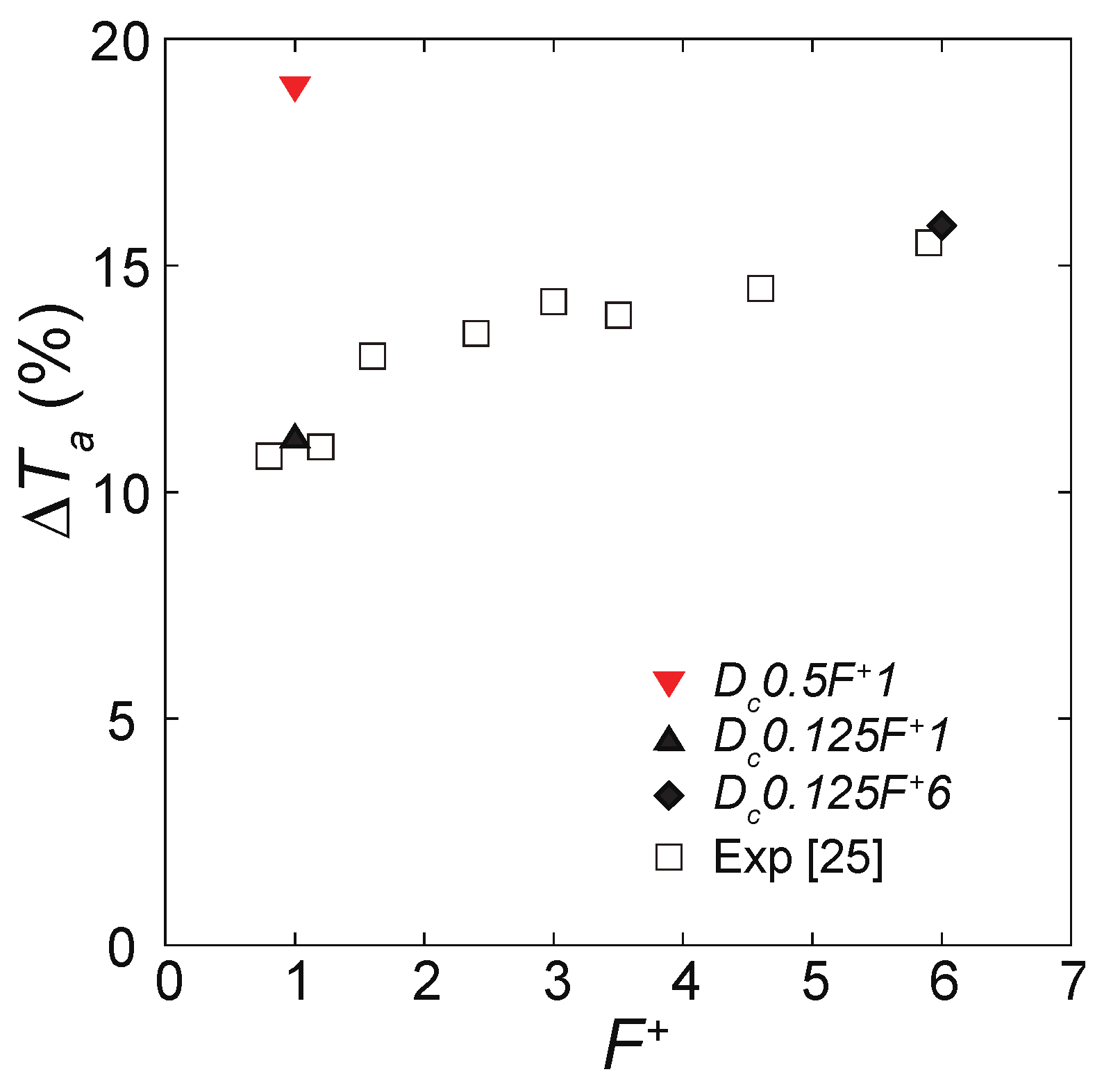
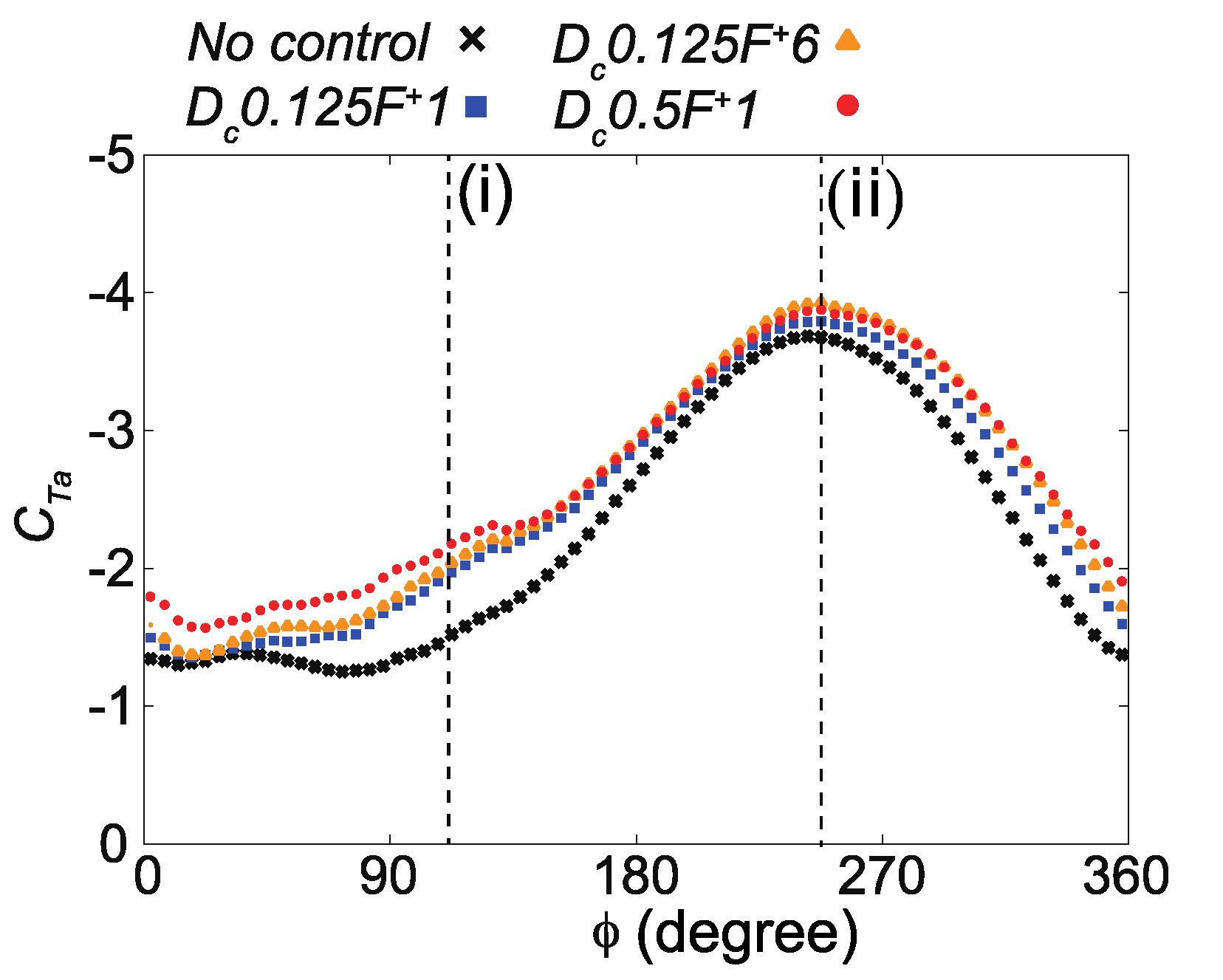
5.1. Effect of DBD-PA on the Cycle-Averaged Axial Torque Output
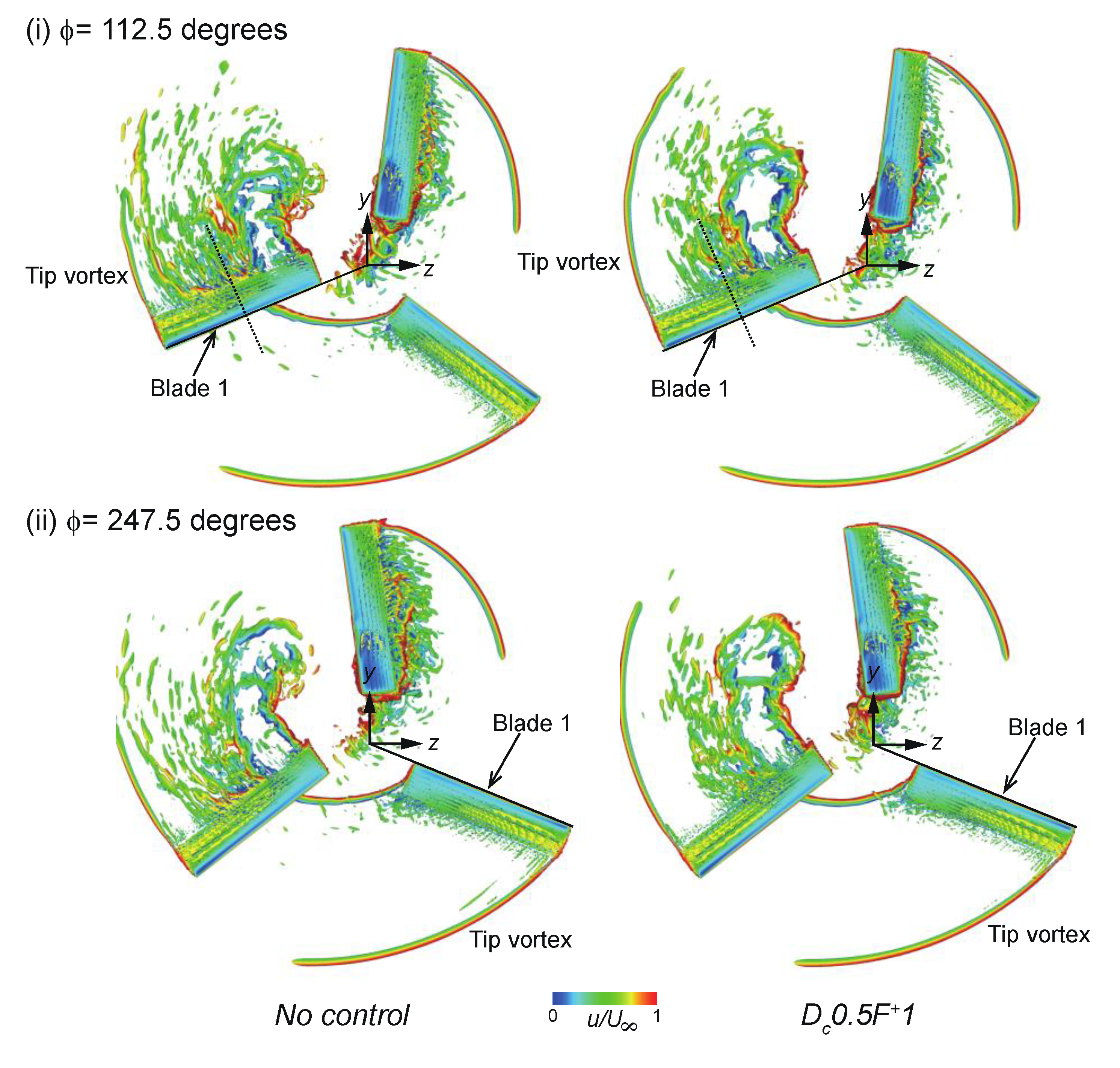
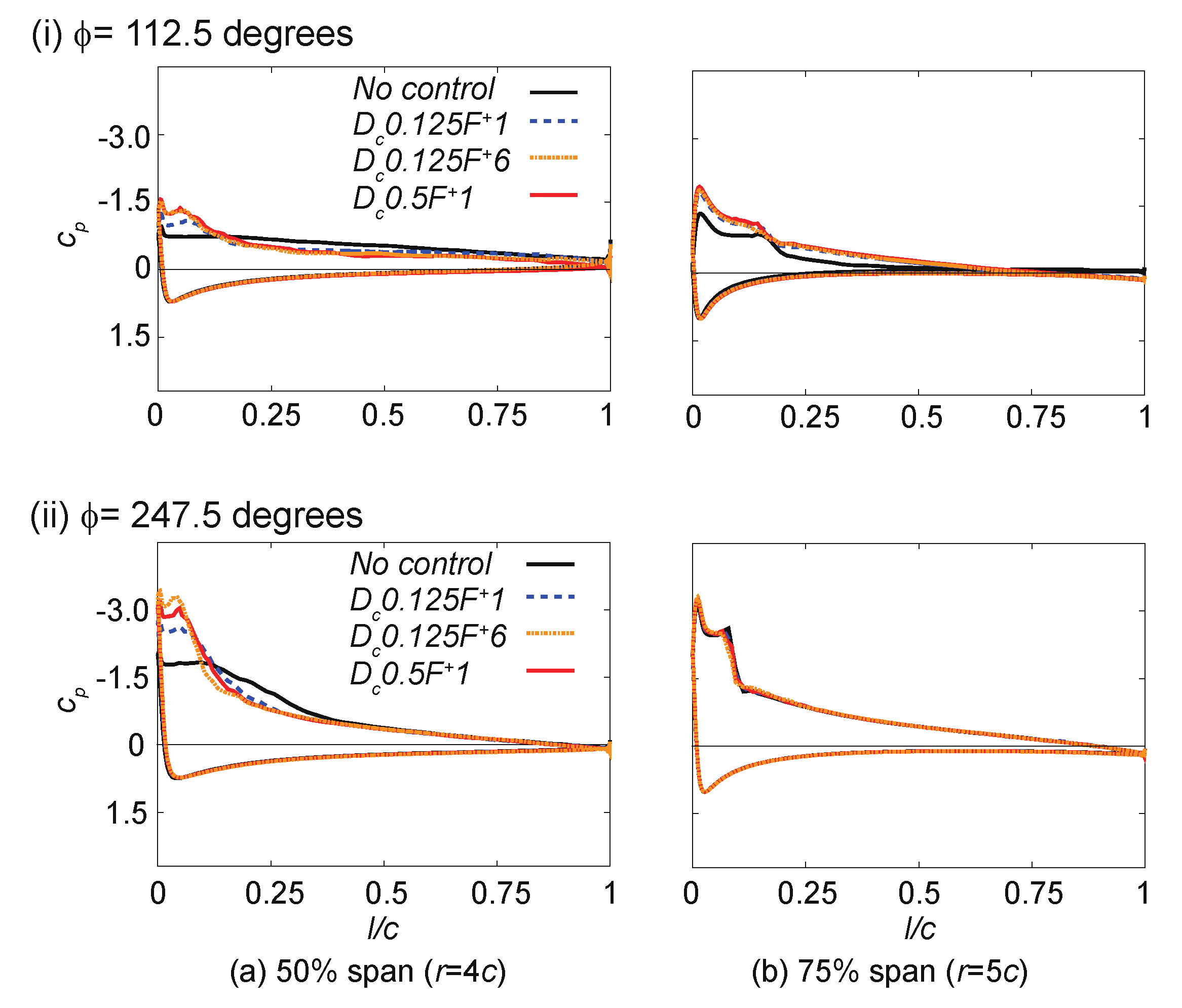
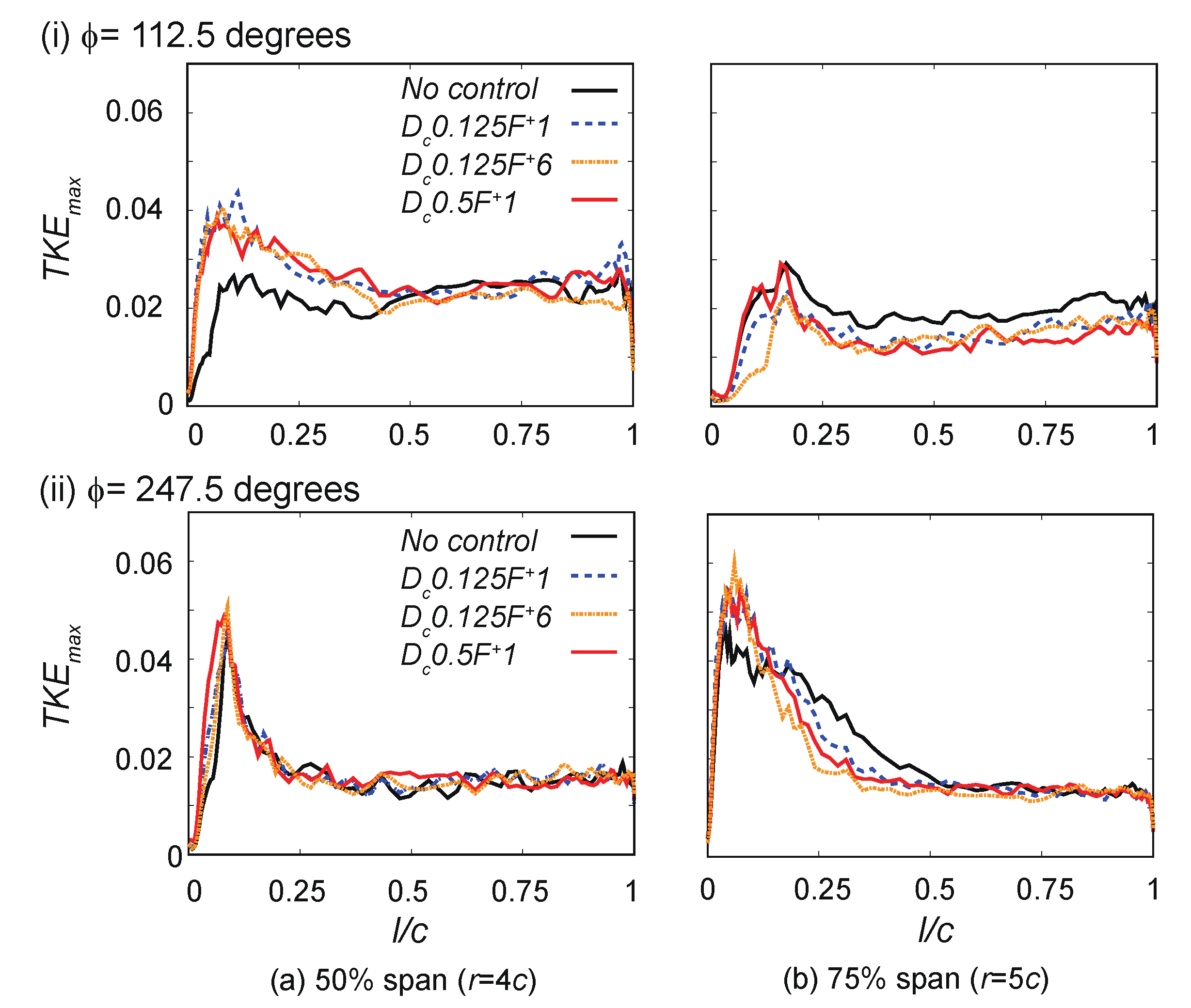
5.2. Phase-Averaged Flow and Aerodynamic Characteristics
5.3. Discussion about Flow Control around the Sophisticated Wind Turbine Airfoil Cross-Section
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sorensen, J.N. Aerodynamic aspects of wind energy conversion. Annu. Rev. Fluid Mech. 2011, 43, 427–448. [Google Scholar] [CrossRef]
- Cattafesta, L.N., III; Sheplak, M. Actuators for active flow control. Annu. Rev. Fluid Mech. 2011, 43, 247–272. [Google Scholar] [CrossRef]
- Roth, J.R.; Sherman, D.M.; Wilkinson, S.P. Boundary layer flow control with a one atmosphere uniform glow discharge surface plasma. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998. [Google Scholar]
- Roth, J.R.; Sherman, D.M.; Wilkinson, S.P. Electrohydrodynamic flow control with a glow-discharge surface plasma. AIAA J. 2000, 38, 1166–1172. [Google Scholar] [CrossRef]
- Roth, J.R.; Dai, X. Optimization of the aerodynamic plasma actuator as an electrohydrodynamic (EHD) electrical device. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar]
- Forte, M.; Jolibois, J.; Pons, J.; Moreau, E.; Touchard, G.; Cazalens, M. Optimization of a dielectric barrier discharge actuator by stationary and non-stationary measurements of the induced flow velocity: Application to airflow control. Exp. Fluids 2007, 43, 917–928. [Google Scholar] [CrossRef]
- Corke, T.C.; Martiqua, L.P.; Orlov, D.M. SDBD plasma enhanced aerodynamics: Concepts, optimization and applications. Prog. Aerosp. Sci. 2007, 43, 193–217. [Google Scholar] [CrossRef]
- Wang, J.-J.; Choi, K.-S.; Feng, L.-H.; Jukes, T.N.; Whalley, R.D. Recent developments in DBD plasma flow control. Prog. Aerosp. Sci. 2013, 62, 52–78. [Google Scholar] [CrossRef]
- Benard, N.; Moreau, E. Electric and mechanical characteristics of surface AC dielectric barrier discharge plasma actuators applied to airflow control. Exp. Fluids 2014, 55, 1846. [Google Scholar] [CrossRef]
- Enloe, C.L.; McLaughlin, T.E.; VanDyken, R.D.; Kachner, K.D.; Jumper, E.J.; Corke, T.C. Mechanisms and responses of a single dielectric barrier plasma actuator: Plasma morphology. AIAA J. 2004, 42, 589–594. [Google Scholar] [CrossRef]
- Moreau, E. Airflow control by non-thermal plasma actuators. J. Phys. D 2007, 40, 605. [Google Scholar] [CrossRef]
- Corke, T.C.; Post, M.L.; Orlov, D.M. Single dielectric barrier discharge plasma enhanced aerodynamics: Physics, modeling and applications. Exp. Fluids 2009, 46, 1–26. [Google Scholar] [CrossRef]
- Sato, M.; Aono, H.; Yakeno, A.; Nonomura, T.; Fujii, K.; Okada, K.; Asada, K. Multifactorial effects of operating conditions of dielectric-barrier-discharge plasma actuator on laminar-separated-flow control. AIAA J. 2015, 53, 2544–2559. [Google Scholar] [CrossRef]
- Sato, M.; Nonomura, T.; Okada, K.; Asada, K.; Aono, H.; Yakeno, A.; Abe, Y.; Fujii, K. Mechanisms for laminar separated-flow control using dielectric-barrier-discharge. Phys. Fluids 2015, 27, 117101. [Google Scholar] [CrossRef]
- Sato, M.; Okada, K.; Asada, K.; Aono, H.; Nonomura, T.; Fujii, K. Unified mechanisms for separation control around airfoil using plasma actuator with burst actuation over Reynolds number range of 103–106. Phys. Fluids 2020, 32, 025102. [Google Scholar]
- Aono, H.; Kawai, S.; Nonomura, T.; Sato, M.; Fujii, K.; Okada, K. Plasma-actuator burst-mode frequency effects on leading-edge flow-separation control at Reynolds number 2.6 × 105. AIAA J. 2017, 55, 3789–3806. [Google Scholar] [CrossRef]
- Sato, M.; Asada, K.; Nonomura, T.; Aono, H.; Yakeno, A.; Fujii, K. Mechanisms for turbulent separation control using plasma actuator at Reynolds number of 1.6 × 106. Phys. Fluids 2019, 31, 095107. [Google Scholar]
- Fujii, K. Three flow features behind the flow control authority of DBD plasma actuator: Result of high-fidelity simulations and the related experiments. Appl. Sci. 2018, 8, 546. [Google Scholar] [CrossRef]
- Matsuda, H.; Tanaka, M.; Goshima, S.; Amemori, K.; Nomura, M.; Osako, T. Experimental study on plasma aerodynamic control for improving wind turbine performance. In Proceedings of the Asian Congress on Gas Turbines, Shanghai, China, 20–22 August 2012. [Google Scholar]
- Matsuda, H.; Tanaka, M.; Amemori, K.; Nomura, M.; Osako, T. Plasma aerodynamic control effect on wind turbine performance. In Proceedings of the Japan Society Mechanical Engineering Annual Meeting, Kanazawa, Japan, 9–12 September 2012. [Google Scholar]
- Tanaka, M.; Matsuda, H.; Amemori, K.; Shimura, N.; Yasui, H.; Osako, T. Torque argument effect of plasma actuator aerodynamic control for field rotor. In Proceedings of the Wind Power Energy Symposium, Tokyo, Japan, 27–28 November 2012. [Google Scholar]
- Matsuda, H.; Tanaka, M.; Osako, T.; Maeda, T.; Kamada, Y. Flow visualization study using tuft method on plasma actuated wind turbine blade flow. In Proceedings of the Symposium of the Visualization Society of Japan Annual Meeting, Tokyo, Japan, 16–17 July 2013. [Google Scholar]
- Tanaka, M.; Osako, T.; Matsuda, H.; Yamazaki, K.; Shimura, N.; Asayama, M.; Kondo, S.; Kawakami, M.; Oryu, Y.; Yoshida, S. Power enhancement effect of plasma aerodynamic control for large scale wing turbine. In Proceedings of the Wind Power Energy Symposium, Tokyo, Japan, 12–13 November 2013. [Google Scholar]
- Matsuda, H.; Tanaka, M.; Osako, T.; Yamazaki, K.; Shimura, N.; Asayama, M.; Oryu, Y. Plasma actuation effect on a MW class wind turbine. Int. J. Gas Turbine Prop. Power Syst. 2017, 9, 47–52. [Google Scholar]
- Mitsuo, K.; Watanabe, S.; Atobe, T.; Ito, T.; Shiohara, T.; Tanaka, M. Aerodynamic characteristics improvement of a wind turbine by plasma actuators. In Proceedings of the Japan Society Mechanical Engineering Annual Meeting, Okayama, Japan, 8–11 September 2013. [Google Scholar]
- Jukes, T.N. Smart control of a horizontal axis wind turbine using dielectric barrier discharge plasma actuators. Renew. Energy 2015, 80, 644–654. [Google Scholar] [CrossRef]
- Nelson, R.; Corke, T.; Othman, H.; Patel, M.; Vasudevan, S.; Ng, T. A smart wind turbine blade using distributed plasma actuators for improved performance. In Proceedings of the 46th Aerospace Science Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008. [Google Scholar]
- Greenblatt, D.; Schulman, M.; Ben-Harav, A. Vertical axis wind turbine performance enhancement using plasma actuators. Renew. Energy 2012, 37, 345–354. [Google Scholar] [CrossRef]
- Ohtake, T.; Motohashi, T. Flow field around NACA0012 airfoil at low Reynolds numbers Part 1 characteristics of airfoil wake. J. Jpn. Soc. Aeronaut. Space Sci. 2009, 57, 397–404. [Google Scholar]
- Shyy, W.; Jayaraman, B.; Anderson, A. Modeling of glow discharge-induced fluid dynamics. J. Appl. Phys. 2002, 92, 6434–6443. [Google Scholar] [CrossRef]
- Orlov, D.M.; Corke, T.C. Numerical simulation of aerodynamic plasma actuator effects. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- Suzen, Y.B.; Huang, P.G.; Jacob, J.D.; Ashpis, D.E. Numerical simulations of plasma based flow control applications. In Proceedings of the 35th Fluid Dynamics Conference and Exhibit, Toronto, Ontario, Canada, 6–9 June 2005. [Google Scholar]
- Aono, H.; Sekimoto, S.; Sato, M.; Yakeno, A.; Nonomura, T.; Fujii, K. Computational and experimental analysis of flow structures induced by a plasma actuator with burst modulations in quiescent air. Mech. Eng. J. 2015, 2, 1–16. [Google Scholar] [CrossRef]
- Kawai, S.; Bouwhuis, T.; Abe, Y.; Yakeno, A.; Nonomura, T.; Aono, H.; Oyama, A.; Hoeijmakers, H.; Fujii, K. Dominant parameters for maximum velocity induced by body-force models for plasma actuators. Theor. Comput. Fluid Dyn. 2018, 32, 805–820. [Google Scholar] [CrossRef]
- Font, G.I.; Enloe, C.L.; McLaighlin, T.E. Plasma volumetric effects on the force production of a plasma actuator. AIAA J. 2010, 48, 1869–1874. [Google Scholar] [CrossRef]
- Aono, H.; Kimura, T.; Honami, S.; Ishikawa, H. Mechanisms of drag reduction due to flow control around circular disk using coaxial type dielectric barrier discharge plasma actuator at low Reynolds numbers. Fluid Dyn. Res. 2020, 52, 015508. [Google Scholar] [CrossRef]
- Fujii, K.; Obayashi, S. High-resolution upwind scheme for vortical-flow simulations. J. Aircr. 1989, 26, 1123–1129. [Google Scholar] [CrossRef]
- Abe, Y.; Nonomura, T.; Iizuka, N.; Fujii, K. Geometric interpretations and spatial symmetry property of metrics in the conservative form for high-order finite-difference schemes on moving and deforming grids. J. Comp. Phys. 2014, 260, 163–203. [Google Scholar] [CrossRef]
- Lele, S.K. Compact finite difference scheme with spectral-like resolution. J. Comp. Phys. 1992, 103, 16–22. [Google Scholar] [CrossRef]
- Gaitonde, D.V.; Visbal, M.R. Pade type higher-order boundary filters for Navier-Stokes equations. AIAA J. 2000, 38, 2103–2122. [Google Scholar] [CrossRef]
- Fujii, K. Simple ideas for the accuracy and efficiency improvement of the compressible flow simulation methods. In Proceedings of the 1st International CFD Workshop of Supersonic Transport Design, Tokyo, Japan, 16–17 March 1998. [Google Scholar]
- Iizuka, N. Study of Mach Number Effect on the Dynamic Stability of a Blunt Re-Entry Capsule. Ph.D. Thesis, University of Tokyo, Tokyo, Japan, 2006. [Google Scholar]
- Chakravarthy, S.R. Relaxation methods for unfactored implicit upwind schemes. In Proceedings of the 22nd Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 1984. [Google Scholar]
- Kobayashi, H.; Ham, F.; Wu, X. Application of a local SGS model based on coherent structures to complex geometries. Int. J. Heat Fluid Flow 2008, 29, 640–653. [Google Scholar] [CrossRef]
- Miyazaki, H.; Kusano, Y.; Okano, H.; Nakada, T.; Seki, K.; Shimizu, N.; Shoji, F.; Uno, A.; Kurokawa, M. K computer: 8.162 PetaFLOPS massively parallel scalar supercomputer built with over 548,000 cores. In Proceedings of the IEEE International Solid-state Circuits Conference, San Francisco, CA, USA, 19–23 February 2012. [Google Scholar]
- Aono, H.; Nonomura, T.; Iizuka, N.; Ohsako, T.; Inari, T.; Hashimoto, Y.; Takaki, R.; Fujii, K. Scalar tuning of a fluid solver using compact scheme for a supercomputer with a distributed memory architecture. CFD Lett. 2013, 5, 143–152. [Google Scholar]
- Abe, Y.; Aono, H.; Nonomura, T.; Fujii, K. Efficient evaluations of symmetric conservative metrics for high-order finite-difference schemes on a rotating grid. In Proceedings of the 2nd Frontiers in Computational Physics: Energy Sciences, Zurich, Switzerland, 3–5 June 2015. [Google Scholar]
- Fujii, K. Unified zonal method based on the fortified solution algorithm. J. Comp. Phys. 1995, 118, 92–108. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Fukumoto, H.; Aono, H.; Watanabe, T.; Tanaka, M.; Matsuda, H.; Osako, T.; Nonomura, T.; Oyama, A.; Fujii, K. Control of dynamic flowfield around a pitching NACA633-618 airfoil by a DBD plasma actuator. Int. J. Heat Fluid Flow 2016, 62, 10–23. [Google Scholar] [CrossRef]


| Parameters | [26] | [19,20] | [25] | [21,22] | [23,24] |
|---|---|---|---|---|---|
| Number of blades | 2 | 3 | 3 | 3 | 3 |
| Diameter (m) | 0.6 | 1.56 | 2.376 | 10 | 66 |
| Chord length c (m) | 0.078 | 0.057 | 0.2 | 0.213 | 1.8 |
| Airfoil (near midspan) | NRELS822 | - | NACA0012 | DU91W210 | DU91W2250 |
| Airfoil (near tip) | NRELS822 | - | NACA0012 | NACA63-618 | NACA63-618 |
| Freestream velocity, U∞ (m/s) | 2 | 6.5 (4.5–12.5) | 7.5, 10, 20 | 6 | 8.3 |
| Yaw angle, Φyaw (degree) | 0 | 0, 15, 30, 45 | 0, −40 | 9 | 0 |
| Rotational frequency, frot (Hz) | 5 (4–6.5) | 30–400 | 170, 174 | 60 | 13.5 (11–16) |
| Tip velocity, Utip (m/s) | 9.42 | 32.6 | 21.6 | 31.4 | 46.7 |
| Nondimensional parameters | |||||
| Reynolds number, Rec | 1.1 × 104 | 2.5 × 104 | 1.3 × 105 | 8.8 × 104 | 1.0 × 106 |
| Tip-speed ratio, λ | 4.6 | 5.0 | 2.2 | 5.2 | 5.6 |
| Reduced frequency, k | 0.61 | 0.18 | 0.18 | 0.11 | 0.15 |
| Parameters | [26] | [19,20] | [25] | [21,22] | [23,24] |
|---|---|---|---|---|---|
| Position (%) | 3, 38 | 0 | 0 | 0 | 0 |
| Peak-to-peak applied voltage, Vpp (kV) | 6.5 | 9.0 (8.0–10.0) | 9 | 5.5 | 10 |
| Base frequency, fbase (Hz) | 14,000 | 15,000 | 9000 | 15,000 | 15,000 |
| Burst frequency, fburst (Hz) | 9–15 | 300 | 20–300 | - | 4.6 |
| Duty ratio (burst ratio) BR (%) | - | 10 | 10 | 10 | 1 |
| Name of Grid | ξ | η | ζ | Total Points |
|---|---|---|---|---|
| Zone 1 (background) | 337 | 495 | 1023 | 170,651,745 |
| Zone 2 (background) | 41 | 495 | 41 | 832,095 |
| Zone 3 (blade-main 1) | 201 | 1501 | 101 | 30,471,801 |
| Zone 4 (blade-tip 1) | 169 | 301 | 101 | 5,137,769 |
| Zone 5 (blade-root 1) | 169 | 301 | 101 | 5,137,769 |
| Zone 6 (actuator of blade 1) | 604 | 1461 | 123 | 108,540,612 |
| Zone 7 (blade-main 2) | 201 | 1501 | 101 | 30,471,801 |
| Zone 8 (blade-tip 2) | 169 | 301 | 101 | 5,137,769 |
| Zone 9 (blade-root 3) | 169 | 301 | 101 | 5,137,769 |
| Zone 10 (actuator of blade 2) | 604 | 1461 | 123 | 108,540,612 |
| Zone 11 (blade-main 3) | 201 | 1501 | 101 | 30,471,801 |
| Zone 12 (blade-tip 3) | 169 | 301 | 101 | 5,137,769 |
| Zone 13 (blade-root 3) | 169 | 301 | 1001 | 5,137,769 |
| Zone 14 (actuator of blade 3) | 604 | 1461 | 123 | 108,540,612 |
| Case Name | F+ | Dc | BR | Fbase |
|---|---|---|---|---|
| No control | NA | NA | NA | NA |
| Dc0.125F+1 | 1 | 0.125 | 0.1 | 170 |
| Dc0.5F+1 | 1 | 0.5 | 0.1 | 170 |
| Dc0.125F+6 | 6 | 0.125 | 0.1 | 170 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aono, H.; Fukumoto, H.; Abe, Y.; Sato, M.; Nonomura, T.; Fujii, K. Separated Flow Control of Small Horizontal-Axis Wind Turbine Blades Using Dielectric Barrier Discharge Plasma Actuators. Energies 2020, 13, 1218. https://doi.org/10.3390/en13051218
Aono H, Fukumoto H, Abe Y, Sato M, Nonomura T, Fujii K. Separated Flow Control of Small Horizontal-Axis Wind Turbine Blades Using Dielectric Barrier Discharge Plasma Actuators. Energies. 2020; 13(5):1218. https://doi.org/10.3390/en13051218
Chicago/Turabian StyleAono, Hikaru, Hiroaki Fukumoto, Yoshiaki Abe, Makoto Sato, Taku Nonomura, and Kozo Fujii. 2020. "Separated Flow Control of Small Horizontal-Axis Wind Turbine Blades Using Dielectric Barrier Discharge Plasma Actuators" Energies 13, no. 5: 1218. https://doi.org/10.3390/en13051218
APA StyleAono, H., Fukumoto, H., Abe, Y., Sato, M., Nonomura, T., & Fujii, K. (2020). Separated Flow Control of Small Horizontal-Axis Wind Turbine Blades Using Dielectric Barrier Discharge Plasma Actuators. Energies, 13(5), 1218. https://doi.org/10.3390/en13051218








