Effects of Jet Induced by String-type Plasma Actuator on Flow Around Three-Dimensional Bluff Body and Drag Force

Abstract

An experimental investigation of active flow control on a three-dimensional (3D) curved surface bluff body was conducted by using a string-type plasma actuator. The 3D bluff body model tested in this study was composed of a quarter sphere and a half cylinder, and the Reynolds number based on the diameter of half cylinder was set at 1.3 × 10⁴. The modulation drive was adopted for flow control, and the control effects of variations in dimensionless burst frequency (f_m⁺) normalized by the width of the model and freestream velocity were studied. Velocity distributions analyzed by particle image velocimetry showed that the recirculation region behind the model shrank due to the flow control. The static pressure distributions on the back surface of the model tended to decrease under any f_m⁺ set in this study, especially in the ranges of 0.40 ≤ f_m⁺ ≤ 0.64. The drag coefficient reached its maximum value under the similar ranges of f_m⁺. Although the aerodynamic wake sharpening was observed due to the flow control, the entrainment of separated flow into the back surface of the model was enhanced. This scenario of wake manipulation was considered to be responsible for increasing drag acting on the model.

1. Introduction

Control of flow around bluff bodies has been studied both actively [1,2,3,4] and passively [5,6]. Bluff bodies are the representative shapes in some parts of various types of actual fluid machinery. Although success is guaranteed when using passive flow control techniques [5,6], an active flow control technique using a plasma actuator (PA) is of interest to the current study because of its advantage [3,4]. Figure 1a shows a schematic illustration of a typical PA. The basic structure of PA was firstly developed by Roth et al. [7], and it consists of a dielectric sheet and a pair of exposed and encapsulated electrodes. When a high voltage current (AC) between electrodes is applied, dielectric barrier discharge (DBD) occurs near one side edge of the exposed electrode. Then, the air around the edge is partially ionized by DBD, and the electric fields formed around the electrodes accelerate the charged particles. As a result, momentum transports due to the collision of the ionized particles with the surrounding neutral particles, and it develops into a one-way tangential jet. The induced flow jet is advected in the direction from the exposed electrode to the encapsulated electrode. This typical PA, called the “sheet-type PA” to distinguish it from the “string-type PA”, used in this study.

To date, experimental [3,4,8,9,10] and numerical [11,12] studies have been conducted and shown the possibilities of improvement in the lift-to-drag ratio and increasing the stall angle using the sheet-type PA installed near the leading edge of the airfoil as well as the effectiveness of modulation drive. Moreover, control methods of flow fields on more complex shaped 3D bluff bodies have been investigated. One of such examples is the Ahmed body [13], designed as a representative automobile model. From the flow structures in the case of without flow control, the longitudinal vortices generated from the slant around the 3D bluff body with slant angle at the rear end strongly correlate with the magnitude of the pressure drag [14]. Since the pressure drag most likely dominates the total drag acting on the 3D bluff body, weakening or transferring the vortices is conducted using flaps or PAs [15,16]. Recently, flow control using a pulse jet controlled by a solenoid valve on a square back shaped 3D bluff body model has been studied [16,17,18]. The correlation between the flow pattern in the wake and the generation of the drag on the square back shaped 3D bluff body due to the pulse jet flow control has been reported [16,17]. Moreover, the effects of the frequency of the pulse jet on flow structures and drag force have been analyzed. Results indicate that the change of frequency of the pulsed jet has a considerable impact on the drag force acting on the square back shaped 3D bluff body [16]. These efforts present certain possibilities of the drag reduction by the active flow control in the case of the square back shaped 3D bluff bodies.

Another example of the 3D bluff body is the generic body of a car door mirror consisting of a half cylinder and a quarter sphere [19,20,21]. This model has a 3D curved surface on the front and the rear end cut off with a sharp corner. Since the car door mirrors are a component installed as a projection on the body surface of a vehicle, they can generate vortices by flow separation that interact with flow around the vehicle. Those vortices cause an increase in aerodynamic drag and noise. Thus, research and development studies related to car door mirrors have been conducted in order to improve vehicle aerodynamic characteristics [22,23]. Furthermore, there are many examples of devices installed as projections on mobilities, such as the landing gears of aircraft [24,25] and pantographs of high-speed trains [26,27], which have complicated shapes and cause deterioration of the aerodynamic performance. On the other hand, to the best of our knowledge, the active flow control on the generic body of a 3D curved surface has not been adequately addressed. Therefore, more studies are required to understand the detailed mechanisms of change in fluid dynamic force on the 3D curved surface bluff bodies due to the flow control. In addition, the knowledge and understanding regarding the flow around the 3D curved surface bluff bodies, including the car door mirror, landing gears, and pantographs, and developing methods for improving aerodynamic performance by active flow control are expected to be useful for many types of fluid machinery with protrusion devices.

On the other hand, unlike the sheet-type PA, a string-type PA developed by Segawa et al. [28] has shown promise in terms of the smooth installation on 3D curved surface objects without the change of the original surface shape. Figure 1b shows the basic structure of a typical string-type PA. The string-type PA consists of a conductive wire coated with highly flexible insulation material preliminarily and an exposed electrode. If a groove for embedding a metal wire is structured on the surface of the test piece, it can be flush mounted to the objects. Using the string-type PA, the suppression of turbine tip clearance flow and feedback control of flow separation on an NACA0015 airfoil have been presented by experiments [28,29]. These cases have verified the performance of the string-type PA in flow control around a two-dimensional curved surface that has been reported by many researchers [8,9,10,11,12].

In this study, the string-type PA is applied to a 3D curved surface bluff body (the car door mirror model) on the surface in which the sheet-type PA might not be easily installed, and the control effects on aerodynamic properties were investigated based on the measurements of static pressures on the model surface, drag forces acting on the model, and velocity distributions around the model analyzed by particle image velocimetry (PIV). Through these experiments and analyses, we found a significant change in the drag coefficient due to the flow control. Although the increase in drag coefficient was observed in all flow control cases, we explored the mechanisms of the drag increase on the model in order to identify the possibility of the drag reduction of the 3D curved surface bluff body using the string-type PA.

2. Experimental Set up

2.1. Tested Model and Flow Condition

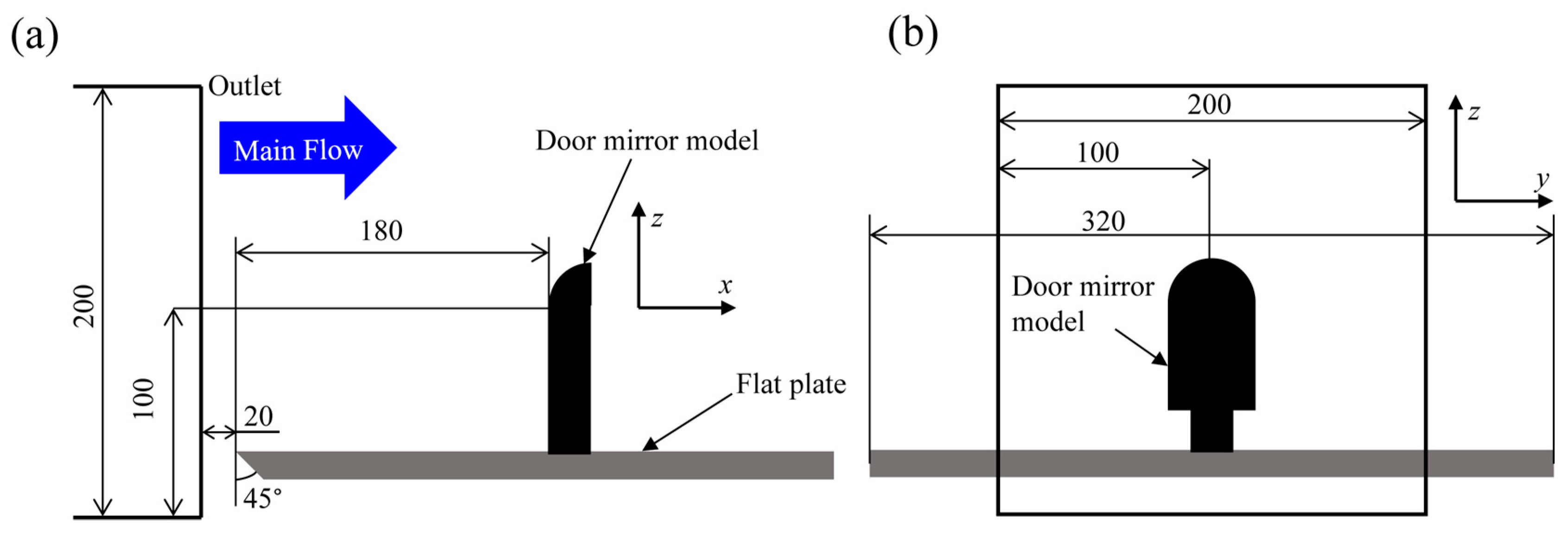
In this study, a 3D bluff body model simulating car door mirror geometry was adopted as the test piece. As shown in Figure 2, this model is a combination of a half cylinder (40 mm in the diameter (D) and 50 mm in height) and a quarter sphere (D = 40 mm), and the total height of the mirror model from the bottom wall was designed as 70 mm. An additional cylinder (20 mm in the diameter, 20 mm in height) used as a support is attached to the bottom surface of the half cylinder. A monocoque structure of the test piece made of heat resistant resin (TSR-884B) was modeled at a molding pitch of 100 μm by using a 3D rapid prototyping apparatus (CMET Inc., ATOM m-4000).

Figure 2b shows a schematic drawing of the model and internal structure in the x–z cross section. In a previous study on the flow around a car door mirror model conducted by Kato et al. [22], the separation point at Re = 10⁵ was approximately 70 degrees. Juke et al. [30] tried to control the flow around a two-dimensional cylinder with sheet-type PAs and indicated that a sheet-type PA located slightly upstream of the separation point was effective in mitigating flow separation. In consideration of this information, for constructing a flush mounted string-type PA, concave grooves (1.5 mm wide, 1.6 mm deep) were molded at the position 60 degrees from the stagnation point, which was presumed to be slightly upstream of the separation point. A copper wire (Cu wire) coated with silicone rubber (outer diameter: 1.3 mm, Cu diameter: 0.6 mm) was buried into the groove, and moisture-curable silicone was filled in the gaps between the model and wires to prevent a step with the mirror model surface. In addition, a conductive epoxy was filled in a V-shaped groove provided upstream of the wire for constructing the exposed electrode. A lead wire bonded to the exposed electrode and embedded Cu wire coated with silicone rubber were derived from inside to outside of the model through a midair hole of the support and connected to the power supply. From a safety perspective, high voltage AC was applied to the Cu wire, and the exposed electrode was connected to the ground (GND).

The model was installed on a flat plate that was fixed downstream of the exit with a 200 × 200 mm cross section in an open-circuit blowout wind tunnel. In this study, the main flow velocity (U_∞) was set at 5 m/s, and the Reynolds number (Re) based on the half cylinder diameter (D) of the test piece as the representative length was Re = 1.3 × 10⁴. The turbulent level of the incoming flow to the test piece was less than 0.4%. As shown in Figure 3, the flat plate was inserted 20 mm downstream from the exit of the wind tunnel contraction section. On the other hand, the test piece was placed at 180 mm downstream from the leading edge of the flat plate, and the highest stagnation point of the half cylinder was adjusted in the middle of the blowout port cross section.

2.2. Particle Image Velocimetry (PIV)

The arrangement of the test section and PIV system is shown in Figure 4. Dioctyl Sebacate (DOS) droplets atomized by a Laskin nozzle to the order of 1 μm in diameter were introduced into the flow as seeding particles, and the flows around the model were visualized using a 15 mJ/pulse double-pulse Nd:YAG laser (Litron Lasers, NANO S30-15PIV), and 300 pairs of flow images were acquired at 3.75 Hz using a cross-correlation camera (TSI Inc., PIVCAM13-8, 1280 × 1024 pixel resolution). An interrogation window of the square grid in 16×16 pixels was chosen, and velocity components (u, v) in the x–y cross section and (u, w) in the x–z cross section were analyzed by the single-step interrogation algorithm using PIV software (TSI Inc., Insight ver. 3.53) with 50% overlap between adjacent interrogation windows. Velocity vectors exceeding a certain magnitude were deleted as error vectors. Velocity vector components in each grid were averaged by the number except for errors.

Since the size of the visualization area was different for each cross section, the image resolutions of each pixel were also varied to d_px = 170.5 μm/pixel in the x–y cross section and 130.0 μm/pixel in the x–z cross section, respectively. The laser pulse interval obtaining a pair of flow images (∆t) was set such that the maximal displacement of seeding particles near the acceleration region around the model during ∆t was less than four pixels. In this study, ∆t = 100 μs and 70 μs were set in the cases for obtaining a pair of images in the x–y and x–z cross sections. Since the minimum displacement of the seeding particle calculated by the sub-pixel interpolation in PIV image processing is about 0.1 pixel, the uncertainties of the velocity components in the x–y and x–z cross sections were calculated to be 0.17 m/s and 0.19 m/s by calculating 0.1 d_px/∆t, respectively. Therefore, the error of velocity in the PIV analysis was estimated to be less than 4% of the main flow velocity.

2.3. Pressure Measurement on the Model Surface

The static pressures on the model surface were measured using the static pressure holes placed at 14 locations on the back surface, as shown in Figure 5. On the opposite side of the model back surface (inside of the model), stainless steel tubes (outer diameter: 1.6 mm) were inserted into 14 concave structures, where through-holes for differential pressure measurements (0.5 mm in diameter) were made in each center. The space between their holes and tubes were glued to prevent leakage. Flexible urethane tubes (inner diameter: 1.37 mm, outer diameter: 2.18 mm) connecting their static holes and a pressure scanner (Pressure Systems Inc., Model 9116) were pulled out of a support hollow to avoid disturbing flow around the model. The pressure scanner is composed of 16 independent silicone semiconductor piezoresistive elements and can measure the differential pressure from the atmospheric pressure. Time series of static pressure fluctuations at 14 locations were acquired at the same time by a sampling rate of 500 Hz. The time-averaged pressure coefficient (C_p) was also computed based on the time-averaged data at the 14 locations. The 60 s (30,000 points by each channel) between 10 and 70 s after the PA started operation were adopted for calculating the time-averaged value. C_p is defined as follows:

$$C_p=\frac{\mathsf{\Delta }p}{\frac{1}{2}\rho U_{{\infty }^2}}$$

where ∆p and ρ are the difference between the pressure measured in the static hole and atmospheric pressure, and air density, respectively. This pressure scanner with the temperature compensation function can measure the differential pressure at each channel ranging from −2.5 kPa to 2.5 kPa relative to atmospheric pressure, and static accuracy including combined errors due to non-linearity, hysteresis, and non-repeatability is shown to be ±0.05% FS in the specifications, which corresponds to the measurement error of 2.5 Pa.

In the pre-process measuring pressure fluctuations, each channel of the pressure scanner was reset to zero under the quiescent flow condition. Before and after PA operation for 80 s, pressure fluctuations without PA operation were obtained for 15 s to estimate the pressure coefficients under the condition of without flow control (before: ∆p (t < 0), after: ∆p (t > 80)). The standard deviation in a series of experiments for the difference between time-averaged ∆p (t < 0) and ∆p (t > 80) was less than 0.25 Pa. On the other hand, the standard deviation of ∆p (t < 0) (or ∆p (t > 80)) was 0.13 Pa at each experiment. From the analysis of these uncertainties, the cumulative error was evaluated as 0.01 in terms of C_p. In addition, the time-averaged ∆p (t < 0) was different in each measurement due to non-repeatability. Therefore, the time-averaged ∆p (t < 0) obtained under various PA driving conditions was averaged in order to determine the baseline. For estimating C_p, conclusively, ∆p under flow control during each measurement was offset by the difference between the time-averaged ∆p (t < 0) and baseline.

2.4. Drag Force Measurement

Aerodynamic drags acting on the model under various PA driving conditions were measured using a three-component force transducer (Kyowa Electronic Instruments Co., Ltd., LSM-B-5NSA 37-P, rated capacity: 5 N). The experimental setup of force measurement is illustrated in Figure 6. Each component force in the x (drag), y, and z axes measured by the three-component force transducer was converted to an analog voltage signal by a strain gauge built into the dynamic strain measurement system (Kyowa Electronic Instruments Co., Ltd., DPM-911B), and then recorded by a digital oscilloscope (Tektronix Inc., DPO-4034). Time series of three component forces were acquired at a sampling rate of 1000 Hz, and here, the drag coefficient (C_D) was evaluated with an averaged value for 60 s (60,000 points). The C_D is defined as follows:

$$C_D=\frac{F_x}{\frac{1}{2}\rho U_{{\infty }^2}S}$$

where F_x is the aerodynamic force in the x-axis component, and S is the projected area of the model. Note that measured y and z axes component forces were referenced to confirm the proper setting of the model and the magnitude of vibration.

In the catalog specification, the measurement accuracy of the three-component force transducer is shown as 0.001 N, which is equivalent to 0.024 in terms of a drag coefficient under the without flow control condition at Re = 1.3 × 10⁴ in this study. In addition, as a result of calibration using a standard weight, the ratio of load to output voltage shows high linearity with changes in load near the maximum load on the test piece. The measurement accuracy of F_x due to non-linearity and non-repeatability was less than 0.03 N in the case of without flow control at Re = 1.3 × 10⁴ in this study.

In measuring the drag force, each channel of the three-component force transducer was reset to zero under the quiescent flow condition at first. Before and after PA operation for 80 s, the drag force fluctuations without PA operation were obtained for 5 s to estimate the drag coefficients without flow control (before: F_x (t < 0), after: F_x (t > 80)). The standard deviation in a series of experiments for the difference between the time-averaged F_x (t < 0) and F_x (t > 80) was less than 0.000015 N. On the other hand, the standard deviation of F_x (t < 0) (or F_x (t > 80)) was 0.00018 N in each experiment. From the analysis of these uncertainties, the cumulative error was 0.02 in terms of C_D. Moreover, time-averaged F_x (t < 0) was varied in each measurement due to non-repeatability at Re = 1.3 × 10⁴. Therefore, the time-averaged F_x (t < 0) obtained under various PA driving conditions was averaged in order to determine the baseline. For estimating C_D, conclusively, F_x under flow control during each measurement was offset by the difference between the time-averaged F_x (t < 0) and baseline.

2.5. Driving Conditions of PA

In this study, the base frequency of sinusoidal voltage (f_p) and peak-to-peak voltage (V_p-p) were set at 10 kHz and 16 kV, respectively, for driving of the string-type PA. The string-type PA was operated in burst modulation control [3,4,9]. Figure 7 shows the waveform patterns of the applied sinusoidal voltage. Unlike the waveform in the case of continuous control (Figure 7a), the burst control (Figure 7b) has the two time periods that the PA switches on (T_on) and off (T_off). Here, the dimensionless burst frequency (f_m⁺) and duty ratio (DR) are defined as follows:

$${f_m}^{+}=\frac{f_{m}D}{U_{\infty }},\mathrm{DR}=\frac{T_{\mathrm{on}}}{T_{\mathrm{on}}+T_{\mathrm{off}}}\times 100\%,$$

where f_m, U_∞, T_on, and T_off indicate the burst frequency, main flow velocity, duration in one cycle for driving PA under burst control, and duration in one cycle for switching PA off under burst control, respectively. In this study, in order to investigate the influences of the f_m⁺ on flow around the model and the drag force acting on the model, f_m⁺ varied from 0.04 to 16 (0.04, 0.07, 0.1, 0.13, 0.16, 0.2, 0.27, 0.32, 0.4, 0.5, 0.53, 0.64, 0.8, 1.0, 1.28, 1.6, 2.0, 3.2, 8.0, and 16) with fixed DR = 20%.

3. Results

3.1. Induced Flow by the String-type PA under Quiescent Flow Condition

Before the flow control effects are discussed, the flow generated by the string-type PA installed in the model under the quiescent flow condition is presented. Figure 8 shows the spatial distribution of the time-averaged velocity (U_p) and turbulence level, which will be defined in Section 3.2, distributions in the x–z cross section of the induced jet around string-type PA.

The applied voltage was set to be V_p-p of 16 kV with DR of 100% (continuous control). Since the maximum velocity of the induced jet (u_max) was approximately 1.8 m/s in the continuous control, lower velocity is expected in the burst control cases. Thus, the ratios of the main flow and induced jet velocities are less than u_max/U_∞ ≈ 0.36 in all flow control cases considered.

3.2. Effects of Flow Control on Wake Structures

Figure 9 shows the time-averaged velocity distributions (x-axis velocity (u), y-axis velocity (v)) in the x-y cross section (z/D = −0.5, which is mid-height of the half cylinder) of the model wake in the cases of without flow control and with the burst control (f_m⁺ = 0.1, 0.5, 16 with DR = 20%). The basic wake structures are similar in all cases. The flow separates from near the rear end of the model, and a recirculation region behind the back surface is formed behind the back side. Figure 10 shows u profiles normalized by U_∞ at x/D = 1.25 and y/D = 0 in the x−y cross section. Based on Figure 10, normalized width (Y_rev/D) and length (X_rev/D) of the recirculation region are defined as the distance between two points where the positive and negative value of u/U_∞ are interchanged at x/D = 1.25 and the distance between x = 0 and the location where u/U_∞ changes from a negative to a positive value, respectively. Here, the Y_rev/D and X_rev/D are compared in order to analyze the control effects between different burst frequencies. Figure 11 plots Y_rev/D and X_rev/D as a function of f_m⁺. The changes of Y_rev/D and X_rev/D are similar with the variation of f_m⁺. Y_rev/D and X_rev/D reach their minimum value in the range of 0.32≤ f_m⁺ ≤ 0.64. Since the dashed lines in Figure 11 indicate the values of Y_rev/D and X_rev/D in the case without control, the recirculation region is shortened regardless of the burst frequencies. The maximum decrease rates of Y_rev and X_rev with respect to those of the case without flow control are approximately 20% and 25%, respectively.

In addition to the x–y section, Figure 12 shows the time-averaged velocity distributions (u, z-axis velocity(w)) in the x−z cross section at y/D = 0 in the cases of without flow control and with burst control (f_m⁺ = 0.1, 0.5, 16 with DR = 20%). It is also found that the recirculation region in the x–z cross section is reduced by driving the string-type PA and the wake approaches the flat plate side. This is because a strong downwash from the tip of the model generates in the wake structure (i.e., negative w region that is indicated by a dashed line in Figure 12). This downwash is formed at approximately x/D = 1.5 without control, and the distance from the model surface to the downwash region in the x-direction is changed due to the flow control. When f_m⁺ approaches 0.5, the distance reaches the minimum. Figure 13a shows u profiles normalized by U_∞ at x/D = 1.25. As shown in Figure 13a, the height of the recirculation region in the z-direction (Z_rev/D) is defined as the distance between z/D = −0.5 and the location at which u/U_∞ changes from a negative to a positive value. Figure 13b plots the Z_rev/D as a function of f_m⁺. Unlike X_rev/D and Y_rev/D, the change of the Z_rev/D due to the flow control is not significant.

Furthermore, turbulent intensity (Tu) was analyzed in order to evaluate the control effects on the separated shear layer by jets generated under burst control. Tu in the x–y cross section (Tu_x-y) and x–z cross section (Tu_x-y) are defined as follows:

$$Tu{}_{x-y}=\frac{\sqrt{\frac{1}{2}\left(\overline{{u^{\prime }}^2}+\overline{{v^{\prime }}^2}\right)}}{U},Tu{}_{x-z}=\frac{\sqrt{\frac{1}{2}\left(\overline{{u^{\prime }}^2}+\overline{{w^{\prime }}^2}\right)}}{U}.$$

Figure 14 and Figure 15 visualize the distribution of the turbulent intensity at z/D = −0.5 in the x–y cross section and at y/D = 0.0 in the x–z cross section under the without flow control condition and the burst control condition (f_m⁺ = 0.1, 0.5, 16 with DR = 20%). In the x–y cross section without flow control, a region with large velocity fluctuations for Tu_x-y > 0.25 was observed in the location where the separated shear layer was formed and in the wake near x/D > 2.0. Whereas, just behind the model, the velocity fluctuation was low (Tu_x-y < 0.1). Under the burst control of the string-type PA at f_m⁺ = 0.5, the region Tu_x-y > 0.5 was observed in the wake near x/D < 1.0, and it extended to the back surface of the model. At the same time, the region where Tu_x-y < 0.1 had shrunk. In addition, the burst control driving the string-type PA at f_m⁺ = 0.5 promoted the growth of the shear layer and reduced the length in the x-axis direction of the shear layer, which was attributed to the enhancement of the entrainment of the separated flow. In the x–z cross section, as in the x–y section, the region of large fluctuation was enlarged, and the x-axis direction of the shear layer was shortened by the same driving condition.

On the other hand, the distributions of turbulent intensity in both cross sections at f_m⁺ = 0.1 and 16 are closer to those of the case without flow control. However, it was observed that the burst control driving the string-type PA at f_m⁺ = 0.1 and 16 certainly promoted the growth of the shear layer and reduced the length in the x-axis direction of the shear layer.

3.3. Effects on Flow Control on Pressure Distributions

C_p at locations illustrated in Figure 5 under the burst control was analyzed in comparison with those under the burst control and without control (Figure 16). As shown in Figure 16a, C_p wholly tended to decrease over the back surface when string-type PA was driven compared without control. Compared to C_p of the case without control, it dropped roughly 20% under the burst control for f_m⁺ = 0.5, DR = 20%. It is remarkable that similar control effects were found at −0.9 ≤ z/D ≤ 0.2 in y/D = 0 (Figure 16b), especially since the flow structure was considered to exhibit strong three-dimensionality at z/D = 0.2 and −0.9. In Section 3.2, it was shown that the low-speed structure caused by the wake was closest to the back surface of the model for f_m⁺ = 0.5, DR = 20% under burst control. Therefore, C_p reduction on the model back surface can be attributed to the approach of the low-speed structure with lower pressure than the surrounding flow. Variations of C_p at the locations A, B, C and D (y or z-direction) shown in Figure 5 under different conditions of burst control were compared in Figure 17 (C_p as a function of f_m⁺ under fixed DR = 20%) in order to clarify the consistency with velocity distributions analyzed by PIV. C_p values of the case without control at three locations (baseline) were drawn by a dashed line. C_p reached its minimum in the ranges of 0.40 ≤ f_m⁺ ≤ 0.64, where X_rev and Y_rev were similarly reduced to the minimum, as shown in Figure 11. For example, at location B, C_p under the burst control decreased from 18% to 21% compared to that of the case without control.

3.4. Effects on Drag Coefficient

Variations of C_D under different conditions of burst control were compared in Figure 18 (C_D as a function of f_m⁺ under fixed DR = 20%) in order to understand the relationship between C_D and the results of velocity and pressure distributions. On the whole, C_D under any flow control condition by PA was increased in comparison with that under no control (baseline) illustrated by a dashed line. In the ranges of 0.40 ≤ f_m⁺ ≤ 0.64, where C_p on the back surface of the model decreased most as presented in Figure 17, C_D reached its maximum value and increased from 4% to 7% compared to that without control.

3.5. Effects of Duty Cycle Ratio on Model Surface Pressure and Drag Coefficients at Fixed f_m⁺

Effects of the duty cycle ratio on C_p and C_D were analyzed. Figure 19 and Figure 20 show the results of the case of different duty cycle ratios (DR) of C_p at selected measured points and drag coefficient (C_D) acting on the model, respectively. Note that the case with DR = 100 corresponds to the continuous operation. The effects of DR on C_p and C_D show nonlinear behavior. Especially, the results of cases with near DR = 20% show the lowest values of C_p at all the measured points. On the other hand, the variation of C_D with change of the DR is slightly different. An increase of C_D is found for most of the DR cases. In the case of continuous operation, C_p and C_D values were found to be a little different from the baseline.

3.6. Vortex Shedding Frequency Estimation based on Surface Pressure Fluctuations

In this section, the effects of flow control by the string-type PA on wake frequency are discussed. It is important to know the optimal range of the dimensionless frequency of modulation in order to realize the effective flow control. For circular cylinder wake control using sheet-type PAs, Jukes and Choi [30,31] reported that in the cases of f_m⁺ larger than 0.6, the suppression of vortex shedding was successful and 32% drag reduction was achieved, while in the cases of f_m⁺, less than 0.6 vortex shedding was locked out of multiple of PA frequencies to amplify the wake oscillations resulting in an 85% increase in lift with 8% drag increase.

By analyzing ∆p, we then attempted to analyze how the vortex shedding frequency of wake changed under burst control. However, the characteristic frequency relevant to f_c was not confirmed in 14 locations on the back surface of the test piece. On the other hand, the remaining two ports of the pressure scanner with 16 channels were used for measuring static pressure fluctuations at the positions ±75 degrees on z/D = 0 in the x−y cross section on the front surface. As shown in Figure 21, the characteristic peak frequency (f_c) of normalized D and U_∞ was identified as St = f_cD/U_∞ = 0.17. It is considered to be corresponding to the vortex shedding frequency St = 0.16, which was detected at 60 degrees from the stagnation point on the front surface of a door mirror model conducted by Kato et al. [22]. However, a frequency shift by jets under the burst control was not confirmed in this study. Therefore, direct measurements of pressure fluctuations at various locations downstream of the test piece, such as near the separated shear layer, will be necessary in future work.

4. Discussion

In the previous section, the results showed that the drag measured was increased by the flow control with all burst frequencies considered while the length (X_rev/D) and width (Y_rev/D) of the recirculation region (the characteristic length of the wake) were decreased. In general, when the recirculation area caused by flow separation shrinks in wake flow around the bluff body, drag force is considered to be decreased because of the velocity deficit reduction. For example, Michelis and Kotsonis [32] also tried to mitigate flow separation on the door mirror of a truck by installing a sheet-type PA in the guide vane adjacent to the side mirror of a full-scale truck and found that momentum deficiency was suppressed by driving the sheet-type PA. However, when the flow around the bluff body is three-dimensional, the drag force can increase, as shown in this study, even if the momentum deficit was recovered in the two-dimensional cross section of velocity distributions. Indeed, the results shown in Section 3.2, 3.3, and 3.4 clarified that C_D under burst control was increased since the entrainment of separation flow into the model back surface was enhanced by driving the string-type PA, and the model was pulled downstream by the low-speed structure that approached the back surface.

In this section, the correlation between the controlled flow patterns and the drag force acting on the model is analyzed and discussed. To discuss the control effects on the pressure on the model surface and the drag acting on the model, the rate of spatial-averaged C_p based on the 14 locations shown in Figure 5 ($\overline{C_p}$) and C_D under control compared to that without control (γ_p and γ_D) [17] are introduced and defined as follows;

$${\gamma }_p=\frac{\overline{C_p}\left(\mathrm{under}\mathrm{control}\right)}{\overline{C_p}\left(\mathrm{without}\mathrm{control}\right)},{\gamma }_D=\frac{C_D\left(\mathrm{under}\mathrm{control}\right)}{C_D\left(\mathrm{without}\mathrm{control}\right)}$$

Figure 22 shows the effects of f_m⁺ on the surface pressure and drag force acting on the model. The change of γ_p with respect to the variation of f_m⁺ correlates with the change of γ_D with respect to the variation of f_m⁺. Also, although the γ_D varies due to the flow control, γ_D becomes larger than that in the cases considered. These results mean the drag forces acting on the model increase in comparison with that of the case without the control. The γ_p and γ_D firstly increase in the ranges of 0.04 ≤ f_m⁺ ≤ 0.53, then both reach their maximum value at near f_m⁺ = 0.53 and start decreasing with an increase in f_m⁺. When f_m⁺ becomes larger than three, the changes of γ_p and γ_D are not significant. The maximum increase in C_D is approximately 7% compared to the case of without control.

Figure 23 visualizes the recirculation region by the contour line of u/U_∞ = 0.0 for the cases with and without the control. The contour lines shown in Figure 23 indicate the change of the recirculation region due to the variation of f_m⁺. The length and width of the recirculation region shrink with the increase in f_m⁺ up to 0.5, but it enlarges when f_m⁺ exceeds 0.5. From the contour lines in the x–z cross section, basically, the response of the length and width of the recirculation region to the variation in f_m is similar to that observed in the x–y cross section. However, due to an asymmetric geometric feature in the z-direction and the presence of the wall beneath the bottom of the model, the recirculation region is formed in the lower part rather than the boundary between the quarter sphere and the half cylinder (z/D = 0). The height (Z_rev/D) of the recirculation region length in x/D < 1.25 increases by the control while the length (X_rev/D) of the recirculation region length below z/D = 0.0 decreases. These flow patterns imply that the recirculating flow in the model wake exhibits the three-dimensionality.

It is interesting that the changes of wake structures (i.e., recirculation region) in the x–y cross section in the cases of the drag increase are similar to those observed in the flow control on a square back shaped 3D bluff body model using the pulsed jets [16,17]. In particular, the drag increased when the recirculation length in the wake was shortened by the flow control with the non-dimensional forcing frequency normalized by the model height and freestream velocity being around 0.8. On the other hand, the drag decreased by the flow control with a higher non-dimensional forcing frequency than four [17], which was not be observed in the results presented in the current study. In the previous study [17], the wake manipulations in terms of the enhancement of the momentum entrainment and recirculation length were responsible for the mechanisms of these drag changes. The enhanced entrainment decreasing the length of the recirculation region was proposed for low-frequency forcing work in all the controlled cases. Although an aerodynamic wake sharpening was also observed in the results of the current study, little reduced entrainment due to the control with high-frequency forcing was observed. This difference observed in the controlled wake structure might cause an increase in drag force acting on the model with high-frequency forcing. In addition, if the direction of the main flow is not parallel to the square back shaped 3D bluff body model, another mechanism of the drag reduction [18] and dependencies of drag change mechanisms on Re and the magnitudes of induced jet velocity were reported [17].

In short, the elongation of the recirculation length in the main flow direction plays an important role in drag reduction based on the observations from the results of current and previous studies [16,17,18]. The main control effect of the string-type PA with the burst modulation on the flow around the curved surface 3D bluff body model is the aerodynamic wake sharpening with the enhanced entrainment. We consider that the mechanism underlying the drag increases by driving the string-type PA is due to a decrease in pressure of the model back surface associated with the movement of the recirculation region. For the future works, 3D base flow around the 3D curved surface bluff body model under different flow conditions (e.g., Re and the angle of main stream) and multiple string-type PAs with different burst frequencies and the flow control with control laws [29,33] should be investigated.

5. Conclusions

In this study, the active flow control using the string-type PA was applied for the door-mirror like bluff body with curved surface at Re of 1.3 × 10⁴. The effects of burst frequencies and duty cycle ratios on flow structures around the model and drag force acting on the model were investigated. Although the drag reduction was not realized by the flow control using the string-type PA, the effects of control on flow structures around the bluff body with the curved surface, as well as the relationship between flow structures and drag force generation, were analyzed in detail. These findings could be used for improving the flow control using the string-and sheet-type PA for bluff bodies at Re of O(10⁴).

In addition, the contribution of this research to the scientific community is considered as follows: (i) to offer further understanding of flow structures around the bluff body with curved surface with/without the string-type PA, (ii) to provide the results of analysis regarding the operational parameters of PA such as duty cycle ratio and modulation frequency, and (iii) to assess the relationship between surface pressure and PIV measurement data and drag force acting on the model in order to explain the reason of drag increase. We consider that all the results and discussions presented in this study can contribute to improving flow control techniques for bluff bodies with three-dimensional curved surfaces.