Transient Natural Convection in a Thermally Insulated Annular Cylinder Exposed to a High Temperature from the Inner Radius

Abstract

Extensive numerical analysis was performed for the unsteady state, natural convection in the annular cylinders. The cylinder’s boundaries were thermally insulated, except the inner surface. The fluid (water) in the cylinder initially was assumed at a cold temperature while the inner surface was subjected to a high temperature. The time history for the heat transfer by diffusion and advection was studied. The time needed for fully charging the storage tank and rate of heat transfer was calculated. The predicted results were compared with the pure heat diffusion process and with a steady-state convection system. Therefore, CFD simulations were performed for natural convection in the storage tank. The main objective of this study was to establish correlations for the rate of heat transfer as a function of time and other controlling parameters. The correlation is needed in designing a thermal energy storage system for domestic and industrial heating processes. One of the drawbacks of the conventional thermal storage systems is the slow charging and discharging, where the heat transfer is mainly diffusion dominated. To overcome such a problem, a system was designed based on the natural convective heat transfer mechanism. Therefore, the heat transfer and fluid flow in a cylindrical storage tank were simulated for a range of Rayleigh numbers (10⁴ to 10⁸) and radius ratio. It was found that a convection-operated storage tank reduces the thermal charging process time drastically compared with the thermally diffusion charging process. The rate of reduction in the charging time mainly depends on the rate of heating and geometric parameter of the tank. To the best of the authors’ knowledge, the work is novel.

1. Introduction

Thermal storage systems are an essential part of domestic and commercial water heating systems, especially solar heating systems, for water heating and power generation. It is crucial to understand the flow and heat transfer in sensible and latent heat thermal storage systems in designing and optimizing the storage system. One of the critical parameters in the design of the system is estimating the charging and discharging times. The steady and unsteady states of natural convection in enclosures have been extensively studied by Hussein et al. [1].

However, very limited data are available on the natural convection in annular geometries, specifically unsteady state convection with thermally insulated boundaries. The operation of thermal storage systems is unsteady due to charging and discharging processes. From the physics of heat transfer, in the very early thermal charging process, the expected mechanism of heat transfer is the diffusion dominated process. At a certain period of the time, which depends on the rate of heating and radius ratio of the annular cylinder, the heat transfer mechanism is dominated by the convection mechanism. It is expected that the convection strength will be high until the heat diffuses and advocates by convection to the far end boundaries. Then, the strength of the convection decays, and the system reaches the equilibrium conditions, where the tank reaches its maximum thermal capacity.

Huang and Hsieh [2] simulated the buoyancy-driven flow in a cylindrical enclosure. The circumferential and top of the cylinder were kept at a cold temperature, while the bottom of the cylinder was kept at a hot temperature. The Rayleigh (Ra) number was varied from 10² to 2 × 10⁵, and Prandtl (Pr) number was varied from 1.0 to 200. The authors found that a unicellular motion existed due to the boundary layers lining each of the differentially heated walls, and the eye of vortex moved steadily closer to the geometric corner of the flow region as the Ra number increased. The net heat transfer increased with the Ra number, which was expected. The effect of the Pr number was observed, but not noted. The authors also found that the major heat was transferred from the bottom wall, and the ceiling could be considered as an insulator.

Papanicolaou and Belessiotis [3] studied transient natural convection in a cylindrical enclosure filled with water at high Ra numbers (10¹⁰ to 10¹⁵). They considered and compared the prediction of different turbulent flow models. They imposed constant heat flux along the circumference of the cylinder. The top and bottom of the cylinder were assumed to be adiabatic. The ratio of the height to the diameter was set to one. The Ra was varied from 10¹⁰ to 10¹³ in the laminar flow regime, and Ra was varied from 5 × 10¹³ to 10¹⁵ in the turbulent flow regime. The results showed that the achievement of a quasi-steady state was attained after fluid undergoes an oscillating pattern and the secondary flows alternatively appeared and vanished. They found that those patterns affected the stratification in the tank. In a turbulent flow regime, the authors found that the low Reynolds k-ϵ model eventually predicted a laminarization. The high-Re, k–ϵ model predicted sustain or very slowly decaying turbulence. The predicted results were fairly compared with the experimental data.

Wang et al. [4] studied natural convection in a circular enclosure embedded with a rectangular enclosure for Ra varied from 10³ to 10⁶, which is in the laminar regime. The flow patterns and isotherms were reported. Also, the local and average Nusselt number average values along the outer and inner walls were reported. The results showed a significant effect of aspect ratio on the flow pattern and thermal stratification. Also, the vortices occurring at the top of the rectangle domain had a significant effect on the average Nusselt number for the aspect ratio greater than 1.2.

Al-Jabair and Habeeb [5] simulated natural convection in a concentric annulus between an outer inclined square enclosure. Two-dimensional, steady-state simulations were performed. The authors assumed Boussinesq approximation in the modeling of the buoyant effect. The time marching method was used in updating the solution of the governing equations. Body-fitted coordinates and coordinate transformation methods were used in modeling the geometry of the system. The results were obtained for Ra numbers of 10³, 10⁴, 10⁵, and 10⁶; aspect ratios of 1.5, 3, and 4.5; and seven various inclination angles of 0, 30, 45, 60, 90, 135, and 180 degrees. The flow and temperature fields were presented in the form of streamlines and isotherms. Nusselt number variations as a function of the geometrical parameters were discussed. The results showed a significant effect of Ra number and aspect ratio on the flow and on the thermal fields, which are expected.

Pelletier et al. [6] studied a natural convection heat transfer from a pair of isothermally heated cylinders filled with water. They noticed that when the cylinders were vertically aligned, the heat transfer on the upper cylinder was affected by buoyancy-induced fluid flow from the lower cylinder. The authors also noticed strong oscillations appear in the local rate of heat transfer and fluid flow patterns. The simulations were performed for Rayleigh numbers varied from 1.7·10⁶ to 5.3·10⁶, and the center-to-center cylinder spacing varied from 1.5 to 4.

Krakov and Nikoforov [7] numerically and analytically investigated the laminar convection in a horizontal cylindrical enclosure heated from below and filled with magnetic nanofluids. The system was heated by a uniform electromagnetic field. The results showed that the outer magnetic field could cause instability of the equilibrium state of magnetic nanofluid and influence gravity convection. The authors considered Prandtl numbers from 0.7 to 700 and Rayleigh numbers of up to 10⁶. The authors found that the magnetic permeability of the magnetic fluid filling the enclosure was an important factor. They studied four modes of fluid flow analytically, and two of them were demonstrated using the numerical simulations. The simulation showed that the outer uniform magnetic field turned to nonuniform in the magnetic fluid heated from below. So, there was a weak convective flow, even for a very small magnetic Rayleigh number.

Li et al. [8] studied the effect of different thermal storage tank structures on temperature stratification and thermal efficiency during the charging process. The authors compared temperature stratification in six kinds of tanks. Also, the thermal charging efficiency of the tanks was compared. The optimal tank shape for charging was developed. The authors also performed CFD simulation and validated their results experimentally and found the relative discrepancy between the CFD model predictions and experimental data was about 5%.

Medebber and Retiel [9] examined the effects of buoyancy and height ratio on the natural convection in a vertical cylinder partially annular. The results showed that the flow field is characterized by simple recirculating zone turning in the clockwise direction. The results indicated that the variation in the Ra number and height ratio have a major influence on the flow structure and isotherm patterns. They noticed two flow regimes for lower Ra number values and the dominance of conduction heat transfer. At higher Ra number values, the heat transfer rate was increased and was dominated by convection mode. Moreover, the results showed that the average Nusselt number increased with the increasing of the Ra number and height ratio, which is consistent with the predications of previously mentioned authors.

Moran and Katz [10] numerically investigated a natural convection heat transfer in an annular cylindrical enclosure with nonuniform boundary conditions using the finite element method. The inner circumferential temperature distribution was assumed to be varied along the inner hot cylinder surface. The outer surface of the cylinder was kept at a constant cold temperature. The simulation was carried on for Ra = 2 × 10⁵ to 1.1 × 10⁷. The authors analyzed the temperature and velocity by comparing the results to the case of uniform boundary conditions. A correction factor was proposed to enable the use of the classical empirical correlations for the uniform boundary conditions. The results showed that the overall heat transfer rate for nonuniform linear temperature distribution was up to 7% higher compared to the cases of uniform temperature equal to the average nonuniform temperature. However, a 7% increase in the rate of heat transfer for an idealized system is not that high for practical applications.

Moldovan et al. [11] experimentally investigated the natural convection flow in an annularly heated vertical cylinder. The work was focused on measuring the flow temperatures and velocities in a crystal grow reactor equivalent setup. The cylinder geometry was scaled to imitate the geometry of existing crystal growth reactors. The Rayleigh number varied from 10⁷ to 10⁸ were investigated. The PIV was used to measure and visualize the flow velocity. The experimental measurements showed that axial heat transfer occurred mainly by advection, and the radial heat transfer occurred primarily by conduction. Also, they mentioned that 3D cells generated by the temperature gradient improved the heat transfer between the cold and hot sections of the setup.

Bai et al. [12] studied thermal stratification in a cylindrical tank due to heat losses in standby mode. The experimental and numerical simulations were performed. The Nusselt number was determined, and a new one-dimensional model for the cooling process was proposed and experimentally validated. The results showed that the aspect ratios, H/D, higher than three had little influence on the thermal stratification.

Goodrich et al. [13] studied natural convection heat transfer and boundary layer transition for vertical heated cylinders. The effect of curvature on the rate of heat transfer and regime transition was experimentally investigated. The authors applied PIV to visualize the flow field and measured the local surface temperature from five heater sizes. The authors provided a continuous, local, and curvature dependent Nusselt number correlation for the laminar, transition, and turbulent regimes for natural convection from vertically heated cylinders.

The thermal storage systems may be coupled with PV-T panels to utilize the waste heat from PV cooling and heat the domestic water. This kind of system, with tube plate PV/T filled with iron, was studied by Huo at al. [14]. The use of iron-filling allows increasing the electrical and thermal efficiency of the PV-T system.

In conclusion, the mentioned works considered different conditions and scenarios for steady and unsteady state heat convection in enclosures. However, to our knowledge, there has been no work done on the annular cylinder with all surfaces thermally insulated except the heated inner surface. Furthermore, no correlation of the rate of heat transfer for such a system has been reported. Hence, it is essential to investigate such a system to estimate the charging and discharging times and rate of heat transfer.

2. Problem Definition and Modelling Details

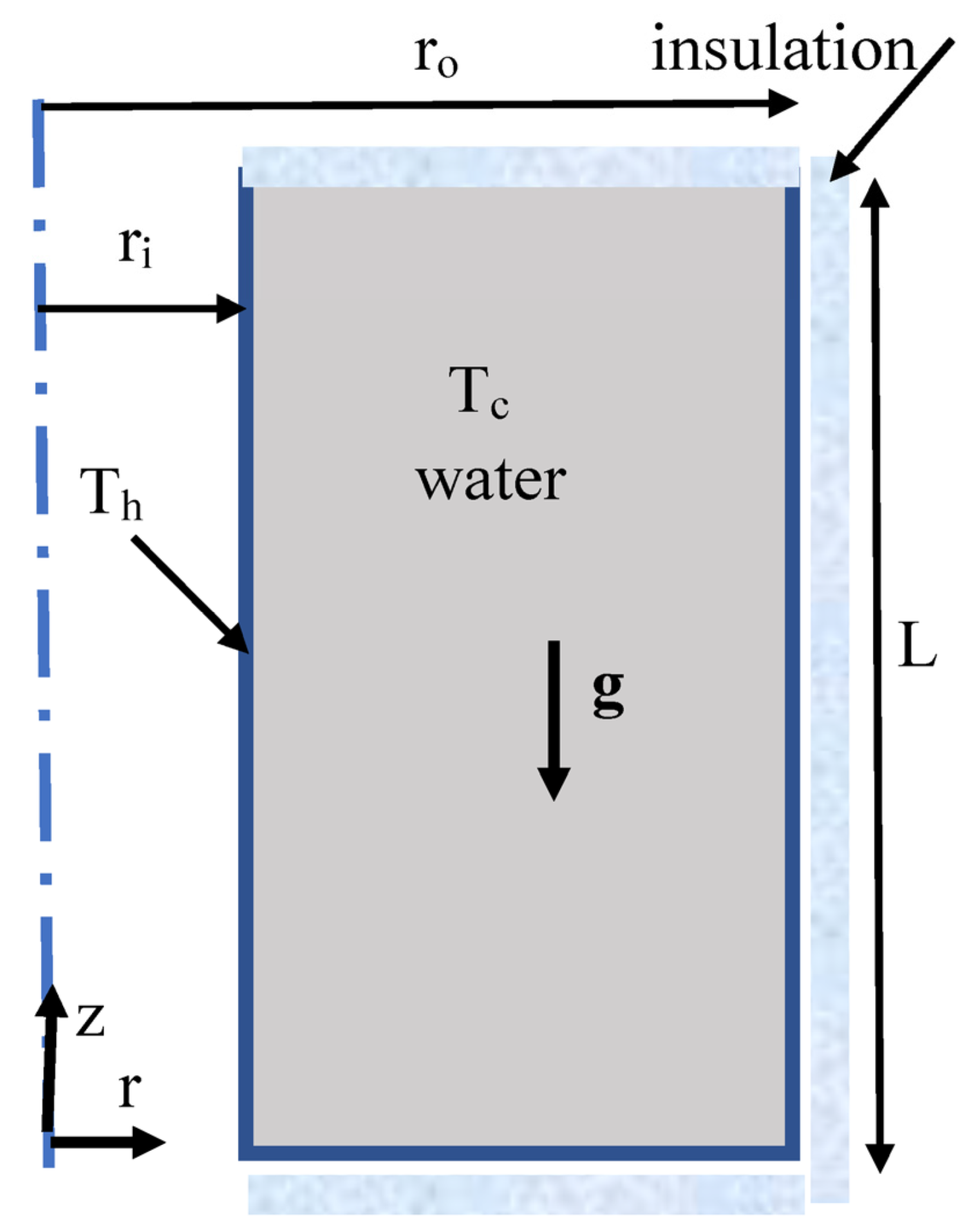
Figure 1 shows the sketch of the problem with coordinate and boundary conditions. The radius aspect ratio R_in = r_i/r_o was set to 0.05, 0.1, and 0.2. The height aspect ratio L* = L/r_o was set to one and two. All the boundaries of the enclosure were assumed thermally insulated, except the inner surface of the annular cylinder, which was suddenly heated to a constant temperature while the water in the encloser was at a cold temperature. The water Prandtl (Pr) number was set to 4.0 (water at a moderate temperature). A range of the rate of heating was explored for Ra = 10⁴ to Ra = 10⁸. The thermophysical properties of the working fluid were assumed constant, except for the change of the density in the buoyancy term, for which the Boussinesq approximation was employed.

Two-dimensional axisymmetric Navier–Stokes equations were solved using the second-order accurate finite-volume method. The governing equations can be written in a nondimensional form.

The continuity equation:

$$\frac{1}{R}\frac{\partial \left(RU\right)}{\partial R}+\frac{\partial V}{\partial Z}=0$$

(1)

The momentum equation:

R-component:

$$\frac{\partial U}{\partial \tau }+U\frac{\partial U}{\partial R}+V\frac{\partial U}{\partial Z}=-\frac{\partial P}{\partial R}+Pr[\frac{1}{R}\frac{\partial }{\partial R}\left(R\frac{\partial U}{\partial R}\right)-\frac{U}{R^2}+\frac{{\partial }^{2}U}{\partial Z^2}]$$

(2)

Z-component:

$$\frac{\partial V}{\partial \tau }+U\frac{\partial V}{\partial R}+U\frac{\partial V}{\partial Z}=-\frac{\partial P}{\partial Z}+Pr\left[\frac{1}{R}\frac{\partial }{\partial R}\left(R\frac{\partial V}{\partial R}\right)+\frac{{\partial }^{2}V}{\partial Z^2}\right]+RaPr\theta$$

(3)

The energy equation:

$$\frac{\partial \theta }{\partial \tau }+U\frac{\partial \theta }{\partial R}+V\frac{\partial \theta }{\partial Z}=\left[\frac{1}{R}\frac{\partial }{\partial R}\left(R\frac{\partial \theta }{\partial R}\right)+\frac{{\partial }^2\theta }{\partial Z^2}\right]$$

(4)

The outer radius of the cylinder was used as a reference length scale. The nondimensional terms were τ = t α/r_o², U = u r_o/α, V = v r_o/α, θ = (T − T_c)/(T_h − T_c), R = r/r_o, where t, V, α, and r_o are time, velocity, thermal diffusivity, and outer radius, respectively.

Equations (1)–(4) are similar to those presented in paper [9], but extended for transient simulation.

The local Nusselt number was based on the heat balance:

$$q=h2\pi r_{i}L\left(T_h-T_c\right)=-k2\pi r_{i}L\frac{\partial T}{\partial r}$$

(5)

$$N{u}_{loc}=\frac{h{r}_i}{k}=-R_{in}\frac{\partial \theta }{\partial R}$$

(6)

where h, k, and R_in represent the convective heat transfer coefficient, thermal conductivity of the fluid, and dimensional inner radius of the cylinder R_in = (r_i/r_o), respectively.

The equilibrium amount of heat stored in the enclosure was:

$$Q=\rho L\pi \left(r_o^2-r_i^2\right)c\left(T_h-T_c\right)$$

(7)

Nondimensionalized:

$$Q^{*}=\frac{Q}{c\rho \pi r_o^2\left(T_h-T_c\right)}=\left(1-R_{in}\right)A$$

(8)

where A = L/r_o.

Also, the equilibrium amount of heat can be calculated as:

$$Q=-{{\displaystyle \int }}_0^t{{\displaystyle \int }}_0^{L}k2\pi r_i\frac{\partial T}{\partial r}{|}_{r_i^{}}dZdt$$

(9)

In the nondimensionalized form:

$$Q^{*}=-2R_{in}{{\displaystyle \int }}_0^{\tau }{{\displaystyle \int }}_0^A\frac{\partial \theta }{\partial R}{|}_{R_{in}}dZd\tau$$

(10)

The nondimensional heat stored in the tank as a function of time was:

$$Q_s=-R_{in}{{\displaystyle \int }}_0^A\frac{\partial \theta }{\partial R}{|}_{R_{in}}dZ$$

(11)

The finite volume method with implicit time discretization scheme was used for solving governing Equations (1)–(4). The computational procedure applied allowed us to obtain the R-velocity and Z-velocity distribution within the tank, as well as temperature distribution within the tank. Those parameters were used to calculate the nondimensional heat stored in the tank as a function of time.

For a fully charged system, Equation (10) should be equal to Equation (8). In the modeling, we used Equation (10) in calculating the amount of energy stored in the system at any time. At the equilibrium state, the prediction of Equation (10) produced the same results of Equation (8). This is an indication that the model correctly predicts the analytical results (Equation (8)). For instance, the dimensionless amount of energy stored for an annular cylinder of R_in = 0.1 and A = 1 was 0.99 (Equation (8)), and the model’s prediction was 0.98994 (Equation (10)).

The numerical predictions results were carefully tested for grid size and time step independence. The grids were clustered near the boundaries. It was found that for Ra up to 10⁶, the grid sizes of 61 × 61 produced independent results for an aspect ratio of one. Figure 2 shows the grid dependency results for Ra = 10⁸ using 81 × 81 and 121 × 121 nonuniform grids. An insignificant difference between the predictions of those grid sizes was noticed. To ensure that the predicted results were grid-independent, 61 × 61 nonuniform grids were used for Ra of 10⁴, 10⁵, and 10⁶. For Ra = 10⁷ and Ra = 10⁸, we used 81 × 81 and 121 × 121, respectively. Also, the time step used in updating the results was tested. For instance, for Ra = 10⁸, the time step was set to 1 × 10⁻⁶. Also, for height aspect ratios more than one, the number of grids increased proportionally along the cylinder height, The average Nusselt number Nu_av was calculated by averaging the local Nusselt number determined based on Equation (6) at the location of r = r_in.

Moreover, the developed model was tested for an annular cylinder heated from the inner surface and cooled from the outer surface with other boundaries that were assumed adiabatic. The model predictions agree well with the analytical solution.

We can claim with confidence that the predicted results are numerically accurate and reliable.

3. Results

In most domestic applications, a water temperature of about 45 °C is used. The Prandtl number of water for the mentioned temperature is about 4.0 [15]. It is well established in the open literature that the rate of heat transfer (Nusselt number) for natural convection in enclosures for fluids of Pr > 1 is not a strong function of Pr. Therefore, keeping Pr at 4.0, the results of the current work should be applicable to the working temperature range.

The typical scenario of fluid flow and heat transfer evolutions are shown in Figure 3 and Figure 4 for streamlines and isotherms, respectively, at different time frames. Figure 3 and Figure 4 are for Ra = 10⁶ and for r_i* = 0.1. At the early stage, τ = 0.01, shown in Figure 3a and Figure 4a, a weak flow circulation took place inside the enclosure. At this stage, the heat transfer was mainly by diffusion. As time increased, the strength of the flow circulation increased (Figure 3b,c.) However, as the time further precedes the strength of the recirculation starts decaying (Figure 3d). Figure 4 shows isotherm (temperature) evolution at different time frames. At early stages (Figure 4a) the thermal plume only evidence at the upper part of the cavity. The convection dominated flow was clear in Figure 4b,c. Also, the flow stratification was evident within those time frames. At a dimensionless time of about 0.5 (Figure 4d), the temperature of the fluid tended toward equilibrium. In other words, the system was fully charged, and the temperature was equal to the hot boundary temperature.

The time series for different Ra numbers compared with the pure heat diffusion process are illustrated in Figure 5, Figure 6 and Figure 7 for R_in = 0.05, 0.1, and 0.2, respectively.

It is clear that as the rate of heating increased, i.e., Ra increased, the fluid in the enclosure reached the thermal equilibrium condition faster compared with a pure diffusion process. The rate of heat transfer (Nusselt number) can be correlated as (

Table 1. Lists the correlation constant a for R_in = 0.1.

Ra	a
104	0.831
105	1.366
106	2.266
107	3.881
108	6.753

):

$$Nu=a{e}^{-2.13a\tau }$$

The coefficient can be correlated as a function of Ra as:

$$a=0.11R{a}^{0.22}$$

(12)

For Ra = 10⁴:

$$Nu=\left(0.287+5.757R\right)e^{-\left(0.518+13.4R\right)\tau }$$

(13)

For Ra = 10⁵, the effect of the radius ratio on Nu can be correlated as:

$$Nu=\left(0.34+10R\right)e^{-\left(0.6+23R\right)\tau }$$

(14)

For Ra = 10⁶:

$$Nu=\left(0.35+19R\right)e^{-\left(0.6+42R\right)\tau }$$

(15)

For Ra = 10⁷:

$$Nu=\left(0.34+35.5R\right)e^{-80R\tau }$$

(16)

For Ra = 10⁸:

$$Nu=\left(0.33+64R\right)e^{-\left(0.34+138R\right)\tau }$$

(17)

Energy Storage

The equilibrium thermodynamic helps us to calculate the amount of energy stored in an enclosure, which is given in dimensional and nondimensional forms in Equations (7) and (8), respectively.

However, the equilibrium thermodynamics does not help us in estimating the time of the process. On the other hand, the heat transfer (nonequilibrium thermodynamics) helps us in estimating the time needed for charging the storage system. Figure 8 shows a typical charging process for an annular tank with a radial aspect ratio of 0.1 and the height aspect ratio of one, for different heating processes (Rayleigh numbers). It is very clear that as the heating rate increased, the charging time decreased due to the enhanced buoyancy force. We estimated that the charging time needed for the heat capacity of the storage system reached 99% of the total heat capacity.

Table 2. Charging time obtained for various Ra values and R_in = 0.1.

Rayleigh Number, Ra	Charging Time	The Charging Time Relative to Diffusion Charging Time
Diffusion	3.769	1
104	3.260	0.865
105	2.392	0.635
106	1.505	0.399
107	0.903	0.239
108	0.518	0.137

summarizes the computationally predicted results for a range of investigated Ra and the aspect ratio of one. The convection results are compared with a pure diffusion process, where the flow assumed to be stagnant. For instance, even for low Ra (Ra = 10⁶), the time needed to charge the enclosure was about 40% of the time needed by the diffusion process.

The above data can be correlated as:

$$\tau =22R{a}^{-0.2}$$

(18)

Some limitations of the model exist. For example, in case of solar air heating, the air temperature decreases along the pipe height L and air inlet temperature changes with time. Therefore, the coupled boundary conditions between the air flowing in the pipe and tank domain should be applied to the model in more detail to conjugate the heat transfer problem [16].

4. Conclusions

Computational fluid dynamics (CFD) was used to simulate unsteady state natural convection in annular cylinders for a range of Ra up to 10⁸ and for radius aspect ratios of 0.05, 0.1, and 0.2. Streamlines, isotherms, and rate of heat transfer (Nusslt number) as a function of time and Rayleigh number were analyzed and reported. The control volume method was employed for discretizing two-dimensional and axisymmetric natural convection problem. The explicit method was used for discretizing time dependent terms of governing equations (continuity, momentum, and energy). The physics of fluid flow and heat transfer in annular heat storage tanks were explained. A few correlations were developed for the rate of heat transfer, which is crucial for designing and operating the thermal storage tanks. The correlations were valid for numbers from 10⁴ to 10⁸ and allowed us to calculate the Nusselt number changes in time of tank charging. Furthermore, the charging period was analyzed and correlated as a function of Ra number. The work has importance in designing hot water storage tanks for solar energy and other domestic or industrial applications and allows the prediction of the charging time of the tank.