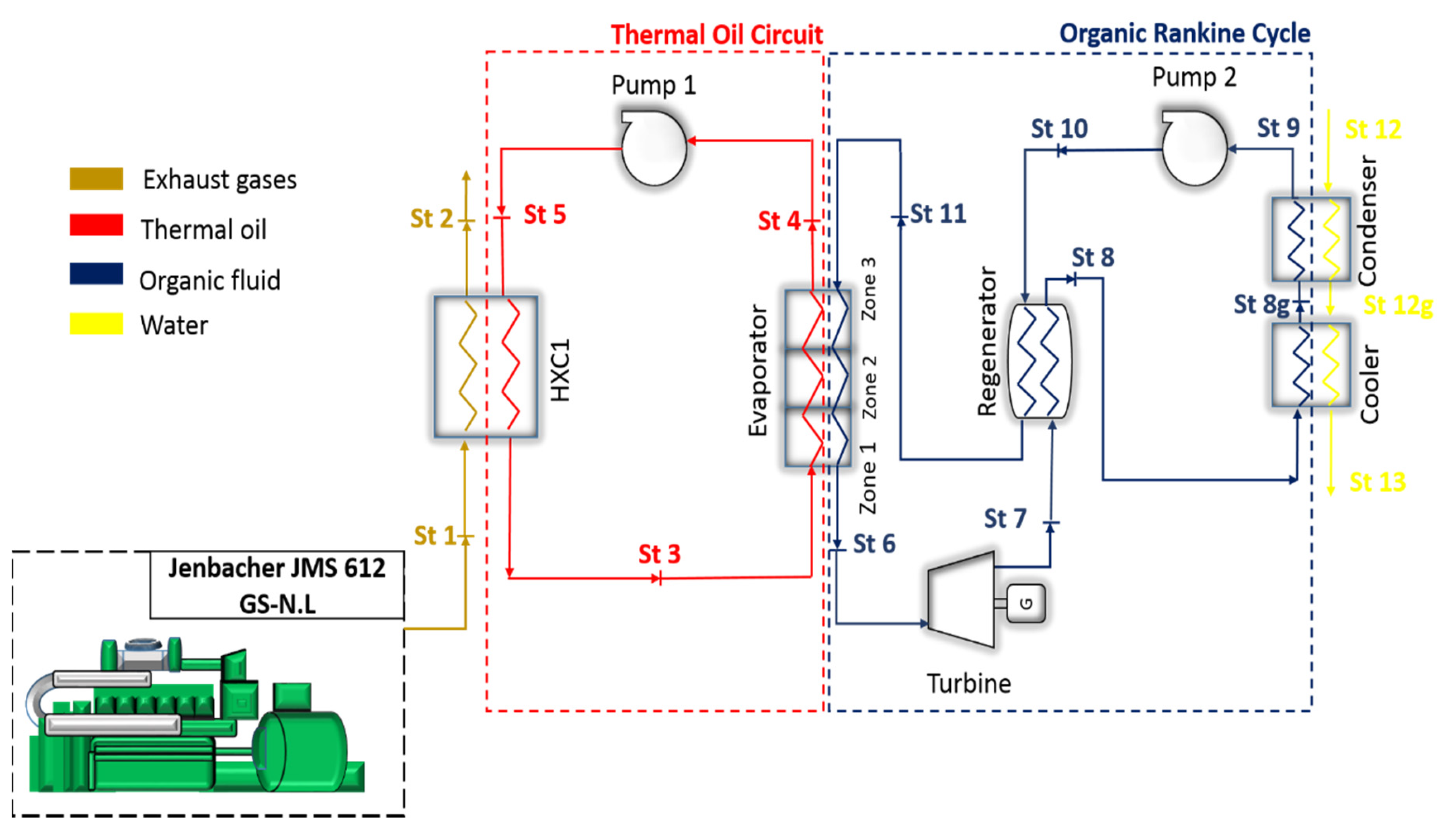
1. Introduction
In the past few years, developed countries have shown interest in the possibility of reducing carbon dioxide emissions, which has been brought about by the rational use of energy, and the drive to decrease the energy consumption generated through fossil fuels [
1]. The Climate Change Convention in 2009 set the limit to 2 °C growth in the global average surface temperature, and based on the Intergovernmental Panel on Climate Change, warming of more than two degrees would be catastrophic for both humans and nature [
2].
The main factor responsible for the enhancement in surface global average temperature is the high atmospheric concentration of Greenhouse Gases (GHGs). At the current growth rate of these gases, there is at least a 77% chance that the growth in average global temperature will exceed 2 °C by 2035. From the gases cited in the Kyoto Protocol as GHGs, carbon dioxide (CO
2) accounts for three quarters, and more than 90% of it originates from the energy transformations that occur in means of transport, industry, and residences. However, today there is no viable technology capable of absorbing CO
2 emissions [
3].
The only way to limit it is through the efficient use of energy in the energy generation systems, and the increase of the green mass of the planet [
4]. Two different methodologies have been proposed to promote rational energy use through the WHRS to increase the energy efficiency of combustion engine systems [
5].
Since a century ago, when the first gasoline engines were produced, the thermal efficiency of the internal combustion engine (ICE) have reached their maximum values, and the energy is still not fully used, because around 65% is a loss to the atmosphere using heat [
6]. Therefore, increasing engine efficiency through WHRSs will lead to a reduction of carbon dioxide emissions, which would reduce the negative impact on the environment through bottoming cycles based on the organic Rankine cycle (ORC) [
7].
Gas engines for power generation have become a high impact alternative for global energy decentralization, which is expected to have an even more significant presence in the industry, due to their high power densities, high efficiencies and low emissions, as well as a high degree of availability [
8].
Natural gas is a successful fuel in replacing conventional liquid fuels such as diesel and gasoline worldwide, since it can be extracted from large fossil fuel reserves [
9]. Thus, natural gas engines are an attractive option to current diesel engine technology in industrial applications due to the price of the fuel, and a growing gas distribution network worldwide [
10]. However, the operating and design conditions of the integrated engine system with a WHRS configuration must be determined to allow the adoption of these systems in practical applications at competitive costs in respect to renewable energies [
11].
The use of an ORC system has several advantages, such as high reliability and easy maintenance, making it a cost-effective system for transforming waste heat from various sources into useful energy [
11]. Among the energy sources that have been studied for WHRS based on the ORC system, are the solar radiation [
12], geothermal energy [
13], the biomass combustion [
14], and the energy source evaluated in this research, which is the waste heat of industrial engines [
15].
The ORC uses an organic working fluid such as hydrocarbons and refrigerants, which have better performance than water, allowing to reduce the heat source temperature [
16]. However, due to the high contamination rates, environmental protection has been chosen as the main criterion, and numerous investigations report the negative impact on the atmosphere of the chlorofluorocarbon (CFC), which makes the selection of the working fluid for the ORC a complex task [
17]. Therefore, different methods have been established in ICE to achieve greater energy efficiency with less environmental impact such as waste to energy technologies based on the ORC cycle operating with environmentally friendly fluids [
18]. Thus, better efficiency in the Jenbacher gas engine JMS 612 GS-N.L, can be achieved by waste heat recovery using the ORC [
19]. However, this arrangement requires a secondary coupling circuit for indirect evaporation, in which the waste heat is used to heat the organic fluid indirectly by first transferring the heat to a thermal oil, which is then used to evaporate the organic fluid.
Additionally, it has been very helpful to introduce working fluids with a lower rate of pollution, which is measured with a low Global Warming Potential (GWP) [
20]. Therefore, Toffolo et al. [
21] oriented its research towards the economic profitability that can be obtained through the choice of an organic working fluid and the adjustment of operational parameters in the ORC system. In this study, the selection of the cycle configuration was developed attending to several criteria together: an original thermodynamic optimization technique of the process, and the design factors that examine all achievable configurations, the design selections about the best values of the objective function, the economic modeling procedure proved on valid cost data and the contemplation of out-of-design behavior. Then, the use of the regenerative organic Rankine cycle (RORC) increases cycle efficiency by 9.29% over the simple ORC cycle [
22]. In environmental aspects, the use and choice of the organic fluid are limited due to the environmental impact involved. For this reason, Suarez et al. [
23] evaluated the reduction of emissions in tons that can be generated by the working fluid in one year of operation, which obtained that benzene delivers the greatest reduction of emissions with a value of 849 tons after one year of operation, followed by heptane with 809 tons of carbon dioxide. The other important aspect is to explore about fluids that can work with the high temperatures of engine exhaust gases and offer good thermal performance. Therefore, the residual thermal energy availability must be considered for organic fluid selection [
24]. Thus, toluene is a high critical temperature or high boiling point fluid that is used in heat sources with temperatures around 300 °C, higher than the refrigerants that normally work at low temperatures, below 200 °C, such as R227ea, R123, R245FA and HFE7000 [
16]. In addition, the toluene was used in an ORC system with a recuperator, which improves operative performance by getting a power of 146.45 kW, and a reduction in s fuel feeding of 7.67% at 1482 rpm [
25].
On the other hand, Zare V. [
26] evaluated the economic behavior of different ORC configurations, where the ORC presents better results. The economic analysis was proposed as a methodology for designing a cost-effective WHRS to determine total investment capital, maintenance, and operating costs. When the equipment costs are not determined, but nominal details are accessible, they could be computed using a percentage of the total equipment cost. Bejan et al. [
27], Smith [
28], and Towler [
29] propose a correlation and cost orientation for many kinds of equipment.
To increase the productivity of the WHRS based on ORC, normally, a regenerator is added, which achieves a 5% increase in efficiency, thus leading to an increase in power output [
30]. Similarly, to increase performance, the components with the greatest irreversibilities in the system are identified using traditional exergetic analysis. However, this analysis does not allow to determine opportunities for improvements in the system [
31]. Thus, the implementation of the advanced exergetic analysis in these cases allows obtaining opportunities for improvement in a specific component or the interaction of this one on the system, providing data on the exergy destruction portion that can be avoided [
32].
Therefore, the main objective of this study is to determine the components with the greatest irreversibility in a WHRS based on a RORC, through the use of three organic working fluids: acetone, heptane, and toluene. The components that have the greatest opportunity for improvement are identified through advanced exergetic analysis, and changes in capital investment cost rates are identified by varying the pressure ratio, condensing temperature, and evaporator pinch point. Thus, this study is based on a specific gas engine application widely used worldwide so that realistic results of the economic viability of the WHRS are obtained. Furthermore, the results are expected to contribute useful information applicable to other engines to achieve economically viable solutions.
4. Conclusions
Another contribution is the methodology suggested for the best design of secondary circuits of ORC systems for WHRS with indirect evaporation, which allows the necessary energy to be supplied to the organic fluid and does not affect the admissible back pressure of the motor. This methodology can be useful to any type of WHRS with indirect evaporation, and is more appropriate for situations where there are restrictions on the back pressure of the heat source with medium and high temperatures, just in cases where ORC equipment has not been extensively applied commercially.
The advanced exergetic analysis allowed to determine opportunities for improvement in the components with the greatest irreversibilities of the waste heat recovery systems based on RORC the system, focusing only on those fractions of exogenous or endogenous exergy destruction that can be avoided. An economic investigation has been conducted to understand the economic dimension and financial viability of the equipment acquisition project. Therefore, such economic evaluation and cost resolution achieve precision in a range of magnitude under a study or previous estimates.
An additional contribution of the present work in the area of WHRS from exhaust- gases in high-powered natural gas engines, is the identification of the design and operation variables that contribute most to the economic viability of the integrated system, which allows focusing future efforts that lead to the application of these solutions in industrial environments.
For the operating states considered in the study, the results showed higher exergy destruction when using toluene and acetone as working fluid, reaching around 70 kW for the evaporator and heat exchanger. For the heptane, the maximum exergy destruction was shown for the evaporator and regenerator with a value of 53 kW. The breakdown of exergy increased opportunities for improvement in Pump 2 of an endogenous nature with a percentage of about 80% by using acetone as a working fluid. Similarly, greater opportunities for improvement were obtained in the turbine with a rate of 77% using heptane and through the use of toluene with a percentage close to 70% for the endogenous turbine, 34%, and 42% for the regenerator and exogenous Pump 2.
The research allowed a variation of the system operation parameters, condensation temperature, pressure ratio, and evaporator pinch point in order to find the adequate fluid and operational values that provide a cost reduction in the system. In such a way that it was achieved for the acetone lower acquisition costs at a pressure ratio of 8, a condensation temperature of 65 °C and a pinch point of the evaporator of 90. Similarly, for heptane, lower costs were achieved at a 70 °C condensation temperature, a pressure ratio of 9, and an evaporator pinch point of 90 °C.
It is necessary to study in detail the heat exchange equipment for the thermal process of the plant, in search of deficiencies and areas of high heat transfer to the environment, or irreversibilities, which would imply an increase in the power recovered. On the other hand, this study must be complemented with a thermo-economic analysis to evaluate in financial terms implementations of new equipment or changes in the process in order to achieve efficient use of the energy and resources available in the exhaust gases of these type of natural gas generation engines.