Comprehensive Analysis of a High-Power Density Phase-Shift Full Bridge Converter Highlighting the Effects of the Parasitic Capacitances ^†

Abstract

A phase-shift full bridge converter is analyzed in detail in continuous conduction mode for one switching cycle for both the leading and lagging legs of the primary bridge. The objective of the study is to determine how the stray capacitance of the transformer, and the capacitances of the diodes in the bridge rectifier affect the converter functionality. Starting from some experimental results, Laplace equivalent circuit models and describing equations are derived for each significant time interval during the switching cycle and are validated through simulations and experimental measurements. The resulting equations are of great interest in the high-power density domain because they can be used to design a clamping circuit for the output rectifier bridge accurately.

1. Introduction

The phase-shift full bridge converter (PSFB) uses parasitic circuits elements, such as capacitances of the semiconductor devices and leakage inductances of the power transformer to provide zero voltage switching (ZVS) without any other active components. During the dead time between switching the transistors of the same leg, the converter can achieve zero voltage ZVS using the energies stored in magnetic components (mainly the power transformer leakage and magnetizing inductance) and the output capacitances of the primary bridge switches. Dead time is usually calculated using a set of predefined conditions, which results in the loss of zero voltage switching condition (ZVS) at light loads [1]. Since the zero voltage switching determines the efficiency of the converter and considering that it depends on the dead time, the relationship between the available energies, the values of the magnetic components and the parasitic capacitances of the semiconductor devices can be determined by analyzing the equivalent circuit models during switching. The values of the magnetic components, the snubbers and the capacitances of the semiconductor devices can be chosen based on this analysis.

When a PSFB is designed for high output voltage, the effect of the stray capacitance of the power transformer together with the parasitic capacitance of the secondary rectifier bridge has a significant effect on its operation [2]. This type of converters are intensely used in many of industrial areas [3], for example: Battery chargers for plug-in-electric vehicles [4,5,6], photovoltaic (PV) power systems (charging batteries or boosting the PV voltage to higher levels) [4], fuel-cell stacks, wind turbines, DC microgrid applications, lighting, etc.

The PSFB topology is represented in Figure 1. As it can be seen, the converter has three modules: The full bridge inverter, the high frequency transformer, and the output rectifier and filter. The converter has a simple topology which can be easily controlled using fixed frequency. Because the description and functional analysis of this type of converter are present in the literature [6,7], in this paper, the effect of the parasitic elements will be emphasized. The main advantages of this topology are: ZVS in a wide load range, simple control methods, low power density, and high efficiency [8].

In most cases, high insulation requirements are needed between the primary and the secondary windings of the power transformer to satisfy the safety standards for this converter. This leads to large leakage inductance in primary and secondary sides. A large number of secondary turns required for high step-up and high voltage applications leads to an increased capacitance between the windings of the transformer, significantly deteriorating the performance of the converter [3,9]. The parallel capacitance of the secondary rectifier diodes adds to the stray capacitance of the transformer further increasing its effects. Another drawback of the converter is the dependency of the ZVS on the load conditions. The loss of ZVS causes not only a decrease in efficiency, but also results in high electromagnetic interference at light load. There are methods to increase the ZVS range by adapting the dead-time based on load condition [10,11]. Moreover, new control methods where used to increase the ZVS at light loads [12,13,14,15]. Modification of the power topology was proposed to extend the ZVS range in References [16,17,18,19]. By properly analyzing the switching behavior of the converter, the ZVS range can be extended without altering the control or the topology of the converter to some extent.

Many studies concentrate on the parasitic elements and how can they degrade the efficiency of the converter. None of these papers considers the stray capacitance of the transformer or the capacitance of the output rectifier. The parasitic elements of the high voltage transformer are analyzed in different papers, but only in predetermined conditions: For example, in Reference [3] only in discontinuous conduction mode (DCM) and for a PSFB converter with pure capacitive filter; in Reference [9] the effect of the transformer capacitance only on the leading leg from current drop perspective; in References [20,21] a discussion on voltage oscillations across secondary diodes in a PSFB converter, but not analyzing in every detail a complete switching interval.

The design of high voltage PSFB converter has many degrees of freedom which complicates the selection of the components [22]. Finding an optimized solution (highest power density, efficiency or lower cost) requires comprehensive analytical models and equations that account for the most harmful parasitic elements. This work concentrates on a detailed analysis of the PSFB converter that accounts parasitic influences, namely: Stray capacitance of the transformer secondary winding and the capacitances of the diodes in the bridge rectifier. The analysis is performed in continuous conduction mode for both the leading and lagging leg of the primary bridge for a complete switching cycle.

2. Motivation

Most articles nowadays start from method explanation and simulations followed by experimental results for validation. In this paper, a different approach is proposed. As presented in Figure 2, one can see the differences between a simulation-based analysis and the waveforms obtained during experimental measurement. Starting from these differences, a mathematical analysis using Laplace equivalent models, together with Spice simulations for the different working time intervals are proposed for better understanding the influence of the parasitic capacitance on the phase shift converter [23]. The Laplace equivalent models emphasize the effects of the parasitic capacitance and provide the designer with an in-depth understanding of how to compensate them in order to provide a better design. The simulations were carried out to validate the theoretical analysis and provide a faster and more intuitive tool for the designers. A complete switching cycle of the converter was considered for the analysis. For an in-depth analysis, this cycle was divided into seven time intervals to better highlight the effect of the parasitic capacitance. For each time interval, Laplace equivalent models are provided in the paper followed by a simulation specific built for each situation. In the simulations, the component values used are the same as for the built experimental model. The results obtained through simulations are compared with the ones obtained during experiments. Comparing the numerical values, it can be seen that the mathematically equivalent model and simulations are validated. In some cases, the small inaccuracies that appear are due to other parasitic elements that were not taken into account intentionally to have a simple equivalent model that can be used with ease. As presented in the paper, the equations obtained can be used for instance as a basis for the design of an active snubber circuit that will increase the efficiency and ease the thermal enclosure design. Choosing the correct components through a minimum number of steps is every designer’s goal.

The experimental model from which the analysis started was used to provide data to check the accuracy of the Laplace equivalent models and simulations.

The phase shift converter was designed for the following specifications: The input voltage of the converter reflected in the secondary is V_in = 250 V, and the output voltage is V_out = 173 V. The primary leakage inductance is L_{r_p} = 5 µH, the transformer ratio is n = 0.6, and the output inductor is L_out = 280 µH.

The secondary peak voltage and the oscillations caused by L_r = 14 µH inductance (the sum of the leakage inductances referred to the secondary that will be explained later) and C_s capacitance—total stray capacitance of the transformer and rectifier capacitances (will be demonstrated later) are presented in Figure 3.

As it can be seen from secondary rectified voltage, the frequency of oscillations is f_r = 4.167 MHz. Thus, C_s capacitance can be estimated as:

$$C_s=\frac{1}{4{\pi }^2{f}_r^2{L}_r}=\frac{1}{4·{\pi }^2·4.167·{10}^6 \mathrm{Hz}·14 \mathsf{\mu }\mathrm{H}}\cong 100 \mathrm{pF}$$

(1)

where L_r =14 µH.

Also, the discharge time interval of C_r (the switches equivalent output capacitance equal to 767 pF) can be estimated as:

$$\mathsf{\Delta }t=\frac{1}{\sqrt{L_r·C_r}}\arcsin \left(\frac{V_{in}}{I_0·\sqrt{L_r/C_r}}\right)=\frac{1}{\sqrt{14 \mathsf{\mu }\mathrm{H}·767 \mathrm{pF}}}·\arcsin \left(\frac{250 \mathrm{V}}{2.3A·\sqrt{\frac{14 \mathsf{\mu }\mathrm{H}}{767 \mathrm{pF}}}}\right)\cong 97 \mathrm{ns}$$

(2)

where I_o = 2.3 A is the output current. Equation (2) will be later demonstrated in the article.

The C_r capacitor is fully charged in about 97 ns as can be observed in Figure 4:

Although simulation tools can always be used for simulating the switching converters in a much easier way, the circuit parameters remain in non-closed form, and it is difficult to tell the impact of a certain design parameter on the results. Moreover, experiments often take time, and additional delay will be expected if changes in magnetic components are needed. On the other hand, a mathematical model can give very intuitive information, which can always help the designer to (1) fully understand the operation of the switching states; (2) reduce the number of iterations for optimization in experiments; (3) find worst case/corner case for testing; (4) analyze component tolerance impacts, etc.

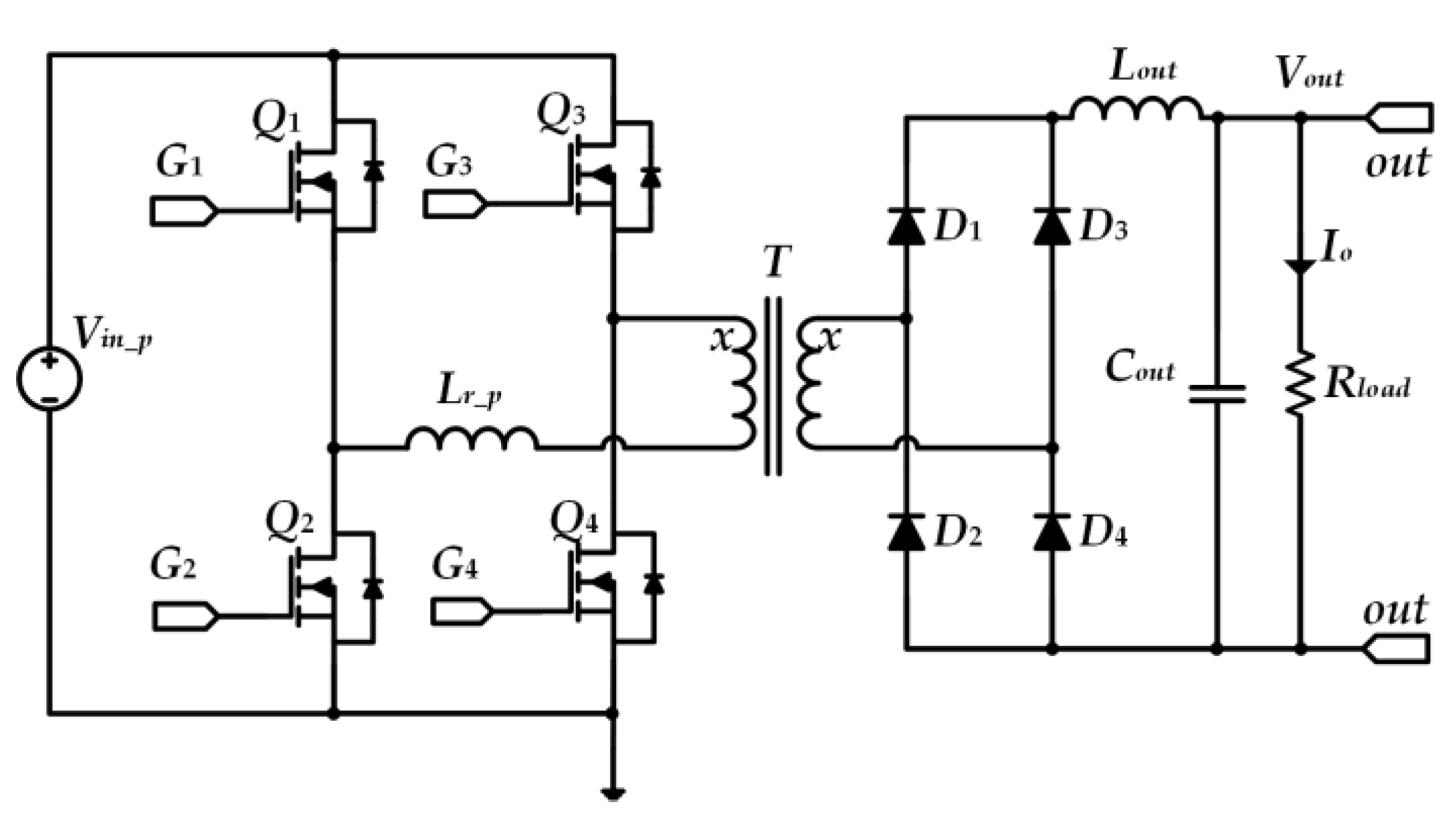
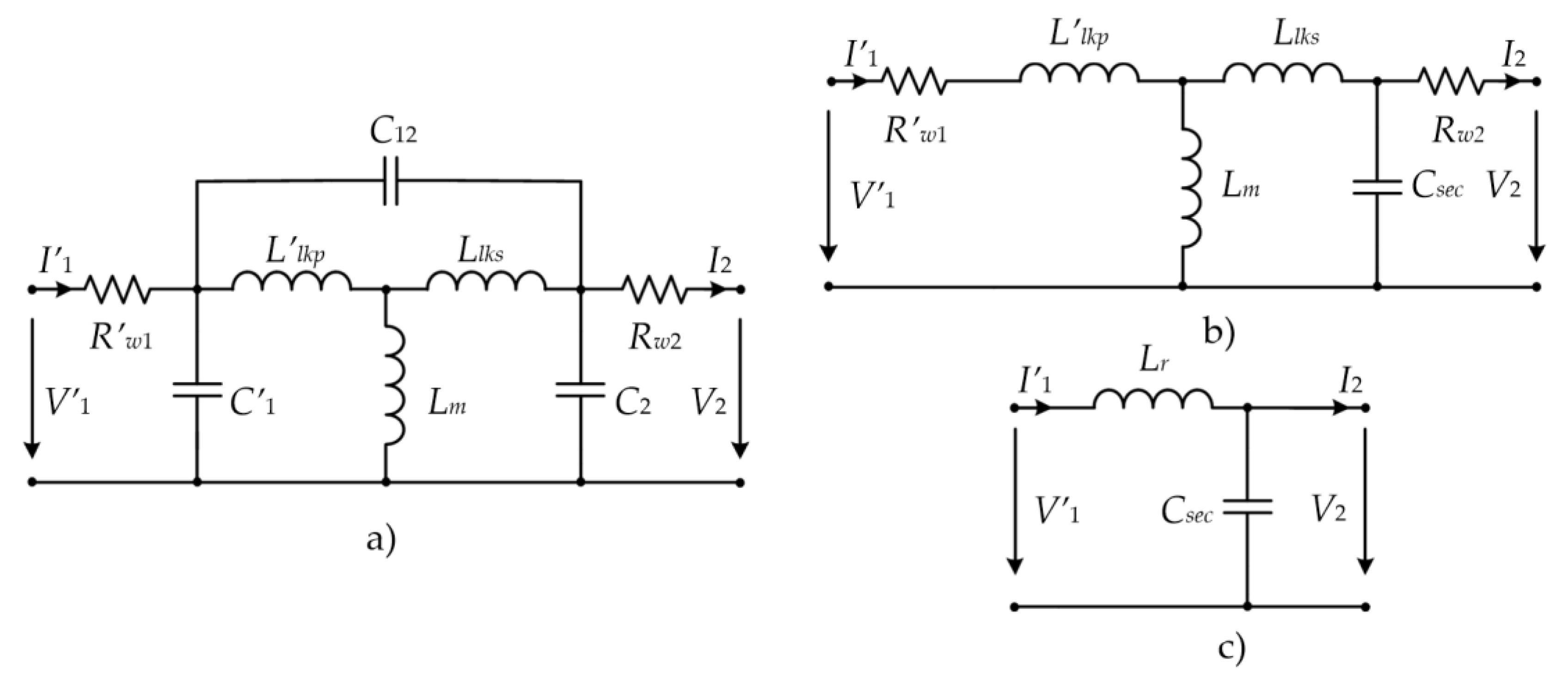
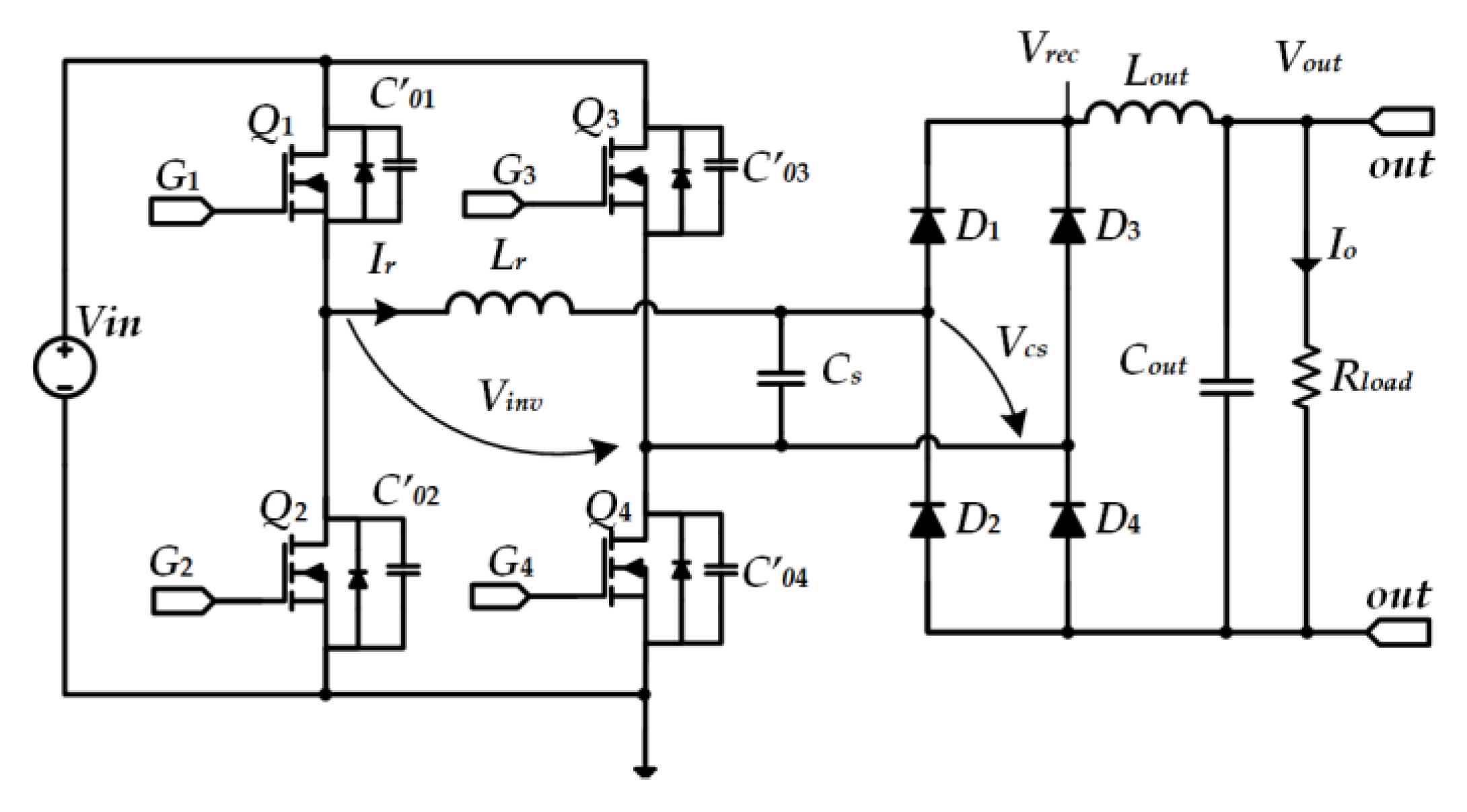
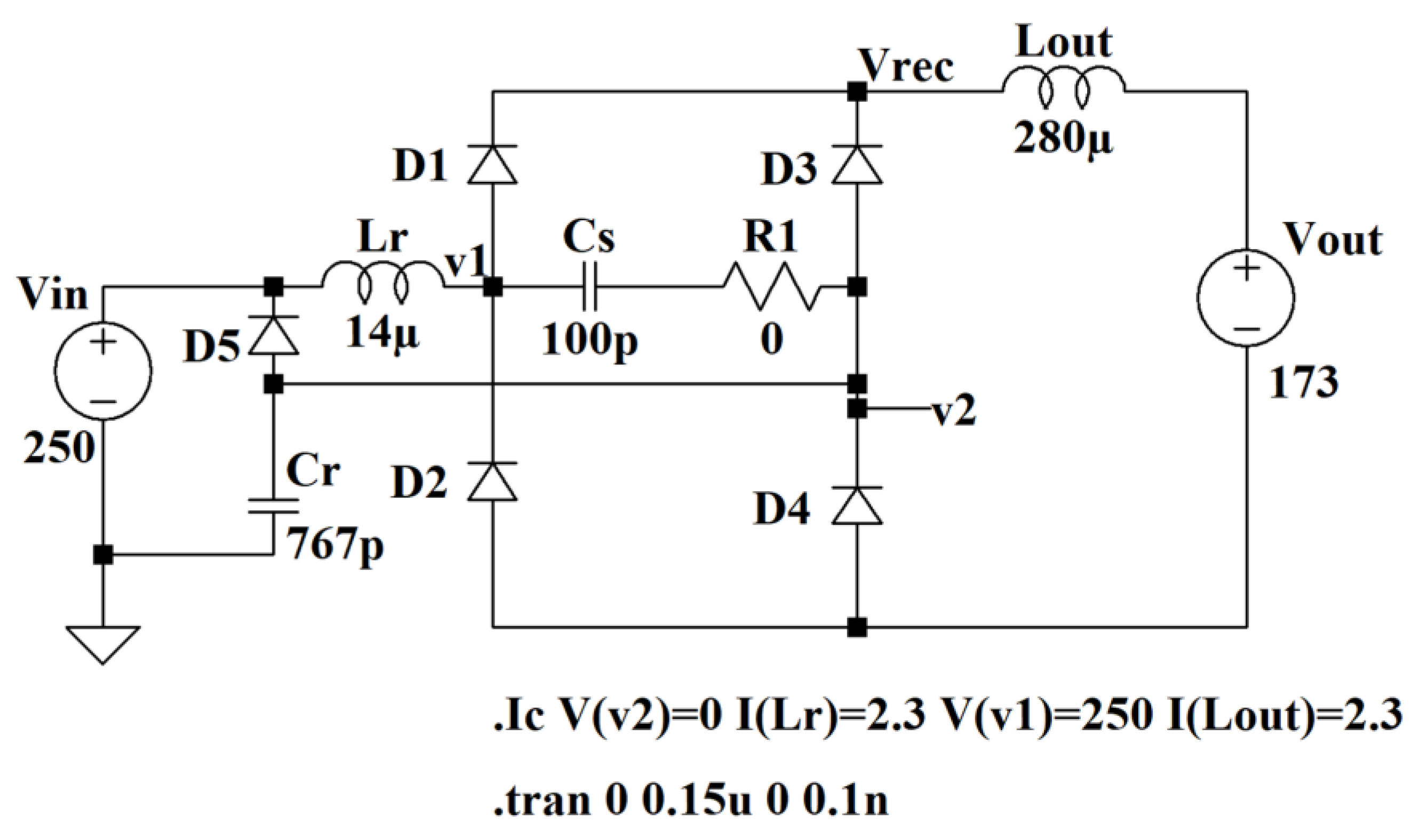
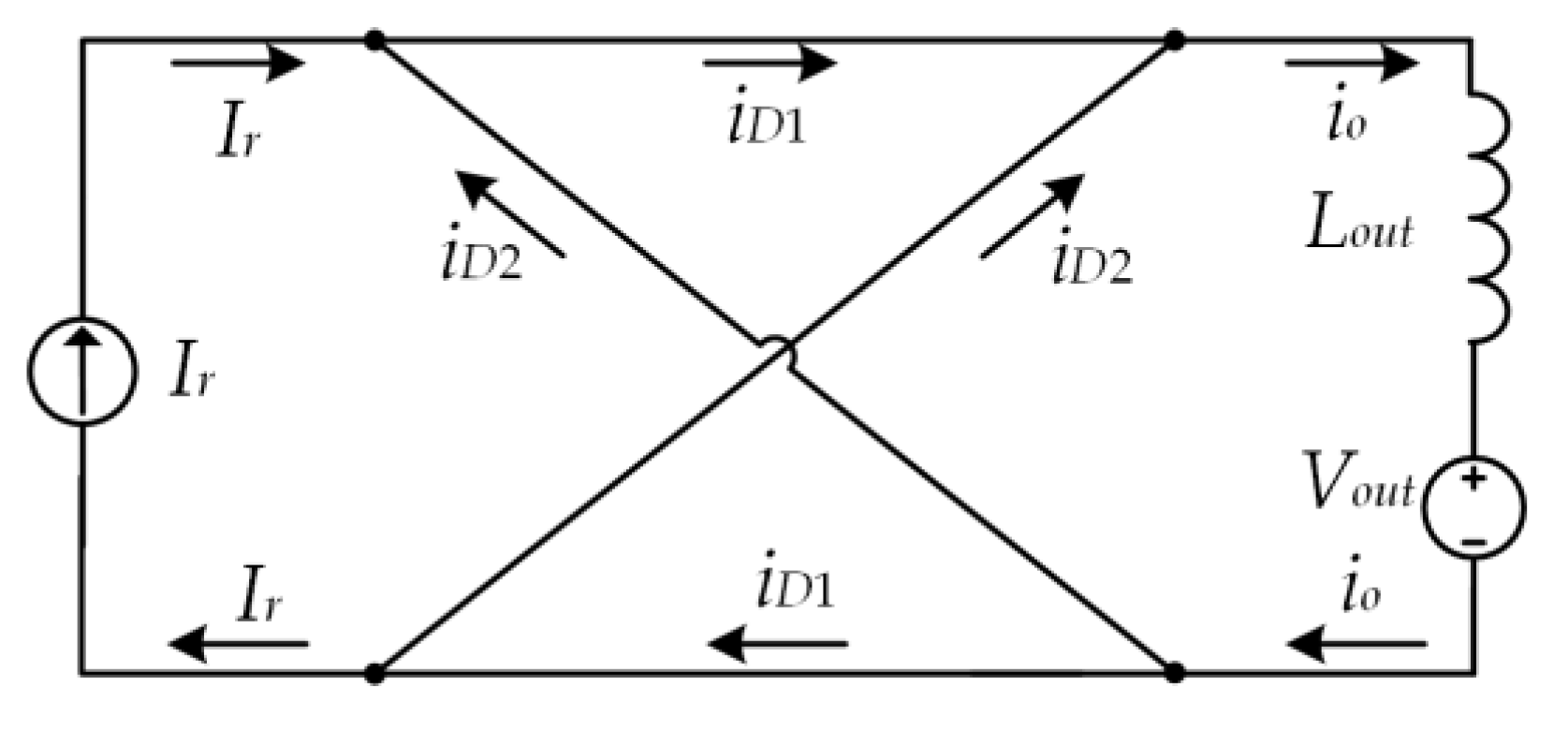
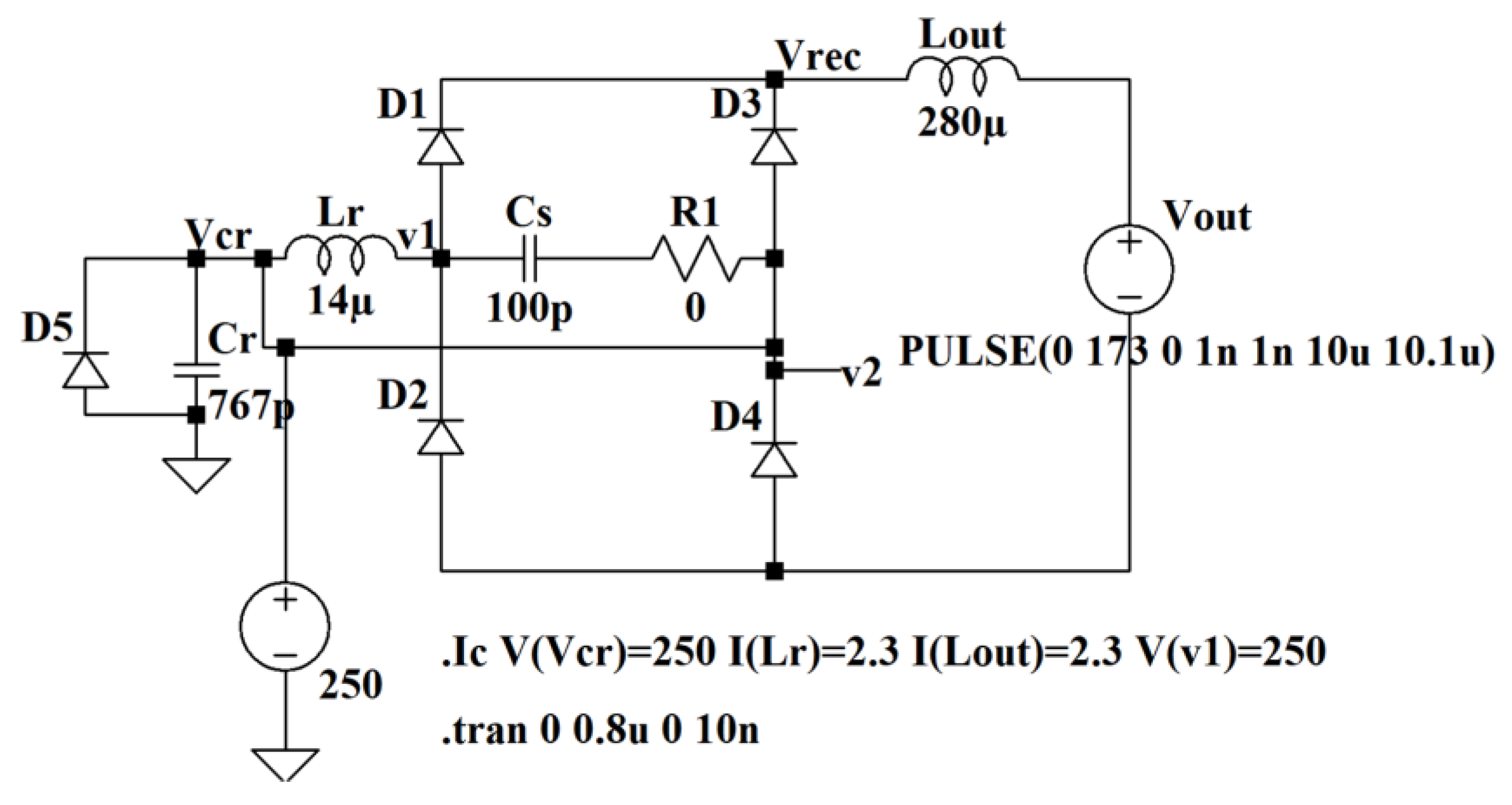
3. The Model of the Converter

In Figure 5a, an equivalent electric circuit of a high frequency transformer is presented, with all the elements referred to the secondary side. R’_w1 and R_w2 are the resistances and L’_lkp, and L_lks are the leakage inductances of the primary and secondary windings, L_m is the magnetizing inductance of the secondary, C’₁ and C₂ are the self-capacitances of the primary and secondary windings, C₁₂ the mutual capacitance between the windings and V’₁, V₂ are the voltages of the primary and secondary sides. For the analyzed converter, the primary and the secondary inductances of the transformer are small compared to the magnetizing inductance. The voltage drop across these inductances is small; thus, the stray parasitic capacitances can be modeled by a single capacitor, connected as in Figure 5b equal to: C_sec ≈ C’₁ + C₂ with C₁₂ neglected.

If the effects of the winding resistances and of the magnetizing inductance are neglected, then a simplified transformer model is obtained, Figure 5c, where L_r is the sum of the leakage inductances.

Due to design considerations, the transformer ratio is equal to 0.6, resulting in the equivalent circuit of the PSFB converter, Figure 6, where G₁, G₂, G₃ and G₄ are the gate drive signals, V_cs is the voltage on the stray capacitance, I_r is the current through the L_r inductance, and V_rec is the secondary rectified voltage. The rectifier capacitances are also included in the total stray capacitance of the transformer C_s = C_sec + C_DIODES. When I_o flows through D₁, D₄ C_DIODES = C_D2 + C_D3 and vice-versa when D₂ and D₃ conduct.

Whenever possible, the parasitic elements (leakage inductances of the transformer associated with semiconductor parasitic capacitances) can be used in an advantageous way to facilitate the resonant transition and to achieve ZVS. In Figure 1 the resonant inductor is depicted by L_{r_p} that can be an external inductor added to the schematic but in this case, the leakage inductances of the transformer will be used as the resonant inductor, L_r, to achieve ZVS: $L_r=L{\prime }_{lkp}+L_{lks}$. C’_o1, C’_o2, C’_o3, C’_o4 are the output capacitances of the switches and I_r and V_inv are values referred to the secondary.

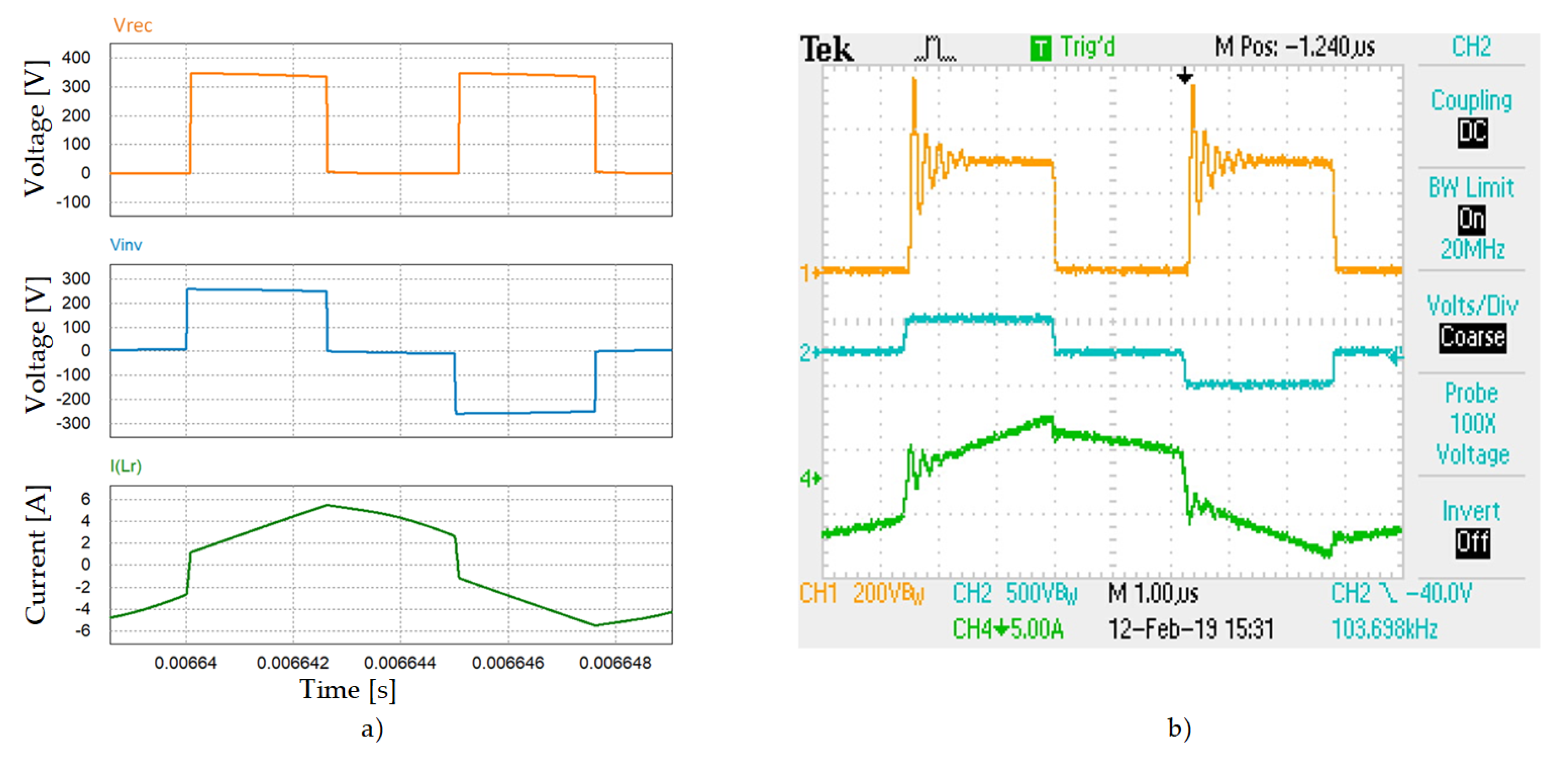
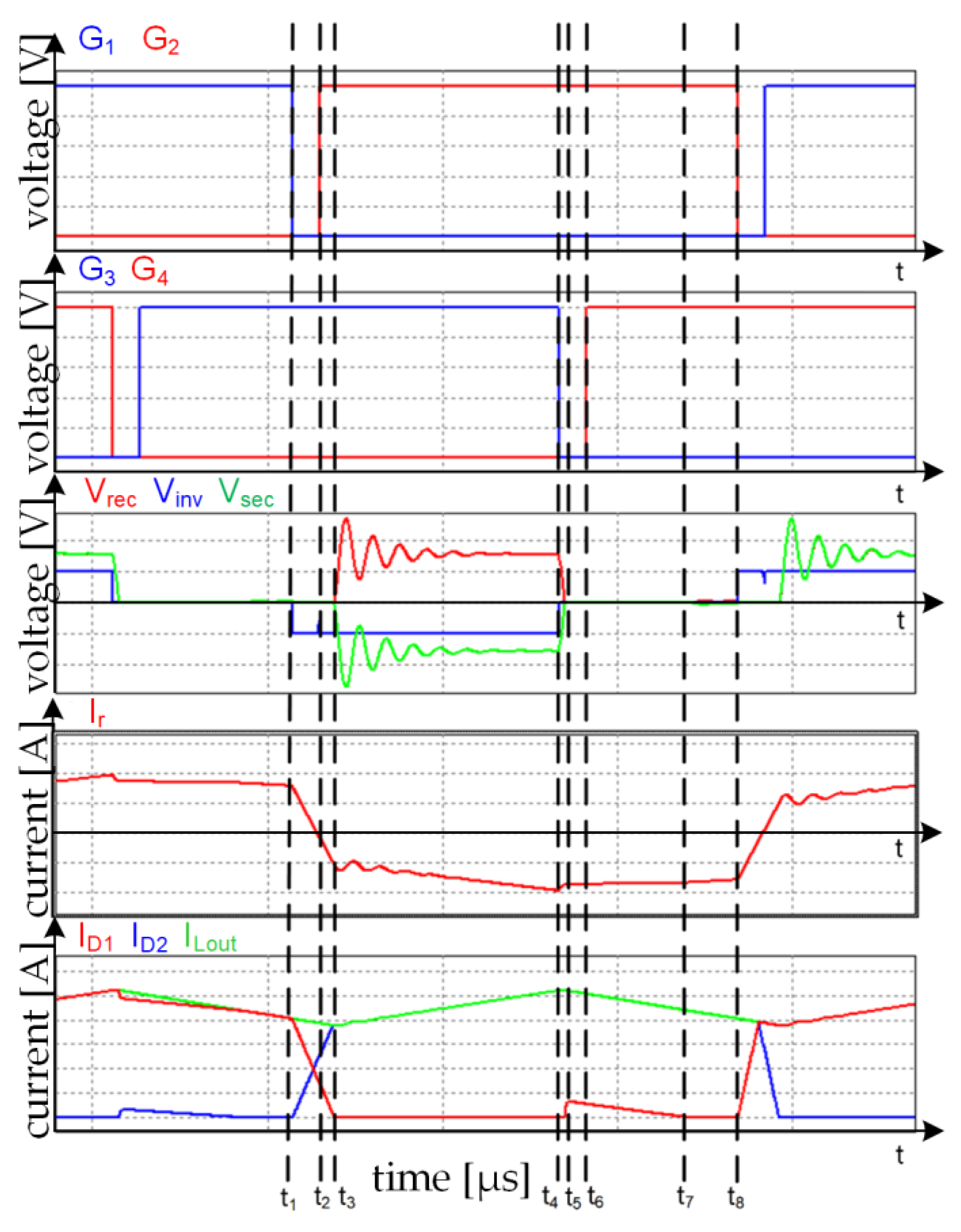
4. Converter Operation

Figure 7 illustrates the operation waveforms of the converter.

4.1. Operation during [t₁-t₃]

In the first analysis, the influence of the capacitance C_s is neglected. Before t₁, transistors Q₁ and Q₃ together with diode D₁ and D₄ are ON. In the same time, the output capacitor C’_o2 of the Q₂ transistor starts discharging. The output current I_o flows through D₁, D₄, D₃ and D₂, so that the following relationships can be written.

$$\{\begin{array}{l}{i}_{D1}=i_{D4}\\ i_{D2}=i_{D3}\\ i_{D1}+i_{D2}=I_o\end{array}$$

(3)

During t₁-t₂, if there is enough energy stored in L_r, C’_o2 capacitor is completely discharged, and C’_o1 is charged to V_in. Thus, at t₂, the body diode of Q₂ turns ON, allowing ZVS turn ON for Q₂. Considering C_r = C’_o1 + C’_o2 the equivalent output capacitance of Q₁ and Q₂ transistors and neglecting the secondary parasitic capacitance C_s, the Laplace equivalent circuit corresponding to this time interval is presented in Figure 8.

The equation describing the circuit in Figure 8 is:

$$I_r(s)\left(s{L}_r+\frac{1}{s{C}_r}\right)=L_r{I}_o$$

(4)

If the angular frequency is ${\omega }_r=\frac{1}{\sqrt{L_r{C}_r}}$ then the current through C_r is:

$$I_r(s)=I_o\frac{s}{s^2+{\omega }_r^2}$$

(5)

Applying the Laplace inverse transform to (5) and shifting to t₁, results that C_r is discharged with the current:

$$i_r\left(t\right)=I_o\cos \left({\omega }_r\left(t-t_1\right)\right)$$

(6)

The C_r capacitor voltage is:

$$v_{cr}(t)=V_{in}-\frac{1}{C_r}{\displaystyle \underset{t_1}{\overset{t}{\int }}{I}_0\cos \left({\omega }_r\left(t-t_1\right)\right)dt}=V_{in}-\frac{I_0}{{\omega }_r{C}_r}\sin \left({\omega }_r\left(t-t_1\right)\right)$$

(7)

From (7) results that the completely discharge time interval of C_r can be estimated as:

$$\mathsf{\Delta }t=\frac{1}{{\omega }_r}\arcsin \left(\frac{V_{in}}{I_o\sqrt{L_r/C_r}}\right)$$

(8)

For the values used in the simulation presented in Figure 9: L_r = 14 µH, V_in = 250 V, I_o = 2.3 A, using (8) Δt will be 97 ns. The same result for the time needed to discharge C_r is obtained in simulation, Figure 10. At t₁ all the diodes (D₁, D₂, D₃, D₄) will start to conduct immediately.

If one considers the influence of the C_s secondary parasitic capacitance, which is assumed to be charged at t₁, the Laplace equivalent schematic of the converter is presented in Figure 11. It will be later demonstrated that C_s is charged (for the worst case) at:

$$V_{cs}(0)=2·V_{out}\frac{L_r}{L_r+L_{out}}$$

(9)

For example, if L_r = 14 µH and L_out = 280 µH, then V_Cs(0) = 16.4 V.

The equations describing the circuit from Figure 11 are:

$$\{\begin{array}{l}{I}_r\left(s\right)+I_{cs}\left(s\right)=\frac{I_o}{s}\\ \frac{V_{cs}}{s}-I_{cs}\left(s\right)\frac{1}{s{C}_s}=L_r{I}_o-I_r\left(s\right)\left(s{L}_r+\frac{1}{s{C}_r}\right)\end{array}$$

(10)

After simple mathematical manipulations (10) becomes:

$$\frac{V_{cs}}{s}+\frac{I_o}{s^2{C}_r}=I_{cs}\left(s\right)\left(s{L}_r+\frac{1}{s{C}_1}\right)$$

(11)

From (11), results that the expression of the current through the C_s capacitor is:

$$I_{cs}\left(s\right)=\frac{V_{cs}{C}_1}{s^2{L}_r{C}_1+1}+\frac{I_{o}s{C}_1}{s^2{C}_r\left(s^2{L}_r{C}_1+1\right)}=\frac{V_{cs}}{\sqrt{L_r/C_1}}\frac{{\omega }_1}{s^2+{\omega }_1^2}+\frac{I_o}{C_r{L}_r{\omega }_1^2}\left(\frac{1}{s}-\frac{s}{s^2+{\omega }_1^2}\right)$$

(12)

In (11) and (12), $C_1=\frac{C_r{C}_s}{C_r+C_s}$ and ${\omega }_1=\frac{1}{\sqrt{L_r{C}_1}}$.

Applying the Laplace inverse transform to (12) and shifting to t₁ results:

$$i_{cs}\left(t\right)=\frac{V_{cs}}{\sqrt{L_r/C_1}}\sin \left({\omega }_1(t-t_1)\right)+\frac{I_o{C}_1}{C_r}\left[1-\cos ({\omega }_1(t-t_1))\right]$$

(13)

From (13) the voltage across the C_s capacitor can be calculated as:

$$v_{cs}\left(t\right)=\frac{V_{cs}}{C_s+C_r}\left[C_s+C_r\cos {\omega }_1\left(t-t_1\right)\right]-\frac{I_o}{C_s+C_r}\left[\left(t-t_1\right)-\frac{1}{{\omega }_1}\sin {\omega }_1\left(t-t_1\right)\right]$$

(14)

Solving the equation v_cs(t) = 0 V one gets: Δt = 30 ns.

The current through the resonant inductor is:

$$i_r(t)=I_o-i_{cs}(t-t_1)$$

(15)

The capacitor C_r will be discharged according to:

$$v_{cr}(t)=V_{in}-\frac{1}{C_r}{\displaystyle \underset{t_1}{\overset{t}{\int }}{i}_r(t)dt}$$

(16)

$$v_{cr}(t)=V_{in}-\left[\frac{I_o}{C_r}\left(1-\frac{C_1}{C_r}\right)t+I_o\frac{C_1}{C_r^2}\frac{1}{{\omega }_1}\sin \left({\omega }_1\left(t-t_1\right)\right)+V_c\frac{C_s}{C_r+C_s}\left(1-\cos ({\omega }_1\left(t-t_1\right)\right)\right]$$

(17)

After Δt = 30 ns the voltage on C_r will be: V_cap = 157 V and I_rt′ = 2.16 A.

The Spice circuit is represented in Figure 12, and the simulation results are shown in Figure 13.

As can be seen in Figure 13 the diodes will turn ON immediately after V_cs reaches zero, starting from its initial value before Q₁ turns OFF. At this moment t’ = 30 ns the voltage on the C_r capacitor that is also discharging reaches the value of 157 V and the current through the L_r inductor is 2.16 A. The C_r capacitor needs in this case 97 ns to completely discharge from its initial value.

In Figure 14, a detailed set of waveforms is presented for the time interval corresponding to [t₁-t₂]. It can be observed that the values obtained with the mathematical and simulation model match closely the experimental measurements. V_cr is the voltage measured on the primary of the transformer and corresponds to V_inv from Figure 6, V_cs is the voltage on the secondary, V_rec is the rectified secondary voltage, and I_Lr is the output current in this case.

At t’ when C_s is discharged, the Laplace equivalent circuit presented in Figure 15 can be used to compute the C_r voltage.

$$V_{diff}=V_{in}-V_{cap}$$

(18)

$$i_r(t)=I_{rt\prime }\cos \left({\omega }_r(t-t\prime )\right)-\frac{V_{diff}}{\sqrt{\frac{L_r}{C_r}}}\sin \left({\omega }_r(t-t\prime )\right)$$

(19)

$$V_{Cr}(t)=V_{cap}-I_{rt\prime }\sqrt{\frac{L_r}{C_r}}\sin ({\omega }_r(t-t\prime ))+V_{diff}[1-\cos ({\omega }_r(t-t\prime ))]$$

(20)

where V_diff is the difference between the input voltage and the initial voltage of C_r at t′ and I_rt′ is the current through L_r at t′.

The diodes D₂, D₃ will start to conduct after t′ when C_s is completely discharged. At t″ = 97 ns when V_cr(t″) = 0 the resonant inductor current, I_r, is flowing through the body diode D_in2 of Q₂, decreasing with a slope equal to V_in/L_r. Now Q₂ can be switched ON. The current through D₁ is decreasing and through D₃ is increasing. At t_3, D₁ current is zero and I_r = I_o.

When C_s is charged at a low voltage, its influence on the C_r discharging time is negligible.

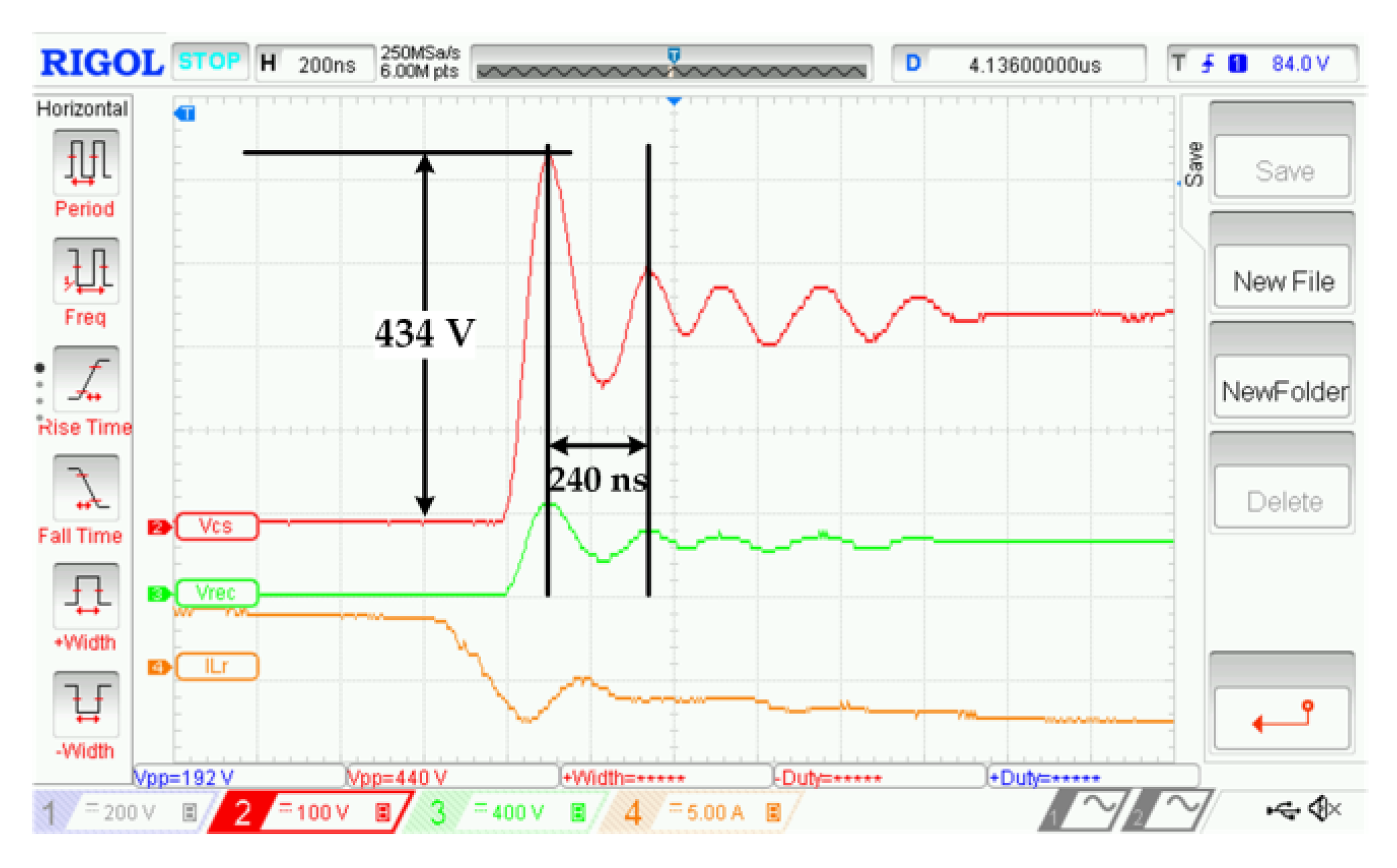
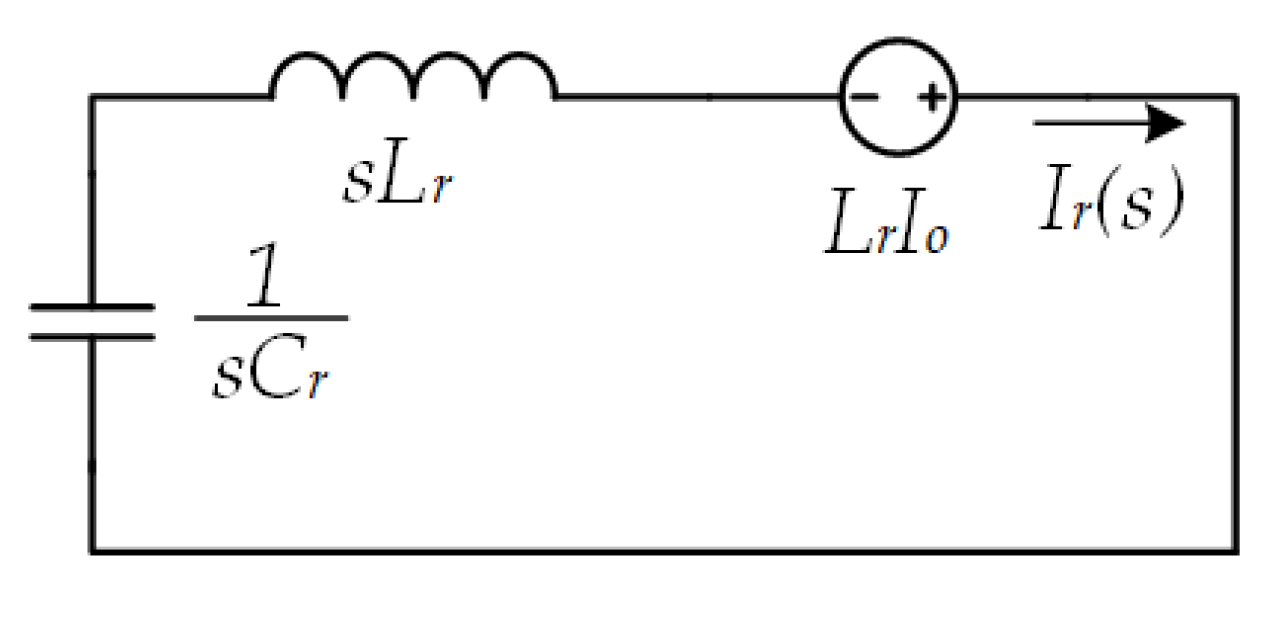
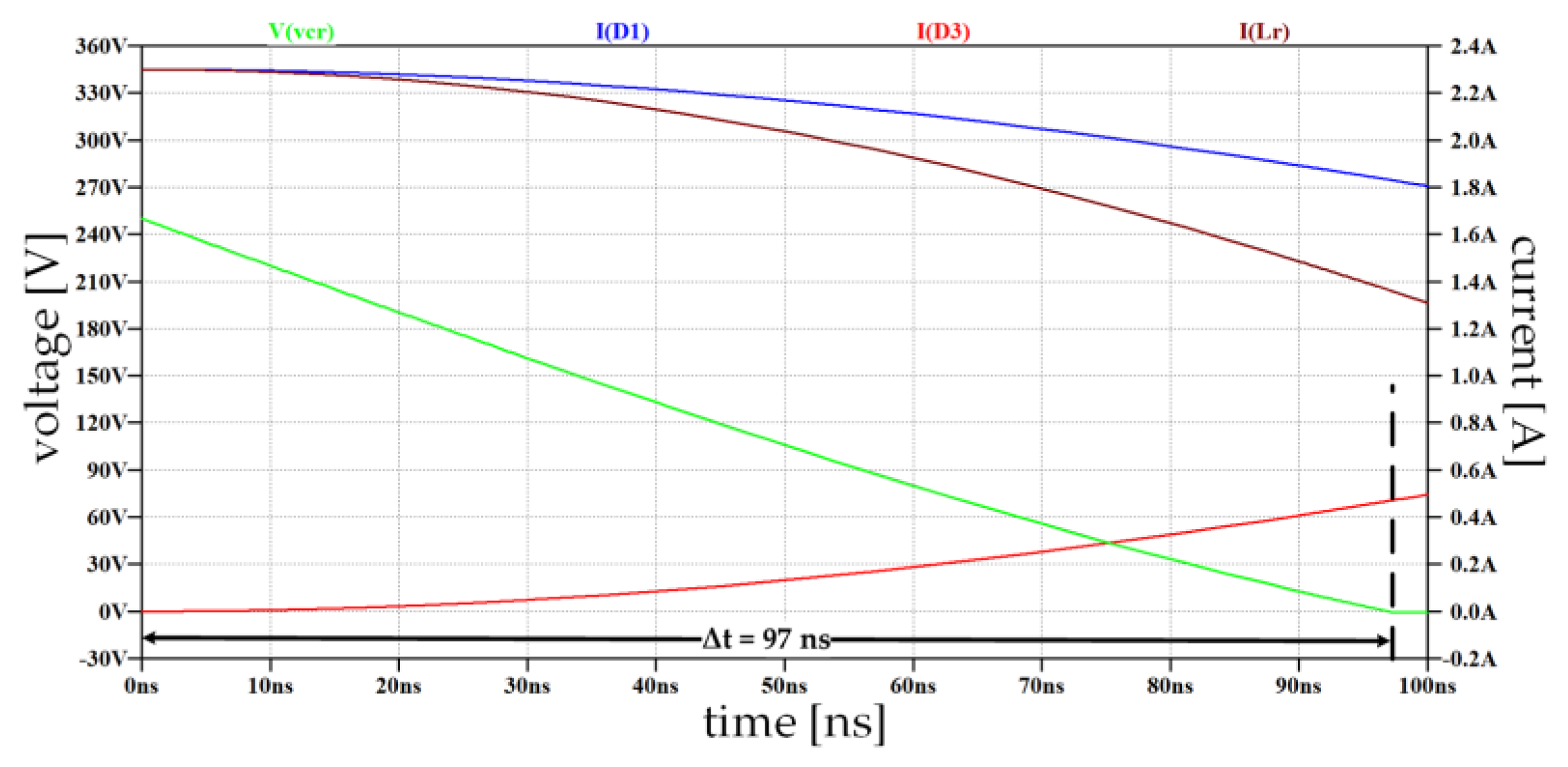
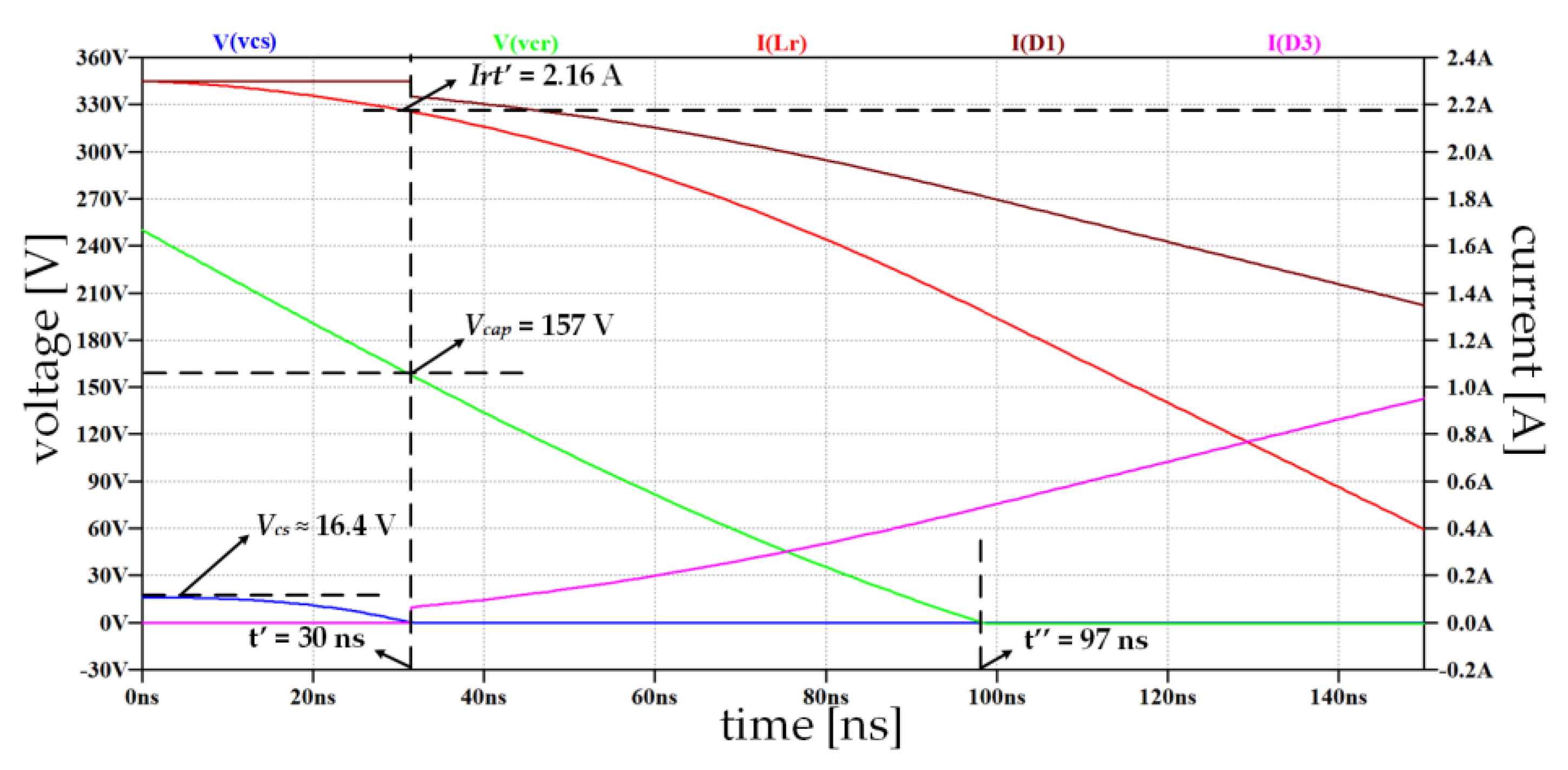
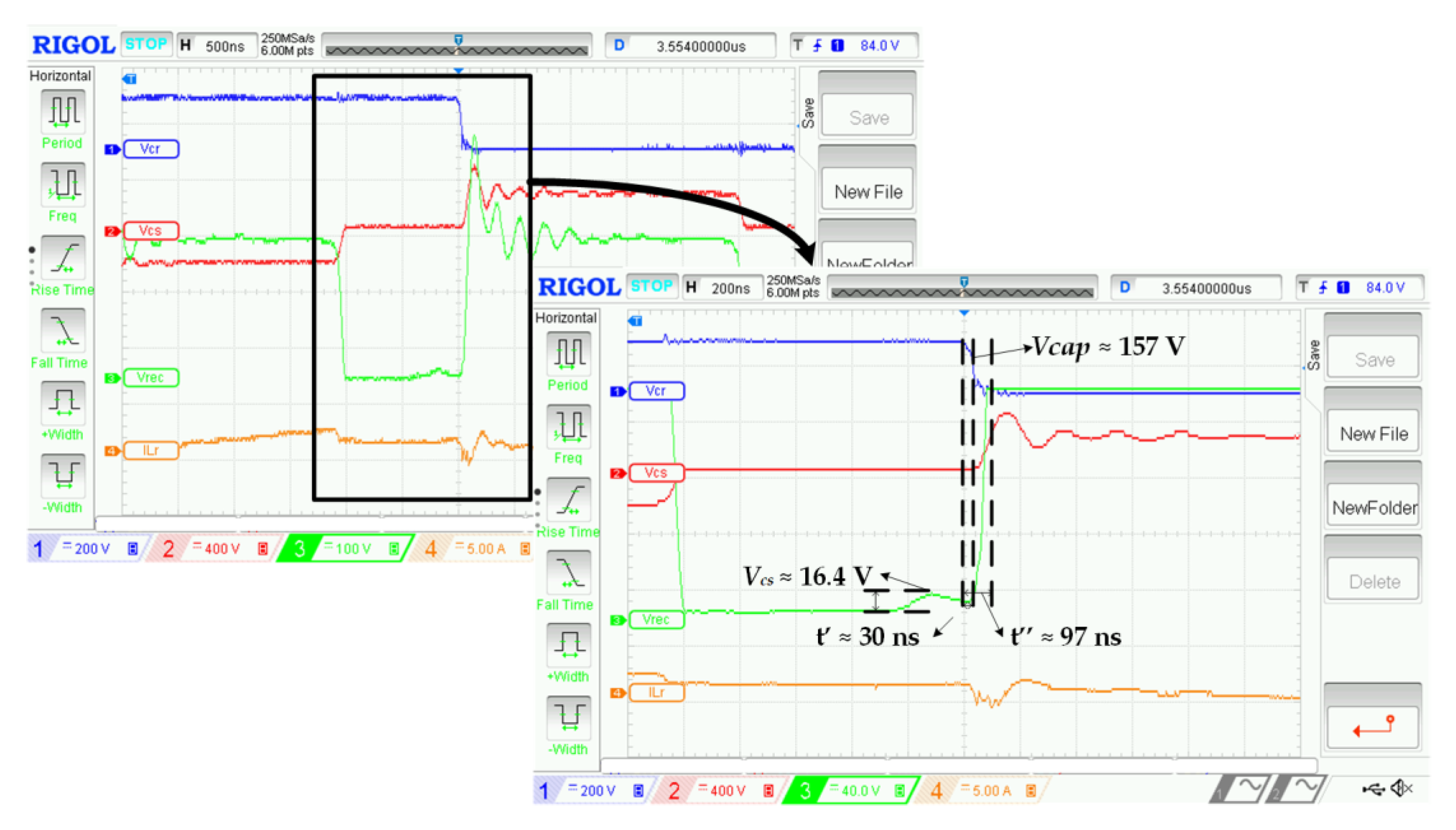
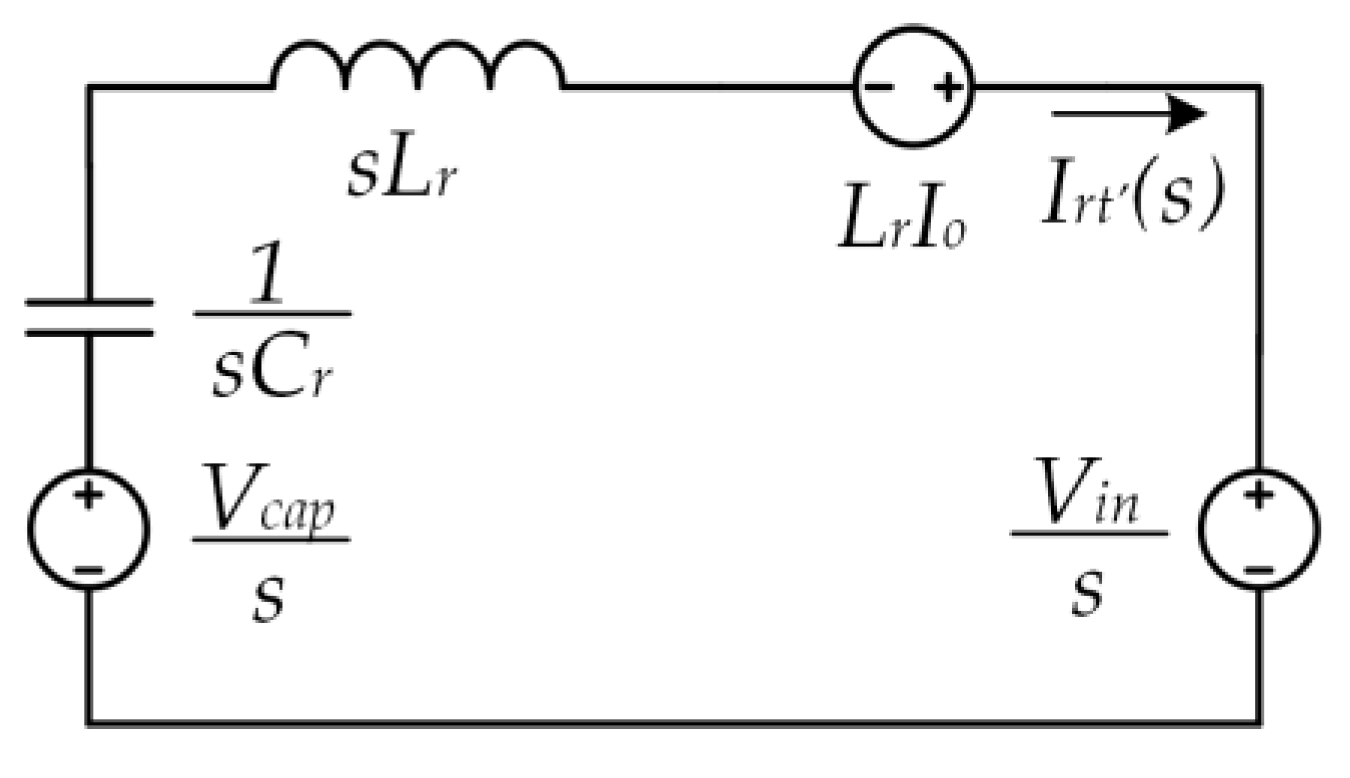
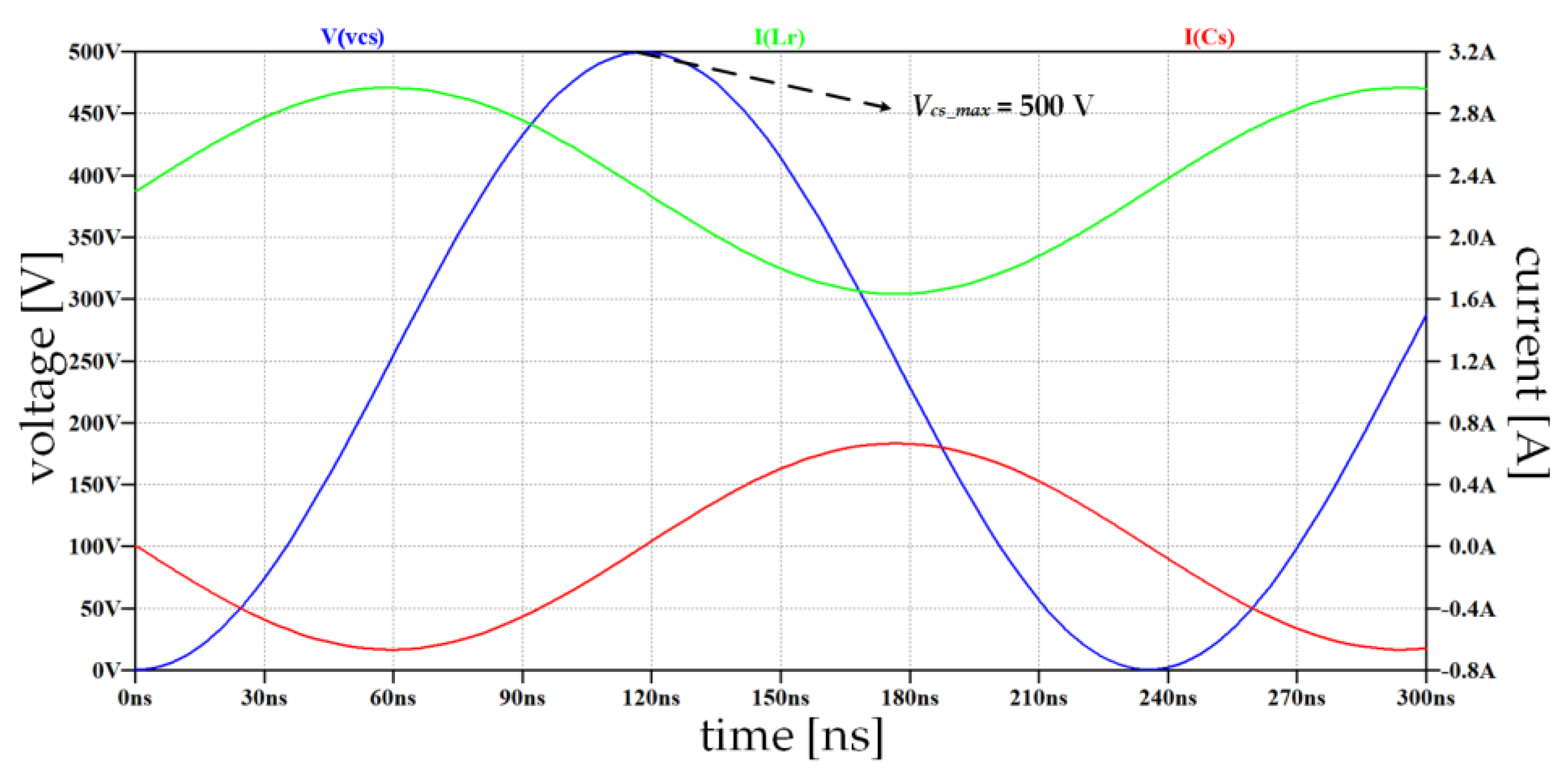
4.2. Operation during [t₃-t₄], immediately after t₃

At t₃, D₁ and D₄ diodes turn OFF, and the output current continues to flow through D₃ and D₂. For a short time after t₃ the current through L_out can be considered constant, and this inductance is replaced by a constant current source.

The Laplace equivalent model corresponding to this time interval is presented in Figure 16.

The equations describing the circuit from Figure 16 are:

$$\{\begin{array}{l}{I}_r\left(s\right)=\frac{I_o}{s}+I_{cs}\left(s\right)\\ \frac{V_{in}}{s}-s{L}_r{I}_r\left(s\right)+L_r{I}_o=\frac{1}{s{C}_s}{I}_{cs}\left(s\right)\end{array}$$

(21)

After simple mathematical manipulation of (21) the expression of the C_s current is:

$$i_{cs}\left(t\right)=\frac{V_{in}}{\sqrt{L_r/C_s}}\sin \left(\omega (t-t_3)\right)$$

(22)

where $\omega =\frac{1}{\sqrt{L_r{C}_s}}$.

The voltage across the C_s capacitor can be calculated as:

$$v_{cs}(t)=\frac{1}{C_s}{\displaystyle \underset{t_3}{\overset{t}{\int }}\frac{V_{in}}{\sqrt{L_r/C_s}}\sin \left(\omega (t-t_3)\right)dt}=V_{in}\left[1-\cos \left(\omega (t-t_3)\right)\right]$$

(23)

As it can be deduced from (23), V_cs voltage reaches its maximum value V_cs.max = 2V_in after a time interval equal to T/2 = π/ω. This equation is very useful for designing the output clamping circuit.

Spice simulation for the schematic in Figure 17 describing the converter immediately after t₃ is presented in Figure 18.

As it can be observed in Figure 18, immediately after t₃ the maximum voltage on the C_s capacitor reaches the double input value, in this case, V_in = 250 V. The value represents the voltage measured on the secondary side of the transformer.

In Figure 19 are highlighted the experimental results for the interval t₃-t₄ immediately after t₃. It can be observed that there is a difference between the simplified model used in the simulation and the experimental values. This difference is due to the fact that the simulation takes into account the worst-case scenario for the maximum possible V_cs voltage (obtained for worst-case R₁ = 0 Ω).

For the experimental setup, if a secondary parasitic equivalent resistance R₁ = 70 Ω is considered, the damping ratio of the secondary voltage is given by:

$$\xi =\frac{R_1}{2\sqrt{\frac{L_r}{C_s}}}=\frac{70 \mathsf{\Omega }}{2\sqrt{\frac{14 \mathsf{\mu }\mathrm{H}}{100 \mathrm{pF}}}}\cong 0.095$$

(24)

From (24) results that secondary peak voltage can be estimated with:

$$V_{c.\max }=V_{in}·\left(1+e^{-\frac{\pi \xi }{\sqrt{ 1-{\xi }^2}}}\right)=250 \mathrm{V}·\left(1+e^{-\frac{\pi ·0.095}{\sqrt{1-{0.095}^2}}}\right)\cong 434 \mathrm{V}$$

(25)

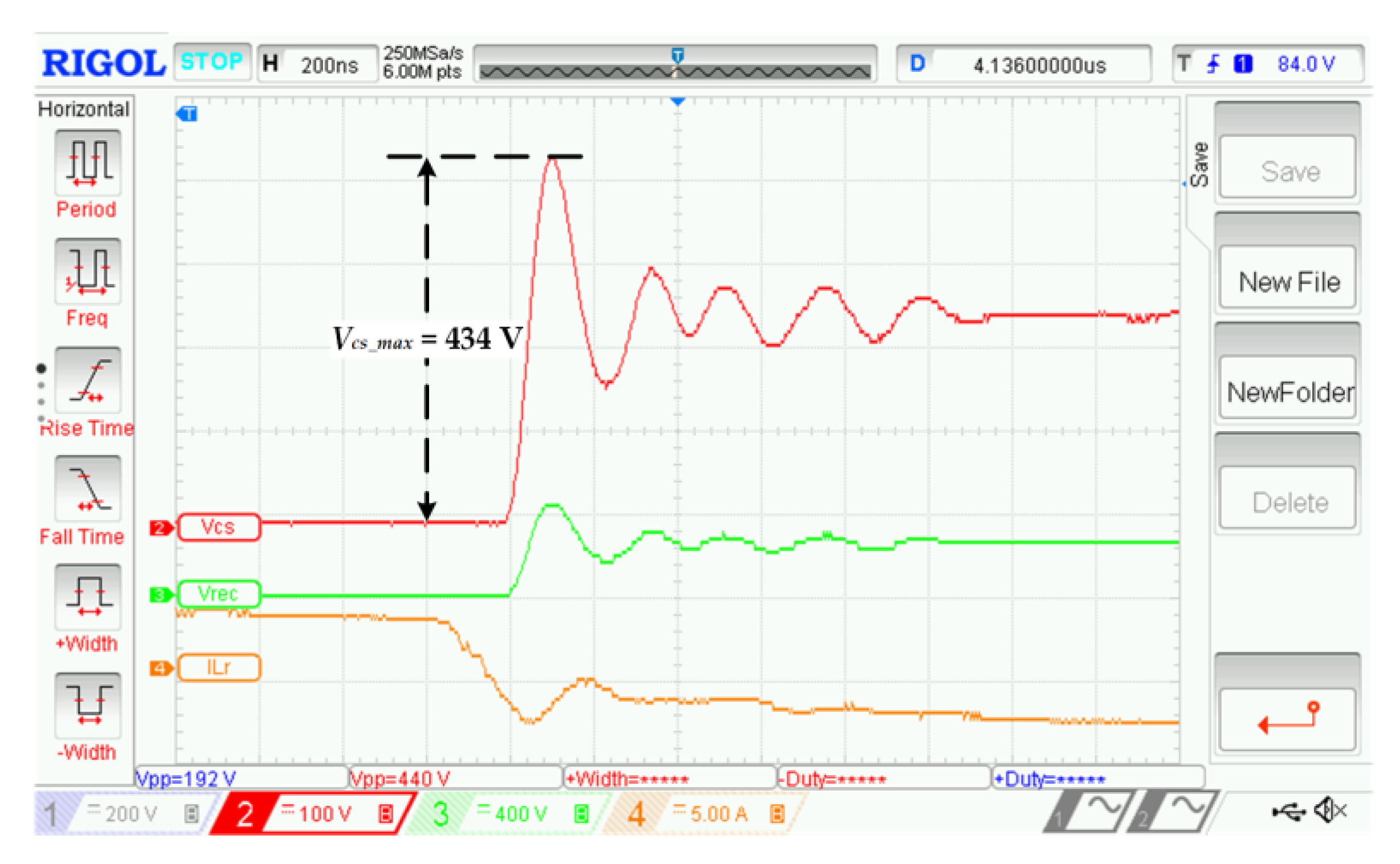
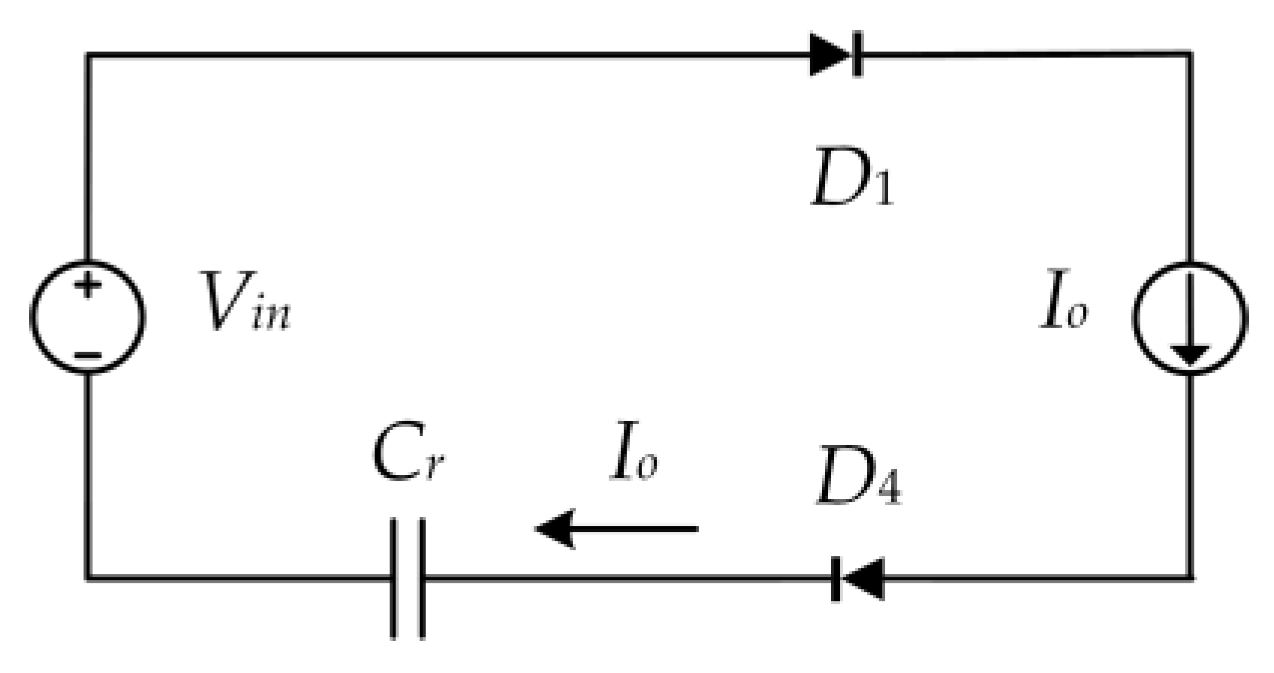
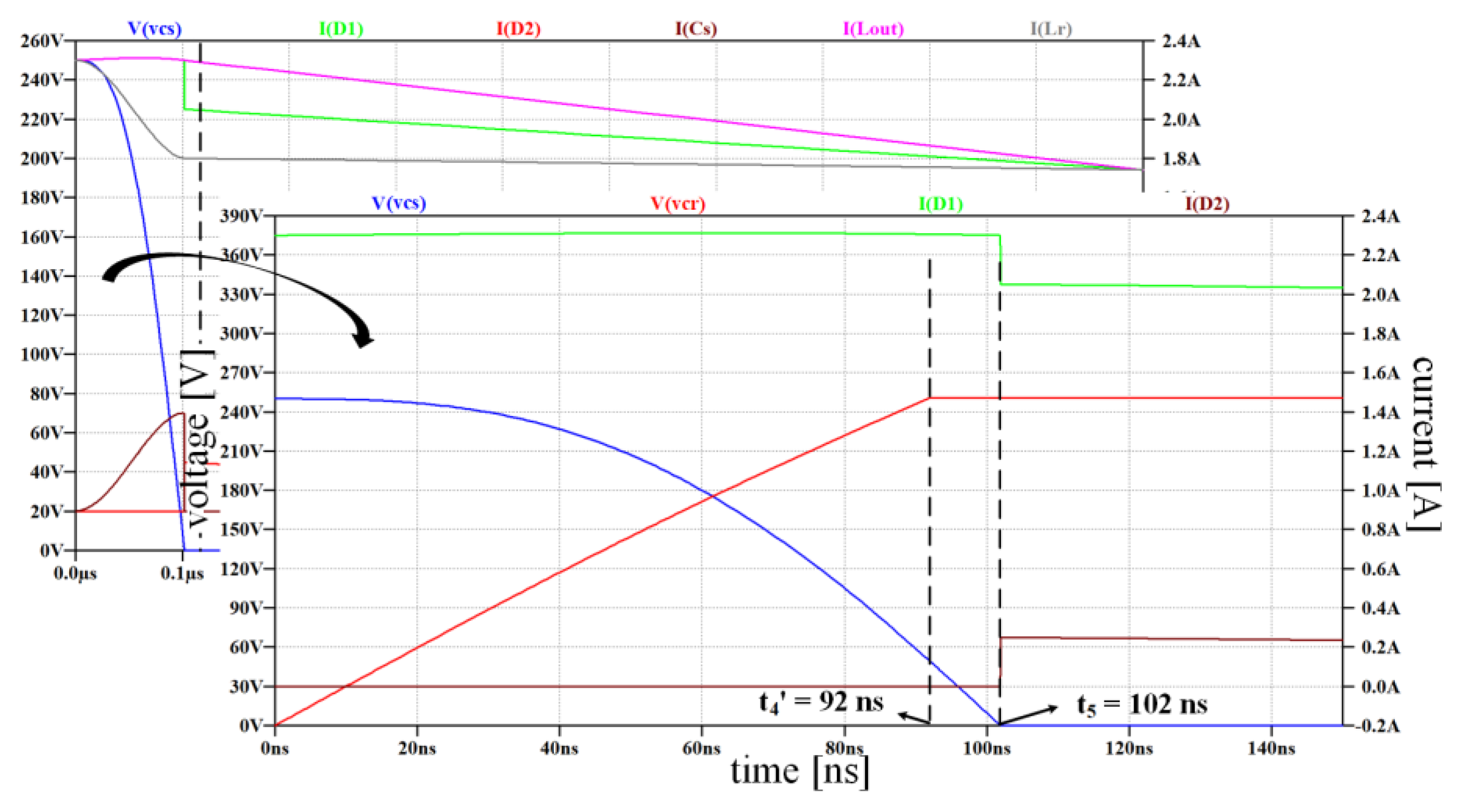
4.3. Operation during [t₄-t₅]

At t₄, Q₃ turns off, and the energy transfer from primary to the output stops. The output capacitor C’_o3 of Q₃ starts to charge, and the output capacitor of Q₄ starts to discharge. If one considers C_r = C’_o3 + C’_o4, then the equivalent schematic of the converter corresponding to this time interval is presented in Figure 20.

Since only D₁ and D₄ are on, results that C_r starts to be charged with an approximatively constant current (the output current I_o), thus in general, this time interval is very narrow.

In this case, the voltage across the C_r capacitor is given by:

$$v_{cr}(t)=\frac{1}{C_r}{\displaystyle \underset{t_4}{\overset{t}{\int }}{I}_{0}dt}=\frac{I_0}{C_r}\left(t-t_4\right)$$

(26)

From Equation (26), results that the charging time interval of the C_r capacitor can be estimated with (27) supposing that during this time interval the capacitor C_s will remain charged at the approximately same voltage V_in. A detailed analysis which takes into account the influence of C_s can be made, as in Section 4.1.

$$t_4^{\prime }-t_4=\frac{V_{in}{C}_r}{I_o}$$

(27)

The equations describing the circuit in Figure 21 are:

$$\{\begin{array}{l}{I}_r\left(s\right)+I_{cs}\left(s\right)=\frac{I_o}{s}\\ \frac{V_{in}}{s}-\frac{1}{s{C}_s}{I}_{cs}\left(s\right)=L_r{I}_o-s{L}_r{I}_r\left(s\right)\end{array}$$

(28)

The equivalent circuit corresponding to this time interval is presented in Figure 22, supposing that C_r is already charged. During [t₄′-t₅] time interval, as seen in Figure 23, the energy stored in C_s shall be evacuated through D₁ and D₄.

From (23) results that C_s current is given by:

$$I_{cs}\left(s\right)=\frac{V_{in}}{\sqrt{L_r/C_s}}\frac{\omega }{s^2+{\omega }^2}$$

(29)

Applying the Laplace inverse transform to (29) and shifting to t₄′, results that C_s is discharged by a sinusoidal current, as in (22). The equation of the voltage across the C_s capacitor becomes in this case:

$$v_{cs}(t)=V_{in}-\frac{1}{C_s}{\displaystyle \underset{t_4\prime }{\overset{t}{\int }}\frac{V_{in}}{\sqrt{L_r/C_s}}\sin \left(\omega (t-t_4\prime )\right)dt}=V_{in}\cos \left(\omega (t-t_4\prime )\right)$$

(30)

As supposed before, the C_r capacitor will start to charge according to Equation (26), while for the first part of this period of time the voltage on the C_s capacitor remains constant at the 250 V in this case. The energy stored in C_s shall be evacuated through the D₁ and D₄ diodes.

In Figure 24 are highlighted the experimental results for the interval t₄-t₅. It can be observed that the results match closely the values obtained with the mathematical and simulation models.

4.4. Operation during [t₅-t₇]

From (30) results that at t₅ (after a time interval equal to T/4 = π/2ω), the voltage across C_s reaches zero, and the I_cs current reaches its maximum value. After this time interval, due to the reverse voltage polarity on C_s, the energy stored in it shall be evacuated almost instantaneous through D₂ and D₃, which turn ON and keep the voltage on C_s equal to zero. At t₆, Q₄ turns ON with ZVS, and the primary output reflected current continues to flow through the body diode D_in4 of Q₄. The D₁ and D₄ diodes are turned ON together with D₃ and D₂ until t₇, when the L_r current reaches again the value of the output current reflected in the primary of the transformer. After t₇, the output current flows again only through D₁ and D₄. If one considers that in [t₅-t₇] time interval the L_r current is approximatively constant and the diode currents i_D1 = i_D4 and i_D3 = i_D2, then the equivalent schematic of the converter corresponding to this time interval is presented in Figure 25.

The equations describing the circuit in Figure 25 are:

$$\{\begin{array}{l}{i}_{D1}-i_{D2}=I_r\\ i_{D1}+i_{D2}=i_o\end{array}$$

(31)

From (31) results that:

$$i_o-I_r=2i_{D2}$$

(32)

Since this difference between the output current and the reflected primary current is given by the current drop through C_s at t₅, results that:

$$\{\begin{array}{l}{I}_{D1}=I_o-\frac{I_{cs.\max }}{2}\\ I_{D2}=\frac{I_{cs.\max }}{2}=\frac{V_{in}}{2\sqrt{L_r/C_s}}\end{array}$$

(33)

where I_D1 and I_D2 are the current values through D₁ and D₂ in t₅ and I_cs.max is the maximum value of the C_s current.

The diodes D₂ and D₃ are turning OFF at t₇, when the current through L_r reaches the value of the current through L_out.

The equations describing the relation between the L_r and L_out currents are:

$$\{\begin{array}{l}{I}_r=I_o-I_{cs.\max }\\ i_{Lo}\left(t\right)=I_o-\frac{V_{out}}{L_{out}+L_r}\left(t-t_5\right)\end{array}$$

(34)

Since the L_r and L_out currents are again equal at t₇, results that:

$$I_o-I_{cs.\max }=I_o-\frac{V_{out}}{L_{out}+L_r}\left(t_7-t_5\right)$$

(35)

From (35) results that [t₅-t₇] time interval can be estimated as: 1.2 µs.

4.5. Operation during [t₇-t₈]

At t₇, D₂ and D₃ diodes turn OFF, and D₁ and D₄ continue to stay ON until t₈, when Q₂ transistor turns OFF. The equivalent circuit from Figure 26 presents the Laplace model of the converter corresponding to [t₇-t₈] time interval. In this case, the initial currents through L_r and L_out have no influence.

The voltage across the C_s capacitor in [t₇-t₈] time interval is:

$$V_{cs}\left(s\right)=\frac{V_{out}}{s}\frac{Z_p}{Z_p+s{L}_{out}}=\frac{V_{out}}{s}\frac{1}{1+\frac{L_{out}}{L_r}+s^2{L}_{out}{C}_s}$$

(36)

$$V_{cs}\left(s\right)=\frac{V_{out}}{L_{out}{C}_s}\frac{1}{s\left(s^2+\frac{L_{out}{L}_r}{L_{out}+L_r}{C}_s\right)}$$

(37)

If $Z_p=\frac{s{L}_r/s{C}_s}{s{L}_r+1/s{C}_s}=\frac{s{L}_r}{1+s^2{L}_r{C}_s}$ is the impedance of the parallel connection L_r-C_s and ${\mathsf{\omega }}_2=\frac{1}{\sqrt{\frac{L_{out}{L}_r}{L_{out}+L_r}{C}_s}}$ then (37) becomes:

$$V_{cs}\left(s\right)=\frac{V_{out}}{L_{out}{C}_s}\frac{1}{s^2(s^2+{\omega }_2^2)}=\frac{V_{out}}{L_{out}{C}_s{\omega }_2^2}\left(\frac{1}{s}-\frac{s}{s^2+{\omega }_2^2}\right)$$

(38)

Applying the Laplace inverse transform to (38), results that the voltage across the C_s capacitor in [t₇-t₈] is:

$$v_{cs}\left(t\right)=\frac{V_{out}{L}_r}{L_{out}+L_r}\left[1-\cos {\omega }_2\left(t-t_7\right)\right]$$

(39)

Spice simulation for the schematic in Figure 27 describing the converter in [t₇-t₈] interval is presented in Figure 28. As can be observed the C_s capacitor charges at the voltage deduced with Equation (9). So this is the worst-case values of V_cs(0) for this specific analysis.

As it can be deduced from (39), v_cs voltage reaches the maximum value V_cs.max = 16.4 V after a time interval equal to T₂/2 = π/ω₂:

$$V_{cs.\max }=2\frac{V_{out}{L}_r}{L_{out}+L_r}$$

(40)

In Figure 29 can be observed that the voltage across the C_s capacitor in [t₇-t₈] is V_cs = 16.4 V corresponding with the value obtained with Equation (40).

Equation (40) is used for determining the initial conditions of [t₁-t₃] time interval, in Section 4.1.

It can be concluded that the simulations strongly agree with the equations’ results. The difference between Figure 2a and Figure 2b are explained with the mathematical models presented.

5. Conclusions

This paper presents a detailed analysis of the PSFB converter that accounts for the stray capacitance of the transformer secondary winding and the capacitances of the diodes in the bridge rectifier. The analysis was performed in continuous conduction mode for both, leading and legging leg of the primary bridge and for a complete switching cycle, starting from an equivalent electric circuit of a high frequency transformer, with all the elements referred to the secondary side. The complete switching cycle considered for the analysis was divided into seven time intervals to better highlight the effect of the parasitic capacitance. A simplified Laplace equivalent circuit for each operation time interval was developed and the corresponding equations where derived. The values obtained through mathematical manipulation are compared with the ones obtained with the Spice simulation models created for each time interval. The simulation models validate the mathematical description on each time interval and provide an intuitive and easy to adapt the method for analyzing a phase shift converter in detail. Equations (9) and (23) can be used to design active snubbers. The effect of the stray capacitance can be observed in the experimental waveforms presented in Figure 29. Because of the short amount of time and small value that the V_cs(0) exhibits most of the time, its presence is ignored by designers resulting in flawed designs. The experimental waveforms were measured on the PSFB converter prototype. 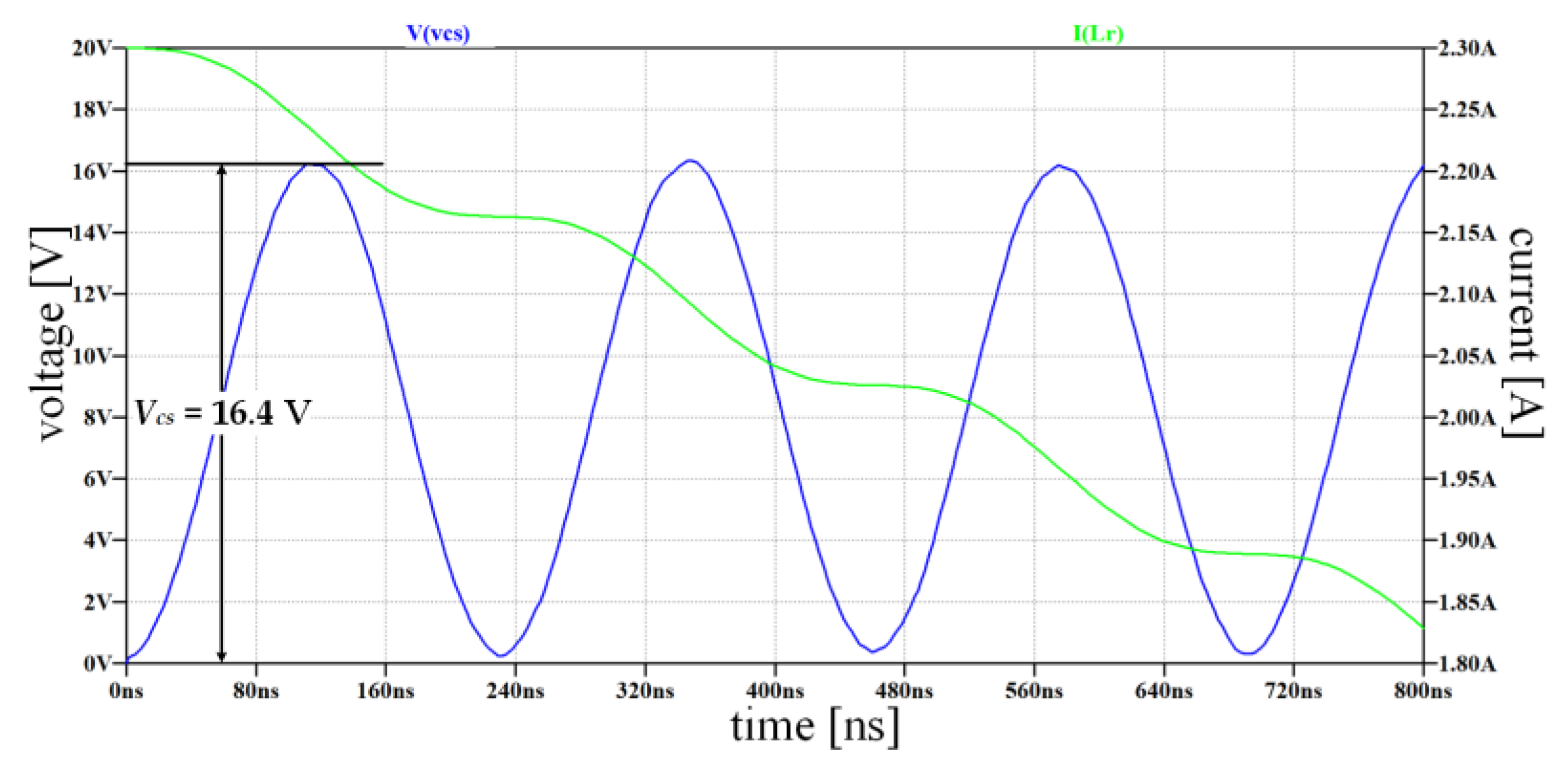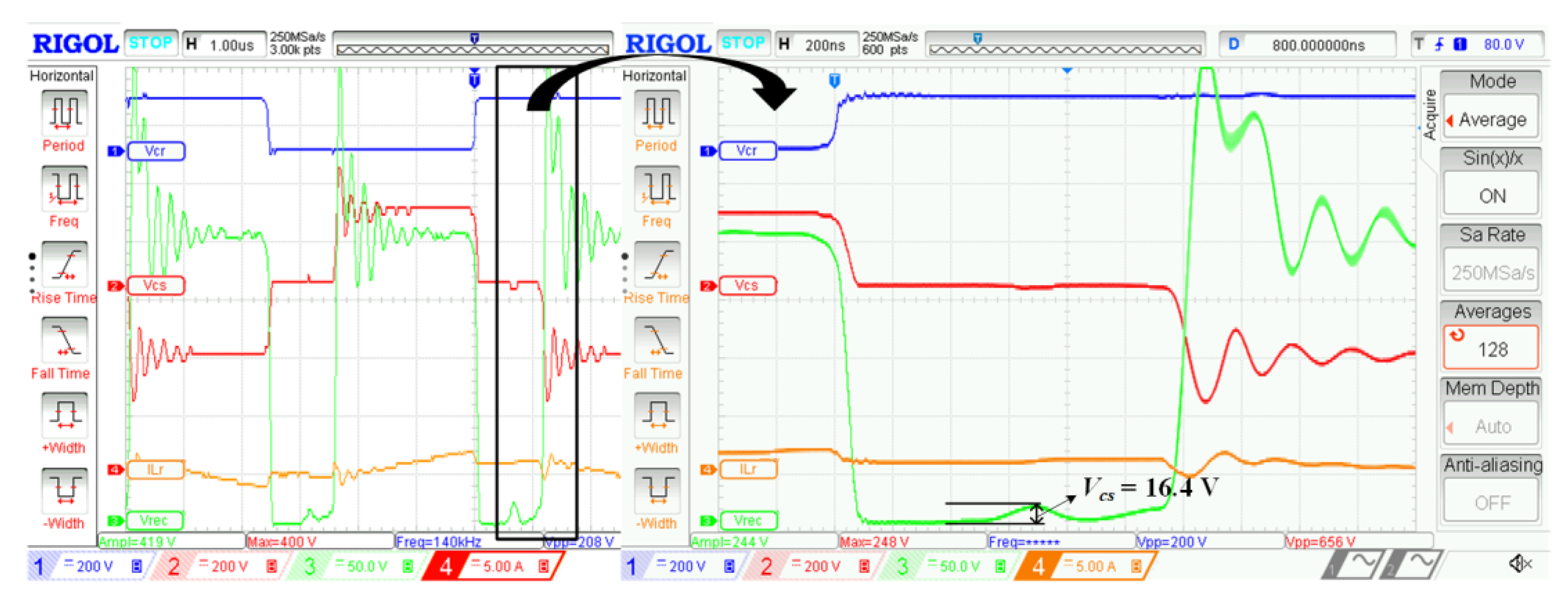It can be observed that the experimental measurement prove that the mathematical model and the equivalent simulation circuits are valid and can be used for design optimizations.

6. Discussion

The main objective of the paper is to highlight and better understand the effects of the parasitic capacitances on the PSFB. By using the equations and simulation models presented in Section 4 the design process of such a converter simplifies, and there is no need for implementing new complicated control techniques if the negative effects of the stray capacitance are taken into account. By determining the maximum voltage on the stray capacitance, an active clamping circuit can be designed. As highlighted in the Introduction section, such high power density converters are needed more and more in the automotive industry, due to the development of electric cars and off and on board charging stations. Using active snubbers in this equipment is necessary, due to high-efficiency requirements and space constraints that affect the heat dissipation needed for the passive snubbers approach. This type of analysis, presented in this paper, helps designers and scientist to better understand the effects that appear in high density power converters. If these effects are ignored it can lead to a design with a very high number of iterations between the simulation stage and experimental measurements. Many times the redesign is the solution adopted.