Analysis and Application of the Direct Flux Control Sensorless Technique to Low-Power PMSMs
Abstract
1. Introduction
2. Theory
2.1. Analysis of the Star Point Voltage Dynamics in Synchronous Machines
2.2. Particularization to PMSMs
2.3. Rotor Position Estimation
2.4. Comparison between the DFC Technique and High-Frequency Injection Techniques
2.5. The Direct Flux Control Technique
3. Experimental Validation
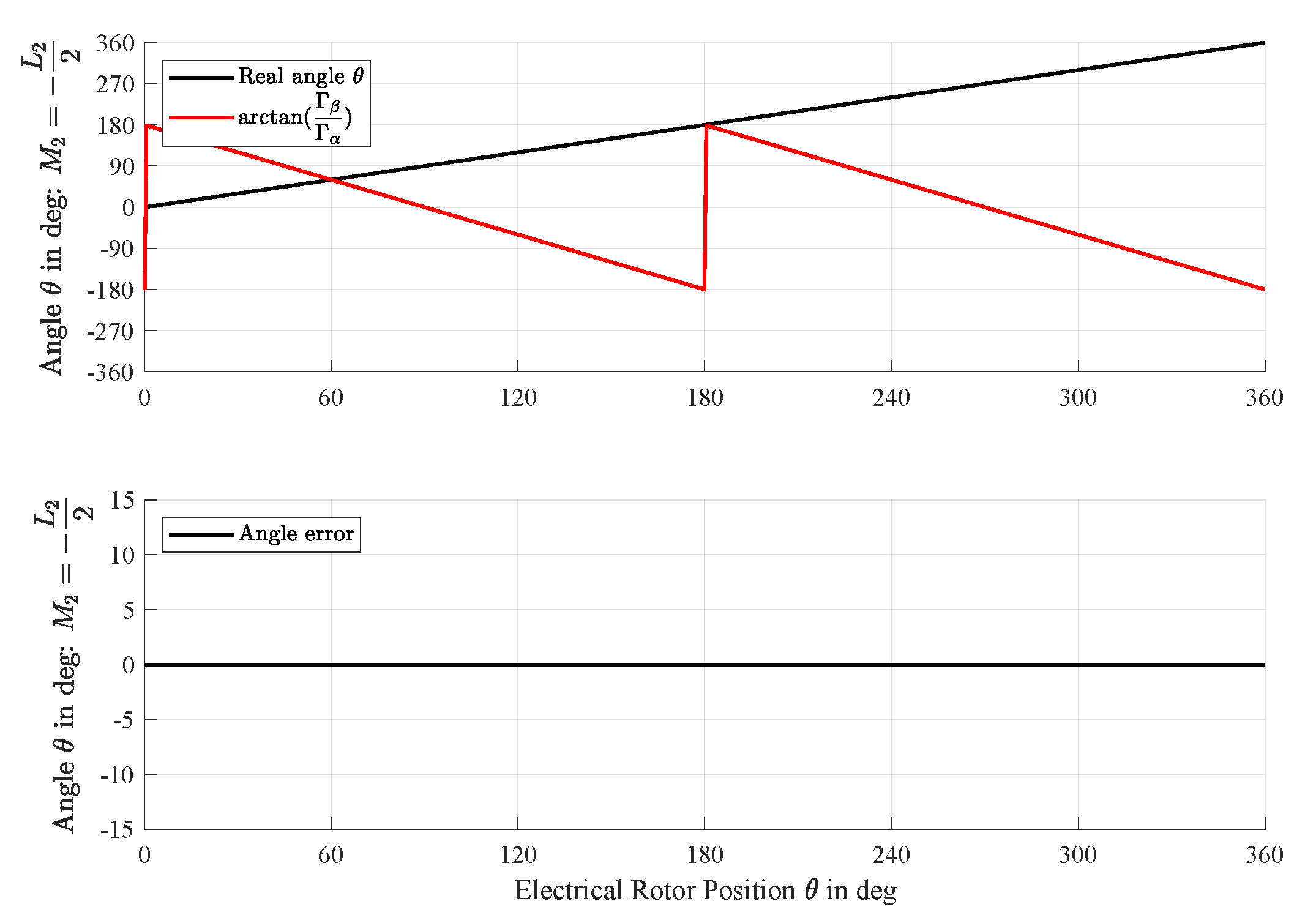
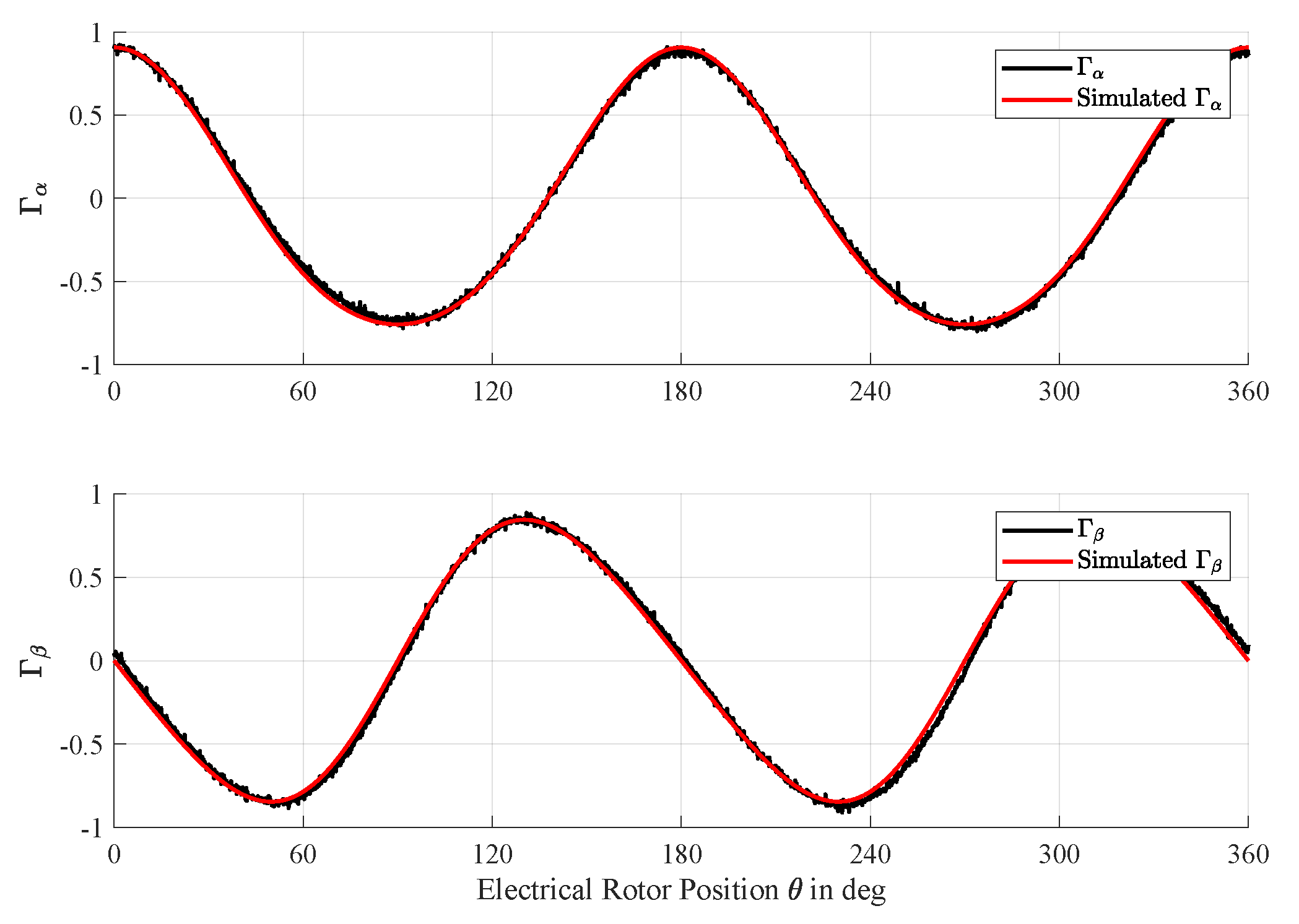
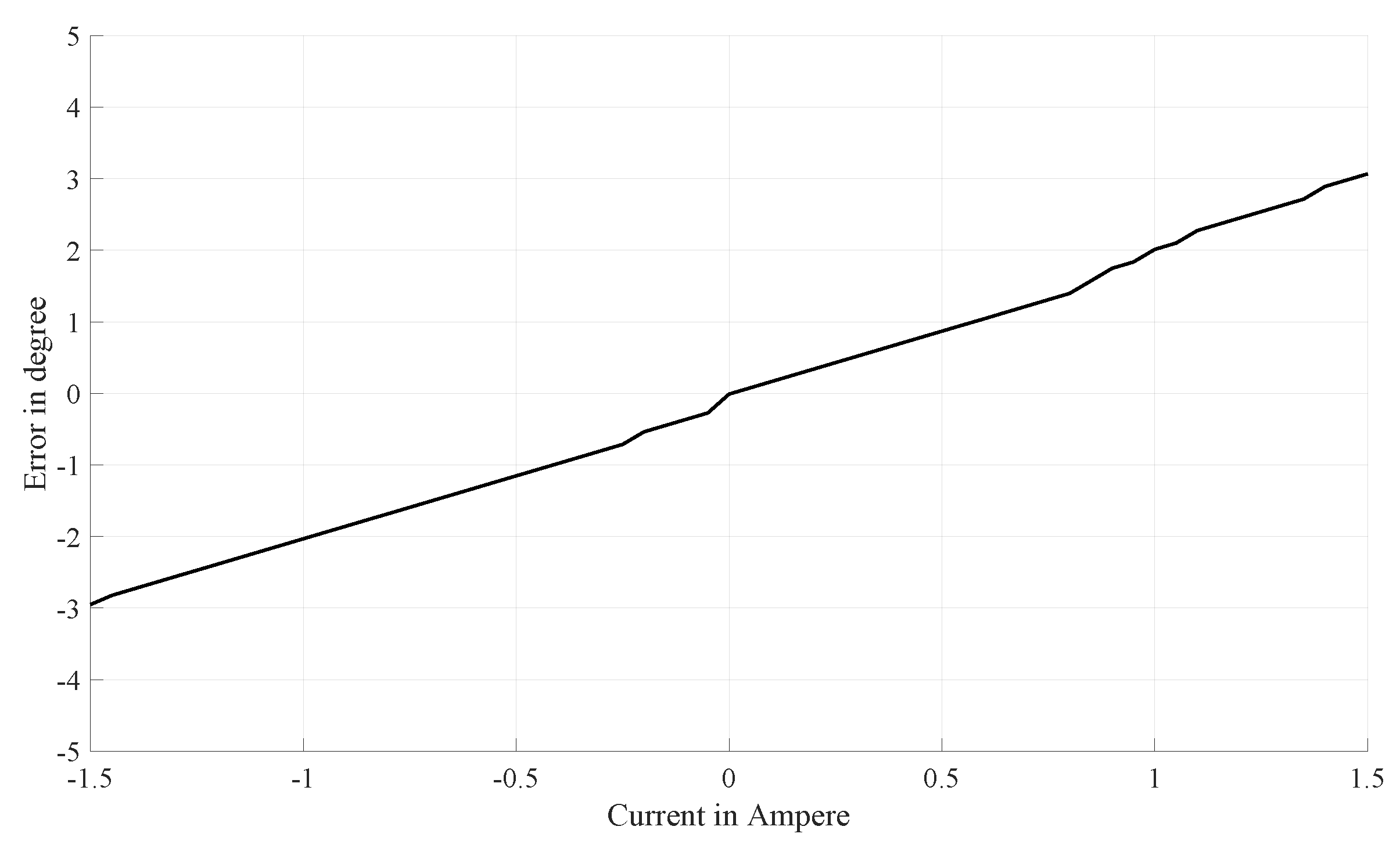
3.1. Measurement and Validation of
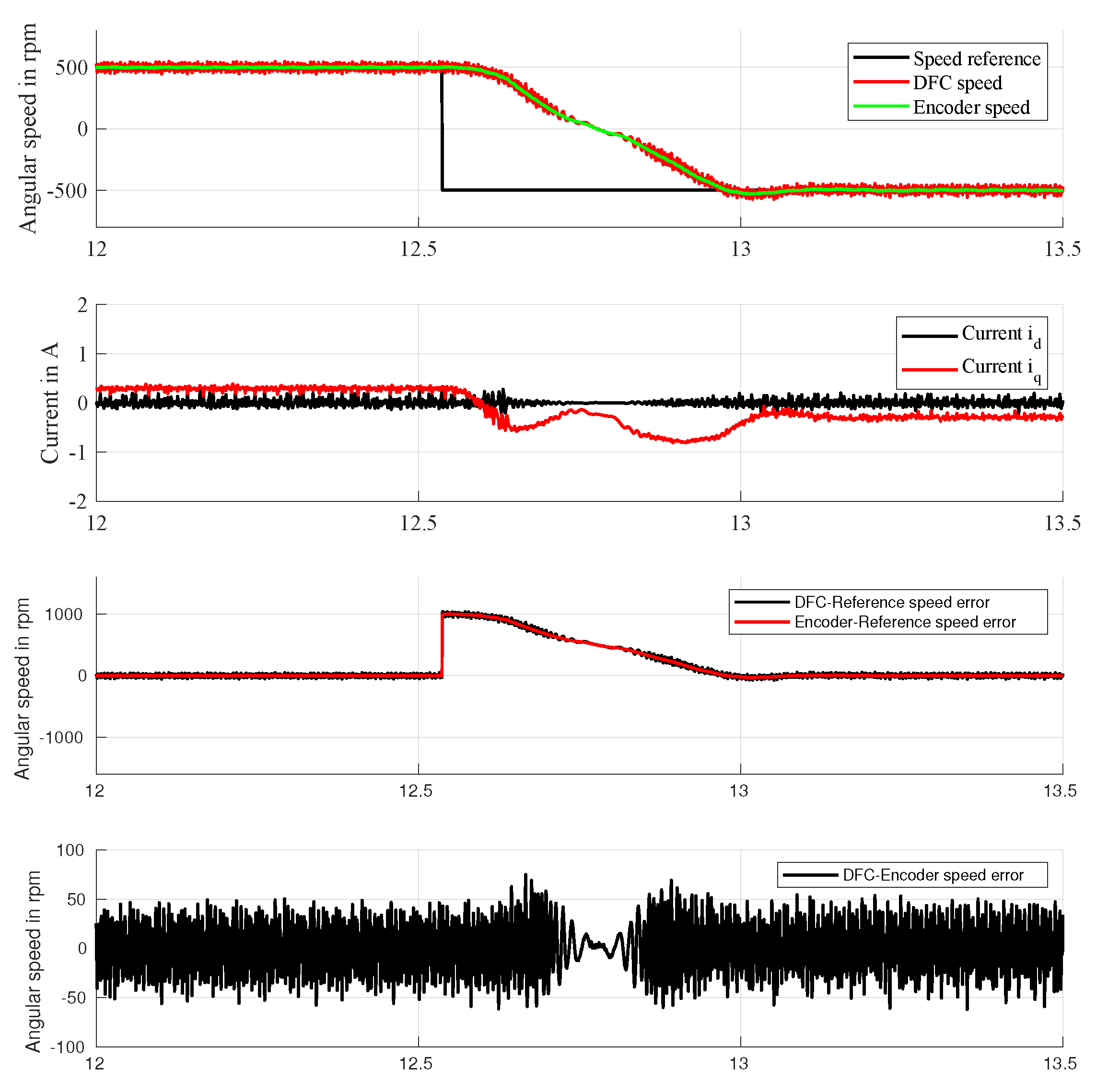
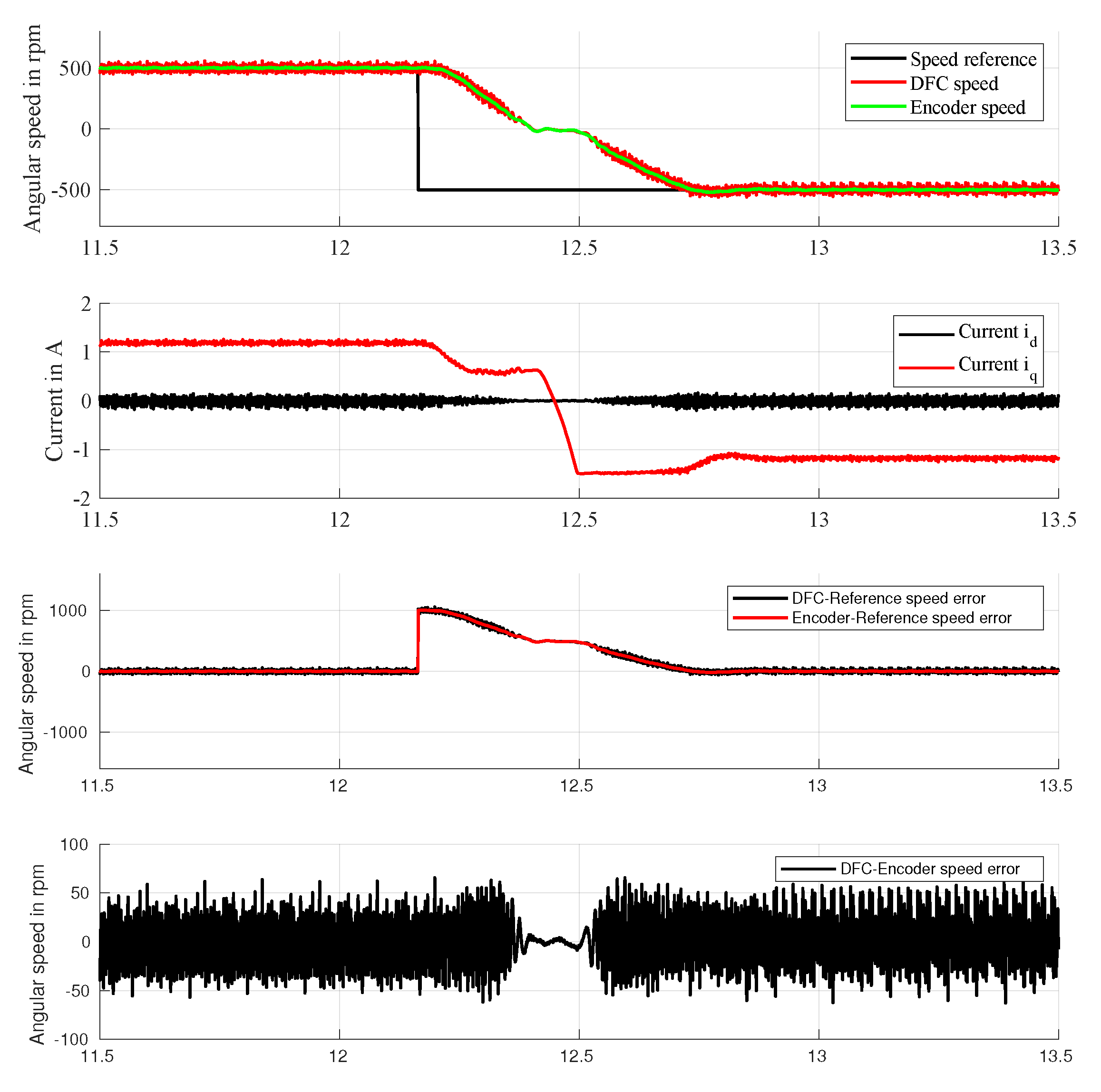
3.2. Validation of the Proposed Technique under Dynamic Conditions
4. Conclusions and Outlooks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, Z.; Shang, F.; Brown, I.P.; Krishnamurthy, M. Comparative Study of Interior Permanent Magnet, Induction, and Switched Reluctance Motor Drives for EV and HEV Applications. IEEE Trans. Transp. Electrif. 2015, 1, 245–254. [Google Scholar] [CrossRef]
- Xu, D.; Wang, B.; Zhang, G.; Wang, G.; Yu, Y. A review of sensorless control methods for AC motor drives. CES Trans. Electr. Mach. Syst. 2018, 2, 104–115. [Google Scholar] [CrossRef]
- Schrödl, M. Sensorless Control of A. C. Machines; Fortschritt-Berichte VDI: Reihe 21, Elektrotechnik; 117; VDI-Verl.: Düsseldorf, Germany, 1992; Volume 117. [Google Scholar]
- Schrödl, M. Sensorless control of AC machines at low speed and standstill based on the “INFORM” method. In Proceedings of the IAS ’96. Conference Record of the 1996 IEEE Industry Applications Conference Thirty-First IAS Annual Meeting, San Diego, CA, USA, 6–10 October 1996; Volume 1, pp. 270–277. [Google Scholar] [CrossRef]
- Lorenz, R.D. Transducerless Position and Velocitv Estimation in Induction and Salient AC Machines. IEEE Trans. Ind. Appl. 1995, 31, 240–247. [Google Scholar]
- Corley, M.; Lorenz, R. Rotor position and velocity estimation for a salient-pole permanent magnet synchronous machine at standstill and high speeds. IEEE Trans. Ind. Appl. 1998, 34, 784–789. [Google Scholar] [CrossRef]
- Linke, M.; Kennel, R.; Holtz, J. Sensorless position control of permanent magnet synchronous machines without limitation at zero speed. In Proceedings of the IEEE 2002 28th Annual Conference of the Industrial Electronics Society (IECON 02), Sevilla, Spain, 5–8 November 2002; Volume 1, pp. 674–679. [Google Scholar] [CrossRef]
- Linke, M.; Kennel, R.; Holtz, J. Sensorless speed and position control of synchronous machines using alternating carrier injection. In Proceedings of the IEEE International Electric Machines and Drives Conference (IEMDC’03), Madison, WI, USA, 1–4 June 2003; Volume 2, pp. 1211–1217. [Google Scholar] [CrossRef]
- Landsmann, P.; Paulus, D.; Stolze, P.; Kennel, R. Saliency based encoderless predictive torque control without signal injection. In Proceedings of the 2010 International Power Electronics Conference - ECCE ASIA, Sapporo, Japan, 21–24 June 2010; pp. 3029–3034. [Google Scholar] [CrossRef]
- Paulus, D.; Landsmann, P.; Kennel, R. Sensorless field- oriented control for permanent magnet synchronous machines with an arbitrary injection scheme and direct angle calculation. In Proceedings of the 2011 Symposium on Sensorless Control for Electrical Drives, Birmingham, UK, 1–2 September 2011; pp. 41–46. [Google Scholar] [CrossRef]
- Paulus, D.; Landsmann, P.; Kennel, R. Saliency based sensorless field- oriented control for permanent magnet synchronous machines in the whole speed range. In Proceedings of the 3rd IEEE International Symposium on Sensorless Control for Electrical Drives (SLED 2012), Milwaukee, WI, USA, 21–22 September 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Consoli, A.; Scarcella, G.; Testa, A. A new zero-frequency flux-position detection approach for direct-field-oriented-control drives. IEEE Trans. Ind. Appl. 2000, 36, 797–804. [Google Scholar] [CrossRef]
- Consoli, A.; Scarcella, G.; Testa, A.; Lipo, T.A. Air-Gap Flux Position Estimation of Inaccessible Neutral Induction Machines by Zero-Sequence Voltage. Electr. Power Components Syst. 2002, 30, 77–88. [Google Scholar] [CrossRef]
- Holtz, J.; Pan, H. Elimination of saturation effects in sensorless position controlled induction motors. In Proceedings of the Conference Record of the 2002 IEEE Industry Applications Conference—37th IAS Annual Meeting (Cat. No.02CH37344), Pittsburgh, PA, USA, 13–18 October 2002; Volume 3, pp. 1695–1702. [Google Scholar] [CrossRef]
- Holtz, J.; Pan, H. Acquisition of Rotor Anisotropy Signals in Sensorless Position Control Systems. IEEE Trans. Ind. Appl. 2004, 40, 1379–1387. [Google Scholar] [CrossRef]
- Holtz, J. Sensorless Control of Induction Machines—With or Without Signal Injection? IEEE Trans. Ind. Electron. 2006, 53, 7–30. [Google Scholar] [CrossRef]
- Consoli, A.; Scarcella, G.; Tutino, G.; Testa, A. Zero frequency rotor position detection for synchronous PM motors. In Proceedings of the 2000 IEEE 31st Annual Power Electronics Specialists Conference—Conference Proceedings (Cat. No.00CH37018), Galway, Ireland, 23 June 2000; Volume 2, pp. 879–884. [Google Scholar] [CrossRef]
- Strothmann, R. Fremderregte Elektrische Maschine. EP Patent EP1005716B1, 14 November 2001. [Google Scholar]
- Thiemann, P.; Mantala, C.; Mueller, T.; Strothmann, R.; Zhou, E. Direct Flux Control (DFC): A New Sensorless Control Method for PMSM. In Proceedings of the 2011 46th International Universities’ Power Engineering Conference, Soest, Germany, 5–8 September 2011. [Google Scholar]
- Mantala, C. Sensorless Control of Brushless Permanent Magnet Motors. Ph.D. Thesis, University of Bolton, Bolton, UK, 2013. [Google Scholar]
- Grasso, E.; Merl, D.; Nienhaus, M. Verfahren und Vorrichtung zum Bestimmen einer Läuferlage eines Läufers einer elektronisch kommutierten elektrischen Maschine. DE Patent DE102016117258A1, 21 March 2018. [Google Scholar]
- Merl, D.; Grasso, E.; Schwartz, R.; Nienhaus, M. A Direct Flux Observer based on a Fast Resettable Integrator Circuitry for Sensorless Control of PMSMs. In Proceedings of the ACTUATOR 2018; 16th International Conference on New Actuators, Bremen, Germany, 25–27 June 2018; p. 4. [Google Scholar]
- Grasso, E.; Mandriota, R.; König, N.; Nienhaus, M. Analysis and Exploitation of the Star-Point Voltage of Synchronous Machines for Sensorless Operation. Energies 2019, 12, 4729. [Google Scholar] [CrossRef]
- Iwaji, Y.; Kokami, Y.; Kurosawa, M. Position-sensorless control method at low speed for permanent magnet synchronous motors using induced voltage caused by magnetic saturation. In Proceedings of the 2010 International Power Electronics Conference (ECCE ASIA), Sapporo, Japan, 21–24 June 2010; pp. 2238–2243. [Google Scholar] [CrossRef]
- Iwaji, Y.; Takahata, R.; Suzuki, T.; Aoyagi, S. Position Sensorless Control Method at Zero-Speed Region for Permanent Magnet Synchronous Motors Using the Neutral Point Voltage of Stator Windings. IEEE Trans. Ind. Appl. 2016, 52, 4020–4028. [Google Scholar] [CrossRef]
- Hara, T.; Aoyagi, S.; Ajima, T.; Iwaji, Y.; Takahata, R.; Sugiyama, Y. Neutral Point Voltage Model of Stator Windings of Permanent Magnet Synchronous Motors with Magnetic Asymmetry. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 1611–1616. [Google Scholar] [CrossRef]
- Xu, P.; Zhu, Z. Novel Carrier Signal Injection Method Using Zero Sequence Voltage for Sensorless Control of PMSM Drives. IEEE Trans. Ind. Electron. 2015, 63. [Google Scholar] [CrossRef]
- Xu, P.L.; Zhu, Z.Q. Novel Square-Wave Signal Injection Method Using Zero-Sequence Voltage for Sensorless Control of PMSM Drives. IEEE Trans. Ind. Electron. 2016, 63, 7444–7454. [Google Scholar] [CrossRef]
- Schuhmacher, K.; Kleen, S.; Nienhaus, M. Comparison of Anisotropy Signals for Sensorless Control of Star-Connected PMSMs. In Proceedings of the 2019 IEEE 10th International Symposium on Sensorless Control for Electrical Drives (SLED), Turin, Italy, 9–10 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Raja, R.; Sebastian, T.; Wang, M. Online Stator Inductance Estimation for Permanent Magnet Motors Using PWM Excitation. IEEE Trans. Transp. Electrif. 2019, 5, 107–117. [Google Scholar] [CrossRef]
- Poltschak, F.; Amrhein, W. Influence of winding layout of PMSM on inductance and its impact on suitability for sensorless vector control. In Proceedings of the SPEEDAM 2010, Pisa, Italy, 14–16 June 2010; pp. 1002–1007. [Google Scholar] [CrossRef]
- Gächter, J.; Hirz, M.; Seebacher, R. The effect of rotor position errors on the dynamic behavior of field-orientated controlled PMSM. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017; pp. 1–8. [Google Scholar] [CrossRef]




















| Case | |||||
|---|---|---|---|---|---|
| 1 | 100 | −50 | 25 | 1 | 24 |
| 2 | 100 | −50 | 25 | 24 | 1 |
| Motor Parameters | Values |
|---|---|
| Phase resistance | 1.1 |
| d-axis inductance | 394 |
| q-axis inductance | 475 |
| Pole pairs | 8 |
| Torque constant | 0.1186 |
| Nominal voltage | 24 V |
| Nominal current | 1.5 A |
| Nominal speed | 500 rpm |
| Nominal torque | 200 mNM |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grasso, E.; Palmieri, M.; Mandriota, R.; Cupertino, F.; Nienhaus, M.; Kleen, S. Analysis and Application of the Direct Flux Control Sensorless Technique to Low-Power PMSMs. Energies 2020, 13, 1453. https://doi.org/10.3390/en13061453
Grasso E, Palmieri M, Mandriota R, Cupertino F, Nienhaus M, Kleen S. Analysis and Application of the Direct Flux Control Sensorless Technique to Low-Power PMSMs. Energies. 2020; 13(6):1453. https://doi.org/10.3390/en13061453
Chicago/Turabian StyleGrasso, Emanuele, Marco Palmieri, Riccardo Mandriota, Francesco Cupertino, Matthias Nienhaus, and Stephan Kleen. 2020. "Analysis and Application of the Direct Flux Control Sensorless Technique to Low-Power PMSMs" Energies 13, no. 6: 1453. https://doi.org/10.3390/en13061453
APA StyleGrasso, E., Palmieri, M., Mandriota, R., Cupertino, F., Nienhaus, M., & Kleen, S. (2020). Analysis and Application of the Direct Flux Control Sensorless Technique to Low-Power PMSMs. Energies, 13(6), 1453. https://doi.org/10.3390/en13061453





