Effect of Axial In-Situ Stress in Deep Tunnel Analysis Considering Strain Softening and Dilatancy
Abstract
:1. Introduction
2. Theoretical Analysis
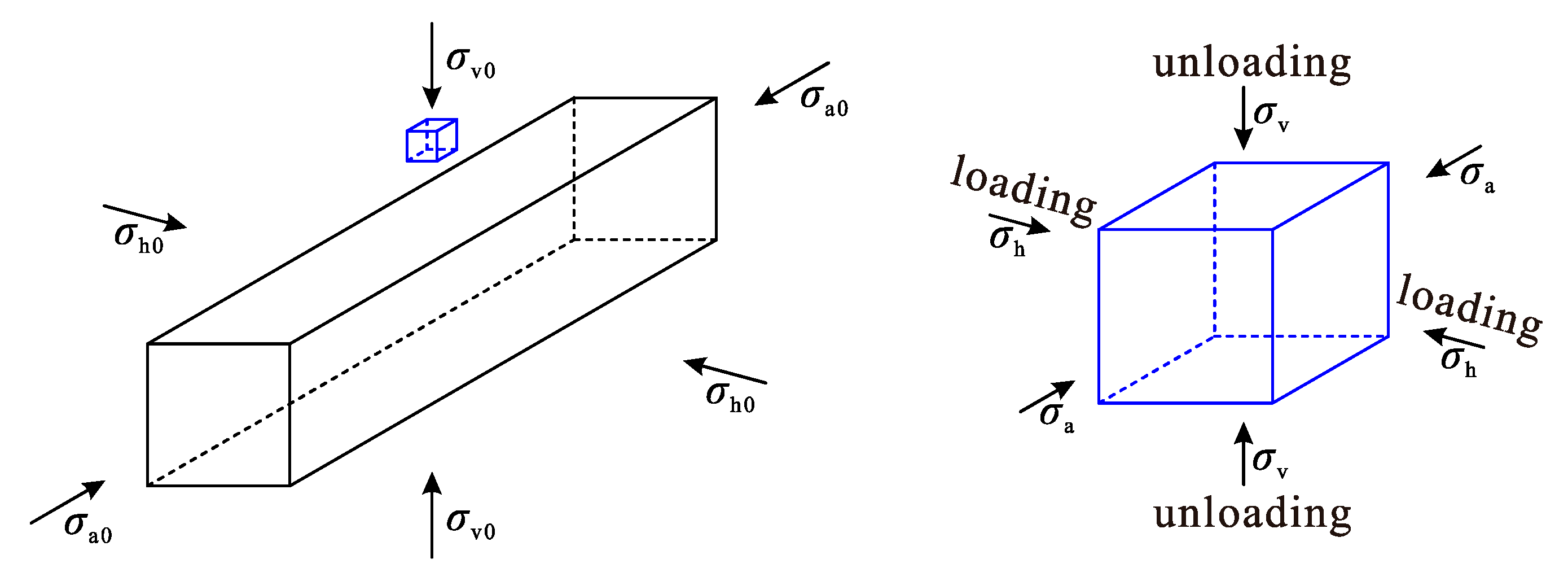
2.1. Description of the Problem
2.2. When σa is σ1 or σ3 at the Initial Yield
2.3. When σa Is σ2 at the Initial Yield
3. Numerical Simulation
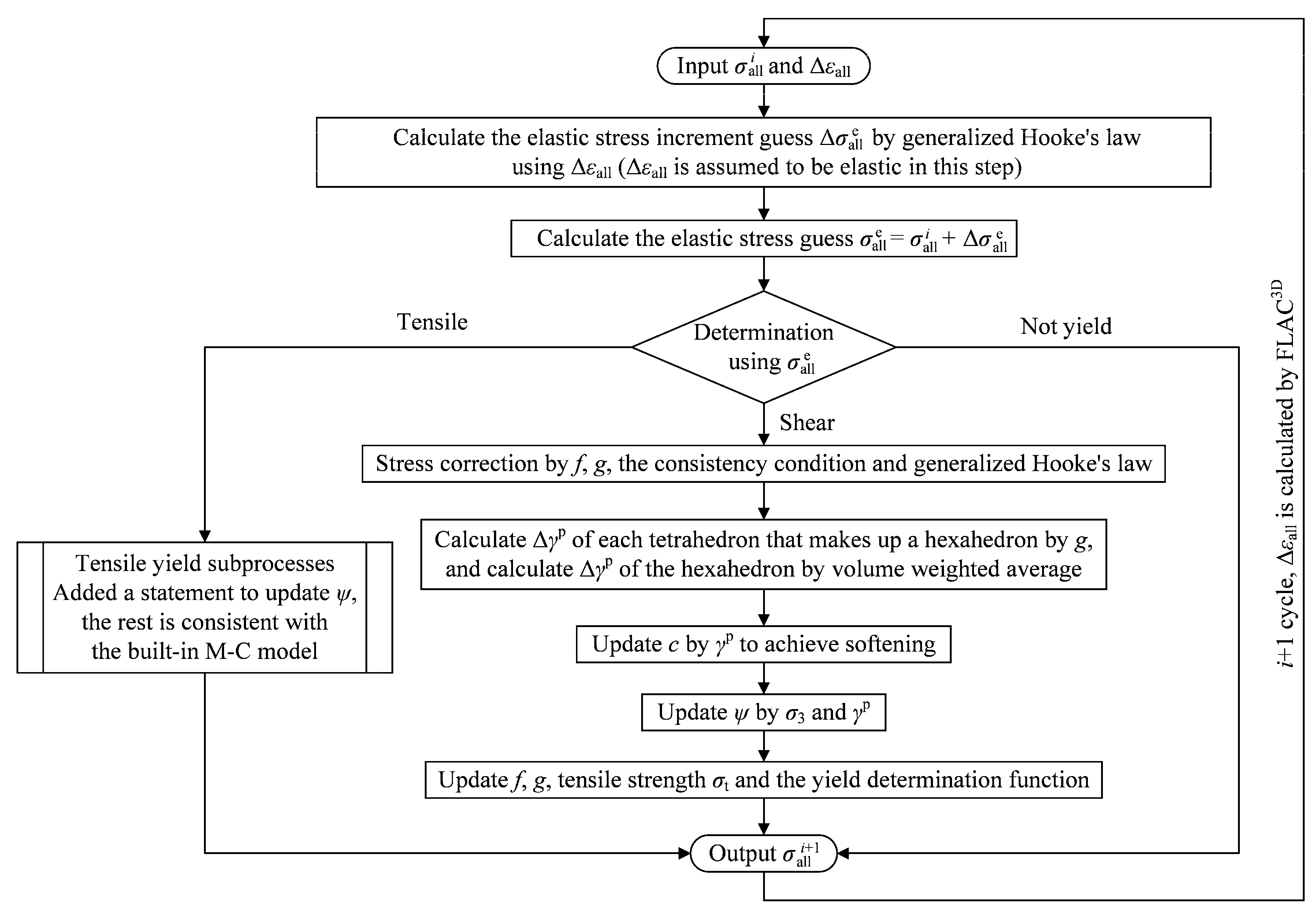
3.1. Constitutive Model Development
3.2. Numerical Model and Schemes
3.3. Analysis of the Roof Subsidence and Plastic Zone Depth
3.4. Analysis of the Stress Adjustment Process
4. Verification via Field Monitoring Data
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kang, H.; Wu, Y.; Gao, F.; Lin, J.; Jiang, P. Fracture characteristics in rock bolts in underground coal mine roadways. Int. J. Rock Mech. Min. Sci. 2013, 62, 105–112. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, N.; Li, J.; Ma, L.; Fan, P. Computational method of large deformation and its application in deep mining tunnel. Tunn. Undergr. Space Technol. 2015, 50, 47–53. [Google Scholar] [CrossRef]
- Tao, M.; Hong, Z.; Peng, K.; Sun, P.; Cao, M.; Du, K. Evaluation of Excavation-Damaged Zone around Underground Tunnels by Theoretical Calculation and Field Test Methods. Energies 2019, 12, 1682. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.-Q.; Chen, M.; Jing, H.-W.; Chen, K.-F.; Meng, B. A case study on large deformation failure mechanism of deep soft rock roadway in Xin’An coal mine, China. Eng. Geol. 2017, 217, 89–101. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, C.; Jiang, B.; Li, N.; Wang, Y. Elastoplastic Coupling Solution of Circular Openings in Strain-Softening Rock Mass Considering Pressure-Dependent Effect. Int. J. Geomech. 2018, 18. [Google Scholar] [CrossRef]
- Cui, L.; Zheng, J.-J.; Dong, Y.-K.; Zhang, B.; Wang, A. Prediction of critical strains and critical support pressures for circular tunnel excavated in strain-softening rock mass. Eng. Geol. 2017, 224, 43–61. [Google Scholar] [CrossRef]
- Song, L.; Li, H.-Z.; Chan, C.L.; Low, B.K. Reliability analysis of underground excavation in elastic-strain-softening rock mass. Tunn. Undergr. Space Technol. 2016, 60, 66–79. [Google Scholar] [CrossRef]
- Lu, A.-Z.; Xu, G.-S.; Sun, F.; Sun, W.-Q. Elasto-plastic analysis of a circular tunnel including the effect of the axial in situ stress. Int. J. Rock Mech. Min. Sci. 2010, 47, 50–59. [Google Scholar] [CrossRef]
- Wang, S.; Wu, Z.; Guo, M.; Ge, X. Theoretical solutions of a circular tunnel with the influence of axial in situ stress in elastic-brittle-plastic rock. Tunn. Undergr. Space Technol. 2012, 30, 155–168. [Google Scholar] [CrossRef]
- Guan, K.; Zhu, W.; Wei, J.; Liu, X.; Niu, L.; Wang, X. A finite strain numerical procedure for a circular tunnel in strain-softening rock mass with large deformation. Int. J. Rock Mech. Min. Sci. 2018, 112, 266–280. [Google Scholar] [CrossRef]
- Alejano, L.R.; Alonso, E. Considerations of the dilatancy angle in rocks and rock masses. Int. J. Rock Mech. Min. Sci. 2005, 42, 481–507. [Google Scholar] [CrossRef]
- Cai, M.; Kaiser, P.K.; Tasaka, Y.; Minami, M. Determination of residual strength parameters of jointed rock masses using the GSI system. Int. J. Rock Mech. Min. Sci. 2007, 44, 247–265. [Google Scholar] [CrossRef]
- Cai, M.; Kaiser, P.K.; Uno, H.; Tasaka, Y.; Minami, M. Estimation of rock mass deformation modulus and strength of jointed hard rock masses using the GSI system. Int. J. Rock Mech. Min. Sci. 2004, 41, 3–19. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. Practical estimates of rock mass strength. Int. J. Rock Mech. Min. Sci. 1997, 34, 1165–1186. [Google Scholar] [CrossRef]
- Hoek, E.; Diederichs, M.S. Empirical estimation of rock mass modulus. Int. J. Rock Mech. Min. Sci. 2006, 43, 203–215. [Google Scholar] [CrossRef]
- Zhao, X.G.; Cai, M.F.; Cai, M. Considerations of rock dilation on modeling failure and deformation of hard rocks: A case study of the mine-by test tunnel in Canada. J. Rock Mech. Geotech. Eng. 2010, 2, 338–349. [Google Scholar]
- Zhao, X.G.; Cai, M. Influence of plastic shear strain and confinement-dependent rock dilation on rock failure and displacement near an excavation boundary. Int. J. Rock Mech. Min. Sci. 2010, 47, 723–738. [Google Scholar] [CrossRef]
- Meng, Q.; Chen, Y.; Zhang, M.; Han, L.; Pu, H.; Liu, J. On the Kaiser Effect of Rock under Cyclic Loading and Unloading Conditions: Insights from Acoustic Emission Monitoring. Energies 2019, 12, 3255. [Google Scholar] [CrossRef] [Green Version]
- Arzua, J.; Alejano, L.R. Dilation in granite during servo-controlled triaxial strength tests. Int. J. Rock Mech. Min. Sci. 2013, 61, 43–56. [Google Scholar] [CrossRef]
- Arzua, J.; Alejano, L.R.; Walton, G. Strength and dilation of jointed granite specimens in servo-controlled triaxial tests. Int. J. Rock Mech. Min. Sci. 2014, 69, 93–104. [Google Scholar] [CrossRef]
- Pérez-Rey, I.; Alejano, L.R.; Alonso, E.; Arzúa, J.; Araújo, M. An Assessment of the Post-peak Strain Behavior of Laboratory Intact Rock Specimens Based on Different Dilation Models. Procedia Eng. 2017, 191, 394–401. [Google Scholar] [CrossRef]
- Lin, P.; Liu, H.; Zhou, W. Experimental study on failure behaviour of deep tunnels under high in-situ stresses. Tunn. Undergr. Space Technol. 2015, 46, 28–45. [Google Scholar] [CrossRef]
- Paterson, M.S.; Olgaard, D.L. Rock deformation tests to large shear strains in torsion. J. Struct. Geol. 2000, 22, 1341–1358. [Google Scholar] [CrossRef]
- Yi, K.; Kang, H.; Ju, W.; Liu, Y.; Lu, Z. Synergistic effect of strain softening and dilatancy in deep tunnel analysis. Tunn. Undergr. Space Technol. 2020, 97, 103280. [Google Scholar] [CrossRef]
- Wang, F.; Qian, D. Difference solution for a circular tunnel excavated in strain-softening rock mass considering decayed confinement. Tunn. Undergr. Space Technol. 2018, 82, 66–81. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Lake, L.W.; Sahimi, M. Insights into rock typing: A Critical Study. SPE J. 2019, 24, 230–242. [Google Scholar] [CrossRef]
- Kang, H.; Yi, B.; Gao, F.; Lu, H. Database and characteristics of underground in-situ stress distribution in Chinese coal mines. J. China Coal Soc. 2019, 44, 23–33. [Google Scholar]
- Cai, W.; Dou, L.; Ju, Y.; Cao, W.; Yuan, S.; Si, G. A plastic strain-based damage model for heterogeneous coal using cohesion and dilation angle. Int. J. Rock Mech. Min. Sci. 2018, 110, 151–160. [Google Scholar] [CrossRef]
- Zou, J.-F.; He, Z. Numerical approach for strain-softening rock with axial stress. Proc. Inst. Civ. Eng. Geotec. 2016, 169, 276–290. [Google Scholar] [CrossRef]
- Pourhosseini, O.; Shabanimashcool, M. Development of an elasto-plastic constitutive model for intact rocks. Int. J. Rock Mech. Min. Sci. 2014, 66, 1–12. [Google Scholar] [CrossRef]
- Vermeer, P.A. Non-Associated Plasticity for Soils, Concrete and Rock. In Physics of Dry Granular Media; Herrmann, H.J., Hovi, J.P., Luding, S., Eds.; Springer: Dordrecht, The Netherlands, 1998; pp. 163–196. [Google Scholar]
- Itasca Inc. FLAC3D: Fast Lagrangian Analysis of Continua in 3 Dimension. Version 5.01; Itasca Inc.: Minneapolis, MN, USA, 2012. [Google Scholar]
- Walton, G.; Diederichs, M.S.; Alejano, L.R.; Arzúa, J. Verification of a laboratory-based dilation model for in situ conditions using continuum models. J. Rock Mech. Geotech. Eng. 2014, 6, 522–534. [Google Scholar] [CrossRef] [Green Version]
- Kang, H.; Fan, M.; Gao, F.; Zhang, H. Deformation and support of rock roadway at depth more than 1000 meters. Chin. J. Rock Mech. Eng. 2015, 34, 2227–2241. [Google Scholar]
- Lu, Y.; Cheng, Y.; Ge, Z.; Cheng, L.; Zuo, S.; Zhong, J. Determination of Fracture Initiation Locations during Cross-Measure Drilling for Hydraulic Fracturing of Coal Seams. Energies 2016, 9, 358. [Google Scholar] [CrossRef] [Green Version]










© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, K.; Liu, Z.; Lu, Z.; Zhang, J.; Dong, S. Effect of Axial In-Situ Stress in Deep Tunnel Analysis Considering Strain Softening and Dilatancy. Energies 2020, 13, 1502. https://doi.org/10.3390/en13061502
Yi K, Liu Z, Lu Z, Zhang J, Dong S. Effect of Axial In-Situ Stress in Deep Tunnel Analysis Considering Strain Softening and Dilatancy. Energies. 2020; 13(6):1502. https://doi.org/10.3390/en13061502
Chicago/Turabian StyleYi, Kang, Zhenghe Liu, Zhiguo Lu, Junwen Zhang, and Shuangyong Dong. 2020. "Effect of Axial In-Situ Stress in Deep Tunnel Analysis Considering Strain Softening and Dilatancy" Energies 13, no. 6: 1502. https://doi.org/10.3390/en13061502
APA StyleYi, K., Liu, Z., Lu, Z., Zhang, J., & Dong, S. (2020). Effect of Axial In-Situ Stress in Deep Tunnel Analysis Considering Strain Softening and Dilatancy. Energies, 13(6), 1502. https://doi.org/10.3390/en13061502




