Analytical Solution for Coupled Diffusion Induced Stress Model for Lithium-Ion Battery
Abstract
:1. Introduction
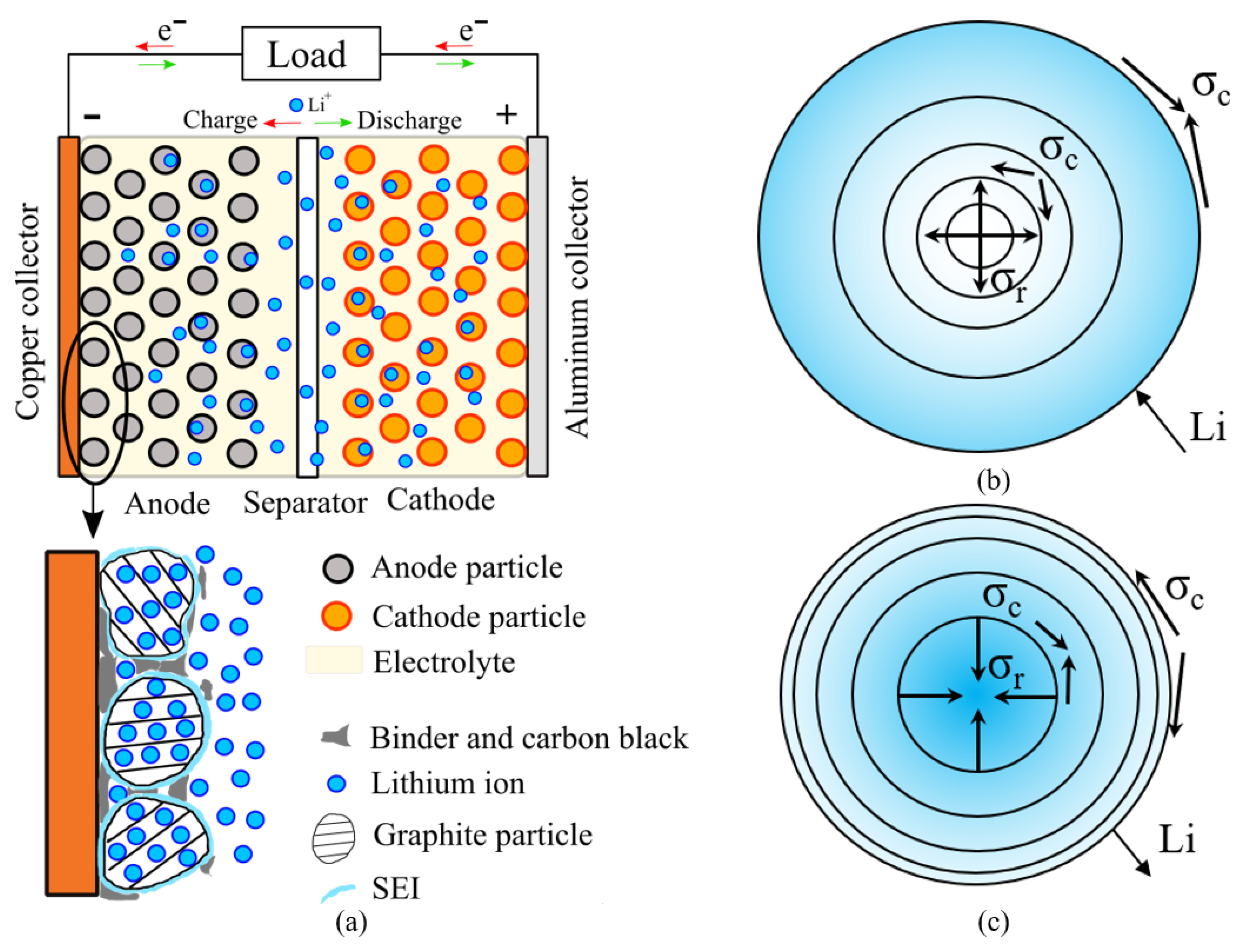
2. Problem Formulation
2.1. Mechanical Problem
2.2. Diffusive Problem
2.3. Uncoupled Problem
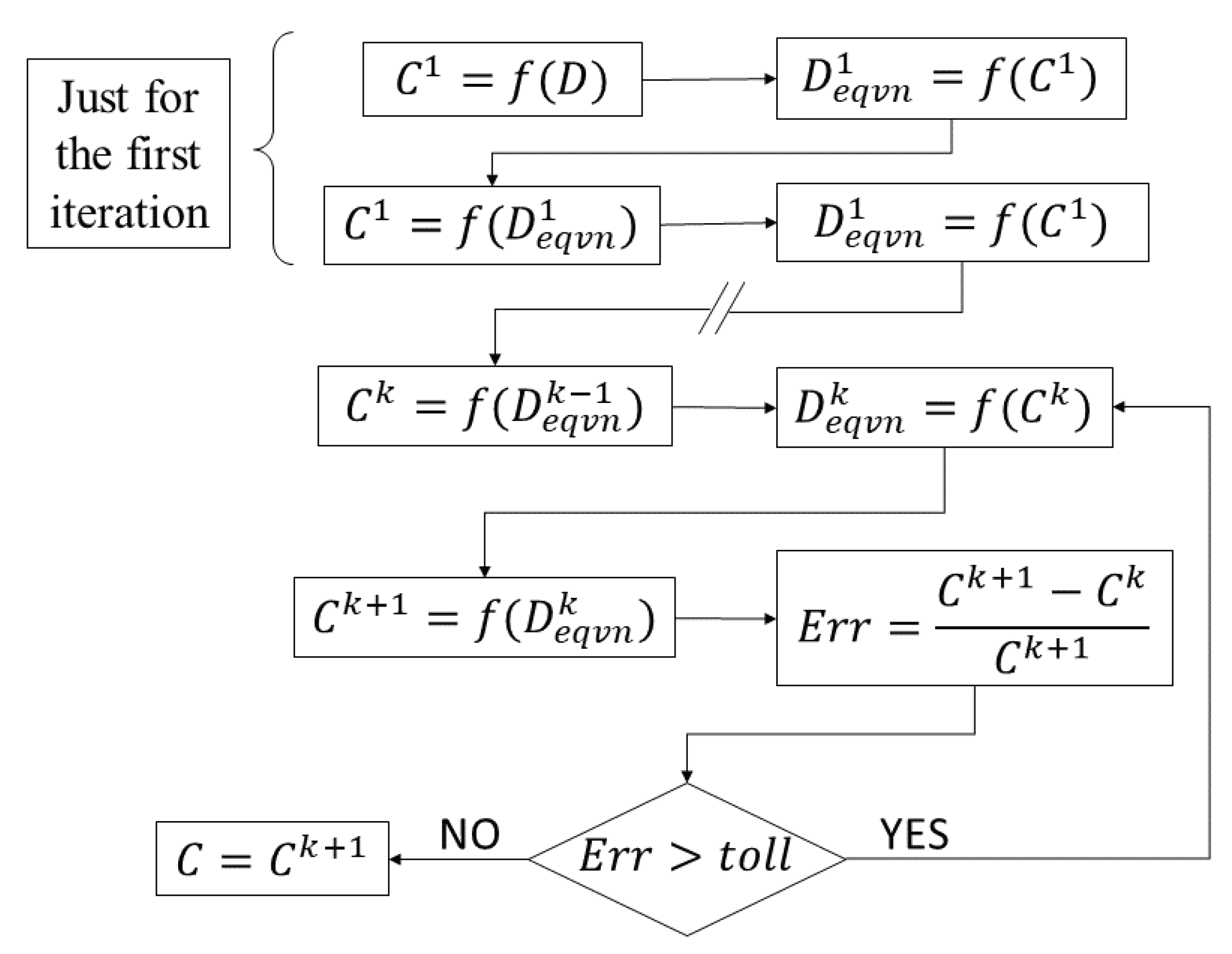
2.4. Coupled Problem
- The concentration field is calculated according to the physical diffusion coefficient.
- The equivalent diffusion coefficient is calculated for each radial position with the concentration function.
- A new concentration function is computed with the equivalent diffusion coefficient computed in the previous iteration.
3. Results and Discussion
3.1. Compatibility between Model Assumptions and Real Material
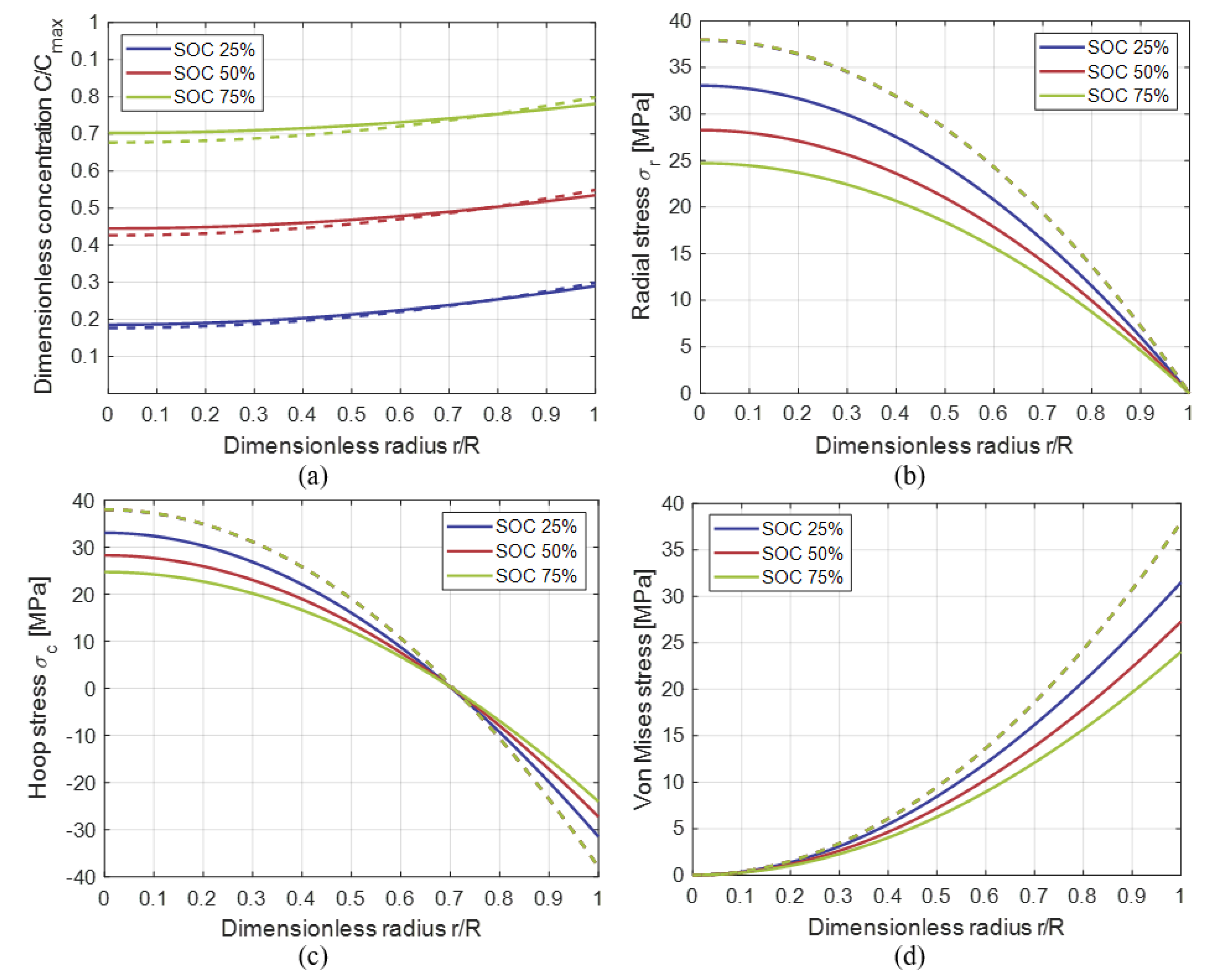
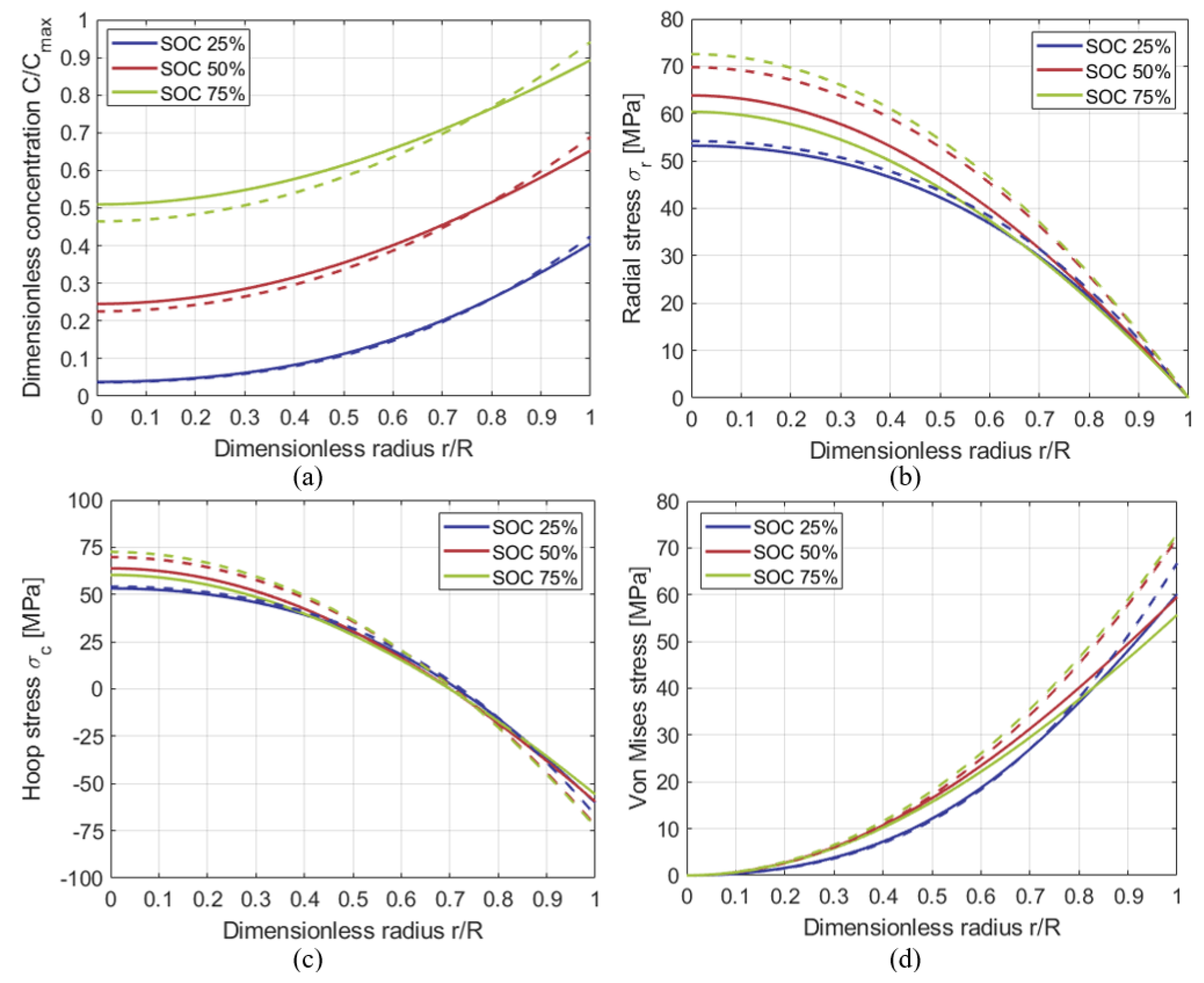
3.2. Comparison with the Results of Numerical Models in Literature
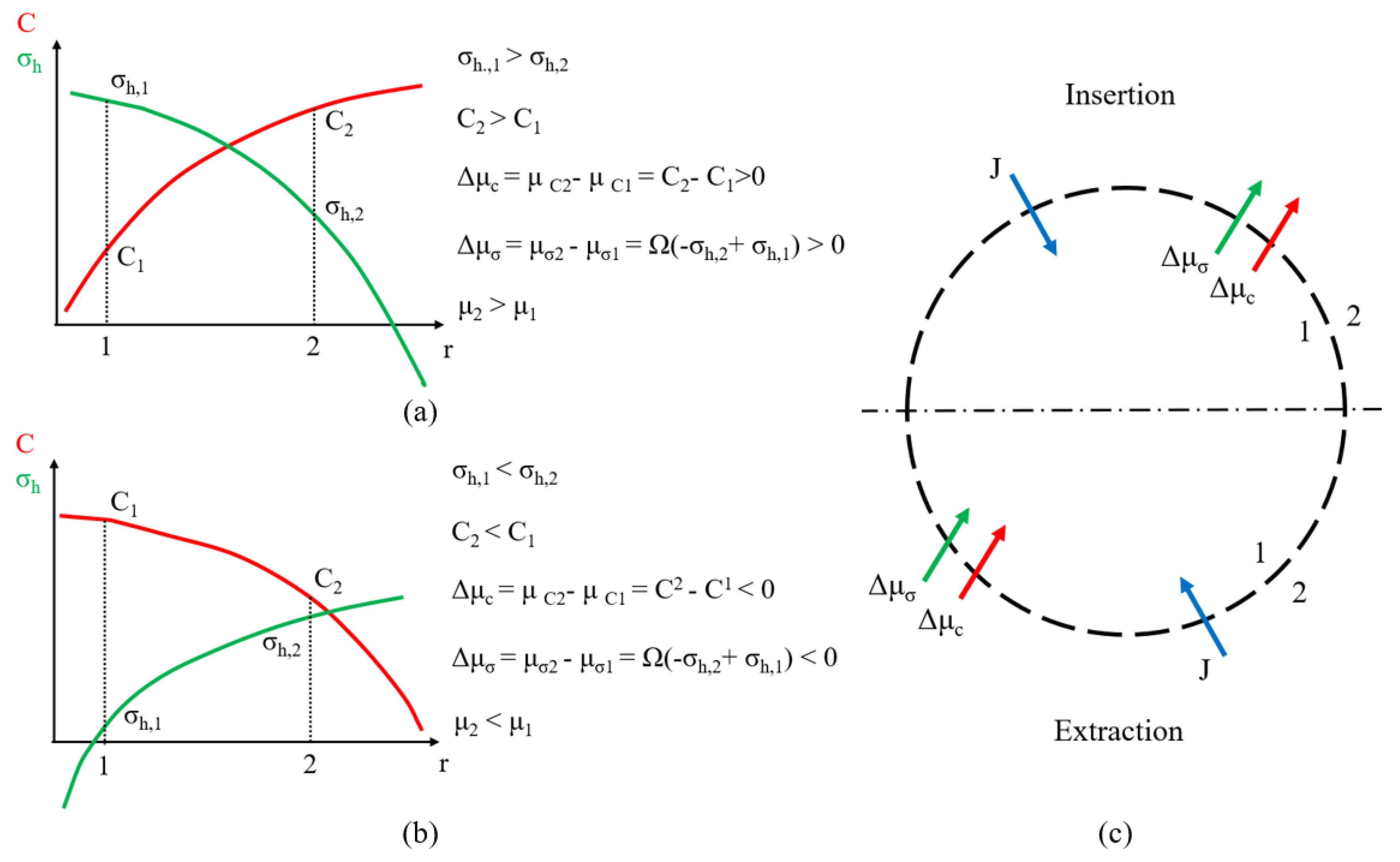
3.3. Insertion under Galvanostatic Control
3.4. Extraction under Galvanostatic Control
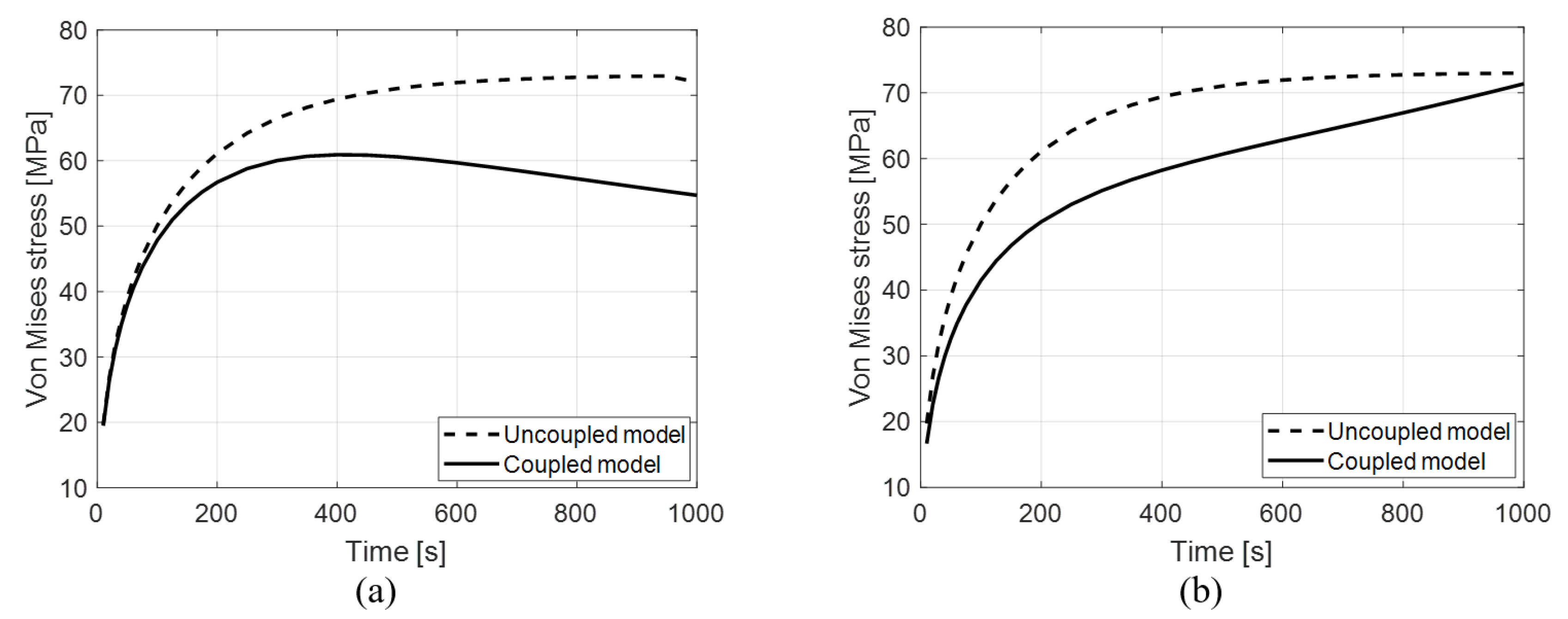
3.5. Evolution of Von Mises Stress in Time
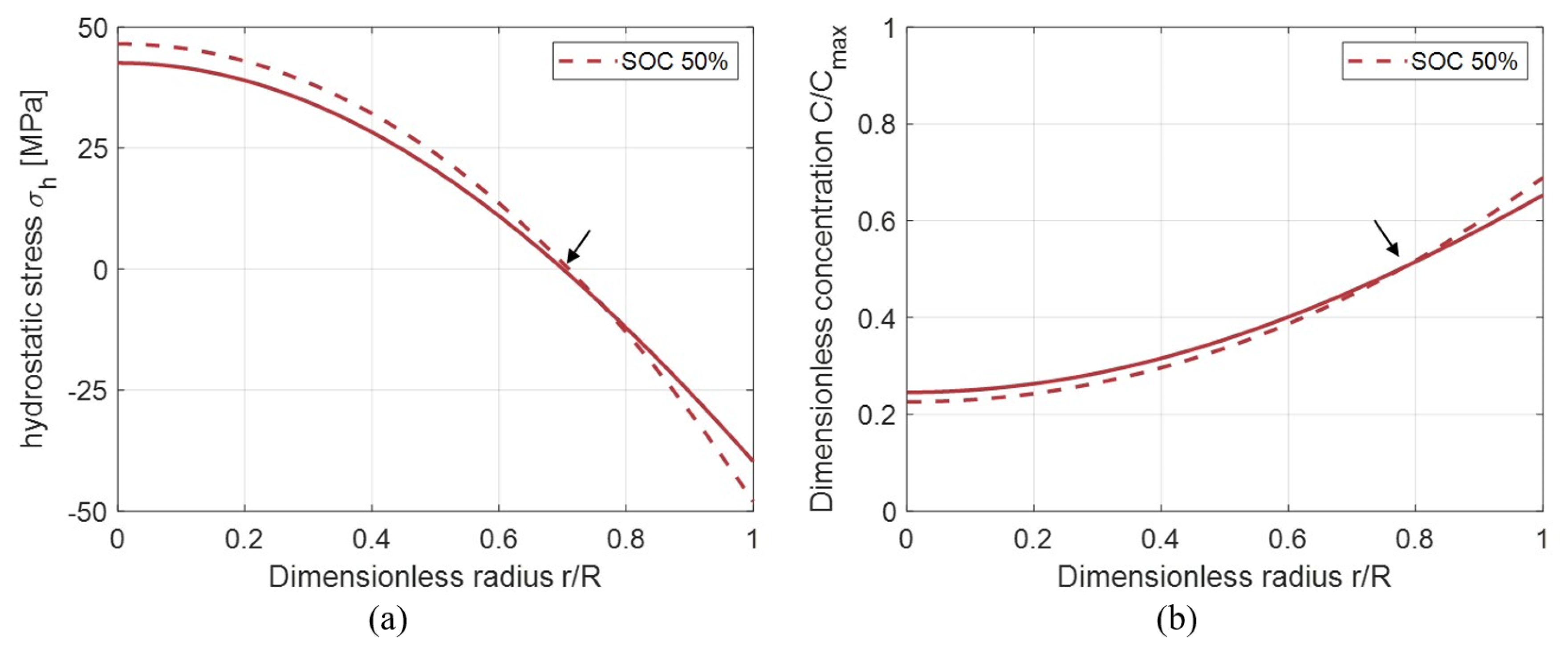
3.6. Influence of Hydrostatic Stress on Concentration
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| C | Concentration | mol/m |
| Initial concentration | mol/m | |
| Maximum concentration | mol/m | |
| Surface concentration | mol/m | |
| D | Diffusion coefficient | m/s |
| Equivalent diffusion coefficient | m/s | |
| E | Young Modulus | |
| F | Faraday constant | 96485.332 As/mol |
| I | Current density | A/m |
| J | Lithium flux | mol/ms |
| M | Mobility | mol· s/Kg |
| r | Radius | m |
| R | Particle radius | m |
| Gas constant | 8.3145 J/mol K | |
| State of charge | - | |
| T | Temperature 298 | K |
| u | Displacement | m |
| x | Normalized radial coordinate | - |
| Hoop strain | - | |
| Chemical strain | - | |
| Radial strain | - | |
| Chemical potential | J/mol | |
| Reference chemical potential | J/mol | |
| Poisson ratio | - | |
| Hoop stress | MPa | |
| Hydrostatic stress | MPa | |
| Radial stress | MPa | |
| Characteristic time | - | |
| Partial molar volume | m/mol |
References
- Miao, Y. Current li-ion battery technologies in electric vehicles and opportunities for advancements. Energies 2019, 12, 1074. [Google Scholar] [CrossRef] [Green Version]
- Soma, A. Hybridization Factor and Performance of Hybrid Electric Telehandler Vehicle. IEEE Trans. Ind. Appl. 2016, 52, 5130–5138. [Google Scholar] [CrossRef]
- Mocera, F. Battery performance analysis for working vehicles applications. IEEE Trans. Ind. Appl. 2019, 56, 644–653. [Google Scholar] [CrossRef]
- Vergori, E. Battery modelling and simulation using a programmable testing equipment. Computers 2018, 7, 20. [Google Scholar] [CrossRef] [Green Version]
- Kleiner, J. Thermal modelling of a prismatic lithium-ion cell in a battery electric vehicle environment: Influences of the experimental validation setup. Energies 2019, 13, 62. [Google Scholar] [CrossRef] [Green Version]
- Gantenbein, S. Capacity fade in lithium-ion batteries and cyclic aging over various state-of-charge ranges. Sustainability 2019, 11, 6697. [Google Scholar] [CrossRef] [Green Version]
- Lee, D. Modeling the Effect of the Loss of Cyclable Lithium on the Performance Degradation of a Lithium-Ion Battery. Energies 2019, 12, 4386. [Google Scholar] [CrossRef] [Green Version]
- Willenberg, L.K. High-Precision Monitoring of Volume Change of Commercial Lithium-Ion Batteries by Using Strain Gauges. Sustainability 2020, 12, 557. [Google Scholar] [CrossRef] [Green Version]
- Qi, Z.; Shan, Z.; Ma, W.; Li, L.; Wang, S.; Li, C.; Wang, Z. Strain Analysis on Electrochemical Failures of Nanoscale Silicon Electrode Based on Three-Dimensional in Situ Measurement. Appl. Sci. 2020, 10, 468. [Google Scholar] [CrossRef] [Green Version]
- Cheng, X. In situ stress measurement techniques on li-ion battery electrodes: A review. Energies 2017, 10, 591. [Google Scholar] [CrossRef]
- Prussin, S. Generation and distribution of dislocations by solute diffusion. J. Appl. Phys. 1961, 32, 1876–1881. [Google Scholar] [CrossRef]
- Larchè, J. A linear theory of thermochemical equilibrium of solids under stress. Acta Metall. 1973, 8, 1051–1063. [Google Scholar] [CrossRef]
- Larchè, J. The effect of self-stress on diffusion in solids. Acta Metall. 1982, 30, 1835–1845. [Google Scholar] [CrossRef]
- Chu, J.L. Chemical stresses in composite circular cylinders. J. Appl. Phys. 1993, 73, 2239–2248. [Google Scholar] [CrossRef]
- Chu, J.L. The effect of chemical stresses on diffusion. J. Appl. Phys. 1994, 75, 2823–2829. [Google Scholar] [CrossRef]
- Cheng, Y.T. Evolution of stress within a spherical insertion electrode particle under potentiostatic and galvanostatic operation. J. Power Sources 2009, 190, 453–460. [Google Scholar] [CrossRef]
- Cheng, Y.T. The influence of surface mechanics on diffusion induced stresses within spherical nanoparticles. J. Appl. Phys. 2008, 104, 083521. [Google Scholar] [CrossRef]
- Christensen, J. Modeling diffusion-induced stress in Li-ion cells with porous electrodes. J. Electrochem. Soc. 2010, 157, 336–386. [Google Scholar] [CrossRef]
- Christensen, J. Stress generation and fracture in lithium insertion materials. J. Solid State Electrochem. 2006, 10, 293–319. [Google Scholar] [CrossRef]
- Christensen, J. A mathematical model of stress generation and fracture in lithium manganese oxide. J. Electrochem. Soc. 2006, 153, 1019–1030. [Google Scholar] [CrossRef]
- Zhang, X. Numerical simulation of intercalation-induced stress in Li-Ion battery electrode Particles. J. Electrochem. Soc. 2007, 154, 910–916. [Google Scholar] [CrossRef]
- Zhang, X. Intercalation-induced stress and heat generation within single lithium-ion battery cathode particles. J. Electrochem. Soc. 2008, 155, 542–555. [Google Scholar] [CrossRef]
- Wang, W.L. Effect of chemical stress on diffusion in a hollow cylinder. J. Appl. Phys. 2002, 91, 9584–9590. [Google Scholar] [CrossRef]
- Wang, W.L. Interaction between diffusion and chemical stresses. Mater. Sci. Eng. A 2005, 409, 153–159. [Google Scholar]
- Zhao, Y. A review on modeling of electro-chemo-mechanics in lithium-ion batteries. J. Power Sources 2018, 413, 259–283. [Google Scholar] [CrossRef]
- Bagheri, A. On the effects of hydrostatic stress on Li diffusion kinetics and stresses in spherical active particles of Li-ion battery electrodes. J. Power Sources 2019, 137, 103–134. [Google Scholar] [CrossRef]
- Eshghinejad, A. The coupled lithium ion diffusion and stress in battery electrodes. Mech. Mater. 2015, 91, 343–350. [Google Scholar] [CrossRef] [Green Version]
- Haftbaradaran, H. Continuum and atomistic models of strongly coupled diffusion, stress, and solute concentration. J. Power Sources 2011, 196, 361–370. [Google Scholar] [CrossRef]
- Wu, B. A consistently coupled multiscale mechanical–electrochemical battery model with particle interaction and its validation. J. Mech. Phys. Solids 2019, 125, 89–111. [Google Scholar] [CrossRef]
- Deshpande, R. Battery cycle life prediction with coupled chemical degradation and fatigue mechanics. J. Electrochem. Soc. 2012, 159, 1730–1738. [Google Scholar] [CrossRef]
- Kotak, N. Electrochemistry-mechanics coupling in intercalation electrodes. J. Electrochem. Soc. 2018, 165, 1064–1083. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y. Simulation of crack behavior of secondary particles in Li-ion battery electrodes during lithiation/de-lithiation cycles. J. Mech. Sci. 2018, 155, 178–186. [Google Scholar] [CrossRef]
- Grantab, R. Pressure-gradient dependent diffusion and crack propagation in lithiated silicon nanowires. J. Electrochem. Soc. 2012, 159, 584–591. [Google Scholar] [CrossRef]
- Verbrugge, M.W. Stress and strain-energy distributions within diffusion-controlled insertion-electrode particles subjected to periodic potential excitations. J. Electrochem. Soc. 2009, 156, 927–937. [Google Scholar] [CrossRef]
- Tang, Z.Y. Determination of the Lithium Ion Diffusion Coefficient in Graphite Anode Material. Acta Phys. Chim. Sin. 2001, 17, 388. [Google Scholar]
- Jun, G.H. Diffusion coefficient of lithium in artificial graphite, mesocarbon microbeads, and disordered carbon. New Carbon Mater. 2007, 22, 7–10. [Google Scholar]
- Barai, P. Stochastic analysis of diffusion induced damage in lithium-ion battery electrodes. J. Electrochem. Soc. 2013, 160, 955–967. [Google Scholar] [CrossRef]
- Korsunsky, A.M. Explicit formulae for the internal stress in spherical particles of active material within lithium ion battery cathodes during charging and discharging. Mater. Des. 2015, 69, 247–252. [Google Scholar] [CrossRef]
- Pimenta, V. Synthesis of Li-Rich NMC: A Comprehensive Study. Mater. Des. 2017, 23, 9923–9936. [Google Scholar] [CrossRef]
- Mendoza, H. Mechanical and Electrochemical Response of a LiCoO2 Cathode using Reconstructed Microstructures. Electrochim. Acta 2016, 190, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Malavé, V. A computational model of the mechanical behavior within reconstructed LixCoO2 Li-ion battery cathode particles. Electrochim. Acta 2014, 130, 707–717. [Google Scholar] [CrossRef]
- Korsunsky, A.M. Generation of Realistic Particle Structures and Simulations of Internal Stress: A Numerical/AFM Study of LiMn2O4 Particles. J. Electrochem. Soc. 2011, 158, 434–442. [Google Scholar]
- Chung, M. Implementing Realistic Geometry and Measured Diffusion Coefficients into Single Particle Electrode Modeling Based on Experiments with Single LiMn2O4 Spinel Particles. J. Electrochem. Soc. 2011, 158, 371–378. [Google Scholar] [CrossRef]
- Ai, W. Electrochemical Thermal-Mechanical Modelling of Stress Inhomogeneity in Lithium-Ion Pouch Cells. J. Electrochem. Soc. 2011, 167, 013512. [Google Scholar] [CrossRef]
- Huang, S. Stress generation during lithiation of high-capacity electrode particles in lithium ion batteries. Acta Mater. 2013, 61, 4354–4364. [Google Scholar] [CrossRef]
- Renganathan, S. Theoretical Analysis of Stresses in a Lithium Ion Cell. J. Electrochem. Soc. 2010, 157, 155–163. [Google Scholar] [CrossRef]
- Xu, R. Computational analysis of chemomechanical behaviors of composite electrodes in Li-ion batteries. Mater. Res. 2016, 31, 2715–2727. [Google Scholar] [CrossRef] [Green Version]
- Goldin, G. Three-dimensional particle-resolved models of Li-ion batteries to assist the evaluation of empirical parameters in one-dimensional models. Mater. Res. 2012, 64, 118–129. [Google Scholar] [CrossRef]
- Wu, B. Mechanical-electrochemical modeling of agglomerate particles in lithium-ion battery electrodes. Mater. Res. 2016, 163, 3131–3139. [Google Scholar] [CrossRef]
- Zhang, T. Effect of reversible electrochemical reaction on Li diffusion and stresses in cylindrical Li-ion battery electrodes. J. Appl. Phys. 2014, 115, 083504. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clerici, D.; Mocera, F.; Somà, A. Analytical Solution for Coupled Diffusion Induced Stress Model for Lithium-Ion Battery. Energies 2020, 13, 1717. https://doi.org/10.3390/en13071717
Clerici D, Mocera F, Somà A. Analytical Solution for Coupled Diffusion Induced Stress Model for Lithium-Ion Battery. Energies. 2020; 13(7):1717. https://doi.org/10.3390/en13071717
Chicago/Turabian StyleClerici, Davide, Francesco Mocera, and Aurelio Somà. 2020. "Analytical Solution for Coupled Diffusion Induced Stress Model for Lithium-Ion Battery" Energies 13, no. 7: 1717. https://doi.org/10.3390/en13071717








