Three-Legs Interleaved Boost Power Factor Corrector for High-Power LED Lighting Application
Abstract
1. Introduction
- Magnetics components size can be reduced;
- Reduced electromagnetic contents and Electromagnetic Interference (EMI) filter;
- RMS current rating decrease in the output capacitance;
- Suitable tailoring of power semiconductor devices;
- Reduction of conduction losses thanks to the parallel structure.
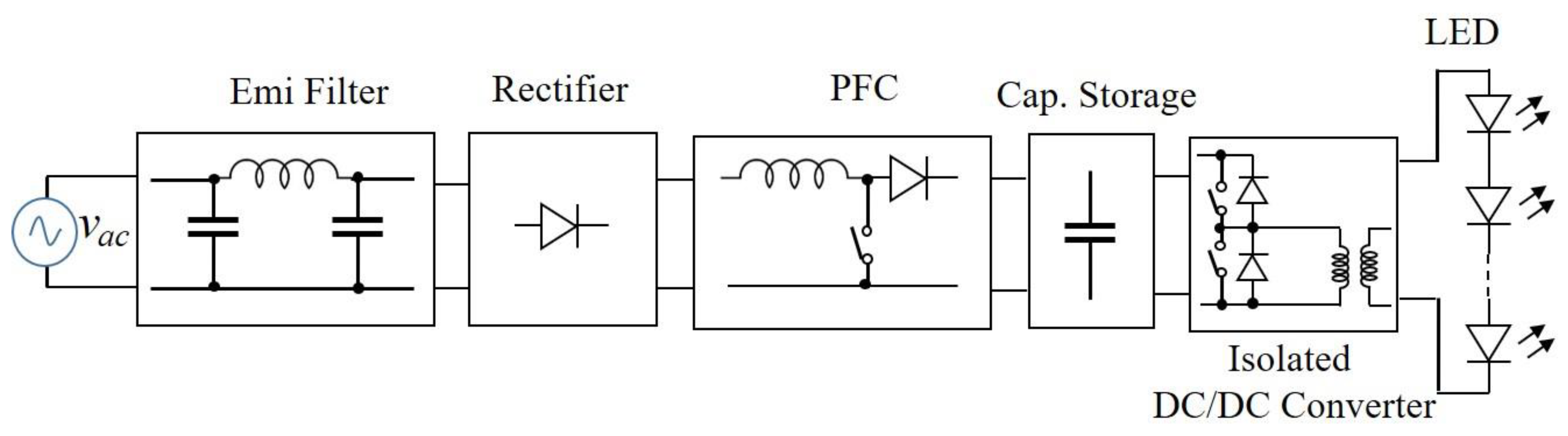
2. Three-Stage Interleaved PFC Converter Operation
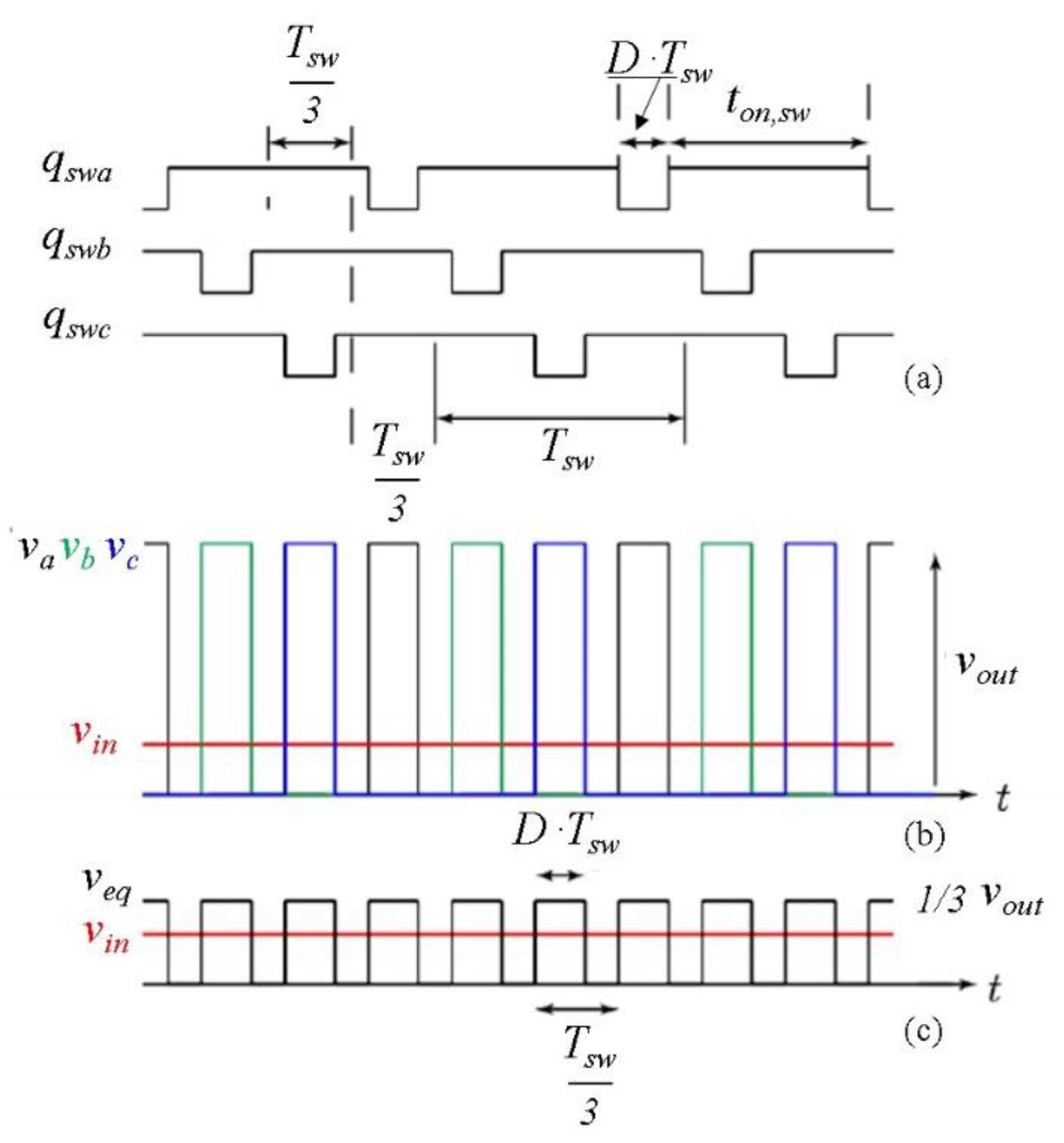
2.1. D < 1/3 Control Condition
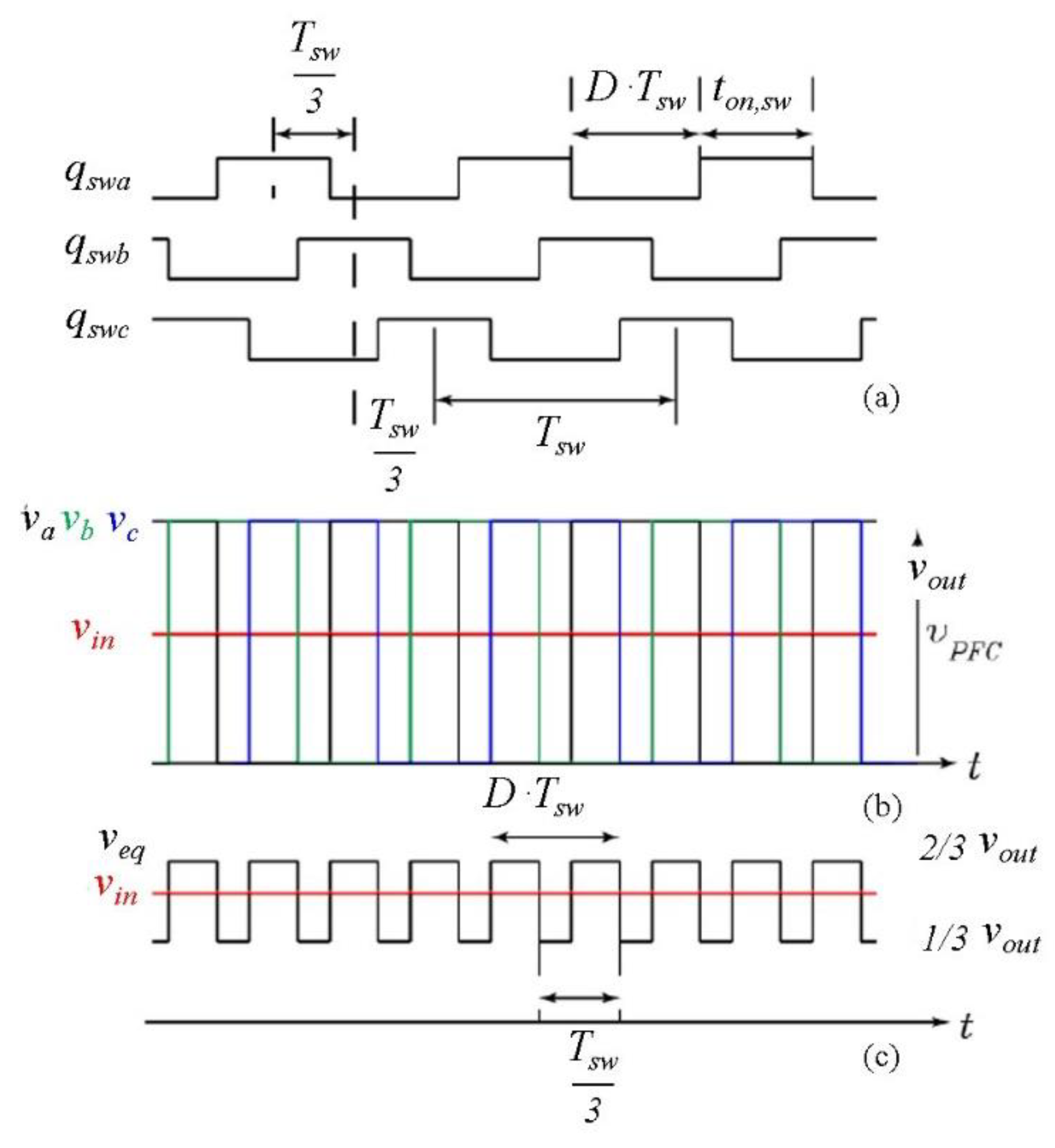
2.2. 1/3 < D < 2/3 Control Condition
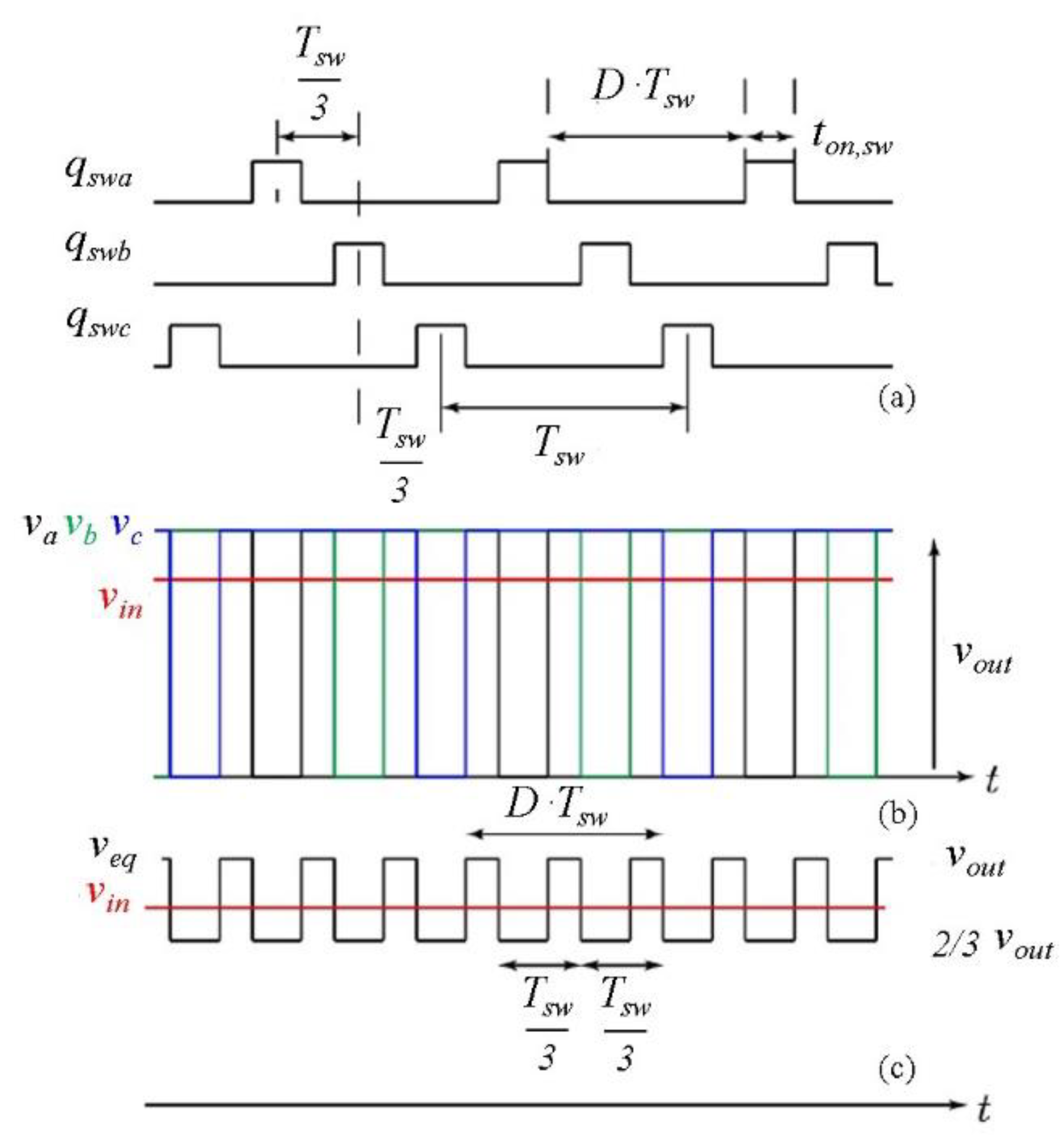
2.3. D > 2/3 Control Condition
2.4. Converter Behavior within the Whole Operating Range
3. Interleaved Boost PFC Design Issues
3.1. Output Capacitor Design
3.2. Power Devices Selection
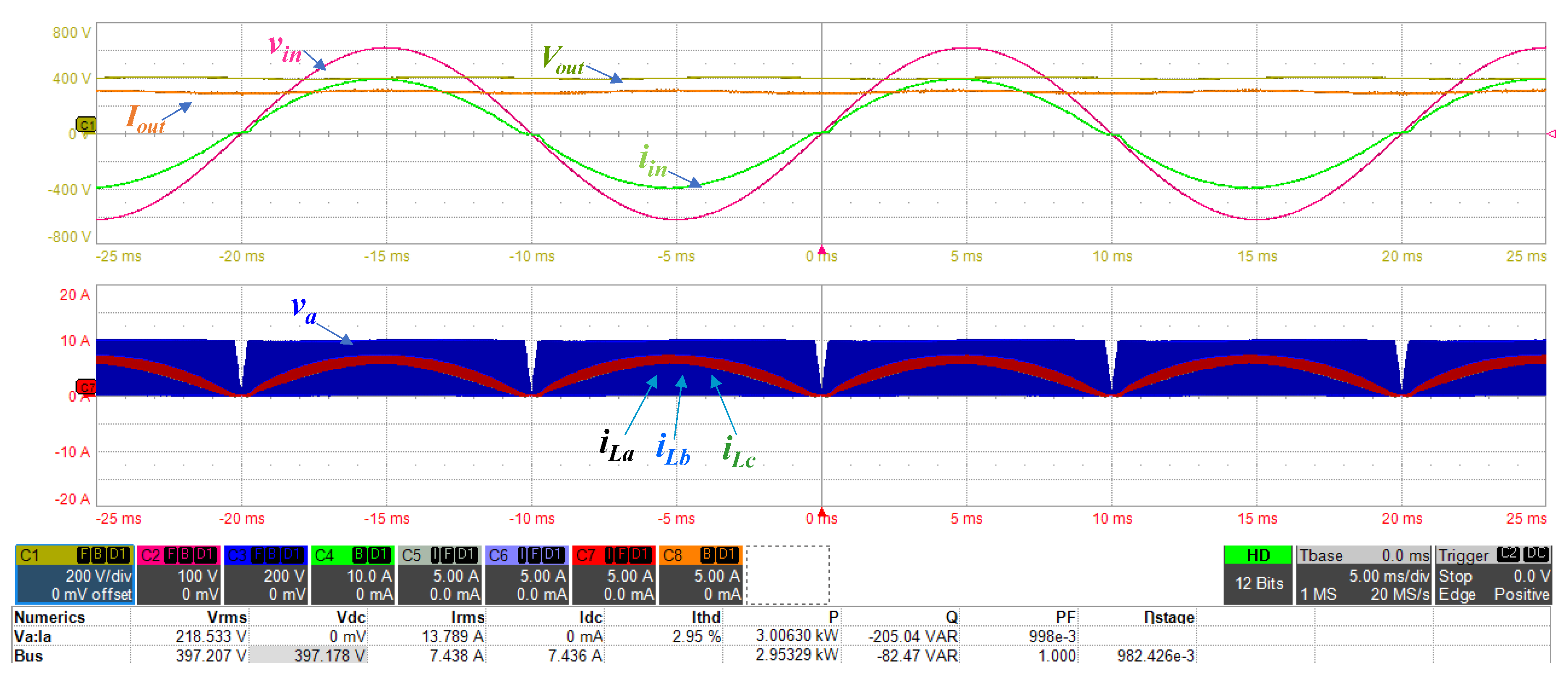
4. Interleaved Boost PFC Experimental Evaluation
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Chen, M.; Lin, S.; Chou, D.; Chen, J. Study of driving source efficiency improvement for high power LED street lighting system using Taguchi method. In Proceedings of the 2016 IEEE International Conference on Industrial Technology (ICIT), Taipei, Taiwan, 14–17 March 2016; pp. 372–377. [Google Scholar]
- Lee, S.; Choe, H.; Yun, J. Performance Improvement of a Boost LED Driver with High Voltage Gain for Edge-Lit LED Backlights. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 481–485. [Google Scholar] [CrossRef]
- di Mauro, S.; Musumeci, S.; Raciti, A. Analysis of electrical and photometric quantities of CFL and LED bulb lamps. In Proceedings of the 2017 IEEE Industry Applications Society Annual Meeting, Cincinnati, OH, USA, 1–5 October 2017; pp. 1–8. [Google Scholar]
- Raciti, A.; Rizzo, S.A.; Susinni, G. Steady-State Electrical Modeling of LED and CF Bulb Lamps Under Variable Voltage on the Main. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–6. [Google Scholar]
- Liu, Z.; Lee, H. A Current-Accuracy-Enhanced Wide-Input-Range DC–DC LED Driver with Feedforward Synchronous Current Control. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 3996–4006. [Google Scholar] [CrossRef]
- Chen, W.; Cheng, K.W.E.; Shao, J. Circuit Topology Analysis for LED Lighting and its Formulation Development. Energies 2019, 12, 4203. [Google Scholar] [CrossRef]
- Kalla, U.K. A PFC based control scheme for LED lighting systems. In Proceedings of the 2016 IEEE 7th Power India International Conference (PIICON), Rajasthan, India, 25–27 November 2016; pp. 1–4. [Google Scholar]
- Raciti, S.; Rizzo, A.; Susinni, G. Parametric PSpice Circuit of Energy Saving Lamp Emulating Current Waveform. Appl. Sci. 2019, 9, 152. [Google Scholar] [CrossRef]
- Balogh, L.; Redl, R. Power-factor correction with interleaved boost converters in continuous-inductor-current mode. In Proceedings of the Eighth Annual Applied Power Electronics Conference and Exposition, San Diego, CA, USA, 7–11 March 1993; pp. 168–174. [Google Scholar]
- Raggl, K.; Nussbaumer, T.; Doerig, G.; Biela, J.; Kolar, J.W. Comprehensive Design and Optimization of a High-Power-Density Single-Phase Boost PFC. IEEE Trans. Ind. Electron. 2009, 56, 2574–2587. [Google Scholar] [CrossRef]
- Liu, J.; Chen, W.; Zhang, J.; Xu, D.; Lee, F.C. Evaluation of power losses in different CCM mode single-phase boost PFC converters via a simulation tool. In Conference Record of the 2001 IEEE Industry Applications Conference, Proceedings of the 36th IAS Annual Meeting (Cat. No.01CH37248), Chicago, IL, USA, 30 September–4 October 2001; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2001; Volume 4, pp. 2455–2459. [Google Scholar]
- Borlo, S.; Cittanti, D.; Gregorio, M.; Mandrile, F.; Musumeci, S. Comparative CCM-DCM Design Evaluation of Power Inductors in Interleaved PFC Stage for Electric Vehicle Battery Chargers. In Proceedings of the 2019 International Conference on Clean Electrical Power (ICCEP), Otranto, Italy, 2–4 July 2019; pp. 180–186. [Google Scholar]
- Kong, P.; Wang, S.; Lee, F.C.; Wang, C. Common Mode EMI Study and Reduction Technique for the Interleaved Multichannel PFC Converter. IEEE Trans. Power Electron. 2008, 23, 2576–2584. [Google Scholar] [CrossRef]
- Nussbaumer, T.; Raggl, K.; Kolar, J.W. Design Guidelines for Interleaved Single-Phase Boost PFC Circuits. IEEE Trans. Ind. Electron. 2009, 56, 2559–2573. [Google Scholar] [CrossRef]
- Biela, J.; Kolar, J.W.; Deboy, G. Optimal design of a compact 99.3% efficient single-phase PFC rectifier. In Proceedings of the 2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Palm Springs, CA, USA, 21–25 February 2010; pp. 1397–1404. [Google Scholar]
- Messina, S.; Torrisi, M.; Cacciato, M. Three-channels interleaved PFC exploiting mixed signal control. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017; pp. P.1–P.10. [Google Scholar]
- Alessandria, A.; Fragapane, L.; Morale, G. Design considerations on Field-Stop Layer processing in a trench-gate IGBT. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–6. [Google Scholar]
- Cristaldi, D.; Musumeci, S.; Raciti, A. Modelling and Simulation of IGBT Thermal Behavior During a Short Circuit Power Pulse. In Proceedings of the International Conference on Clean Electrical Power, 2015 IEEE, ICCEP 15, Taormina, Italy, 16–18 June 2015; pp. 542–547. [Google Scholar]
- Musumeci, S.; Pagano, R.; Raciti, A.; Frisina, F.; Melito, M. Transient behavior of IGBTs submitted to fault under load conditions. In Proceedings of the 2002 IEEE Industry Applications Conference. 37th IAS Annual Meeting (Cat. No.02CH37344), Pittsburgh, PA, USA, 13–18 October 2002; Volume 3, pp. 2182–2189. [Google Scholar]
- Raciti, A.; Musumeci, S.; Xibilia, F.; Chimento, F.; Privitera, G. A bi-dimensional model for power MOSFET devices accounting for the behavior in unclamped inductive switching conditions. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 134–139. [Google Scholar]
- Musumeci, S.; Cristaldi, D.; Portoghese, F. Super-junction power MOSFET in half bridge DC-DC zero-voltage converter for energy conversion management. In Proceedings of the 2015 International Conference on Clean Electrical Power (ICCEP), Taormina, Italy, 16–18 June 2015; pp. 755–760. [Google Scholar]
- Cheng, L.; Kai, Y.; Xiaoguang, W.; Dezhang, L. A design of single phase inverter with three-channel interleaved PFC module. In Proceedings of the 19th International Conference on Electrical Machines and Systems, ICEMS 2016, Chiba, Japan, 13–16 November 2016; pp. 1L–5L. [Google Scholar]
- Kolar, J.W.; Drofenik, U.; Minibock, J.; Ertl, H. A new concept for minimizing high-frequency common-mode EMI of three-phase PWM rectifier systems keeping high utilization of the output voltage. In Proceedings of the PEC 2000. Fifteenth Annual IEEE Applied Power Electronics Conference and Exposition), New Orleans, LA, USA, 6–10 February 2000; Volume 1, pp. 519–527. [Google Scholar]
- Jiang, C.; Nene, H.; Choudhury, S. Efficiency and THD Optimization Based on an Interleaved PFC Converter Using Digital Controller with Integrated Valley Switching Control Feature. In Proceedings of the 2019 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 7–8 February 2019; pp. 1–5. [Google Scholar]
- Musumeci, S.; Bojoi, R.; Borlo, S.; Armando, E. IGBT based Three Channel Interleaved PFC Boost Converter for Inverter Front-End Application. In Proceedings of the 2019 AEIT International Annual Conference (AEIT), Florence, Italy, 18–20 September 2019; pp. 1–6. [Google Scholar]








| Vin,max [V] | Pout,min [W] | Vout [V] | fsw [kHz] | ηmin |
|---|---|---|---|---|
| 264.5 | 1000 | 400 | 60 | 0.95 |
| Vin [V] | Vout [V] | Pout [W] | fSW [KHz] | La = Lb = Lc [μH] | Cdc [μF] |
|---|---|---|---|---|---|
| 230 ± 10% | 400 | 3000 | 60 | 900 | 1800 |
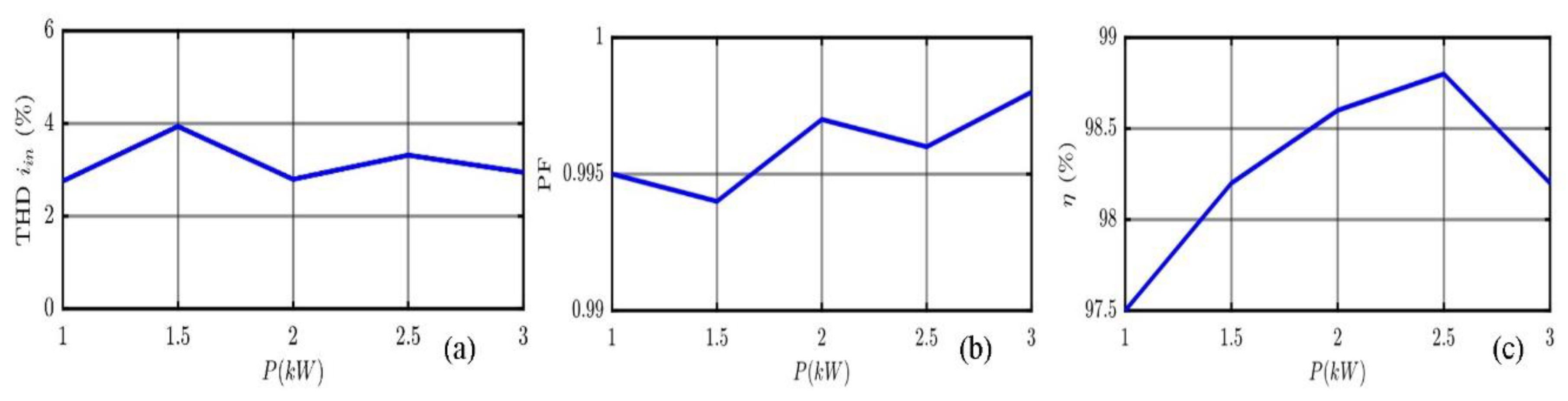
| N | Pin [kW] | iin,rms [A] | Iout [A] | iTHD | PF | η | N of Cells |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 4.6 | 2.5 | 2.76 | 0.995 | 0.975 | 1 |
| 2 | 1.5 | 6.8 | 3.6 | 3.94 | 0.994 | 0.982 | 2 |
| 3 | 2 | 9.2 | 4.9 | 2.80 | 0.997 | 0.986 | 2 |
| 4 | 2.5 | 11.5 | 6.2 | 3.32 | 0.996 | 0.988 | 3 |
| 5 | 3 | 13.8 | 7.4 | 2.95 | 0.998 | 0.982 | 3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Musumeci, S.; Bojoi, R.; Armando, E.; Borlo, S.; Mandrile, F. Three-Legs Interleaved Boost Power Factor Corrector for High-Power LED Lighting Application. Energies 2020, 13, 1728. https://doi.org/10.3390/en13071728
Musumeci S, Bojoi R, Armando E, Borlo S, Mandrile F. Three-Legs Interleaved Boost Power Factor Corrector for High-Power LED Lighting Application. Energies. 2020; 13(7):1728. https://doi.org/10.3390/en13071728
Chicago/Turabian StyleMusumeci, Salvatore, Radu Bojoi, Eric Armando, Stefano Borlo, and Fabio Mandrile. 2020. "Three-Legs Interleaved Boost Power Factor Corrector for High-Power LED Lighting Application" Energies 13, no. 7: 1728. https://doi.org/10.3390/en13071728
APA StyleMusumeci, S., Bojoi, R., Armando, E., Borlo, S., & Mandrile, F. (2020). Three-Legs Interleaved Boost Power Factor Corrector for High-Power LED Lighting Application. Energies, 13(7), 1728. https://doi.org/10.3390/en13071728






