Hydrodynamic Performance of a Pitching Float Wave Energy Converter
Abstract
:1. Introduction
2. Theoretical Considerations
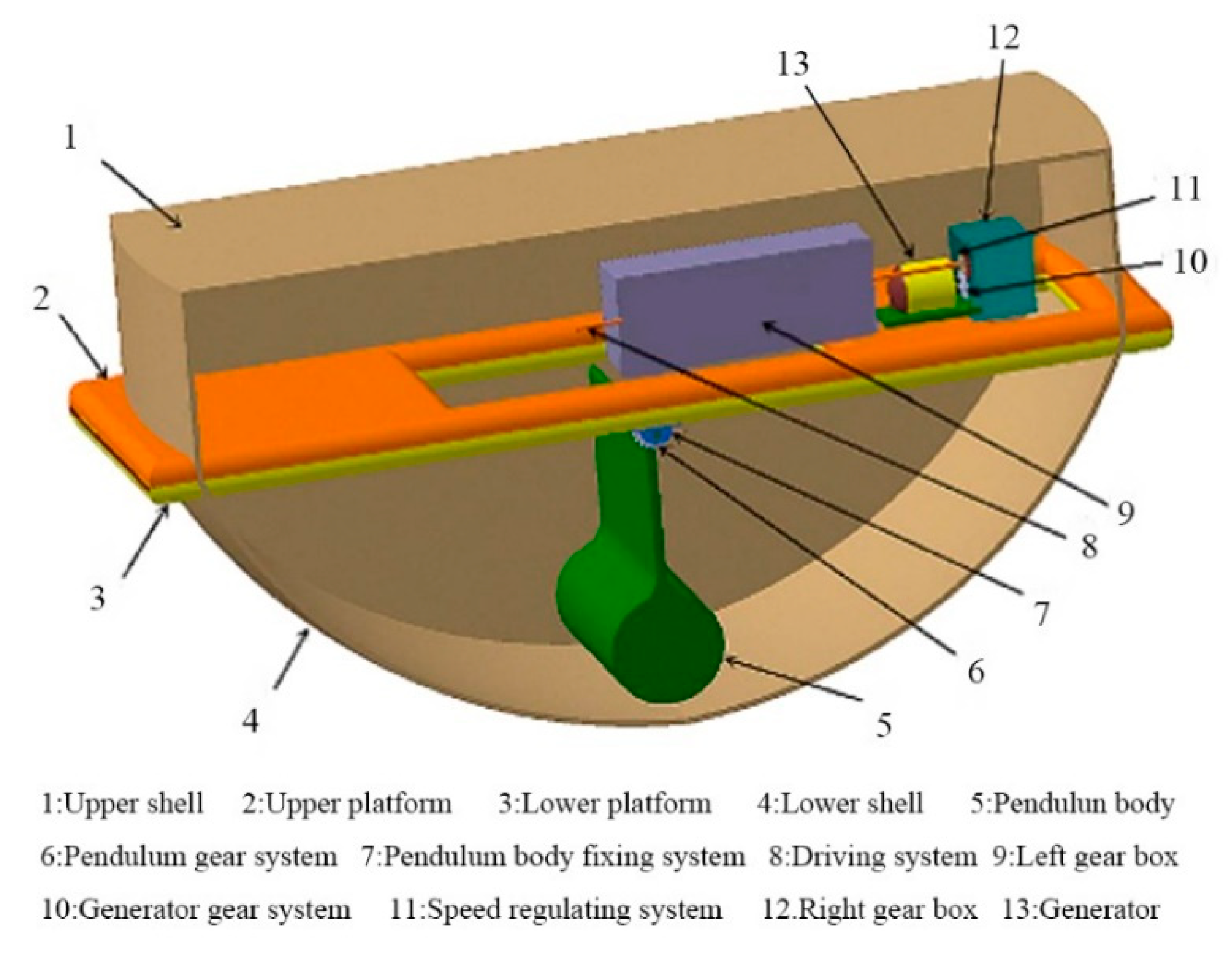
2.1. Converter Dynamics Model
2.2. Frequency Domain Analysis Method
2.3. Time Domain Analysis Method
2.4. Numerical Model Verification
3. Hydrodynamic Device Characteristics
3.1. Analysis of the Hydrodynamic Performance in the Frequency Domain
3.1.1. Pitching Response RAO
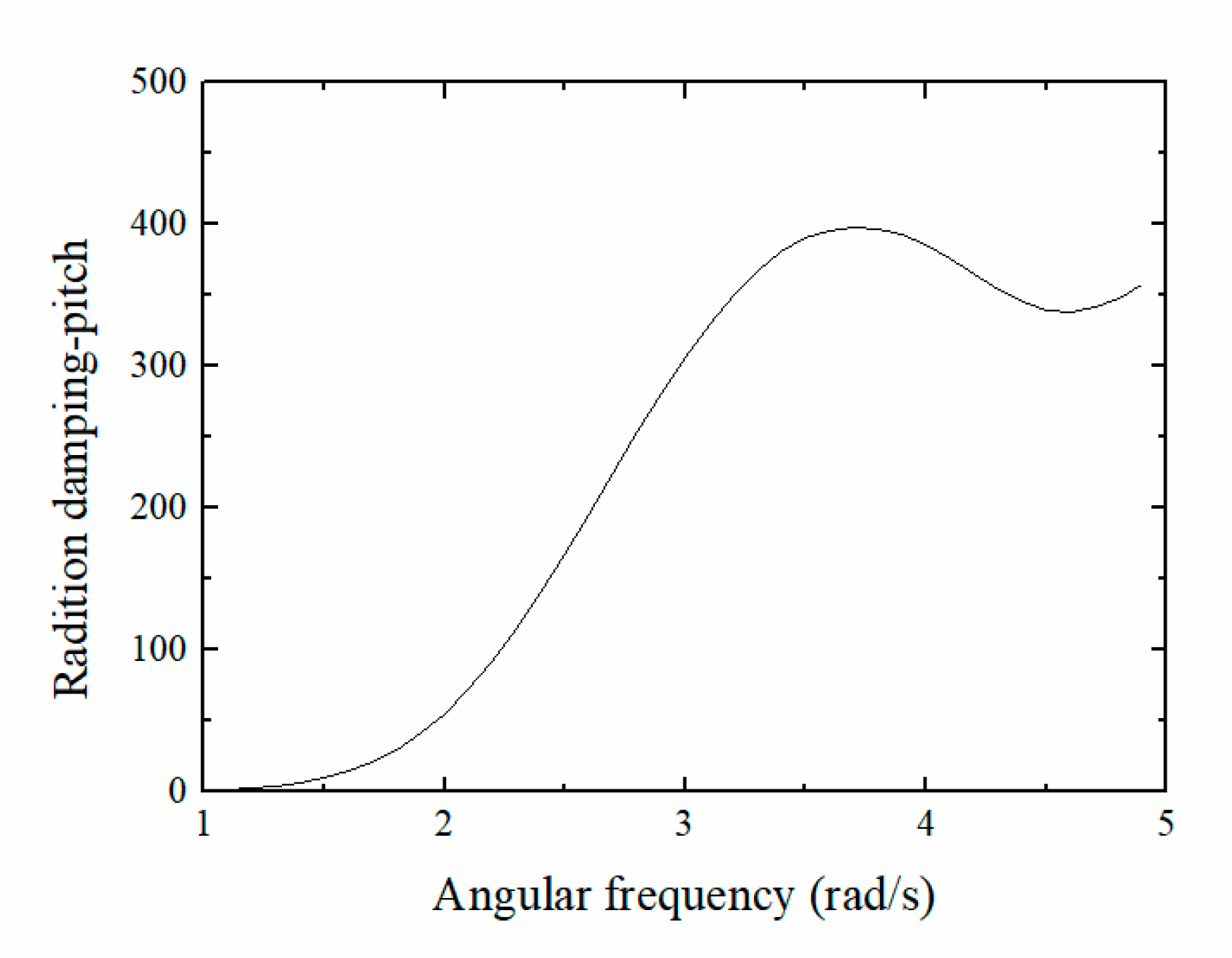
3.1.2. Radiation Damping
3.1.3. Wave Motivator
3.1.4. Additional Mass Force
3.2. Analysis of the Hydrodynamic Performance in the Time Domain
3.2.1. Effect of Mooring Point Position on Float Hydrodynamic Performance
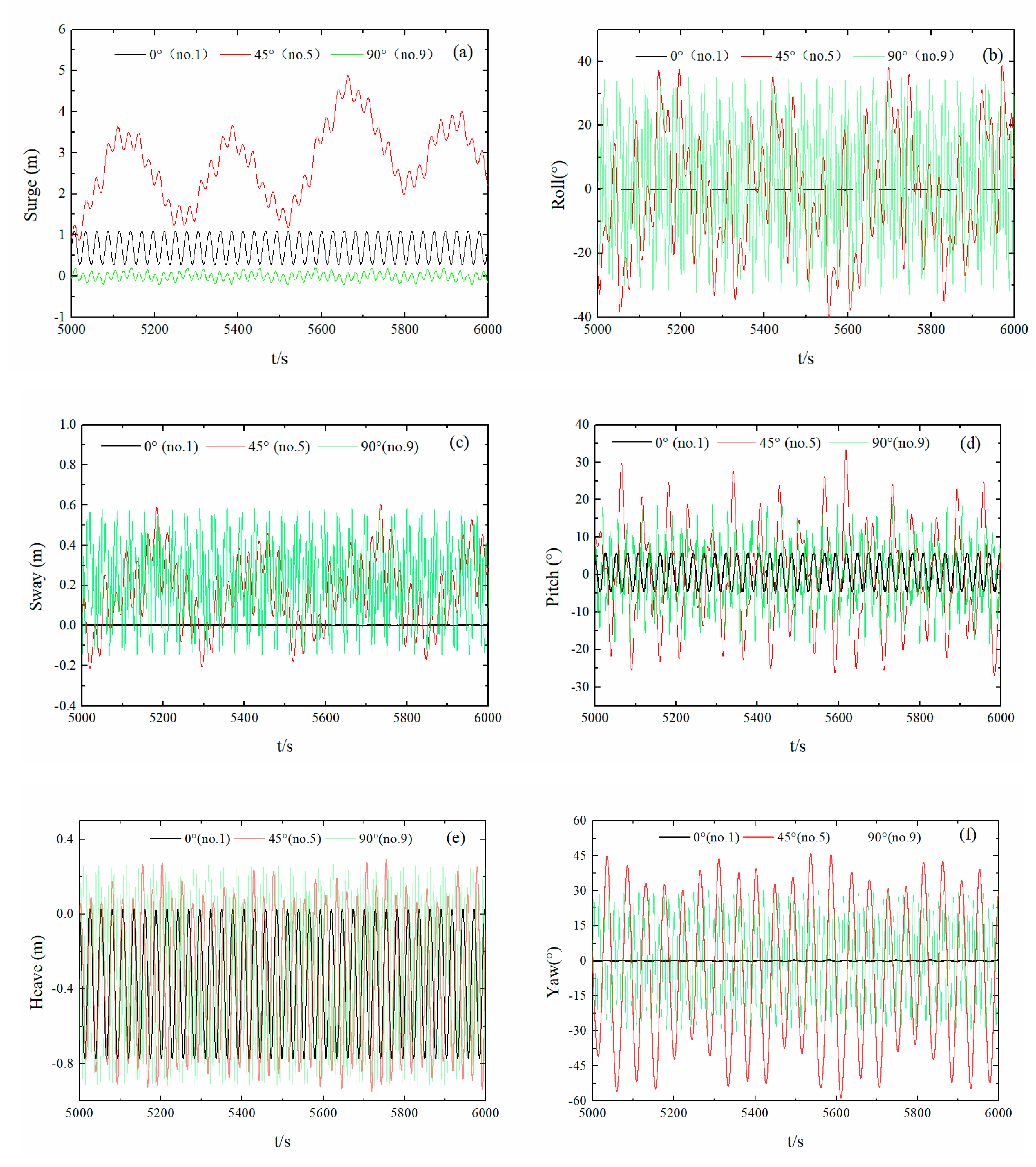
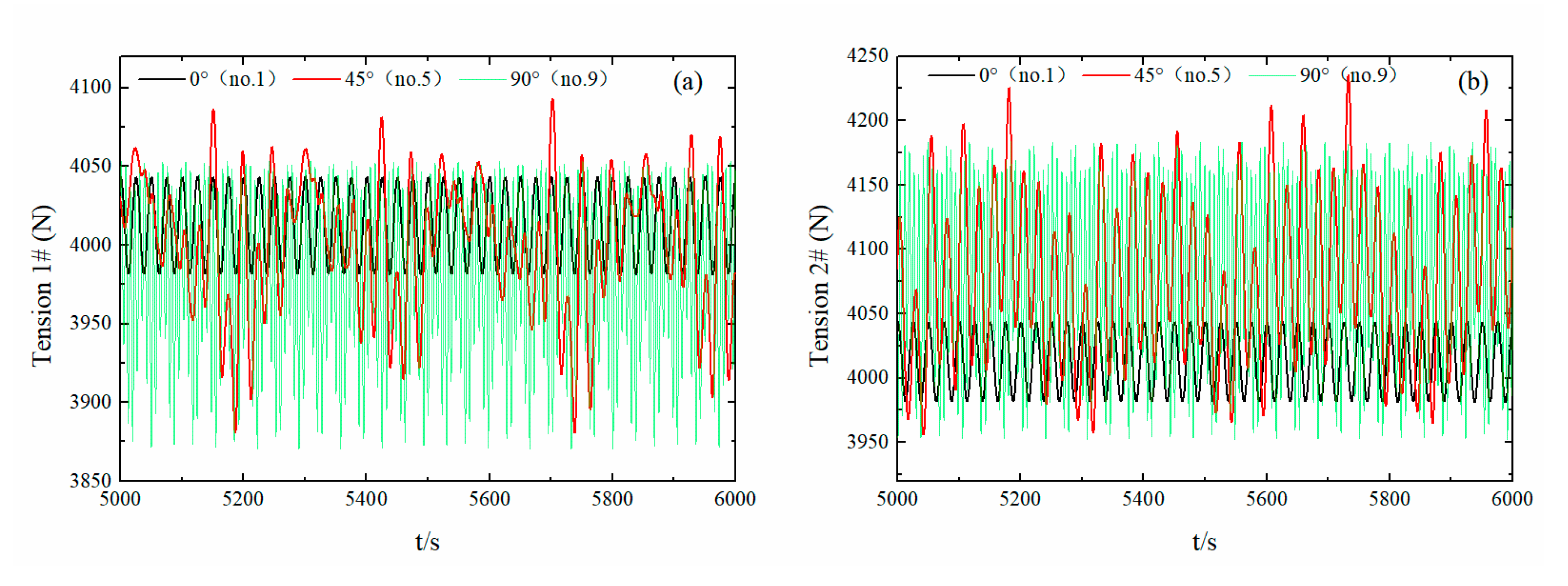
3.2.2. Effect of Wave Angle on Hydrodynamic Float Performance
3.2.3. Effect of Wave Period on Hydrodynamic Float Performance
3.3. Irregular Waves
3.3.1. Effect of Mooring Point Position on Hydrodynamic Float Performance
3.3.2. Effect of Wave Angle on Hydrodynamic Float Performance
3.3.3. Effect of Start and End Frequency on Hydrodynamic Float Performance
4. Conclusions
- (1)
- The frequency hydrodynamic performance of the designed float conforms to the specifications of a marine mobile platform, with excellent pitching response performance. It was verified that the float radiation damping coefficient, additional mass force, and wave excitation yielded optimum pitching performance.
- (2)
- Under regular wave conditions, mooring point positions that were closer to the center of mass resulted in better device stability. The angle arrangement of the anchor-chain mooring method fully conformed to the safety requirements. The 45° wave direction angle subjected the unit to the greatest overall force with the most intense movement. Wave cycles that were closest to the peak period resulted in a larger overall force on the device and more intense movement, with a maximum force of 4061.34 N for a wave period of 2.7 s. The device can therefore operate safely, steadily, and with high reliability under all tested operating conditions.
- (3)
- Under irregular wave conditions, mooring point positions that were closer to the center of mass also resulted in better device stability. The angle arrangement of the anchor-chain mooring method fully conformed to the safety requirements. A 45° wave direction angle resulted in the greatest overall force on the unit and the most intense movement. The irregular wave frequency area at 2.5–3.0 rad/s yielded the most concentrated energy, the most force ingested by the float, and the most intense movement. The device was deemed to operate safely, steadily, and with high reliability under all operating conditions.
- (4)
- The superior performance of the pitching float-type wave power generator was verified based on the frequency and time-domain analysis. These results are significant for the use of wave-energy generators in the South China Sea and expansion of the wave-energy capture range.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Float Number | Location of Mooring Point | Wave Direction (deg) | Wave Period (s) |
|---|---|---|---|
| 1 | centroid | 0° | 2.5 |
| 2 | centroid | 0° | 2.6 |
| 3 | centroid | 0° | 2.7 |
| 4 | centroid | 0° | 6 |
| 5 | centroid | 45° | 2.5 |
| 6 | centroid | 45° | 2.6 |
| 7 | centroid | 45° | 2.7 |
| 8 | centroid | 45° | 6 |
| 9 | centroid | 90° | 2.5 |
| 10 | centroid | 90° | 2.6 |
| 11 | centroid | 90° | 2.7 |
| 12 | centroid | 90° | 6 |
| 13 | waterline | 0° | 2.5 |
| 14 | waterline | 0° | 2.6 |
| 15 | waterline | 0° | 2.7 |
| 16 | waterline | 0° | 6 |
| 17 | waterline | 45° | 2.5 |
| 18 | waterline | 45° | 2.6 |
| 19 | waterline | 45° | 2.7 |
| 20 | waterline | 45° | 6 |
| 21 | waterline | 90° | 2.5 |
| 22 | waterline | 90° | 2.6 |
| 23 | waterline | 90° | 2.7 |
| 24 | waterline | 90° | 6 |
| 25 | vertex | 0° | 2.5 |
| 26 | vertex | 0° | 2.6 |
| 27 | vertex | 0° | 2.7 |
| 28 | vertex | 0° | 6 |
| 29 | vertex | 45° | 2.5 |
| 30 | vertex | 45° | 2.6 |
| 31 | vertex | 45° | 2.7 |
| 32 | vertex | 45° | 6 |
| 33 | vertex | 90° | 2.5 |
| 34 | vertex | 90° | 2.6 |
| 35 | vertex | 90° | 2.7 |
| 36 | vertex | 90° | 6 |
References
- Krzyszczak, J.; Baranowski, P.; Zubik, M.; Hoffmann, H. Temporal scale influence on multifractal properties of agro-meteorological time series. Agric. For. Meteorol. 2017, 239, 223–235. [Google Scholar] [CrossRef]
- Castañeda-Miranda, A.; Icaza-Herrera, M.D.; Castaño, V.M. Meteorological Temperature and Humidity Prediction from Fourier-Statistical Analysis of Hourly Data. Adv. Meteorol. 2019, 2019, 1–13. [Google Scholar] [CrossRef]
- Yang, Z.C. Hourly ambient air humidity fluctuation evaluation and forecasting based on the least-squares Fourier-model. Measurement 2019, 133, 112–123. [Google Scholar] [CrossRef]
- Stoyanov, D.B.; Nixon, J.D. Alternative operational strategies for wind turbines in cold climates. Renew. Energy 2020, 145, 2694–2706. [Google Scholar] [CrossRef]
- Castañeda-Miranda, A.; Castaño, V.M. Smart frost control in greenhouses by neural networks models. Comput. Electron. Agric. 2017, 137, 102–114. [Google Scholar] [CrossRef]
- Li, C.; Zhou, D.; Wang, H.; Lu, Y.; Li, D. Techno-economic performance study of stand-alone wind/diesel/battery hybrid system with different battery technologies in the cold region of China. Energy 2020, 192, 116702. [Google Scholar] [CrossRef]
- Konispoliatis, D.N.; Mavrakos, S.A. Natural frequencies of vertical cylindrical oscillating water column devices. Appl. Ocean Res. 2019, 91, 101894. [Google Scholar] [CrossRef]
- Zheng, S.; Zhu, G.; Simmonds, D.; Greaves, D.; Iglesias, G. Wave power extraction from a tubular structure integrated oscillating water column. Renew. Energy 2020, 150, 342–355. [Google Scholar] [CrossRef]
- Singh, U.; Abdussamie, N.; Hore, J. Hydrodynamic performance of a floating offshore OWC wave energy converter: An experimental study. Renew. Sustain. Energy Rev. 2020, 117, 109501. [Google Scholar] [CrossRef]
- Zhang, H.; Xi, R.; Xu, D.; Wang, K.; Shi, Q.; Zhao, H.; Wu, B. Efficiency enhancement of a point wave energy converter with a magnetic bistable mechanism. Energy 2019, 181, 1151–1165. [Google Scholar] [CrossRef]
- Alamian, R.; Shafaghat, R.; Safaei, M.R. Multi-objective optimization of a pitch point absorber wave energy converter. Water 2019, 11, 969. [Google Scholar] [CrossRef] [Green Version]
- Yue, X.; Chen, Q.; Wang, Z.; Geng, D.; Yan, D.; Jiang, W.; Wang, W. A novel nonlinear state space model for the hydraulic power take-off of a wave energy converter. Energy 2019, 180, 465–479. [Google Scholar]
- Rosa-Santos, P.; Taveira-Pinto, F.; Rodríguez, C.A.; Ramos, V.; López, M. The CECO wave energy converter: Recent developments. Renew. Energ. 2019, 139, 368–384. [Google Scholar] [CrossRef]
- Aderinto, T.; Li, H. Ocean wave energy converters: Status and challenges. Energies 2018, 11, 1250. [Google Scholar] [CrossRef] [Green Version]
- Prakash, S.S.; Mamun, K.A.; Islam, F.R.; Mudliar, R.; Pau’u, C.; Kolivuso, M.; Cadralala, S. Wave Energy Converter: A Review of Wave Energy Conversion Technology. In Proceedings of the 2016 3rd Asia-Pacific World Congress on Computer Science & Engineering, Nadi, Fiji, 5–6 December 2016; pp. 71–77. [Google Scholar]
- Yurchenko, D.; Alevras, P. Parametric pendulum based wave energy converter. Mech. Syst. Signal. Pr. 2018, 99, 504–515. [Google Scholar] [CrossRef] [Green Version]
- Zheng, S.; Zhang, Y. Analytical study on hydrodynamic performance of a raft-type wave power device. J. Mar. Sci. Tech. 2017, 22, 620–632. [Google Scholar] [CrossRef]
- Nicola, P.; Giovanni, B.; Biagio, P.; Antonello, S.S.; Giacomo, V.; Giuliana, M.; Gianmaria, S. Wave tank testing of a pendulum wave energy converter 1:12 scale model. Int. J. Appl. Mech. 2017, 9, 1750024. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Yang, Q.; Bao, G. Latching control using optimal control method for a raft-type wave energy converter. Ships. Offshore. Struc. 2018, 13 (Suppl. S1), 138–154. [Google Scholar] [CrossRef]
- Mustapa, M.A.; Yaakob, O.B.; Ahmed, Y.M.; Rheem, C.K.; Koh, K.K.; Adnan, F.A. Wave energy device and breakwater integration: A review. Renew. Sustain. Energ. Rev. 2017, 77, 43–58. [Google Scholar] [CrossRef]
- Malara, G.; Arena, F. Response of U-Oscillating Water Column arrays:Semi-analytical approach and numerical results. Renew. Energ. 2019, 138, 1152–1165. [Google Scholar] [CrossRef]
- Yang, S.; He, H.; Chen, H.; Wang, Y.; Li, H.; Zheng, S. Experimental study on the performance of a floating array-point-raft wave energy converter under random wave conditions. Renew. Energ. 2019, 139, 538–550. [Google Scholar] [CrossRef]
- Gao, H.; Li, B. Establishment of motion model for wave capture buoy and research on hydrodynamic performance of floating-type wave energy converter. Pol. Marit. Res. 2015, 22, 106–111. [Google Scholar] [CrossRef]
- Budal, K.; Falnes, J. Wave power conversion by point absorbers:A Norwegian project. Int. J. Ambie. Energ. 1982, 3, 59–67. [Google Scholar] [CrossRef]
- Sjökvist, L.; Göteman, M. Peak forces on a point absorbing wave energy converter impacted by tsunami waves. Renew. Energ. 2019, 133, 1024–1033. [Google Scholar] [CrossRef]
- Dang, T.D.; Phan, C.B.; Ahn, K.K. Design and investigation of a novel point absorber on performance optimization mechanism for wave energy converter in heave mode. Int. J. Pr. ENG. Man-GT 2019, 6, 477–488. [Google Scholar] [CrossRef]
- Xu, Q.; Li, Y.; Xia, Y.; Chen, W.; Gao, F. Performance assessments of the fully submerged sphere and cylinder point absorber wave energy converters. Mod. Phys. Lett. B 2019, 33, 1950168. [Google Scholar] [CrossRef]
- Prado, M. Archimedes Wave Swing (AWS). In Ocean Wave Energy; Cruz, J., Ed.; Springer: Berlin, Germany, 2008; pp. 297–304. [Google Scholar]
- Zhao, A.; Wu, W.; Sun, Z.; Zhu, L.; Lu, K.; Chung, H.; Blaabjerg, F. A Flower Pollination Method Based Global Maximum Power Point Tracking Strategy for Point-Absorbing Type Wave Energy Converters. Energies 2019, 12, 1343. [Google Scholar] [CrossRef] [Green Version]
- Abdelkhalik, O.; Zou, S. Control of small two-body heaving wave energy converters for ocean measurement applications. Renew. Energy 2018, 132, 587–595. [Google Scholar] [CrossRef]
- Liu, C.; Yu, H.; Liu, Q.; Zhong, W.; Zhu, H. Research on a double float system for direct drive wave power conversion. IET Renew. Power. Gen. 2017, 11, 1026–1032. [Google Scholar] [CrossRef]
- Amiri, A.; Panahi, R.; Radfar, S. Parametric Study of Two-Body Floating-Point Wave Absorber. J. Marine. Sci. Appli. 2016, 15, 41–49. [Google Scholar] [CrossRef]
- Antonio, F.D.O. Wave energy utilization: A review of the technologies. Renew. Sustain. Energ. Rev. 2010, 14, 899–918. [Google Scholar]
- Zhang, H.; Xu, D.; Zhao, H.; Xia, S.; Wu, Y. Energy extraction of wave energy converters embedded in a very large modularized floating platform. Energy 2018, 158, 317–329. [Google Scholar] [CrossRef]
- Huang, S.; Sheng, S.; Gerthoffert, A.; Cong, Y.; Zhang, T.; Wang, Z. Numerical design study of multipoint mooring systems for the floating wave energy converter in deep water with a sloping bottom. Renew. Energ. 2019, 136, 558–571. [Google Scholar] [CrossRef]
- Do, H.-T.; Dang, T.-D.; Ahn, K.K. A multi-point-absorber wave-energy converter for the stabilization of output power. Ocean Eng. 2018, 161, 337–349. [Google Scholar] [CrossRef]
- Author, D.E.N.; Ungar, E.E. Mechanical Vibration Analysis and Computation. Acoust. Soc. Am. 1992, 88, 2506. [Google Scholar]
- Airy, G.B. Tides and waves. Encyc. Metrop. 1845, 192, 241–396. [Google Scholar]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of Wind-Wave Growth and Swell Decay During the Joint North Sea Wave Project (JONSWAP); Deutches Hydrographisches Institut: Hamburg, Germany, 1973; pp. 8–12. [Google Scholar]
- Liu, Y. Design and Analysis of Built-in Wave Energy Converter. Master’s Thesis, Ocean University of China, Qingdao, China, 2014. [Google Scholar]
- China Classification Society, Rules for Classification of Mobile Offshore Units; China Communication Press: Beijing, China, 2012.











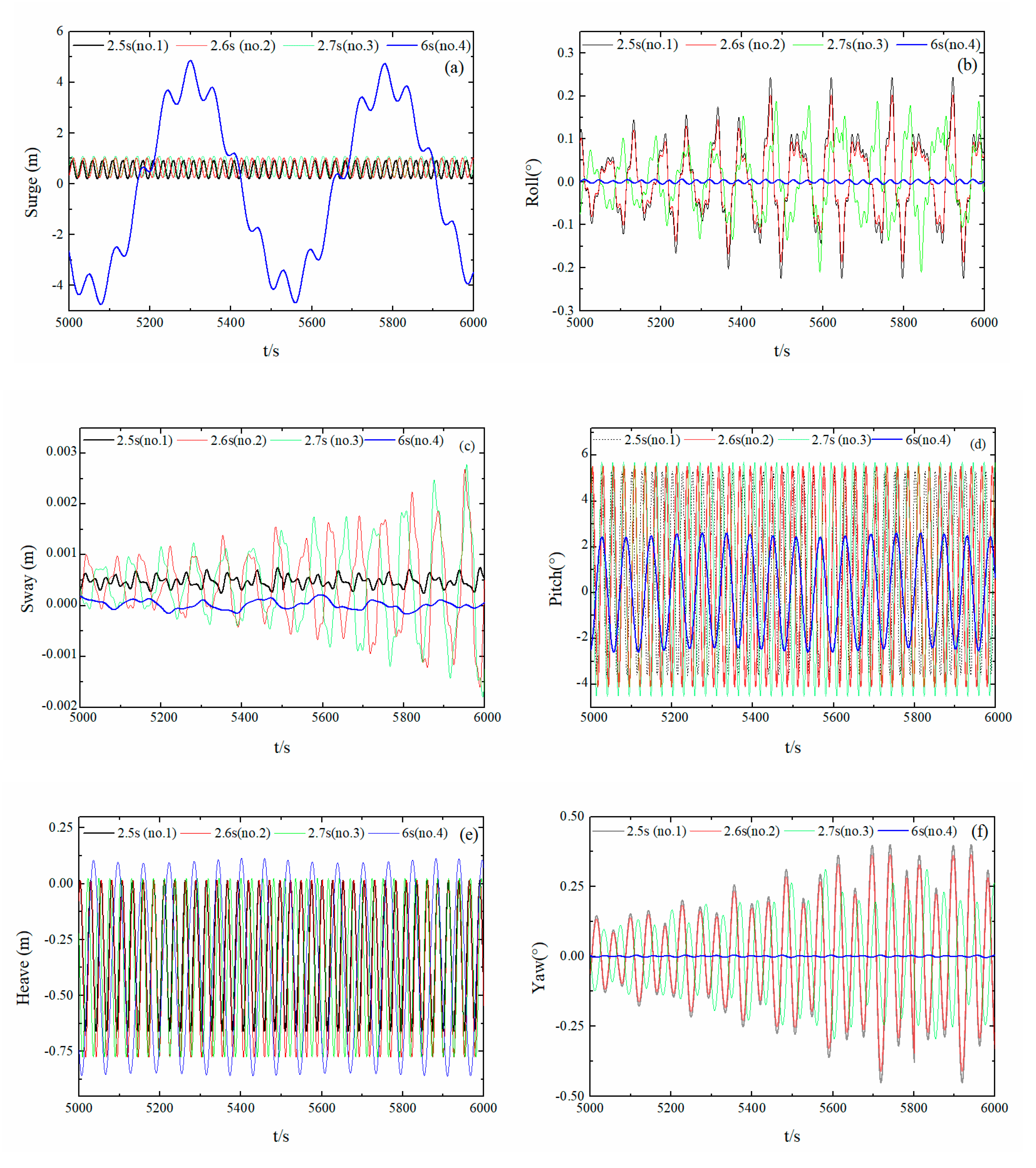





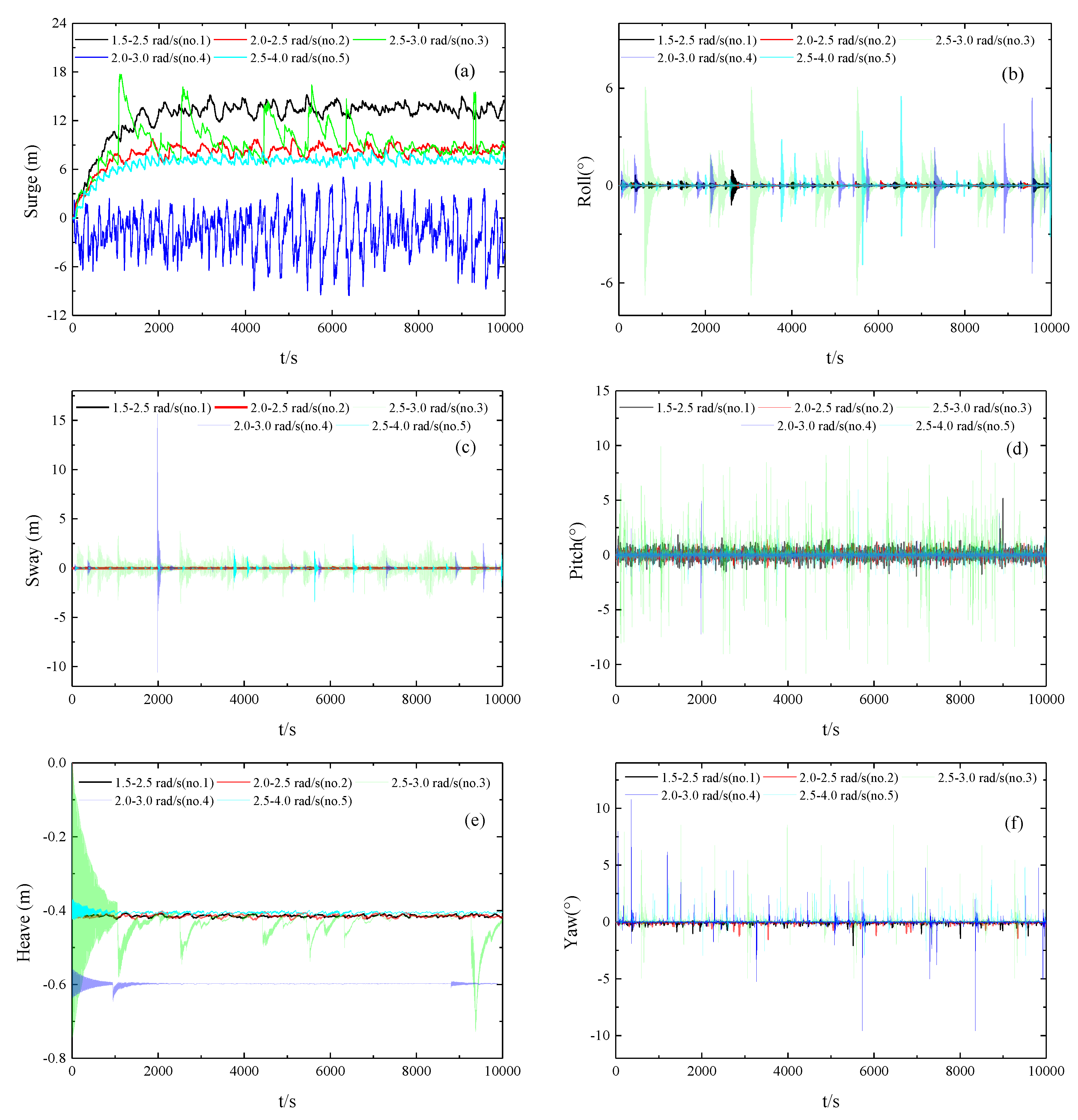

| Float Number | Regular Wave Period (s) | Irregular Wave Period (rad/s) |
|---|---|---|
| 1 | - | 1.5–2.5 |
| 2 | 2.5 | 2.0–2.5 |
| 3 | 2.6 | 2.5–3.0 |
| 4 | 2.7 | 2.0–3.0 |
| 5 | 6.0 | 2.5–4.0 |
| Contrasting Terms | Float Number | Mooring Point Location | Wave Direction (º) | Frequency Region of Irregular Wave (rad/s) |
|---|---|---|---|---|
| Mooring point | 1 | Centroid | 0° | 1.5–2.5 |
| Mooring point | 16 | Waterline | 0° | 1.5–2.5 |
| Mooring point | 31 | Vertex | 0° | 1.5–2.5 |
| Wave direction | 1 | Centroid | 0° | 1.5–2.5 |
| Wave direction | 16 | Centroid | 45° | 1.5–2.5 |
| Wave direction | 31 | Centroid | 90° | 1.5–2.5 |
| Frequency region | 1 | Centroid | 0° | 1.5–2.5 |
| Frequency region | 2 | Centroid | 0° | 2.0–2.5 |
| Frequency region | 3 | Centroid | 0° | 2.5–3.0 |
| Frequency region | 4 | Centroid | 0° | 2.0–3.0 |
| Frequency region | 5 | Centroid | 0° | 2.5–4.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Ai, S.; Yang, L.; Zhang, A.; Liu, S.; Zhou, B. Hydrodynamic Performance of a Pitching Float Wave Energy Converter. Energies 2020, 13, 1801. https://doi.org/10.3390/en13071801
Ma Y, Ai S, Yang L, Zhang A, Liu S, Zhou B. Hydrodynamic Performance of a Pitching Float Wave Energy Converter. Energies. 2020; 13(7):1801. https://doi.org/10.3390/en13071801
Chicago/Turabian StyleMa, Yong, Shan Ai, Lele Yang, Aiming Zhang, Sen Liu, and Binghao Zhou. 2020. "Hydrodynamic Performance of a Pitching Float Wave Energy Converter" Energies 13, no. 7: 1801. https://doi.org/10.3390/en13071801





