Deployment of a Bidirectional MW-Level Electric-Vehicle Extreme Fast Charging Station Enabled by High-Voltage SiC and Intelligent Control
Abstract
:1. Technical Challenges of EV Extreme Fast Charging Stations
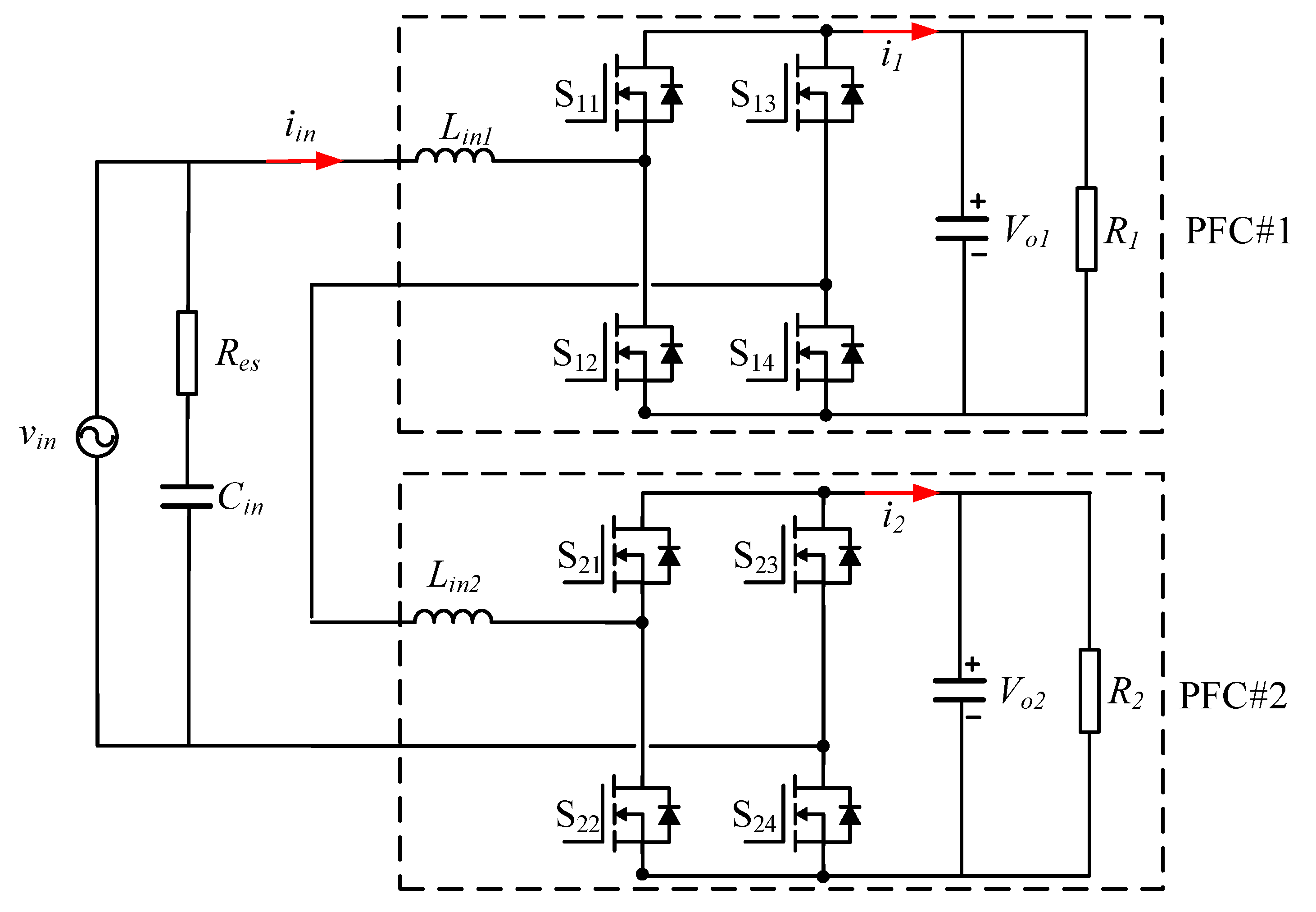
2. PFC-Stage Control
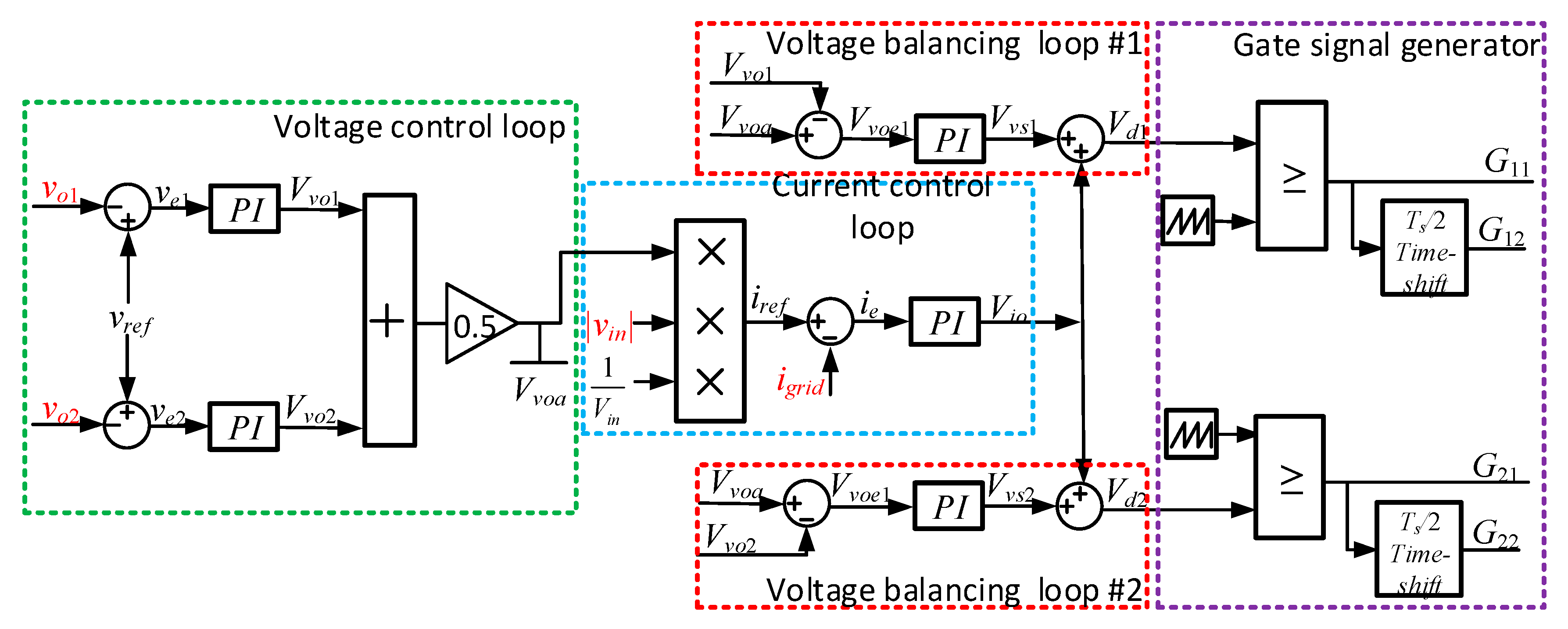
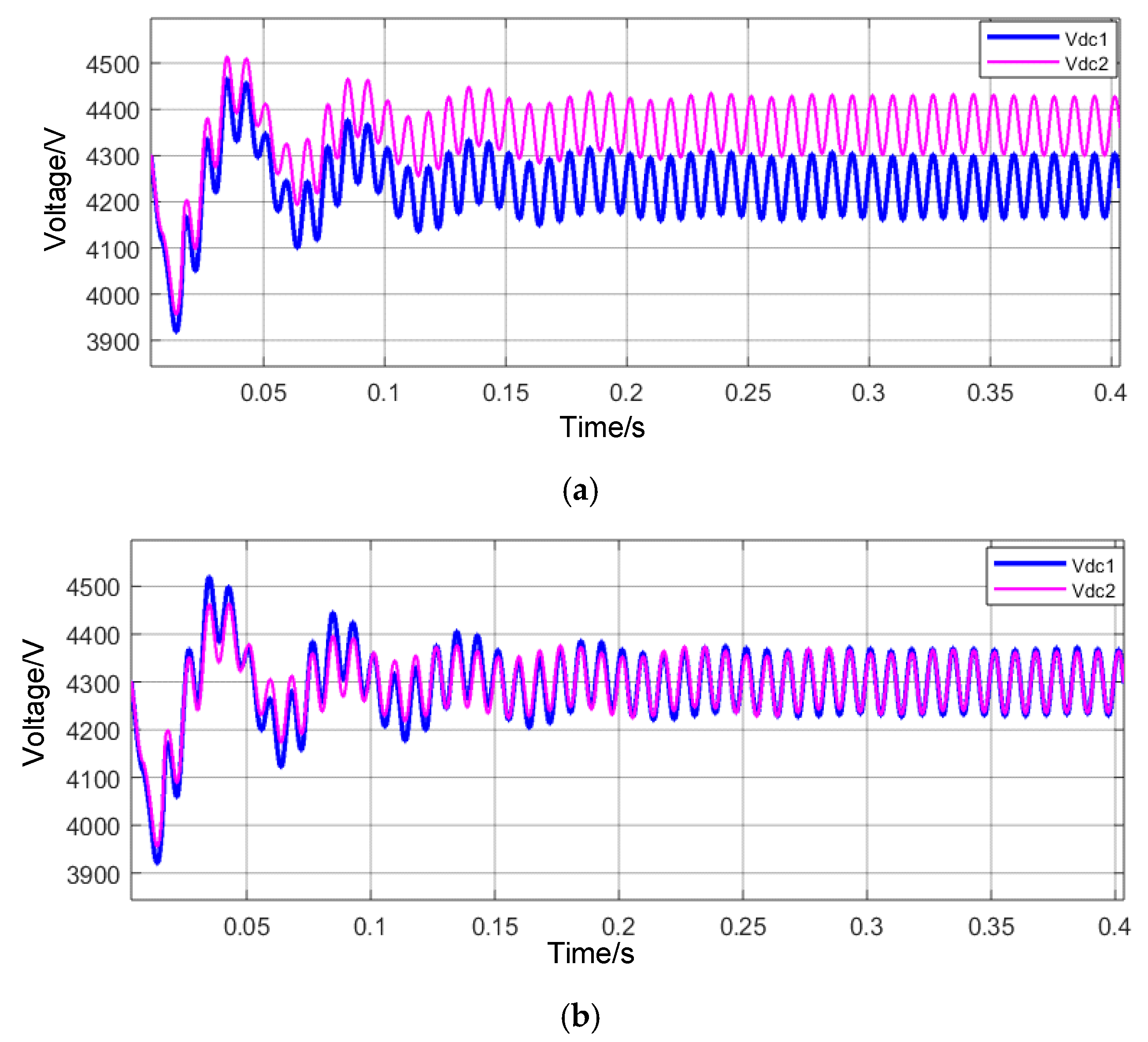
2.1. Power Balancing
2.2. Interleaving Control
3. DCX Stage Control
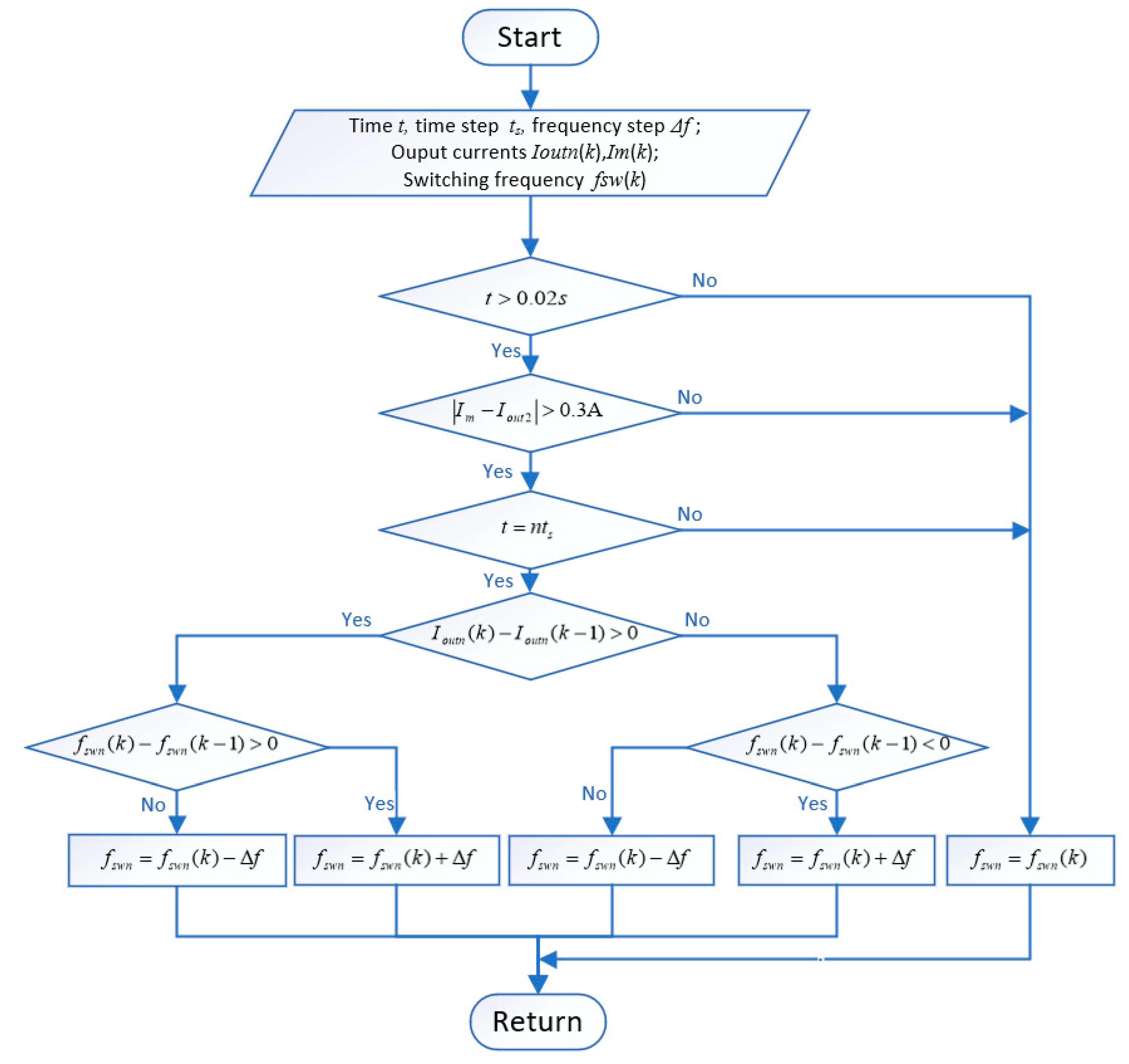
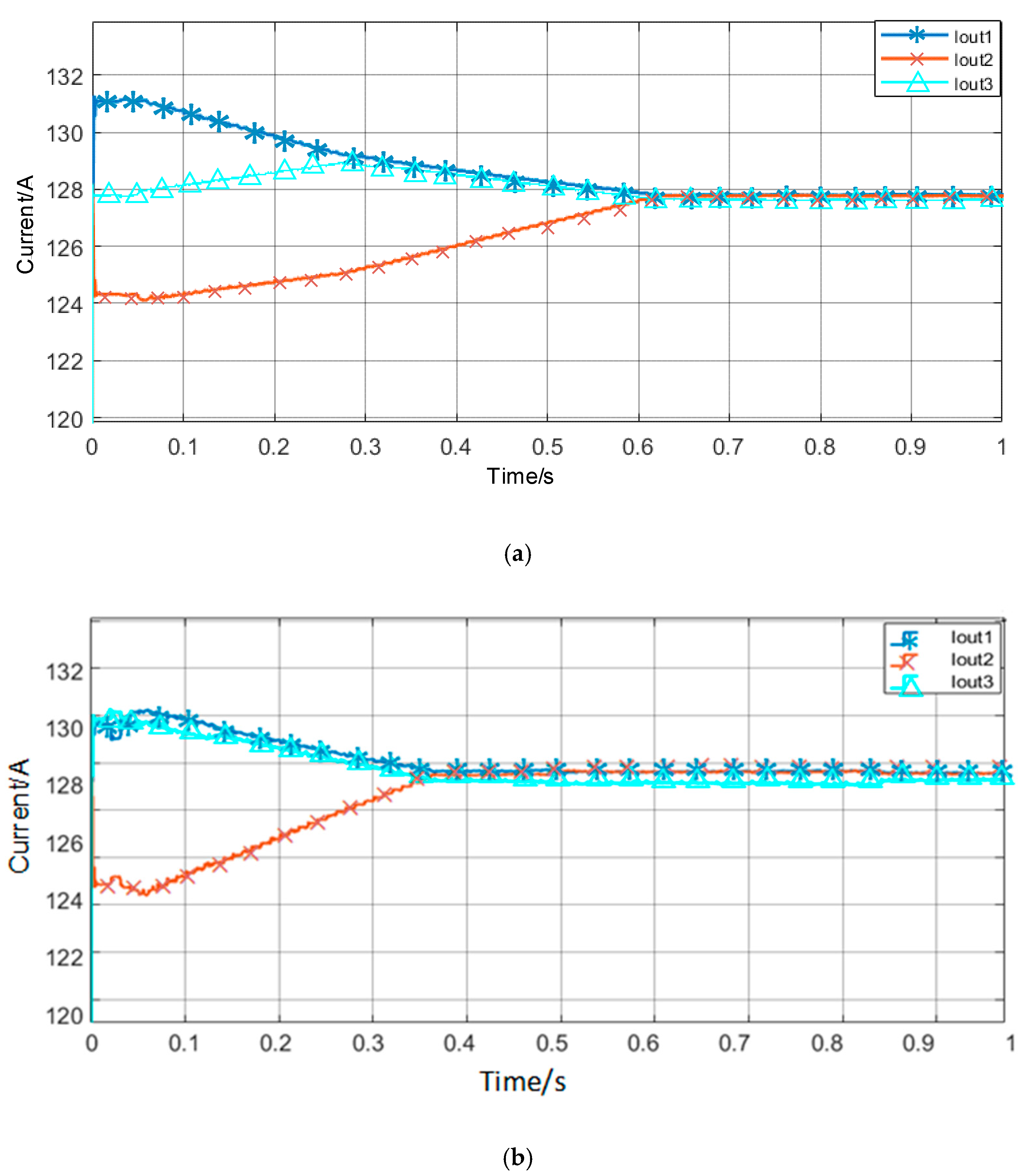
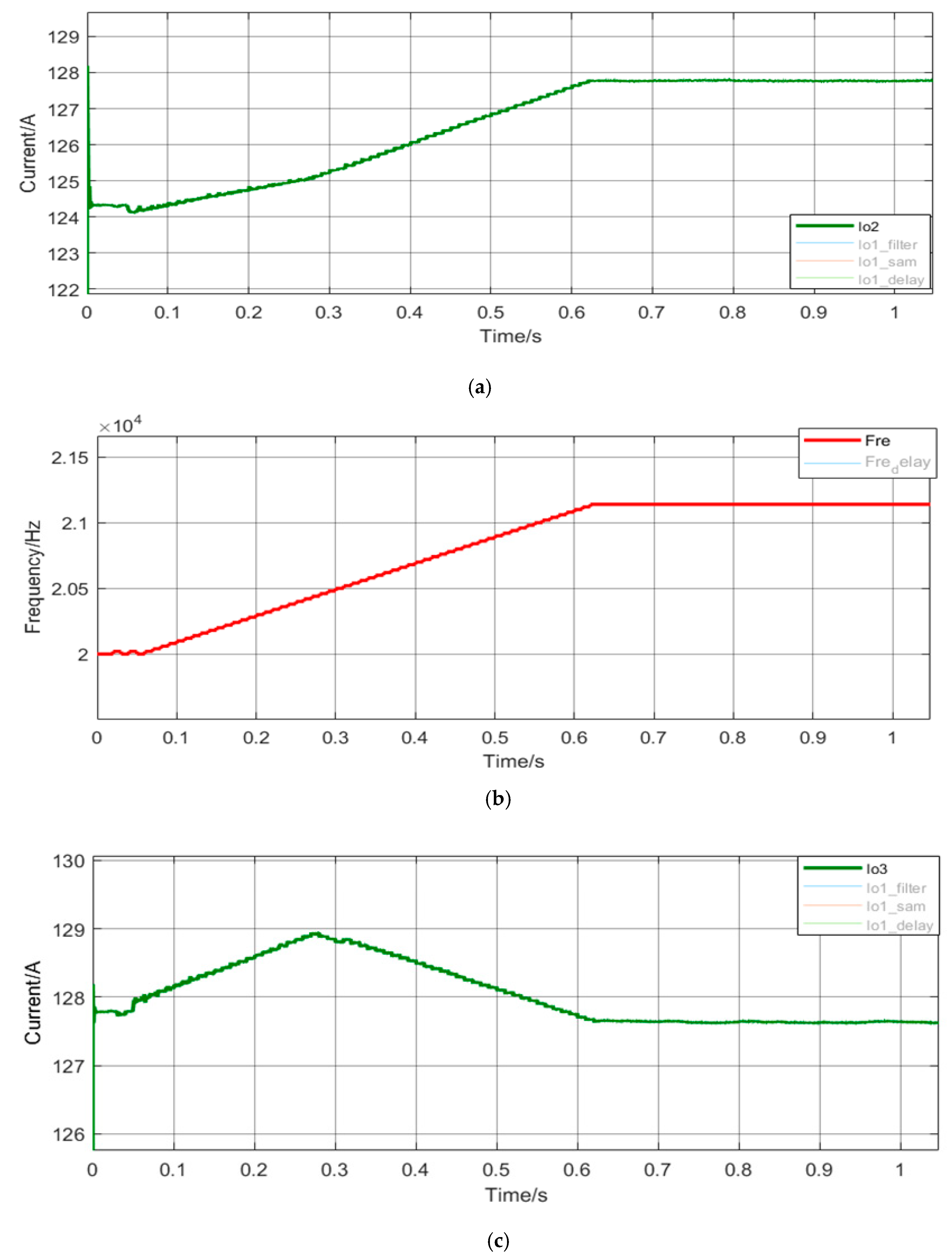
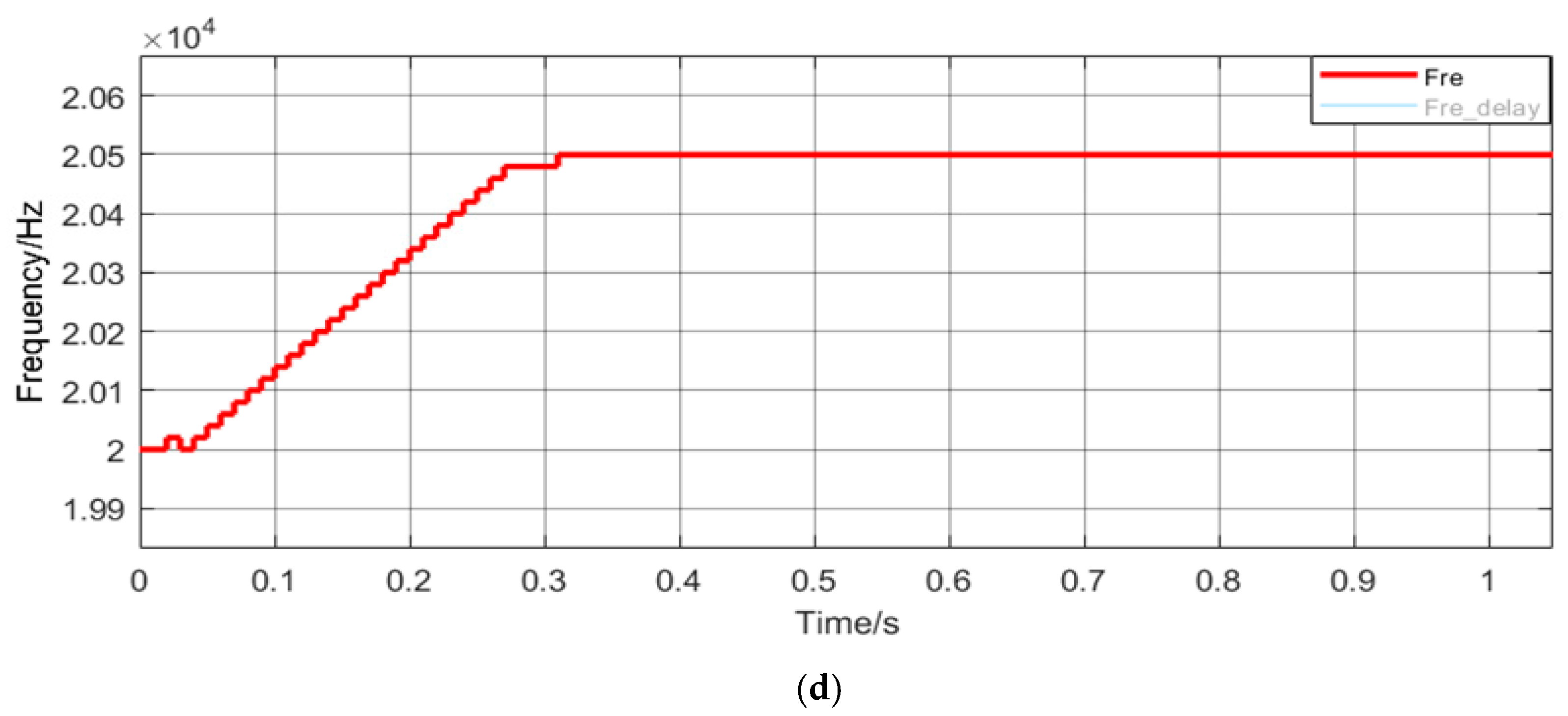
3.1. Power Balancing Control
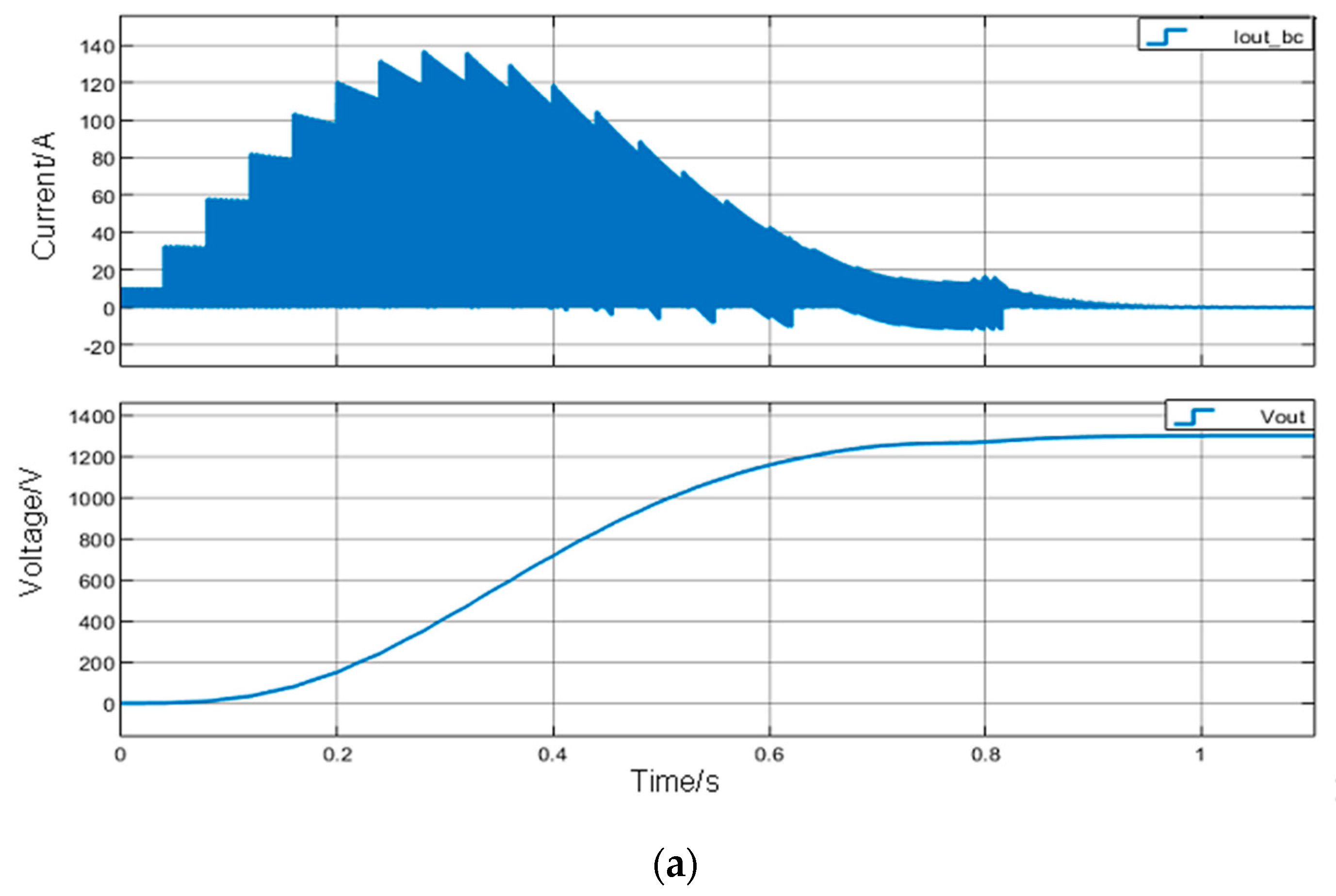
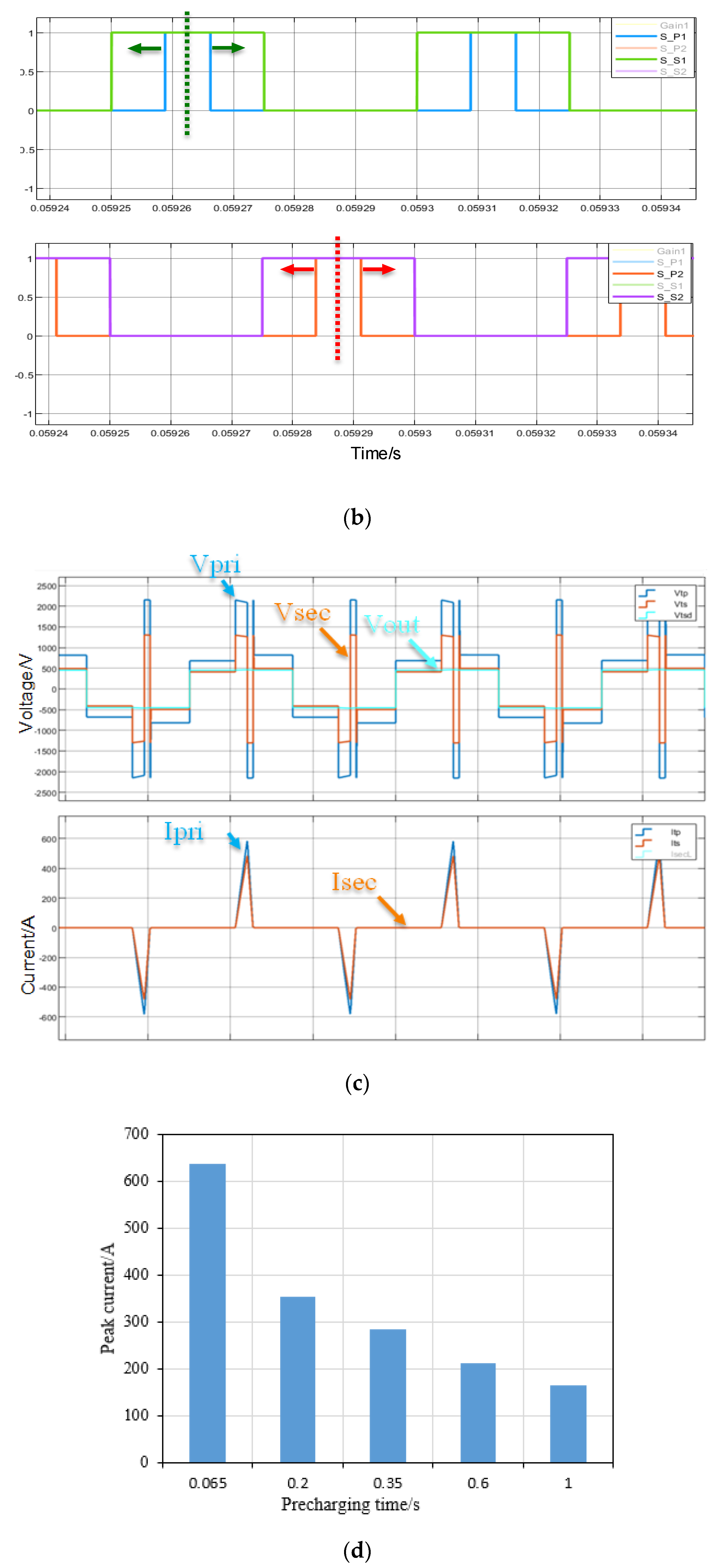
3.2. Pre-Charging Process
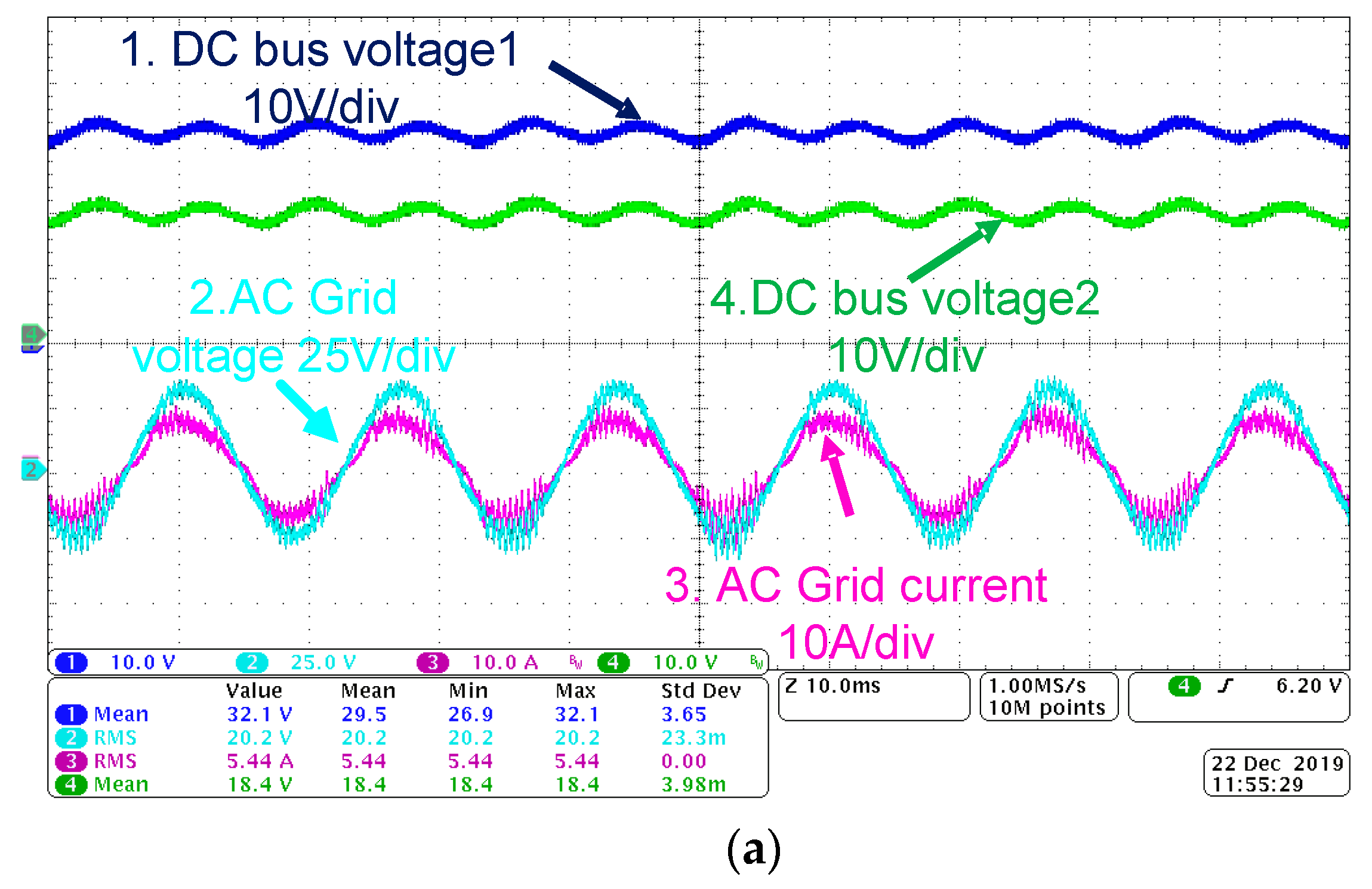
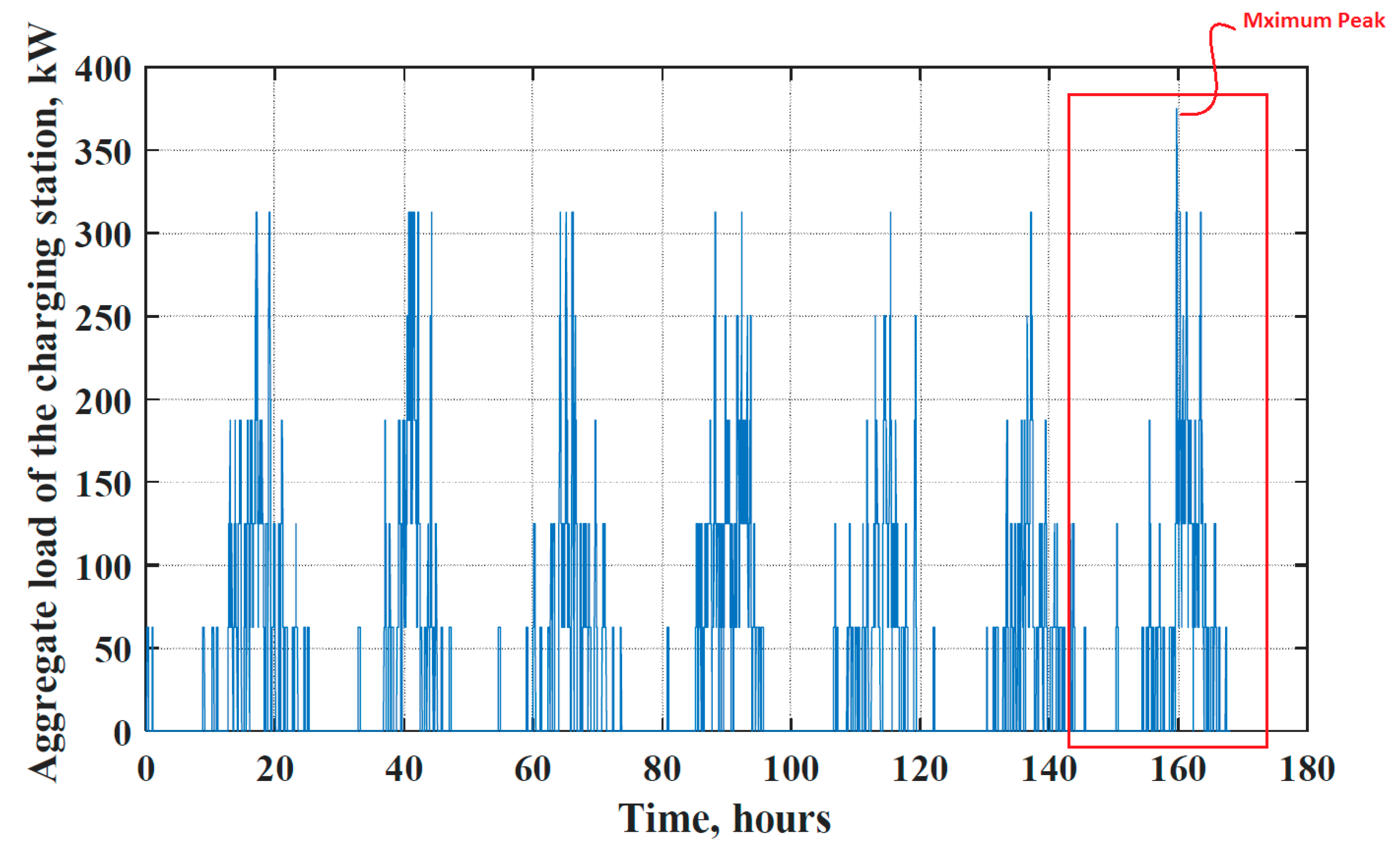
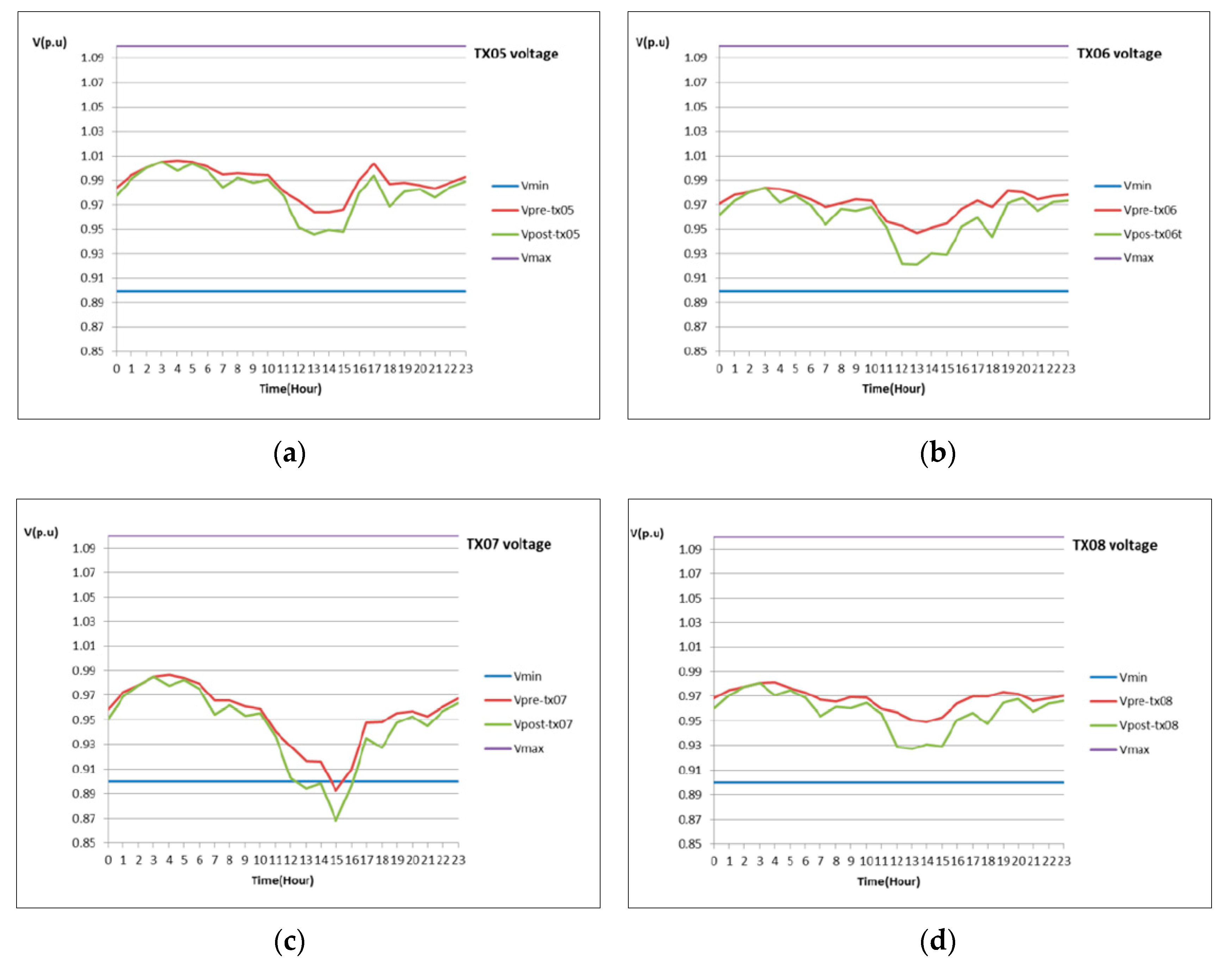
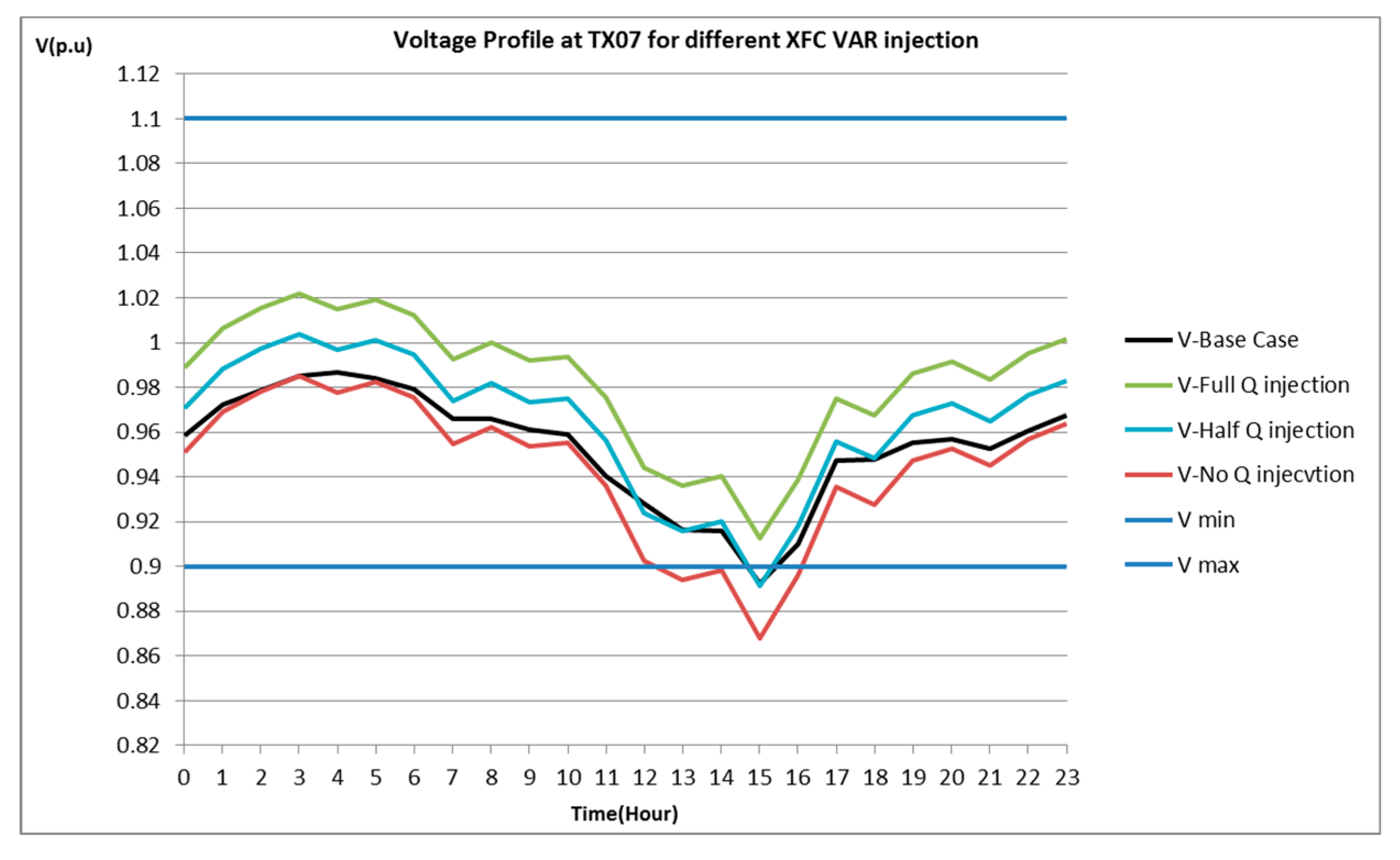
4. Interaction with the Grid
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| AC | Alternating Current |
| CCM | Continuous Conduction Mode |
| Cr | Resonant Capacitance |
| DAB | Dual Active Bridge |
| DC | Direct Current |
| DCX | DC Transformer |
| DC/DC | DC to DC |
| d1, d2 | Duty Cycles for PFC stage |
| EMS | Energy Management System |
| EV | Electric Vehicle |
| FPGA | Field Programmable Gata Array |
| fr | Resonant Frequency |
| fs | Switching Frequency |
| finitial | Initial working frequency |
| Lrd | Designed resonant inductance |
| Crd | Designed resonant capacitance |
| HV | High Voltage |
| ISOP | Input Series Output Parallel |
| Lr | Resonant Inductance |
| LVDC | Low-Voltage DC |
| MOSFET | Metal Oxide Semiconductor Field Effect Transistor |
| MTTF | Mean Time To Failure |
| MV | Medium Voltage |
| MW | Megawatt |
| PFC | Power Factor Correction |
| PWM | Pulse Width Modulation |
| RMS | Root Mean Square |
| R1, R2 | PFC Load Resistances |
| Si | Silicon |
| SiC | Silicon Carbide |
| SOC | State of Charge |
| Ts | Switching Period |
| THD | Total Harmonic Distortion |
| VAC | AC Voltage |
| VAR | Reactive Power |
| VDC | DC Voltage |
| Vin | Input Voltage |
| Vo1, Vo2 | PFC Output Voltages |
| Vvoa | Average Output Voltage |
| WBG | Wide Bandgap |
| XFC | Extreme Fast Charger |
| XFMR | Transformer |
| η | Efficiency |
References
- Hajian, M.; Zareipour, H.; Rosehart, W.D. Environmental benefits of plug-in hybrid electric vehicles: The case of Alberta. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–6. [Google Scholar]
- Lulhe, A.M.; Date, T.N. A technology review paper for drives used in electrical vehicle (EV) & hybrid electrical vehicles (HEV). In Proceedings of the 2015 International Conference on Control, Instrumentation, Communication and Computational Technologies (ICCICCT), Kumaracoil, India, 18–19 December 2015; pp. 632–636. [Google Scholar]
- Ahmed, S.; Bloom, I.; Jansen, A.N.; Tanim, T.; Dufek, E.J.; Pesaran, A.; Burnham, A.; Carlson, R.B.; Dias, F.; Hardy, K.; et al. Enabling fast charging—A battery technology gap assessment. J. Power Sources 2017, 367, 250–262. [Google Scholar]
- Tu, H.; Feng, H.; Srdic, S.; Lukic, S.M. Extreme Fast Charging of Electric Vehicles: A Technology Overview. IEEE Trans. Transp. Electrif. 2019, 5, 861–878. [Google Scholar] [CrossRef]
- Ji, S.; Huang, X.; Zhang, L.; Palmer, J.; Giewont, W.; Wang, F.; Tolbert, L.M. Medium voltage (13.8 kV) transformer-less grid-connected DC/AC converter design and demonstration using 10 kV SiC MOSFETs. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 1953–1959. [Google Scholar]
- Chow, T.P. Wide bandgap semiconductor power devices for energy efficient systems. In Proceedings of the 2015 IEEE 3rd Workshop on Wide Bandgap Power Devices and Applications (WiPDA), Blacksburg, VA, USA, 2–4 November 2015; pp. 402–405. [Google Scholar]
- Armstrong, K.O.; Das, S.; Cresko, J. Wide bandgap semiconductor opportunities in power electronics. In Proceedings of the 2016 IEEE 4th Workshop on Wide Bandgap Power Devices and Applications (WiPDA), Fayetteville, AR, USA, 7–9 November 2016. [Google Scholar]
- Zhao, B.; Song, Q.; Liu, W.; Sun, Y. Overview of dual-active-bridge isolated bidirectional DC–DC converter for high-frequency-link power-conversion system. IEEE Trans. Power Electron. 2014, 29, 4091–4106. [Google Scholar] [CrossRef]
- Wen, H.; Gong, J.; Yeh, C.-S.; Han, Y.; Lai, J. An investigation on fully zero-voltage-switching condition for high-frequency GaN based LLC converter in solid-state-transformer application. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 797–801. [Google Scholar]
- Li, B.; Li, Q.; Lee, F.C. A WBG based three phase 12.5 kW 500 kHz CLLC resonant converter with integrated PCB winding transformer. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 469–475. [Google Scholar]
- Everts, J.; Krismer, F.; Keybus, J.V.D.; Driesen, J.; Kolar, J.W. Optimal ZVS modulation of single-phase single-stage bidirectional DAB AC–DC converters. IEEE Trans. Power Electron. 2013, 29, 3954–3970. [Google Scholar] [CrossRef] [Green Version]
- Khalid, U.; Shu, D.; Wang, H. Hybrid modulated reconfigurable bidirectional CLLC converter for V2G enabled PEV charging applications. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 3332–3338. [Google Scholar]
- Singh, B.; Chandra, A.; Al-Haddad, K.; Pandey, A.; Kothari, D.P. A review of single-phase improved power quality ac~dc converters. IEEE Trans. Ind. Electron. 2003, 50, 962–981. [Google Scholar] [CrossRef] [Green Version]
- Jovanovic, M.; Jang, Y. State-of-the-art, single-phase, active power-factor-correction techniques for high-power applications—an overview. IEEE Trans. Ind. Electron. 2005, 52, 701–708. [Google Scholar] [CrossRef]
- Sankar, U.A.; Mishra, S.; Viswanathan, K.; Naik, R. Control of a series input boost pre-regulator with unbalanced load. In Proceedings of the IECON 2014 - 40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 4582–4588. [Google Scholar]
- Mukhopadhyay, A.; Mishra, S. FPGA based novel voltage balancing technique for series input boost pre-regulator. In Proceedings of the IECON 2017 - 43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 1160–1165. [Google Scholar]
- Li, H.; Jiang, Z. On automatic resonant frequency tracking in LLC series resonant converter based on zero-current duration time of secondary diode. IEEE Trans. Power Electron. 2015, 31, 4956–4962. [Google Scholar] [CrossRef]
- Kundu, U.; Chakraborty, S.; Sensarma, P. Automatic resonant frequency tracking in parallel LLC boost DC–DC converter. IEEE Trans. Power Electron. 2014, 30, 3925–3933. [Google Scholar] [CrossRef]
- Yang, X.; Chen, H.; Shi, J.; Hu, W.; Wang, L.; Liu, J.; Hu, P.; Xiaonan, Y.; Hongkun, C.; Jing, S.; et al. A novel precharge control strategy for modular multilevel converter. In Proceedings of the 2015 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Brisbane, QLD, Australia, 15–18 November 2015; pp. 1–5. [Google Scholar]
- Deng, Q.; Tripathy, S.; Tylavsky, D.; Stowers, T.; Loehr, J. Demand Modeling of a dc Fast Charging Station. In Proceedings of the 2018 North American Power Symposium (NAPS), Fargo, ND, USA, 9–11 September 2018; pp. 1–6. [Google Scholar]





| Figures of Merit | Traditional 500 kVA System | HV SiC Enabled 500 kVA System |
|---|---|---|
| Power losses (%/kW) | η = ηxfmr × ηfast charger = 94.38% @ rated power Plosses = 28.09 kW | η ≥ 97.75% @ rated power Plosses ≤ 11.25 kW η ≥ 95% @ 5% rated power Plosses ≤ 1.25 kW |
| Size–footprint (dm) | Areatotal = 3.5 m2 | Areatotal ≤ 0.875 m2 |
| Size–form factor (dm3) | Vtotal = 5190 liters | Vtotal ≤ 1298 liters |
| Weight (kg) | Wtotal = 3537 kg | Wtotal ≤ 530 kg |
| Specific Power | 0.14 kVA/kg | >5 kVA/kg |
| Power Density | 0.09 kVA/L | >9.2 kVA/L |
| Cooling Method | Air Cooled/Oil Filled | Liquid Cooled |
| MTTF (Targets) | 68,960 h (7.9 years) (PFC + DCX) | 75,856 h (8.66 years) (PFC + DCX) |
| Parameter | DAB | CLLC | DCX |
|---|---|---|---|
| Peak Current [A] | 112 | 275 | 250 |
| RMS Current [A] | 93 | 193 | 170 |
| Maximum Switching-off Current [A] | 112 | 154 | 15 |
| CDC (DC-bus cap between PFC and DCDC [mF]) | 0.8 | 0.6 | 0.01 |
| Cout (DC-bus cap at output [mF]) | 0.085 | 0.085 | 1 × 2 |
| Cr (resonant cap [µF]) | N/A | 0.316 | 12.665 |
| Transformer [kVA] | 420 | 423 | 592 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Z.; Merced, D.; Jalalpour, M.; Bai, H. Deployment of a Bidirectional MW-Level Electric-Vehicle Extreme Fast Charging Station Enabled by High-Voltage SiC and Intelligent Control. Energies 2020, 13, 1840. https://doi.org/10.3390/en13071840
Liang Z, Merced D, Jalalpour M, Bai H. Deployment of a Bidirectional MW-Level Electric-Vehicle Extreme Fast Charging Station Enabled by High-Voltage SiC and Intelligent Control. Energies. 2020; 13(7):1840. https://doi.org/10.3390/en13071840
Chicago/Turabian StyleLiang, Ziwei, Daniel Merced, Mojtaba Jalalpour, and Hua Bai. 2020. "Deployment of a Bidirectional MW-Level Electric-Vehicle Extreme Fast Charging Station Enabled by High-Voltage SiC and Intelligent Control" Energies 13, no. 7: 1840. https://doi.org/10.3390/en13071840
APA StyleLiang, Z., Merced, D., Jalalpour, M., & Bai, H. (2020). Deployment of a Bidirectional MW-Level Electric-Vehicle Extreme Fast Charging Station Enabled by High-Voltage SiC and Intelligent Control. Energies, 13(7), 1840. https://doi.org/10.3390/en13071840





