1. Introduction
The smart grids of today encourage building consumers to deliver demand response (DR) through load curtailment. DR programs are designed to utilise this distributed and flexible energy resource for managing the supply-demand balance in the grid. Such DR programs are key enablers of reliable grid operation, particularly in scenarios where intermittent renewable energy generation and electric vehicle charging are higher. In electricity markets such as the United States of America (USA), Great Britain (GB), most of continental Europe and Oceania, depending on the services availed, the transmission system operator or the distribution system operator plays the additional role of a DR program operator [
1]. The building consumers participating in DR programs deliver DR to the grid either directly or through third-party DR aggregators [
2]. Together, they are referred to as DR participants here. The DR program operator incentivises the DR participants based on their contribution to the energy balance of the grid through load curtailment. This is specifically facilitated by the incentive-based DR programs [
3].
While residential buildings are encouraged to participate in DR programs in many of the electricity markets, this study focuses only on large consumer (commercial and industrial) buildings. For building consumers participating in incentive-based DR programs, capacity scheduling is the task of estimating their load curtailment availability for different forecast horizons such as the hour-ahead to the week-ahead or even the month-ahead. They may be required to notify the DR program operator about this availability in advance. However, it is possible that the forecasted load curtailment and subsequently the scheduled capacity is inaccurate due to errors in the forecast model used by the DR participant. This is one of the uncertainties faced by the DR program operators [
4]. Deviations from the scheduled DR capacity would necessitate additional real-time balancing and reserve energy resources to guarantee the security of supply in the grid [
5]. Often, such deviations result in penalties to the DR participants, who may be discouraged to continue delivering DR. Operator prescribed models for DR capacity scheduling are absent in many of the incentive-based DR programs. As a result, DR participants commit their own estimates of the capacity availability for a given forecast horizon. In this context, the presented study attempts to develop a reliable model for DR capacity scheduling that can potentially be prescribed by the DR operators and adopted by the large consumer building DR participants. Due to the increasing demand for flexibility in the grid, DR participation is also expected to scale up. Catering to this scenario, the presented study focuses not only on the reliability of the models, but also on aspects related to their wider adoption and deployment in DR capacity scheduling.
1.1. Literature Review
Depending on the load curtailment strategy used, the capacity scheduling task for building DR participants can involve either total load forecasting or flexible load forecasting. Building load forecasting is a widely studied domain and extensive literature is available on this subject. Physics based building load forecast models, as reviewed in [
6], are highly accurate since detailed information relating to ambient weather, geographic location and orientation, building design and geometry, thermo-physical aspects of building materials, characteristics of the HVAC system, occupancy information and operating schedule, among others are used in the model development [
7]. However, such detailed level of information and datasets are not always available nor accessible from building consumers participating in DR programs. This limits the applicability of physics based models for DR capacity scheduling. In addition, when a large number of building consumers are participating in DR programs, physics-based models provide minimal opportunity for replication, making their deployment in live operation a tedious process. Machine learning (ML) based data-driven building load forecasting is based on implementations of functions deducted from samples of measured data describing the behaviour of a building load. The ML based building load forecast models have been extensively reviewed in: [
8,
9,
10,
11,
12,
13]. Some of these models are developed for specific application areas such as building performance measurement and verification [
14,
15,
16,
17], building control [
18,
19,
20] and demand-side management [
21,
22], whereas a significant number of studies are application agnostic. Literature demonstrates the capability of supervised ML algorithms such as artificial neural networks (ANN) [
23], support vector machines (SVM) [
24], decision trees [
25,
26], Gaussian processes [
27,
28,
29] and nearest neighbours [
30], among others, in developing reliable building load forecast models. In contrast to the physics based models, the ML based load forecast models require lesser amount of information from the buildings. Using training data, the supervised ML algorithms are capable of learning the nonlinear relationships between influencing (predictor) variables and the building load. With repeated training using the new incoming data, the supervised ML algorithms can learn patterns from the more recent changes (such as addition of a new load). This makes them more adaptable to deployment and operational scenarios. For these reasons, ML based load forecast models are observed to be quite suitable for DR related tasks.
Few previous studies have explored the use of ML for DR related tasks such as capacity scheduling. Nghiem and Jones [
31] developed a Gaussian processes based supervised regression ML model for predicting the load available for DR from commercial buildings using DR signals and weather variables as predictors. Jung et al. [
32] estimated the available flexible DR capacity in two large buildings based on an ML model using data from building variables such as temperature/humidity/light sensors, carbon dioxide sensors, passive infrared sensors and smart plug power meters; the model is claimed to be better than the conventional manual audit processes used to estimate DR capacity. Yang et al. [
33] developed ML based forecast models for energy consumption of heating, ventilation and air conditioning (HVAC) subsystems by using building data and weather forecast information, towards optimising the building energy management system operation as part of DR. Studies have also implemented ML based building load modelling for other DR related tasks such as baseline load estimation towards accurately quantifying the energy delivered as part of DR [
34].
1.2. Contribution
Previous studies on ML based building load forecasting have seldom focussed on deployment of the models in a production environment. This is not necessarily warranted when the modelling efforts are application agnostic. However, when it comes to ML based building load forecast modelling for specific applications, it is worth giving attention to the deployment related aspects that matters in a production environment, right from the beginning. Such a design thinking helps avoid pitfalls at later stages. The presented study demonstrates this by developing reliable ML based building load forecast models for DR capacity scheduling, guided by deployment-centric design criteria such as computational efficiency and scalability. Each of the ML model development tasks performed as part of the modern data science practices are carefully assessed based on these criteria, without compromising the reliability of the models. Furthermore, deployment of the ML models is proposed as an ML pipeline that implements different workflows with sequential and repetitive tasks, suiting the production environment for DR capacity scheduling. Through this approach, the study contributes to the development of a data-driven DR capacity scheduling method that can be easily replicated and widely adopted by the DR industry. This is expected to increase reliable flexibility in the grid and minimise revenue losses for the DR participants. Such efforts are rarely seen in the applied ML literature. This adds to the novelty of the presented work.
1.3. Hypothesis and Objective
The study hypothesises that ML based modelling can present a standardised approach to DR capacity scheduling for large consumer buildings. It is also expected that ML pipelines can enable faster, cost-effective and large-scale deployment of ML models in such DR related tasks. The objective of the study is to develop reliable ML based building load forecast models that are computationally efficient as well as scalable for application in DR capacity scheduling. The ML model development tasks such as data collection, data pre-processing, training-testing dataset preparation, cross-validation, algorithm selection, hyperparameter optimisation, feature ranking, model selection and model evaluation are guided by the focus on deployment in a production environment that supports live operations.
1.4. Deployment-Centric Model Development in Brief
Towards achieving the objective, day-ahead and week-ahead building load forecast models are developed for a retail building. Data collection focuses only on variables that are realistically accessible during deployment. The use of weather forecast predictors with inherent errors are minimised. Instead, alternatives such as lag values accounting for the weather related information from the past are used. Data pre-processing methods for outlier removal, gap filling and feature transformation chosen during model development can be applied on the live data feed in the production environment. The sizes of the testing sets are selected based on the forecast horizon required for capacity scheduling, i.e., day-ahead and week-ahead. A custom forward sliding window method of cross-validation is employed, in order to simulate the actual training and forecasting process in deployment. The selection of a gradient boosted tree (GBT) based supervised regression algorithm for building load forecasting is primarily guided by its computational efficiency. The feature importance output from the GBT algorithm is used to identify the most informative predictors. The study adopts a random-search hyperparameter optimisation method over the commonly used manual-search and the grid-search methods as it is computationally efficient and reliable. A recursive feature elimination method is adopted for feature ranking in order to ensure that a minimal set of the most informative predictors is used. This helps reduce the impact of data gaps on the deployed models. The model selection process identifies the best performing ML models with the smallest set of predictors as well as the least training sizes. This helps reduce the processing power requirements of the models in production and also saves costs while scaling up. The ML model evaluation discussed in the study simulates the training and forecasting process and acts as a pre-production test. The ML model performances are evaluated using the absolute, over-prediction and under-prediction error metrics. These are compared against the error metrics of the persistence models used as alternatives to the ML models. While the ML models show better performance, it is proposed that the persistence models can be used as backups in the production environment.
1.5. Article Structure
The ML model development for building load forecast towards DR capacity scheduling is discussed in
Section 2. Aspects related to deployment of the ML models are detailed in
Section 3. A discussion of the performance of the proposed ML-based DR capacity scheduling is presented in
Section 4.
Section 5 concludes the study.
2. Machine Learning (ML) Model Development
In this section, the tasks involved in ML based model development for building load forecasting are discussed in detail. This starts with the ML problem definition that directs the modelling required towards achieving the end goal. This is followed by data collection and data exploration, within which outliers, data gaps and patterns in the collected data are investigated. The section on feature transformation discusses the necessary changes made to the collected variables towards helping the ML algorithm learn the data relationships. Furthermore, the data preparation activity presents the global dataset and its adaptation for training the ML algorithm. The selection of a suitable ML algorithm and the reasoning behind the same is discussed next, followed by a mathematical description of the selected algorithm. Sections on selection of a suitable hyperparameter optimisation method as well as a feature ranking method, advises the succeeding section on ML model selection. The model development process concludes with the ML model evaluation task that compares the performance of the selected ML models with the persistence models.
2.1. ML Problem Definition
The aim of this research is to develop building load forecast models using ML for DR capacity scheduling. This is demonstrated using a total load curtailment strategy as well as a flexible load curtailment strategy commonly observed in DR practices from large consumer buildings. Total load curtailment can be achieved only if the building site has backup resources such as diesel generators or large batteries. In such cases, the ML problem is to forecast the total load for different horizons. Flexible load curtailment can be achieved by turning off loads such as HVAC for a small duration without affecting the building thermal comfort or business processes. The ML problem here is to forecast how much of that flexible load is available for curtailment. The load forecast horizon depends on the requirements of the DR programs. It has to be noted that the DR program contractual agreements also specify the duration for which loads such as HVAC can be curtailed at a stretch. In order to demonstrate different use cases, day-ahead and week-ahead forecast models are developed for the total load and flexible load in a large consumer building. This results in four different building load forecast models that are then deployed for DR capacity scheduling.
2.2. Data Collection and Exploration
One year long smart meter data are collected from a retail building located in GB at 30 min intervals. This meter dataset includes recordings of the total building load as well as that of the flexible loads such as air conditioners and chillers. These data are resampled from 30 min to 1 h resolution using the mean values.
The collected meter data have few outliers standing out in magnitude from the remaining recorded values. For example, if the absolute value of the maximum rated building load is 500, the meter data values such as 10,000 are acknowledged as outliers in this study. These are removed using the Tukey fences method [
35], according to which, for a dataset with
as the lower quartile (25th percentile),
as the upper quartile (75th percentile) and
as the interquartile range, the data samples outside the following range
for
are identified as outliers. In order to remove outliers from the data that may feed into the model in deployment at a later stage, the Tukey fences are recorded.
Removal of the outliers leave gaps. Single timestamp gaps are filled by imputing with the mean of preceding and succeeding values. In the case of two or more consecutive gaps, the data samples are removed from the dataset. After dealing with the data gaps, the meter data are scaled using the maximum rated building load. This is primarily done for the purpose of data anonymisation. A one week snapshot of these scaled data are shown in
Figure 1. It can be seen that the flexible loads (air conditioners and chillers) constitute about 25–40% of the maximum rated building load. The other loads are assumed to be non-flexible for the purpose of providing DR.
In ML terms, the total load and flexible load are considered as target variables that should be forecasted. Since the values of each of these target variable are continuous, the modelling employs a regression algorithm that can forecast them with the help of predictor variables (or predictors).
In order to understand the temporal influence on the energy consumption patterns in the retail building, load profiling is performed on the collected smart meter data. The time-of-day variations for the scaled total and flexible loads across day-of-week and month-of-year are shown in
Figure 2 and
Figure 3, respectively. The plotted lines represent annual mean values for day-of-week and monthly mean values for month-of-year.
The time-of-day load variations across day-of-week capture the operational hours of the retail building. For most of the days, except Sundays, the energy consumption is consistently high between 7:00 a.m. and 8:00 p.m., possibly correlated with the building occupancy, controlled by temperature or ventilation setbacks. From the time-of-day load variations across month-of-year, it can be observed that this consumption pattern is more pronounced during the winter months. During the summer months, the energy consumption peak is observed only during the midday hours and this could be attributed to the cooling energy requirements in proportion with the ambient temperature. Since temporal variables such as time-of-day, day-of-week and month-of-year show clear influence on the building loads, they are considered as the default set of predictors for all the building load forecast models.
Local weather variables such as temperature, humidity, wind speed and solar radiation influence building energy consumption [
36]. Among these, temperature has the highest influence on building loads such as HVAC. In addition, temperature variations are usually consistent within a considerable distance from the building location [
37]. For this study, temperature recordings from the nearest available meteorological station are collected at one hourly resolution. Wet bulb temperature recordings are preferred over dry bulb temperature recordings since the latter takes into account humidity as well. No outliers were observed in the temperature dataset. Nevertheless, the Tukey fences method as discussed earlier is used to help weed out potential outliers that may feed into the model in deployment at a later stage. Temperature is considered as a candidate predictor for all the building load estimation models, albeit with certain transformations as discussed in the next section.
2.3. Feature Transformation
Feature transformations are the changes made to the collected raw variables that enable the ML algorithm to learn patterns easily. These may be performed either based on the data type or based on domain expertise. Some of these are discussed below.
2.3.1. Categorical to Dummy Variables
Categorical variables such as day-of-week and month-of-year are converted to dummy variables in order to help the supervised ML algorithm learn their relationship with the target variable [
38]. This means that, instead of using values such as 1 for Monday and 2 for Tuesday, dummy variables such as ’is Monday’ and ’is Tuesday’ are derived with values 0 or 1. Hence, a data sample for Monday will have value 1 for ’is Monday’ and 0 for the remaining dummy variables derived for day-of-week.
2.3.2. Degree Days
Temperature and humidity levels maintained inside a building determine its thermal comfort. Base temperature is defined as the ambient temperature at which the HVAC systems do not need to operate in order to maintain thermal comfort. A base temperature of 15.5 °C is widely used in the GB. When ambient temperature is below the base temperature, the heating system provides heat proportional to the temperature difference. The heat energy consumption over a period of time relates to the summation of temperature differences between the ambient temperature and the base temperature. This is referred to as the heating degree days (HDD). Similarly, cooling systems operate when the ambient temperature is above the base temperature, and the summation of their differences over a period of time gives the cooling degree days (CDD) [
39]. HDD and CDD are good indicators of building thermal energy consumption and hence used as predictors in the building load estimation model. Since the ambient temperature data are collected at hourly intervals, an hourly method is used for calculating the daily HDD (
) and daily CDD (
), based on the equations below:
where
is the base temperature, and
is the ambient temperature at the
hour of the day. The plus symbol (+) highlights that the negative temperature differences are equated to zero [
39]. The weekly degree days
and
are calculated based on the summation of daily degree days over a week.
2.3.3. Temperature Estimates
The mean, maximum and minimum values of the ambient temperature over different time periods such as the day or the week are derived to capture seasonal trends in local weather conditions and enrich the information fed into the ML model.
2.3.4. Lag Values to Replace Forecasts
Use of weather variables for training ML algorithms brings in the responsibility of feeding their forecast values into the model once it is deployed. Errors in weather forecasts add to the errors of the building load forecast model, affecting its overall performance. This issue is not given enough attention in many of the applied ML modelling studies since deployment is not always a priority. The meteorological office in the United Kingdom claims that 92% of their day-ahead temperature forecasts are accurate within 2 °C [
40]. However, it is accepted that, as the forecast horizon increases, the weather forecast accuracy declines [
41,
42]. A possible solution to address this uncertainty is the use of time-shifted lag values of the weather data to train the ML models. In this study, the day-ahead building load forecast models use the daily temperature estimates from the previous day (
day_temp_min_lag1,day_temp_mean_lag1,day_temp_max_lag1) and daily degree days from the previous day (
day_HDD_lag1,day_CDD_lag1) as candidate predictors. Similarly, weekly temperature estimates from the previous week (
week_temp_min_lag1,week_temp_mean_lag1,week_temp_max_lag1) and weekly degree days from the previous week (
week_HDD_lag1,week_CDD_lag1) are used in the week-ahead forecast models.
2.4. Data Preparation
From the data exploration and the subsequent feature transformation performed earlier, candidate predictors are identified for the day-ahead and week-ahead building load forecast models. These are listed in
Table 1. Along with the target variables, they form the global dataset for the respective ML forecast models.
The simplest approach to ML model development is to train an algorithm on some data samples and test it on unseen samples using error metrics. To improve the generalisation capability of an ML model while making the best use of the available data, the training-testing process is repeated on different samples using cross-validation. The k-fold is a widely implemented cross-validation technique in which the data samples are randomly split into
k parts of roughly equal sizes. In each iteration, a unique part is held-out for testing and the remaining
parts are used for training. The general forecast performance of the model is then estimated using the average of the error metrics for each iteration. Such cross-validation techniques do not represent the real-world timeseries forecasting problems and results in data leakages [
43]. Hence, a custom cross-validation technique as explained below is used for this deployment-centric ML modelling.
The number of data samples required in a testing set (i.e., the testing set size) is determined based on the forecast horizon of the model. For example, the testing set size for the week-ahead models is the number of hourly values in one week. The training set samples are taken from the preceding days of the testing set without gaps in between to ensure that the latest data are used for training. The training-testing sets are selected for cross-validation using a forward sliding window method as shown in
Figure 4. The training-testing sets slide forward in steps equal to the size of the testing set. This also simulates the real-world operation of the ML models that we would want in deployment for DR capacity scheduling.
Prior to performing cross-validation, each global dataset in timeseries is split into a development set and an evaluation set in the ratio 75:25, respectively. The training-testing sets generated using the forward sliding window method in the development set are used to perform ML model selection (elaborated in
Section 2.8), whereas those generated in the evaluation set are used to compare the ML models’ performance against the persistence models (discussed in
Section 2.9).
2.5. Algorithm Selection
Selection of an appropriate ML algorithm is an important task within ML model development. A simple linear regression algorithm can comprehend nonlinear relationships between predictors and building load with the help of custom transformations such as polynomial functions. Since load characteristics are unique for each building, it is not easy to identify custom functions while developing ML models for a large number of buildings involved in DR programs. Hence, the linear regression algorithm is not adopted for ML model development in this study. Compared against the linear regression algorithm, deep learning algorithms can naturally learn nonlinear relationships but with the help of extremely complex architectures. Application of different ML algorithms in building load forecasting has shown that a deep learning based model, while using higher computational resources and complex training schemes do not produce any better results on a one year dataset than the shallow algorithms [
44]. Shallow algorithms such as artificial neural networks (ANN), support vector machines (SVM), decision trees, ensembles [
45], Gaussian processes [
46] and nearest neighbours [
47] are good at learning nonlinear relationships. There is no requirement to use custom transformations of predictors to establish nonlinear relationships with the target variable. They have proven predictive performances on building load data and are computationally less demanding than deep learning algorithms. While the methodology used in this study is replicable on any supervised ML algorithm, a decision trees based ensemble algorithm namely gradient boosted trees (GBT) is selected for developing the building load forecast models. The GBT algorithm architecture is discussed in detail in the section below.
Gradient Boosted Trees (GBT) Regression Algorithm
This is an ensemble of the decision trees (DT) algorithm. Starting from a root node, the DT algorithm generates a set of if-then-else rules at each decision node below, until the tree terminates at the leaf nodes. The set of decision rules in the DT algorithm are highly interpretable and easy to implement, making it a favoured ML algorithm. Based on its architecture, the DT algorithm also can handle heterogeneous data [
48]. For this reason, predictor data scaling has not been performed in this study. However, it has to be noted that algorithms such as ANN would require mandatory data scaling prior to training.
This study adopts the classification and regression trees (CART) based DT algorithm, discussed in [
49]. The mathematical formulation for CART given further is derived from [
45]. The DT regression algorithm examines a training set
S to find a predictor and split-value that partitions the data samples into two groups (
and
), starting from the root node. This is based on the minimisation of a splitting criterion such as the sum of squared errors (
):
where
and
are the averages of the target variable values within the
and
groups, respectively. The predictor withe lowest
splits a node into two new nodes below and this continues until the leaf node. This recursive partitioning grows the tree until the number of samples in the leaf node falls below a threshold represented by the hyperparameter
minimum samples in leaf. The distance from the root node to the farthest leaf node is quantified in terms of the hyperparameter
maximum number of nodes. It is important to find an optimal DT for a given training data because increase in the tree size increases the complexity of decision rules and may result in over-fitting. The DT hyperparameters
minimum samples in leaf and
maximum number of nodes can be used to optimise the size of the DT.
The DT algorithm generates feature importance scores through the measurement of relative importance of predictors during training. This is achieved by aggregating the reduction in SSE (or other splitting criterion used) for the training set over each predictors. Intuitively, the predictors being split in the upper nodes of the tree or those used multiple times are inferred to have more influence on the predictions [
48]. This capability is utilised for deriving feature rankings, discussed in
Section 2.7.
DT based models have high variance and a small change in the training data could result in a different set of splits. Ensembles are particularly useful in solving this problem. Boosting ensembles based on the gradient boosting machines developed by Friedman [
48] follow the principle: given a loss function (such as least squares) and a weak learner (a trained base model with poor forecast performance), the algorithm seeks to find an additive model that minimises the loss function. The DT base models are good candidates for boosting since they can be easily generated, optimised and added sequentially. In the GBT ensemble algorithm, additive models of the following form are considered:
where
represents the DT base models of fixed size and
the weight parameter. The models are built in a forward stage-wise fashion such that the model at the
mth stage is:
Given the model fit
on
n samples of the training set,
is obtained by minimising the loss function:
using steepest descent optimisation. Loss functions such as least squares (LS), least absolute deviation (LAD) or Huber can be used for this purpose [
48].
The hyperparameters of GBT algorithm considered in this research are the loss function, the number of base models, the maximum number of nodes and the minimum samples in leaf. These hyperparameters are optimised based on the method discussed in the next section.
2.6. Hyperparameter Optimisation Method
Hyperparameter optimisation is the process of selecting the optimal set of hyperparameters in an algorithm that gives the best forecast performance to an ML model [
50]. This process usually begins with defining an initial pool of hyperparameter values from which different trial sets are selected. The performance of the models using these selected trial sets are then tested through cross-validation.
One of the most common methods for selection of trial sets is by manual-search where the values are hand-picked from an initial pool using experience based judgement, as demonstrated in [
51,
52]. While manual-search is a simple method, it is not easily replicable since human judgement is not consistent. Furthermore, manual-search becomes complicated with an increasing number of hyperparameters that are required to be optimised. Grid-search is another widely adopted method where the trial hyperparameter sets are formed using all possible combinations from the initial pool, as demonstrated in [
53,
54]. In comparison with manual-search, grid-search selects the most optimal values. However, as the number of hyperparameters increases, the computational cost of grid-search also escalates. As a computationally efficient alternative to grid-search, the random-search method was proposed by Bergstra and Bengio [
55]. In this method, trial sets are randomly selected from the initial pool using a predetermined sampling size. The sampling size can be varied based on the available computational resources, giving better control to the modeller. Since ML model development in this study is driven by criteria such as computational efficiency and scalability, the random-search method is adopted for hyperparameter optimisation of the GBT algorithm.
2.7. Feature Ranking
A simple ML model should use the minimum number of predictors and still be able to generate the best forecasts. This is particularly important in deployment since issues such as data gaps in each predictor would affect the entire model. Feature ranking methods help identify the best predictors and eliminate the redundant. In this study, based on the load profiling performed earlier, the temporal predictors are considered as the minimal set of predictors required for forecasting. Hence, feature rankings are derived only for the weather predictors listed in
Table 1 based on a method referred to as recursive feature elimination [
56]. For this purpose, all weather predictors are used to train a GBT algorithm on the entire development set and those with the lowest feature importance scores are eliminated in each instance of the training. The weather predictor that remains until the final training instance is given the rank 1. It has to be noted that the GBT algorithm applied at this stage uses a fixed set of hyperparameters (
loss function = LS, number of base models = 100, max. number of nodes = 2, minimum samples in leaf = 2). This is done purely for the purpose of feature ranking prior to model selection, discussed in the succeeding section. When large number of candidate predictors are available, feature ranking becomes an important strategy to help develop simple ML models.
Table 2 shows feature ranking of the weather predictors for the four different building load forecast models.
2.8. ML Model Selection
Model selection is the process of identifying the version of a given algorithm that gives the best forecast performance with the minimal set of predictors, sufficient training data and optimal hyperparameters.
As part of the preparations for model selection, different feature sets are generated for each forecast model as follows. The first feature set (set-1) includes the temporal predictors only. The second feature set (set-2) contains the temporal predictors as well as the rank-1 weather predictor for a particular model. Furthermore, set-3 contains the temporal, rank-1 weather predictor and the rank-2 weather predictor. This continues and the final feature set (set-6) contains all the predictors. In the proposed mode for deployment, the models are expected to be trained regularly. Taking this requirement into consideration, it is ideal for the deployed models to have the smallest training size and yet yield the best forecast performance. For this purpose, the following training sizes are considered: past-2-weeks, past-4-weeks, past-6-weeks and past-8-weeks of hourly values. For each building load forecast model, model selection is performed through an iterative process as summarised using the psuedo codes below (Algorithm 1).
| Algorithm 1 Model selection process |
- 1:
for features [Set-1, Set-2, Set-2,…, Set-6] do - 2:
for training-size [Past-2-weeks, Past-4-weeks,…, Past-8-weeks] do - 3:
Perform hyperparameter optimisation - 4:
end for - 5:
end for
|
The process starts with the selection of the first feature set (set-1), iteratively followed by the set-2, the set-3, and so on, up to set-6. For each feature set selected, the process continues with the selection of a training size from those proposed earlier (past 2–8 weeks). For each feature set and training size selected, random-search hyperparameter optimisation is performed to identify a good candidate model as follows.
Based on the available computational resources, a sampling size of 25 is chosen and the hyperparameter values of the GBT algorithm are randomly selected from the initial pool listed in
Table 3.
A given feature set, a training size and a set of hyperparameter values (for example,
loss function = LAD, number of base models = 130, max. number of nodes = 11, minimum samples in leaf = 4), are together identified as a model. Hence, for a given feature set and a given training size, the random sampling of hyperparameters results in 25 different models. For each of these models, forward sliding window cross-validation is performed on the training-testing sets in the development set (discussed in
Section 2.4). Model forecast performance is measured based on the mean absolute error (MAE) metric given in the equation below:
where
is the forecasted value and
is the actual value. After cross-validation, average MAE is calculated for each model and the one with the lowest average MAE is identified as a candidate model. Hence, for a given feature set and training size, only one candidate model with the best forecast performance is selected.
When all iterations over the six feature sets and four training sizes are complete, 24 candidate models are obtained for each building load forecast category (i.e., total load week-ahead, flexible load week-ahead, total load day-ahead and flexible load day-ahead). Based on their recorded average MAE values, relative model rankings are derived for each of these categories such that a model with the lowest recorded average MAE is given rank 1 and selected as the best candidate. The model rankings are displayed as heatmaps in
Figure 5 and
Figure 6.
For the total load week-ahead model, the best candidate uses feature set-2 and training size of past-6-weeks. Feature set-2 for this model includes temporal predictors (time_of_day, day_of_week, month_of_year) and minimum temperature from past week (week_temp_min_lag1). The flexible load week-ahead model shows best performance with set-1 (temporal predictors only) and training size of past-4-weeks.
For the total load day-ahead model, the best candidate uses feature set-3 and training size of past-6-weeks. Feature set-3 for this model includes temporal predictors as well as weather predictors such as maximum temperature from past day (day_temp_max_lag1) and mean temperature from past day (day_temp_mean_lag1). The best candidate for flexible load day-ahead model uses feature set-5 and training size of past-4-weeks. Feature set-5 of this model includes temporal predictors and weather predictors such as mean temperature from past day (day_temp_mean_lag1), maximum temperature from past day (day_temp_max_lag1), daily CDD from past day (day_CDD_lag1) and daily HDD from past day (day_HDD_lag1).
The optimised hyperparameters of all the best candidate models are listed in
Table 4. These models are selected for model evaluation, elaborated in the next section.
2.9. ML Model Evaluation
As mentioned in
Section 2.4 on data preparation, 25% of all the global datasets are kept untouched for ML model evaluation. These datasets are used to simulate the operation of the best candidate ML models identified from the model selection process, in a production-like environment. Hence, model evaluation is also a pre-production test for the best candidate ML models where the training-forecasting process is simulated using the training-testing sets in the respective evaluation set (selected based on the forward sliding window method discussed in
Section 2.4). For day-ahead models, this results in a continuous set of forecasts that are produced in daily steps based on the training data behind. Here, the training data size depends on that of the best candidate ML model. Similarly, for the week-ahead models, the forecasts are produced in weekly steps. These forecasts are then compared against the actual values and model performances are quantified using the error metrics, mean absolute percentage error (MAPE), mean overprediction percentage error (MOPE) and mean underprediction percentage error (MUPE), given below:
where
is the forecasted value and
is the actual value. The selection of the over-prediction and under-prediction metrics are motivated by the use case i.e., DR capacity scheduling. Specifically, over-prediction and under-prediction errors in the scheduled capacities could impact revenues for the DR participant and also affect the grid balance. The percentage errors are selected for anonymising the actual load values. The values of the MAPE, MOPE and MUPE metrics of each building load forecast models are recorded for benchmarking purposes.
The evaluation for ML based building load forecast models is incomplete without comparing their performances against naive alternatives. For this purpose, four persistence models are developed as alternatives to the four ML based building load forecast models. The day-ahead persistence models use the meter data values from the previous similar day. For instance, the forecasted total load for the upcoming Monday will be the same as the metered total load for the previous Monday. The week-ahead forecast models use the meter data values from the preceding week. In order to avoid ambiguity due to dissimilarities in energy consumption, public holidays are removed from the evaluation sets. The testing sets in the evaluation set that were used to evaluate the ML models are used to evaluate the persistence models as well. The performances of the persistence models are also measured using the MAPE, MUPE and MOPE metrics.
Figure 7 and
Figure 8 displays the forecasts for the week-ahead and the day-ahead models, respectively. Using these figures, a visual comparison can be made between the forecast performances of the ML models and the persistence models for a period of one week taken from the evaluation set. It can be observed that the ML based forecasts are closer to the actual recorded values in most of the instances. Furthermore, a comparison of the model performance metrics for the ML and persistence models is shown in
Figure 9.
3. ML Pipeline for DR Capacity Scheduling
The model evaluation performed in the previous section acts as a pre-production test for the selected forecast models. The performances of the ML models are found to be better than that of their naive alternatives. The next logical step is to deploy these models into the production environment. This section presents the scope for an ML pipeline that facilitates faster, cost-effective and large-scale deployment of ML models for DR capacity scheduling. Related aspects such as ML workflow, computational resource requirements and systems for monitoring and visualisation are discussed in detail.
3.1. ML Workflow
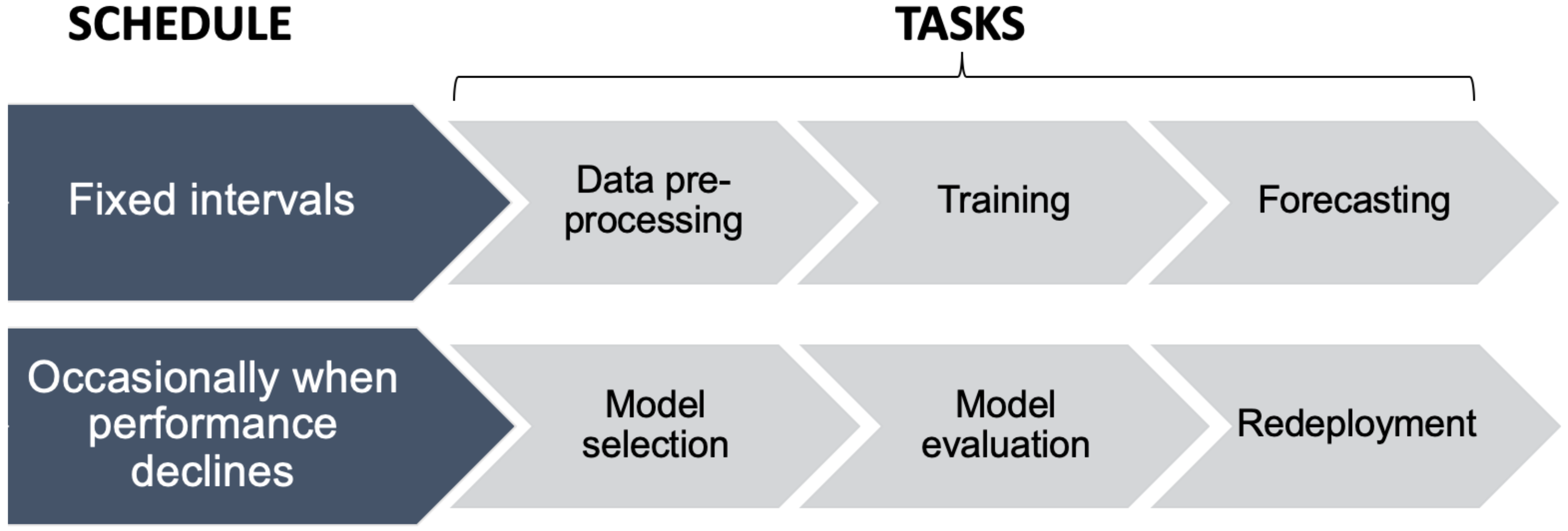
A workflow is a sequence of tasks that repeats over time. The ML workflow for supervised ML based DR capacity scheduling involves tasks such as data pre-processing, training and forecasting. Data pre-processing refers to activities such as data cleaning, data gap filling and feature transformation that are performed on the raw dataset.
During the ML model development process, data cleaning for the building load forecast models were performed with the help of Tukey fences and those values were recorded. In production, these recorded values are used to remove outliers from the live data feeding into the models. The strategy used for gap filling during the model development process is also implemented in production so that forecasts are reliable. Feature transformations used in the final set of predictors for each deployed models are applied on the respective live data feeds. For example, HDD and CDD are derived from the live temperature data feed before passing the values into an ML model. The functions used to derive these transformations are also recorded in a library for future use. This saves time when deploying other load forecast models with similar requirements.
In deployment, ML model training can be performed occasionally or regularly depending on the computational resources available. For DR capacity scheduling, the forecast horizon and the frequency of forecasts are determined based on the DR program requirements. For instance, a week-ahead model may need to update the forecasts weekly or daily or even hourly. Furthermore, the model performance may decline over time in comparison with the benchmark error metrics recorded during model evaluation. In such cases, the model selection and evaluation processes may need to be repeated to re-deploy the best version. Although scheduled to run occasionally, these tasks also become part of the ML workflow. This complete ML workflow is represented in
Figure 10.
When a large number of ML models are deployed into production, the unique scheduling requirements for their workflows necessitate the need for workflow management systems. Such systems are useful to schedule repetitive and sequential tasks very effectively. The open-source packages such as Apache Airflow [
57] and Luigi [
58] are good examples of workflow management systems that support ML pipelines.
3.2. Computational Resource Requirements
Computational resources such as database servers, processing power and programming environments form the backbone of an ML pipeline.
Data that flow through the ML pipeline are stored in databases at different stages. For instance, a database stores live incoming data from various sources continuously. For the building load forecast models developed in this study, the raw dataset includes meter data and weather data. Data pre-processing is performed on this raw dataset and the processed data are also stored for easy querying towards training and forecasting. The trained ML models with their parameters are stored for subsequent repeated forecasting on unseen data. The forecasted results and error metrics such as MAPE, MOPE and MUPE are also stored in the database for monitoring the model performances continuously.
Model development is a computationally intensive process. Depending on the type of algorithm and the size of data used, the processing power requirements could also change. Due to their complexity, deep learning algorithms usually require graphical processing units (GPUs) for faster training. ML models based on shallow algorithms such as GBT used in this study can be easily trained using the ubiquitous central processing units (CPUs). For the purpose of this study, the model development is performed on a computer with the following specification: Intel i5, four cores 2.71 GHz CPU and 8 GB RAM. The computational times for different processes are listed in
Table 5. For the computer specifications used, the model selection process takes between 48 and 53 min. This can be altered by changing the sampling size of the random-search hyperparameter optimisation method. Each instance of training-forecasting for the selected ML models takes between 8.1 and 8.6 seconds.
Tasks such as model selection, model evaluation, data pre-processing, training and forecasting that are part of the ML workflow are codified in a programming environment. The presented study has made use of the Python environment and its Scikit-Learn ML package.
3.3. Systems for Monitoring and Visualisation
In production, forecast models may fail because of data gaps or technical issues with computational resources. In such cases, backup models may need to be triggered to ensure business continuity. The persistence models used in this study with relatively good forecast performances (as shown in
Figure 9) could serve as backup models in such occasions. Systems capable of monitoring the models in production and alerting the right people towards taking corrective measures tend to be very useful. Many of the workflow management systems provide such monitoring capabilities.
In addition to monitoring, visualisation of the forecast results supports better decision-making.
Figure 11 shows the total and flexible load forecasts for the week-ahead as well as the actual load values over a selected window in a representative visualisation dashboard. The DR capacity scheduled for each building and their deviations from the actual availability could be visualised in this way and the outputs could be directed to appropriate channels.
4. Results and Discussion
The presented research attends to the need for reliable capacity scheduling in incentive-based demand response (DR). Since this DR task is not standardised at the moment, inaccurate forecasts from DR participants such as large consumer buildings result in deviations from their scheduled capacities. This affects the energy balance of the electricity grid and leads to penalties for the consumers. In this study, supervised machine learning (ML) based forecast models are developed for total and flexible loads of a retail building that can be used to schedule DR capacity availability for the day-ahead and the week-ahead. Persistence models are also developed as alternatives to each category of the ML models. For benchmarking purposes, the ML and the persistence models are compared against each other using the MUPE, MOPE and MAPE metrics that are relevant for the DR capacity scheduling application.
From the results given in
Figure 9, it can be seen that the forecast errors (referring to MUPE, MOPE and MAPE metrics) of the ML models are generally lower than their respective persistence model alternatives. The difference in MAPE between the persistence and ML methods, for the day-ahead models is 1.41 (total load) and 2.4 (flexible load), while that for week-ahead models is 0.8 (total load) and 1.25 (flexible load). It can be concluded that, in comparison to the persistence models, ML models are more reliable for the day-ahead DR capacity scheduling as well as for the flexible load DR capacity scheduling. Nevertheless, the persistence models also perform well, making them good backup models in the production environment.
The study also considers the scenario of increasing DR participation from large consumer buildings towards supplementing the grid flexibility. In order to encourage wider adoption, the ML based building load forecast model development performed in this study is focused on deployment in a production environment. Subsequently, the model development is guided by design criteria such as computational efficiency and scalability, while ensuring reliability of the models. These factors distinguish the presented study from the previous literature on ML based building load forecasting. The specific deployment-centric model development processes presented in this study are evaluated below:
Data collection for the retail building focuses only on variables such as smart meter data and ambient weather data that are realistically accessible in a production environment. The use of weather predictors such as temperature forecast that comes with inherent errors are attempted to be minimised. Instead lag values of the measured temperature data are used. If accessibility to other weather predictors such as solar radiation, humidity and wind speed is guaranteed during model development and in production, it is highly encouraged to use them as candidate predictors. Using feature ranking methods, the less informative predictors could then be removed.
Data pre-processing methods for outlier removal and gap filling are selected such that they are applicable on the new data feeds after deployment. Feature transformations are used to improve the learning capability of the ML algorithm and the functions used for this purpose are stored in a library for future use. This saves time and cost when repeating similar modelling on other building loads.
As part of data preparation, the testing sizes are selected on the basis of the forecast horizon (day-ahead or week-ahead) required for capacity scheduling. The use of cross-validation methods such as k-fold is avoided to minimise data leakage. Instead, a custom forward sliding window method of cross-validation is employed that also simulates the actual training and forecasting process in deployment.
Computational efficiency guides the selection of gradient boosted tree (GBT) based regression algorithm for building load forecasting. The feature importance output from the GBT algorithm is utilised to identify the best predictors. Among the nonlinear regression algorithms, while the use of deep learning algorithms for building load forecasting is observed to be computationally demanding, other shallow algorithms may be used to replace the GBT algorithm. Since computational efficiency need not be a limiting factor for DR participants with access to powerful computational resources, it is also worth exploring how deep learning algorithms perform in this context. However, this is beyond the scope of the presented study.
A random-search hyperparameter optimisation method is preferred over the manual-search and the grid-search methods as it provides more control to the modeller by letting select a sampling size based on the available processing power.
Feature ranking is performed using a recursive feature elimination method to ensure that a minimal set of predictors is used to develop the best ML models. This helps reduce the impact of data gaps in predictors on the models in production and hence minimise model failures.
The demonstrated model selection process ensures that the best performing ML models with the smallest set of predictors as well as the least training sizes are identified such that processing power requirements of the models in production are reduced, saving costs in the process. The savings are more significant when a large number of models are in production.
The model evaluation acts as a pre-production test that simulates the training and forecasting process. Metrics that quantify the absolute, over-prediction and under-prediction errors are used to evaluate the model performances. Persistence models considered as alternatives for the ML models are also evaluated using the same metrics. Against the persistence models, the ML models show better performance. Nevertheless, it is proposed that the persistence models can be used as backups in production if the ML models fail due to issues such as data gaps.
To support the efforts towards faster, cost-effective and large-scale deployment of ML models, the research proposes an ML pipeline for DR capacity scheduling. The ML pipeline implements ML workflows of different sequential and repeating tasks scheduled with the help of workflow management systems. These include tasks such as data pre-processing, training and forecasting that are repeated at fixed intervals as well as tasks such as model selection, model selection and model redeployment that are triggered occasionally when the model performance declines over a period of time. The ML pipeline also accounts for computational resource requirements such as the database servers, processing power and programming environments. In addition, systems for monitoring and visualisation are observed to be vital components of the ML pipeline.
While DR capacity scheduling is an important aspect within DR operations, the actual availability of the forecasted load curtailment depends on other factors as well. These are discussed below:
For a building with a generator or a battery that can backup the total load, scheduled DR capacity assumes that the backup sources are available on demand to switch the total load away from the grid. The total load models implemented through the ML pipeline can continuously make forecasts to different horizons such as day-ahead or week-ahead, as mandated by the DR program requirements. In practice, when the program operator requests the scheduled DR capacity to be delivered for a few hours, the generator may end up being non-functional. It is also possible that the battery runs out of energy to backup the total load for the suggested duration. These situations result in non-delivery of the scheduled DR capacity, regardless of how good the total load forecast models are. Such events could be minimised with proper planning and management on-site.
A building DR participant with flexible loads could make use of the flexible load forecast models implemented through the ML pipeline to schedule their DR capacity. Depending on the DR program requirements, the scheduling may be done for different forecast horizons. However, the actual utilisation of this scheduled DR capacity is constrained by the building internal factors. In the case of flexible loads such as air conditioners, the curtailment decision takes into account thermal comfort of the occupants. Subsequently, such curtailments cannot be prolonged for hours. Similarly, curtailment of chiller loads for long duration could affect the quality of consumables in a retail building. Many of the DR programs that facilitate flexible load based DR address such practical limitations in their contractual agreements.
5. Conclusions
The study demonstrates the applicability of ML based building load forecasting for DR capacity scheduling in a retail building. Results show that, in comparison with timeseries based persistence models, reliable ML based models can be developed for DR capacity scheduling, while also giving weightage to design criteria such as computational efficiency and scalability. The modelling methodology is easily replicable on other large consumer buildings. If more weather predictors are available, it may be worth considering them in the model development process. While the study employs the GBT based supervised regression algorithm, it is possible to build similar models with other competent algorithms. These tasks are beyond the scope of the presented study and hence considered for a future presentation.
A highly flexible grid can support the integration of renewable energy and electric vehicle charging towards its complete decarbonisation. In order to realise this, increased DR delivery must be expected from participants such a large consumer buildings with total or flexible load curtailment capability. The ML pipeline proposed in this study facilitates faster, cost-effective and large-scale deployment of reliable DR capacity scheduling models for such DR participants. If the DR aggregators and the program operators adopt such ML pipelines for DR related tasks, grid flexibility can be improved without affecting its reliability. This also helps minimise revenue losses for the DR participants who otherwise get penalised for deviations from their scheduled capacities. In aggregated scales, these ML pipelines could also pave the way for increased automation in smart grid operations. While open-source ML and computational resources are abundantly available, data quality issues such as outliers and data gaps should be minimised for effective functioning of these data-driven ML pipelines. This can be achieved through regulatory and industry-wide efforts towards improving data quality in the smart grids.
Author Contributions
Conceptualization, G.K.; methodology, G.K.; software, G.K.; validation, G.K.; formal analysis, G.K.; investigation, G.K.; resources, G.K. and A.K.; data curation, G.K.; writing—original draft preparation, G.K.; writing—review and editing, A.K.; visualization, G.K.; supervision, A.K.; project administration, A.K.; funding acquisition, A.K. All authors have read and approved the final version of the manuscript.
Funding
This study was conducted at Flexitricity Limited in collaboration with University of Edinburgh. It received funding from the European Union’s Seventh Framework Programme for research, technological development and demonstration under Grant Agreement No. 607774 and the Department for Business, Energy and Industrial Strategy (BEIS), United Kingdom.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ANN | Artificial Neural Networks |
| CART | Classification and Regression Tree |
| CDD | Cooling Degree Days |
| CPU | Central Processing Unit |
| DR | Demand Response |
| DT | Decision Tree |
| GB | Great Britain |
| GBT | Gradient Boosted Tree |
| GPU | Graphical Processing Unit |
| HDD | Heating Degree Days |
| HVAC | Heating, Ventilation and Air Conditioning |
| LAD | Least Absolute Deviation |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MOPE | Mean Overprediction Percentage Error |
| MUPE | Mean Underprediction Percentage Error |
| ML | Machine Learning |
| SVM | Support Vector Machine |
| USA | United States of America |
References
- Paterakis, N.G.; Erdinç, O.; Catalão, J.P. An overview of Demand Response: Key-elements and international experience. Renew. Sustain. Energy Rev. 2017, 69, 871–891. [Google Scholar] [CrossRef]
- Mohammad, N.; Mishra, Y. The Role of Demand Response Aggregators and the Effect of GenCos Strategic Bidding on the Flexibility of Demand. Energies 2018, 11, 3296. [Google Scholar] [CrossRef]
- Shi, Q.; Chen, C.; Mammoli, A.; Li, F. Estimating the Profile of Incentive-Based Demand Response (IBDR) by Integrating Technical Models and Social-Behavioral Factors. IEEE Trans. Smart Grid 2020, 11, 171–183. [Google Scholar] [CrossRef]
- Li, P.; Wang, H.; Zhang, B. A Distributed Online Pricing Strategy for Demand Response Programs. IEEE Trans. Smart Grid 2019, 10, 350–360. [Google Scholar] [CrossRef]
- Liu, Z.; Zeng, X.; Meng, F. An Integration Mechanism between Demand and Supply Side Management of Electricity Markets. Energies 2018, 11, 3314. [Google Scholar] [CrossRef]
- Foucquier, A.; Robert, S.; Suard, F.; Stéphan, L.; Jay, A. State of the art in building modelling and energy performances prediction: A review. Renew. Sustain. Energy Rev. 2013, 23, 272–288. [Google Scholar] [CrossRef]
- Harish, V.; Kumar, A. A review on modeling and simulation of building energy systems. Renew. Sustain. Energy Rev. 2016, 56, 1272–1292. [Google Scholar] [CrossRef]
- Yildiz, B.; Bilbao, J.; Sproul, A. A review and analysis of regression and machine learning models on commercial building electricity load forecasting. Renew. Sustain. Energy Rev. 2017, 73, 1104–1122. [Google Scholar] [CrossRef]
- Daut, M.A.M.; Hassan, M.Y.; Abdullah, H.; Rahman, H.A.; Abdullah, M.P.; Hussin, F. Building electrical energy consumption forecasting analysis using conventional and artificial intelligence methods: A review. Renew. Sustain. Energy Rev. 2017, 70, 1108–1118. [Google Scholar] [CrossRef]
- Deb, C.; Zhang, F.; Yang, J.; Lee, S.E.; Shah, K.W. A review on time series forecasting techniques for building energy consumption. Renew. Sustain. Energy Rev. 2017, 74, 902–924. [Google Scholar] [CrossRef]
- Amasyali, K.; El-Gohary, N.M. A review of data-driven building energy consumption prediction studies. Renew. Sustain. Energy Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Wang, Z.; Srinivasan, R.S. A review of artificial intelligence based building energy use prediction: Contrasting the capabilities of single and ensemble prediction models. Renew. Sustain. Energy Rev. 2017, 75, 796–808. [Google Scholar] [CrossRef]
- Raza, M.Q.; Khosravi, A. A review on artificial intelligence based load demand forecasting techniques for smart grid and buildings. Renew. Sustain. Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
- Burkhart, M.C.; Heo, Y.; Zavala, V.M. Measurement and verification of building systems under uncertain data: A Gaussian process modeling approach. Energy Build. 2014, 75, 189–198. [Google Scholar] [CrossRef]
- Gallagher, C.V.; Leahy, K.; O’Donovan, P.; Bruton, K.; O’Sullivan, D.T. Development and application of a machine learning supported methodology for measurement and verification (M|&V) 2.0. Energy Build. 2018, 167, 8–22. [Google Scholar] [CrossRef]
- Attanasio, A.; Savino Piscitelli, M.; Chiusano, S.; Capozzoli, A.; Cerquitelli, T. Towards an Automated, Fast and Interpretable Estimation Model of Heating Energy Demand: A Data-Driven Approach Exploiting Building Energy Certificates. Energies 2019, 12, 1273. [Google Scholar] [CrossRef]
- Maritz, J.; Lubbe, F.; Lagrange, L. A Practical Guide to Gaussian Process Regression for Energy Measurement and Verification within the Bayesian Framework. Energies 2018, 11, 935. [Google Scholar] [CrossRef]
- Peng, Y.; Rysanek, A.; Nagy, Z.; Schlüter, A. Using machine learning techniques for occupancy-prediction-based cooling control in office buildings. Appl. Energy 2018, 211, 1343–1358. [Google Scholar] [CrossRef]
- Drgoňa, J.; Picard, D.; Kvasnica, M.; Helsen, L. Approximate model predictive building control via machine learning. Appl. Energy 2018, 218, 199–216. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, J.; Chen, H.; Li, G.; Liu, J.; Xu, C.; Huang, R.; Huang, Y. Machine learning-based thermal response time ahead energy demand prediction for building heating systems. Appl. Energy 2018, 221, 16–27. [Google Scholar] [CrossRef]
- Chae, Y.T.; Horesh, R.; Hwang, Y.; Lee, Y.M. Artificial neural network model for forecasting sub-hourly electricity usage in commercial buildings. Energy Build. 2016, 111, 184–194. [Google Scholar] [CrossRef]
- Wang, L.; Lee, E.W.; Yuen, R.K. Novel dynamic forecasting model for building cooling loads combining an artificial neural network and an ensemble approach. Appl. Energy 2018, 228, 1740–1753. [Google Scholar] [CrossRef]
- Runge, J.; Zmeureanu, R. Forecasting Energy Use in Buildings Using Artificial Neural Networks: A Review. Energies 2019, 12, 3254. [Google Scholar] [CrossRef]
- Ahmad, A.; Hassan, M.; Abdullah, M.; Rahman, H.; Hussin, F.; Abdullah, H.; Saidur, R. A review on applications of ANN and SVM for building electrical energy consumption forecasting. Renew. Sustain. Energy Rev. 2014, 33, 102–109. [Google Scholar] [CrossRef]
- Pang, Y.; Jiang, X.; Zou, F.; Gan, Z.; Wang, J. Research on Energy Consumption of Building Electricity Based on Decision Tree Algorithm. In Proceedings of the Fourth Euro-China Conference on Intelligent Data Analysis and Applications, Malaga, Spain, 9–11 October 2018; Krömer, P., Alba, E., Pan, J.S., Snášel, V., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 264–271. [Google Scholar]
- Yu, Z.; Haghighat, F.; Fung, B.C.; Yoshino, H. A decision tree method for building energy demand modeling. Energy Build. 2010, 42, 1637–1646. [Google Scholar] [CrossRef]
- Heo, Y.; Zavala, V.M. Gaussian process modeling for measurement and verification of building energy savings. Energy Build. 2012, 53, 7–18. [Google Scholar] [CrossRef]
- Prakash, A.K.; Xu, S.; Rajagopal, R.; Noh, H. Robust Building Energy Load Forecasting Using Physically-Based Kernel Models. Energies 2018, 11, 862. [Google Scholar] [CrossRef]
- Goliatt, L.; Capriles, P.V.Z.; Duarte, G.R. Modeling Heating and Cooling Loads in Buildings Using Gaussian Processes. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Valgaev, O.; Kupzog, F.; Schmeck, H. Building power demand forecasting using K-nearest neighbours model —Practical application in Smart City Demo Aspern project. CIRED Open Access Proc. J. 2017, 2017, 1601–1604. [Google Scholar] [CrossRef]
- Nghiem, T.X.; Jones, C.N. Data-driven demand response modeling and control of buildings with Gaussian Processes. In Proceedings of the American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 2919–2924. [Google Scholar] [CrossRef]
- Jung, D.; Krishna, V.B.; Temple, W.G.; Yau, D.K.Y. Data-driven evaluation of building demand response capacity. In Proceedings of the IEEE International Conference on Smart Grid Communications (SmartGridComm), Venice, Italy, 3–6 November 2014; pp. 541–547. [Google Scholar] [CrossRef]
- Yang, C.; Létourneau, S.; Guo, H. Developing Data-driven Models to Predict BEMS Energy Consumption for Demand Response Systems. In Modern Advances in Applied Intelligence; Ali, M., Pan, J.S., Chen, S.M., Horng, M.F., Eds.; Springer International Publishing: Cham, Switzelrand, 2014; pp. 188–197. [Google Scholar]
- Song, T.; Li, Y.; Zhang, X.P.; Li, J.; Wu, C.; Wu, Q.; Wang, B. A Cluster-Based Baseline Load Calculation Approach for Individual Industrial and Commercial Customer. Energies 2018, 12, 64. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley: Boston, MA, USA, 1977. [Google Scholar]
- Hunn, B.D. Fundamentals of Building Energy Dynamics; MIT Press: Cambridge, MA, USA, 1996; Volume 4. [Google Scholar]
- Arens, E.A.; Williams, P.B. The effect of wind on energy consumption in buildings. Energy Build. 1977, 1, 77–84. [Google Scholar] [CrossRef]
- Grotenhuis, M.T.; Thijs, P. Dummy variables and their interactions in regression analysis: Examples from research on body mass index. arXiv 2015, arXiv:stat.AP/1511.05728. [Google Scholar]
- Mourshed, M. Relationship between annual mean temperature and degree-days. Energy Build. 2012, 54, 418–425. [Google Scholar] [CrossRef]
- UK Met Office. Global Accuracy at a Local Level. 2019. Available online: https://www.metoffice.gov.uk/about-us/what/accuracy-and-trust/how-accurate-are-our-public-forecasts (accessed on 12 December 2019).
- OFGEM. Review of Met Office Weather Forecast Accuracy. 2019. Available online: https://www.ofgem.gov.uk/ofgem-publications/111122 (accessed on 12 December 2019).
- Paret, M.; Martz, E. Weather Forecasts: Just How Reliable Are They? Technical Report; Minitab: Ferguson Township, PA, USA, 2015. [Google Scholar]
- Tashman, L.J. Out-of-sample tests of forecasting accuracy: An analysis and review. Int. J. Forecast. 2000, 16, 437–450. [Google Scholar] [CrossRef]
- Fan, C.; Xiao, F.; Zhao, Y. A short-term building cooling load prediction method using deep learning algorithms. Appl. Energy 2017, 195, 222–233. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Berlin, Germany, 2016. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Hastie, T.; Friedman, J.; Tisbshirani, R. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin, Germany, 2017. [Google Scholar]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Loh, W.Y. Classification and regression trees. Wires Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for Hyper-parameter Optimization. In Proceedings of the 24th International Conference on Neural Information Processing Systems, NIPS’11, Guangzhou, China, 14–18 November 2011; Curran Associates Inc.: Red Hook, NY, USA, 2011; pp. 2546–2554. [Google Scholar]
- Ruiz, L.G.B.; Cuéllar, M.P.; Calvo-Flores, M.D.; Jiménez, M.D.C.P. An Application of Non-Linear Autoregressive Neural Networks to Predict Energy Consumption in Public Buildings. Energies 2016, 9, 684. [Google Scholar] [CrossRef]
- Li, Q.; Meng, Q.; Cai, J.; Yoshino, H.; Mochida, A. Predicting hourly cooling load in the building: A comparison of support vector machine and different artificial neural networks. Energy Convers. Manag. 2009, 50, 90–96. [Google Scholar] [CrossRef]
- Massana, J.; Pous, C.; Burgas, L.; Melendez, J.; Colomer, J. Short-term load forecasting in a non-residential building contrasting models and attributes. Energy Build. 2015, 92, 322–330. [Google Scholar] [CrossRef]
- Kontokosta, C.E.; Tull, C. A data-driven predictive model of city-scale energy use in buildings. Appl. Energy 2017, 197, 303–317. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene Selection for Cancer Classification Using Support Vector Machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Apache Airflow. Documentation. 2019. Available online: https://airflow.apache.org/docs/stable/ (accessed on 20 January 2020).
- Luigi. Documentation. 2019. Available online: https://luigi.readthedocs.io/en/stable/index.html (accessed on 20 January 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).