Numerical Study of Heat Transfer in Gravity-Driven Particle Flow around Tubes with Different Shapes †
Abstract
:1. Introduction
2. Physical Model and Computational Method
2.1. Physical Model
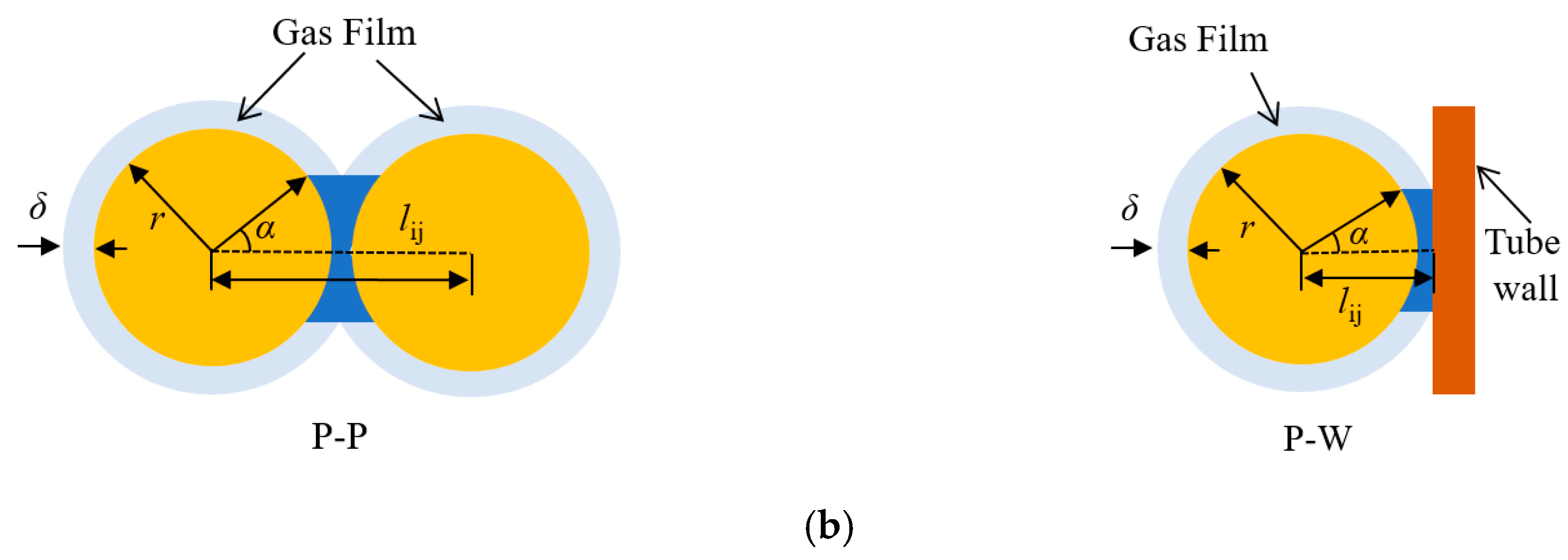
2.2. DEM Method and Heat Transfer Model
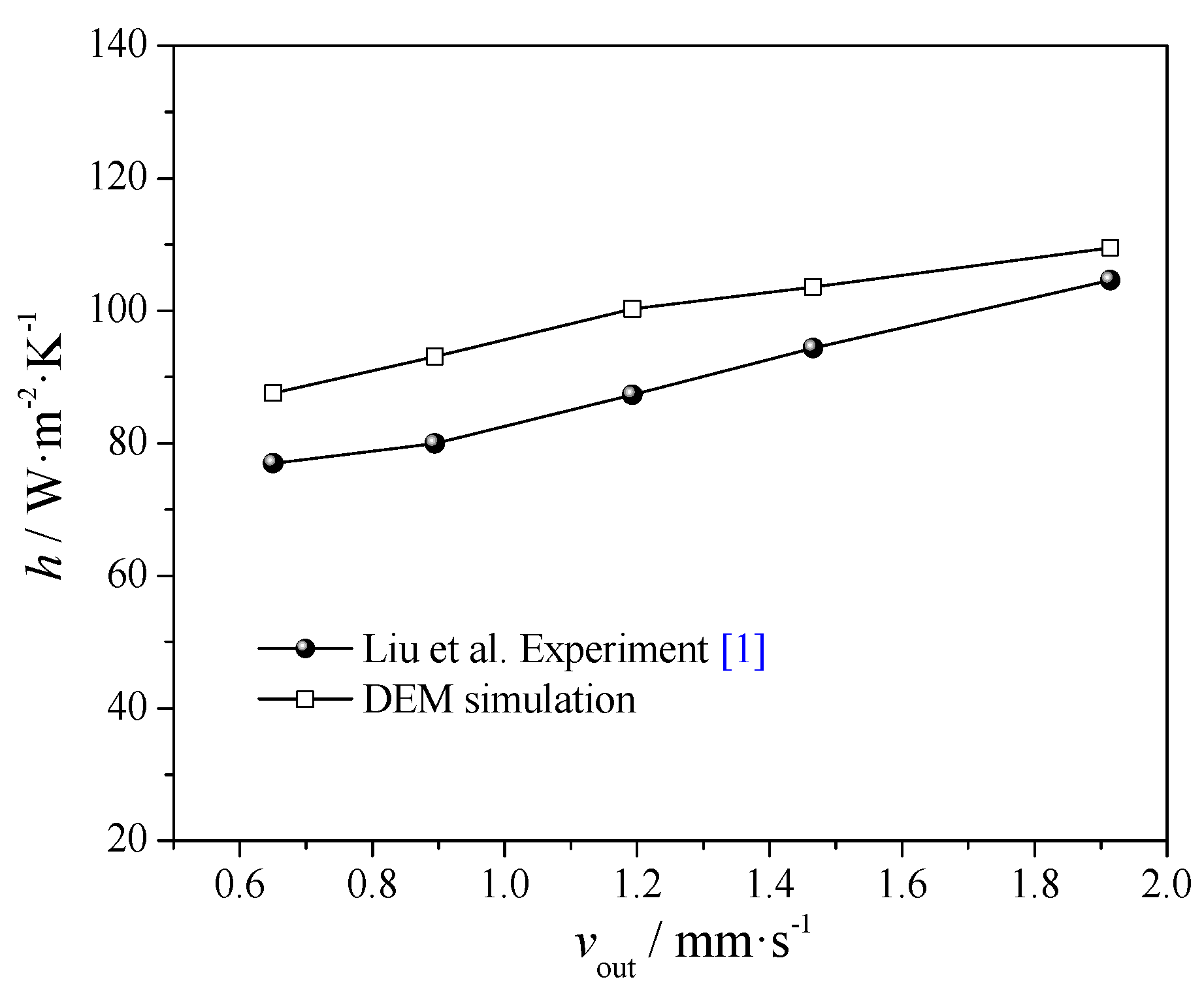
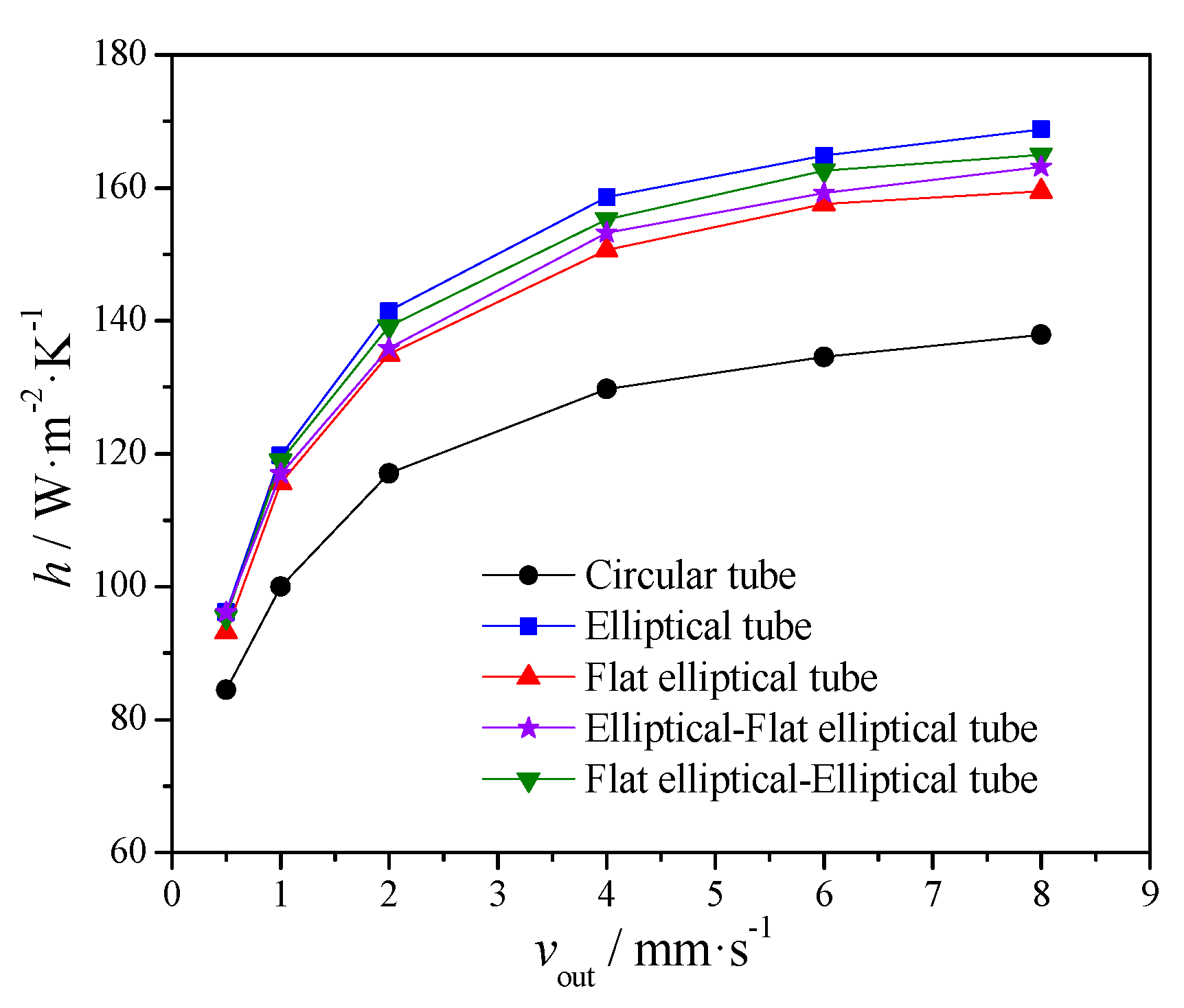
2.3. Model Validations
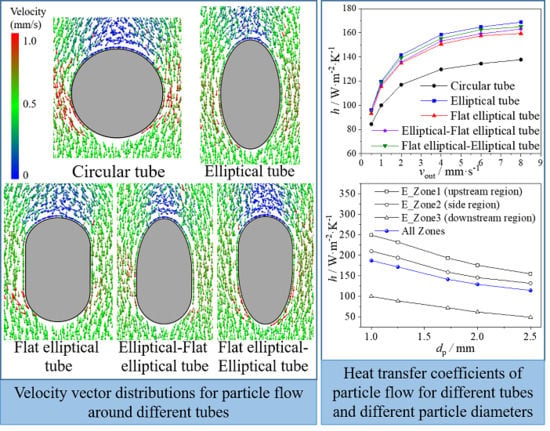
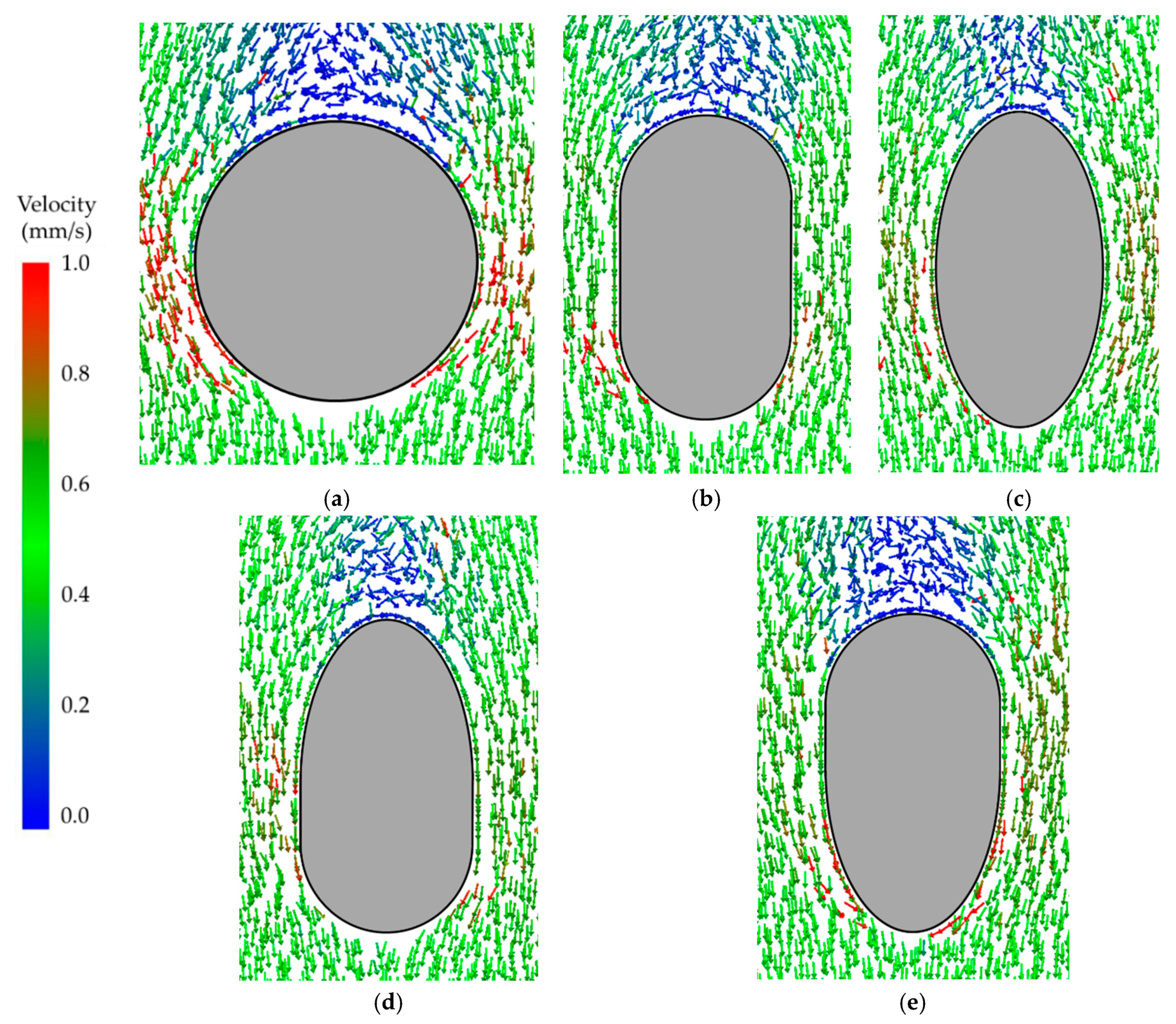
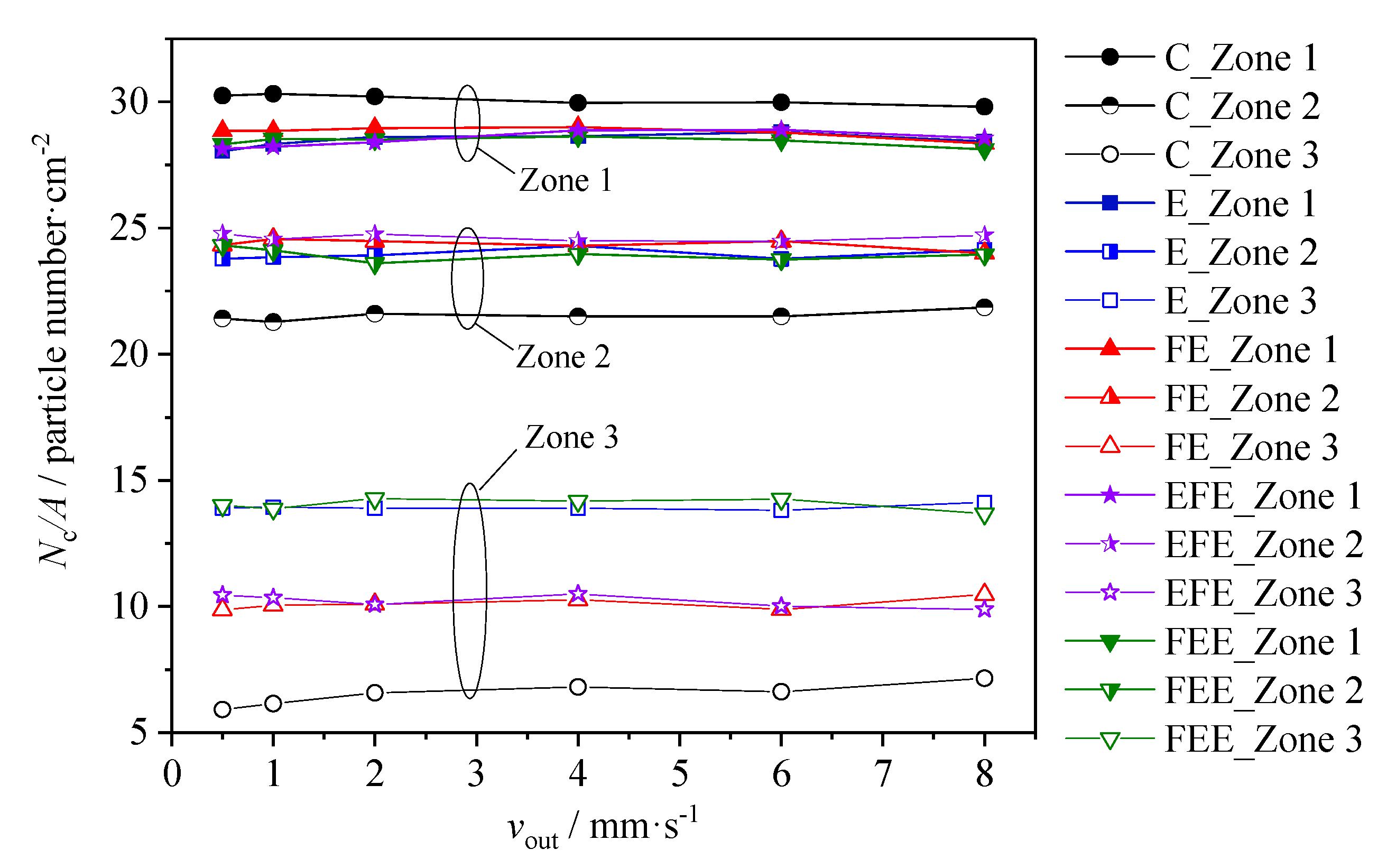
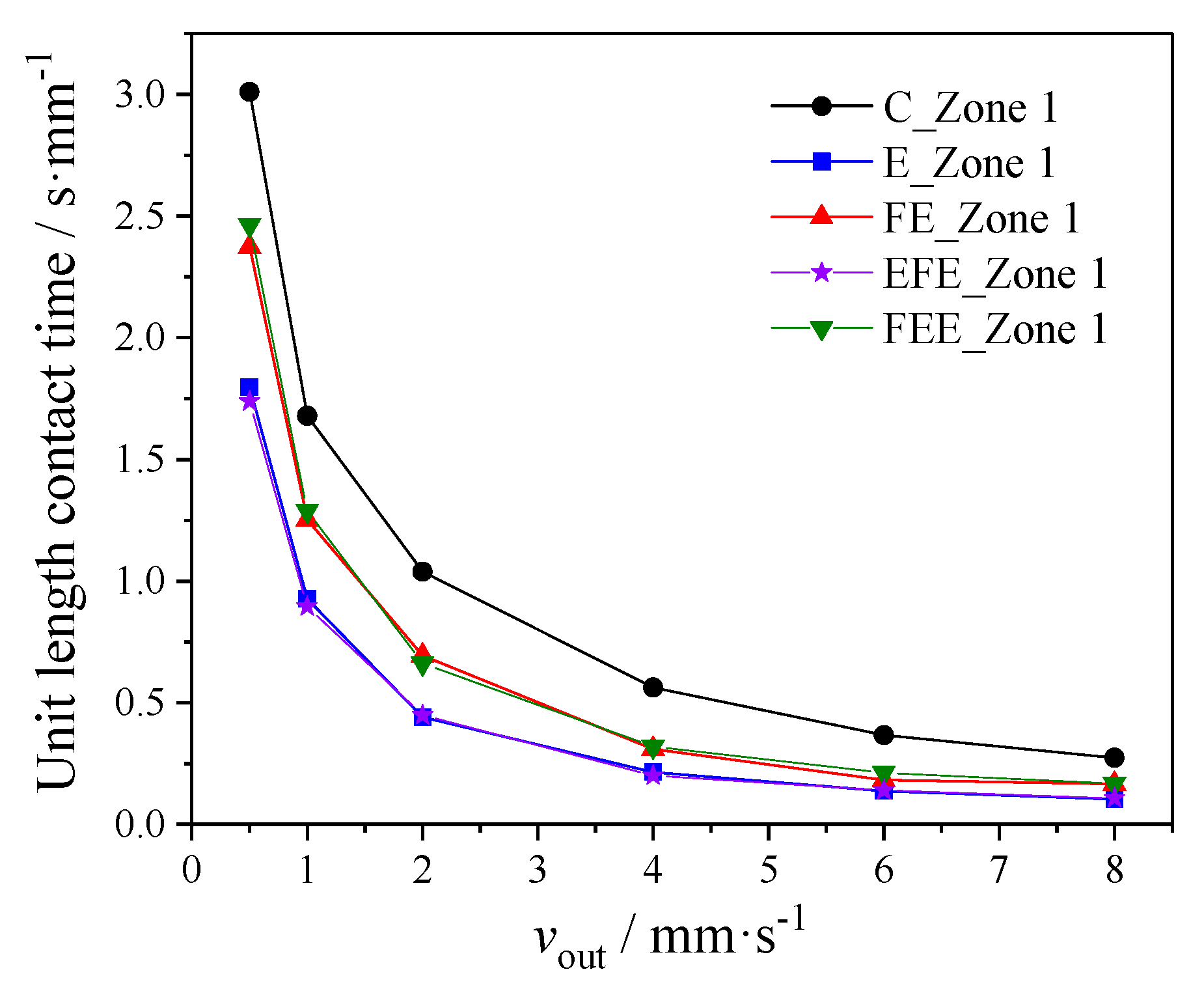
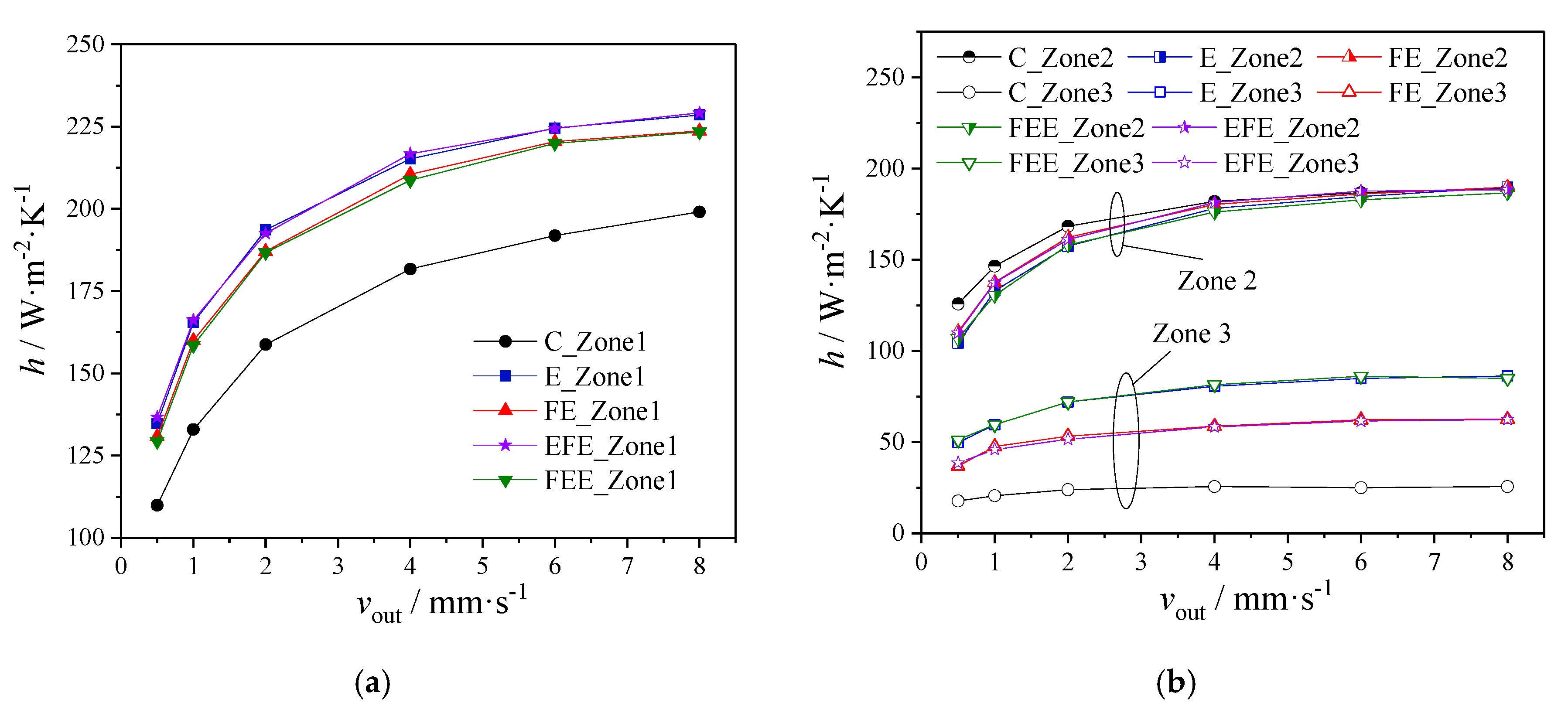
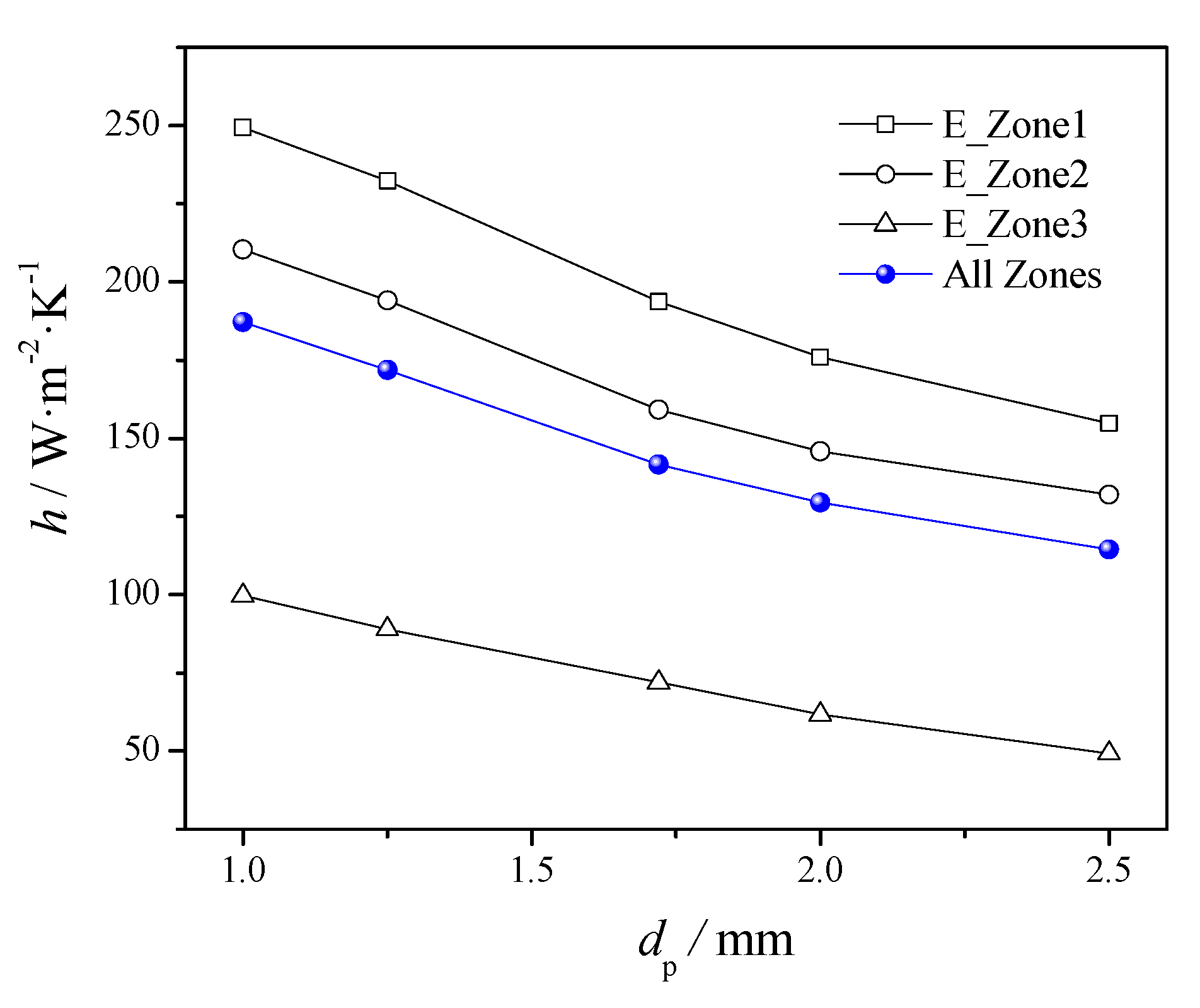
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | area (m2) |
| ae | major axis length of elliptical tube cross section (m) |
| be | minor axis length of elliptical tube cross section (m) |
| cp | specific heat (J/(kg·K)) |
| dp | particle diameter (m) |
| D | distance from tube wall (m) |
| e | restitution coefficient |
| E | Young modulus (GPa) |
| Fn | normal component of the contact force (N) |
| Ft | tangential component of the contact force (N) |
| g | gravitational acceleration (m/s2) |
| H | channel height (m) |
| h | heat transfer coefficient (W/(m2·K)) |
| k | thermal conductivity (W/(m·K)) |
| L | channel length (m) |
| l | distance of particle-particle or particle-wall (m) |
| lfe | side length of flat elliptical tube (m) |
| m | mass (kg) |
| N | particle number |
| Nc | particle contact number |
| Q | heat (J) |
| q | heat flux (W) |
| R | thermal resistance (K/W) |
| r | particle radius (m) |
| rc | circular tube radius (m) |
| rfe | flat elliptical tube radius (m) |
| T | temperature (K) |
| t | time (s) |
| v | velocity (m/s) |
| Vnrel | relative normal translational velocity (m/s) |
| Vtrel | relative tangential translational velocity (m/s) |
| W | channel width (m) |
| Greek Letters | |
| α, β, Θ | angles (rad) |
| δ | gas film thickness (m) |
| δn | normal displacement (m) |
| δt | tangential displacement (m) |
| ε | surface emissivity |
| μs | translational friction coefficient |
| ρ | density (kg/m3) |
| σ | Stefan–Boltzmann constant (W/(m2·K4)) |
| φ | porosity |
| Subscripts | |
| eq | equivalent parameters |
| g | gas |
| i, j | index |
| in | inlet |
| n | normal direction |
| out | outlet |
| s | solid |
| Abbreviations | |
| DEM | discrete element method |
| G-C | only contact with gas film |
| MBHE | moving bed heat exchanger |
| P-C | physical contact |
| p-p | particle-particle |
| p-w | particle-wall |
References
- Liu, J.; Yu, Q.; Peng, J.; Hu, X.; Duan, W. Thermal energy recovery from high-temperature blast furnace slag particles. Int. Commun. Heat Mass Transf. 2015, 69, 23–28. [Google Scholar] [CrossRef]
- Zheng, Y.; Cai, J.J.; Dong, H.; Feng, J.S.; Liu, J.Y. Experimental investigation of volumetric exergy transfer coefficient in vertical moving bed for sinter waste heat recovery. Energy 2019, 167, 428–439. [Google Scholar] [CrossRef]
- Rahman, A.; Rasul, M.; Khan, M.M.K.; Sharma, S. Assessment of energy performance and emission control using alternative fuels in cement industry through a process model. Energies 2017, 10, 1996. [Google Scholar] [CrossRef] [Green Version]
- Lee, W.J.; Kim, D.Y.; Choi, J.H.; Lee, J.W.; Kim, J.S.; Son, K.; Ha, M.J.; Kang, J. Utilization of petroleum coke soot as energy storage material. Energies 2019, 12, 3195. [Google Scholar] [CrossRef] [Green Version]
- Baumann, T.; Zunft, S. Development and performance assessment of a moving bed heat exchanger for solar central receiver power plants. Energy Procedia 2015, 69, 748–757. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Z.; Guo, Z.; Tan, Z.; Yang, J.; Wang, Q. Waste heat recovery from high-temperature solid granular materials: Energy challenges and opportunities. Renew. Sustain. Energy Rev. 2019, 116, 109428. [Google Scholar] [CrossRef]
- Wang, S.; Xu, C.; Liu, W.; Liu, Z. Numerical study on heat transfer performance in packed bed. Energies 2019, 12, 414. [Google Scholar] [CrossRef] [Green Version]
- Vogtenhuber, H.; Pernsteiner, D.; Hofmann, R. Experimental and numerical investigations on heat transfer of bare tubes in a bubbling fluidized bed with respect to better heat integration in temperature swing adsorption systems. Energies 2019, 12, 2646. [Google Scholar] [CrossRef] [Green Version]
- Zheng, B.; Sun, P.; Liu, Y.; Zhao, Q. Heat transfer of calcined petroleum coke and heat exchange tube for calcined petroleum coke waste heat recovery. Energy 2018, 155, 56–65. [Google Scholar] [CrossRef]
- Natarajan, V.V.R.; Hunt, M.L. Heat transfer in vertical granular flows. Exp. Heat Transf. 2007, 10, 89–107. [Google Scholar] [CrossRef]
- Takeuchi, H. Particles flow pattern and local heat transfer around tube in moving bed. Part. Technol. Fluid. 1996, 42, 1621–1626. [Google Scholar] [CrossRef]
- Qoaider, L.; Thabit, Q.; Kiwan, S. Innovative sensible heat transfer medium for a moving bed heat exchanger in solar central receiver power plants. Appl. Sol. Energy 2017, 53, 161–166. [Google Scholar] [CrossRef]
- Al-Ansary, H.; El-Leathy, A.; Al-Suhaibani, Z.; Jeter, S.; Sadowski, D.; Alrished, A.; Golob, M. Experimental study of a sand–air heat exchanger for use with a high-temperature solar gas turbine system. J. Sol. Energy Eng. 2012, 134, 041017. [Google Scholar] [CrossRef]
- Nguyen, C.; Sadowski, D.; Alrished, A.; Al-Ansary, H.; Jeter, S.; Abdel-Khalik, S. Study on solid particles as a thermal medium. Energy Procedia 2014, 49, 637–646. [Google Scholar] [CrossRef] [Green Version]
- Chehata, D.; Zenit, R.; Wassgren, C.R. Dense granular flow around an immersed cylinder. Phys. Fluids 2003, 15, 1622. [Google Scholar] [CrossRef]
- Tian, X.; Yang, J.; Guo, Z.G.; Wang, Q.W.; Sunden, B. Numerical study of flow and heat transfer in gravity-driven particle flow around a circular or elliptical tube. Chem. Eng. Trans. 2019, 76, 235–240. [Google Scholar]
- Bartsch, P.; Zunft, S. Numerical investigation of dense granular flow around horizontal tubes: Qualification of CFD model with validated DEM model. Sol. Energy 2019, 182, 298–303. [Google Scholar] [CrossRef]
- Bartsch, P.; Zunft, S. Granular flow around the horizontal tubes of a particle heat exchanger: DEM-simulation and experimental validation. Sol. Energy 2019, 182, 48–56. [Google Scholar] [CrossRef]
- Niegsch, J.; Köneke, D.; Weinspach, P.M. Heat transfer and flow of bulk solids in a moving bed. Chem. Eng. Process. 1994, 33, 73–89. [Google Scholar] [CrossRef]
- Guo, Z.G.; Tian, X.; Tan, Z.T.; Yang, J.; Wang, Q.W. Optimization of gravity-driven granular flow around the tube for heat transfer enhancement. Chem. Eng. Trans. 2019, 76, 247–252. [Google Scholar]
- Morris, A.B.; Pannala, S.; Ma, Z.; Hrenya, C.M. A conductive heat transfer model for particle flows over immersed surfaces. Int. J. Heat Mass Transf. 2015, 89, 1277–1289. [Google Scholar] [CrossRef] [Green Version]
- Morris, A.B.; Ma, Z.; Pannala, S.; Hrenya, C.M. Simulations of heat transfer to solid particles flowing through an array of heated tubes. Sol. Energy 2016, 130, 101–115. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Zhou, Z.; Yu, A.B.; Kim, S.Y.; Jung, S.K. Discrete particle simulation of solid flow in a melter-gasifier in smelting reduction process. Powder Technol. 2017, 314, 641–648. [Google Scholar] [CrossRef]
- Hilton, J.E.; Tordesillas, A. Drag force on a spherical intruder in a granular bed at low Froude number. Phys. Rev. E. Stat. NonlinearSoft Matter Phys. 2013, 88, 062203. [Google Scholar] [CrossRef] [PubMed]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Mindlin, R.D.; Deresiewicz, H. Elastic spheres in contact under varying oblique forces. J. Appl. Mech. 1953, 20, 327–344. [Google Scholar]
- Zhang, R.; Yang, H.; Lu, J.; Wu, Y. Theoretical and experimental analysis of bed-to-wall heat transfer in heat recovery processing. Powder Technol. 2013, 249, 186–195. [Google Scholar] [CrossRef]
- Molerus, O. Heat transfer in moving beds with a stagnant interstitial gas. Int. J. Heat Mass Transf. 1997, 40, 4151–4159. [Google Scholar] [CrossRef]
- Chen, R.; Guo, K.; Zhang, Y.; Tian, W.; Qiu, S.; Su, G.H. Numerical analysis of the granular flow and heat transfer in the ADS granular spallation target. Nucl. Eng. Des. 2018, 330, 59–71. [Google Scholar] [CrossRef]
- Bu, C.S.; Liu, D.Y.; Chen, X.P.; Liang, C.; Duan, Y.F.; Duan, L.B. Modeling and coupling particle scale heat transfer with DEM through heat transfer mechanisms. Numer. Heat Transf. Part A Appl. 2013, 64, 56–71. [Google Scholar] [CrossRef]
- Vargas, W.L.; Mccarthy, J.J. Stress effects on the conductivity of particulate beds. Chem. Eng. Sci. 2002, 57, 3119–3131. [Google Scholar] [CrossRef]
- Antwerpen, W.V.; Rousseau, P.G.; Toit, C.G.D. Multi-sphere unit cell model to calculate the effective thermal conductivity in packed pebble beds of mono-sized spheres. Nucl. Eng. Des. 2012, 247, 183–201. [Google Scholar] [CrossRef]




| L (mm) | W (mm) | H (mm) | rc (mm) | rfe (mm) | lfe (mm) | ae (mm) | be (mm) |
|---|---|---|---|---|---|---|---|
| 39 | 18 | 45 | 7.5 | 4.87 | 8.29 | 19.48 | 9.74 |
| Parameter | ρs (kg/m3) | ks (W/(m·K)) | cp,s (J/(kg·K)) | kg (W/(m·K)) |
|---|---|---|---|---|
| Value | 2848 | 0.55 | 1210 | 0.0257 |
| Mechanical Parameters | Value | Mechanical Parameters | Value |
|---|---|---|---|
| E (particle, GPa) | 0.55 | Static friction coefficient (p-p) | 0.154 |
| E (wall, GPa) | 182 | Rolling friction coefficient (p-w) | 0.1 |
| Poisson’s ratio (particle) | 0.25 | Rolling friction coefficient (p-p) | 0.1 |
| Poisson’s ratio (wall) | 0.30 | Restitution coefficient (p-w) | 0.5 |
| Static friction coefficient (p-w) | 0.154 | Restitution coefficient (p-p) | 0.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, X.; Yang, J.; Guo, Z.; Wang, Q.; Sunden, B. Numerical Study of Heat Transfer in Gravity-Driven Particle Flow around Tubes with Different Shapes. Energies 2020, 13, 1961. https://doi.org/10.3390/en13081961
Tian X, Yang J, Guo Z, Wang Q, Sunden B. Numerical Study of Heat Transfer in Gravity-Driven Particle Flow around Tubes with Different Shapes. Energies. 2020; 13(8):1961. https://doi.org/10.3390/en13081961
Chicago/Turabian StyleTian, Xing, Jian Yang, Zhigang Guo, Qiuwang Wang, and Bengt Sunden. 2020. "Numerical Study of Heat Transfer in Gravity-Driven Particle Flow around Tubes with Different Shapes" Energies 13, no. 8: 1961. https://doi.org/10.3390/en13081961
APA StyleTian, X., Yang, J., Guo, Z., Wang, Q., & Sunden, B. (2020). Numerical Study of Heat Transfer in Gravity-Driven Particle Flow around Tubes with Different Shapes. Energies, 13(8), 1961. https://doi.org/10.3390/en13081961