Thermo-Chemical Instability and Energy Analysis of Absorption Heat Pumps

Abstract

This paper presents the results of energy analysis of absorption heat pumps. The thermo-chemical instability term was introduced for absorption heat pumps used for heating or cooling or heating and cooling. A higher thermo-chemical instability results in the equipment being more sensitive with regard to the variation of the heat source flux. This sensitivity can be taken into account when heat sources are chosen for a certain absorption machine. Absorption heat pumps having thermo-chemical compressors were compared from energy demand and energy efficiency points of view with heat pumps having mechanical compressors. As it is shown, for certain evaporation and condensation temperature values, an absorption heat pump with similar efficiency to that of the heat pump with a mechanical compressor can always be found.

1. Introduction

The aim of the European Union is to reduce the energy consumption by 32.5% compared to the level of energy use in 2007 [1]. The building sector is responsible for 40% of the total energy use in the European Union [2]; thus, it would be advantageous to increase the energy efficiency of this sector. A first step can be the reduction of the energy demand of buildings [3,4,5]. Naturally, in the case of new buildings, low energy demand can be met with energy conscious design [6,7,8,9]. In the case of existing buildings, thermal improvement of the building envelope will result in lower energy demand [10,11,12]. Furthermore, it is essential to choose proper basic data for the design of heating, ventilation, and air conditioning (HVAC) systems [13,14,15,16]. Moreover, the position of workplaces in the building has to be identified, in order to provide proper microenvironmental parameters for occupants [17,18]. Energy saving can be obtained by improving the energy efficiency of HVAC systems, or by optimizing these systems from an exergy point of view [19,20,21,22]. Last but not least, the energy consumption can be reduced by decreasing the heat waste during the operation of HVAC systems. Heat waste can be reduced by proper thermal insulation of HVAC elements or reusing these heat quantities in the buildings’ energy flow [23,24,25].

Heat pumps are often used for heating and cooling of buildings [26,27,28]. In the case of operation of these machines, cool energy (at the evaporator) and warm energy (at the condenser) are produced simultaneously. However, in a certain period of time, these machines are used for heating or for cooling. On the other side of the machine, the cool energy or the warm energy is practically wasted. If the cool and warm energy produced simultaneously but in a different amount by heat pumps can be usefully expended, important energy savings could be obtained.

2. Theoretical Background

With heat pumps, warm and cool energy is produced simultaneously. Usually, only one of these two energy types is used, while the other one is energy waste (let us call this operation mode single use). In the case of the utilization of both warm and cool energy, then the machine will be in total energy use operation mode (let us call this operation mode double use). Total energy use heat pumps are provided with mechanical or thermo-chemical compressors. For both cases, quantitative indices can be defined in order to describe the energy efficiency of the machine. In the case of machines with mechanical compressors, these indices are the coefficient of performance and the energy efficiency ratio, while, in the case of absorption heat pumps, in addition to the coefficient of performance, the other index is the thermo-chemical efficiency. The coefficient of performance is the ratio between the desired energy results and required energy input. The desired energy is the cooling capacity in the case of cooling mode, while it is the heat released in the condenser in the case of heating mode [29,30,31]. In the case of total energy use of a heat pump, the desired energy is the sum of the cooling capacity and the heat released in the condenser. In the case of double-use machines, the coefficient of performance is the sum of the coefficients of performance of the two operation modes [32].

$$CO{P}_{R,ER}=CO{P}_{R,C}+CO{P}_{R,H}=\frac{{\dot{Q}}_0}{P}+\frac{{\dot{Q}}_C}{P},$$

(1)

where COP_R,C and COP_R,H are the coefficients of performance in the cooling and heating mode (machine with mechanical compressor), respectively, ${\dot{Q}}_0$ is the cooling capacity (W), ${\dot{Q}}_C$ is the heat released in the condenser (W), and P is the electric power consumed by the machine (W).

The maximum value of the COP is obtained in the case of heat pumps working on a reversed Carnot cycle [29,30,31]. The efficiency of a double-use heat pump working on a reversed Carnot cycle is as follows [32]:

$$CO{P}_{RC,ER}=CO{P}_{RC,C}+CO{P}_{RC,H}=\frac{T_L}{T_H-T_L}+\frac{T_H}{T_H-T_L}=\frac{T_H+T_L}{T_H-T_L},$$

(2)

where COP_RC,C and COP_RC,H are the maximum values of the coefficients of performance in the cooling and heating mode (machine with mechanical compressor), respectively, T_L is the temperature of evaporation of the working fluid (K), and T_H is the temperature of condensation of the working fluid (K).

The energy efficiency (second-law efficiency) of a heat pump is the ratio between the real coefficient of performance and ideal case (heat pump working based on the reversed Carnot cycle) [29,30,31]. In the case of a double-use heat pump (machines with mechanical compressor), the second-law efficiency is as follows [32]:

$${\eta }_{R,ER}(\%)=\frac{CO{P}_{R,ER}}{CO{P}_{RC,ER}}=\frac{{\dot{Q}}_0+{\dot{Q}}_C}{P}·\frac{T_H-T_L}{T_H+T_L}.$$

(3)

Absorption and adsorption heat pumps work with thermo-chemical compressors. The required energy input is the sum of consumed heat in the generator (${\dot{Q}}_G$) and the pumping power requirement of the solution pump (P_p). However, the consumed heat in the generator is considerably higher than the pumping power requirement (${\dot{Q}}_G\gg P_p$); thus, it is usually neglected in the COP calculation [29,30,31]. In the case of a double-use heat pump (absorption machine), the coefficient of performance is the sum of coefficients of performance of the cooling [29,30,31] and heating [29,30,31] modes. This relationship is given by Equation (4) [32].

$$CO{P}_{A,ER}=\frac{{\dot{Q}}_0+{\dot{Q}}_A+{\dot{Q}}_C}{{\dot{Q}}_G}=\frac{{\dot{Q}}_0}{{\dot{Q}}_G}+\frac{{\dot{Q}}_A+{\dot{Q}}_C}{{\dot{Q}}_G}=CO{P}_{A,C}+CO{P}_{A,H},$$

(4)

where COP_A,C and COP_A,H are the coefficients of performance in the case of cooling and heating operation mode (absorption machine), respectively, ${\dot{Q}}_A$ is the heat released in the absorber (W), and ${\dot{Q}}_G$ is the heat consumed in the generator (W).

The maximum value of the coefficient of performance can be obtained in the case of a reversed Carnot cycle (cooling and heating mode [29,30,31], cooling–heating mode [32]).

$$\begin{gathered} CO{P}_{AC,ER}=CO{P}_{AC,C}+CO{P}_{AC,H}=\frac{T_L}{T_G}·\frac{T_G-T_A}{T_H-T_L}+\frac{T_G·T_H-T_A·T_L}{T_G·\left(T_H-T_L\right)}= \\ CO{P}_{AC,ER}=\frac{T_G·\left(T_H+T_L\right)-2·T_A·T_L}{T_G·\left(T_H-T_L\right)}=CO{P}_{RC,ER}-\frac{2·T_A·T_L}{T_G·\left(T_H-T_L\right)}, \end{gathered}$$

(5)

where COP_AC,C and COP_AC,H are the maximum values of the coefficients of performance in the cooling and heating mode (absorption machine), respectively.

The ratio between the real and ideal coefficient of performance is the thermo-chemical efficiency of the absorption machine (second-law efficiency) [29,30,31].

$${\eta }_{A,ER}(\%)=\frac{CO{P}_{A,ER}}{CO{P}_{AC,ER}}.$$

(6)

During the operation of these machines, heat is consumed and released in the compressor at the same time. The ratio between these two heat quantities represents the thermo-chemical performance index [33].

$$\beta =\frac{{\dot{Q}}_A}{{\dot{Q}}_G}.$$

(7)

The two extreme values of the thermo-chemical performance index are 0 and the ratio T_A/T_G (the latter is always lower than 1) [33]. The two extreme values can only occur theoretically.

Using this index, both the coefficient of performance and the thermo-chemical efficiency can be given. The coefficients of performance in the cooling mode [33], heating mode [33], and heating and cooling mode are as follows [32]:

$$CO{P}_{A,C}=\frac{T_L}{T_A}·\frac{T_H-T_A}{T_H-T_L}·\beta +\frac{T_L}{T_G}·\frac{T_G-T_H}{T_H-T_L},$$

(8)

$$CO{P}_{A,H}=\frac{T_L}{T_A}·\frac{T_H-T_A}{T_H-T_L}·\beta +\frac{T_H}{T_G}·\frac{T_G-T_L}{T_H-T_L},$$

(9)

$$CO{P}_{A,ER}=CO{P}_{A,C}+CO{P}_{A,H}=2·\frac{T_L}{T_A}·\frac{T_H-T_A}{T_H-T_L}·\beta +\frac{T_G·\left(T_H+T_L\right)-2·T_H·T_L}{T_G·\left(T_H-T_L\right)}.$$

(10)

The thermo-chemical efficiencies in the cooling mode [33], heating mode [33], and heating and cooling mode are as follows [32]:

$${\eta }_{A,C}(\%)=\frac{T_G}{T_A}·\frac{T_H-T_A}{T_G-T_A}·\beta +\frac{T_G-T_H}{T_G-T_A},$$

(11)

$${\eta }_{A,H}(\%)=\frac{T_G·T_L}{T_A}·\frac{T_H-T_A}{T_G·T_H-T_A·T_L}·\beta +\frac{T_H·\left(T_G-T_L\right)}{T_G·T_H-T_A·T_L},$$

(12)

$${\eta }_{A,ER}(\%)=2·\frac{T_G·T_L}{T_A}·\frac{T_H-T_A}{T_G·\left(T_H+T_L\right)-2·T_A·T_L}·\beta +\frac{T_G·\left(T_H+T_L\right)-2·T_H·T_L}{T_G·\left(T_H+T_L\right)-2·T_A·T_L}.$$

(13)

Equations (8)–(13) describe a linear relationship, and the slope of the line is not negative. Upon analyzing these equations, it can be observed that the maximum values (COP_AC,C/H/ER and 100%) can be obtained in two cases. The first case is the thermo-chemical performance index taking its maximum value (β = T_A/T_G), and the second possibility is when the temperatures in the absorber and condenser are equal (T_A = T_H) (in this case, the slope of the function is 0, and the second term of the sum is COP_AC and 1). If the thermo-chemical performance index is minimum (β = 0), then the quantitative indices of the heating or cooling or heating and cooling processes will meet the minimum value. If the slope of the linear function is positive, then it has a minima; if the slope of the function is negative, then it has a maxima. The minimum values of the coefficients of performance are as follows [32]:

$$CO{P}_{A,min,C}=\frac{T_L}{T_G}·\frac{T_G-T_H}{T_H-T_L},$$

(14)

$$CO{P}_{A,min,H}=\frac{T_H}{T_G}·\frac{T_G-T_L}{T_H-T_L},$$

(15)

$$CO{P}_{A,min,ER}=\frac{T_G·\left(T_H+T_L\right)-2·T_H·T_L}{T_G·\left(T_H-T_L\right)}.$$

(16)

The minimum values of the thermo-chemical efficiencies are as follows [32]:

$${\eta }_{A,min,C}(\%)=\frac{T_G-T_H}{T_G-T_A},$$

(17)

$${\eta }_{A,min,H}(\%)=\frac{T_H·\left(T_G-T_L\right)}{T_G·T_H-T_A·T_L},$$

(18)

$${\eta }_{A,min,ER}(\%)=\frac{T_G·\left(T_H+T_L\right)-2·T_H·T_L}{T_G·\left(T_H+T_L\right)-2·T_A·T_L}.$$

(19)

3. Results

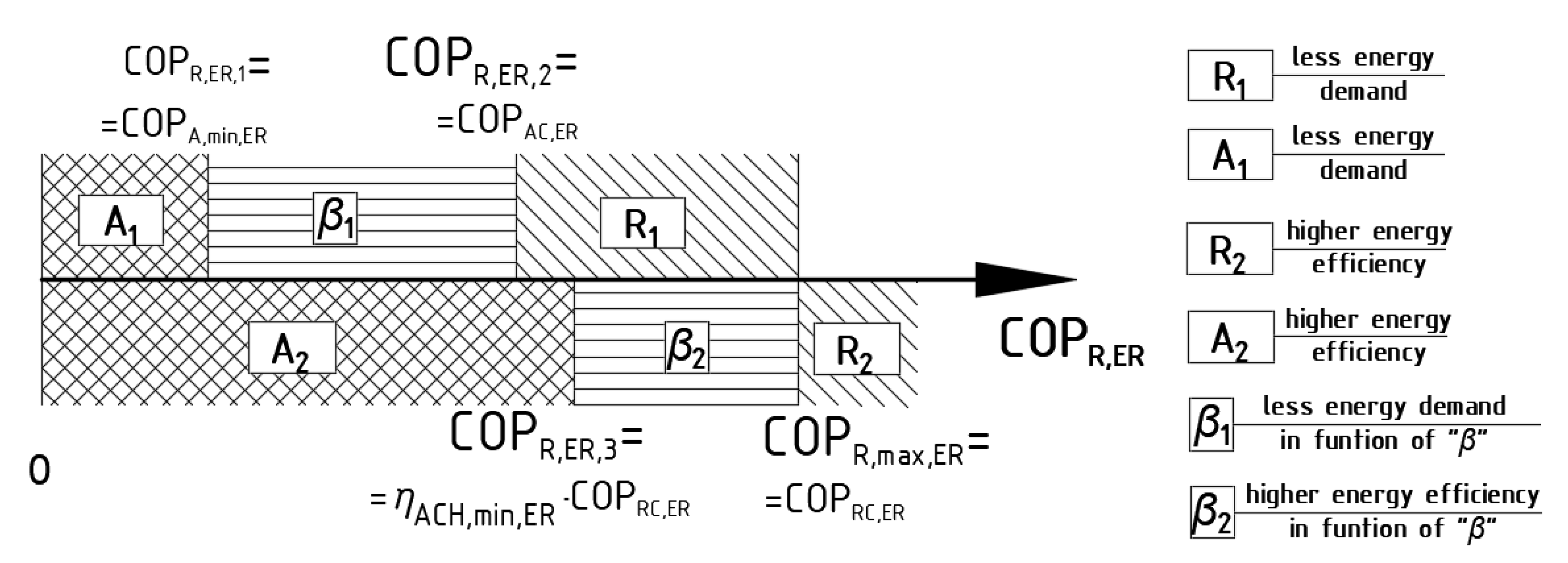
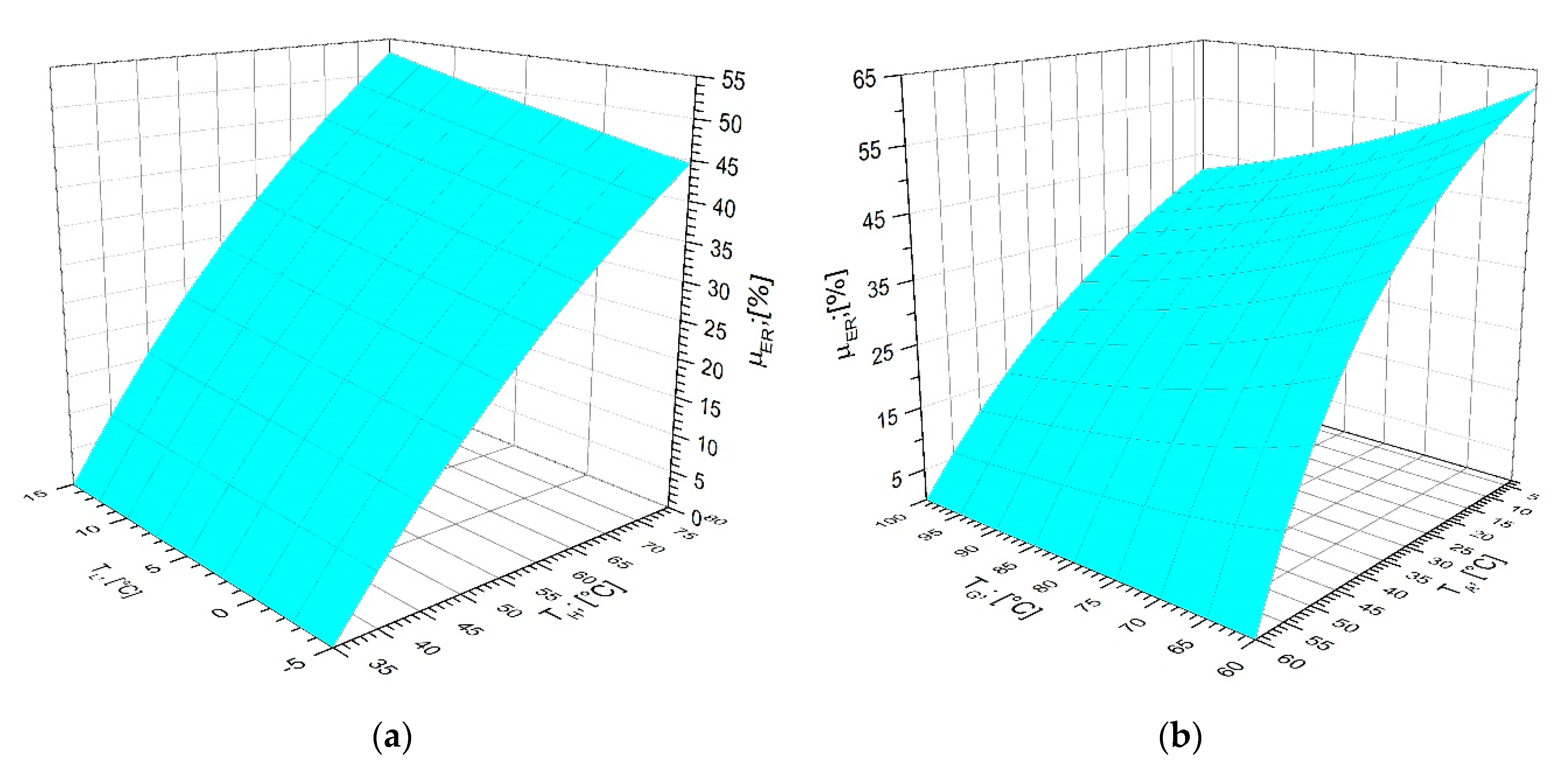
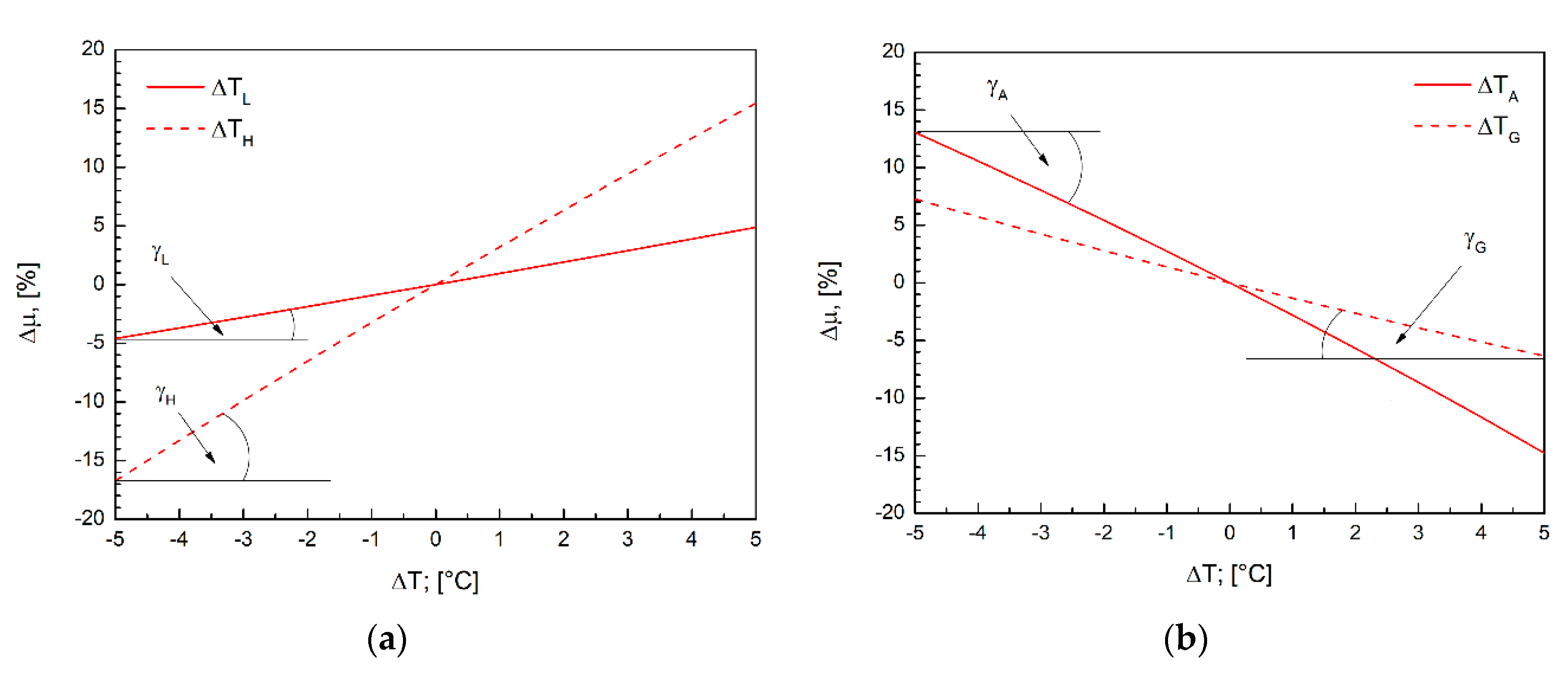
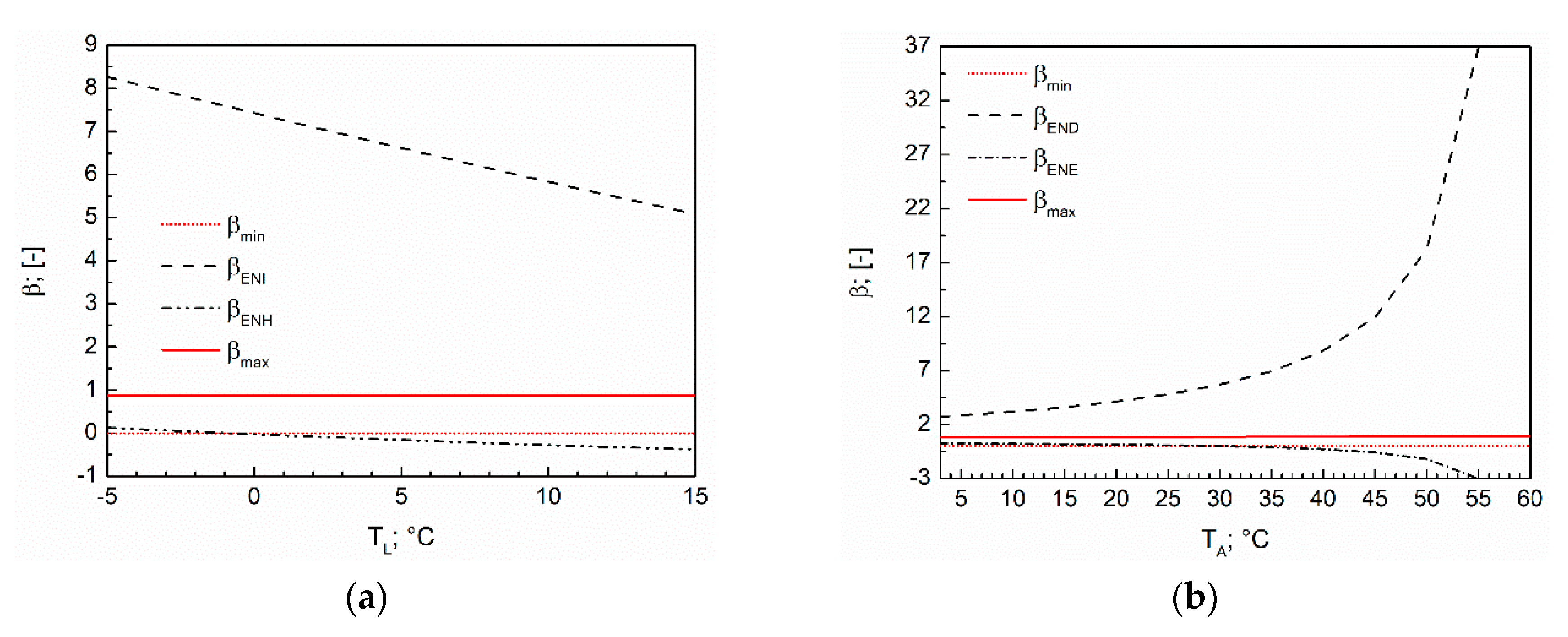
3.1. Instability of Absorption Heat Pumps

It can be observed that both the coefficient of performance and the thermo-chemical efficiency depend on the thermo-chemical performance index, while their extreme values are independent of it. The thermo-chemical performance index is a ratio of heat fluxes; thus, its value describes a certain moment of the controlled operation process. This means that, if it is applied when the machine is only quantitative controlled, then the quantitative indices of the machine will vary during operation between the two extreme values. A smaller difference between the two extreme values compared to the maximum value results in a smaller difference due to the control between the quantitative indices for a partial and full load. Let us call this index “thermo-chemical instability”. The thermo-chemical instability indices of the machine in the case of cooling, heating, and heating–cooling modes are as follows:

$${\mu }_C (\%)=\frac{CO{P}_{AC,C}-CO{P}_{A,min,C}}{CO{P}_{AC,C}}=\frac{{\eta }_{A,max,C}-{\eta }_{A,min,C}}{{\eta }_{A,max,C}}=1-\frac{CO{P}_{A,min,C}}{CO{P}_{AC,C}}=1-{\eta }_{A,min,C},$$

(20)

$${\mu }_H (\%)=\frac{CO{P}_{AC,H}-CO{P}_{A,min,H}}{CO{P}_{AC,H}}=\frac{{\eta }_{A,max,H}-{\eta }_{A,min,H}}{{\eta }_{A,max,H}}=1-\frac{CO{P}_{A,min,H}}{CO{P}_{AC,H}}=1-{\eta }_{A,min,H},$$

(21)

$${\mu }_{ER} (\%)=\frac{CO{P}_{AC,ER}-CO{P}_{A,min,ER}}{CO{P}_{AC,ER}}=\frac{{\eta }_{A,max,ER}-{\eta }_{A,min,ER}}{{\eta }_{A,max,ER}}=1-\frac{CO{P}_{A,min,ER}}{CO{P}_{AC,ER}}=1-{\eta }_{A,min,ER}.$$

(22)

Introducing Equations (5) and Equations (14)–(19) into Equations (20)–(22), the following formulas can be obtained:

$${\mu }_C (\%)=\frac{T_H-T_A}{T_G-T_A},$$

(23)

$${\mu }_H (\%)=\frac{T_L·\left(T_H-T_A\right)}{T_H·T_G-T_L·T_A},$$

(24)

$${\mu }_{ER} (\%)=\frac{2·T_L·\left(T_H-T_A\right)}{T_G·\left(T_H+T_L\right)-2·T_A·T_L}.$$

(25)

As it can be observed, the thermo-chemical instability depends only on the four operational temperatures. A lower value denotes a smaller fluctuation of the quantitative indices (assuming constant operational temperatures).

Usually, absorption heat pumps use generator waste heat or renewable energy. However, the temperature of the heat sink or the heat flux may fluctuate. At higher values of thermo-chemical instability, the generated cool or warm energy quantity will fluctuate to a higher extent. If the used heat sink shows large variations of the delivered heat flux, the operational temperatures have to be chosen so as to obtain minimal thermo-chemical instability indices.

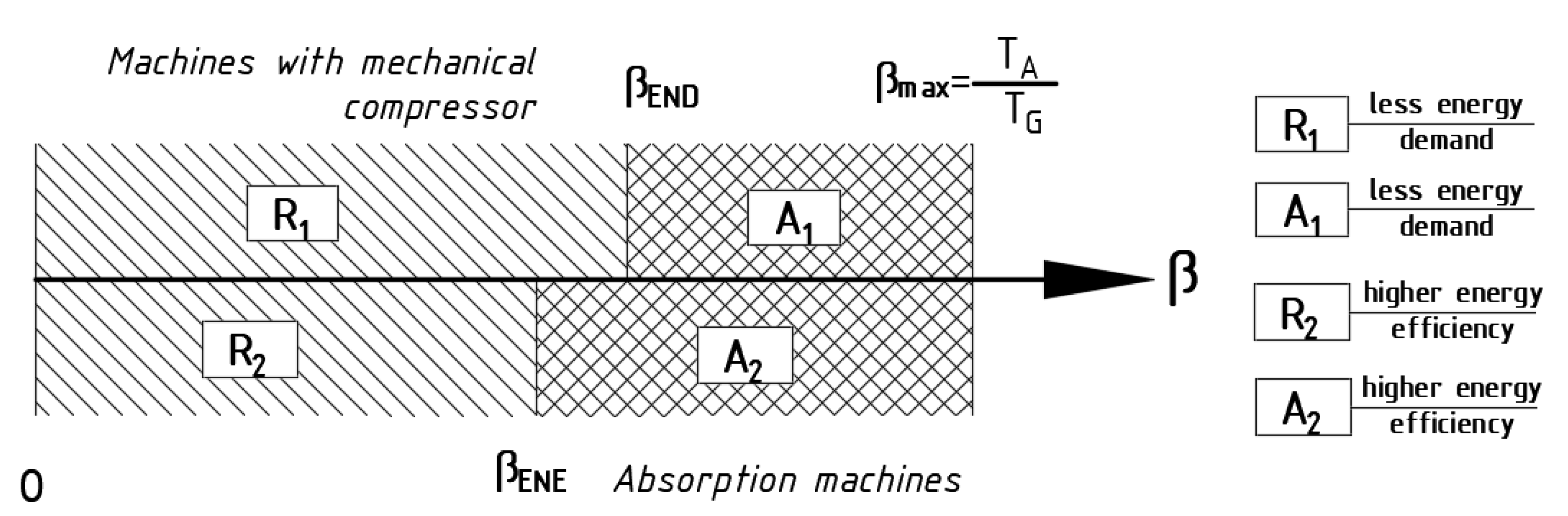
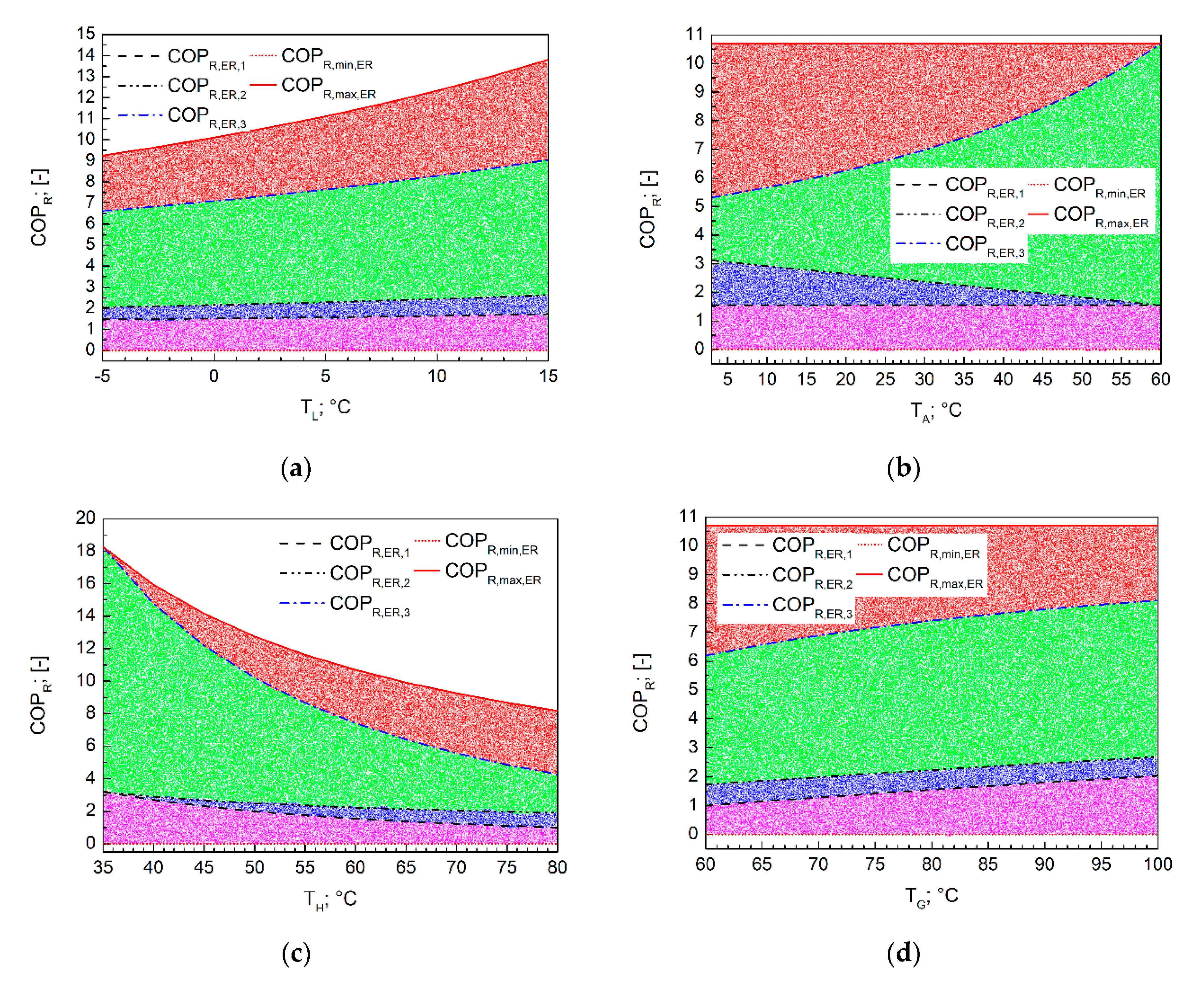
3.2. Energy Comparison of Machines Having Mechanical and Thermo-Chemical Compressors

From an energy demand point of view, a machine with a thermo-chemical compressor will show better results in comparison with a machine with a mechanical compressor if the following relationship is fulfilled:

$${\dot{Q}}_G<P.$$

(26)

Naturally, for similar values of the delivered energy, the following statement applies:

$$CO{P}_{R,ER}<CO{P}_{A,ER}.$$

(27)

Substituting Equation (10) into Equation (27), and introducing the thermo-chemical performance index, the following equation is obtained:

$$\frac{1}{2}·\frac{T_H-T_L}{T_L}·\frac{T_A}{T_H-T_A}·CO{P}_{R,ER}+\left[\frac{T_H}{T_G}-\frac{T_H+T_L}{2·T_L}\right]·\frac{T_A}{T_H-T_A}<{\beta }_{END}.$$

(28)

From an energy efficiency point of view, a machine with a thermo-chemical compressor will show better results in comparison with a machine with a mechanical compressor if the following relationship is fulfilled (i.e., the second-law efficiency is higher):

$${\eta }_{R,ER}<{\eta }_{A,ER.}$$

(29)

Substituting Equations (2) and (3) and Equation (13) into Equation (29), and introducing the thermo-chemical performance index, the following equation is obtained:

$$\frac{1}{2}·\frac{T_H-T_L}{T_L}·\frac{T_A}{T_H-T_A}·\left[1-\frac{2·T_A·T_L}{T_G·\left(T_H+T_L\right)}\right]·CO{P}_{R,ER}+\left[\frac{T_H}{T_G}-\frac{T_H+T_L}{2·T_H}\right]·\frac{T_A}{T_H-T_A}<{\beta }_{ENE}.$$

(30)

These two criteria are illustrated in Figure 1.

As it can be observed, at higher values of the thermo-chemical performance index, it is more likely that the machine with a thermo-chemical compressor will perform better. If the absorption machine performs better from an energy demand point of view, its efficiency will be higher in comparison with the machine having a mechanical compressor.

The comparison between these two machines can also be done depending on the coefficient of performance of the double-use traditional heat pump with a mechanical compressor. Taking into account Equations (28) and (30), the machines with thermo-chemical compressors will perform better if the following conditions are realized:

$$2·\frac{T_H-T_A}{T_A}·\frac{T_L}{T_H-T_L}·\beta +\frac{T_H+T_L}{T_H-T_L}-2·\frac{T_H}{T_G}·\frac{T_L}{T_H-T_L}>CO{P}_{R,ER,END},$$

(31)

$$\frac{1}{2}·\frac{T_L}{T_A}·\frac{T_H-T_A}{T_H-T_L}·\frac{T_G·\left(T_H+T_L\right)}{T_G·\left(T_H+T_L\right)-2·T_A·T_L}·\beta +\frac{T_H+T_L}{T_H-T_L}·\frac{T_G·\left(T_H+T_L\right)-2·T_H·T_L}{T_G·\left(T_H+T_L\right)-2·T_A·T_L}>CO{P}_{R,ER,ENE}.$$

(32)

The thermo-chemical performance index has two extreme values. By introducing the extreme values in Equations (31) and (32), a group of relationships can be obtained which are suitable for choosing between the two machines.

By writing Equation (31) as a function of thermo-chemical performance index (first the lowest, and then the highest value), the following relationship is obtained (A—absorption machine, R—machine with mechanical compressor):

$$CO{P}_{R,ER,END}\left\{\begin{array}{l}<\frac{T_H+T_L}{T_H-T_L}-2·\frac{T_H}{T_G}·\frac{T_L}{T_H-T_L}=CO{P}_{A,min,ER}=CO{P}_{R,ER,1}\to “A”\\ CO{P}_{R,ER,1}\langle ;\rangle CO{P}_{R,ER,2}\to “A”or“R”,infunctionof“\beta ”\\ >\frac{T_H+T_L}{T_H-T_L}-\frac{2·T_A·T_L}{T_G·\left(T_H-T_L\right)}=CO{P}_{AC,ER}=CO{P}_{R,ER,2}\to “R”\end{array}\right\}.$$

(33)

By introducing the extreme values of the thermo-chemical performance index in Equation (32), the following group of relationships is obtained (A—absorption machine, R—machine with mechanical compressor):

$$CO{P}_{R,ER,ENE}\left\{\begin{array}{l}<\frac{T_H+T_L}{T_H-T_L}·\frac{T_G·\left(T_H+T_L\right)-2·T_H·T_L}{T_G·\left(T_H+T_L\right)-2·T_A·T_L}={\eta }_{A,min,ER}·CO{P}_{RC,ER}=CO{P}_{R,ER,3}\to “A”\\ CO{P}_{R,ER,3}\langle ;\rangle CO{P}_{R,ER,4}\to “A”or“R”,infunctionof“\beta ”\\ >\frac{T_H+T_L}{T_H-T_L}=CO{P}_{RC,ER}=CO{P}_{R,ER,4}=CO{P}_{R,max,ER}\to “R”\end{array}\right\}.$$

(34)

Figure 2 illustrates the Equations (33) and (34).

It can be observed that, in any case, there exists an absorption heat pump with similar efficiency to the efficiency of a heat pump with a mechanical compressor. To obtain a machine with a mechanical compressor which performs better than an absorption heat pump, its coefficient of performance should exceed the coefficient of performance of a machine working on a Carnot cycle. However, such a machine does not exist in practice.

4. Case Study

In order to show the applicability of the mathematical model presented above, the technical data of two machines were used. In this section, these data are used as a reference (

Table 1. Reference data.

	Denomination	Notation	Value
Common data	Evaporation temperature	TL	3 °C
	Condensing temperature	TH	60 °C
	Cooling capacity	${\dot{Q}}_0$	105 kW
	Type unit	Single stage
Machine with a mechanical compressor	Coefficient of performance (cooling)	COPR,C	3
	Coefficient of performance (heating)	COPR,H	4
	Resultant coefficient of performance	COPR,ER	7
	Heating capacity	${\dot{Q}}_C$	135 kW
	Electric power consumed by the machine	P	35 kW
	Working fluid	R410A
Absorption machine	Temperature in the absorber	TA	35 °C
	Temperature in the generator	TG	80 °C
	Thermo-chemical performance index	β	0.574
	Maximum value of thermo-chemical performance index	TA/TG = βmax	0.873
	Coefficient of performance (cooling)	COPA,C	0.5
	Coefficient of performance (heating)	COPA,H	1.5
	Coefficient of performance in double-use operation mode	COPA,ER	2
	Thermo-chemical instability index (cooling)	μC	55.6%
	Thermo-chemical instability index (heating)	μH	21.2%
	Thermo-chemical instability index (double-use operation mode)	μER	30.7%
	Heating capacity	${\dot{Q}}_C$$+{\dot{Q}}_A$	315 kW
	Heat consumed in the generator	${\dot{Q}}_H$	210 kW
	Working fluid	Water/Li-BR

).

The variation of the thermo-chemical instability of a double-use absorption heat pump was investigated depending on the evaporation temperature and condensation temperature (Figure 3a). The effects of absorber temperature and generator temperature on the thermo-chemical efficiency are illustrated in Figure 3b. These temperature values might occur during normal operation of the machines.

It can be observed that the thermo-chemical instability can be reduced by decreasing the evaporation temperature and condensation temperature and by increasing the absorber temperature and the generator temperature. In the analyzed temperature intervals, the thermo-chemical instability can be changed by 8.48% (by varying the evaporation temperature), 53.05% (by varying the condensation temperature), 62.38% (by varying the temperature in absorber), and 20.35% (by varying the temperature in the generator).

Then, the variation of thermo-chemical instability was analyzed upon changing the temperatures given in Table 1 by ± 5 °C. The results are shown in Figure 4.

As can be seen, the variation of the thermo-chemical efficiency was linear, whereby the inclination angle to the horizontal gave information on the sensitivity of the thermo-chemical instability for the analyzed temperatures. The largest effect on the thermo-chemical instability was registered in the case of absorber temperature (γ_A = 72.75°) followed by the condensation temperature (γ_H = 70.23°), then the temperature in the generator (γ_G = 53.69°); the smallest effect was obtained in the case of evaporation temperature (γ_L = 43.47°).

Figure 5 shows the thermo-chemical performance index values needed at different temperature values in order to obtain a better performance of an absorption machine in comparison with a machine with a mechanical compressor. The red lines illustrate the lowest and the highest values of the thermo-chemical performance index. That parts of the β_END and β_ENE curves which are not presented between the minimum and maximum values are only theoretical values (such values cannot be obtained in practice).

It can be observed that the reference machine with a mechanical compressor, in any case, will perform better than an absorption machine (β_END > βmax). In most cases, the efficiency of the absorption machine is higher than the efficiency of the machine with a mechanical compressor. The maximum value of the thermo-chemical efficiency index (β = 0.610) is needed when the condensation temperature is equal to the temperature in the generator. In other cases, its value is around 0.5.

We then analyzed which machine performs better depending on the coefficient of performance (machine with a mechanical compressor) and on the operation temperatures (absorption machine) (Figure 6).

In all cases, four zones (red, green, blue, and purple) can be identified. In the red zone, the machine with a mechanical compressor has a lower energy demand, but the energy efficiency depends on the thermo-chemical efficiency index of the absorption machine. In the green zone, the energy demand of the machine with a mechanical compressor is lower, but the absorption machine will be more energy-efficient. In the blue zone, the energy efficiency of the absorption machine will be higher, but the energy demand depends on the thermo-chemical performance index of the absorption machine. Finally, in the purple zone, the absorption machine will perform better from both an energy demand and an energy efficiency point of view. The COP value of the reference machine with a mechanical compressor is 7, which means that the machine will work in zones 1 or 2 depending on the operation temperature values of the absorption machine.

5. Conclusions

In this paper, the thermo-chemical instability of absorption heat pumps was introduced and discussed. Its value can vary between 0% and 100%. For certain operation values of absorption machines, the quantitative indices have linear variation as a function of the thermo-chemical performance index. As the thermo-chemical performance index has two extreme values, the indices of absorption machines will similarly have two extreme values. The thermo-chemical instability of an absorption machine is the difference between the maximum and minimum correlated to the maximum value of the quantitative indices. A higher thermo-chemical instability represents a higher sensitivity of the absorption machine to the variation of heat flux at the heat source. The absorption machine with a low thermo-chemical instability can perform better in the case of heat sources with variable heat fluxes (solar energy). The thermo-chemical instability can be reduced by decreasing the operation temperatures. The largest effect on the thermo-chemical instability was obtained upon increasing the temperature in the absorber, followed by decreasing the condensing temperature, increasing the temperature in the generator, and decreasing the evaporation temperature.

The absorption heat pumps were compared with heat pumps with mechanical compressors. If the absorption machine is better from an energy demand point of view, its efficiency will also be higher (this is not true for machines with mechanical compressors).

It was shown that an absorption heat pump with similar efficiency to that of the machine with a mechanical compressor can always be found. Moreover, in the case of a machine with a mechanical compressor which cannot realize a reversed Carnot cycle, an absorption heat pump will perform better.