1. Introduction
As one of the global efforts to counter global warming and climate change, an international cooperation system has been created to reduce emissions of greenhouse gases, including carbon dioxide. The carbon emission allowance market was established from the results of several international conferences on climate change. It operates by optimally allocating and trading carbon dioxide emissions among potential pollutants. In other words, this market was introduced in accordance with the goal of controlling global carbon emissions by utilising the efficient pricing mechanism of an organised exchange. As this system uses a centralised transaction method, it aims to achieve the target level of carbon emission reduction with minimal economic loss.
However, to achieve the target that this system expects, it is necessary to assume that the price of carbon emission allowance is effectively determined in the market. Efficiency in this study refers to informational efficiency, whereby all information related to price formation is reflected quickly and sufficiently in price. If the price of an emission right is being determined in an inefficient market, this means that it is difficult to properly manage risk to cope with changes in the emission price from a market participant’s point of view and due to technology that can reduce carbon emissions by companies that use a large number of fossil fuels. This may result in delaying investment in technology for carbon emission reduction. This means that if the transaction price of carbon emission allowance is determined inefficiently, it is difficult to effectively realise the goals pursued by the system.
According to this practical need, the degree of informational efficiency of the carbon credit trading market has attracted the attention of market participants, market managers, and policymakers, and it has been studied as an important empirical analysis target in academia. Empirical studies are centred on the EU Allowance Unit (EUA, of one tonne of CO
2) price of the European Emissions Market, which is operated according to the European Union Emissions Trading Scheme (EU ETS), which is the largest and most active carbon trading market. For example, Miclaus et al. [
1], Krishnamurti and Hoque [
2], Daskalakis [
3], and Gregoriou et al. [
4] report empirical results that show that the EU carbon trading market is efficient. On the other hand, Daskalakis and Markellos [
5], Lu and Wang [
6], Crossland et al. [
7], and Aatola et al. [
8] report research results indicating that the carbon emission market is inefficient. Meanwhile, Montagnoli and de Vries [
9], Charles et al. [
10], Niblock and Harrison [
11], and Yang et al. [
12] report that the carbon emission trading market is efficient only in some periods.
It is believed that the previously mentioned research did not lead to any consistent conclusions for the following reasons. First, it is possible that the degree of market efficiency changes depending on the analysis target and the analysis time. The EU ETS has updated its system several times in the past 20 years, and, as a result, it is possible that the efficiency of EUA price movements has changed. For this reason, the results of the empirical analysis may differ depending on the period of the sample. Second, the results of the empirical analysis may be different due to differences in analysis methods. In particular, the efficiency of the carbon market may be different when EUA prices rise and fall. In this study, we contribute to the research area and strictly examine the informational efficiency of the carbon market and its changes by paying attention to these two aspects.
The main results of the analysis are as follows. First, there are multifractal characteristics in the price movement of the carbon credit market, and these characteristics are different in the market ups and downs. Second, the informational efficiency of the carbon credit market has changed over time. Third, the informational efficiency of the carbon credit market has experienced continuous improvement. Fourth, during Phase III, the inefficiency in the upward period was higher than that of the downward period.
The remaining sections of this paper are as follows. The literature review is presented in
Section 2. The current status and institutional changes in the EU ETS are given in
Section 3. The methodology used in this study is presented in
Section 4. The sample data and empirical findings are explained in
Section 5. The conclusions of the study are summarised in
Section 6.
2. Literature Review
For the EU ETS system to effectively reduce carbon emissions, the premise that the carbon credit market must be operated efficiently is required. In this regard, several studies have conducted an empirical analysis to determine whether the movement of the EUA price is efficient. These studies can be grouped into three main strands.
The first strand corresponds to those studies that found evidence that the movement of carbon credit market prices is informationally efficient. For example, by using the event study method, Miclaus et al. [
1] reported that the EU ETS emissions’ market was efficient during Phase I. Krishnamurti and Hoque [
2] performed a regression analysis based on the put-call parity approach and reported that the carbon emission options market was efficient for the 2008–2010 period (part of Phase II). The results of technical analysis by Daskalakis [
3], who used methods to predict emissions prices between 2008 and 2011 (part of Phase II), showed that as the market matured it became weakly efficient after 2010. Gregoriou et al. [
4] reported that the EU ETS emissions market was efficient during 2005–2012 (Phase I and Phase II), based on the fact that the spread of spot and futures prices is a stable time series.
The second strand is the studies that report that the EU carbon market is not efficient. For example, using a methodology that predicts the daily yield movements of emission prices during Phase I, Daskalakis and Markellos [
5] found that this market cannot be viewed as a weak-form efficient market. They explained that this was because the market was a new-born market that was not mature and did not allow for short selling and banking of credits. Using the variance ratio test, Lu and Wang [
6] found that the EU ETS emission market was inefficient in 2005–2010 (part of Phase I and Phase II). However, they reported that efficiency was improved in Phase II compared with Phase I. Crossland et al. [
7] used the EUA daily spot price data from the EU ETS between February 2008 and June 2011 (part of Phase II) and found the creation of momentum in the movement of carbon credit prices. This means that the EUA market is not efficient. Aatola et al. [
8], using a technical analysis technique, found that investing could yield excess returns in 2007–2010 (part of Phase II). This means that the EU ETS market was not informationally efficient during that period.
The third strand consists of the studies in which the EU ETS market is efficient only occasionally. For example, employing a variance ratio test, Montagnoli and de Vries [
9] and Charles et al. [
10] found that the EU ETS market was not efficient during Phase I and was efficient during Phase II. Similarly, Yang et al. [
12] used several variance ratio tests to find that the EU ETS market was not efficient during either Phase I or Phase III and was efficient only during Phase II. Niblock and Harrison [
11] analysed the predictability of the daily price of the EU ETS emission market during Phase II (2008–2012) and reported that the carbon market was inefficient during the global financial crisis, but it became more efficient after the crisis.
The empirical studies on informational efficiency in the carbon emission allowance market listed previously have not reached a consistent conclusion. This is because empirical studies use different analytical methods and different samples. In this study, we use a sample period that is divided into sub-samples based on the institutional changes in the EU ETS and employ a recently developed technique, the asymmetric multifractal detrended fluctuation analysis (A-MF-DFA) method introduced, to analyse the informational efficiency of the carbon market.
3. Institutional Changes in the EU ETS
An ETS is a system that allows transactions of quotas after allocating the Assigned Count Unit to countries with obligations to reduce greenhouse gas emissions. The allocation of allowances is divided basically into “Cap and Trade” and “Baseline and Credit.” The Cap and Trade method sets emission limits and allocates allowances to trade them. The EU ETS and Chicago Climate Exchange are typical markets for Cap and Trade. The Baseline and Credit method establishes the reference emissions and allows the residuals to be traded with each other if they are released below the baseline. The Clean Development Mechanism and the Joint Implementation on the Kyoto Protocol are typical markets for Baseline and Credit [
13,
14].
An ETS has advantages in terms of system flexibility, measurement of performance, recycling of resources, and management of overall emissions when compared with a carbon tax, another policy to reduce greenhouse gas emissions. In particular, it is easy to manage overall emissions explicitly with an ETS, and it has the advantage of attracting the development of greenhouse gas reduction technologies while effectively achieving the reduction targets set by society as a whole through the trading of allowances, which is used as a means to reduce greenhouse gas emissions in many advanced countries. On the other hand, there is also the downside movement problem of unstable emission prices and the lack of optimal resource allocation if there is a restriction on the smooth operation of the trading market, which can result in social losses. Therefore, efficient operation of the trading market is important.
Under the Kyoto Protocol, the EU was obliged to reduce greenhouse gas emissions by 8% over Phase I. To facilitate greenhouse gas reduction, the European Commission (EC) announced its plan to introduce an ETS by 2005. Through the discussion process within Europe, the EC agreed to introduce the Cap and Trade-based ETS in 2003 and, in 2004, approved additional guidelines to link the EU ETS with the Kyoto Protocol’s international allowances. Between 2005 and 2007, Phase I was conducted for 25 EU members. Starting in 2008, Phase II was expanded to 31 member countries, including new members [
15]. Phase III is in operation between 2013 and 2020, and Phase IV is scheduled to run from 2021 to 2030. The key features of each phase are summarised in
Table 1.
The EU assessed that it was able to secure accurate data by establishing a process for monitoring, reporting, and verifying emissions of companies subject to the ETS, along with the infrastructure to freely trade emissions across the EU during Phase I–II. Transactions during Phase I rose to 321 million tonnes in 2005, 1.1 billion tonnes in 2006, and 2.1 billion tonnes in 2007, according to the World Bank’s annual carbon market report. The EU ETS established a key position in the international carbon market during Phase II, and EU emissions’ trading accounted for 84% of the global carbon markets in 2010.
During Phase III, the EU has successfully demonstrated that pricing and trading allowances through the EU ETS have been effective in reducing emissions. In addition, the EU ETS system predicts that greenhouse gas emissions will be reduced by more than 8% compared to the beginning of Phase III and by 21% in 2020 [
14].
In 2018, the EU amended the EU ETS to achieve its 2030 emissions’ reduction target before entering Phase IV. The revised Directive ((EU) 2018/410), which took effect in April 2018, focuses on increasing annual emissions reduction rates to 2.2% from 2021 and strengthening the Market Stability Reserve (MSR) that the mechanism established by the EU to reduce the surplus of emission allowances in the carbon market and to improve the EU ETS’s resilience to future shocks. In response, the EU predicts that greenhouse gas emissions will be further reduced by 43% in 2030 when Phase IV, which applies to the revised system, ends [
16].
Table 2 shows that, during 2005–2018 (i.e., Phase I–III), the traded volume of allowances in the EU ETS generally increased, and the actual amount of emissions mainly decreased. Based on the above figures, we can expect that changes and development in the EU ETS system would have contributed to actual emissions’ reductions. However, it is also necessary to analyse the impact of these changes on the informational efficiency of the carbon market.
4. Methodology
There are several methods for assessing the informational efficiency of the financial market. The multi-fractal fluctuation detrended analysis (MF-DFA) approach has been used frequently in recent studies [
18,
19,
20]. However, the general MF-DFA method has a weakness resulting from the excessively restrictive assumption that the rising and falling dynamics of the price in a time series are symmetric. In this study, we use the asymmetric-MF-DFA (A-MF-DFA) method, which allows asymmetric behaviours for the upward and the downward price movements in the time series [
21,
22,
23].
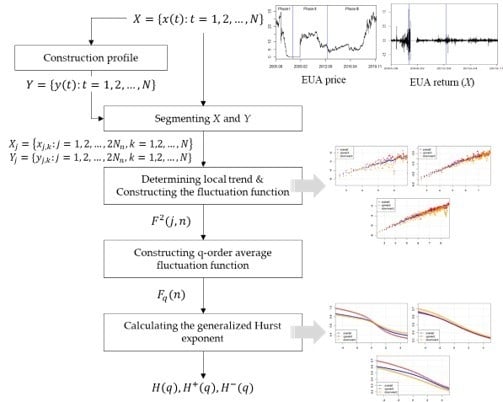
Figure 1 shows the overall process of the A-MF-DFA method. Assuming a time series
with length
, the A-MF-DFA method generally proceeds as follows:
(1) Step 1: Constructing the Profile
The profile
represents the magnitude of the local fluctuation and is defined as the following Equation.
where
and
represent the
j-th value and the mean of the
, respectively. So, the profile
represents the cumulative sum of the deviation from first to
t-th in the time series.
(2) Step 2: Segmenting the Time Series and its Profile
We divide the time series
into
non-overlapping segments with length
, where
is the largest integer less than
. Peng et al. [
24] suggest
from 5 to
. If
is not a multiple of
, then the length of the last segment is shorter than
. To consider this remainder of
, we also divide from the opposite end of
. That way, we get
segments from
. Equally, we repeat this procedure for
, resulting in
segments.
The
and
represent the
j-th segment for
and
, respectively, and are defined as follows:
(3) Step 3: Determining the Local Trend and Constructing the Fluctuation Function
The local trend of the profile segment
can be identified from the linear fit
as follows:
where
represents the horizontal position. The fluctuation function of the profile segment
is computed using:
Also, we estimate the linear fit for , which represents the local linear trend for the time series segment . We consider the sign of as the linear trend .
(4) Step 4: Construct -Order Average Fluctuation Functions
As the traditional MF-DFA method does not consider the trend of the time series, it uses the general average fluctuation functions, as follows:
On the other hand, the A-MF-DFA method makes
-order average fluctuation functions depending on the linear trend of
to consider asymmetric characteristics in the time series. For
, the standard MF procedure is retrieved [
18]. We only consider the sign of
which is the slope of
, to identify the linear trend of
. That is, if
, then
has a positive trend, otherwise, it has a negative trend. The directional
-order average fluctuation functions are defined as follows:
where
and
represent the
-order fluctuation function with a positive trend and a negative trend, respectively. For all
from one, to
, if
for all
, then
.
(5) Step 5: Calculating the Generalised Hurst Exponent
If a power-law relationship is captured in a time series, it means that the time series has a long-range correlation, i.e., long memory. Then the scaling satisfies
where
,
, and
represent the scaling exponents of the overall, upward, and downward periods, respectively. The scaling exponents of the fluctuation functions are derived from the logarithmic form of
,
and
versus
. These scaling exponents are called the generalised Hurst exponents.
is the Hurst exponent corresponding to the scaling exponent of
, which indicates the autocorrelation (
) within the time horizon [
25]. If
equals 0.5, the time series follows a random walk process. That is, there are not any correlations in the behaviour of the time series. If
is under 0.5, the correlation of the time series is an anti-persistent process. It means that an increase (decrease) is likely to be followed by another decrease (increase). Whereas, if
is above 0.5, the correlations of the time series are long-term persistent, that is, an increase (decrease) is likely to be followed by another increase (decrease) [
18,
22,
25,
26].
The time series is multifractal if varies depending on . Additionally, if , the correlations of the time series are asymmetric. This means that the correlations for the upward and the downward periods are different. The indicates the magnitude of the fluctuation, that is, the large (small) represents the large (small) fluctuation. So, if , , , and represent the scaling dynamics of overall, upward, and downward for large fluctuations, respectively. Generally, the scaling exponents of the multifractal time series tend to decrease as grows.
6. Conclusions
The main goal of the EU ETS (emission trading scheme) system is to enable participating countries to achieve their greenhouse gas reduction targets in a cost-effective and economically optimal way. This is the basic premise. The efficiency of the CO2 emissions’ market is especially important for energy and carbon hedge fund investors and risk managers, companies with high carbon emissions, and energy and environmental policymakers.
In this study, the level and change of informational efficiency of the EU ETS carbon trading market, which is the largest and most active ETS market, were analysed according to phases. For this purpose, the European Emissions Market daily price from 4 August 2005 to 31 December 2019 and the asymmetric multi-fractal fluctuation detrended analysis technique was used. The main results obtained in this study are as follows. First, there were multifractal characteristics in the price movement of the carbon credit market, and these characteristics were different in the market ups and downs. Additionally, the degree of asymmetry of the multifractal characteristics was greater during Phase III than during both Phase I and Phase II. Second, the informational efficiency of the carbon credit market has changed over time, with the lowest informational efficiency in Phase I and the highest informational efficiency in Phase III. Third, measuring the market inefficiency scale showed that the market efficiency was lowest during Phase I and highest during Phase III. During Phase III, the value of the upward period was higher than that of the downward period, indicating that the inefficiency in the upward period was higher.
From the empirical analysis results of this study, it can be seen that the informational efficiency of the carbon credit market has improved continuously. However, it has not yet reached the level of informational efficiency demanded by the efficient market hypothesis. Therefore, EU ETS policymakers need to tighten regulations to improve the information flow in the carbon market and reduce market manipulation. Basically, the EU ETS is a system for which it is difficult to find similar cases in the past for reference, and improvement of the system through trial and error is inevitable.
Furthermore, even if the carbon credit trading market operates efficiently, climate change due to carbon emissions cannot be sufficiently suppressed. As pointed out by Lehmann and Gawel [
29] and del Rio [
30], the carbon credit trading system focuses on very limited and short-term goals and does not account for the technological aspects of changing the way that energy is used. Thus, the EU ETS may not be able to control climate change appropriately. In this regard, to better respond to climate change caused by carbon emissions, it is necessary to increase the informational efficiency of the carbon credit trading market and promote other effective policies, such as supporting renewable and clean energy production and consumption.